Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Revista Latinoamericana de Psicología
Print version ISSN 0120-0534
rev.latinoam.psicol. vol.42 no.2 Bogotá May/Aug. 2010
Robustez de cinco estadísticos univariados para analizar diseños Split-Plot en condiciones adversas
Robustness of five univariate statistics in analyzing Split-Plot desings under adverse conditions
Paula Fernández
Guillermo Vallejo
Universidad de Oviedo
Pablo Livacic-Rojas
Universidad de Santiago de Chile
Reconocimiento: Este trabajo ha sido realizado con la ayuda concedida por el MCI (Ref. PS-I2008-03624).
Correspondencia: Paula Fernández García, Universidad de Oviedo, Departamento de Psicología, Plaza Feijóo, s/n, E-33003 Oviedo, Spain, E-mail address: paula@uniovi.es (P. Fernández), Tel.: +34 985 104167, Fax: +34 985 104144
Recibido: 30 de Junio de 2009 Aceptado: 17 de Mayo de 2010
Resumen
En esta investigación examinamos el comportamiento de cinco estadísticos univariados para analizar datos en un diseño Split-Plot. Cuatro de ellos asumen que la matriz de desviación subyacente es no esférica. Sin embargo, existe una clara distinción entre dos alternativas, dos procedimientos presuponen que la correlación entre los datos no sigue un patrón determinado y otros dos asumen que existe autocorrelación serial de primer orden. Todos ellos fueron comparados con respecto a su robustez para poner a prueba las fuentes de variación intra-sujeto (tratamiento e interacción) bajo distribución no normal en ausencia de esfericidad y en ambas situaciones, bajo correlación serial de primer orden y bajo correlación arbitraria. Los resultados muestran que cuando la distribución es no normal simétrica todos los procedimientos muestran una tasa de error de Tipo I similar a la obtenida bajo distribución normal. Conforme el grado de sesgo y curtosis incrementa, todos los procedimientos experimentan una alteración en su estimación de la tasa de error de Tipo I y que depende de la estructura de la matriz de covarianza que subyace a los datos. En el conjunto de condiciones sometidas a estudio los procedimientos más robustos fueron HCH, JN y LEC.
Palabras clave: Robustez; autocorrelación serial de primer orden; ausencia de esfericidad; ausencia de normalidad.
Abstract
In this research we examine the behaviour of five univariate statistics for analyzing the data of a Split-Plot design. Four of them assume that the dispersion matrix underlying is not spherical. However, they do so with a clear distinction between two alternatives, insofar as two of them presuppose that the correlation between the data does not have a certain structure and other two assume that there exists first-order serial autocorrelation. All of them were compared with regard to their robustness to test the sources of variation within-subject (treatment and interaction) under non-normality in the absence of sphericity, both when there was first-order serial autocorrelation and when the underlying correlation was arbitrary. The results show that when the distribution is non-normal symmetric all the procedures show a Type I error rate similar to the obtained one under normal distribution. As the degree of skewness and kurtosis increases, all the procedures experience an alteration in their estimation of the Type I error rate and that it depends on the structure of covariance matrix underlying in the data. In the set of conditions submitted to study the most robust procedures were HCH, JN and LEC.
Key words: Robustness; first-order serial autocorrelation; absence of sphericity; absence of normality.
Introducción
Los diseños de medidas repetidas son, quizá, los más utilizados para abordar el estudio de procesos biológicos, psicológicos y sociales que experimentamos a lo largo del tiempo (Keselman, Algina & Kowalchuk, 2001). La estructura del diseño habitualmente más utilizada tiene dos factores: uno entre-sujetos (A), y otro, intra-sujeto (B). Los sujetos (i=1,..., nj, Σ nj=N) son clasificados en función de los niveles del factor entre-sujetos (j=1,..., p) o asignados aleatoriamente a ellos, y, con posterioridad, son observados y medidos en todos los niveles del factor intra-sujeto (k=1,..., q), ya sean diferentes tratamientos o un reducido número de ocasiones en tiempos fijos y equidistantes.
Para analizar los datos así recogidos hay disponible una gran variedad de técnicas univariadas y multivariadas (véase, Fernández, Livacic-Rojas & Vallejo, 2007, y las referencias contenidas en este trabajo). Es conocida la baja potencia de las técnicas multivariadas cuando los tamaños muestrales son relativamente pequeños, añadiendo además, que si el número de sujetos dentro de cada grupo es menor que el número de medidas repetidas menos una (debe suceder que N-p≥ q-1) ningún estadístico multivariado podrá calcularse debido a que la matriz de covarianzas resultará singular. Si este es el caso, al investigador sólo le resta utilizar estadísticos univariados. De todos ellos, el Análisis Univariado de la Varianza (AVAR) es, sin duda, el más robusto y potente cuando se satisfacen los supuestos del modelo (Keselman, Lix & Keselman, 1996), esto es: normalidad conjunta multivariada, independencia entre los vectores de observaciones de las diferentes unidades experimentales, homogeneidad de las matrices de dispersión (Σ) y esfericidad de las mismas.
No obstante, puede suceder que la respuesta a los distintos tratamientos exija el registro de distintas escalas de medida o que la variable intra-sujeto sea la edad o el tiempo. Si es así, es posible que en el primer caso las varianzas de los tratamientos resulten arbitrariamente heterogéneas arrastrando con ello una heterogeneidad de covarianzas también sin ninguna estructura definida. En el segundo caso, es probable que se observen determinadas tendencias ligadas a algún proceso de maduración o de aprendizaje manifestando efectos residuales y/o de autocorrelación, pudiéndose producir además determinada heterogeneidad en las varianzas de los tratamientos. En ambas circunstancias, la matriz Σ que subyace a los datos se desvía del patrón de esfericidad requerido, pero con una diferencia, en la primera la correlación entre las observaciones es arbitraria y en la segunda la correlación entre las observaciones sigue un patrón determinado. La consecuencia inmediata de la violación de este supuesto es que las hipótesis nulas de los efectos del diseño son falsamente rechazadas más veces de lo debido, y en mayor medida, conforme mayor sea la desviación (Collier, Baker, Mandeville & Hayes, 1967).
Para resolver este problema, y en función de si las matrices de dispersión son o no homogéneas, varios autores han desarrollado alternativas univariadas orientadas a corregir los valores críticos de la F univariada (v.g. Greenhouse & Geisser, 1959; Huynh & Feldt, 1976 y Quintana & Maxwell, 1994). La corrección se realiza multiplicando los grados de libertad (df) por un valor que indica la desviación de la matriz Σ del patrón de esfericidad requerido (ε), y que es calculado desde la matriz de covarianza promediada de los datos del diseño (Σ). Sin embargo, todas ellas asumen que la correlación entre las observaciones en distintos puntos del tiempo no es una función de la distancia temporal entre ellas.
Así pues, como en los datos puede subyacer algún tipo de dependencia serial, algunos autores han propuesto procedimientos univariados que la tienen en cuenta (v.g. Andersen, Jensen & Schou, 1981; Azzalini, 1984; Hearne, Clark & Hatch, 1983; Jones, 1985). No obstante, ninguno de ellos, a diferencia de alguno de los anteriormente referidos, ha sido sometido suficientemente a estudio en los diseños de medidas repetidas, algunos de ellos nunca, ni están integrados en los paquetes de software estadístico más utilizados por los investigadores aplicados de las Ciencias Sociales y de la Salud (SAS® y SPSS).
Un enfoque univariado más flexible y versátil es el Modelo Lineal Mixto (MLM). Este enfoque extiende el modelo clásico a situaciones donde los supuestos de independencia y homogeneidad no son requeridos y las variables son fijas y/o aleatorias. Además, existen muchas ventajas que lo convierten en una técnica analítica muy recomendable para realizar inferencias, tanto de los efectos fijos (Kowalchuck, Keselman, Algina & Wolfinger, 2004; y Littel, Milliken, Stroup, Wolfinger & Schabenberger, 2006) como de los efectos aleatorios (Núñez-Antón & Zimmerman, 2001); a saber: 1) Permite analizar datos completos e incompletos, 2) Modelar las variaciones intra y entre-sujetos que existen en los datos (Vallejo, Fernández & Secades, 2004). El módulo PROC MIXED del SAS y el comando MIXED del SPSS facilitan el ajuste de diversas estructuras de covarianza usando criterios de selección de modelos tales como los Criterios de Información de Akaike (AIC; Akaike, 1974) y Bayesiano (BIC; Schwarz, 1978), 3) Manejar covariaciones cambiantes a lo largo del tiempo, y, finalmente, 4) El MLM es relativamente fácil de generalizar a situaciones multivariantes (Vallejo, Arnau & Ato, 2007).
No obstante, el MLM también tiene puntos débiles, resaltamos dos. De una parte, las dificultades surgidas con los criterios AIC y BIC para identificar el verdadero proceso generador de los datos cuando la estructura de covarianza es compleja y el tamaño de muestra reducido (Keselman, Algina, Kowalchuck & Wolfinger, 1999; Vallejo, Ato & Valdés, 2008; Vallejo, Fernández & Ato, 2003). De otra, los estimadores de precisión e inferencia se basan en su distribución asintótica, de ahí que generalmente ajusten bien con muestras grandes (Wolfinger, 1996), pero pueden ocasionar problemas cuando se trabaja con muestras reducidas (Vallejo, Arnau, Bono, Cuesta, Fernández & Herrero, 2002).
Abundan las investigaciones que han puesto a prueba el comportamiento de los procedimientos univariados que corrigen la ausencia de esfericidad sin reparar en la existencia de una estructura de correlación definida, y también aquellas que han puesto a prueba el MLM (revisiones excelentes sobre el comportamiento de las mismas se pueden consultar en Keselman et al., 1996; Keselman et al., 2001; Blanca Mena, 2004 & Fernández et al., 2007). Sin embargo, son muy escasas las investigaciones sobre los procedimientos univariados orientados a corregir los efectos de la dependencia serial. Dos de ellos, los procedimientos de Hearne et al. (1983) y Jones (1985), merecen atención en esta investigación por dos razones fundamentales. De una parte, porque su cálculo es sencillo y está exento de dificultad. Ambos otorgan prioridad a la autocorrelación serial de primer orden, y, una vez calculada, el primero computa el valor de sobre (matriz estimada de covarianza asumiendo que los datos manifiestan autocorrelación serial de primer orden) y después modifica los df multiplicando éstos por el valor de ε calculado. El segundo propone modificar el cálculo de las sumas de cuadrados del AVAR incorporando la correlación serial en ellas y restando un df en el error intra-sujeto. De otra parte, porque sólo podemos destacar cuatro investigaciones donde alguna de ellas se ha sometido a estudio, y que pasamos a comentar.
Edwards (1991) examinó la robustez de los procedimientos de Greenhouse y Geisser (1959) (GG), y de Hearne et al. (1983) (HCH) para un diseño simple de medidas repetidas bajo distribución normal y dos tipos de matrices de covarianza, autorregresivas de primer orden estacionarias (AR[1]), y autorregresivas de primer orden heterogéneas estructuradas (AREH[1]) (varianzas crecientes a través del tiempo). Concluye que cuando la autocorrelación serial es pequeña, el comportamiento del estadístico HCH es muy superior al del estadístico GG, sin embargo, para niveles elevados de autocorrelación, las diferencias entre ellos desaparecen siendo tan ventajoso uno como el otro.
Fernández y Vallejo (1996 y 1997) estudiaron bajo distribución normal y no normal (asimetría positiva y negativa) y matrices de covarianza AR[1] (ρ=.80 y ε=.47) y no estructurada (NE) (ρ=0 y ε=.47), la robustez de los procedimientos AMVAR (Análisis Multivariado de la Varianza), AVAR, GG, el procedimiento de Huynh-Feldt (1976) (HF) y el de Jones (1985) (JN) en un diseño Split-Plot (2x8) balanceado. Concluyen que el procedimiento JN es sin duda el mejor procedimiento cuando la matriz subyacente es AR[1] bajo distribución normal (resultado en sintonía con los obtenidos por Edwards, 1991), pero su estimación es liberal en ausencia de normalidad. Cuando la matriz subyacente fue NE, el AMVAR y GG obtuvieron mejores resultados, comportándose el procedimiento JN de modo liberal.
Recientemente, Fernández, Vallejo, Livacic-Rojas, Herrero y Cuesta (2010) examinaron la robustez de los estadísticos univariados AVAR, GG, HF, corrección de Lecoutre (1991) (LEC), HCH, y JN en un diseño Split- Plot de medidas repetidas balanceado bajo distribución normal. Observaron su robustez bajo una gran variedad de matrices de covarianza, niveles intrasujeto y tamaños muestrales. Sus resultados mostraron que los procedimientos AVAR, HF y JN fueron los menos robustos y los más dependientes de todas las variables manipuladas (este aspecto, referente al procedimiento JN, no se pudo observar en las dos investigaciones anteriormente mencionadas debido a las condiciones tan concretas en que había sido estudiado; sin embargo, en las combinaciones de variables coincidentes con aquellas sí coincidieron los resultados). Los procedimientos GG, LEC y HCH mantuvieron en más ocasiones el error de Tipo I dentro de los límites de robustez. Las diferencias entre ellos se debían a la estructura de la matriz Σ subyacente. Cuando la matriz fue AR[1] y AREH[1] decreciente, los procedimientos más robustos fueron HCH y JN (en mayor medida HCH), siendo su estimación independiente de ρ, nj y q; sin embargo, cuando la matriz fue AREH[1] creciente y autorregresiva de primer orden heterogénea arbitraria (ARAH[1]) los más robustos fueron GG y LEC. Cuando la matriz fue NE el estadístico GG mostró el mejor comportamiento, y el AVAR y JN fueron los menos robustos.
Con posterioridad, Fernández, Vallejo y Livacic-Rojas (2008) compararon mediante simulación los procedimientos GG, LEC, HCH y JN junto con el MLM (con la matriz correctamente identificada) bajo las mismas condiciones matriciales que en la investigación anterior. Los resultados obtenidos con los procedimientos GG, LEC, HCH y JN replicaron los del trabajo anterior. El MLM mostró menos robustez que los anteriores cuando las matrices subyacentes fueron AREH[1] decreciente y NE.
En las dos investigaciones anteriores se puso de manifiesto que los procedimientos realizaban mejor estimación bajo autocorrelación serial (sobre todo cuando era positiva) que bajo correlación arbitraria. Sin embargo, sólo HCH, JN y el MLM dependían significativamente de su magnitud, HCH y JN realizaban mejor estimación conforme mayor era ρ y el MLM conforme era menor. GG, LEC, HCH y JN mostraban mejor estimación conforme la matriz estaba más cercana a la esfericidad, pero el MLM no resultó afectado por el valor de ε. Para un mismo tamaño de muestra, los procedimientos GG, LEC y MLM fueron más robustos conforme menor era q. HCH y JN fueron los menos dependientes de q, excepto cuando la matriz subyacente fue ARAH[1], en este caso, para un mismo tamaño de muestra la estimación de ambos mejoraba conforme mayor era q. Todos los procedimientos mejoraron su estimación cuanto mayor fue el tamaño de la muestra, siendo GG y MLM los más dependientes de esta variable.
Infortunadamente, cuando se trabaja con datos reales es habitual que los datos se ajusten a una distribución no normal (v.g. Micceri, 1989). Bajo estas condiciones, han sido ampliamente estudiados los procedimientos orientados a corregir la ausencia de esfericidad sin reparar en la existencia de una estructura de correlación definida (v.g. Keselman et al., 1996; Mendoza, Toothaker & Nicewander, 1974; Rasmussen, Heumann, Heumann & Botzum, 1989 y Wilcox, 1993) y también el MLM (v.g. por Keselman et al., 1999; Keselman, Kowalchuck & Boik, 2000 y Wright & Wolfinger, 1996), y se ha visto que todos ellos son vulnerables, particularmente cuando el tamaño de muestra es pequeño. Sin embargo, hasta la fecha no ha sido examinada la robustez del procedimiento HCH bajo distribución no normal, y sólo en una ocasión, bajo las condiciones limitadas y concretas antes descritas, la robustez del procedimiento JN.
Así las cosas, el objetivo general de esta investigación es evaluar la robustez, cuando los datos no se distribuyen de modo normal, de los procedimientos que en las investigaciones realizadas por Fernández et al. 2008a y 2008b tuvieron más controlado el error de Tipo I (GG, LEC, HCH y JN). También, y a modo de comparación, se estudian junto con el procedimiento AVAR. Para llevarlo a cabo, se va a manipular una variedad importante de niveles de otras variables que pasamos a comentar en el siguiente apartado.
Método
Con ánimo de someter a examen la robustez de los procedimientos llevamos a cabo un estudio de simulación Montecarlo para un diseño Split-Plot de medidas repetidas (3xq) balanceado (modelo no aditivo). Se examinó la robustez bajo no normalidad en conjunción con la ausencia de esfericidad, tanto bajo correlación serial como bajo correlación arbitraria.
Descripción de los procedimientos que se someten a investigación. En lo que respecta a la formulación de los procedimientos no nos vamos a detener, de una parte, porque el cálculo de todos ellos es muy simple y no entraña ninguna dificultad, y de otra, porque la estrategia de análisis del AVAR, GG y LEC es muy popular y está contenida en numerosas publicaciones (v.g. Vallejo, 1991 y Fernández et al., 2007), y la referida a los procedimientos HCH y JN, además de haber sido comentada brevemente en el apartado anterior, está claramente expuesta y explicada en Hearne et al., (1983) una, y en Jones (1985) la otra.
Variables manipuladas. Se manipularon cuatro variables: tamaño total de la muestra, ocasiones de medida, estructura de la matriz de covarianza, y tipo de distribución no normal subyacente en los datos.
El comportamiento de los estadísticos fue investigado con tres tamaños totales de muestra (N): N=15 (nj=5), N= 30 (nj=10) and N= 46 (nj=16). Los tamaños de grupo nj=10 y 16 se encuentran con frecuencia en investigación sobre Psicología Animal y Psicología Educativa, sin embargo, tamaños de grupo de nj=5 son más frecuentes en Psicología Clínica. Se eligió someter a estudio cuatro niveles del factor intra-sujeto (q): 4, 6, 8 y 12. Someter a estudio 4 y 8 niveles es habitual en la literatura, sin embargo, y con ánimo de observar la tendencia del error de Tipo I en función del número de niveles de la variable intra-sujeto en combinación con el resto de variables manipuladas, elegimos estudiar también 6 y 12 niveles.
Los datos fueron generados utilizando tres estructuras de covarianza AR[1], ARH[1] y NE. Las matrices AR[1] manifiestan estacionariedad en las varianzas y la correlación entre la κth y la κ'th observación es ρκ-κ'. Se han construido a través de la expresión Σ=σ2 (1/1- ρ2) V, donde σ2 (1/1- ρ2), es la varianza intra-sujeto común (σ2 =10, ρ= [-0.8:0.8: (0.2)] en nuestro caso), y V=D1/2 R D1/2. V es idéntica a la matriz de correlación diseñada de tamaño qxq y DΞIq. Las ARH[1] expresan matrices de covarianza con el mismo diseño de correlación serial positiva y negativa que las matrices AR[1], pero las varianzas son heterogéneas. En esta investigación consideramos tres estructuras diferentes. Dos de ellas exhiben heterogeneidad intra-sujeto que denominamos estructurada porque las varianzas varían a través de q en progresión aritmética creciente o decreciente. Así pues, de éstas contemplamos dos condiciones de no estacionariedad: creciente AREH[1]-C y decreciente AREH[1]-D . La expresión que se ha utilizado para diseñar cada una de estas matrices de covarianza es la misma que para las matrices AR[1], pero con dos variaciones: σ2 =1 y D es una matriz escalar qxq cuyos elementos de la diagonal principal son las respectivas varianzas. Las covarianzas para AR[1] y ARH[1] declinan exponencialmente cuando la correlación es positiva y convergen uniformemente cuando es negativa.
Las matrices AR[1] y AREH[1] tienen una desviación de la esfericidad que puede ser calculada mediante ó ρ, y cuyo tamaño está en función de cada uno de los elementos utilizados en su construcción (Edwards, 1991), Tabla 1. De interés prioritario en esta investigación, es observar la robustez de los procedimientos en condiciones de ausencia de normalidad cuando para una misma magnitud y dirección de autocorrelación serial de primer orden existe diferente desviación de la esfericidad, y contemplar si la estimación del error de Tipo I resulta más afectada por la magnitud y sentido (positiva o negativa) de ρ, o por el tamaño de ε. Para este cometido, hemos construido matrices de covarianza con el mismo diseño de correlación serial positiva y negativa que las matrices AR[1], pero que exhiben heterogeneidad intra-sujeto arbitraria y, por tanto, las varianzas varían a través de q sin ninguna estructura definida. Las denominamos ARAH[1]. Estas matrices fueron construidas con dos desviaciones de la esfericidad (ε=.50 y ε=.75). El estudio de la hipótesis anterior se completó con la introducción en la investigación de matrices NE que no presentan autocorrelación serial (ρ=0) pero sí ausencia de esfericidad. Estas últimas matrices también son no estacionarias arbitrarias, y por lo tanto, las varianzas como las covarianzas varían sin ninguna estructura definida. Fueron construidas mediante el algoritmo desarrollado por Cornell, Young y Bratcher (1991) y dos desviaciones de la esfericidad (ε=.56 y ε=.75).
Por último, con ánimo de investigar los efectos de la forma de distribución de los datos sobre el error de Tipo I de los cinco procedimientos, todas las combinaciones de las variables anteriores se observaron bajo las distribuciones Doblemente Exponencial o de Laplace, Exponencial y Lognormal.
Comparaciones efectuadas. En cada una de las condiciones que hemos expuesto efectuamos comparaciones con respecto a las medidas empíricas de la probabilidad de cometer errores Tipo 1 ( ). Estas se obtuvieron tabulando el número de veces que cada estadístico excedió el valor crítico (α) y dividiéndolo por el número de replicaciones efectuadas. Se ha tomado como criterio de robustez el intervalo de Bradley para α=0.05, esto es (0.025-0.075).
). Estas se obtuvieron tabulando el número de veces que cada estadístico excedió el valor crítico (α) y dividiéndolo por el número de replicaciones efectuadas. Se ha tomado como criterio de robustez el intervalo de Bradley para α=0.05, esto es (0.025-0.075).
Generación de datos. Para explorar los posibles efectos de la forma de distribución de los datos sobre la robustez de los procedimientos, generamos datos no normales mediante las distribuciones g y h introducidas por Tukey (1977). Sometimos a estudio tres formas de distribución: (a) g = 0 y h = .109, una distribución que tiene el mismo grado de sesgo y de curtosis que la doblemente exponencial o de Laplace (γ1=0, γ2=3), (b) g = .76 y h = -.098, una distribución que tiene el mismo grado de sesgo y de curtosis que la distribución exponencial (γ1=2, γ2=6) y (c) g = 1 y h = 0, una distribución que tiene el mismo grado de sesgo y de curtosis que la distribución lognormal (γ1=6.18, γ2=110.94). Las distribuciones g y h fueron obtenidas mediante la transformación de las variables normales estandarizadas (Zijk), generadas con el algoritmo propuesto por Kinderman y Ramage (1976), en Z*ijk=g1[exp(g Zijk)-1] exp(hZ2 ijk/2), donde g y h son números reales que controlan el grado sesgo y de curtosis respectivamente. Finalmente, los vectores de observaciones pseudoaleatorios y'ij1,...,y'ijq con matriz de covarianza Σ fue obtenida a través de la descomposición triangular de Σj, γijk=T x (Z*ijk-μgh) donde T es la matriz triangular inferior que satisface la ecuación Σj=TT', y μgh={exp[g2/(2-2h)]-1}/[g(1-h)1/2] es la media de la población de la distribución g y h (se pueden ver los detalles en Headrick, Kowalchuk y Sheng, 2008). Mediante un programa escrito en GAUSS realizamos tantas simulaciones como condiciones experimentales anteriormente detalladas. En cada una de ellas se realizaron 10000 observaciones independientes para cada uno de los procedimientos.
Resultados
Las tablas que acompañan a la descripción de los resultados representan un subconjunto seleccionado de las condiciones investigadas que muestran adecuadamente las diferencias entre los diferentes procedimientos y la tendencia que siguen en función de las variables manipuladas.
Error de Tipo I para el efecto principal intra-sujeto
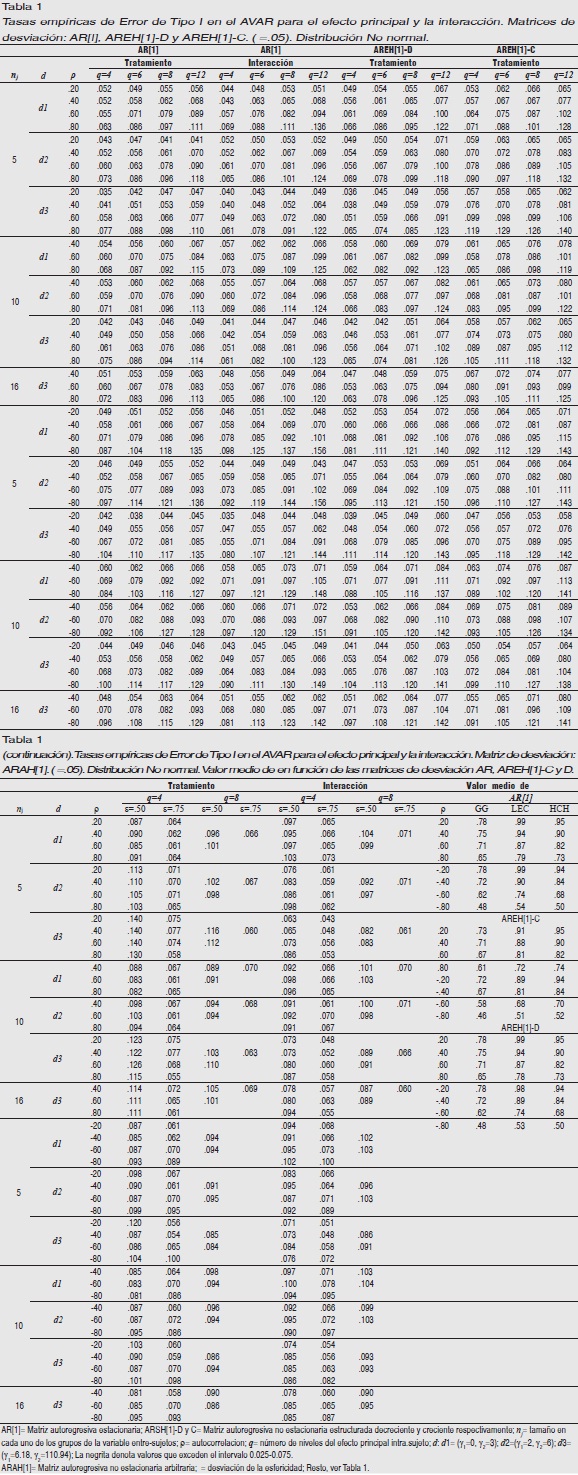
Matrices subyacentes AR[1] y AREH[1]-D: Tablas 1 y 2. No se exponen los resultados obtenidos cuando la matriz de desviación subyacente es AREH[1]-D para los procedimientos LEC, GG, HCH y JN debido a la gran similitud (ningún procedimiento difiere significativamente en los resultados) con los obtenidos cuando la matriz de desviación subyacente es AR[1]. Tampoco se exponen los resultados cuando nj=16 y la distribución es d1 y d2 debido a que el procedimiento AVAR obtiene resultados muy similares a los obtenidos en d3 y el resto de procedimientos son robustos en estas condiciones.
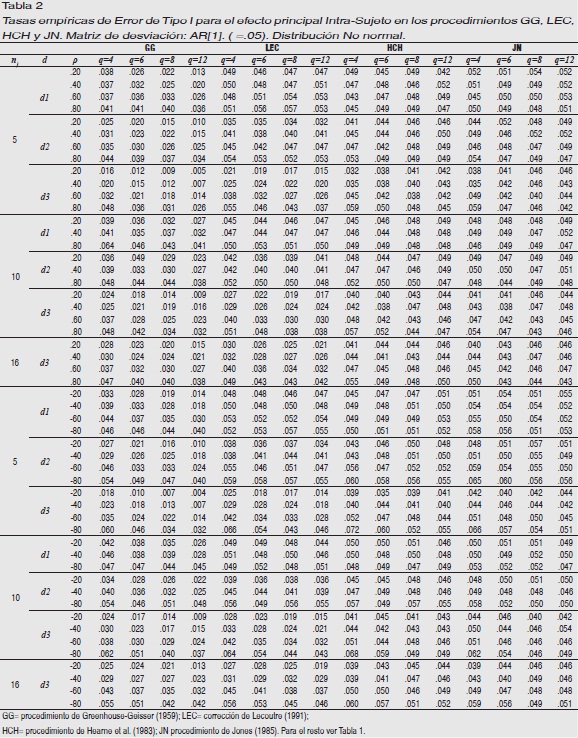
En las Tablas 1 y 2 podemos observar cómo el AVAR abandona la robustez con independencia de la distribución que subyace a los datos y del tamaño de la muestra cuando ρ≥.60 en mayor proporción cuando ρ es negativa, y GG se muestra conservador para nj=5 cuando ρ≤.40 y q≥8 en d1; ρ≤.40 y q≥6 en d2, y ρ≤.60 en todo q en d3, apreciándose cómo un mayor tamaño de muestra incrementa su robustez.
El procedimiento LEC ajusta el error de Tipo I al nivel nominal en d1 y d2. Cuando la distribución subyacente es d3 y nj= 5, se muestra conservador para ρ≤.40, en mayor medida cuanto mayor es q. Ambos, GG y LEC son insensibles a la dirección de ρ, no varían su comportamiento sea ésta positiva o negativa.
Los procedimientos HCH y JN tienen un comportamiento excelente con independencia de ρ (magnitud y dirección), nj, q y d.
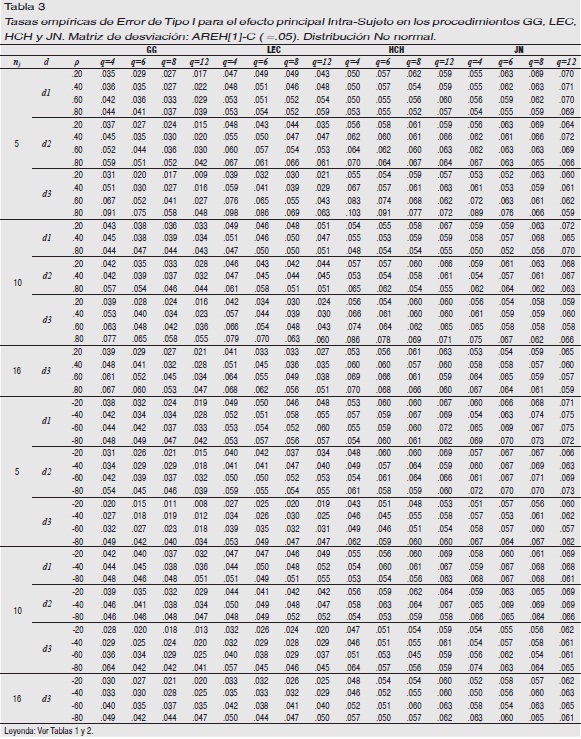
Matriz subyacente AREH[1]-C: Tablas 1 y 3. No se exponen los resultados cuando nj=16 y la distribución es d1 y d2 debido a que todos los procedimientos son robustos en estas condiciones.
En la Tabla 1 observamos que el AVAR, con independencia de la forma de distribución, es robusto cuando ρ≤±.20 en todo nj y q. Cuando ρ es positiva y ≥.40 su robustez depende de la forma de distribución. Es más liberal cuanto mayor es d (en mayor medida a >q y <nj). Cuando ρ es negativa, un incremento en ρ y q repercute en una estimación más liberal, pero del mismo modo en todo d y nj.
En la Tabla 3 advertimos que cuando la distribución es d1 y d2 GG se muestra robusto si nj≥10, sin embargo, cuando nj=5 se comporta de modo conservador en elevados valores de q siempre que ρ≤±40. Cuando en los datos subyace una forma de distribución d3 su comportamiento es conservador si ρ≤ .40, en mayor medida cuanto mayor es q (más cuando la correlación es negativa), y liberal cuando ρ=.80 y q=4.
El procedimiento LEC se muestra robusto en todo ρ, nj y q en las condiciones de forma de distribución de los datos d1 y d2. Cuando la distribución es d3 experimenta un comportamiento conservador para ρ=±.20 en elevados valores de q, y liberal en q=4 y autocorrelaciones positivas elevadas.
Los procedimientos HCH y JN son robustos cuando ρ es negativa en todo nj, q y d. También es así cuando ρ es positiva si la distribución subyacente es d1 y d2 en todo nj y q. Sin embargo, bajo la distribución d3 se muestra liberal para valores elevados de ρ, en mayor medida cuando menores son q y nj.
Matriz subyacente ARAH[1]: Tablas 1cont. y 4 que se puede apreciar con claridad la evolución que sigue la tasa de error, no se exponen los resultados para ρ=±.80. Tampoco se exponen cuando ρ es negativa y la distribución es d1 debido a que no varían significativamente con respecto a los hallados en d2.
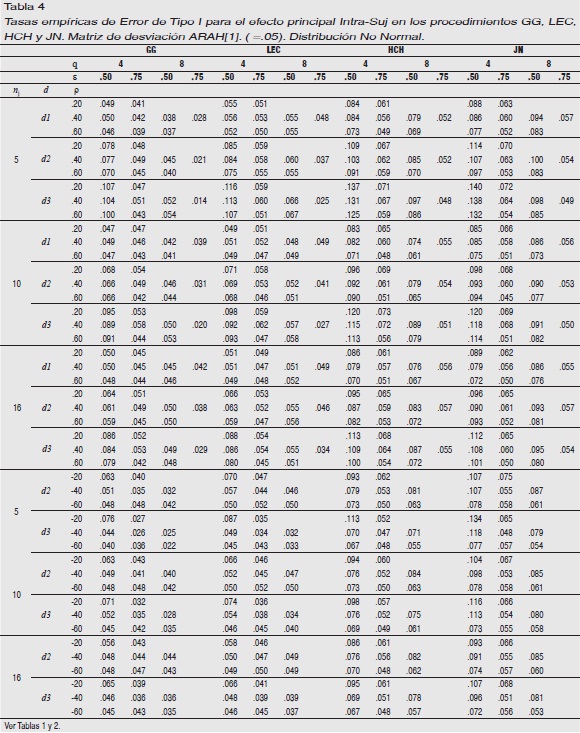
En la Tablas 1cont. observamos que el AVAR realiza una estimación liberal siempre que ε=.50 en todo ρ (dirección y magnitud), q y nj, en mayor medida cuando la distribución que subyace a los datos es d3 que cuando es d2, y en ésta, que cuando la distribución subyacente es d1.
En la Tabla 4 observamos que GG y LEC son robustos cuando ρ es positiva y la distribución es d1, y cuando ρ es negativa con alguna excepción bajo distribución d3 y ε=.50. Cuando ρ es positiva ambos son liberales si la distribución es d2 (ρ≤40, nj=5, q=4 y ε=.50), y GG conservador si la distribución es también d2 (ρ≤.40, nj=5, q=8 y ε=.75). Cuando la forma de distribución subyacente es d3, el comportamiento de ambos es liberal en q=4 y ε=.50 en todo ρ y nj, y GG conservador en q=8 y ε=.75 en todo ρ y nj.
El procedimiento HCH es liberal cuando ρ es positiva para ε=.50 en todo q sólo cuando ρ≤.40 bajo la distribución d1, y para todo valor de ρ cuando la distribución es d2 y d3. Siempre es robusto cuando ε= .75. Cuando ρ es negativa siempre es robusto si ρ≥.60 y ε=.50 en todo q, y en todo ρ y q cuando ε=.75.
El procedimiento JN tiene el mismo comportamiento que HCH cuando ρ es positiva, aunque mayor error. Cuando ρ es negativa manifiesta un mal comportamiento cuando ε=.50 en todo q, nj y d.
Matriz subyacente NE: En la Tabla 5 observamos que cuando ε=.56, los procedimientos AVAR, HCH y JN son liberales bajo las distribuciones d1 y d2 con independencia de q y nj, comportándose mejor cuando la distribución es d3. Los procedimientos GG y LEC son robustos bajo las distribuciones d1 y d2, y éste último también en d3, excepto para elevados valores de q (q≥8, en mayor medida para nj=5).
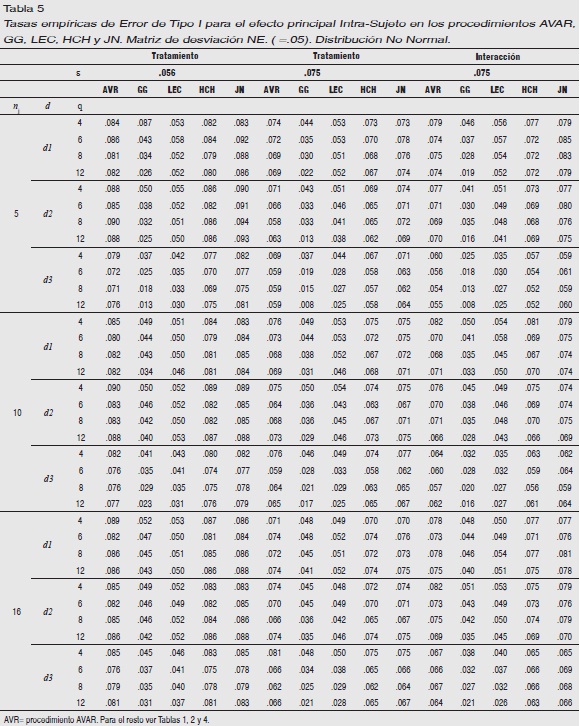
De otra parte, cuando ε=.75 observamos que LEC y HCH son robustos en todo d, nj y q. También observamos que JN es liberal bajo la distribución d1 y GG conservador bajo la distribución d3.
Error de Tipo I para la interacción
Matrices subyacentes AR[1] y AREH[1]-D: Tablas 1 y 6. La razón de los resultados no expuestos es la misma que la expresada para las matrices de desviación homólogas para el tratamiento intra-sujeto.
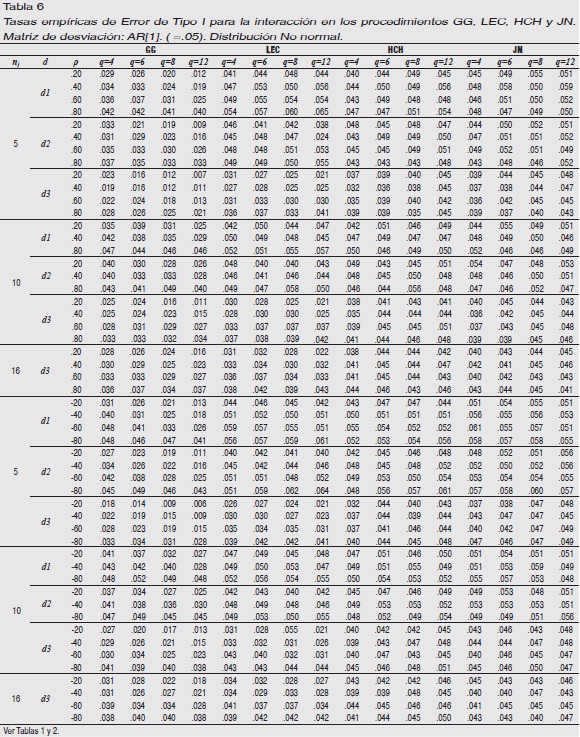
Los estadísticos AVAR, GG, y LEC acusan una estimación del error superior a la experimentada para el tratamiento y, como consecuencia de esta tendencia, GG y LEC resultan favorecidos con respecto al efecto principal, en mayor medida LEC, resultando robusto en más ocasiones. Sin embargo, la estimación del error para el AVAR resulta aún más perjudicada que lo estaba para el tratamiento, sobre todo en niveles elevados de ρ y q. HCH y JN son robustos con independencia de ρ, nj, q y d.
Matriz subyacente AREH[1]-C: No se exponen estos resultados porque no varían de modo significativo con respecto a los obtenidos para el tratamiento. Por esta razón nos remitimos a lo allí expuesto.
Matriz subyacente ARAH[1]: Tablas 1cont. y 7. Los resultados que no se exponen se deben a la misma razón expresada para la matriz de desviación homóloga en el tratamiento intra-sujeto. Observamos que el AVAR estima de modo liberal siempre que ε=.50 en todo valor de ρ (dirección y magnitud), q y nj, en mayor medida cuanto mayor es d. También cuando ε=.75 y la autocorrelación serial es elevada negativa.
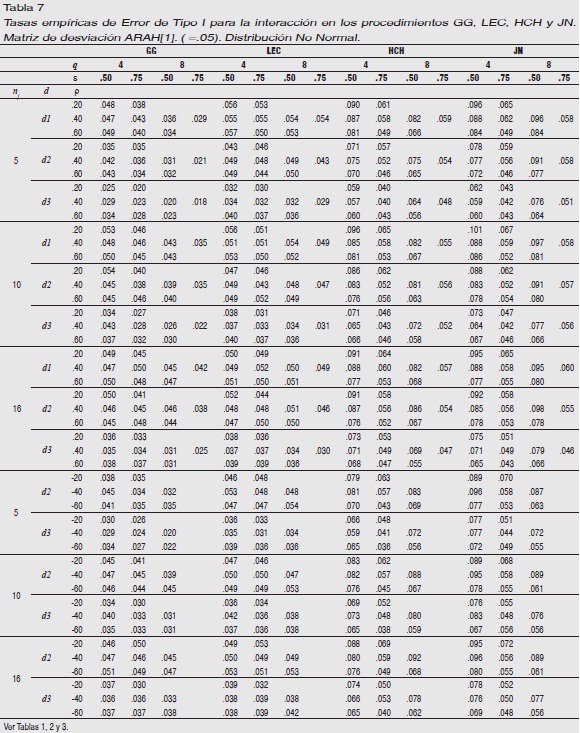
El procedimiento GG realiza una estimación robusta excepto cuando la distribución subyacente a los datos es d2 (ρ≤.40, nj=5, q=8 y ε=.75), y cuando la distribución es d3 (nj=5) excepto en q=4 y ε=.50.
LEC tiene un comportamiento excelente con independencia de ρ (magnitud y dirección), nj, q y d. HCH y JN son robustos cuando ε=.75 en todo q. Cuando ε=50 también lo son si la distribución es d3 en todo nj, y en d2 (nj=5). Los límites de la robustez son violados en más ocasiones por JN que por HCH.
Matriz subyacente NE: En la Tabla 5 advertimos que cuando ε=.56 todos los procedimientos se comportan del mismo modo que para el tratamiento. Sin embargo, cuando ε=.75 el procedimiento LEC es robusto en todo d, nj y q. También se puede ver que cuando la distribución es d1 y d2 JN se comporta de modo liberal, y GG bajo la distribución d3 de modo conservador. Estos dos últimos procedimientos son los que más veces violan los límites de la robustez cuando la desviación de la esfericidad es leve.
Discusión y conclusiones
El objetivo de esta investigación fue someter a comparación el comportamiento, cuando la distribución de los datos cursa de modo no normal, de los procedimientos univariados AVAR, GG, LEC, HCH y JN respecto a las tasas de error empírico de Tipo I en el modelo no aditivo de un diseño de medidas repetidas Split-Plot (3xq). Dos matices la hacen inédita. De una parte, el hecho de observar procedimientos que difieren en el modo de abordar la ausencia de esfericidad, bien sin reparar en la existencia de una estructura de correlación definida (GG y LEC), bien asumiendo autocorrelación serial de primer orden (HCH y JN), con el añadido de que la robustez en condiciones de ausencia de normalidad del procedimiento HCH nunca ha sido observada mediante simulación Montecarlo, y la robustez de los procedimientos JN y LEC solamente bajo unas condiciones muy concretas y en una sola ocasión cada uno de ellos, el primero en Fernández y Vallejo (1996) y el segundo en Beasley (2002). De otra parte, el hecho de ser sometidos a comparación en una gran variedad de estructuras de desviación subyacentes en los datos todas ellas carentes de esfericidad donde, además de las habitualmente estudiadas en los procedimientos AVAR y GG (AR[1], AREH[1] y NE), se introdujo la condición ARAH[1] que nos permitirá observar qué variable interviene en mayor medida en la cuantía del error de Tipo I empírico, si la ausencia de esfericidad, o el sentido y magnitud de la autocorrelación serial de primer orden. Los resultados obtenidos han puesto de relieve los siguientes patrones de comportamiento:
Comportamiento que adquieren los diferentes procedimientos cuando no se mantienen dentro de los límites de robustez. Los procedimientos AVAR, HCH y JN siempre son liberales. GG y LEC siempre son conservadores, con dos excepciones muy concretas donde son liberales y únicamente para la fuente de variación del tratamiento intra-sujeto (no para la interacción): una de ellas cuando la matriz subyacente es AREH[1]-C, d3, ρ≥.60, q≤6 y nj=5 y 10, y otra cuando la matriz es ARAH[1], d2 y d3, nj=5, q=4 y ε=.50.
Condiciones vulnerables de los diferentes procedimientos en las cuales trasgreden los límites de robustez: AVAR, ρ≥.60 y q≥6; GG y LEC, ρ≤.40 y q≥6 (más vulnerable GG); HCH y JN, ρ≤.40 del mismo modo en todo q; los procedimientos AVAR, LEC, HCH y JN muestran mejor comportamiento cuando ε=.75, y GG cuando ε=.50. Los resultados hallados para el AVAR, GG y LEC por Beasley (2002), Chen y Dunlap (1994), Fernández et al. (2008 y 2010), Huynh (1978), Huynh y Feldt (1976), Keselman y Keselman (1990), Keselman, Keselman y Lix (1995), *Keselman et al. (1996), Mendoza et al. (1974), Quintana y Maxwell (1994), Rasmussen et al. (1989), Rogan, Keselman y Mendoza (1979) y Wilcox (1993), y los hallados para JN por Edwards (1991) y Fernández y Vallejo (1996 y 1997), y para HCH por Fernández et al. (2008 y 2010) muestran los mismos patrones de comportamiento y vulnerabilidad para estos procedimientos en las condiciones concretas que coinciden con las aquí estudiadas. (Es necesario precisar que en las investigaciones antes referidas sólo se estudia uno, o a lo sumo dos, de los procedimientos de interés en este trabajo. En adelante, un asterisco, **, indicará que también allí es conveniente este aserto).
Proporción de error cometido por los diferentes procedimientos en función de la estructura de la matriz de desviación que subyace en los datos. Bajo las estructuras AR[1] y AREH[1]-D, los cinco estadísticos realizan prácticamente la misma estimación, tanto en lo que respecta al efecto principal intra-sujeto como a la interacción. Keselman y Keselman (1990) y Keselman et al. (1995) construyeron matrices no estacionarias estructuradas similares a las matrices AREH[1]-D sometidas a estudio en esta investigación obteniendo para el procedimiento GG los mismos resultados. Bajo la estructura matricial AREH[1]-C se produce un mayor error de estimación que en las dos condiciones matriciales anteriores en todos los procedimientos (en mayor medida en las situaciones vulnerables anteriormente indicadas). Cuando la matriz tiene la forma ARAH[1] aun se observa un mayor error que en las matrices anteriores en todos los procedimientos, sobre todo en las situaciones más vulnerables que son ε=.50 y d2 y d3. Huynh (1978) utilizando matrices muy similares a estas (ARHA[1]) obtuvo para el procedimiento GG resultados similares a los hallados en esta investigación. Por último, cuando la matriz de desviación es NE, excepto el procedimiento LEC que tiene un comportamiento excelente en todo ε, q y d, y del mismo modo para el tratamiento que para la interacción, el resto de ellos muestran una peor estimación cuando ε=.50. También, y al contrario que bajo el resto de estructuras matriciales estudiadas, todos los procedimientos realizan una mejor estimación del error de Tipo I cuando la distribución es Lognormal.
Comportamiento de los procedimientos en comparación con el mostrado cuando en los datos subyace distribución normal.
- Para todos los procedimientos, tanto para el tratamiento como para la interacción, cuando la distribución que subyace a los datos es d1 (Laplace), y tanto cuando ρ es positiva como cuando es negativa, el comportamiento es prácticamente el mismo que bajo distribución normal (Beasley, 2002; Fernández & Vallejo, 1996 y 1997; Fernández et al., 2008 y 2010; Wilcox, 1993). Otros investigadores (v.g. Vallejo, Fernández, Cuesta & Herrero, 2006 y Vallejo, Fernández, Herrero & Conejo, 2004), sometiendo a prueba en los diseños de medidas repetidas el MLG junto con otros procedimientos de análisis diferentes a estos han hallado similares resultados bajo esta distribución no normal simétrica.
- Todos los procedimientos son vulnerables cuando los datos se distribuyen de modo Exponencial (d2) y Lognormal (d3), en mayor medida en esta última tanto cuando existe correlación positiva como negativa (en menor medida cuando es negativa), y sea la matriz estacionaria como no estacionaria estructurada y como no estacionaria arbitraria. Con las siguientes particularidades:
- Matrices AR[1] y AREH[1]-D: Tanto para el tratamiento como para la interacción los procedimientos GG y LEC estiman de modo conservador o por debajo del nivel nominal en cualquier caso (mucho más GG) cuanto mayor es d. El AVAR estima de modo liberal pero sólo depende levemente de d y los estadísticos HCH y JN realizan una estimación excelente con independencia de d. **Beasley (2002), Fernández y Vallejo (1996 y 1997), Fernández et al. (2008 y 2010), Keselman y Keselman (1990), Keselman et al. (1995), *Keselman et al. (1996), Mendoza et al. (1974), Rasmussen et al. (1989) y Wilcox (1993) obtienen con respecto al AVAR y GG resultados muy similares. En la literatura podemos observar cómo estadísticos robustos para analizar los datos de medidas repetidas también experimentan este comportamiento (v.g. Livacic, Vallejo & Fernández, 2006; Vallejo et al., 2004 y Vallejo et al., 2006).
- Matriz AREH[1]-C: Todos los procedimientos experimentan la misma tasa de error que en AR[1] y AREH[1]-D para la interacción, sin embargo, para el tratamiento todos incrementan su estimación viéndose perjudicados claramente el AVAR (más a mayor d) y también HCH y JN en d3, pero favorecidos los procedimientos GG y LEC.
- Matrices ARAH y NE: En ambas matrices no estacionarias arbitrarias con y sin correlación serial respectivamente son destacables los siguientes patrones de comportamiento divergentes:
- Matriz ARAH[1]: Con independencia de la dirección de la autocorrelación, cuando mayor es d, más liberales son todos los procedimientos en el tratamiento y en la interacción (mucho menos en ésta), en mayor medida cuanto menores son nj y, q. Existe una clara diferencia entre el AVAR y el resto de procedimientos. La estimación del AVAR depende de d y nj, pero no de ρ ni de q. La estimación del resto de procedimientos en cada d y nj, depende de ρ y q (pero sólo en d2 y d3). Bajo esta matriz de desviación un incremento del tamaño de la muestra mejora la estimación de todos los procedimientos.
- Matriz NE: Con independencia de nj, q y ε, todos los procedimientos realizan una mejor estimación (menos liberales) para el tratamiento y la interacción cuanto mayor es d. Las diferencias entre d1 y d2 no existen, pero sí con d3, donde mejora claramente el comportamiento de todos los procedimientos. También es destacable que no se modifican los resultados debido a un incremento del tamaño de la muestra.
Bajo esta última estructura matricial (NE) en condiciones de no normalidad, han sido observados el AVAR y GG en muchas ocasiones, y en otras muchas el AVAR junto otros procedimientos robustos para analizar medidas repetidas. Es destacable que los resultados allí encontrados son convergentes con los hallados en esta investigación. (v.g. Beasley, 2002; Fernández & Vallejo, 1996 y 1997; Fernández et al., 2008 y 2010; Wilcox, 1993; Vallejo et al., 2004 & Vallejo et al., 2006).
¿Qué influye más en la estimación empírica del error de Tipo I, ε o ρ? En esta investigación, como en las llevadas a cabo por Fernández et al. (2008 y 2010) y en todas las investigaciones referenciadas en este artículo**, hemos comprobado cómo la robustez de todos los procedimientos se acentúa cuando ε= .75, excepto para el procedimiento GG que obtiene como regla general mejor comportamiento cuando ε= .50. Dilucidar este punto ha sido un objetivo prioritario en esta investigación y, por tanto, extendemos la siguiente hipótesis. Si observamos el valor del coeficiente medio de esfericidad para el conjunto de simulaciones efectuadas bajo las matrices AR[1] y AREH[1] para todas las magnitudes de correlación estudiadas (Tabla 1), apreciamos que cuando las matrices tienen correlación serial positiva, los valores medios de ε disminuyen muy gradualmente conforme incrementa la magnitud de ρ; sin embargo, cuando la correlación serial es negativa, los valores de ε disminuyen notablemente cuanto mayor es la magnitud de ρ. Esta es la razón del comportamiento de los procedimientos estudiados, tanto en función de ε y tamaño de ρ, como en función de la dirección de ρ. A la luz de esta curiosidad, el error de Tipo I empírico está más determinado por la magnitud de la desviación de la esfericidad que por la magnitud de la correlación serial cuando la matriz de desviación subyacente es AR[1] y AREH[1], pero también cuando la matriz subyacente es ARAH[1].
Las conclusiones más relevantes a tenor de los resultados obtenidos en esta investigación son:
Si tenemos en cuenta el conjunto de las tres formas de distribución no normal que subyacen a los datos aquí sometidas a estudio (Laplace, Exponencial y LogNormal) concluimos que:
- Los procedimientos HCH y JN tienen un comportamiento excelente para poner a prueba tanto el efecto principal intra-sujeto como la interacción cuando la matriz que subyace a los datos es AR[1], AREH[1] (D y C), para todo valor de ρ (magnitud y dirección), nj, q y d.
- El procedimiento LEC tiene un excelente comportamiento para poner a prueba el efecto principal intra-sujeto cuando la matriz subyacente a los datos es ARAH[1] y la autocorrelación es negativa. Cuando la autocorrelación es positiva, su comportamiento es excelente cuando ε=.75 y q=4, y también para toda desviación de la esfericidad cuando q=8. En cuanto a la interacción, el procedimiento LEC es excelente en todo momento sea cual sea la distribución que subyace a los datos.
- El procedimiento LEC tiene un comportamiento excelente para poner a prueba tanto el efecto principal intra-sujeto como la interacción cuando la matriz subyacente es NE en todo ε, y el procedimiento HCH cuando ε=.75 sea cual sea la distribución que subyace a los datos.
- Si tenemos en cuenta únicamente la distribución no normal simétrica Laplace y la distribución no normal asimétrica Exponencial que, como Micceri (1989, p. 163) señaló, "es difícil encontrarse con situaciones más extremas que éstas..." el procedimiento LEC es el que muestra el mejor comportamiento (el más estable) para todo valor de ρ (magnitud y dirección), nj, q, d y Σ tanto para el tratamiento como para la interacción, con alguna excepción detallada en el apartado de resultados. Beasley (2002) ha mostrado cómo el estadístico de Lecoutre (1991) proporciona resultados satisfactorios al ser aplicada en distribuciones asimétricas con carácter exponencial, y simétricas con alta densidad en las colas.
Lo inmediatamente antes señalado es de suma importancia. De una parte, porque uno de ellos, el procedimiento HCH, a pesar de haber sido gestado en 1983, hasta el año 2008 (Fernández et al., a y b) nunca había sido sometido a estudio intensivamente mediante simulación, y el procedimiento LEC (Lecoutre, 1991) solamente en escasas ocasiones (Beasley, 2002; Chen & Dunlap, 1994; Fernández et al., 2008 y 2010; Quintana & Maxwel, 1994) y en condiciones muy concretas. De otra parte, porque aunque ninguno de estos procedimientos ha sido incorporado aún a los paquetes estadísticos más utilizados por los investigadores que trabajan en disciplinas integradas en las Ciencias Sociales y de la Salud (SPSS y SAS), su cálculo es sumamente sencillo y fácil de llevar a cabo.
Al amparo de los resultados hallados por Fernández et al (2008 y 2010) bajo distribución normal (ver allí las recomendaciones extendidas por los autores) y los resultados hallados en esta investigación, la elección del mejor procedimiento para poner a prueba las hipótesis de un diseño Split-Plot balanceado de medidas repetidas quedaría reducido a tres procedimientos, LEC, HCH y GG, siendo recomendable observar en primer lugar la estructura de las varianzas de la matriz Σ, la existencia o no de correlación serial de primer orden (estas dos características también Edwards (1991) las indicó como prioritarias para seleccionar un estadístico de análisis para un diseño simple de medidas repetidas), la cuantía de la esfericidad, el número de niveles de la variable intra-sujeto y el tamaño de la muestra.
No debemos olvidar que en investigaciones aplicadas otras condiciones adversas pueden sumarse a éstas, como heterogeneidad entre grupos de las matrices de covarianza y desigualdad en el tamaño de los grupos, con el añadido de que el apareamiento entre ambas condiciones puede ser positivo o negativo. Por esta razón, son varios los procedimientos robustos que se han desarrollado para poner a prueba las hipótesis en los diseños de medidas repetidas. Autores como *Keselman et al. (1996), Keselman et al. (2001), Blanca Mena (2004) y Fernández et al. (2007) realizan excelentes revisiones de estos procedimientos y aportan recomendaciones ad hoc para seleccionar el estadístico de análisis más adecuado en estas circunstancias. Sin embargo, los procedimientos HCH, JN y LEC nunca han sido puestos a prueba en las condiciones adversas anteriores y por esta razón una futura investigación debería estar orientada en ése sentido.
Referencias
Akaike, H. (1974). A new look at the statistical model identification. IEEE Transactions on Automatic Control, AC-19, 716-723. [ Links ]
Andersen, A.H.; Jensen, E.B. & Schou, G. (1981). Two-way analysis of variance with autocorrelated errors. International Statistical Review, 49, 153-157. [ Links ]
Azzalini, A. (1984). Estimation and hypothesis testing for collections of autoregressive time series. Biometrika, 71, 85-90. Correction: 74 (1987), 667. [ Links ]
Blanca Mena, Mª. (2004). Alternativas de análisis estadístico en los diseños de medidas repetidas. Psicothema, 16 (3), 509-518. [ Links ]
Beasley, T.M. (2002). Multivariate aligned rank test for interactions in multiple group repeated measures designs. Multivariate Behavioral Research, 37 (2), 197-226. [ Links ]
Chen, S.R. & Dunlap, W.P. (1994). A Monte Carlo study on the performance of a corrected formula for suggested by Lecoutre. Journal of Educational Statistics, 19, 119-126. [ Links ]
Collier, R. O., Baker, F. B., Mandeville, G. K., & Hayes, T. F. (1967). Estimates of test size for several test procedures based on conventional variance ratios in the repeated measures designs. Psychometrika, 32, 339-353. [ Links ]
Cornell, J.E.; Young, D.M. & Bratcher, T.L. (1991). An algorithm for generating covariance matrices with specified departures from sphericity. Journal of Statistical Computation and Simulation, 34, 240-243. [ Links ]
Edwards, L.K. (1991). Fitting a serial correlation pattern to repeated observations. Journal of Educational Statistics, 16 (1), 53-76. [ Links ]
Fernández, P. & Vallejo, G. (1996). Análisis de un diseño de medidas repetidas con dependencia serial en el error cuando la asunción de normalidad es violada. Psicológica. Revista de Metodología y Psicología Experimental, 17 (3), 533- 558. [ Links ]
Fernández, P. & Vallejo, G. (1997). Diseño de medidas repetidas con dependencia serial en el error. Psicothema 9 (3), 619-635. [ Links ]
Fernández, P.; Livacic-Rojas, P. & Vallejo, G. (2007). Cómo elegir la mejor prueba estadística para analizar un diseño de medidas repetidas. International Journal of Clinical and Health Psychology, 7 (1), 153-175. [ Links ]
Fernández, P.; Vallejo, J.; Livacic-Rojas; Herrero, J. & Cuesta, M. (2010). Comparative robustness of six tests in repeated measures designs with specified departures from sphericity. Quality & Quantity, Quality & Quantity, 44 (2), 289-301. DOI: 10.1007/ S11135-008-9198-3. [ Links ]
Fernández, P.; Vallejo, G. & Livacic-Rojas, P. (2008, July). Comparison of the robustness of the SPSS MIXED procedure with regard to another three univariate statistics in repeated measures designs with specified departures from sphericity. Paper presented at the III European Congress of Methodology, Oviedo (Spain). [ Links ]
GAUSS. (2008). The Gauss System. (Vers. 9.0). Washington: Aptech Systems, Inc. [ Links ]
Greenhouse, S. W., & Geisser, S. (1959). On methods in the analysis of profile data. Psychometrika, 24, 95-112. Headrick, T. C., Kowalchuk, R. K. & Sheng. (2008). [ Links ]
Parametric probability densities and distribution functions for Tukey g-and-h transformations and their use for fitting data. Applied Mathematical Sciences, 2, 449-462. [ Links ]
Hearne, E.M.; Clark, G.M. & Hatch, J.P. (1983). A test for serial correlation in univariate repeated-measures analysis. Biometrics, 39, 237-243. [ Links ]
Huynh, H. (1978). Some approximate tests for repeated measurement designs. Psychometrika, 43 (2), 161-175. [ Links ]
Huynh, H. & Feldt, L. S. (1976). Estimation of the Box correction for degrees of freedom from sample data randomized block and split-plot designs. Journal of Educational Statistics, 1, 69-82. [ Links ]
Jones, R.H. (1985). Repeated measures, interventions, and time series analysis. Psychoneuroendocrinology, 10 (1), 5-14. [ Links ]
Keselman, H. J., Algina, J. & Kowalchuck, R. K. (2001). The analysis of the repeated measures design: A review. British Journal of Mathematical and Statistical Psychology, 54, 1-20. [ Links ]
Keselman, H.J., Algina, J., Kowalchuck, R.K. & Wolfinger, R.D. (1999). A comparison of recent approaches to the analysis of repeated measurements. British Journal of Mathematical and Statistical Psychology, 52, 63-78. [ Links ]
Keselman, J.C. & Keselman, H.J. (1990). Analysis unbalanced repeated measures designs. British Journal of Mathematical and Statistical Psychology, 43, 265-282. [ Links ]
Keselman, H.J., Keselman, J.C. & Lix, L.M. (1995). The analysis of repeated measures: Univariate test, multivariate, or both? British Journal of Mathematical and Statistical Psychology, 48, 319-338. [ Links ]
Keselman, H.J., Kowalchuck, R. & Boik, R. (2000). An examination of robustness of the empirical bayes and other approaches for testing main interaction effects in repeated measures designs. British Journal of Mathematical and Statistical Psychology, 53, 51-67. [ Links ]
Keselman, J., Lix, L. & Keselman H. J. (1996). The analysis of repeated measurements designs: A quantitative research synthesis. British Journal of Mathematical and Statistical Psychology, 49, 275-298. [ Links ]
Kinderman, A.J. & Ramage, J.G. (1976). Computer generation of normal random numbers. Journal of American Statistical Association, 77, 893-896. [ Links ]
Kowalchuck, R.K., Keselman, H.J., Algina, J. & Wolfinger, R.D. (2004). The analysis of repeated measures with mexed-model adjusted F test. Educational and Psychological Measurements, 64, 224-242. [ Links ]
Lecoutre, B. (1991). A correction for the approximate test in repeated measures designs with two or more independent groups. Journal of Educational Statistics, 16, 371-372. [ Links ]
Livacic-Rojas, P., Vallejo, G. & Fernández, P. (2006). Procedimientos estadísticos alternativos para evaluar la robustez mediante diseños de medidas repetidas. Revista Latinoamericana de Psicología, 38, 579-598. [ Links ]
Littell, R.C., Milliken, G.A., Stroup, W.W., Wolfinger, R.D. & Schabenberger, O. (2006). SAS System for Mixed Models, Cary, NC: SAS Institute Inc. [ Links ]
Mendoza, J.L., Toothtaker, L.E. & Nicewander, W.A. (1974). A Monte Carlo comparison of the univariate and multivariate methods for the groups by trials repeated-measures design. Multivariate Behavioral Research, 9, 165-177. [ Links ]
Micceri, T. (1989). The unicorn, the normal curve, and other improbable creatures. Psychological Bulletin, 92, 778-785. [ Links ]
Núñez Antón, V. & Zimmerman, D.L. (2001). Modelización de datos longitudinales con estructuras de covarianza no estacionarias: Modelos de coeficientes aleatorios frente a modelos alternativos. Qüestiió, 25, 225- 262. [ Links ]
Quintana, S. & Maxwell, S. E. (1994). A Monte Carlo comparison of seven 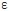 -adjustment procedures in repeated measures designs with small sample sizes. Journal of Educational Statistics, 19, 57-71. [ Links ]
-adjustment procedures in repeated measures designs with small sample sizes. Journal of Educational Statistics, 19, 57-71. [ Links ]
Rasmussen, J.L. Heumann, K.A., Heumann, M.T. & Botzum, M. (1989). Univariate and multivariate groups by trials analysis under violations of variance-covariance and normality assumptions. Multivariate Behavioral Research, 24, 93-105. [ Links ]
Rogan, J.C., Keselman, H.J. & Mendoza, J.L. (1979). Analysis of repeated measurements. British Journal of Mathematical and Statistical Psychology, 32, 269-286. [ Links ]
Schwarz, G. (1978). Estimating the dimension of a model. Annals of Statistics, 6, 461-464. [ Links ]
Tukey, J.W. (1977). Modern techniques in data analysis. NSF-sponsored regional research conference at Southern Massachusetts University (North Dartmouth, Massachusetts). [ Links ]
Vallejo, G. (1991). Análisis univariado y multivariado de los diseños de medidas repetidas de una sola muestra y de muestras divididas. Barcelona, PPU. [ Links ]
Vallejo, G., Arnau, J. & Ato, M. (2007). Comparative robustness of recent methods for the analysis of multivariate repeated measuses designs. Educational & Psychological Measurement, 67, 410-432. [ Links ]
Vallejo, G., Arnau, J., Bono, R., Cuesta, M., Fernández, P. & Herrero, J. (2002). Análisis de diseños de series temporales cortas. Metodología de las Ciencias del Comportamiento, 4 (2), 301-323. [ Links ]
Vallejo, G., Ato, M. & Valdés, T. (2008). Consequences of misspecifying the error covariance structure in linear mixed models for longitudinal data. Methodology, 4, 10-21. [ Links ]
Vallejo, G., Fernández, P & Ato, M. (2003). Tasas de potencia de dos enfoques robustos para analizar datos longitudinales. Psicológica, 24, 109-122. [ Links ]
Vallejo, G.; Fernández, P.; Cuesta, M. & Herrero, F. J. (2006). A comparison of the bootstrap-F, Improved General Approximation and Brown-Forsythe approaches in a mixed repeated measures design. Educational and Psychological Measurement, 66, 35-62. [ Links ]
Vallejo, G.; Fernández, P.; Herrero, F.J. & Conejo, N.M. (2004). Alternative procedures for testing fixed effects in repeated measures designs when assumptions ere violated. Psicothema, 16 (1), 498-508. [ Links ]
Vallejo, G., Fernández, J. R., & Secades, R. (2004). Application of a mixed model approach for assessment of interventions and evaluation of programs. Psychological Reports, 95, 1095-1118. [ Links ]
Wilcox, R.R. (1993). Analysing repeated measures or randomized block designs using trimmed means. British Journal of Mathematical and Statistical Psychology, 46, 63-76. [ Links ]
Wright, S.P. & Wolfinger, R.D. (1996, October). Repeated measures analysis using mixed models: Some simulations results. Paper presented at the Conference on Modelling Longitudinal and Spatially Correlated data: Methods, Applications, and Future directions. Nantucket, Massachusetts. [ Links ]
Wolfinger, R.D. (1996). Heterogeneous variance-covariance structures for repeated measurements. Journal of Agricultural, Biological, and Enviromental Statistics, 1, 205-230. [ Links ]














