Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Revista Colombiana de Ciencias Pecuarias
Print version ISSN 0120-0690On-line version ISSN 2256-2958
Rev Colom Cienc Pecua vol.20 no.2 Medellín Apr./June 2007
Comparación de modelos matemáticos: una aplicación en la evaluación de alimentos para animales
Comparison of mathematical models: an application forevaluation of animal food
Sandra L Posada1*, Zoot, MS; Ricardo Rosero Noguera1, Zoot, MS, PhD.
1Grupo de Investigación en Ciencias Agrarias-GRICA. Facultad de Ciencias Agrarias, Universidad de Antioquia, AA 1226, Medellín, Colombia.
slposada@agronica.udea.edu.co
(Recibido: 6 febrero, 2007; aceptado: 24 mayo, 2007).
Resumen
La digestibilidad y las tasas de degradación de los alimentos pueden ser estimadas a través de la técnica in vitro de producción de gases. Las curvas de producción de gases que se generan pueden ser descritas por diversos modelos matemáticos (exponenciales, logísticos, empíricos). El objetivo de este trabajo fue presentar algunos modelos matemáticos empleados para describir las curvas de producción de gases y las herramientas estadísticas que sirven para evaluar su capacidad de ajuste. Dos modelos, uno logístico propuesto por Schofield et al y uno empírico propuesto por France et a, fueron utilizados para ajustar los perfiles de producción de gases de seis especies forrajeras, y los criterios seleccionados para evaluar su capacidad de ajuste fueron: 1) el cuadrado medio del error (CME), 2) el criterio de información de Akaike (AIC), 3) el criterio de información bayesiano (BIC), 4) el coeficiente de determinación (R2), 5) el análisis de los residuos, y 6) la dócima de Durban-Watson (DW). Los mejores modelos son aquellos que presentan el mejor balance entre la capacidad de ajuste de los datos y la coherencia biológica, siendo necesaria su evaluación en las más variadas condiciones experimentales, a fin de escoger el mejor para cada situación.
Palabras clave: ajuste, digestibilidad, estadístico, gas, in Vitro, producción.
Summary
The digestibility and degradation rates of food can be estimated through the in vitro gas production technique. The gas curves generated can be described by diverse mathematical models (exponential, logistic, and empirical). The objective of this work was to present some mathematical models commonly used to describe gas production curves and to review some statistical tools useful to evaluate their adjustment capacity. Two models, either a logistic or an empirical proposed by Schofield et al, and France et al, respectively, were used to fit the profiles of gas production of six forage species. The selected criteria for evaluation of their adjustment capacity were: 1) square means error (CME), 2) Akaike (AIC) or 3) Bayesian (BIC) information criteria, 4) coefficient of determination (R2), 5) residual analysis, and 6) Durban-Watson dosim (DW). The best models for evaluation of gas production are those that present the best balance between data adjustment capacity and biological coherence, being necessary their evaluation under the most varied experimental conditions, in order to choose the best model for each specific situation.
* Autor para el envío de la correspondencia y la solicitud de separatas. Carrera 75 N° 65-87, Facultad de Ciencias Agrarias, Universidad de Antioquia, Medellín, Colombia. E-mail: slposada@agronica.udea.edu.co
Keywords: accuracy, digestibility, gas, in vitro, statistics, production.
Introducción
La producción de leche y el crecimiento de los rumiantes están limitados por la calidad del alimento disponible, por tanto, la evaluación de su valor nutricional es importante. Cuando los alimentos son incubados en fluido ruminal y solución tampón, su digestibilidad y tasas de degradación pueden ser estimadas por la medición de la producción de gas in vitro (1, 17). La descripción estadística por modelos matemáticos de las curvas de producción de gas permite la comparación de los sustratos, la evaluación de diferentes ambientes de fermentación, y proporciona información sobre las tasas de fermentación de los constituyentes solubles y estructurales (8, 12).
Diferentes modelos están disponibles para estimar los parámetros de fermentación a través de las curvas de producción de gas, todos ellos con diferencias de ajuste estadístico dependiendo de las condiciones experimentales y del tipo de sustrato, lo que hace necesaria su evaluación (12). No obstante, la escogencia del modelo no debe tener solamente en cuenta consideraciones de ajuste matemático, sino también la coherencia biológica de los parámetros (21). El objetivo de este trabajo es presentar algunos de los modelos estadísticos empleados para describir las curvas de producción de gas y herramientas matemáticas que sirven para evaluar y comparar su capacidad de ajuste, tales como el cuadrado medio del error, el criterio de información de Akaike, el criterio de información bayesiano, el coeficiente de determinación, el análisis de los residuales y la dócima de Durban-Watson.
Modelación de la cinética de producción de gas
El incremento en la frecuencia de las lecturas de la producción de gas conduce a la obtención de perfiles muy detallados (21). Los perfiles de producción de gas obtenidos con un limitado número de datos pueden ser descritos por simples modelos exponenciales, basados en cinéticas de primer orden, en los que se asume una tasa fraccional constante de fermentación (3, 8). La introducción de más avanzados y sensibles equipos de medición de la producción de gas, hace necesaria la utilización de modelos multifásicos (8, 12) que separan el sustrato evaluado en las fracciones más rápida o más lentamente fermentables (21).
Las curvas de producción de gas presentan forma sigmoidal y en ellas se puede distinguir tres fases: una fase inicial, de lenta producción de gas; una fase exponencial, de rápida producción de gas; y una fase asintótica, donde existe una lenta o casi nula producción de gas. Durante la fase inicial ocurre la hidratación y colonización del sustrato insoluble por los microorganismos ruminales (2). Cuando el sustrato es saturado con microorganismos y enzimas, la fase exponencial toma lugar; durante esta fase, la parte más degradable del sustrato insoluble es degradada primero, y el sustrato menos digestible precisa de más tiempo para ser degradado. Finalmente, cuando la fracción potencialmente degradable ha sido digerida, la producción de gas es cero (1).
Para evaluar los resultados es necesario un modelo que describa la producción de gas en el tiempo, que permita un adecuado ajuste estadístico de los datos y cuantifique con precisión los parámetros con significado biológico. Diferentes ecuaciones han sido desarrolladas con este propósito (5, 19).
Modelos
Modelos exponenciales simples. El método de digestión “in vitro” de la fibra desarrollado por Tilley y Terry (18) y modificado por Goering y Van Soest
(7) ha sido ampliamente utilizado para determinar las tasas de digestión de la fibra insoluble. Los dados de estos experimentos son ajustados a través de funciones exponenciales:
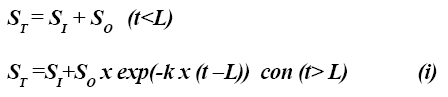
Donde ST es el residuo total de fibra en el tiempo t, SI es la fibra indigestible, SO es la fibra inicial digestible, k es una tasa constante de digestión (h-1) y L es el tiempo de colonización (9). Para emplear este modelo en la técnica de producción de gas, la ecuación debe ser modificada porque la aparición de un producto es considerada antes de la desaparición de un sustrato:
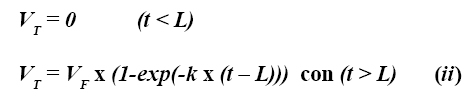
Donde VT corresponde al volumen de gas en el tiempo t, VF es el volumen de gas correspondiente a la completa digestión del sustrato (asíntota), k es la tasa de producción de gas (h-1) y L fue definida en la ecuación (i) (14). Esta ecuación exponencial simple puede ser derivada del supuesto de que la tasa de producción de gas depende únicamente del sustrato disponible para la fermentación una vez alcanzado el tiempo de colonización.
Muchos alimentos para animales contienen una mezcla de carbohidratos que presentan diferentes tasas de degradación. Para el análisis de la cinética de producción de gas, el sustrato puede ser considerado como una única entidad con una tasa de degradación que no varía con el tiempo (monocompartimental) o como una entidad múltiple constituida por una fracción de rápida degradación y otra fracción de lenta fermentación, cada una de las cuales presenta una tasa de degradación característica (multicompartimental) (8). La ecuación (ii) puede ser modificada para estimar cada una de estas fracciones:
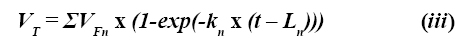
Donde n representa cada una de las fracciones fermentables dentro del sustrato.
Modelos logísticos. El modelo exponencial asume que el único factor limitante en la tasa de producción de gas es la cantidad de fibra digestible. Una función de crecimiento logístico (22) asume que la producción de gas es proporcional al tamaño de la población microbiana y al sustrato digestible. En el inicio de la fermentación, la población microbiana constituye el factor limitante, ya en el final de la fermentación es la disponibilidad de sustrato fermentable lo que limita la tasa de producción de gas (15). En consecuencia, una curva logística es inherentemente sigmoidal y la máxima tasa de producción de gas ocurre cuando la mitad del sustrato ha sido fermentado. El modelo que representa este tipo de comportamiento puede ser descrito como:
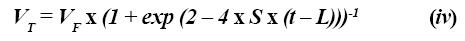
Las expresiones fueron definidas en la ecuación (ii) y S representa una tasa específica semejante a la tasa de degradación. La ecuación (iv) puede ser descrita en su forma multicompartimental:
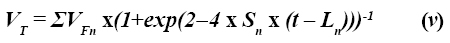
Esta ecuación es más versátil para el ajuste de las curvas de producción de gas. La principal diferencia entre las ecuaciones (iii) y (v) se encuentra en el tiempo de colonización (L). La ecuación (iii) es una función discontinua y L determina el punto de discontinuidad. Por el contrario, la ecuación (v) es válida para todos los valores positivos de t (15).
Modelos empíricos. Para el ajuste de las curvas de producción de gas, Groot et al (8) propusieron la siguiente ecuación:
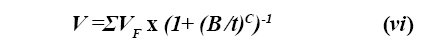
Donde VF es el volumen de gas producido, B corresponde al tiempo (horas) en el cual la mitad del volumen total de gas ha sido producido, y C es un valor positivo que cambia simultáneamente con B y determina la forma de la curva. Cuando C ≤ 1, la curva no tiene punto de inflexión y presenta la forma de una función exponencial; y cuando C ≥ 1, la curva es sigmoidal (14). La ecuación (vi) es muy versátil y permite reproducir las curvas de producción de gas con una buena aproximación, aunque infortunadamente el parámetro C es difícil de interpretar en términos biológicos.
La primera ecuación publicada como una alternativa a la ecuación exponencial simple (ii) fue propuesta por France et al (5). La ecuación propuesta por ellos conserva el concepto de tiempo de colonización (L, h-1) y la tasa de degradación µ (h-1) fue postulada para variar con el tiempo t. La expresión matemática que representa este modelo es:
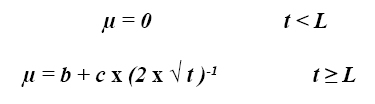
Si VF es el volumen total de gas producido (asíntota), la ecuación que describe el volumen de gas acumulado VT con el tiempo t sería:
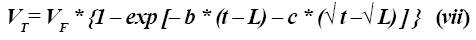
El término b no tiene interpretación biológica.
Criterios de selección para evaluar la capacidad de ajuste de los modelos
El objetivo de la evaluación de modelos es seleccionar aquellos que presenten el mejor balance entre la capacidad de ajuste de los datos y su complejidad. Modelos con un mayor número de parámetros tienden a ajustar mejor una base de datos, no obstante tienden a ser más inestables y a modelar la variabilidad de esos datos más que su tendencia. Los modelos pueden ser evaluados de acuerdo con los siguientes criterios:
1. Cuadrados medios del residuo (o del error) (CME). El CME es una medida que agrupa la variabilidad de aquellos factores que no tiene en cuenta el investigador. La varianza de n residuales ei se representa como:
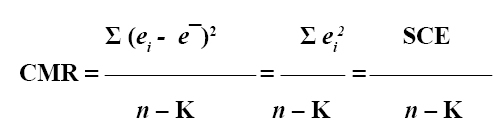
Donde, e¯ es la media de n residuales (número de observaciones), que en todos los casos corresponde a cero (11), K es el número de parámetros estimados en el modelo (4) y SCE es la suma de cuadrados de las distancias verticales de los puntos desde la curva de regresión (residuales) (10).
Toda vez que el CME corresponde a la varianza residual, los modelos seleccionados por su mayor capacidad de ajuste son aquellos que expresan el menor valor en este criterio.
2. Criterio de información de Akaike (AIC) y criterio de información bayesiano (BIC). Cuando se tiene una serie de modelos M1, M2,/serial/rccp/v20n2. con parámetros K1, K2,…, respectivamente, una metodología para compararlos corresponde a la función de máxima verosimilitud (likelihood). La máxima verosimilitud permite seleccionar el modelo que realiza el mejor ajuste de los datos pero no penaliza su complejidad, lo que si sucede cuando se emplean medidas de contraste como el AIC y el BIC. Ambos criterios hacen uso del Log-likelihood (log Lik), que es el logaritmo de máxima verosimilitud, y sustraen un término proporcional al número de parámetros (K) en el modelo, así: log Lik -αK, donde α corresponde a 2 para el AIC y a log(N) para el BIC (6).
Criterio de información de Akaike (AIC). El criterio combina la teoría de máxima verosimilitud, información teórica y la entropía de información (10), y es definido por la siguiente ecuación:
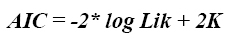
Este criterio tiene en cuenta los cambios en la bondad de ajuste y las diferencias en el número de parámetros entre dos modelos (6). Los mejores modelos son aquellos que presentaron el menor valor de AIC.
Cuando los valores de AIC están muy cercanos, la escogencia del mejor modelo se puede realizar con base en el cálculo de la probabilidad (pesos de Akaike) y la probabilidad relativa (relación de evidencia), a través de las siguientes ecuaciones:

Donde, ∆ es la diferencia entre los valores de AIC (10).
3. Criterio de información bayesiano (BIC). El BIC es calculado para los diferentes modelos como una función de la bondad de ajuste del log Lik, el número de parámetros ajustados (K) y el número total de datos (N). El modelo con el más bajo valor de BIC es considerado el mejor en explicar los datos con el mínimo número de parámetros (6). El BIC está definido por la ecuación:
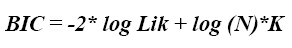
4. Coeficiente de determinación (R2). El R2 mide el porcentaje de variación total en Y debido a las variables que toma el investigador; en nuestro caso, informa sobre la fracción de la varianza total de Y (volumen de producción de gas, ml/g MS incubado) que es explicada por los modelos y se expresa en porcentaje. Este valor se obtiene a partir de la suma de cuadrados del error (SCE) y de la suma de cuadrados total (SCT), a partir de la ecuación:
R2 = 1.0 - SCE / SCT
La SCE corresponde a la suma de cuadrados de las distancias de los puntos desde la curva de mejor ajuste determinada por regresión no lineal, en tanto que la SCT es la suma de cuadrados de las distancias de los puntos desde una línea horizontal correspondiente a la media de todos los valores de Y (10).
5. Análisis de los residuos (términos de error) para verificar el cumplimiento de supuestos teóricos. Los residuales de cada modelo son calculados como la diferencia entre los valores observados y los predichos (ei = Yi - Yλ i). Para el análisis de los residuos se puede probar constancia de la varianza del error, independencia de los términos de error y ausencia de datos extremos (outliers). Para verificar el primer supuesto, los residuos son graficados frente a los valores estimados, buscando determinar si la magnitud de los sesgos incrementa o disminuye con la magnitud de los valores estimados. La independencia de los términos de error les asigna la mayor capacidad de ajuste a los modelos que registren la menor correlación entre residuales sobre el tiempo, para lo cual los residuales del tiempo i son graficados contra aquellos del tiempo de incubación precedente i-1. Para determinar la ausencia de outliers se grafican los residuales estandarizados, obtenidos como ei /√CME, frente al tiempo, identificando que no se registren puntos superiores a cuatro o más desviaciones estándar desde el punto cero (11). Para los supuestos teóricos, el tiempo de incubación es considerado una variable independiente.
6. Dócima de Durbin-Watson (DW). Esta dócima demuestra la existencia de autocorrelación serial de primer orden entre residuales, caso en el cual el modelo aproxima los datos con errores sistemáticos. DW se calcula a partir de la siguiente ecuación:
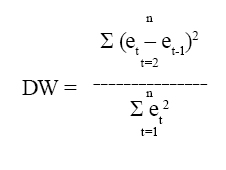
Donde et = residual al tiempo t, y et-1 = residual al tiempo t-1 (20).
Los modelos con menor autocorrelación ofrecen residuales más pequeños y no tendenciosos. El coeficiente de DW se evalúa contra el valor crítico tabulado (dL y dμ) (α=0.05).
Si DW>dμ, se concluye que no hay correlación serial de primer orden entre residuales
Si DW< dL, se concluye que hay correlación serial de primer orden entre residuales
Si dL≤ DW≤ dμ, el test es inconcluyente (11).
Materiales y métodos
Comparación de dos modelos de producción de gas
Dos modelos fueron utilizados para ajustar los perfiles de producción de gas de seis especies forrajeras e ilustrar los criterios considerados para su comparación. El primero fue el modelo logístico propuesto por Schofield et al (15); el segundo fue el modelo empírico propuesto por France et al (5). La información fue obtenida de un trabajo realizado por Posada (13), en el cual el ajuste de los datos a cada modelo y las estimativas de los parámetros se realizaron a través del proceso iterativo del algoritmo Marquardt del procedimiento para modelos no lineales PROC NLIN de SAS (16).
Resultados
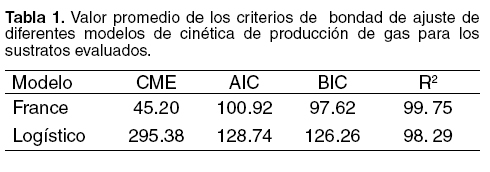
El valor promedio de los criterios de bondad de ajuste para los dos modelos considerados se muestra en la tabla 1, en donde se observa que el modelo France fue el que explicó en mayor magnitud la cinética de producción de gas.
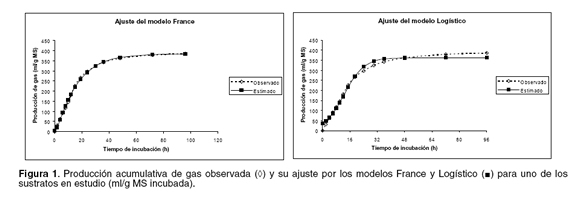
En la figura 1 se presenta la producción acumulativa de gas observada y estimada por los modelos evaluados en uno de los sustratos utilizados del experimento. Se observa que el modelo France ofreció un adecuado ajuste en las primeras horas del proceso fermentativo, así como también durante la fase exponencial y asintótica de la curva, en tanto que el modelo logístico no presentó esta característica, una vez que los valores estimados distan de los observados en varios puntos de la curva.
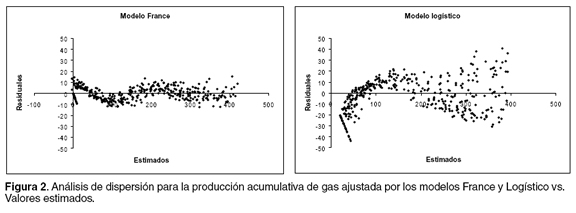
La diferencia entre la producción acumulativa de gas observada y la estimada por los modelos permite obtener los residuales, los cuales son presentados en la figura 2 para los sustratos en estudio. La mejor distribución residual se obtuvo para el modelo France, una vez que es el que ajustó los datos con la más pequeña SCE. El modelo logístico fue el que presentó residuales más grandes y con mayor tendencia a sobreestimar y subestimar grandes secciones de la curva de producción acumulativa de gas. Se observa que ambos modelos presentaron residuales positivos y negativos a medida que el tiempo de incubación aumentó (valores estimados conforme avanza el tiempo de incubación), no obstante, la constancia de la varianza del error fue más evidente para el modelo France, toda vez que la distribución de sus residuales siguió un patrón más aleatorio alrededor de la línea cero.
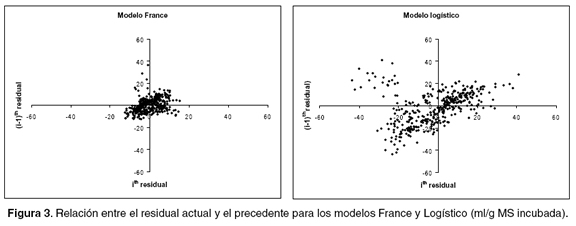
Otra propiedad de los residuales relacionada con la constancia de la varianza del error es la independencia de los términos de error, la cual asigna la mejor capacidad de ajuste a los modelos que registren la menor correlación entre los residuales sobre el tiempo. En la figura 3 se aprecia el valor de los residuales contra aquellos del tiempo de incubación precedente para los sustratos en estudio.
Discusión
Tomando en cuenta que la proporción de la varianza explicada por los modelos (R2) fue alta, 99.75 y 98.29%, ambos pueden considerarse válidos para describir los perfiles de producción de gas, lo cual no fue confirmado por los demás criterios considerados. De acuerdo con estos resultados se concluye que el R2 no debe ser el principal, ni mucho menos el único criterio para definir si un modelo es adecuado, toda vez que no indica si el ajuste realizado es sensible en términos de coherencia biológica. Altos valores de R2 pueden ser observados en modelos con limitada capacidad de predicción.
Como la SCT es siempre la misma para un conjunto de datos, el valor de la SCE depende exclusivamente del buen ajuste del modelo. En este caso, el modelo France fue el que mejor representó el conjunto de datos al ofrecer menor SCE, que es utilizada para estimar el CME. Esta conclusión fue avalada por el AIC y el BIC. Si bien ambos criterios balancean el cambio en la bondad de ajuste, evaluado por la suma de cuadrados, con el cambio en el número de parámetros (10), los valores obtenidos permiten concluir que el modelo France fue el mejor en explicar la cinética de producción de gas, no obstante, su mayor número de parámetros.
El análisis gráfico presentado en la figura 3 permite seleccionar el modelo de mejor ajuste con base en dos criterios: a) proximidad de la nube de puntos al punto cero, lo que indica residuales de menor magnitud, b) ubicación de los puntos en los cuadrantes II y IV, lo que muestra que un residual positivo es precedido por uno negativo o viceversa, una vez que residuales del mismo signo estarían indicando que el modelo sobre o subestima determinadas secciones de la curva a lo largo del tiempo. Para este estudio, la menor correlación serial entre residuales se registró para el modelo France, que a su vez es el presentó valores más próximos al punto de encuentro de las coordenadas (0,0), lo que revela residuales más pequeños que ajustan los datos con menor SCE.
El análisis realizado por DW mostró una evidente correlación serial de primer orden para el modelo logístico en el 100% de las curvas, en tanto que el modelo France exhibió un resultado inconcluyente en el 95.83% de ellas. La autocorrelación positiva permite concluir que los residuales adyacentes et y et-1 tendieron a ser de la misma magnitud y presentaron pequeñas diferencias, lo que condujo a un coeficiente DW menor. Cuando el resultado es inconcluyente, en principio más observaciones son requeridas.
Los resultados en términos de bondad de ajuste de los modelos para describir la cinética de degradación de alimentos son muy variables entre experimentos. Esto hace necesaria su evaluación en diferentes condiciones y con una amplia variedad de sustratos, permitiendo escoger el mejor modelo para cada situación y no la utilización indiscriminada de un único modelo.
En conclusión, no hay un método único para evaluar similitudes o diferencias entre modelos de regresión no lineal y para probar cuál de ellos debe ser usado para ajustar de una forma más adecuada la cinética de producción de gas. Un gran número de procedimientos están disponibles para este fin, permitiendo escoger el más consistente para las condiciones intrínsecas del experimento. No obstante, la selección de un modelo para explicar un conjunto particular de datos no debe estar basada enteramente sobre medidas estadísticas, ya que algunas condiciones de orden biológico, en relación con los parámetros del modelo tienen que ser satisfechas.
Agradecimientos
Los autores expresan sus agradecimientos a la profesora Diana Bolívar (Universidad Nacional sede Medellín, Colombia) por su disponibilidad para el desarrollo del proyecto y al Grupo de Investigación en Ciencias Animales (GRICA) por su apoyo económico para la ejecución de la propuesta
Referencias
1. Beuvink JMW, Kogut J. Modeling gas production kinetics of grass silages incubated with buffered ruminal fluid. J Anim Sci 1993; 71:1041-1046. [ Links ]
2. Cheng KJ, Fay JP, Howarth RE, Costerton JW. Sequence of events in the digestion of fresh legume leaves by rumen bacteria. Applied Environ Microbiol 1980; 40:613-625. [ Links ]
3. Cone JW, Van Gelder AH, Driehuis F. Description of gas production profiles with a three-phasic model. Anim Feed Sci Technol 1997; 66:31-45. [ Links ]
4. Ellis WC, Mahlooji M, Matis JH. Models for estimating parameters of neutral detergent fiber digestion by ruminal microorganisms. J Anim Sci 2005; 83:1591-1601. [ Links ]
5. France J, Dhanoa MS, Theodorou MK, Lister SJ, Davies DR, et al. A model to interpret gas accumulation profiles associated with in vitro degradation of ruminant feeds. J Theor Biol 1993; 163:99-111. [ Links ]
6. Gaona LM. Matrices de covarianza estructuradas en modelos con medidas repetidas. Tesis de maestría, Recinto Universitario de Mayagüez, Universidad de Puerto Rico, 2005. 118p. [ Links ]
7. Goering HK, Van Soest PJ. Forage fiber analysis. Agric. Handbook No. 379. Washington: Agricultural Research Service-USDA; 1970. [ Links ]
8. Groot JCJ, Cone JW, Williams BA, Debersaques FMA, Lantinga EA. Multiphasic analysis of gas production kinetics for in vitro fermentation of ruminant feeds. Anim Feed Sci Technol 1996; 64:77-89. [ Links ]
9. Mertens DR, Loften JR. The effect of starch on forage fiber digestion kinetics in vitro. J Dairy Sci 1980; 63:1437- 1446. [ Links ]
10. Motulsky H, Christopoulos A. Fitting models to biological data using linear and nonlinear regression. Versión 4. San Diego CA: GraphPad PRISM®. 2003. URL: http://www.graphpad.com.351p. [ Links ]
11. Neter J, Wasserman W. Applied lineal statistical models. USA: Richard D. Irwin, Inc. 1972. 842p. [ Links ]
12. Noguera RR, Saliba EO, Mauricio RM. Comparación de modelos matemáticos para estimar los parámetros de degradación obtenidos a través de la técnica de producción.de gas. Livestock Res Rural Develop 2004; 16 (11).URL: http://www.cipav.org.co/lrrd/lrrd16/11/nogu16086.htm [ Links ]
13. Posada SL. Valoración de las heces y el líquido ruminal como inóculos en la técnica in vitro de producción de gases. Tesis de maestría, Facultad de Ciencias Agrarias, Universidad de Antioquia, Medellín, 2006. 78p. [ Links ]
14. Schofield P. Gas production methods. Farm animal metabolism and nutrition. Wallingford (UK): CAB International; 2000. 450p. [ Links ]
15. Schofield P, Pitt RE, Pell AN. Kinetics of fiber digestion from in vitro gas production. J Anim Sci 1994; 72: 2980-2991. [ Links ]
16. Statistical analysis systems. SAS®, versión 8.2 para Windows. User´s Guide. Statistics. Statistical Analysis Systems Institute. Inc., Cary, NC. 2001. [ Links ]
17. Theodorou MK, Williams BA, Dhanoa MS, McAllan AB, France J. A simple gas production method using a pressure transducer to determine the fermentation kinetics of ruminant feeds. Anim Feed Sci Technol 1994; 48: 185-197. [ Links ]
18. Tilley JMA, Terry RA. A two stage technique for the in vitro digestion of forage crops. J Br Grass Soc 1963;18:104111. [ Links ]
19. Van Milgen J, Murphy MR, Berger LL. A compartmental model to analyze ruminal digestion. J Dairy Sci 1991; 74:2515-2529. [ Links ]
20. Vargas B, Koops WJ, Herrero M, Van Arendonk JAM. Modeling extended lactations of dairy cows. J Dairy Sci 2000; 83:1371-1380. [ Links ]
21. Williams BA. Cumulative gas-production techniques for forage evaluation. In: Givens DI, Owen E, Omed HM, Axford RFE (eds). Forage Evaluation in Ruminant Nutrition. Wallingford (UK): CAB International; 2000. 475p. [ Links ]
22. Zwietering MH, Jongenburger L, Rombouts FM, Van`t Tiet K. Modelling of the bacterial growth curve. Appl Envirom Microbiol 1990; 56:1875-1881. [ Links ]














