Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Revista Colombiana de Ciencias Pecuarias
Print version ISSN 0120-0690On-line version ISSN 2256-2958
Rev Colom Cienc Pecua vol.20 no.2 Medellín Apr./June 2007
Diagramas de estructura en el análisis de varianza
Diagrams of structure in analysis of variance
Luis F Restrepo B1*, Estad, Esp estad bioma.
1 Grupo de Investigación Grica, Facultad de Ciencias Agrarias, Universidad de Antioquia, AA 1226, Medellín, Colombia.
lusitano@agronica.udea.edu.co
(Recibido: 31 mayo, 2006; aceptado: 26 abril, 2007).
Resumen
Los diagramas de estructura fueron definidos por Warren H Taylor Jr y H. Gill Milton para diseños experimentales balanceados estándar. El método requiere reconocer las características del conjunto de factores que son usados en interacción o anidamiento. El cuadrado medio esperado, el F Ratio y los componentes estimados de varianza pueden derivarse empleando la simbología de los diagramas de estructura. El diagrama de estructura facilita entender el diseño de clasificación experimental y las hipótesis asociadas con dicho modelo, es una representación visual que permite entender las relaciones o interacciones existentes entre los factores seleccionados por el investigador.
Palabras clave: anidado, diagrama de estructura, factor, modelo.
Summary
Diagrams of structure were defined by Taylor Jr and Milton for standard experimental balanced designs. The method requires recognizing the characteristics of the set of factors used in the interaction or nested. The expected main square, the F Ratio and the estimated variance components can be driven by using diagrams of structure symbols. Diagram of structure facilitates understanding the design of experimental classification and hypotheses associated with the above mentioned model, it is a visual representation that allows understanding the relationship or existing interactions between the factors selected by the researcher.
Key words: diagram of structure, factor, model, nested.
* Autor para el envío de la correspondencia y la solicitud de separatas. Facultad de Ciencias Agrarias, Universidad de Antioquia, AA 1226, Medellín, Colombia. E-mail: lusitano@agronica.udea.edu.co
Introducción
Cuando se modela se debe tener presente el tipo de factor (fijo, aleatorio, mixto) y los niveles de cada factor dispuesto; además, que factores se cruzarán y cuales serán anidados. Los diagramas de estructura son bastante útiles cuando se tiene un número considerable de factores. También se tiene que tener presente el correcto modelo lineal.
El diagrama de estructura es una representación visual de la descripción verbal dada por el investigador para definir el modelo lineal (9). En el diagrama no es usual anotar los subíndices del factor, el diagrama da confianza para verificar el modelo y diagramar computacionalmente el proceso con la información generada a partir del diseño elegido, y así poder establecer el estadístico F de prueba idóneo para cada fuente de variación a partir de los componentes de varianza. Cuatro conceptos deben tenerse en cuenta para la aplicación de los diagramas de estructura:
1. Entender la relación entre factores y describir el diseño de efectos que aparecen en el análisis estadístico.
2. Conocer el concepto formal de interacción entre efectos y derivar las interacciones del diagrama de estructura.
3. Entender las reglas de Thumb (24) para calcular los estadísticos.
4. Dar el diseño de efectos relacionados con la variable respuesta.
Comúnmente el diagrama de estructura se conoce como diagrama de Hasse. Es un resultado de conceptos matemáticos referidos a estructura Latice y diseños de estructura experimental, discutidos por Trockmorton (22), Kempthorne (9, 10, 19), Zyskind (11) y Kemthorne en asocio con Folks (10, 19).
La relación de anidamiento y el cruzamiento de factores son fundamentales para explicar el concepto de estructura experimental (1, 2, 3), como es llamado comúnmente el diseño de experimentos. El anidamiento o cruzamiento de factores es indicado por la presencia o ausencia de conectores entre los factores presentes. Si dos factores no se unen por una línea está indicando que se cruzan o interactúan. Y si un factor está conectado por debajo de otros factores se dice que es anidado.
Un factor es cruzado con otro factor si cada nivel de uno de los factores se combina con todos los niveles del otro factor. Existen experimentos en los que interesa que los niveles de un factor combinen con todos los niveles del otro factor, lo que corresponde al concepto de anidamiento (6). Puede darse el caso en que unos factores sean cruzados y otros anidados.
Los siguientes son esquemas representativos de factores cruzados y anidados, donde A, B, C son factores y a, b, c son los niveles para cada factor.
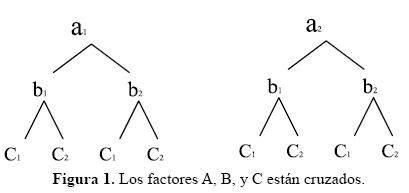
Ahora si los factores son cruzados o anidados depende de la estructura del modelo aditivo lineal del experimento, y a su vez, del modelo lineal depende las fuentes de variación asociadas con el análisis de la varianza. Conocer las fuentes de variación y los cuadrados medios esperados permite hacer un correcto análisis de varianza; además definir el error experimental (23).
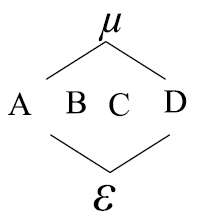
Para ilustrar el diagrama de estructura suponga que se tienen tres factores A, B, C y se desea cruzar dichos factores, entonces el diagrama se define así:
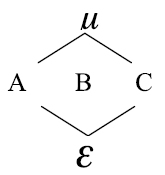
Donde µ, es el efecto promedio; µ anida a todos los demás componentes. A, B, C son los factores de interés. ε: Error experimental, el cual esta anidado en todos los factores o componentes.
El modelo lineal estadístico correspondiente al diagrama de estructura anterior es:
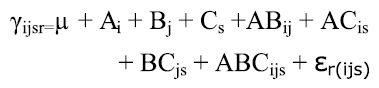
Donde i,j,s,r están asociados con los niveles del factor, por ejemplo si i= 1,2,3 indica que tiene tres niveles el factor A; j son los niveles del factor B; s representa los niveles del factor C, r indica las Cabe anotar que Cindica que el factor C esta replicaciones asociadas al error experimental.
El rango de un factor es igual al número de niveles En el próximo esquema, B está anidado en A y la con los que cuenta el factor en el diseño. El rango del interacción AC está cruzada al igual que la interacción factor puede ser indicado en el diagrama por un número BC. entre paréntesis adjunto al factor (7). El diagrama puede tener efectos fijos y aleatorios, el factor fijo en un diagrama estructura se representa con la letra del factor colocándole debajo del símbolo
El modelo es:
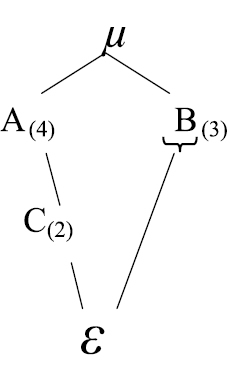
Para el siguiente diagrama el modelo es:
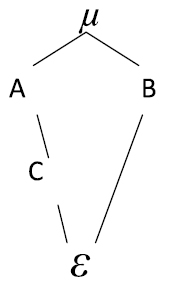
A es aleatorio, B factor fijo, C aleatorio al igual que ε, µ se puede omitir si se desea. En el diagrama anterior, A tiene 4 niveles, B tres, C dos. El rango de los factores es A = 4, B = 3, C = 2.
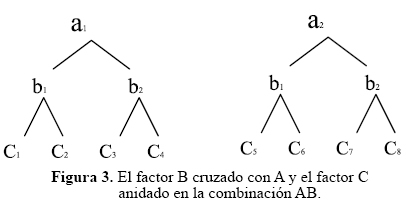
En el siguiente diagrama, A está cruzado con B, C está cruzado con B y anidado en A:
El modelo lineal es:
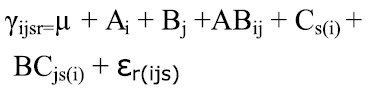
Cabe anotar que Cs(i) indica que el factor C esta anidado en A.
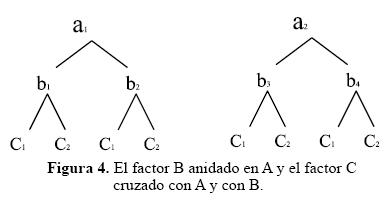
En el próximo esquema, B está anidado en A y la interacción AC está cruzada al igual que la interacción BC.
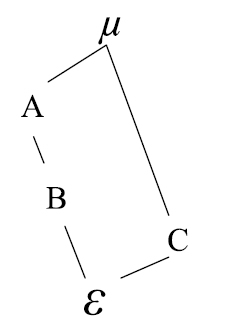
El modelo es:
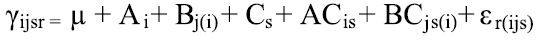
Para el siguiente diagrama el modelo es:
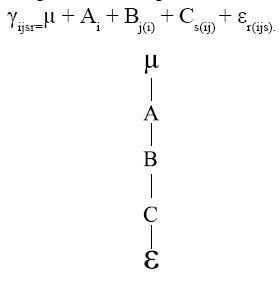
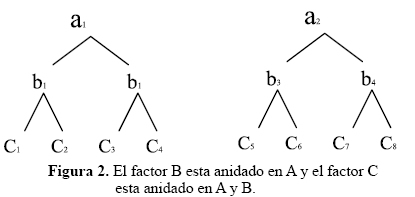
Como puede observarse, el factor B está anidado El modelo es: en A y el factor C está anidado en A y B. En el diagrama que se muestra a continuación, los factores están cruzados:
y el modelo correspondiente es:
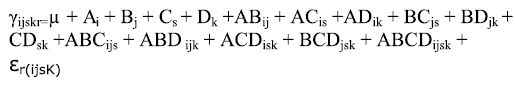
En el próximo diagrama, se tienen las siguientes consideraciones:
Los factores A, B, C están cruzados:
D esta anidado en A y cruzado con E, F, B, C y G.
E esta anidado en A y cruzado con D, F, B y C.
F anidado en A, y en B, y cruzado con D, E y C.
G anidado en A, E, F, B y cruzado con D y C.
ε anidado en todos los factores
μ anida a todos los factores.
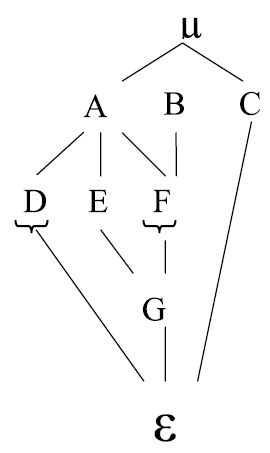
El modelo es:
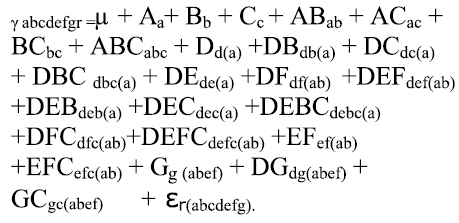
D y F son factores fijos y los demás son aleatorios.
El conjunto de todos los factores en un diseño experimental se llama conjunto diseño (5, 12, 19). Cada efecto en un modelo del conjunto diseño puede ser dividido en una función más pequeña de grupos, llamada conjunto de factores. El principio básico para entender el concepto del conjunto de factores es conocer los efectos del modelo, únicamente se parte el conjunto diseño en conjuntos disjuntos que se requieren para elaborar el proceso computacional del análisis de la varianza.
Se usa la terminología de factores vivos, muertos y ausentes para obtener los resultados estadísticos asociados con la esperanza del cuadrado medio. Los factores que aparecen en el nombre del correspondiente efecto para los subíndices sin paréntesis son llamados factores vivos. Los factores que anidan otros factores, es decir los que señalan los subíndices dentro del paréntesis, son denominados factores inertes o muertos. Los factores restantes que no aparecen nombrados como un factor, ni anidan factor alguno, se llaman ausentes. Esta clasificación parte el conjunto diseño en tres conjuntos disjuntos de factores.
Reglas para establecer el modelo aditivo lineal
1. El primer término del modelo es siempre el parámetro poblacional µ que es el efecto promedio del experimento (4).
2. Cada factor del experimento está representado en el modelo por su efecto respectivo. Por ejemplo A por α, B por β, C por γ.
3. Entre dos o más factores cruzados hay interacción y el efecto debe estar representado en el modelo (16).
4. En un factor anidado que antecede a otro cruzado, existe interacción y por ende su efecto está representado en el modelo.
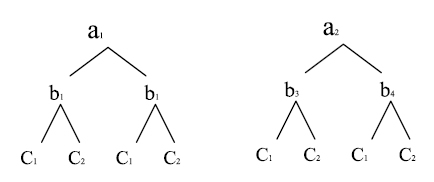
B esta anidado en A y C esta cruzado con B.
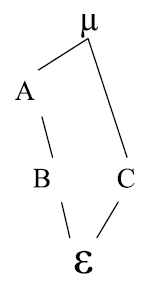
5. Entre un factor cruzado que antecede a uno anidado, no hay interacción (2, 12) y por lo tanto no aparecerá en el modelo ejemplo:
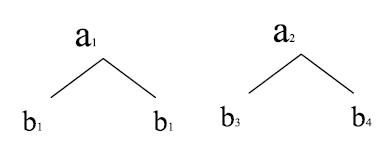
En el esquema anterior no hay interacción.
6. Entre dos o más factores anidados no hay interacción.
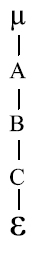
En este modelo no hay interacción entre ningún factor.
7. Un modelo tendrá una variable respuesta o dependiente denotada como Y (15).
8. El termino βj(i) i indica en un modelo que el factor B esta anidado en el factor A.
Grados de libertad
Corresponden a una cantidad que permite introducir una corrección matemática en los cálculos estadísticos para restricciones impuestas en los datos (18). Por grados de libertad se entiende el número efectivo de observaciones que contribuyen a la suma de cuadrados asociada al análisis de varianza menos el número de datos que son combinación lineal de otros.
Los grados de libertad para cualquier efecto, se puede obtener a partir del diagrama de estructura por la distinción entre factores vivos e inertes asociados a la fuente de variación de interés. Los grados de libertad permiten calcular el cuadrado medio asociado a cada factor o interacción de factores.
Forma de determinar los grados de libertad para las fuentes de variación en al análisis de varianza
1. Los grados de libertad asociados a la fuente de variación total son iguales al producto de los niveles de todos los factores menos uno.
2. Los grados de libertad de la interacción entre dos o más factores cruzados son iguales al producto de sus respectivos grados de libertad, anotando que para un factor en particular es el número de niveles menos uno (13).
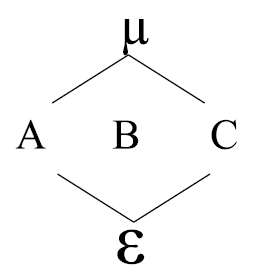
Para la interacción ABC los grados de libertad son (a – 1), (b – 1), (c – 1) donde a,b,c representan los niveles de cada uno de los factores A, B y C.
3. Los grados de libertad de un factor anidado en un factor cruzado, son iguales al producto de los grados de libertad del factor anidado por el número de niveles del factor cruzado (8, 15).
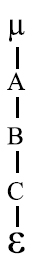
Los grados de libertad para la fuente de variación B(A) son (b – 1)a.
En el siguiente diagrama, los grados de libertad para el factor Cs(ij) son: (c – 1) ab.
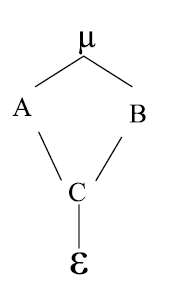
4. Si un factor está anidado en otro factor pero a la vez interacciona con un tercer factor. Los grados de libertad para la interacción son iguales a los grados de libertad del factor anidado multiplicado por el número de niveles del factor en que se anida y por los grados de libertad del factor con el que se cruza.
Acá los grados de libertad para la fuente de variación BC(A) son: (b – 1) a(c – 1)
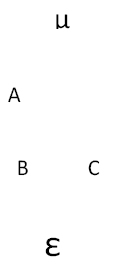
5. Los grados de libertad para repeticiones son componente que siempre está anidado en las combinaciones de todos los demás factores; por lo anterior, los grados de libertad son (r - 1) por el número de niveles de los demás factores (20, 21).
6. Los grados de libertad para factores principales son simplemente el número de niveles que tenga el factor menos uno (14).
7. Los grados de libertad del error experimental se pueden hallar a partir de la diferencia de los grados de libertad de la fuente de variación total menos las demás fuentes de variación presentes en el modelo de clasificación experimental (17).

Los grados de libertad de cualquier término del modelo corresponden al producto del número de niveles asociados con cada subíndice pasivo y el número de niveles menos uno, asociados con cada subíndice activo (1).
Referencias
1. Calzada J. Métodos estadísticos para la investigación. Diversidad de la Molina. Lima.1970. 643p. [ Links ]
2. Cochran WG. Cox GM. Experimental designs. 2ed. John Wiley, New York, 1957. 611p. [ Links ]
3. Cochran WG, Cox GM. Diseños experimentales. Trillas. México.1981. 611p. [ Links ]
4. Conover WJ. Practical nonparametric statistics. 2ed. John Wiley, New York, 1980. 578p. [ Links ]
5. Cordeiro GM. Modelos lineares generalizados. Unicamp, Campinas.1986. 286p. [ Links ]
6. Dobson F. An introduction to linear models, Chadpman- Hall. Second edition New York.1991. 221p. [ Links ]
7. Federer WT. Experimental design. New York, the MaCmillan Company. 1953. 554p. [ Links ]
8. Gaylor DW, Hopper FN. Estimating the degress of freedom for linear combination of mean squares by satherthwaite´s formula, Technometrics 1969; 4:691-706. [ Links ]
9. Hinkelman K, Kempthorne O. Design and analysis of experiments. Vol 1, John Wiley, 1994.512p. [ Links ]
10. Kempthorne O, Folks L. Probability statistics and data analysis. Ames, Iowa. Iowa State University Press. 1961. 551p. [ Links ]
11. Kempthorne O, Zyskind G. Analysis of variance procedures. Aeron Res Lab Techn Repo 1961. 149 p. [ Links ]
12. Lemma AF. Hipoteses estatisticas com amostras desequilibradas, Fac Sci Agrom Gembloux, Bélgica. 1991. 64p. [ Links ]
13. Little TM, Hills FJ. Métodos estadísticos aplicados en agricultura, editorial Trillas México, 1976. 270p. [ Links ]
14. Martínez GA. Diseños experimentales Colegio de Postgrado de Chapingo. México D F. 1983. 1058p. [ Links ]
15. Mccullag P, Nelder J. Generalized linear models. Prentice Hall, London, 1989. 511p. [ Links ]
16. Montgomery DC. Design and analysis of experiments. New York, John Wiley, 1981. 418p. [ Links ]
17. Moore PG, Tukey JW. Answer to query No. 112. Biometrics.1954; 10:562-568. [ Links ]
18. Ostle B. Estadística aplicada. Limusa-Wiley S.A. México DF. 1973. 629p. [ Links ]
19. Schlesselman J. Power families: a note on the Box and Cox transformation. J Royal Stat Soc 1971; 33:307-311. [ Links ]
20. Senedecor GW. Métodos estadísticos aplicados a la investigación agrícola y biológica. México; Continental S.A. 1970. 503p. [ Links ]
21. Sokal R, Rohlf J. Introducción a la bioestadística: Reverte S.A. New York. 1980.363p. [ Links ]
22. Throckmorton TN. Structures of classification data, unpublished PhD, dissertation. Iowa State University. Dept Statistical.1961; 32:927-950. [ Links ]
23. Torrie JH. Bioestadística. Principios y procedimientos. México: McGraw-Hill. 1981. 666p. [ Links ]
24. Warren H, Taylor Jr. H, Gill H. A structure diagram symbolization for analysis of variance.1981; 35:85-93. [ Links ]














