Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Revista Colombiana de Ciencias Pecuarias
Print version ISSN 0120-0690On-line version ISSN 2256-2958
Rev Colom Cienc Pecua vol.25 no.2 Medellín Apr./June 2012
REVISIONES DE LITERATURA
Cattle genetic evaluation: a historical perception¤
La evaluación genética de vacunos: una percepción histórica
A avaliação genética de bovinos: uma percepçã
Carlos A Martínez Niño1*, Zoot, MSc; Carlos Manrique Perdomo1, Zoot, MSc, PhD; Mauricio A Elzo2, MV, PhD.
* Autor para correspondencia: Carlos A Martínez Niño. Departamento de Producción Animal, Universidad Nacional de Colombia. Carrera 30 # 45–03, Bogotá, Colombia. Teléfono 3165000 ext. 19409. Correo electrónico: camartinezn@unal.edu.co
1 Grupo de Estudio en Mejoramiento y Modelación Animal GEMA, Departamento de producción animal, Universidad Nacional de Colombia, Bogotá, Colombia.
2 Department of Animal Sciences, University of Florida, Gainesville, FL 32611–0910, USA.
(Recibido: 13 junio, 2011; aceptado: 20 febrero, 2012)
Summary
Mixed model methodology has been the main statistical tool for unbiased genetic animal evaluation and selection of domestic animals, such as bovines, for over thirty years. Since the use of linear mixed models to obtain the best linear unbiased prediction of the breeding value of the individuals in a population was proposed, there have been scientific advances at the statistical and computational level that have led to implement more complex models describing different biological situations and data structures. This work briefly reviews the history of genetic evaluation in cattle emphasizing on the mixed model methodology in which these evaluations are based. The following topics are discussed in this paper: The unibreed animal model, the derivation of the mixed model equations, some extensions of the unibreed animal model (additive direct and maternal effects, random environmental effects, multiple traits model), the mutibreed animal model, models for the genetic evaluation of longitudinal data and, finally, a brief description of genomic evaluation.
Key words: cattle, genetic predictions, mixed models.
Resumen
La metodología de modelos mixtos ha sido la principal herramienta estadística para la evaluación y la selección de animales domésticos tales como el vacuno durante más de 30 años. Desde que se propuso el uso de modelos lineales mixtos para obtener los mejores predictores lineales insesgados de los valores genéticos de los individuos en una población se han dado avances científicos a nivel estadístico y computacional que han permitido implementar modelos más complejos, los cuales describen diferentes situaciones biológicas y estructuras de datos. En el presente trabajo se hace una breve revisión de la historia de las evaluaciones genéticas en vacunos haciendo énfasis en la metodología de modelos mixtos en la cual se han basado dichas evaluaciones. Los siguientes tópicos son descritos en este documento: El modelo animal unirracial, la derivación de las ecuaciones de modelos mixtos, algunas extensiones del modelo animal unirracial (efectos aditivos directos y maternos, efectos ambientales aleatorios, modelo para múltiples caracteres), el modelo animal multirracial, modelos para la evaluación genética de datos longitudinales y finalmente una breve descripción de la evaluación genómica.
Palabras clave: bovinos, modelos mixtos, predicciones genéticas.
Resumo
A metodologia dos modelos mistos tem sido a principal ferramenta estatística para a avaliação e seleção de animais domésticos, como ocorreu em bovinos há mais de trinta anos. Desde sua proposta, o uso de modelos lineares mistos, para obter os melhores preditores lineares imparciais dos valores genéticos de indivíduos de uma população, têm sofrendo avanços científicos a nível estatístico e computacional, tornando–se possível implementar modelos mais complexos que descrevem diferentes situações biológicas e estruturas de dados. No presente trabalho, é feita uma breve revisão histórica sobre as avaliações genéticas em bovinos, com ênfase na metodologia de modelos mistos, na qual estas avaliações são baseadas. Os seguintes tópicos são descritos neste documento: o modelo animal unirracial, a derivação das equações de modelos mistos, algumas extensões do modelo animal unirracial (efeitos aditivos direto e materno, efeitos aleatórios ambientais, modelos multicaracterísticas), o modelo animal multirracial, modelos para a avaliação genética de dados longitudinais e, finalmente, uma breve descrição da avaliação genômica.
Palavras chave: bovinos, predições genéticas, modelos mistos.
Introducción
La evaluación genética es un proceso que permite obtener el valor genético de los animales para una o más características y así seleccionar como reproductores aquellos con mayor mérito genético (Ruales et al., 2007). Un gran avance se dio con el desarrollo teórico e implementación de la metodología estadística de modelos lineales mixtos aplicada a la genética cuantitativa por parte de Henderson, que permitió separar los efectos genéticos de los no genéticos (Manrique, 1995; Garrick y Golden, 2009). La metodología de modelos mixtos permite obtener el BLUP (Best Linear Unbiased Prediction) o MPLI (Mejor Predicción Lineal Insesgada) del valor genético de los animales evaluados en función de sus propios registros y registros de sus parientes (Kennedy et al., 1988). Las ecuaciones de modelos mixtos permiten el cómputo simultáneo de los mejores estimadores lineales insesgados de los efectos fijos y de los mejores predictores lineales insesgados de valores genéticos.
Durante los últimos 30 años el adelanto en metodologías estadísticas, de computación, métodos numéricos y genética cuantitativa ha sido vertiginoso (Elzo y Cerón–Muñoz, 2009; Golden et al., 2009), este hecho ha permitido un rápido avance en el desarrollo e implementación de modelos estadísticos para la evaluación genética de animales (Bullock y Pollak, 2009). Según Kennedy et al. (1988) en ciencias animales el objetivo es ajustar un modelo práctico que describa la situación biológica lo más cerca posible a la realidad. En el caso de la genética cuantitativa se emplean modelos para la predicción de los valores genéticos, la estimación de la respuesta a la selección y la estimación de parámetros genéticos. Evaluaciones genéticas de alta exactitud mejoran la capacidad de los productores para tomar decisiones de selección acertadas (Bullock y Pollak, 2009; Golden et al., 2009).En el presente trabajo se realizó una breve revisión de la historia de las evaluaciones genéticas haciendo énfasis en la metodología de modelos mixtos en la cual se han basado dichas evaluaciones.
Algo de historia
Los trabajos de Juan Gregorio Mendel mediante los cuales se definieron los mecanismos de la herencia fueron publicados en 1865 (Ossa, 2003), este hecho marca el inicio del estudio de la genética. Posteriormente el matemático inglés Goldfrey Harold Hardy y el médico alemán Wilhelm Weinberg establecieron en 1908 la ley de Hardy– Weinberg (Ruales et al., 2007), Sir Ronald Fischer y Sewall Wright desarrollaron la genética de poblaciones con base a las leyes de Mendel aplicada a caracteres económicos y cuantitativos. Un aporte de gran relevancia fue el realizado por Lush, quien en los años 40 creó las teorías de selección (Galeano, 2004), además trabajó de manera notable en el establecimiento de metodologías para calcular los parámetros genéticos y estableció la importancia del cálculo de los mismos en los programas de mejoramiento animal (Lush, 1940).
En sus trabajos Lush comenzó a direccionar y estructurar los programas de mejora genética, discutió aspectos importantes como la interacción genética–medio ambiente, destacó la importancia de la estadística en la genética cuantitativa y trabajó en la implementación de los índices de selección como herramienta para la identificación genética de los reproductores potenciales (Lush, 1951); fueron Lush y Michael Lerner los pioneros en la aplicación de los principios de la genética cuantitativa en mejoramiento animal (Ossa, 2003).
Con los índices de selección, se obtienen los mejores predictores lineales del valor genético de los individuos (Henderson, 1973). Sin embargo, esta metodología enfrenta dos problemas principales (Henderson, 1973; Elzo, 1996a; Mrode, 2005): En primer lugar los registros deben ser pre–ajustados por los efectos fijos, los cuales se asumen conocidos, pero usualmente no lo son, especialmente cuando no existe información previa para nuevas subclases de efectos fijos. Esto debido a que con el mejor predictor lineal las medias y varianzas de las variables aleatorias involucradas deben ser conocidas con certeza. En segundo lugar, se requiere de la inversa de la matriz de covarianzas de los datos, cuyo computo puede ser no factible en grandes conjuntos de datos.
En 1973 Henderson publicó una completa base teórica en la cual exponía la implementación de modelos estadísticos en la evaluación genética de animales (Henderson, 1973; Manrique, 1995), además contribuyó con el desarrollo de estrategias computacionales para que dichos modelos se implementaran en grandes conjuntos de datos (Elzo, 2006), como es el caso de las evaluaciones genéticas realizadas en la actualidad. Entre tales estrategias se destaca la creación de un conocido algoritmo para invertir la matriz de parentesco (Henderson, 1976). Estos procedimientos fueron inicialmente aplicados a poblaciones de ganado lechero. Aplicaciones a poblaciones de ganado de carne tuvieron que esperar el desarrollo de modelos que consideraran efectos propios de los animales (efectos directos) e influencia materna (efectos maternos), los cuales fueron desarrollados por Quaas y Pollak (Quaas y Pollak, 1980; Pollak y Quaas, 1981).
Según Golden et al. (2009), un problema que se tuvo desde 1972 hasta 1995 fueron las limitaciones en el desempeño de los computadores. Ya se tenían desarrollos teóricos para el cálculo de los valores genéticos, y la continua toma de datos estaba haciendo que las bases de datos aumentaran su tamaño a un ritmo acelerado lo cual implicaba requerimientos computacionales considerables para la época. De esta manera, se realizaron desarrollos que buscaban reducir el número de ecuaciones a resolverse. Entre estos se pueden destacar la inclusión del abuelo materno en lugar de la madre del animal para caracteres con efectos maternos y el desarrollo del modelo animal reducido por parte de Quaas y Pollak (Quaas y Pollak, 1980).
En el modelo animal reducido las ecuaciones se escriben en términos de los padres del animal, lo cual reduce los cómputos y la ventaja es que este modelo es equivalente al modelo animal, lo cual implica que las predicciones de los valores genéticos serán las mismas. Una vez se obtienen las soluciones para los padres, estas se emplean para el computo de las predicciones de los animales “nopadres ” (Henderson, 1988). Con el advenimiento de computadores con mayor capacidad, se pudieron implementar a gran escala, los modelos multivariados o de múltiples caracteres. En estos modelos se calculan de manera simultánea los valores genéticos de dos o más caracteres haciendo uso de las correlaciones genéticas y residuales existentes entre los mismos, lo cual aumenta la exactitud de las predicciones.
Debido al interés en la comparación directa de valores genéticos de animales de diferentes razas o composiciones raciales y a la necesidad de obtener predicciones de valores genéticos en términos aditivos y no aditivos en poblaciones multirraciales, otro hecho importante fue el desarrollo de métodos estadísticos que permitieron resolver tal problema. En 1983 Elzo desarrolló una metodología para evaluar animales en poblaciones multirraciales dentro de un país y entre países (Elzo, 1983; Elzo y Famula, 1985; Elzo y Bradford, 1985), sus desarrollos permitieron la evaluación genética de animales en poblaciones multirraciales (Ossa, 2003).
Según Bullock y Pollak (2009), desde finales de la década de 1980, se han dado grandes avances en biología molecular, en principio se pensó que las predicciones del mérito genético con base en evaluación molecular reemplazarían las metodologías clásicas de evaluación genética, sin embargo ahora se sabe que se deben integrar. Fernando y Grossman (1989) expusieron una metodología para incorporar información proveniente de un marcador molecular en los modelos de evaluación genética, buscando incrementar la exactitud de las predicciones. A esta forma de evaluación genética se le llamo Selección Asistida por Marcadores Moleculares, MAS por sus siglas en ingles. Sin embargo, gracias al desarrollo en técnicas de biología molecular que permitió la obtención mapas densos de SNP (Single Nucleotide Polymorphism) distribuidos en todo el genoma, en un influyente artículo Meuwissen et al. (2001) propusieron el uso de la información de miles de marcadores (SNP) para el cómputo de valores genéticos de los animales. A esta forma de evaluación genética se le denominó selección genómica o selección a lo largo del genoma.
Los avances en la metodología de evaluación genética y su aplicación han cambiado dramáticamente la población de ganado de carne en países como los Estados Unidos. La evolución de este procedimiento ha llevado la toma de las decisiones de selección con base en observaciones fenotípicas de los individuos a la predicción genética de dichos individuos basada en el análisis de millones de registros de fuentes nacionales e internacionales a través de múltiples razas (Bullock y Pollak, 2009).
El modelo animal
El modelo animal es simplemente un modelo mixto donde el efecto aleatorio se refiere al animal que tiene registros (Elzo, 1996a). Sin embargo, como se discutirá más adelante, se pueden incluir efectos aleatorios adicionales. El desarrollo de este modelo permitió una predicción de los valores genéticos mucho más ajustada a las situaciones reales que los índices de selección, pues con estos se obtenía el mejor estimador lineal insesgado, el cual se puede obtener si se conoce la media real de los efectos fijos, hecho que en la práctica rara vez se tiene, pues estos se estiman a partir de los datos (Mrode, 2005).Existen diferentes tipos de modelos animales según la situación biológica y estructura de los datos (Kennedy et al., 1988). Por lo tanto, se puede ver al modelo animal como una familia de diferentes modelos estadísticos utilizados para la predicción del mérito genético de los animales en una población, estimación del progreso genético y de componentes de varianza que varían según la estructura de los datos y de los efectos genéticos considerados. Los denominados modelos animales aproximados corresponden a aquellos en los cuales se consideran ancestros del animal con registros (Elzo, 1996a), tales como el padre (modelo de padre o de toro), padre y madre (modelo de padre y madre), y padre y abuelo materno (modelo de padre y abuelo materno).
El modelo animal unirracial para efectos aditivos directos
Cuando se consideran animales de una misma raza en el proceso de evaluación genética se tiene un modelo animal unirracial, en el cual se consideran generalmente solo efectos genéticos aditivos (que pueden ser directos o maternos). De acuerdo con Henderson (1988) un modelo animal unicarácter de efectos aditivos directos en notación matricial se describe como sigue:
y = Xβ + Zu + e
En donde:
y es el vector aleatorio que contiene las observaciones, β es un vector desconocido de efectos fijos, u es un vector aleatorio y desconocido de efectos genéticos aditivos directos de los animales, e es un vector de efectos residuales aleatorios, X y Z son matrices de incidencia conocidas que relacionan el vector de observaciones con los vectores β y u respectivamente.
Si todos los individuos tienen un solo registro, entonces Z es una matriz de identidad de orden n, siendo n el número de individuos evaluados. Si algunos animales en el pedigrí no tienen registros, la matriz Z es de orden m × n, m<n, con n – m filas correspondientes a animales sin registros eliminadas.
Si se asumen las siguientes condiciones: genes no ligados, un número muy grande de genes controlando la característica y efecto muy pequeño de cada gen; los supuestos de distribución son:
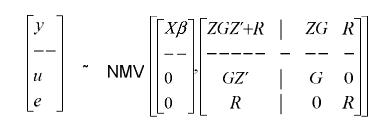
La matriz G = Aσa2, donde A es la matriz de parentesco entre los individuos evaluados y σa2es el componente de varianza genética aditiva, y la matriz R = Iσe2, donde I = matriz identidad, y σe2 es el componente de varianza residual.
Según Henderson (1988), los mejores predictores lineales insesgados del valor genético maximizan el valor esperado de los individuos seleccionados.
Ecuaciones de modelos mixtos (EMM) de Henderson
El procedimiento descrito por Henderson se produjo en un hallazgo que hizo mientras buscaba un procedimiento más viable para encontrar estimadores de β (Elzo, 1996a). Henderson encontró que al resolver el set de ecuaciones resultantes de maximizar la función de densidad conjunta de los registros (y) y de los efectos genéticos (u), i.e., f(y,u) escrita como f(y|u)f(u), él podía obtener estimadores de máxima verosimilitud (EMV) de β (β0=(X'V–1X)–X'V–1y). En lugar de condicionar sobre β y u, Henderson condicionó solamente sobre u (Elzo, 1996a), y maximizó:
f(y|u) = f(y|u)f(u)
La derivación de las ecuaciones de modelos mixtos de Henderson abajo sigue de cerca la derivación presentada por Elzo (1996a).
Por la distribución normal conjunta de los vectores aleatorios y y u se tiene:
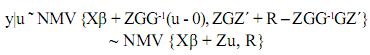
Además u~NMV {0,G}
Denotemos por L la siguiente función:
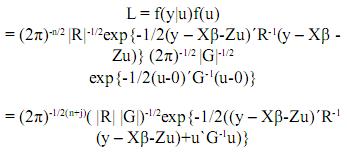
Esta es una función de los parámetros y tiene la propiedad de que sus valores máximos están ubicados en los mismos lugares que los máximos de su logaritmo natural(denotado como log(L)). Por lo tanto, maximizar log(L) es equivalente a maximizar L. La ventaja es que resulta más sencillo optimizar log(L). Entonces:
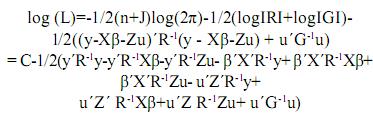
Agrupando términos comunes se tiene:
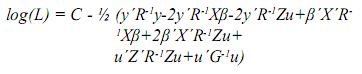
C = –1/2(n+J)log(2π)–1/2(log|R|+log|G|), esto es, las constantes de la función log(L).
Ahora empleando la diferenciación matricial se deriva la función respecto a los parámetros y se iguala a cero para encontrar los valores de β y u que la maximizan.
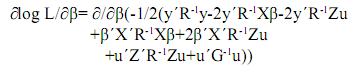
Por la linealidad de la derivada se tiene:
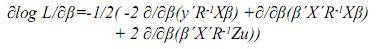
Empleando las reglas de diferenciación matricial:
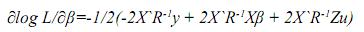
Igualando este término a cero, se tiene:
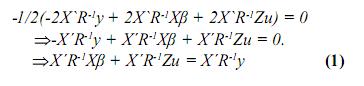
Ahora, derivando el logaritmo de L respecto a u se obtiene:
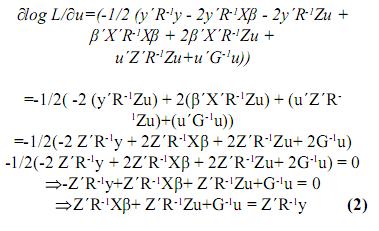
De 1 y 2 se tiene un sistema de ecuaciones matriciales, en las cuales β y u son los vectores por hallar, entonces este sistema se puede llevar a la siguiente forma:
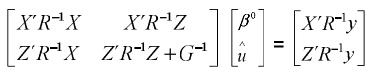
Estas son las ecuaciones de modelos mixtos de Henderson, o simplemente las ecuaciones de modelos mixtos, las cuales se deben solucionar para obtener los mejores predictores lineales insesgados (MPLI) de los valores genéticos, esto es, û =MPLI(u) = GZ'V–1(y–Xβ0) y simultáneamente estimadores de mínimos cuadrados generalizados de β, β0=(X'V–1X)–X'V–1y, de aquí y por el teorema de Gauss–Markov se tiene que el BLUE de K'β, dado que K'β es estimable es K'β0 (Searle, 1971). Teniendo en cuenta los anteriores resultados el MPLI de w = K‘β + L‘g (notado como 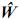 ) es:
) es:
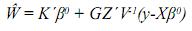
El sistema matricial representado en las EMM es de la forma: Cx=b; nótese que si la matriz X no es de rango columna completo, la matriz C tampoco lo será. El sistema será consistente si y solo si:CC–b=b En donde C– corresponde a una inversa generalizada de la matriz de coeficientes del sistema C. De aquí una solución particular del sistema es: xo = C–b.
Que para las ecuaciones de modelos mixtos es:
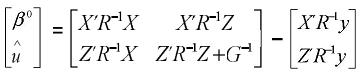
Este procedimiento es posible si el número de ecuaciones es pequeño, y por ende se puede calcular la inversa generalizada. Si por el contrario el número de ecuaciones es grande, el sistema debe resolverse por métodos iterativos, como por ejemplo el de Gauss–Seidel o el de Jacobi (Golub y Van Loan, 1996). Se puede demostrar que la suma del producto de G–1 por el vector û es igual a cero. Si el modelo tiene grupos genéticos, el producto de la matriz de grupos genéticos (e.g., Q) multiplicada por G–1û es cero, i.e., Q' G–1û = 0, lo cual indica que la suma de las predicciones genéticas dentro de grupos genéticos son cero. Estas igualdades se pueden utilizar para comprobar si los programas de computación utilizados produjeron estimaciones de efectos fijos y predicciones de efectos aleatorios correctas.
Modelo animal para caracteres múltiples
En este modelo se obtienen de manera simultánea BLUP de valores genéticos y BLUE de funciones de los efectos fijos para diferentes características teniendo en cuenta las correlaciones genéticas y residuales entre estas. Esto resulta en un aumento en la exactitud de las predicciones (Henderson, 1984; Henderson, 1988). Por lo tanto en estos modelos se emplean las matrices de covarianzas (genéticas y residuales) entre los rasgos evaluados. Un problema asociado a estos modelos es que requieren muchos recursos computacionales, además si el número de caracteres es muy grande se presentan problemas de sobreparametrización (Elzo, 1996b; Meyer y Hill, 1997). Para dos variables dependientes el modelo de múltiples características en forma matricial se representa así:
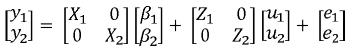
En donde:
yi ,i=1,2 corresponde al vector de observaciones para la i–ésima característica βi, ui y ei, i = 1,2, son respectivamente los vectores de efectos fijos, valores genéticos y residuales para a la i–ésima característica, Xi y Zi, i = 1,2 son las matrices de incidencia para efectos fijos y valores genéticos de la i–ésima característica. Sean G0 y R0las matrices de covarianza genética aditiva y residual entre las características evaluadas, en este caso, serán matrices de orden 2x2 de la siguiente forma:
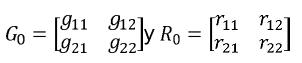
La entrada ij, i≠j de G0y R0 son respectivamente, las covarianzas genética aditiva y residual entre los caracteres i y j, mientras que los elementos diagonales corresponden a las varianzas genética aditiva y residual de cada carácter.
Se asume:
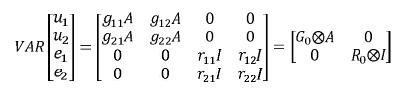
Donde 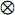 representa el producto directo o producto Kronecker e I es la matriz idéntica.
representa el producto directo o producto Kronecker e I es la matriz idéntica.
Cuando el único efecto aleatorio es el animal y las matrices de diseño (X y Z) son iguales para todas las características estudiadas, es decir, todos los efectos fijos afectan las características y todos los animales tienen registros en cada una de las mismas, es posible reducir un modelo para n características a n análisis univariados (Mrode, 2005). Esto se logra si la matriz de covarianza de efectos genéticos aditivos es semi–definida positiva y la matriz de covarianzas de los residuales es definida positiva, a través un procedimiento denominado transformación canónica, en el cual, mediante el uso de una matriz especial se transforman las observaciones en nuevas variables no correlacionadas y cuya varianza residual es uno, se dice entonces, que estas variables están en escala canónica (Meyer y Hill, 1997). Estas variables se analizan mediante técnicas univariadas convencionales y una vez se obtienen los BLUP de u y BLUE de β, estos se llevan a la escala original de los registros mediante la inversa de la matriz de transformación. Este procedimiento reduce los costos computacionales y genera predicciones idénticas a las obtenidas con el modelo de múltiples características. Cuando se cumplen las condiciones antes mencionadas, pero algunos animales tienen registros perdidos, existe un método presentado por Ducrocq y Besbes (1993), para aplicar la transformación canónica.
Modelo animal con efectos ambientales aleatorios
En ciertas ocasiones, por ejemplo cuando se tienen datos medidos a través del tiempo (caso que se discute más adelante) o cuando la naturaleza de un efecto ambiental es aleatoria dichos efectos se deben considerar como tal en el modelo (Mrode, 2005). En tal caso, dichos efectos se adicionan al modelo como efectos aleatorios no correlacionados con los efectos genéticos. Así, se tienen uno o más componentes de varianza por estimar. Para el caso de un efecto aleatorio ambiental el modelo correspondiente es:
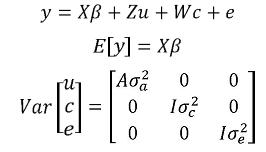
Aquí, el vector c contiene los efectos aleatorios ambientales, y la matriz w es la matriz de incidencia que relaciona los elementos contenidos en c a los registros, 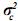 es el componente de varianza del efecto ambiental y los demás elementos del modelo se definen como se hizo en el modelo animal de efectos aditivos. Como se observa en la estructura de varianzas del modelo, no existe covarianza y por lo tanto no existe correlación entre el efecto genético aditivo y el efecto ambiental aleatorio.
es el componente de varianza del efecto ambiental y los demás elementos del modelo se definen como se hizo en el modelo animal de efectos aditivos. Como se observa en la estructura de varianzas del modelo, no existe covarianza y por lo tanto no existe correlación entre el efecto genético aditivo y el efecto ambiental aleatorio.
Modelo animal con efectos maternos
Como se discutió previamente, la situación biológica y la estructura de los datos definen el tipo de modelo a emplear. En esta sección se discute el caso en el cual se contemplan efectos aleatorios correlacionados (efectos maternos).
En ganado de carne, se tiene la particularidad de que muchos caracteres están influenciados por efectos maternos. Esto es, existe un efecto debido a la madre del animal y de esta manera el desempeño del mismo depende de los denominados efectos genéticos directos y del ambiente proveído por la madre (Willham, 1963; Quaas y Pollak, 1980; Elzo, 1996a; Mrode, 2005) el cual debe tenerse en cuenta en el modelo empleado, ya que de lo contrario, los valores genéticos de los animales se verán alterados. Ejemplos de este tipo de caracteres son los caracteres de crecimiento medidos antes del destete.
Una formulación matricial para el modelo animal con efectos maternos sería:
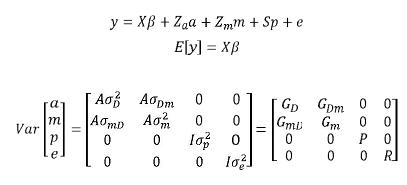
En donde: a = Vector aleatorio desconocido con los efectos genéticos aditivos directos de cada animal, m = Vector aleatorio desconocido de efectos genéticos aditivos maternos, p = vector aleatorio desconocido con efectos de ambiente permanente de la madre (factores como producción de leche, efectos no aditivos de la madre, etc.), σ2D = varianza aditiva para efectos directos, σ2m = varianza aditiva para efectos maternos, 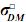 = covarianza entre efectos aditivos directos y efectos aditivos maternos,
= covarianza entre efectos aditivos directos y efectos aditivos maternos, 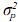 = varianza de efectos de ambiente permanente materno, los demás componentes se definen de igual forma que en el modelo animal de efectos aditivos directos.
= varianza de efectos de ambiente permanente materno, los demás componentes se definen de igual forma que en el modelo animal de efectos aditivos directos.
Se debe considerar que los efectos maternos son genéticos para la hembra y ambientales para su progenie (Elzo 1996a).Estos modelos pueden extenderse a casos más complejos, como por ejemplo modelos con efectos maternos que consideren múltiples caracteres y/o aquellos que consideren efectos de ambiente permanente tanto del animal como de la madre (Henderson, 1988; Elzo, 1996a)
Modelo animal unirracial para efectos aditivos y no aditivos
Desde el comienzo de la implementación de modelos lineales mixtos en la evaluación genética de animales, se estudiaron modelos genéticos que iban más allá de los efectos aditivos (directos o maternos). Al igual que para el caso de efectos aditivos Henderson expuso la teoría acerca de cómo obtener los BLUP para efectos no aditivos y diferentes estimadores de componentes de varianza no aditivos (Henderson, 1985a; Henderson 1985b; Henderson, 1988).
Las primeras aproximaciones, asumieron poblaciones no consanguíneas y se modelaron interacciones entre los diferentes tipos de efectos, por ejemplo aditivo*aditivo, aditivo*dominancia, aditivo*aditivo*dominancia, etc. (Henderson 1984; Henderson 1985; Mrode, 2005). Cuando se consideran efectos de dominancia en estos métodos se emplea la matriz de dominancia D, la cual se usa de manera análoga en a la matriz A en las ecuaciones de modelo mixto para efectos no aditivos. Esta matriz puede ser calculada a partir de los elementos de la matriz A. Los elementos dii son todos iguales a 1, mientras que si el individuo f tiene padres h e i y el individuo g tiene padres j y k se tiene: dfg=(1/4)(ahj aik +ahk aij),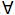 f≠g (Henderson 1984; Mrode, 2005). Por lo tanto en un modelo para efectos aditivos y no aditivos, que incluya dentro de los efectos no aditivos dominancia y aditivo*aditivo se tendrán las siguientes matrices de (co)varianza: Var (u)= Aσa 2, Var (d) = Dσd 2, Var(a*a)= A#Aσaa2, en donde u, d y a*a son vectores que contienen los BLUP de los efectos aditivos, no aditivos de dominancia e interacción aditivo*aditivo, σa2, σd2 y σaa2 son los componentes de varianza genético aditivo, de dominancia y de interacción aditivo*aditivo y finalmente # denota el producto Hadamard.
f≠g (Henderson 1984; Mrode, 2005). Por lo tanto en un modelo para efectos aditivos y no aditivos, que incluya dentro de los efectos no aditivos dominancia y aditivo*aditivo se tendrán las siguientes matrices de (co)varianza: Var (u)= Aσa 2, Var (d) = Dσd 2, Var(a*a)= A#Aσaa2, en donde u, d y a*a son vectores que contienen los BLUP de los efectos aditivos, no aditivos de dominancia e interacción aditivo*aditivo, σa2, σd2 y σaa2 son los componentes de varianza genético aditivo, de dominancia y de interacción aditivo*aditivo y finalmente # denota el producto Hadamard.
Asumiendo no correlación entre los diferentes tipos de efectos, al final el mérito genético total de un individuo es calculado como la sumatoria de los méritos incluidos en el modelo, en el ejemplo anterior sería: Merito genético total = u+d+a*a. Henderson (1984) mostró modelos lineales para la evaluación genética de cruzamientos entre líneas y razas, incluyendo o no efectos maternos. La estructura fue muy similar al caso anterior. Henderson (1984) mostró como calcular la covarianza entre individuos pertenecientes al mismo cruce o entre individuos de diferentes cruces. Además de la dominancia se pueden modelar diferentes tipos de interacciones, aditivo*aditivo, aditivo*dominancia, etc.
Modelo animal multirracial
En 1983 Elzo desarrolló una metodología lineal mixta para evaluar animales en poblaciones multirraciales; esta metodología incluyó efectos directos y maternos aditivos y no aditivos y heterogeneidad de varianzas y covarianzas a través de combinaciones de grupos raciales (Elzo, 2003). Elzo también contribuyó con el de desarrollo de algoritmos de inversión rápida de las matrices multirraciales de efectos aditivos y no aditivos (Elzo, 1990a, b). Además, Elzo (1996b) desarrolló dos procedimientos sin restricciones los cuales garantizan que los estimadores de todas las varianzas genéticas y las varianzas ambientales cumplan la condición de ser mayores que cero, y las correlaciones estimadas se encuentren dentro del rango permitido mayor que –1 y menor que 1. Estos procedimientos fueron denominados puntajes parciales (Partial Scoring) y maximización de Cholesky (Cholesky Maximization), los cuales buscan que las matrices de covarianza estimadas sean definidas positivas (Elzo, 1996b). Tales desarrollos teóricos y computacionales permitieron la evaluación genética de animales puros y cruzados en poblaciones multirraciales. Esta metodología permite obtener la predicción de valores genéticos de animales en poblaciones multirraciales.
De acuerdo con Elzo y Wakeman (1998) una población multirracial se define como aquella en la cual se tienen animales puros y animales cruzados los cuales se aparean entre sí. En estas poblaciones los efectos aditivos y no aditivos son una importante fuente de variación (Elzo y Wakeman, 1998), lo cual implica que el valor genético de un toro perteneciente a una población multirracial depende de estos dos tipos de efectos. Por lo tanto, en evaluaciones multirraciales se predicen diferencias aditivas esperadas de progenie (DAEP) y diferencias no aditivas esperadas de progenie (DNEP), y mediante la suma de estos dos valores se obtienen diferencias multirraciales esperadas de progenie (DMEP) (Manrique et al., 1998). Los elementos básicos de un modelo multirracial son similares a los de un modelo unirracial con efectos aditivos y no aditivos. La mayor complejidad de los modelos multirraciales se debe a que tienen que explicar efectos ambientales, genéticos aditivos y genéticos no aditivos en poblaciones formadas por grupos de animales de dos o más razas puras y por grupos cruzados de varias proporciones de combinaciones raciales(Elzo, 2006). Según Elzo (2006) un modelo multirracial unicarácter contiene los siguientes efectos:
1. Grupo contemporáneo multirracial.
2. Otros efectos fijos como por ejemplo edad de la madre.
3. Grupo genético aditivo.
4. Grupo genético no aditivo.
5. Efecto genético aditivo animal.
6. Efecto genético no aditivo animal.
7. Residuo.
En un estudio conducido por Manrique et al. (1997), se encontró que las predicciones genéticas se alteraban al comparar evaluaciones multirraciales con evaluaciones genéticas que involucraban solamente efectos genéticos aditivos. El modelo multirracial propuesto por Elzo se puede escribir matricialmente de la siguiente manera (Elzo, 2007):
y= Xb + ZaQaga + ZnQngn + Zaaa+ Znan + e.
También se asume distribución normal multivariada de los vectores aleatorios del modelo con los siguientes momentos:
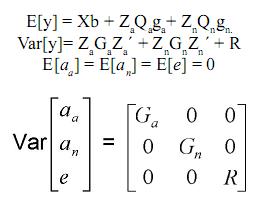
En donde:
y es el vector de registros, b es el vector de efectos fijos desconocidos (grupos contemporáneos, sexo del ternero, edad de la madre, etc.), ga es el vector de efectos desconocidos aditivos de grupo (raza, raza por año de nacimiento), gn es el vector de efectos desconocidos no aditivos de grupo (heterosis en 1 locus, heterosis en 2 loci), aa es el vector de efectos aleatorios desconocidos genéticos aditivos, an es el vector de efectos aleatorios desconocidos genéticos no aditivos, e es el vector de efectos aleatorios desconocidos residuales, Za es la matriz de incidencia conocida, que relaciona los registros a los elementos del vector aa, Zn es la matriz de incidencia conocida, que relaciona los registros a los elementos del vector an, Qa es la matriz de incidencia conocida, que relaciona los efectos genéticos aditivos aleatorios a los grupos genéticos aditivos en el vector ga, Qn es la matriz de incidencia conocida, que relaciona los efectos genéticos no aditivos aleatorios a los grupos genéticos no aditivos en el vector gn, Ga es la matriz de (co)varianza del vector aa, Gn es la matriz (co) varianza del vector an, R = diag {σ2ei}, donde σ2ei es la varianza residual del i–ésimo animal, se pueden modelar varianzas homogéneas para todos los animales o varianzas heterogéneas entre animales de diferente grupo racial.
Las ecuaciones del modelo animal multirracial son las siguientes:
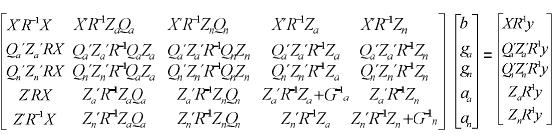
Como se puede ver es un conjunto de ecuaciones más complejo y por lo tanto demanda mayor costo computacional para ser resuelto. Análogamente al caso unirracial, al resolver el sistema se obtienen los BLUP de aa y an y los BLUE de b, ga y gn. Las DAEP se calculan como la suma del BLUE de ga y del BLUP de aa y las DNEP como la suma del BLUE de gn y del BLUP de an. Finalmente, las DMEP son iguales a DAEP + DNEP.
Evaluación genética de datos longitudinales
Cuando se tienen datos tomados a través del tiempo para varios individuos, se tiene una estructura de datos longitudinales, la cual merece un tratamiento estadístico especial (Verbeque y Molenberghs, 2000), los registros de crecimiento a diferentes edades son un ejemplo de este tipo de estructuras (Littel et al., 2006).
Varias formas de tratar estos datos han sido propuestas. Los modelos para caracteres repetidos pueden clasificarse en dos grupos, de dimensión finita y de dimensión infinita. El primer tipo de modelos evalúa rasgos a una edad determinada, si bien los resultados de estos modelos pueden ser satisfactorios estos pueden mostrar parámetros con tendencias muy variables y de difícil interpretación. Es lógico pensar que el crecimiento de un animal presente una trayectoria armoniosa, sin los picos que presentan los análisis de múltiples características. Para resolver este problema se recurre al segundo tipo de modelos, en los cuales se asume que el fenotipo es una función continua del tiempo, (Kirkpatrick et al., 1990). En el sentido matemático, dada la función y = f(x), esta se dice continua en p si 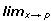 f(x) = f(p) y se dice que f es continua en un intervalo real [a,b] si
f(x) = f(p) y se dice que f es continua en un intervalo real [a,b] si 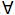 p
p  [a,b] se satisface la condición anterior. Sin embargo, cuando se emplean funciones continuas del tiempo (por ejemplo edad de los animales) para poder calcular la covarianza entre pares de variables medidas en cualquier momento dentro del rango considerado (tales funciones se denominan funciones de covarianza) se trabaja en el espacio vectorial
[a,b] se satisface la condición anterior. Sin embargo, cuando se emplean funciones continuas del tiempo (por ejemplo edad de los animales) para poder calcular la covarianza entre pares de variables medidas en cualquier momento dentro del rango considerado (tales funciones se denominan funciones de covarianza) se trabaja en el espacio vectorial 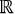 3, por lo tanto la anterior definición se debe extender:
3, por lo tanto la anterior definición se debe extender:
Una función escalar f, de dos variables (edades en este caso) se dice continua en un punto (a,b) Dom f
Dom f 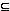
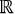 2 si
2 si 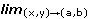 f(x,y) = f(a,b) y se dice que f es continua en un conjunto A
f(x,y) = f(a,b) y se dice que f es continua en un conjunto A 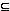 Dom f si es continua en todo punto de A.
Dom f si es continua en todo punto de A.
En mejoramiento animal se usan principalmente tres tipos de modelos para tratar medidas tomadas a través del tiempo, estas se citan a continuación.
Modelo de repetibiilidad
Esta fue la primera aproximación para la evaluación genética de mediciones tomadas a través del tiempo en los individuos de una población bajo modelo animal (Mrode, 2005). Este modelo se caracteriza por su simpleza y por requerir pocos recursos computacionales, esto debido al bajo número de parámetros por estimar (Van der Werf, 2001). Se asume que todas las mediciones son hechas sobre la misma característica (Henderson, 1984; Albuquerque, 2004), por lo tanto se basa en el supuesto de que las correlaciones genéticas entre mediciones son iguales a 1, así todas las varianzas y covarianzas genéticas entre las mediciones (edades) son iguales. Se asume también que las correlaciones ambientales entre pares de registros son iguales, hecho que no siempre se cumple, especialmente en características tenidas en cuenta en las evaluaciones genéticas de rutina como lo son el crecimiento (pesajes a diferentes edades) y producción de leche, siendo este hecho la principal desventaja de este modelo. En este modelo la varianza fenotípica puede descomponerse en tres componentes causales: Varianza genética (aditiva y no aditiva), varianza debida a entorno permanente y varianza debida a entorno específico.
En notación matricial el modelo de repetibilidad es como sigue:
y = Xβ + Zu + Wpe + e
Donde los vectores y, β, u y e y las matrices X y Z son iguales al caso del modelo animal sin efectos ambientales aleatorios, pe es un vector aleatorio desconocido que contiene los efectos de ambiente permanente, los cuales se predicen solamente para animales con registros, W es una matriz de incidencia que relaciona los registros a los efectos de ambiente permanente.
Se asume: Var(pe)=Iσpe2, Var(e)=Iσe2=R, Var(u) = Aσa2 = G.
En donde σpe2, σe2 y σa2 son los componentes de varianza de ambiente permanente, residual y genética aditiva respectivamente, A es la matriz de parentesco e I es la matriz de identidad.
Además E(pe) = E(e) = E(u) = 0, por lo tanto:
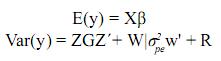
Así definido el modelo, los efectos genéticos no aditivos están incluidos dentro de los efectos de entorno permanente. La relación 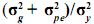 se conoce como repetibilidad y expresa la correlación existente entre registros de un individuo.
se conoce como repetibilidad y expresa la correlación existente entre registros de un individuo.
Modelo de múltiples características
Como se mencionó previamente, un modelo de múltiples características o multivariado, considera varios caracteres de manera simultánea. Para el caso de datos longitudinales, Henderson (1988) mostró como las medidas repetidas pueden ser vistas como modelos de múltiples características en los cuales cada una de las medidas se trata como una característica diferente, hecho que concuerda mucho mejor con la realidad, por ello se considera que el modelo de múltiples características es una mejor aproximación para la evaluación genética de datos longitudinales que el modelo de repetibilidad (Mrode, 2005). El modelo de repetibilidad y el modelo de múltiples características son equivalentes cuando la correlación genética entre las mediciones es 1 (Henderson, 1988).
Además de la alta demanda computacional, Van der Werf (2001) reportó los siguientes inconvenientes de la aproximación de dimensión finita (representada en el modelo de múltiples características) para el caso de mediciones que cambian con el tiempo y pueden ser representadas por una trayectoria:
1. En primer lugar, se ajusta una estructura de covarianzas discontinua, siendo esta realmente continua.
2. La segunda desventaja es que resultaría más tedioso modelar adecuadamente el hecho de tener más mediciones en el mismo periodo de tiempo. Un ejemplo se presenta en los sistemas de producción lechera, pues muchas fincas miden la producción de leche una vez cada mes de lactancia, pero algunas fincas pueden medirla diariamente.
3. En tercer lugar, la matriz de covarianzas es no estructurada y al tratarse de mediciones tomadas a través del tiempo (a través de una trayectoria), la estructura de covarianzas debe tener en cuenta el ordenamiento de las mediciones en el tiempo, esto es, la correlación entre mediciones debe estar relacionada a la magnitud de tiempo que existe entre las mismas.
Sumada a las anteriores, Meyer y Hill (1997) señalaron la siguiente desventaja adicional. Cuando se pretende estimar componentes de varianza, a menos que en cada ocasión se tomen varias mediciones en el animal, no se puede separar la variación debida al entorno permanente de aquella causada por el entorno específico.
Modelos de regresión aleatoria
En estos modelos se mide la evolución de la característica estudiada en función del tiempo, mediante coeficientes de regresión asociados a cada uno de los individuos. Como los individuos son tratados como efectos aleatorios, los coeficientes asociados a cada uno de estos también son tratados como aleatorios, a diferencia de los modelos que emplean coeficientes de regresión fija, los cuales son comunes para todos los individuos de la población (Resende et al., 2001). En el modelo de regresión aleatoria se emplea un coeficiente de regresión fija para determinar la tendencia media de la población y las curvas genéticas de cada animal se expresan como desviaciones de la curva fija, por lo tanto a diferencia del modelo de múltiples características lo que se encuentran son predicciones de valores genéticos para los coeficientes de regresión aleatorios (Van der Werf, 2001; Albuquerque, 2004). Cuando se habla de modelos de regresión aleatoria es preciso definir las funciones de covarianza (FC), las cuales son el equivalente (en dimensión infinita) a la matriz de covarianzas del modelo para múltiples características, tales funciones fueron propuestas por Kirkpatrick et al. (1990) y permiten describir la estructura de las covarianzas a través del tiempo.
La aproximación de Kirkpatrick et al. (1990) se basó en la típica descomposición de la varianza fenotípica en las siguientes fuentes de varianza causales: genética (aditiva y no aditiva), de ambiente permanente, ambiente específico, etc. Sin embargo en este caso se trata de funciones continuas, por lo tanto la trayectoria de crecimiento de un individuo es definida como la suma de dos funciones continuas, la primera representa el componente genético aditivo que se hereda de los padres y la segunda se atribuye a efectos ambientales y efectos de dominancia. En su trabajo Kirkpatrick et al. (1990) formularon la metodología para estimar funciones de covarianza genética aditiva a partir de la matriz observada de covarianzas genéticas aditivas entre las diferentes mediciones. Los autores presentan la estimación completa, es decir el orden de ajuste (k) es igual al número de mediciones repetidas (t edades) y un ajuste de menor grado, es decir k<t. Más adelante se discutirán los aspectos principales de cada metodología.
Bajo el supuesto de que las covarianzas genéticas no cambian de manera discontinua se estiman funciones de covarianza usando curvas suaves. En este caso, como se estableció previamente, se trabaja en el espacio vectorial 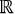 3, por lo tanto, se habla de una superficie y no de una curva suave.
3, por lo tanto, se habla de una superficie y no de una curva suave.
Los métodos que más se ha empleado para estimar las FC, son aquellos mediante los cuales se estiman funciones ortogonales de los datos, pues los coeficientes obtenidos permiten estudiar patrones de variación genética a través de la trayectoria que se está modelando (Kirkpatrick et al, 1990; Meyer y Hill 1997; van der Werf, 2001). El análisis de tales patrones se realiza mediante los valores propios y las funciones propias de la función de covarianza estimada; las funciones propias son el análogo, en la aproximación de dimensión infinita, a los vectores propios.
Un par de funciones continuas e integrables 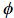 ji y
ji y 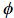 j se dicen normalizadas y ortogonales en un intervalo real [a,b] si satisfacen la siguiente condición:
j se dicen normalizadas y ortogonales en un intervalo real [a,b] si satisfacen la siguiente condición:
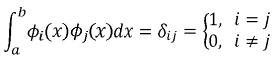
En donde ij se conoce como el delta de Kronecker. Los polinomios de Legendre pertenecen a la familia de los polinomios ortogonales, están definidos en el intervalo [–1,1] y son de aplicación sencilla, razón por la cual fueron propuestos por Kirkpatrick et al. (1990) para la estimación de las FC. En notación escalar una FC tiene la siguiente forma:
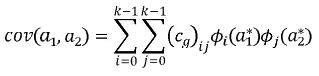
En donde:
(Cg)ij es la entrada ij de la matriz de coeficientes asociados a la FC (CG), 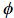 i y
i y 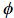 j son el i–ésimo y j–ésimo polinomios ortogonales (i,j=1,2,…,k–1), siendo k el orden de ajuste, a1* y a2* son las edades a1 y a2 (entre las cuales se quiere calcular la covarianza) estandarizadas al intervalo para el cual se definen los polinomios empleados, que en el caso de los polinomios de Legendre es [–1, 1]. Así la i–ésima edad estandarizada a1 se calcula como sigue:
j son el i–ésimo y j–ésimo polinomios ortogonales (i,j=1,2,…,k–1), siendo k el orden de ajuste, a1* y a2* son las edades a1 y a2 (entre las cuales se quiere calcular la covarianza) estandarizadas al intervalo para el cual se definen los polinomios empleados, que en el caso de los polinomios de Legendre es [–1, 1]. Así la i–ésima edad estandarizada a1 se calcula como sigue:
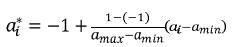
En donde amax y amin, son respectivamente, la máxima y mínima edad a las cuales se tomaron registros.
Estimación completa de la FC
Cuando se realiza una estimación completa, la matriz de covarianza genética puede escribirse como:
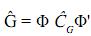
En donde Φ de dimensión txk contiene polinomios ortogonales, como t=k, la matriz es cuadrada; así definida la matriz, se tiene que existe su inversa, por lo tanto: 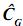 = Φ–1
= Φ–1 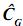 (Φ')–1. En este caso, para las edades en las cuales se tomaron los registros, las estimaciones obtenidas de la CF son idénticas a las contenidas en la matriz
(Φ')–1. En este caso, para las edades en las cuales se tomaron los registros, las estimaciones obtenidas de la CF son idénticas a las contenidas en la matriz 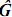 .
.
Estimación de orden reducido de la FC
Cuando se ajusta una función de covarianza de orden reducido (k<t), buscando así tener un modelo parsimonioso, se deben obtener coeficientes tales que el ajuste de la FC a la matriz 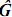 sea optimo y se debe tener en cuenta el error de muestreo, el cual corresponde a la diferencia entre las covarianzas predichas por la FC y las observadas (Mrode, 2005). Kirkpatrick et al. (1990) propusieron el método de mínimos cuadrados generalizados para estimar tales coeficientes, propusieron también una metodología para expresar la matriz
sea optimo y se debe tener en cuenta el error de muestreo, el cual corresponde a la diferencia entre las covarianzas predichas por la FC y las observadas (Mrode, 2005). Kirkpatrick et al. (1990) propusieron el método de mínimos cuadrados generalizados para estimar tales coeficientes, propusieron también una metodología para expresar la matriz 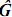 como función lineal del vector de coeficientes de la FC y el error de muestreo, en dicho proceso se vectorizan las matrices implicadas y se eliminan los términos redundantes ya que
como función lineal del vector de coeficientes de la FC y el error de muestreo, en dicho proceso se vectorizan las matrices implicadas y se eliminan los términos redundantes ya que 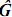 es simétrica; todo esto para construir un modelo lineal. También se detalla la construcción de la matriz de coeficientes de dicho modelo. Una vez se ha construido el modelo parsimonioso, los autores desarrollaron un procedimiento mediante el cual se construye un estadístico de prueba que sigue una distribución chi–cuadrada aproximada para inferir acerca de la bondad de ajuste de la nueva FC a
es simétrica; todo esto para construir un modelo lineal. También se detalla la construcción de la matriz de coeficientes de dicho modelo. Una vez se ha construido el modelo parsimonioso, los autores desarrollaron un procedimiento mediante el cual se construye un estadístico de prueba que sigue una distribución chi–cuadrada aproximada para inferir acerca de la bondad de ajuste de la nueva FC a 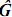 .
.
Métodos alternativos para la estimación de las FC
Como una alternativa para la estimación de los coeficientes de la FC, Meyer y Hill (1997) presentaron una metodología para la estimación de las mismas directamente de los datos mediante máxima verosimilitud restringida empleando una reparametrización de un modelo de múltiples características, la cual permite reescribir la función de verosimilitud restringida en términos de las matrices de coeficientes de las FC genética aditiva y residual. Otra forma de obtener estimaciones de los coeficientes de la FC es mediante regresión aleatoria, pues la estimación de las covarianzas entre coeficientes de regresión aleatoria produce estimativas de las FC (van der Werf, 2001). En este caso se escribe un modelo en el cual los efectos aleatorios del mismo son reemplazados por una FC, lo que se conoce como modelos de regresión aleatoria y funciones de covarianza, FC–RR por sus siglas en ingles. Asumiendo no correlación entre los diferentes efectos aleatorios, las FC son aditivas, al igual que las matrices de covarianza en la aproximación de dimensión finita. Una vez se tiene este modelo la estimación de los coeficientes puede hacerse vía máxima verosimilitud restringida o mediante muestreo de Gibbs.
Cuando se hace un ajuste completo, el modelo FC–RR es equivalente (primer y segundo momentos idénticos) al modelo de múltiples características (Meyer y Hill, 1997).
Un modelo FC–RR en notación matricial es el siguiente:
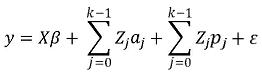
En donde y, β, ε y X se definen como en los modelos presentados anteriormente, Zj es una matriz de orden nxq del j–ésimo polinomio, siendo n el total de observaciones y q el número de animales evaluados, esta matriz contiene las variables de regresión, i.e., los coeficientes son los pertenecientes a los polinomios contenidos en Φ, aj y pj, y son vectores aleatorios que contienen los coeficientes de regresión aleatoria de los efectos genéticos aditivos y de entorno permanente respectivamente, K es el orden de ajuste de los polinomios, en el modelo presentado, el orden es el mismo para efectos genéticos aditivos y de entorno permanente.
Si se ordenan los registros por animal, se puede formar un solo vector a con los vectores aj y un solo vector p con los vectores pj. ordenando cada vector también por animal el modelo puede reescribirse como:
y = Xβ + Z*a + Z*p + ε
En donde Z* es una matriz diagonal en bloques de orden nxkq, cada bloque corresponde a un animal, el bloque 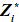 = Φi (Van der Werf, 2001).
= Φi (Van der Werf, 2001).
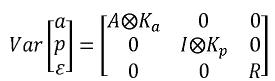
En donde ka y kp son las matrices de coeficientes de las funciones de covarianza genética aditiva y de entorno permanente, A es la matriz de parentesco I, es la matriz de identidad y 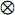 representa el producto directo o de Kronecker. Una ventaja de la estimación vía REML sobre los mínimos cuadrado generalizados, es que con el primer método, la matriz de coeficientes es definida positiva, mientras que con el segundo esta propiedad no está garantizada.
representa el producto directo o de Kronecker. Una ventaja de la estimación vía REML sobre los mínimos cuadrado generalizados, es que con el primer método, la matriz de coeficientes es definida positiva, mientras que con el segundo esta propiedad no está garantizada.
Kirkpatrick et al. (1990), van der Werf (2001) y Bertrand et al. (2006) presentaron las siguientes ventajas de los modelos de dimensión infinita cuando se estudia el fenómeno del crecimiento:
1. Se predice la evolución completa de la trayectoria de crecimiento.
2. Provee un método para analizar patrones de variación genética los cuales permiten identificar posibles cambios evolutivos en la trayectoria.
3. El método presenta un sesgo reducido en la estimación de la varianza genética.
4. Se tiene en cuenta adecuadamente el espaciamiento entre las mediciones tomadas.
5. Ofrecen mayor flexibilidad al permitir el uso de datos tomados en cualquier momento sin tener que ajustarlos a una edad de referencia.
6. Permite proyectar la evolución de las curvas de crecimiento, aun cuando los datos empleados para modelar el efecto de la selección y los usados para modelar la herencia, fueron tomados a diferentes edades.
Evaluación genómica
Gracias a los adelantos en biología molecular que permitieron obtener genotipos de los animales para uno o varios marcadores moleculares, fue posible involucrar tal información en los procedimientos de evaluación genética dando paso a la denominada selección asistida por marcadores moleculares (Fernando y Grossman, 1989). Una suposición que se hace en este caso, es que el o los marcadores considerados están ligados con uno o más QTL (Quantitative Trait Loci) que afectan la característica, lo cual implica que se heredan juntos. La metodología presentada por Fernando y Grossman (1989) muestra un modelo lineal mixto en el cual se incluye información de un marcador molecular polimórfico. Cada individuo tendrá dos copias de un marcador, una heredada del padre y otra de la madre. Por lo tanto, lo que se hace es predecir los efectos de los marcadores para cada animal y sumarlos a los efectos poligénicos modelados a través de la matriz de parentesco. En dicho trabajo se expuso además la forma de calcular la matriz de covarianzas de los marcadores.
Una vez fue posible obtener genotipos de los animales para miles de SNP (Single Nucleotide Polymorphism) distribuidos a lo largo del genoma, apareció un nuevo paradigma en la evaluación genética animal. En un importante documento, Meuwissen et al. (2001) propusieron métodos para utilizar toda la información genómica disponible para predecir los valores genéticos. El modelo lineal mixto propuesto por Meuwissen et al. (2001) contempla efectos fijos ambientales y efectos genéticos aditivos aleatorios de cada uno de los haplotipos de dos marcadores. Sin embargo, también se han empleado los efectos de cada uno de los marcadores en lugar de los haplotipos (Calus et al., 2008; Van Raden, 2008).
Una vez obtenidos los valores aditivos de cada uno de los marcadores (haplotipos) el valor genético aditivo de un animal se obtiene como una suma ponderada de los efectos de cada uno de los marcadores (haplotipos). Los pesos de cada efecto corresponden al número de copias de un alelo de referencia que posee el animal. El alelo que se toma como referencia suele llamarse segundo alelo (Van Raden, 2008). Estos modelos genómicos suponen que los marcadores están en equilibrio de ligamiento y que cada uno de estos marcadores esta en desequilibrio de ligamiento (likage disequilibrium) con uno o más QTL. Desde el punto de vista estadístico, el equilibrio de ligamiento implica que los efectos de cada uno de los marcadores son independientes. Por ello, dado que la varianza aditiva es la varianza de la suma de los efectos de todos los marcadores, ella puede calcularse simplemente como la suma de las varianzas de los efectos de cada marcador (ya que todas las covarianzas son cero). Es necesario mencionar que la varianza explicada por los marcadores podría ser muy diferente a la varianza genética a menos que los marcadores estén en QTL (Gianola et al., 2009).
Además del método MPLI, Meuwissen et al. (2001) propusieron dos métodos bayesianos jerárquicos denominados Bayes A y Bayes B. En el primero, se asume una distribución a priori del vector de efectos de los marcadores normal multivariada con esperanza cero y varianza desconocida la cual se asume sigue una distribución chi–cuadrado escalonada invertida. Con Bayes B, se asigna varianza cero a ciertos marcadores, lo cual pretende establecer que sus efectos sobre el carácter estudiado son nulos.
Las críticas que se han hecho a estos métodos (Gianola et al., 2009), incluyen:
1. La realidad de las poblaciones animales es la existencia de desequilibrio de ligamiento, bien sea por deriva genética, mutación o selección.
2. Así planteados, Bayes A y Bayes B son muy sensibles a los valores a priori.
3. En el caso de Bayes B, el hecho de que la varianza a priori de los efectos de los marcadores sea cero, no implica, desde un punto de vista Bayesiano, que el parámetro valga cero. En realidad puede tomar cualquier valor. Lo que implica varianza a priori cero, es que el valor se conoce con total certeza.
Para corregir estos problemas, Gianola et al. (2009) sugirieron crear grupos de marcadores a los cuales se les asigne la misma varianza o emplear valores a priori no informativos para el parámetro de escala y los grados de libertad en Bayes A. En el caso de Bayes B, los autores propusieron fijar el efecto de ciertos marcadores en cero en lugar de su varianza. Esto dio paso al método denominado Bayes C. Con Bayes C, se asume que una alta proporción de los marcadores (denotada generalmente como π) no tiene efecto sobre el carácter.
Al involucrar la información genómica en los modelos de evaluación se logran mayores exactitudes en las DEP's y estas se pueden interpretar de manera tradicional (Bullock y Pollak, 2009). VanRaden (2008), reportó incrementos de exactitud de 30% en predicciones del mérito lechero neto de toros jóvenes en ganado de leche al utilizar una combinación de información fenotípica, genómica, y de parentesco (ancestros y colaterales) comparada con la metodología tradicionalque utiliza solamente información fenotípica y de parentesco (ancestros y colaterales). Según VanRaden (2008),otra de las grandes ventajas de la incorporación de información genómica en la evaluación genética es que se aumenta el progreso genético y se reduce el costo de las pruebas de progenie al permitir a los criadores preseleccionar animales que heredan porciones de cromosomas de mayor mérito. Además, este mismo autor indica que las evaluaciones basadas en SNP se pueden computar tan pronto como se obtiene una muestra del ADN del animal, lo cual hace posible la selección en ambos sexos a corta edad. Legarra y Misztal (2008) resaltan el aumento en los requerimientos computacionales a nivel de almacenamiento y tiempo, como uno de los aspectos más importantes cuando se implementa la evaluación genómica. Esto se generaría debido a que se pueden incluir miles de covariables (marcadores SNP) en el modelo lo cual aumenta la cantidad de parámetros a estimar y hace que las ecuaciones de modelo mixto se vuelvan densas. Los requerimientos de memoria aumentarían linealmente con ciertos métodos y cuadráticamente con otros a medida que aumenta el número de marcadores incluidos en el modelo (Legarra y Misztal, 2008). Según Legarra y Misztal (2008), las estrategias para enfrentar este obstáculo se deben basar en el tipo de almacenamiento y los algoritmos de solución empleados, por esta razón ellos llevaron a cabo un estudio en el cual se evaluaron diferentes métodos computacionales y se compararon sus ventajas y desventajas.
Con el advenimiento de paneles de SNP más densos (800.000 SNP) los retos a nivel computacional y estadístico aumentarán. Si bien al incrementar la densidad de los paneles se espera que aumente el nivel de desequilibrio de ligamiento entre los marcadores y los QTL que afectan el carácter evaluado, al incluir tal cantidad de marcadores no solamente aumenta el requerimiento computacional, sino que se tendrán ecuaciones altamente co–lineales. En teoría, los métodos bayesianos discutidos previamente pueden manejar la situación de muchos parámetros–pocos datos (Gianola et al., 2009). Sin embargo, esta cantidad de SNP es aproximadamente 16 veces mayor a la que contiene uno de los chip más utilizados hasta el momento (Illumina Bovine SNP50 Bead Chip Assay; Illumina Inc., San Diego, CA) y por lo tanto la factibilidad del uso de tales chips en evaluación genética debe ser valorada. Algunos estudios han reportado que en ganado de carne la inclusión de información genómica por sí sola no es aun suficiente para llevar acabo análisis genéticos y que aun se debe incluir la información de pedigrí (efectos poligénicos) en los modelos (McNeil et al., 2009; Mujibi et al, 2011; Snelling et al., 2011; Goddard, 2009).
Bolormaa et al. (2011) sugirieron que la densidad de los paneles debe aumentar para tener mejores resultados en la selección genómica lo cual incentiva el uso de paneles más densos. Por otro lado, ciertas investigaciones han mostrado como un grupo reducido de marcadores derivado de uno de los chips disponibles en el comercio pueden ser empleados para poblaciones y caracteres específicos (Bolorma et al. 2011; Nalaila et al., 2011; Snelling et al., 2011).
Estos escenarios plantean un interesante campo de investigación el cual presenta nuevos retos a nivel computacional, genético y estadístico. Un aspecto que también ha de tenerse en cuenta es el costo de estos chips. Las diferentes ventajas que brinda la evaluación genómica deben ir acompañadas de análisis económicos en los cuales se valore el impacto de la selección genómica en términos de las ganancias de los productores, ya que el último paso en un programa de mejora genética es un análisis económico de los costos y beneficios del mismo (Garrick y Golden, 2009).
Perspectivas de las evaluaciones genéticas en vacunos
En cuanto a las evaluaciones genéticas multirraciales, Elzo (2006) comenta que se tiene enfrente un largo camino hacia la implementación de sistemas multirraciales cuyo objetivo sea la predicción del producto del apareamiento individual de animales de diferentes razas o grupos raciales en términos de valores genéticos totales (aditivos + no aditivos). Elzo (2006) también resalta la necesidad de una estrecha colaboración entre sectores comerciales y de investigación con el fin de obtener suficiente información para la implementación de modelos apropiados para cada población multirracial. Gianola (2006) comenta que los modelos semiparamétricos tendrán gran importancia en la evaluación de grandes cantidades de datos genómicos. De igual manera Gianola (2006) discute la utilidad de los modelos de mezcla finita (finite mixtures models) en la selección para resistencia a mastitis y la necesidad de crear e implementar software para aplicar estos modelos en evaluaciones genéticas nacionales. Otro tipo de modelos que según Gianola pueden ser de utilidad son los modelos cero–inflados (zero–inflated models) que resultan útiles cuando las variables respuesta son conteos; su principal observación es la futura utilidad de los modelos semiparamétricos y no paramétricos (Gianola, 2006). La emergente y poco costosa biotecnología de genotipificación para SNP ha traído un nuevo paradigma en la evaluación genética basada en selección genómica o selección a través del genoma (Legarra y Misztal, 2008), por lo tanto se deben seguir generando metodologías estadísticas y computacionales que permitan realizar evaluaciones genéticas en grandes conjuntos de datos involucrando la información proveniente de la genotipificación de los individuos.
Comentarios finales
La evaluación genética de animales se vuelve cada vez más sofisticada y específica. Los desarrollos teóricos y computacionales permiten el uso de modelos que describen mejor los fenómenos biológicos estudiados, y como resultado se logran predicciones de valores genéticos y estimaciones de componentes de varianza cada vez más confiables. Para seguir avanzando se requiere la cooperación entre la comunidad científica y los productores, así como la formación de investigadores en esta área del conocimiento.
Referencias
1. Albuquerque LG. Regressão aleatória: Nova tecnologia pode melhorar a qualidade as avaliações genéticas. Memorias del V simpósio da sociedade brasileira de melhoramento animal 2004; [Fecha de acceso: junio 3 de 2011] URL: http://www.sbmaonline.org.br/anais/v/palestras/pdfs/palest11.pdf [ Links ]
2. Bertrand JK, Misztal I, Robins KR, Bohmanova J, Tsuruta S. Implementation of random regression models for large scale evaluations for growth in beef cattle. Proceedings of the 8th World Congress on Genetic Applied to Livestock Production 2006; III: 03–04 [ Links ]
3. Bullock KD, Pollak JE. Beef symposium: The evolution of beef cattle genetic evaluation. J Anim Sci 2009; 87 Suppl E:E1–E2. [ Links ]
4. Bolormaa S, Porto Neto LR, Zhang YD, Bunch RJ, Harrison BE, Goddard ME, Barendse W. A genome–wide association study of meat and carcass traits in Australian cattle. J Anim Sci 2011; 89:2297–2309. [ Links ]
5. Calus MPL, Meuwissen THE, de Roos APW, Veerkamp RF. Accuracy of genomic selection using different methods to define haplotypes. Genetics 2008; 178:553–561. [ Links ]
6. Ducroq V, Besbes B. Solutions of multiple trait animal models with missing data on some traits. J Anim Breed Genet 1993; 110:81–89. [ Links ]
7. Elzo MA. Multibreed sire evaluation within and across countries. Ph. D. Dissertation. Department of Animal Sciences, University of California, Davis. 1983 [ Links ]
8. Elzo MA. Recursive procedures to compute the inverse of the multiple trait additive genetic covariance matrix in inbred and non inbred multibreed populations. J Anim Sci 1990a; 68:1215– 1228. [ Links ]
9. Elzo MA. Covariances among sire by breed group of dam interaction effects in multibreed sire evaluation procedures. J Anim Sci 1990b; 68:4079–4099. [ Links ]
10. Elzo MA. Animal breeding notes. University of Florida 1996a; [Fecha de acceso: 1 junio de 2009] URL:http://www.animal.ufl.edu/elzo/Publications/Animal%20Breeding%20Notes/Index%20Animal%20Breeding%20Notes_a.htm [ Links ]
11. Elzo MA. Unconstrained procedures for the estimation of positive definite covariance matrices using restricted maximum likelihood in multibreed populations. J Anim Sci 1996b; 74:317–328. [ Links ]
12. Elzo MA, Bradford GE. Multibreed sire evaluation across countries. J Anim Sci 1985; 60:953–963. [ Links ]
13. Elzo MA, Famula TR. Multibreed sire evaluation within a country. J Anim Sci 1985; 60:942–952. [ Links ]
14. Elzo MA, Manrique C, Ossa G, Acosta O. Additive and non additive genetic variability for growth traits in the Turipaná Romosinuano–Zebu multibreed herd.J Anim Sci 1998 76:1539– 1549. [ Links ]
15. Elzo MA, Wakeman DL. Covariance components and prediction for additive and non additive preweaning growth genetic effects in an Angus–Brahman multibreed herd. J Anim Sci 1998; 76:1290–1302. [ Links ]
16. Elzo MA. Evaluación genética de animales en poblaciones multirraciales de bovinos utilizando modelos lineales. Arch Latinoam Prod Anim 2006; 14 Suppl4:154–160. [ Links ]
17. Elzo MA. Animal breeding notes. University of Florida 2007; [Fecha de acceso 1 junio de 2009] URL:http://www.animal.ufl.edu/elzo/Publications/Animal%20Breeding%20Notes/Index%20Animal%20Breeding%20Notesa.htm [ Links ]
18. Elzo MA, Cerón–Muñoz MF, editores. Modelación aplicada a las ciencias animales: Genética cuantitativa, Medellín: L. Vieco e Hijas Ltda; 2009. [ Links ]
19. FEDEGAN (Col). Plan estratégico de la ganadería colombiana 2019. Bogotá D.C: San Martín Obregón y Cía.; 2006. [ Links ]
20. Fernando RL, Grossman M. Marker assisted selection using best linear unbiased prediction. Genet Sel Evol 1989; 21:467– 477. [ Links ]
21. Galeano AP. El modelo del día de control (Test day model) como herramienta para el mejoramiento genético. Tesis de pregrado. Facultad de Medicina Veterinaria y de Zootecnia, Universidad Nacional de Colombia, Bogotá. 2004. [ Links ]
22. Garrick DJ, Golden BL. Producing and using genetic evaluations in the United States beef industry of today. J Anim Sci; 87:E11–E18. [ Links ]
23. Gianola D. Statistics in animal breeding: angels and demons. Proceedings of the 8th World Congress on Genetic Applied to Livestock Production 2006; 00–03. [ Links ]
24. Gianola D, de los Campos G, Hill WG, Manfredi E, Fernando R. Additive genetic variability and the bayesian alphabet. Genetics 2009; 183:347–363. [ Links ]
25. Golub GE, Van Loan CF. Matrix Computations, 3rd ed. USA: The John Hopkins University Press; 1996. [ Links ]
26. GoldenBL, Garrick DJ, Benyshek LL. Milestones in beef cattle genetic evaluation. J Anim Sci 2009; 87:E3–E10. [ Links ]
27. Goddard M. Genomic selection: prediction of accuracy and maximization of long–term response. Genetica 2009; 136:245– 257. [ Links ]
28. Henderson CR. Sire evaluation and genetic trends. Proceedings of the Animal Breeding and Genetic symposium in honor of Jay L. Lush 1973; 10–41. [ Links ]
29. Henderson CR. A simple method for computing the inverse of a numerator relationship matrix used in prediction of breeding values. Biometrics 1976; 32:69–83. [ Links ]
30. Henderson CR. Applications of linear models in animal breeding. 1sted. Canada: University of Guelph; 1984. [ Links ]
31. Henderson CR. Best linear unbiased prediction of non additive genetic merits in non inbred populations. J Anim Sci 1985a; 60:111–117. [ Links ]
32. Henderson CR. MIVQUE and REML estimation of additive and non additive genetic variances. J Anim Sci 1985b; 61:113–121. [ Links ]
33. Henderson CR. Theoretical basis and computational methods for a number of different animal models. Proceedings of the animal model workshop. J Dairy Sci 1988; 71 Suppl 2:1–16. [ Links ]
34. Kennedy BW, Schaeffer LR, Sorensen DA. Genetic properties of animal models. Proceedings of the animal model workshop. J Dairy Sci 1988; 71 Suppl 2:17–26. [ Links ]
35. Kirkpatrick M, Lofsvold D, Bulmer M. Analysis of the inheritance, selection and evolution of growth trajectories. Genetics 1990; 124:979–993. [ Links ]
36. Legarra A, Misztal I. Technical note: Computing strategies in genome–wide selection. J Dairy Sci 2008; 91:360–366. [ Links ]
37. Littell RC, Milliken GA, Stroup WW, Wolfinger RD, Schabenberger O.SAS® for mixed models. 2nd ed. Cary (NC): SAS Institute Inc.; 2006. [ Links ]
38. Lush JL. Intra–sire correlations or regressions of offspring on dam as a method of estimating heritability of characteristics. J Anim Sci 1940; 1940:293–301. [ Links ]
39. Lush JL. The impact of genetics in animal breeding. J Anim Sci 1951; 10:311–321. [ Links ]
40. Manrique C. Uso de modelos mixtos en evaluación genética animal. Memorias del Simposio internacional de estadística. Estadística en agricultura y medio ambiente 1995; 65–76. [ Links ]
41. Manrique C, Elzo MA, Odenya WO, Mcdowell LR, Wakeman DL. Predicción de efectos genéticos aditivos y no aditivos del peso al destete mediante un procedimiento de evaluación multirracial. Corpoica Cienc Tecnol Agropecu 1997; 2 Suppl 1:17–21. [ Links ]
42. Manrique C, Elzo MA, Odenya WO, Mcdowell LR, Wakeman DL. Cambios en la predicción de valores genéticos para peso al destete en evaluaciones multirraciales que utilizan valores séricos de calcio, fósforo o magnesio. Rev Corpoica 1998; 2 Suppl 2:49–56. [ Links ]
43. MacNeil MD, Nkrumah JD, Woodward BW, Northcutt SL. Genetic evaluation of Angus cattle for carcass marbling using ultrasound and genomic indicators. J Anim Sci 2009; 88:517– 522. [ Links ]
44. Meyer K, Hill WG. Estimation of genetic and phenotypic covariance functions for longitudinal or “repeated” records by restricted maximum likelihood. Livest Prod Sci 1997; 47:185–200. [ Links ]
45. Meuwissen THE, Hayes BJ, Goddard ME. Prediction of total genetic value using genome–wide dense marker maps. Genetics 2001; 157:1819–1829. [ Links ]
46. Mrode RA. Linear models for the prediction of animal breeding values. 2nd ed. Oxfordshire (OX): CABI Publishing; 2005. [ Links ]
47. Mujibi FDN, Nkrumah JD, Durunna ON, Stothard P, Mah J, Wang Z, Basarab J, Plastow G, Crews DH Jr., Moore SS. Accuracy of genomic breeding values for residual feed intake in crossbred beef cattle. J Anim Sci 2011(In press) [Fecha de acceso: agosto 10 de 2011]URL://jas.fass.org/content/ early/2011/06/03/jas.2010–3361. [ Links ]
48. Nalaila SM, Stochard P, Moore SS, Li C, Wang Z. Wholegenome QTL scan for ultrasound and carcass merit traits in beef cattle using Bayesian shrinkage method. J. Anim. Breed. Genet. 2011 (In press) [Fecha de acceso: agosto 12 de 2011] URL: http://onlinelibrary.wiley.com/doi/10.1111/j.1439– 0388.2011.00954.x/pdf [ Links ]
49. Odenya WO, Elzo MA, Manrique C, Mcdowell LR, Wakeman DL. Genetic and environmental factors affecting serum macrominerals and weights in an Angus–Brahman multibreed Herd: I. Additive and non additive group genetic effects of serum calico, phosphorus, and magnesium and weight at weaning. J Anim Sci 1992; 70:2065–2071. [ Links ]
50. Ossa GA. Mejoramiento genético aplicado a los sistemas de producción de carne. 1ra ed. Bogotá: Produmedios; 2003. [ Links ]
51. Peacock CM, Palmer AZ, Carpenter JW, Koger M. Breed and heterosis effects on carcass characteristics of Angus, Brahman, Charolais and crossbred steers. J Anim Sci 1979; 49:391–395. [ Links ]
52. Pollak JE. Multibreed genetic evaluation of beef cattle in United States. Proceedings of the 8th World Congress on Genetic Applied to Livestock Production 2006; III: 03–01. [ Links ]
53. Pollak EJ, Quaas RL. Monte Carlo study of within–herd multiple trait evaluation of beef cattle growth traits. J Anim Sci 1981; 52:248–256. [ Links ]
54. Quaas RL, Pollak EJ. Mixed model methodology for farm and ranch beef cattle testing programs. J Anim Sci 1980; 51:1277– 1287. [ Links ]
55. Resende MDV, Rezende GDSP, Fernandes JSC. Regressão aleatória e funções de covariância na análise de medidas repetidas. Rev Mat Estad 2001; 19:21–40. [ Links ]
56. Ruales FR, Manrique C, Cerón MF. Fundamentos en mejoramiento animal. 1ra ed. Medellín (Antioquia): L. Vieco e hijasLtda; 2007. [ Links ]
57. Searle SR. Linear models.1st ed. USA: John Wiley and Sons; 1971. [ Links ]
58. Snelling WM, Allan MJ, Keele JW, Kuehn LA, Thallman RM, Bennett GL, Ferrell CL, Jenkins TG, Freetly HC, Nielsen MK, Rolfe KM. Partial–genome evaluation of postweaning feed intake and efficiency of crossbred beef cattle. J Anim Sci 2011; 89:1731–1741. [ Links ]
59. VanRaden VM. Efficient methods to compute genomic predictions. J Dairy Sci 2008; 91:4414–4423. [ Links ]
60. Van der Werf J. Random regression in animal breeding. Course notes. University of New England 2001; [Fecha de acceso: junio 1 de 2010] URL: http://www–personal.une.edu.au/~jvanderw/CFcoursenotes.pdf. [ Links ]
61. Vergara OD, Ceron–Muñoz MF, Arboleda EM, Orozco Y, Ossa GA. Direct genetic, maternal genetic, and heterozygocity effects on weaning weight in a Colombian multibreed beef cattle population. J Anim Sci 2009; 87:516–521. [ Links ]
62. Verveque G, Molenberghs G. Linear mixed models for longitudinal data. 1sted. New York: Springer; 2000. [ Links ]
63. Willham RL. The covariance between relatives for characters composed of components contributed by related individuals. Biometrics 1963; 19:18–27. [ Links ]
Notas
¤ Para citar este artículo: Martínez CA, Manrique C, Elzo MA. La evaluación genética de vacunos: una percepción histórica. Rev Colomb Cienc Pecu 2012; 25:293–311.














