Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Revista Colombiana de Ciencias Pecuarias
Print version ISSN 0120-0690
Rev Colom Cienc Pecua vol.26 no.2 Medellín Apr./June 2013
ORIGINAL ARTICLES
Variance components and genetic parameters for milk production of Holstein cattle in Antioquia (Colombia) using random regression models¤
Componentes de varianza y parámetros genéticos para producción de leche en ganado Holstein de Antioquia (Colombia), utilizando modelos de regresión aleatoria
Componentes de variância e parâmetros genéticos para produção de leite em gado Holandês da Antioquia, (Colombia) utilizando modelos de regressão aleatória
Ana C Herrera*, Zoot, MS; Oscar D Múnera, Zoot, MS student; Mario F Cerón-Muñoz, Zoot, MS, Dr.
* Corresponding author: Ana Cristina Herrera Rios. Grupo de investigación GaMMA, Facultad de Ciencias Agrarias, Universidad de Antioquia. Carrera 75 No. 65-87, Bloque 47-233. Ciudadela de Robledo. AA 1226, Medellìn, Colombia. Tel (574) 2199140. e-mail: anacristinah@gmail.com
Grupo de Genética, Mejoramiento y Modelación Animal,(GaMMA),Facultad de Ciencias Agrarias e Instituto de Biología, Universidad de Antioquia, Medellín Colombia.
(Received: September 9, 2012; accepted: December 18, 2012)
Summary
Background: genetic parameters of lactation curve in dairy cattle can be analyzed as longitudinal data using random regression models (RRM). Objective: the goal of the present study was to estimate variance components and genetic parameters for milk production in Holstein cattle located in Antioquia province using RRM. Methods: a total of 3,158 monthly controls corresponding to 741 first lactations of Holstein cows were evaluated. The RRM included several Legendre polynomials to estimate the population fixed-curve coefficients and to predict the direct additive genetic and the permanent environment effects. Additionally, heterogeneous residual variances were considered by grouping the days in milk into 5 and 10 classes. Eleven models with first to fourth order polynomials were used to describe the direct additive genetic and the permanent environment effects. The residue was modeled by considering five variance classes. Models were compared using Schwartz Bayesian and Akaike's information criteria. Results: the best model was obtained by fourth order Legendre polynomials to estimate the fixed curve of the population, genetic and permanent environment effects. In addition, 5 kinds of days were used to model the residual variances. The variance for the animal genetic, phenotypic, permanent environment, and residual effects decreased as days increased. Milk production heritability in early lactation was 0.36, increasing until 95 days (0.41), with subsequent decrease, reaching 0.10 at 245 days. The permanent environment variance values decreased to 125 days (0.13) and then increased to 215 days (0.21), to finish at the last stage of lactation with values of 0.05. The genetic and phenotypic correlations between milk yields at different days of lactation decreased as days intervals increased. Conclusion: the findings of this study suggest that in the first 150 days of lactation animals better express their genetic potential and that after 180 days there is greater environmental effect.
Key words: dairy cattle, genetic evaluation, heritability.
Resumen
Antecedentes: los parámetros genéticos de la curva de lactancia en ganado de leche pueden ser analizados como datos longitudinales usando modelos de regresión aleatoria (RRM). Objetivo: el objetivo de este estudio fue estimar componentes de varianza y parámetros genéticos para la producción de leche en vacas Holstein en el departamento de Antioquia, utilizando RRM. Métodos: se utilizaron 3.158 controles mensuales de 741 primeras lactancias. Se usaron RRM con diferentes grados de polinomios de Legendre para estimar los coeficientes de la curva fija de la población y la predicción de los efectos genético aditivo directo y de ambiente permanente y se consideraron 5 y 10 clases de varianzas residuales heterogéneas. Se emplearon once modelos con polinomios de primer a cuarto orden, para describir los efectos genético aditivo directo y ambiente permanente. Los modelos fueron comparados mediante los criterios de información bayesiano de Schwartz y de Akaike. Resultados: el mejor modelo presentó polinomios de cuarto orden 4, 4 y 4 de la curva fija, del efecto genético aditivo y de ambiente permanente, respectivamente, y con 5 clases de varianzas heterogéneas (444.het5). La varianzas para los efectos genético animal, fenotípico, de ambiente permanente y residual disminuyeron con el aumento de los días. La heredabilidad de la producción de leche al inicio de la lactancia fue de 0,36 y fue aumentando hasta los 95 días (0,41), con posterior disminución, llegando a 0,10 a los 245 días. Para la trayectoria de la proporción de ambiente permanente los valores descendieron hasta los 125 días (con 0,13), luego aumentaron hasta los 215 días (con 0,21), para finalizar en la última etapa de la lactancia con valores de 0,05. Las correlaciones genéticas y fenotípicas entre producciones de leche en los diferentes días de lactancia disminuyeron con el aumento del intervalo de los días. Conclusión: los resultados encontrados en este estudio sugieren que en los primeros 150 días de lactancia los animales expresan mejor su potencial, y que despues de 180 días hay mayor impacto ambiental.
Palabras clave: evaluaciones genéticas, ganado de leche, heredabilidad.
Resumo
Antecedentes: os parâmetros genéticos da curva de lactação em gado leiteiro podem ser analisados como dados longitudinais usando modelos de regressão aleatória (RRM). Objetivo: o objetivo deste estudo foi estimar os componentes de variância e os parâmetros genéticos para produção de leite de vacas holandesas em Antioquia, utilizando um modelo de regressão aleatória (RRM). Métodos: foram utilizados 3.158 controles mensais de 741 primeiras lactações. Usaram-se RRM com diferentes graus de polinômio ortogonal de Legendre para estimar os coeficientes da curva fixa da população e a predição dos efeitos genéticos aditivos diretos e de ambiente permanente. Consideraram-se 5 e 10 classes de variâncias residuais heterogêneas. Foram empregados 11 modelos com polinômios de primeira ate quarta ordem para descrever os efeitos genéticos aditivos diretos e de ambiente permanente. Os modelos foram comparados mediante os critérios de informação bayesiano de Schwartz e de Akaike. Resultados: o melhor modelo foi o de quarto ordem (4, 4 e 4) da curva fixa, do efeito genético aditivo e de ambiente permanente, respectivamente, e com cinco classes de variâncias heterogéneas (444.het5). A variância para os efeitos genético animal, fenotípico, de ambiente permanente e residual diminuiu com o aumento dos dias. A herdabilidade da produção de leite ao inicio da lactação foi de 0.36 e foi aumentando até os 95 dias (0.41), com posterior diminuição, chegando até 0.10 aos 245 dias. Para a trajetória da proporção de ambiente permanente os valores descenderam até os 125 dias (com 0.13), com posterior aumento até os 215 dias (com 0.21), para finalizar na última etapa da lactação com valores de 0.05. As correlaciones genéticas e fenotípicas entre produções de leite nos diferentes dias de lactação diminuíram com o aumento do intervalo dos dias. Conclusão: os resultados encontrados sugerem que nos primeiros 150 dias da lactação os animais expressaram melhor seu potencial genético.
Palavras chave: avaliações genéticas, gado de leite, herdabilidade.
Introduction
Genetic evaluations in dairy cattle require estimating the variance components and genetic parameters of populations. To accomplish this objective, several methods taking total, partial, and daily milk yield (DMY) records into account have been used. The simplest model uses milk production adjusted to 305 days. Some models include a more sophisticated level of complexity (Mark, 2004). Among these is the Test-Day model, which uses measurements spanning a period of time of complete lactation to describe milk production and milk constituents at any given point on the curve (Rodriguez-Zas et al., 2000). The DMY can be analyzed using repeated measures throughout the lactation length using random regression models (RRM), which describe the covariance structure over time in a continuous manner to estimate the genetic parameters on any lactation day for an animal by using polynomials and other functions of days in milk as a covariate (Henderson, 1982; Schaeffer and Drekkers, 1994; Jamrozik et al., 1997; Kistemaker et al., 1997; Meyer, 2004).
The RRM also allow us to model deviations of phenotypic trajectories, which may have different shapes and can be more easily described by Legendre polynomials (Kirkpatrick et al., 1990) facilitating the prediction of missing records and improving convergence (Meyer, 2004). In addition, it is necessary to consider heterogeneous residual variances to improve the total variance partition, despite the increase in the number of parameters to be estimated for the maximization process of the likelihood function (Meyer, 1999; Olori et al., 1999a; Muir et al., 2007).
According to some literature reports, researchers have used RRM with differing degrees of Legendre polynomials and several heterogeneous variance classes with high heritability values throughout the milk production curve (Van der Werf, 2001; Strabel and Misztal, 1999; Veerkamp and Thompson, 1999, Liu et al, 2000; Albuquerqe and Meyer, 2001). In addition, such studies have proposed the use of heterogeneous residual variances by grouping classes with similar variations (Meyer, 1999; Olori et al. 1999a). Consequently, the purpose of this study was to estimate variance components and genetic parameters for milk production of Holstein cows in Antioquia using a random regression model.
Materials and methods
A total of 3,158 monthly controls from 741 first lactation Holstein cows were used. Lactations occurred between November 2007 and October 2011 in 32 dairy herds in northern and eastern Antioquia. The herds are subscribed to the Milk Control Program of Antioquia Holstein Corporation and the University of Antioquia. The program included individual milk measurements collected using A4 methodology (ICAR, 2002) with monthly visits and two milking controls (morning and afternoon). Lactations with more than 4 monthly records were considered in the analysis; the pedigree file included 8,032 animals.
Controlled herds are located in a very humid premontane forest (bmh-PM), with an average temperature of 16 °C, an altitude between 2,000 and 3,000 m above sea level, and annual rainfall between 2,000 and 4,000 mm which falls onto a flat and undulating topography. Animals grazed mostly on kikuyu grass (Pennisetum clandestinum) and some ryegrass associations. Animals were supplemented with commercial concentrate feed according to production stage and herd management criteria.
Varying degrees of the Legendre polynomial were used in the RRM to estimate population fixed curve coefficients and to predict direct genetic and permanent environment effects, considering 5 and 10 classes of heterogeneous residual variances. Days in milk intervals of 5-90, 91-120, 121-190, 191-250, 251-305 d were used for the 5 variance classes, while 1-30, 31-64, 65-92, 93-121, 122- 155, 156-188, 189-211, 212-255, 256-290, 291- 323 d intervals were considered for the 10 variance classes. The fixed effect of contemporary group (farm, season and year of birth) was also included. Calving seasons were defined as: 1 (December to February), 2 (March to May), 3 (June to August), and 4 (September to November).
The random regression model used was as follows:
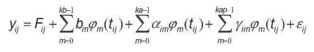
Where:
yij = Milk production at the jth control of the ith animal;
Fij = Contemporary group fixed effect of the jth control of the ith animal;
bm = mth fixed regression coefficient for kb regressors;
Φmt(ij) = mth Legendre polynomial evaluated at the jth control day of the ith animal;
αim = mth random regression coefficients for the additive genetic effect of the ith animal;
γim = mth random regression coefficients for the permanent environment effect of the ith animal;
kb-1, ka–1, and kap-1= Legendre polynomials order to describe the mean curve and the additive genetic and permanent environment effects, respectively;
εij = Random error associated to the jth control the ith animal.
The (co) variance components and genetic parameters were obtained with the restricted maximum likelihood method using the WOMBAT statistical program (Meyer, 2007). The random regression models were compared using Akaike information criterion (AIC; Akaike, 1974) and Bayesian information criterion (BIC; Schwarz, 1978), which allow comparing non-nested models and penalize models having a high number of parameters, BIC being the most rigorous (Nunez- Anton and Zimmerman, 2000). Low AIC and BIC values correspond to a better model fit.
Results
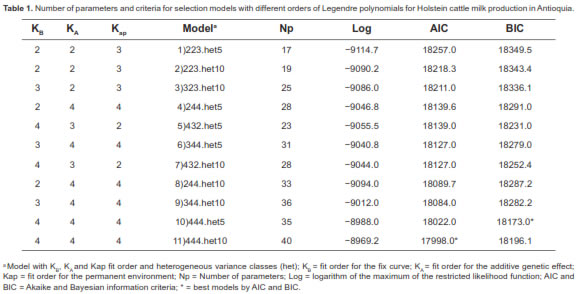
The AIC and BIC results for each model tested are shown in table 1. The lowest AIC value corresponded to the polynomial-degree model 4, 4, and 4 of the fixed curve, additive genetic, and permanent environment effect, respectively, and 10 heterogeneous variance classes (444.het10). The lowest BIC value was for the model with the same polynomial degree above, but with 5 heterogeneous classes (444.het5). In this study, (co) variance components and genetic parameters were estimated using model 444.het5, since it showed the lowest BIC value, was more parsimonious and displayed faster convergence.
The first eigenvalue (λ) accounted for 83.89% of the total additive genetic covariance matrix, and the first three eigenvalues explained it by 99.99%. For the permanent environmental effect, the first eigenvalue accounted for 80.33% of the total permanent environmental variance and the first three values explained it by 99.99% (Table 2).
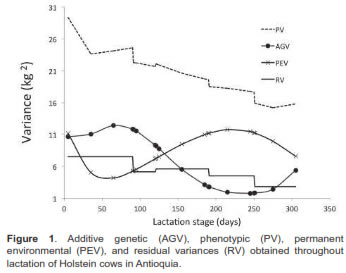
Variance trajectories are shown in figure 3. The direct genetic variance increased until d70 (12.44 kg2) with subsequent decrease until d239 (1.75 kg2). The permanent environment interaction was higher at the beginning of lactation (12.67 kg2), with subsequent reduction to d59 (4.11 kg2), followed by an increase to d224 (11.8 kg2). The residual variance showed a downward trend from d5 (7.5 kg2) to d305 (2.8 kg2). The highest phenotypic variance occurred at the beginning of lactation (29.3 kg2), decreasing to d305 (15.8 kg2).
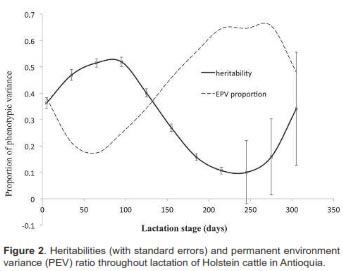
Milk yield heritability in early lactation was 0.36. It increased up to d95 (0.41), with a subsequent decrease, reaching 0.10 at d245, with low standard errors fluctuating between 0.013 and 0.021. Heritabilities increased during the last lactation phase (up to 0.34), but had high standard errors (0.14 to 0.21). The permanent environment trajectory values decreased to d125 (0.13), then increased to d215 (0.21), finishing at 0.05 during the final lactation stage (Figure 2).
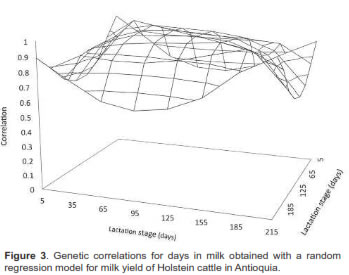
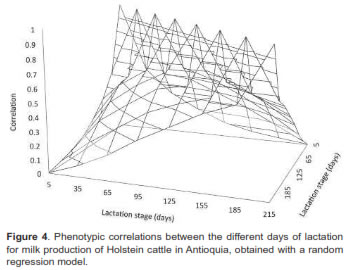
Genetic and phenotypic correlations between milk yields at different lactation days are presented in figures 3 and 4, respectively. In general, genetic correlations decreased as day intervals increased, with positive values between 0.04 and 0.99. These results were higher than those obtained for phenotypic correlations, but followed the same path with values between 0.004 and 0.66.
Discussion
The AIC and BIC values decreased as the number of parameters increased for each model evaluated. The best models were 444.het10 (for AIC) and 444. het5 (for BIC). Several researchers have tested different orders of Legendre polynomials for milk production. Assuming homogeneous residuals variance, Cobuci et al. (2006) and Cobuci et al. (2011) reported that model 555 with homogeneous residual variances was best (for both AIC and BIC). Albuquerque et al. (2011) also found models with polynomial orders 2 through 5 to be better for the same effects using 5 heterogeneous residual variances. Olori et al. (1999) tested RA models with 3 to 5 polynomial orders for different effects, using 10 classes of heterogeneous residual variances. The best models found were those of higher order (i.e., the fourth order, having more number of classes of heterogeneous residual variances).
It can be considered that higher adjustment orders for Legendre polynomials increase the flexibility of RA models. Furthermore, due to the mathematical properties of orthogonal Legendre polynomials, they are considered the most appropriate for daily milk production analysis (Schaeffer, 2004; Strabel and Jamrozik, 2006). However, biological interpretation of these coefficients is more difficult compared to other parametric functions, such as the Wilmink function and the Ali and Schaeffer polynomial functions. Some researchers, such as Cobuci (2005) and Bignardi (2011), tested these functions, obtaining the best results with models that used Legendre polynomials with orders from 4 to 7.
The decline is very pronounced after 150 days and up to 275 for the additive variance. Similarly, Gonzalez-Pena et al. (2007), using heterogeneous residual variances, reported the highest value for the additive variance (σ2a) on d5 and the lowest on d302. A similar trend was estimated by Strabel and Jamrozik (2006) using fourth order Legendre polynomials for the additive effect of the animal.
Different results were reported by Fujii (2006), who found the lowest animal variance at the beginning of lactation, and the highest at its conclusion. This was similar to results for Holstein cows in Brazil, where 3, 4 and 5 orders Legendre polynomials were used for fixed effects, animal genetic, and permanent environment, respectively (Vieira, 2006). Similarly, permanent environment variance was found to sharply decrease for the first 30 days, remaining relatively constant for the majority of lactation, and increasing at the end of it (Fujii, 2006). Other studies have reported that permanent environment variance decreased from the start of lactation to 250 days, approximately, and increased at the end of it above the initial values (Strabel and Jamrozik, 2006).
Heritabilities found at the beginning and up to 150 days were greater than 0.30, indicating that considerable genetic variability exists in the studied population. Similar values were reported by Strabel and Jamrozik (2006) who found that the heritability curve increases as lactation proceeds to 150 days or so, decreasing slightly afterwards, and increasing at the end of the curve. Herrera et al. (2011), using ordinary test-day models for Holstein cows in Antioquia, found milk production heritability values of 0.31 for the first months of lactation, declining thereafter.
According to the present study, in the first five months of lactation animals express better their genetic potential (higher genetic variances and heritabilities), and after six months there are environmental effects which have a greater influence than the genetic factors. Although heritabilities were high during late lactation, standard errors were also high, mainly due to the reduction in the number of lactating animals and the exclusion of females reaching advanced pregnancy. The heritability curve for milk production in the evaluated population suggested that it is possible to achieve a greater efficiency in animal selection up to the first five months of lactation.
Gonzalez-Pena et al. (2007) and Olori et al. (1999) reported heritabilities greater than 0.50 for some stages of the lactation curve. These oscillations during lactation have no clear biological explanation. It is assumed that they can result from using higher-order functions to explain the random effects in the model. On the other hand, Albuquerque (2011), DeGroot et al. (2007), and Muir et al. (2007) reported lower heritabilities than those observed in this study, with values ranging between 0.10 and 0.16.
Genetic correlations for milk production between lactation days prior to day 215 were greater than 0.60. Similar results were found by Takma et al. (2007) and Olori et al. (1999) in Holstein cows at first calving where genetic correlations were high for consecutive days, decreasing as the interval between them increased.
Phenotypic correlations between start and end days of lactation (e.g., day 35 with 305, and 65 with 305) were close to zero and negative. These results are usually obtained with Legendre polynomials (Brotherstone et al., 2000; Cobuci, 2005; Gonzales- Herrera et al., 2008), because the parametric functions do not model the association between production at the beginning and at the end of the lactation curve. Small numbers of observations for the extreme ages, distance of the average and over parameterized models are reported as possible causes of these problems (de Sousa, et al., 2011).
It can be concluded that there is a high genetic variability for milk production of first-calving Holstein cows in Antioquia.
Notes
¤ To cite this article: Herrera AC, Múnera OD, Cerón- Muñoz MF. Variance components and genetic parameters for milk production of Holstein cattle in Antioquia (Colombia) using random regression models. Rev Colomb Cienc Pecu 2013; 26:90-97.
Acknowledgements
Financial support to this study was provided by Colciencias (Evaluación genético-económica de bovinos Holstein en sistemas de producción de leche en Antioquia).
References
Akaike H. A new look at the statiscal model identification. Trans Autom Control 1974; 19:716-723. [ Links ]
Albuquerque LG, Meyer K. Estimates of covariance functions for growth from birth to 630 days of age in Nelore cattle. J Anim Sci 2001; 79:2776-2789. [ Links ]
Bignardi AB, El Faro L, Cardoso VL, Machado PF, Albuquerque LG. Random regression models using different functions to model test-day milk yield of Brazilian Holstein cows. Gen and Mol Res 2011; 92:4634-4640. [ Links ]
Brotherstone S, White IM, Meyer K. Genetic modeling of daily yields using orthogonal polynomials and parametric curves. Anim Sci 2000; 70:407-415. [ Links ]
Cobuci JA, Costa CN, Braccini JN, Freitas AF. Genetic parameters for milk production by using random regression models with different alternatives of fixed regression modeling. Rev Bras Zootec 2011; 40:1397-1404. [ Links ]
Cobuci JA,Costa CN,Teixeira NM, Freitas AF. Utilização dos polinômios de Legendre e da função de Wilmink em avaliações genéticas para persistência na lactação de animais da raça Holandesa. Arq Bras de Med Vet e Zoot 2006; 58:614-623. [ Links ]
Cobuci, JA, Euclydes RF, Lopes PS, Costa CN, Torres RA, y Pereira CS. Estimation of genetic parameters for test-day milk yield in Holstein cows using a random regression model. Genet Mol Biol 2005; 28:75-83. [ Links ]
De Sousa JE, Almeida e Silva M, Sarmento JL, de Sousa WH, de Souza MS, Ferreira IC. Estimates of covariance functions for growth of Anglo-Nubian goats. Rev Bras Zootec 2011; 40:106- 114. [ Links ]
DeGroot BJ, Keown JF. Estimates of genetic parameters for Holstein cows for test-day yield traits with a random regression cubic spline model. Genet Mol Res 2007; 6:434-444. [ Links ]
Fujii SM. Comparison of homogeneity and heterogeneity of residual variance using random regression test-day models for first lactation Japanese Holstein cows. J Anim Sci 2006; 77:28- 32. [ Links ]
Gonzalez-Herrera LG, El Faro L, Albuquerque LG, Tonhati H, Cavallari C.H. Estimativas de parâmetros genéticos para produção de leite e persistência de lactações em vacas gir, aplicando modelos de regressão aleatória. Rev Bras Zootec 2008; 37:1584-1589. [ Links ]
González-Peña D, Espinoza JL, Palacios A y Luna de la Peña R. Estimación de componentes de (co)varianza para la producción de leche del día del control en ganado siboney utilizando un modelo de regresión aleatoria. INCI 2007; 32:702-706. [ Links ]
Henderson J. Analysis of covariance in the mixed model: higher level, nonhomogeneous, and random regressions. Biometrics 1982; 38:623-640. [ Links ]
Herrera AC, Múnera OD, Molina LM, Cerón-Muñoz MF. Componentes de varianza para producción de leche, grasa y proteína en el día de control en vacas Holstein del departamento de Antioquia. Rev Nac de Agron Med 2011; 64: S1-89:26-30. [ Links ]
ICAR. Frequency of milk visits. In: International agreement of recording practices. Section 2.3.15.2. 2002. [Acess date: January 3, 2012] URL: http://www.icar.org [ Links ]
Jamrozik JG, Kistemaker J. Comparison of possible covariates for use in a random regression model for analyses of test day yields. J Dairy Sci 1997; 80:2550-2556. [ Links ]
Kirkpatrick M, Lofsvold D, Bulmer M. Analysis of the inheritance, selection and evolution of growth trajectories. Genetics 1990; 124:979-993. [ Links ]
Kistemaker GJ . PhD Thesis. University of Guelph, 1997. pp26- 124. [ Links ]
Liu Z, Reinhardt F, Reents R. Estimating parameters of a random regression test day model for first three lactation milk production traits using the covariance function approach. Interbull Bull 2000; 25:74-80. [ Links ]
Mark T. Applied genetic evaluations for production and functional traits in dairy cattle. J Dairy Sci 2004; 87:2641-2652. [ Links ]
Meyer K. Estimates of genetic and phenotypic covariance functions for post weaning growth and mature weight of beef cows. J Anim Breed Genet 1999; 116:181-205. [ Links ]
Meyer K. Scope for a random regression model in genetic evaluation of beef cattle for growth. Livest Prod Sci 2004; 86:69-83. [ Links ]
Meyer K. WOMBAT- A program for mixed models analyses in quantitative genetics by REML. J Zhejiang Uni SCIENCE B. 2007; 8:815-821. [ Links ]
Muir BL, Kistemaker G. Genetic parameters for a multiple-trait multiple-lactation random regression test-day model in Italian Holsteins. J Dairy Sci 2007; 90:1564-1574. [ Links ]
Nunez-Anton V and Zimmerman DL. Modeling nonstationary longitudinal data. Biometrics 2000; 56:699-705. [ Links ]
Olori VE, Hill WG. Estimating variance components for test day milk records by restricted maximum likelihood with a random regression animal model. Liv Prod Sci 1999; 61:53-63. [ Links ]
Olori VE, Hill WG. The structure of the residual error variance of test day milk in random regression models. Interbull Bulletin; 1999a.p20:6-9. [ Links ]
Rodríguez-Zas S, Gianola D, Shook G. Evaluation of models for somatic cell score lactation patterns in Holsteins. Liv Prod Sci 2000; 67:19-30. [ Links ]
Schaeffer LR, Jamrozik J, Kistemaker GJ, Van Doormaal BJ. Experience with a test-day model. J Dairy Sci 2000; 83:1135- 1144. [ Links ]
Schaeffer LR, Dekkers JCM. Random regressions in animal models for test-day production in dairy cattle. Proceedings of the 5th World Congr Genet Appl Livest Prod, Guelph. 1994. p433-446. [ Links ]
Schwarz G. Estimating the dimension of a model. Ann Stat 1978; 6:461-464. [ Links ]
Strabel T, Misztal I. Genetic parameters for first and second lactation milk yields of Polish Black and White cattle with random regression. J Dairy Sci 1999; 82:2805–2810. [ Links ]
Strabel T, Jamrozik J. Genetic analysis of milk production traits of polish black and white cattle using large-scale random regression test-day models. J Dairy Sci 2006; 89:3152-3163. [ Links ]
Takma C, Akbas Y. Estimates of genetic parameters for test day milk yields of a Holstein Friesian herd in Turkey with random regression models. Arch Tierz Dummerstorf 2007; 4:327-336. [ Links ]
Van der Werf J. Random regression in animal breeding. Course notes. University of New England 2001; [Access date: June 1, 2011] URL: http://www-personal.une.edu.au/~jvanderw/CFcoursenotes.pdf [ Links ]
Veerkamp RF, Thompson R. A Covariance function for feed intake, live weight, and milk yield estimated using a random regression model. J Dairy Sci 1999; 82:1565–1573. [ Links ]
Vieira CT, Costa CN, Torres RA, Araújo SI, Lopes PS, Regáis AJ, Silva C, Araújo J, Rocha JL. Uso de funções ortogonais para descrever a produção de leite no dia de controle por meio de modelos de regressão aleatória. Rev Bras Zootec 2006; 35:967-974. [ Links ]