Introduction
The Wye Angus cattle herd was established in 1937. It was founded on 19 Aberdeen Angus animals; a bull and 18 heifers, ten of which were half-sisters, daughters of the same father. No other female was ever introduced into the herd. Between 1942 and 1958, 19 Angus bulls imported from the British Isles were introduced in the herd and are responsible for about 75% of its current germplasm (Lingle et al., 2001). The Wye Angus herd was transferred to the University of Maryland (USA) in 1979 and remains closed since 1958. The closed nature, reliable data documentation, strong, direct selection, and breadth and depth of the Wye Angus pedigree provide an excellent opportunity to understand the breeding mechanisms involved in the expression of productive and reproductive traits of this herd.
Recently, Monte Carlo methods based on Markov chains, such as the Gibbs sampler (Neal, 1993), have been used to provide a Bayesian probabilistic methodology to assess the genetic merit in an animal population by obtaining marginal distributions of the parameters of interest. When using a full relationship matrix, Bayesian inference allows to obtain breeding values and genetic parameters of populations that have gone through direct selection and preferred breeding.
Therefore, the main objective of this study was to evaluate parameters and genetic trends associated with the reproduction traits of the Wye Angus herd between 1937 and 2012.
Materials and Methods
The data were obtained from the Wye Research and Education Center, University of Maryland, MD, USA. We used pedigree information of 11.692 individuals from a closed Angus herd, born between 1937 and 2012, for scrotal circumference (SC) at weaning, age at first calving (AFC), and calving interval (CI) (Table 1).
Table 1 Descriptive analysis for Aberdeen Angus cattle.

N: number of observations; SD: standard deviation; Min: minimum; Max: maximum; A-1: animals in the relationship matrix; GG: number of contemporary groups (CG) for characteristics.
The (co)variance and breeding values were determined using uni- and bi- variate models and GIBBS3F90 software (Misztal, 2012). Contemporary groups were formed according to their gender and birth season (month and year), and groups containing less than five animals were not studied further.
For SC we used a model that included random genetic effects (direct and maternal), and permanent environmental effects on the (dam), the covariate age of the (dam) at calving (linear and quadratic), the animal’s age as covariate (linear), and the effect of contemporary groups. The matrix model used for SC was: y = Xβ + Zɑ + Mm + Wep + e. Where: y = is the vector of observations of the dependent variable (SC); β = is the vector of contemporary group, associated with y through the incidence matrix of X ; a = is the vector of random effects of additive genetic value of the animal associated with y through the incidence matrix Z; m = is the vector of random effects of maternal additive genetic value, associated with y through the incidence matrix M ; ep = vector of random effects of permanent environment (dam), associated with y through the incidence matrix W ; e = is the vector of residual effects. The contemporary group used for the SC model was equal to the other characteristics, however, excluding the female sex. For CI, the same effects were included, with the addition of permanent environmental effect on the animal. The matrix model was: y = Xβ + Zɑ + Wep + e. Where: y = is the vector of observations of the dependent variable (CI); β = is the vector of contemporary group, associated with y through the incidence matrix of X ; a = is the vector of random effects of additive genetic value of the animal associating a with y through the incidence matrix Z ; ep = is the vector of random effects of permanent environment of the animal associated with y through the incidence matrix W ; e = is the vector of residual effects.
The model for AFC included only the direct genetic effect and the effect of contemporary group. The matrix model was: y = X β + Zɑ + e . Where: y = vector of observations of the dependent variable (AFC); β = vector of contemporary group, associated with y through the incidence matrix of X ; a = vector of random effects of additive genetic value of the animal associated with y through the incidence matrix Z ; e = vector of residual effects.
For the Bayesian analysis the complete model used had the following assumptions: y|b,a,m,pm, e~N(X b +Z a +M m +W ep +I e );a|σ 2 a ~N(0 , Aσ 2 a);m|σ 2 m~N(0,Aσ 2 m );ep|σ 2 pm~N(0,IVσ 2 ep );e|σ 2 e ~N(0,INσ ² e). Where: σ 2 a, σ ² m, σ 2 ep and σ 2 e = are the additive genetic, maternal, permanent environmental, and residual variance components, respectively; A = is the numerator relationship matrix coefficient ; I = is the identity matrix of an order equal to the number of animals with observations.
For the Bayesian analysis, the effects included in the model were considered to be random variables. For the value of b, an informative a priori distribution based on bibliographic reference values for the breed in the study was assumed.
Estimates of genetic trends, direct and maternal, for the characteristics were obtained by linear regression of the average of the dependent variable (breeding values) over the birth year, obtained by the PROC REG of SAS software, version 8.2 (SAS Institute Inc., Cary, NC, USA; 2000).
For all traits, a single chain of 200,000 interactions was used, with a period of disposal (“burn-in”) with 20,000 iteractions, and a sampling interval (“thinning”) of 50. The convergence of the Gibbs chain was tested by the criterion of Geweke (Geweke, 1992), which diagnoses the convergence of the Markov chain based on equality test of the means of the first and last part of the Markov chain (usually the first 10, and the last 50%). The convergence of the algorithm was verified with a significance level of 5% for the test, under the null hypothesis. In this case, the test considers the null hypothess to be the convergence of the chain; therefore the larger the p-value (˃ 0.05) the greater is the convergence of the chain (Geweke, 1992).
Descriptive statistics and credibility intervals and/ or the high density interval were obtained using the BOA package from the R software (http://www.R-project.org). The high density interval provides the density range for the upper 95% of the sample. In addition to being a measure of reliability, this interval can also be applied to non-symmetric distributions (Hyndman, 1996).
Results
The means, medians and modes were similar for the estimates of the (co)variance components and genetic parameters for SC (Table 2). In contrast to the SC-related parameters, those of AFC and CI showed different results for the position measurements (Table 2), and non-symmetric distributions.
The genetic trend (provided by a linear regression) of the direct effect for SC was significant (p<0.0001), and equal to 0.0105 cm/year, equivalent to 0.66 cm over the 63 years of the study (Figure 1).
The genetic trend (as the linear regression) for AFC was not significant (p>0.0767) (Figure 2).
For CI, the genetic tendency (as the linear regression) was significant (p<0.0001) for the direct effect (-0.097 days/year) equivalent to -6.15 days of the 63-years study (Figure 3), and represented an annual decrease of 0.025% for the average of CI.
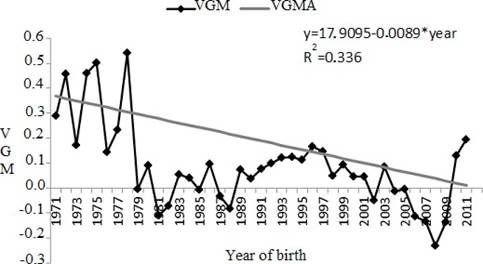
The genetic trend for maternal effect (as the linear regression) was significant (p<0.0001) for SC (Figure 4); however there was a decrease of-0.0089 cm/year.
Table 2 Genetic parameters for scrotal circumference (SC), age at first calving (AFC), and calving interval (CI) in the Wye Angus herd.
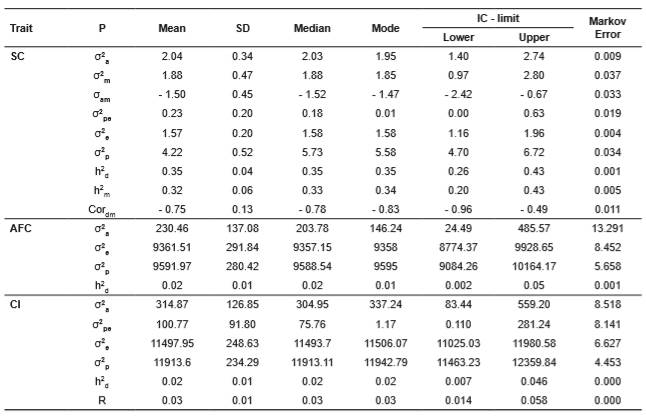
(1)σ2a: additive genetic variance; σ2m: maternal genetic variance; σam: covariance between direct and maternal effects; σ2pe: permanent environmental variance; σ2e: residual variance; σ2p: phenotypic variance; h2: direct heritability; h2m maternal heritability; Cordm: genetic correlation between direct and maternal effects, and R: repeatability; P: parameter. SD: standard deviation; IC: credibility interval.
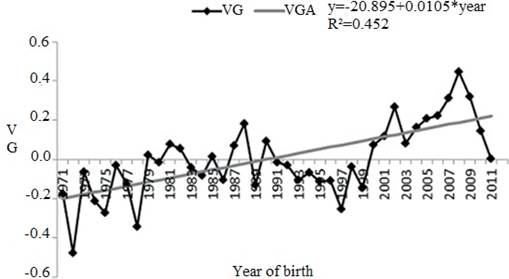
Figure 1 Genetic trend for scrotal circumference (SC) between 1971 and 2011. VG: genetic value in cm (scrotal circumference); VGA: genetic value in cm estimate from linear tendency (*p<0.0001).
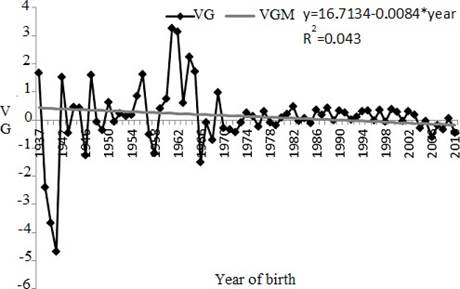
Figure 2 Genetic trend for age at first calving (AFC) between years 1937 and 2010. VG: genetic value in days (age at first calving); VGM: maternal genetic value in days estimate from linear tendency (* p>0.0767).
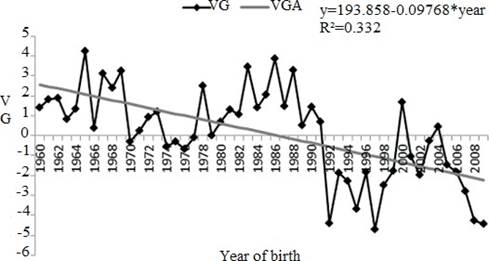
Figure 3 Genetic trend for calving interval (CI) between years 1960 and 2008. VG: genetic value in days (calving interval); VGA: genetic value in days estimate from linear tendency (* p<0.0001).
Discussion
The behavior of the SC is in accordance with that found by Carlin and Louis (2009), who claimed that similar estimates are expected for a marginal density when it is represented by a normal distribution. According to Wright et al. (2000), the mode is the most appropriate position measure for posterior distributions because it best reflects values of greater frequency (‘maximum distribution’). Therefore, we used the modal values of the parameters to describe the studied characteristics.
The magnitudes of the estimated heritability for SC indicate the possibility of obtaining genetic gain through direct selection. The estimate of direct heritability for CI indicating a lack of variability for direct selection. For this work, we emphasized the quality of the information and the depth and integrity of the pedigree database to obtain estimates of the (co)variance with small Markov errors for most measured traits.
The estimate of direct heritability for SC is close to the 0.33 reported by Carrillo and Siewerdt (2012), who used the Restricted Maximum Likelihood (REML) on the Wye Angus herd. The magnitude of the estimate of this parameter indicated that this trait suffered limited influence from the environment, and thereby allows use of SC as a selection criterion as it focuses mainly on semen quality and libido. In addition, others have claimed that SC is positively correlated with age at puberty, and age at first calving, and that such good results can be achieved by indirectly selecting for SC (Oliveira et al., 2007). Several authors have reported that heritability of SC is of medium to large magnitudes in several breeds, including, Aberdeen Angus (USA: Knights et al., 1984), Nellore (Yokoo et al., 2007), Canchim (Gianlorenço et al., 2003), Hereford (Brazil: Oliveira et al., 2004), and Hereford (USA: Evans et al., 1999). Currently, measurement of SC is often used as a selection criterion to improve reproductive efficiency in beef cattle, mainly because it is easy to measure, and has a medium to large heritabilities (Silva et al., 2000; Pereira et al. 2002; Gianlorenço et al. 2003).
The modal value for the direct heritability for AFC (0.01) indicates little possibility of genetic gain by direct selection. The small estimates for direct heritability of AFC reported in the literature (Talhari et al., 2003; Pereira et al., 2001; Vergara et al., 2009) indicate that AFC is minimally influenced by environmental and non-additive effects. Reports in the literature (Silveira et al., 2004; Dias et al., 2004) have identified several breeding-management factors that may contribute to the negligible effect of heredity on AFC, e.g., the time during the reproductive season that the heifers breed, and the length of the breeding season.
The Wye Angus herd has certain reproductive- management peculiarities that may have contributed to this small value, with the primary peculiarity being that in the past 30 - 40 years, breeding of the heifers often first occurs at ˂1 year of age, so that most heifers calve between 650 and 750 days of age. However, if a heifer did not become pregnant during the first breeding season, she remained barren for a year. This type of management may contribute to a large environmental variance, thereby reducing the heritability value. Models that use censored/penalized data can provide a measure of this parameter.
Similar values (0.08) for the heritability of AFC in Brazilian Nelore herds were reported by Pereira et al. (2010). Larger values for direct heritability of AFC and of CI were reported by Gutierrez and colleagues (2002), and Goyache and Gutierrez (2001) (AFC = 0.23 and 0.27, respectively, and CI = 0.12 in both cases) with data from herds of the Asturiana de los Valles breed estimated using the REML method, as did Vergara et al. (2009) (0.15) for Angus and crossbred Angus/Zebu cattle in Colombia. Also using the frequentist methodology and a model that did not include a component for the maternal effect, Bormann and Wilson (2010) estimated averaged heritabilities as 0.28 for US Angus cattle; however, these values increased to 0.66 when the maternal effect was included in the model because it increased the genetic variance.
Larger values for direct heritability of CI (both 0.12) were reported by Gutiérrez et al. (2002), Goyache and Gutierrez (2001) using data for Asturiana de los Valles cattle and the REML method. Vergara et al. (2009) reported a heritability value of 0.11 for the interval between the first and second calving, and a value of 0.18 for the interval between the second and third calving in Angus and crossbred Angus/Zebu cattle in Colombia. The small direct heritability value for CI that we found indicates that this trait is strongly influenced by environmental conditions; therefore, improvements in nutrition and reproductive management would probably have reduced the CI more than genetic selection.
One way of performing this monitoring is by determining the genetic progress of the population under selection (Boligon et al., 2007), as the genetic tendency measures the change caused by a selection process for certain characteristics over the years, and is the best way to observe the genetic progress. This increase over the years, although moderate, may be the result of direct selection for SC, which allows results for correlated reproductive traits to be obtained, including sexual precocity in males and females, and especially for libido and semen quality. In terms of the annual genetic change, it represented an increase of 0,049% over the average SC phenotype and demonstrated a genetic gain.
Laureano et al. (2011) also found a null genetic tendency (-0.003 days/year) between 1984 and 1995 in a Brazilian Nellore herd. However, from 1996 to 2006 the genetic trend improved (-3.024 days/year), indicating considerable reduction in the trait. The Wye Angus herd has sufficient genetic variability to obtain gain through selection on SC. The heritabilities for AFC and CI were~ 0 despite the limited genetic gain owing to CI. Because heritability of AFC and CI are minimal within the herd, it seems that reproductive management has achieved favorable breeding results for the heifers.