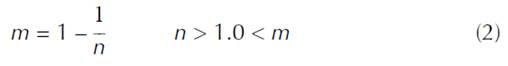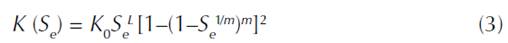INTRODUCTION
The agricultural applications of HYDRUS include irrigation, drainage design, salinization of irrigated lands, pesticide leaching and volatilization, virus movement in the soil subsurface, and the analysis of riparian systems. Typical non-agricultural problems include the design of radioactive waste disposal sites, contaminant leaching from landfills, design and analysis of capillary barriers, transport and degradation of chlorinated hydrocarbons, and recharging from deep vadose zones. Any of these applications, in principle, may involve the estimation of soil hydraulic parameters.
An effective system for measuring the hydraulic parameters is needed when they are used in predicting parameters for modeling the ecosystem and the movement of the groundwater. This is why such a system needs to contribute to these parameters when using modern irrigation techniques and different methods of fertilization. Mathematical models of the movement of water and salts are important tools for analysis and understanding However, using models is not easy, especially with the huge number of parameters that must be known before implementing them to fulfill their purpose. The success of forecasting and achieving high correlation depends on similar and identical parameters that appear clearly during the modeling process (Minasny & McBratney, 2002). Estimating hydraulic parameters requires great effort and work, and it takes a long time, be it by measurement in a laboratory or in the field. To overcome this problem, indirect methods have been used to predict soil hydraulic parameters, the most prominent being inverse modeling, which has yielded good results (Simunek et al., 1998a and Hopmans et al., 2002). Inverse modeling is one of the methods to predict many of these parameters through measurements of the water movement in the soil. With this information, functions can be predicted with high accuracy and flexibility. This method is a modern scientific technique based on secondary easy-to-measure characteristics associated with the parameters under study. It is more flexible than other methods, it is relatively simple to implement, and it can be assimilated to all experimental conditions (Hopmans et al., 2002). Inverse modeling has been characterized as an effective method for estimating soil hydraulic parameters, which is evidenced by a series of repeated measurements of soil moisture content during converged periods, where soil water movement models are linked with the best appropriate algorithm (Levenberg-Marquardt) in order to find the best set of constants to reduce error. It is an advanced method suitable for any range of sites, and it can accommodate differences in conditions such as the number of variables and the surrounding conditions, as well as being an innovative method that addresses the sensitivity of numerical solutions (Ritter et al., 2003; Simunek & van Genuchten, 2008).
Samani and Fatah (2009) and Simunek et al. (2011) used inverse modeling to find values for soil hydraulic parameters and stated that estimating these parameters in this way could result in a high degree of accuracy to predict the water movement and the heterogeneity of the groundwater level. The most important aspect of inverse modeling is its ability to analyze all changes in the porous system of the soil, as well as to give accurate predictions while having a high flexibility towards the data that is used. This method is considered to be the best simulating model because it is very sensitive when comparing the real measured parameter values with the predictions made (Simunek et al., 2012). Soil hydraulic parameters can also be obtained by means of inverse modeling procedures in HYDRUS-1D using simple water diffusion in soil columns. The derived parameters are capable of accurately describing water movement over extended periods of time, as well as alternative flow through the scenarios to which they were fitted (Kirkham et al., 2019).
Hachimi et al. (2019) used a direct and inverse method on the values obtained from the field measurements of cumulative infiltration and water contents to obtain soil hydraulic parameters. The results of their study showed a high correlation between the simulated and measured values, and they stated that that HYDRUS is highly efficient at predicting soil hydraulic parameters. Fujimaki and Yanagawa (2019) used the evaporation data from two tension meters to inversely determine water retention and hydraulic conductivity functions in a relatively low-cost and fast laboratory method for different soil textures. Amini et al. (2019) concluded that using the inverse procedure to determine soil hydraulic properties constituted a relatively simple and rapid reliable alternative method to estimate both soil water retention and hydraulic conductivity curves. Guellouz et al. (2020) used infiltration flow, soil water contents, and pressure heads, which were measured during ponded infiltration and internal drainage tests, as input data for the inverse problems. They also estimated unsaturated soil hydraulic parameters to predict water dynamic transport through a vertical soil profile under the effects of irrigation, drainage, and evapotranspiration, which is imperative for managing soils in arid regions.
The aim of this research is to use the inverse modeling of the HYDRUS-1D software to obtain the values of soil hydraulic parameters through water movement during evaporation in heterogeneous soils. This is carried out by determining the optimal evaporation time for optimal estimation processes, as well as by reducing the HYDRUS-1D software to the lowest possible period for calculation. The inverse model of estimated values for soil hydraulic properties can be validated as follows: (i) by comparing simulated cumulative infiltration with field data and (ii) with the degree of agreement between the water retention curves, which were computed from inverse simulated data, and the laboratory-measured data.
MATERIALS AND METHODS
Field and laboratory experiments
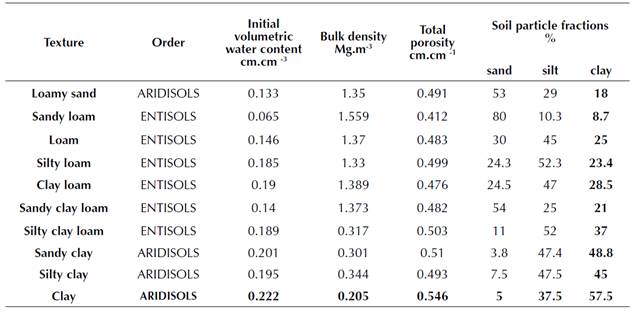
Ten surface samples, taken from 0-30 cm depths and with different textures ranging from sandy loam to clay (Figure 1, Table 1), were collected from different areas in the Nineveh Governorate in Iraq, 223 m above the sea level under semi-arid climate. Some physical properties of the soil were measured according to Klute (1986), as shown in Table 1. A pressure plate device (a Model 1500 pressure extractor from Soilmoisture Equipment Corp., CA, USA) was used to determine the characteristic tension curve under following pressures: 33. 100. 300. 500. 700. 900. 1100. and 1500 Kpa. The Mulaem-van Genuchten (MVG) equation was used, and its θs, θr, α, and n parameters were fitted from the water retention curve using Microsoft Excel and the nonlinear optimization technique. The soil bulk density was measured by means of cores with a 5 cm diameter and a 5 cm height.
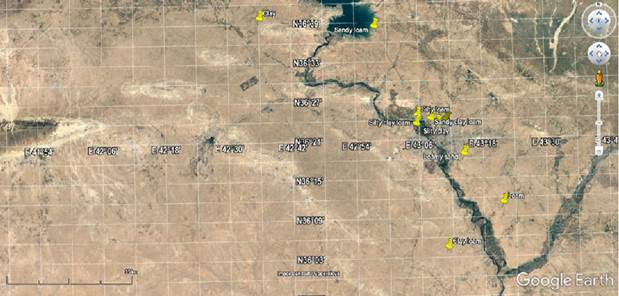
Figure 1 Map of the Nineveh Governorate in Iraq (36° 34’ N, 43° 13’ E) and the soil sample locations
Inverse modeling was carried out using the HYDRUS-1D software package (Simunek et al., 2013) to predict the soil hydraulic parameter values of θs, θr, α, and n, which were obtained from the change in moisture content values of soil water evaporation in a micro-lysimeter at laboratory temperature (a 25.4 cm diameter and 40 cm long cylinder filled with soils of different textures). Soil water evaporation was measured through the soil samples taken by a micro auger from the following depths: 0-5. 5-10. 10-15-, 15-50. and 20-30 cm. A plot of 2x2 m was used for measuring evaporation in the field at each of the four sites. The aforementioned soil samples were taken at the following times: 5. 10. 20. and 45 days. Simulation processes were carried out by feeding the program data according to the changing values of the soil moisture content.
Double rings with diameters of 0.3 and 0.6 m were used for measuring the water infiltration rate.
Soil hydraulic parameters
In this study, the MVG model (van Genuchten, 1980; Mualem, 1976) were used for the soil hydraulic functions, as shown in Equations (1) to (4).
where θ is the volumetric water content (L3L-3), K(h) is the hydraulic conductivity (LT-1), θr and θs the residual and saturated water content , Ks is the saturated hydraulic conductivity (LT-1), h is the soil water matric pressure head (L), α is the inverse of the bubbling pressure (1/L), n is the pore size distribution index, l is the pore connectivity parameter, m is the shape parameter of soil water characteristic, and Se is the effective saturation. The value of parameter l was considered to be 0.5. resulting from average conditions in a range of soils.
The θs, θr, α, and n parameters of the MVG model were fitted by the Excel Solver using a nonlinear optimization technique to minimize the sum of square error (SSE) between the measured and predicted values of soil water contents at h = 33. 100. 300. 500. 700. 900. 1100. and 1500 Kpa. The soil water retention curve, θ(h), was determined using the fitted MVG parameters (θs, θr, α, and n).
Theoretical background for inverse modeling
Hydraulic parameters of soil could be indirectly estimated from transient flow and/or transport using a parameter optimization approach. Minimizing the difference between the observed values and the predicted response of the system, which is known as the objective function, is typically the basis of inverse methods.
The numerical solution of the flow equation, the initial and boundary conditions, and some transport parameters and parameterized hydraulic functions all represent the system response. The Levenberg-Marquardt algorithm is used to improve the optimized system parameters, estimated initially by iteratively reducing the errors to achieve the objective function.
The data column outflow generated in the laboratory and the steady state water flow field transport data are obtained by applying this methodology. Simunek and van Genuchten (1999) and Simunek et al. (2013) are the references for conducting this methodology.
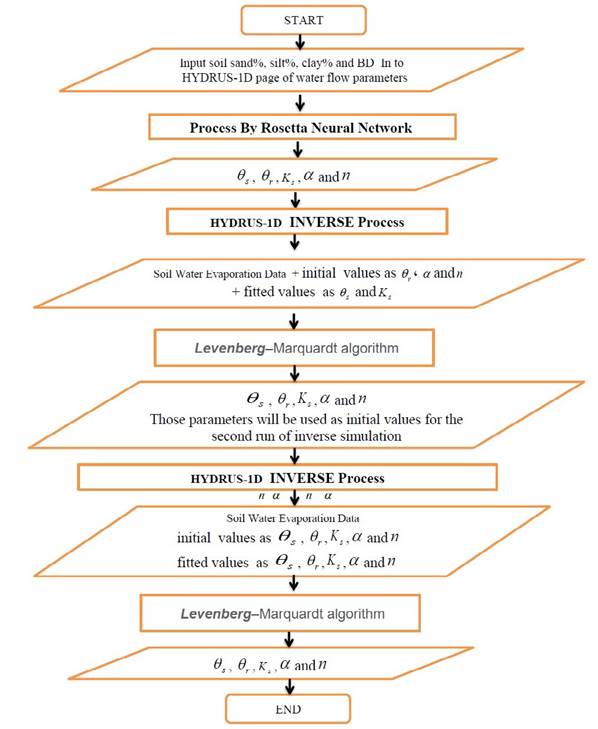
Special technique program
Many steps were performed on the HYDRUS -1D software to achieve inverse modeling and reduce the implementation time to the minimum period possible (1 to 5 seconds only). However, traditional methods can take many hours. This technique has been used successfully to obtain our results, as explained by the flowchart in Figure 2.
RESULTS
The measured and predicted values of the soil hydraulic parameters are shown in Table 2. These results showed a good agreement between the predicted and measured values. Nevertheless, it was noticed that all soil hydraulic parameters reported a low agreement between the measured and predicted values as the percentage of clay increased. The difference in the results was about 20%.
Table 2 Values of the soil hydraulic parameters for θs, θr, α, and n, measured and predicted using inverse modeling under field conditions at 5, 10, 20 and 45 days
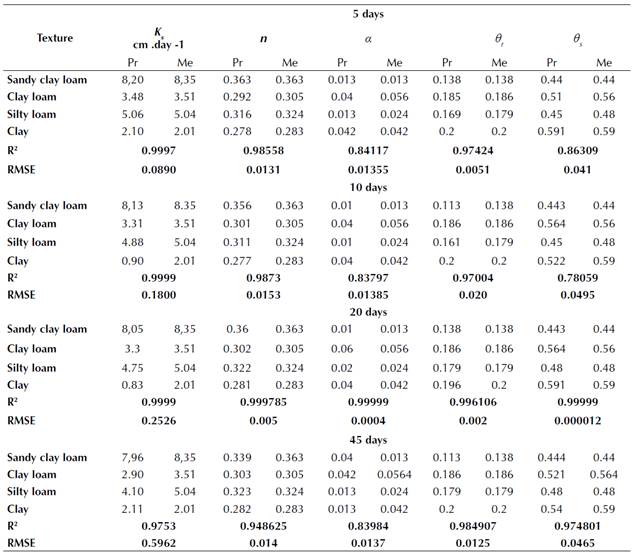
Pr=predicted Me=Measured
The predicted and measured saturated hydraulic conductivity values (Ks) during all the periods of evaporation measurement were in very good agreement, especially at 20 and 45 days, thus resulting in a coefficient of determination (R2) of 0.9998 and root mean square error (RMSE) values ranging from 0.341 to 0.6290. as shown in Table 3.
Table 3 Values of the soil hydraulic parameters for θs, θr, α, and n, measured and predicted using inverse modeling under laboratory conditions at 5, 10, 20 and 45 days
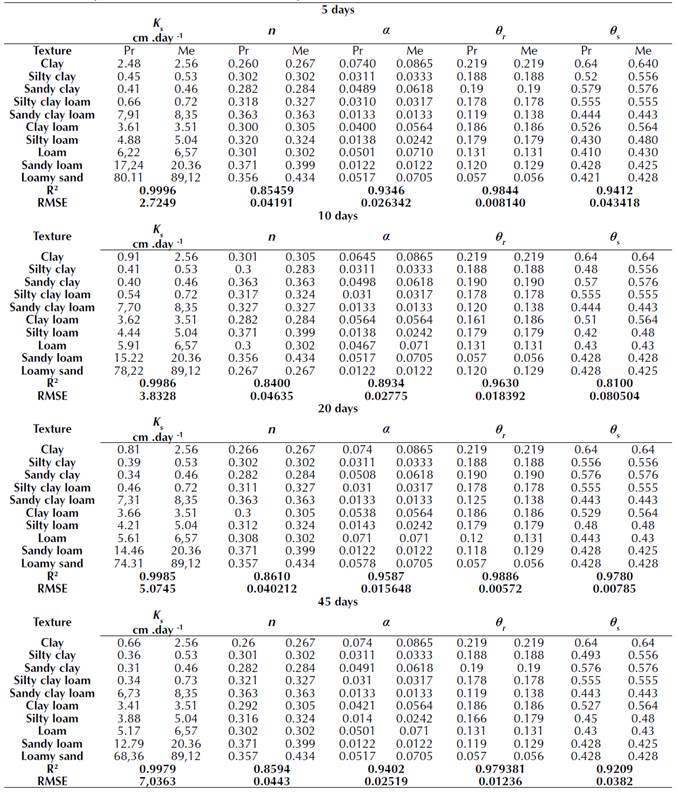
Pr=predicted Me=Measured
The deviation percentage between the measured and predicted values of Ks did not exceed 6% for all soil textures.
The laboratory measurements also showed a good agreement between the measured and the predicted values of hydraulic parameters when using inverse modeling by means of HYDEUS-1D, which is also the case for field measurements.
Table 4 showed a high correlation between θr and Ks, n and θs, and n and (θs, θr), as shown in the bold entries of Table 5. implying a significance level of 0.05. This Table also evidences a good correlation between θr, n, and Ks and each of the silt%, sand%, and soil bulk density.
Table 4 Correlation matrix and variance inflation factor between soil hydraulic parameters and some soil characteristics
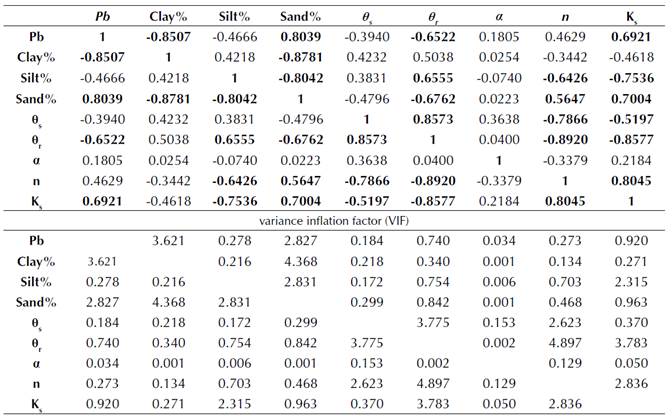
Note: bold entries mean a significance level of 0.05
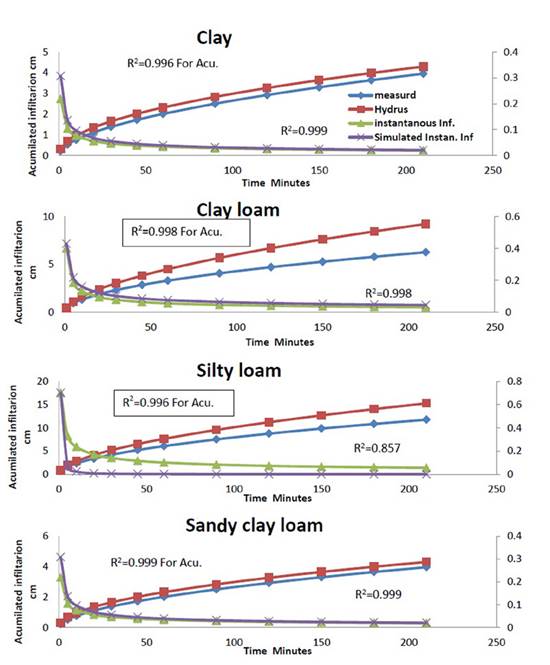
The predicted values of the hydraulic parameters were obtained through inverse simulation conducted in the laboratory with soil water evaporation measurement data for 5 days. These values were used to simulate and predict the soil water infiltration values using HYDRUS-1D (Figure 3).
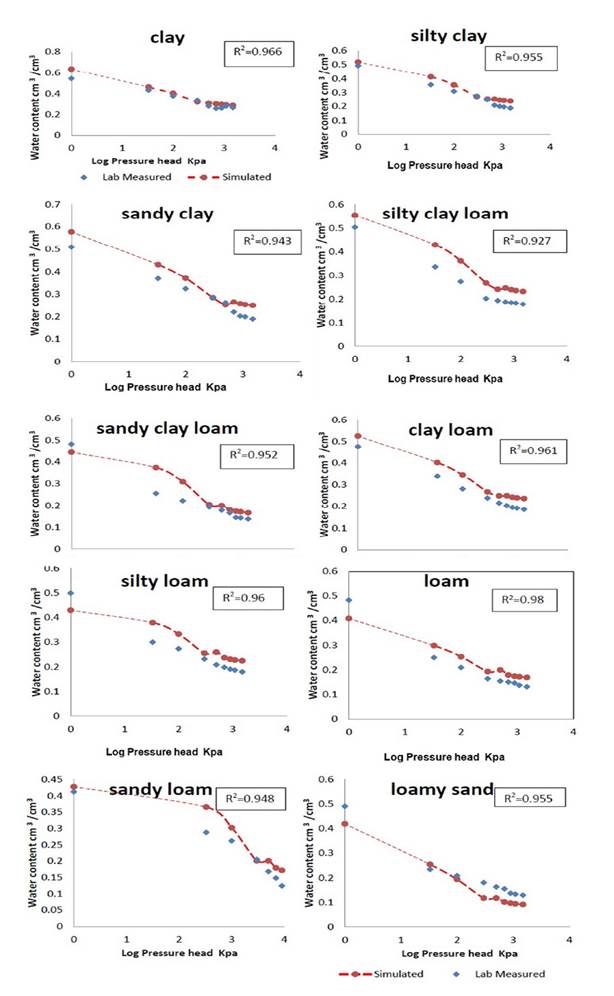
Figure 4 shows the soil moisture characteristic tension curve, which was computed using the van Genuchten parameters from Table 3. These results show a different degree of agreement between the predicted and measured water content values.
DISCUSSION
The measured and predicted values of the soil hydraulic parameters shown in Table 2 show a good agreement between the predicted and the measured values, with a coefficient of determination (R2) ranging from 0.78 to 0.9999, and the values of the root mean square error (RMSE) ranging from to an extremely small value of 0.000012 up to 0.146. However, the highest and the lowest values of both the R2 and RMSE (0.99 and 0.00012. respectively) were obtained at 20 days of evaporation. These results agree with Minasny and McBratney (2002) and Simunek et al. (2012) who indicated the possibility of using inverse modeling to predict the values of some soil hydraulic parameters under field conditions. The low agreement resulting from the simulation of the parameter n at 10 and 45 days of evaporation meant the lowest and highest values for R2 and RMSE (0.948 and 0.0153. respectively). Moreover, the results showed a good agreement between the predicted and the measured values of Ks for all periods of evaporation. The values of R2 ranged from 0.975 to 0.999, but the RMSE values ranging from 0.18 to 0.25 at two measurement periods (10 and 20 days in the relay). The estimation of the values of θr, Ks, and n is predominantly better than that for θs and α over the entire periods of evaporation measurement (Table 2). The predicted values of the soil hydraulic parameters (θs, θr, α, and n obtained through inverse modeling were close to the measured ones. This is due to the capabilities of the HYDRUS-1D software concerning inverse modeling for field conditions and soil characteristics. Moreover, this method yielded the least variations and had a high accuracy. These results are validated by Hopmans et al. (2002), Simunek and van Genuchten (2008), Samani and Fathi (2009), and Simunek et al. (2012). Moreover, they allow stating that inverse modeling is simple to implement and does not take a long time. It also constitutes a predictive function with high flexibility and precision under field conditions.
The θs, n, α, and θr values, which were predicted through the inverse modeling under laboratory conditions were close to their measured values. This was confirmed by the statistical indices (the R2 ranged from 0.81 to 0.99, and the RMSE ranged from 0.0057 to 0.6291). The highest correlation appeared at 20 days of evaporation measurement. These results confirm the efficiency of inverse modeling on the HYDRUS software to predict van Genuchten equation parameters, as indicated by Kelleners et al. (2005), Scharnagl et al. (2011), Simunek et al. (2011), and Schelle et al. (2012).
The results in Table 4 showed a high correlation between θ r and K s , and also between n and θ s . which indicate parameter nonuniqueness and a correspondingly high uncertainty these results agree with the Kirkham et al (2019), also a good correlation between the paramters of θ r , n , and K s with each of the silt %, sand% and soil bulk density,can be used to a predicte these soil hydraulic parameters values from the routin soil analysis. This correlation can be used to predict soil hydraulic parameter values. This result agrees with Mohammed et al. (2019), who used Artificial Neural Networks (ANNs) to estimate soil hydraulic parameters from some soil characteristics with high accuracy. The values of variance inflation factor (VIF) in Table 4 show that there was no multicollinearity between the variables under study, as the values were less than 10.
The predicted and measured values of the cumulative infiltration curves and the instantaneous infiltration rate showed a good agreement for all soils of different textures under study, with R2 values ranging from 0.998 to 0.999 (Figure 4). These results agree with those in Amini et al. (2020).
The values of the van Genuchten parameters in Table 3 were used to obtain the soil moisture characteristic tension curve, and they were compared with measured values, thus showing a good agreement between them, with R2 values ranging from 0.927 to 0.981 (Figure 4). A little variation is noticed between predicted and measured values of the soil water retention curves, which may be due to the soil hysteresis phenomenon, as mentioned by Rezaei et al. (2016).
Several pressure heads were used to predict the moisture content of all soil samples with ten different soil textures. Different degrees of agreement were found, as it can be noticed from the R2 (0.6130. 0.8609, 0.8574. 0.8780. 0.8732. 0.9559, 0.9045. 0.8828, and 0.9085) and the RMSE values (0.053. 0.042. 0.025. 0.028, 0.020. 0.034. 0.039, 0.039, and 0.042) for soil water content at pressure heads of 33. 100. 300. 500. 700. 900. 1.100. and 1.500 Kpa, respectively. The lowest and highest agreement between the predicted and measured values of the water content were obtained at pressures of 0 and 700 Kpa in ten different soil textures. The variation of these results may be due to the anisotropy of the soil, as reported by Šimůnek et al. (1998b), who argued that “the overprediction of θs for the inverse solution could be caused by the anisotropy of the soil” as they work on parameter estimation of the hydraulic properties of unsaturated soil.
CONCLUSIONS
Inverse modeling using the HYDRUS-1D software could be used successfully and accurately with low computation times to predict some soil hydraulic parameters from data obtained from soil water evaporation measured both in the field and in a laboratory. This showed a good agreement relationship with the measured data for the ten different soil textures.
The inverse model of HYDRUS-1D was used with high accuracy to predict the accumulated infiltration values from soil water evaporation data for 5 days in a laboratory experiment.
Meanwhile, this model was applied to the predicted van Genuchten parameters to get the volumetric soil water content at each different pressure heads, thus resulting in a good agreement with the measured values. The inverse modeling procedure using laboratory soil evaporation data was very good for predicting some soil hydraulic parameters and estimating a cumulative infiltration and soil water retention curve with a relatively fast, simple, and reliable alternative method, in addition to reducing the costs and time of determining laboratory and field measurements.