** Mágister en Ingeniería de Sistemas. Docente Facultad de Ingeniería, Universidad de Antioquia, Medellín, Colombia. amarin@udea.edu.co

*** Doctor en Ingeniería de Sistemas. Director de áreas de programas curriculares de la Facultad de Minas, Universidad Nacional de Colombia, Medellín, Colombia.. jwbranch@unalmed.edu.co

Con la facilidad que da la Internet y, en particular la Web, cada día es más fácil acceder a nuevas fuentes de información puestas a disposición en cualquier lugar del mundo. Los usuarios buscan información específica de acuerdo a sus necesidades particulares, a través de la Web. Ellos pueden hacer búsquedas ya sea mediante motores de búsqueda tales como Google o Yahoo!, o también mediante bases de datos particulares de bibliotecas o sistemas de información. Sin embargo, los resultados de consultas en motores de búsqueda, sistemas de catálogos de acceso público en línea, y en general sistemas de consulta en la Web, pueden saturar a un usuario por la abundancia de resultados, causando pérdida de efectividad del sistema de búsqueda. Para resolver este problema, la investigación "Agrupamiento de resultados obtenidos de consultas distribuidas en sistemas de catálogos públicos en línea (OPAC)", de la que se deriva este artículo, propone dos algoritmos de agrupamiento de resultados orientados a sistemas en línea concurrentes, con características de bajo consumo de ciclos de procesador y memoria, los cuales se usan en un prototipo de software.

Palabras clave: k-means, clustering, OPACS, data mining, information retrieval.

Cómo citar este artículo: MARíN, Andrés y BRANCH B, John W. Aplicación de dos nuevos algoritmos para agrupar resultados de búsquedas en sistemas de catálogos públicos en línea (OPAC). Revista Interamericana de Bibliotecología. Ene.-Jun. 2008, vol. 31, no. 1, p. 47-65.

Abstract

With the ease of Internet use, and particularly the Web, today it is easier to gain access to new information sources available in anywhere in the world. Through the web, users search for specific information according to their own necessities. They may search either by means of search machines, such as Google and Yahoo, or specific library data bases or information systems. However, information seeking results on searching machines, online public access catalog systems, and in general, on the web search system can saturate a user because of the abundance of results, which leads to a loss of effectiveness. To solve this problem, the research "Agrupamiento de resultados obtenidos de consultas distribuidas en sistemas de catálogos públicos en línea (OPAC)", from which this paper derives, proposes two results clustering algorithms focused on concurrent online systems characterized by low consume of processor and memory cycles, which are used in a prototype of software.

Key words: k-means, clustering algorithm, OPACS, data mining, information retrieval

How to cite this article: MARíN, Andrés y BRANCH B, John W Application of two new algorithms to group search results in on line public access catalogs (OPAC). Revista Interamericana de Bibliotecología. Ene.-Jun. 2008, vol. 31, no. 1, p. 47-65.

El acceso público a los catálogos de las bibliotecas ha venido cambiando el perfil de los usuarios de dichos catálogos. Mientras que antes eran más frecuentados por personal capacitado en bibliotecología, ahora los mismos catálogos son mas frecuentados por los usuarios directos de la información buscada. Los usuarios con el nuevo perfil no tienen un conocimiento de los modelos de interfaz, de almacenamiento y de codificación empleados en los catálogos en línea; ellos sólo cuentan, en ciertos casos, con una idea vaga del material documental que requieren. Estos usuarios, al emplear los catálogos bibliotecarios en línea, encuentran así una serie de dificultades que les impiden encontrar documentos relevantes para sus intenciones de búsqueda.

El agrupamiento de datos ha sido investigado en varias áreas del conocimiento, particularmente en minería de textos y recuperación de información [13]. El agrupamiento no supervisado ha sido propuesto para examinar una colección de documentos o para organizar resultados retornados por un motor de búsqueda ante una consulta de un usuario [2][5][22]. Recientemente se habla de documentos de naturaleza efímera, que son aquellos obtenidos dinámicamente como resultados de búsquedas ante consultas de usuarios sobre la Web o sistemas de catálogos de acceso público en línea [8]. El agrupamiento de este tipo de documentos introduce nuevos requerimientos; específicamente se requieren algoritmos muy rápidos, dado que en sistemas en línea no se debe obligar al usuario a esperar demasiado tiempo. Nosotros proponemos dos nuevas variantes del algoritmo K-means [3] que toman ventaja de una representación binaria de datos para obtener grupos en un tiempo lineal pero con menos requerimientos de memoria que el algoritmo bisecting-K-means [17].

Este artículo se organiza como sigue: en la sección 2 se plantea la situación problemática, en la sección 3 se presenta el marco teórico, en la sección 4 se dan detalles de los algoritmos propuestos, en la sección 5 se muestra un ejemplo de resultados con el prototipo desarrollado, en la sección 6 se presentan los experimentos y los resultados obtenidos y en la sección 7, las conclusiones y trabajos futuros.

Con las facilidades que da la red Internet, y en particular la Web, cada día es más fácil acceder a nuevas fuentes de información puestas a disposición en cualquier lugar del mundo. Los usuarios requieren buscar información específica de acuerdo a sus necesidades particulares, a través de la Web. Ellos pueden hacer búsquedas, ya sea mediante motores de búsqueda tales como google o yahoo! entre otros, o también mediante bases de datos particulares de bibliotecas o sistemas de información. Esta facilidad de acceso a distintas fuentes de información, trae consigo la dificultad de causar una sobresaturación de información al usuario, debido a la abundancia de resultados que se puede obtener al efectuar una consulta determinada.

En estudios sobre sistemas de catálogos de acceso público en línea Opac se han detectado dificultades que se pueden mirar desde dos puntos de vista; primero desde la interfaz de sistema Opac e interacción hombre máquina; y segundo, desde el método interno de búsqueda y recuperación de información. Con respecto al primer punto de vista se han encontrado problemas con el uso de los operadores de tipo lógico o booleano, los cuales, a pesar de ser usados corrientemente en nuestro vocabulario, no son bien utilizados por los usuarios en los sistemas Opac, lo cual puede causar que el sistema retorne muchos resultados, muchos de ellos no relevantes o que el sistema retorne cero o pocos resultados quedando por fuera otros posibles resultados relevantes. Otros problemas ocurren cuando la búsqueda produce demasiados resultados, con lo que, aparte de consumir mucho tiempo de cómputo, el usuario se puede saturar ante una vasta cantidad de resultados, además que poco se usan las opciones avanzadas de búsqueda que permiten filtrar los resultados.

Estas dificultades aun persisten cuando los usuarios efectúan consultas [1][11][10][20], especialmente porque las bibliotecas usan vocabularios controlados y normalizados al incluir nuevos materiales a sus sistemas de información, y estos vocabularios no necesariamente son conocidos por usuarios finales. El usuario, al intentar obtener resultados no nulos, usualmente adopta una estrategia de búsqueda general, pero esto implica que muchos de los resultados de su búsqueda no serán relevantes y el orden en que estos resultados le son entregados no necesariamente será el más adecuado para él. La idea de usar técnicas de agrupamiento de resultados para mejorar los niveles de relevancia ya ha sido solicitada por especialistas en bibliotecas, como característica que debe ser tenida en cuenta para las interfaces de usuario sobre sistemas de consulta [9]. Por otra parte, en consultas hechas sobre motores de búsqueda en la Web, si los términos de búsqueda son muy generales, los resultados igualmente pueden ser muy generales y numerosos. El agrupamiento de estos resultados obtenidos de búsquedas sobre la Web ha sido propuesto en varios estudios [22][8][21].

Se quiere plantear un método de agrupamiento no supervisado, orientado hacia sistemas en línea con documentos efímeros que, por una parte sea veloz, y por otra que consuma pocos recursos de memoria con el fin de poder atender a múltiples usuarios concurrentes en un mismo sistema.

3. Marco teórico

3.1. Modelo de espacio vectorial

El modelo de espacio vectorial ó vector space model (VSM) en Inglés, se basa en el álgebra lineal y trata los documentos y las consultas de usuario como vectores de números, los cuales contienen los valores correspondientes a la ocurrencia de palabras o términos en sus documentos respectivos [14]. Sea t el número de términos y n el número de documentos. Entonces, tanto una consulta Q así como todos los documentos D_i , i = 1 . . . n, se pueden representar como vectores t-dimensionales así: D_i= [a_i1, a_i2, . . . , a_it] y Q = [a_q1, a_q2, . . . , a_qt] en donde los coeficientes aik y aqk representan los valores asociados del término k en el documento Di o consulta Q, respectivamente [15].

Los valores en las posiciones individuales de los vectores de documentos corresponden a la ocurrencia de términos en estos documentos. Estos valores llamados pesos, describen la importancia del término en el contexto global del documento. El mismo término puede tener diferentes pesos en diferentes documentos. El método más simple para asignar pesos es el binario, esto es, si el término aparece en el documento irá un 1, de lo contrario iría un 0. Este método puede causar que se pierda información valiosa en grandes colecciones de documentos porque sólo se sabe que el término está o no está, pero se desconoce si se utiliza muchas o pocas veces, es decir, no se sabe qué tan importante es pero requiere mínimos recursos de almacenamiento computacional. Otro método es el de frecuencia de términos o tf, que asigna a cada posición del vector, un valor igual al número de ocurrencias del término dentro del documento correspondiente. Para minimizar el crecimiento lineal en el valor del término, se pueden usar raíces cuadradas o normalizaciones. Este método puede mostrar cómo es la frecuencia de un término con respecto a la colección completa de documentos.

Mediante la representación vectorial, el encontrar documentos relevantes a una consulta o saber qué tan similar es un documento con respecto a otro, se traducen en el cálculo de un valor de similaridad o distancia. La medida de similaridad más usada es el coeficiente coseno, el cual es igual al coseno del ángulo de los dos vectores t-dimensionales que se comparan [15] (Ver Tabla 1).

El uso de esta representación matricial es ventajoso debido a que el soporte del álgebra lineal permite fácilmente ejecutar operaciones matemáticas. Además, se pueden usar estructuras de datos simples y eficientes, se pueden usar arreglos y matrices dispersas.

Una desventaja de este modelo es que se pierde la estructura original de los documentos, porque el modelo espacio vectorial solamente guarda la ocurrencia de palabras en documentos y no considera el orden de los términos, tampoco maneja información sobre la proximidad entre palabras, esto es, no utiliza el contexto de los términos para mejorar las consultas.

3.2. Agrupamiento no supervisado

Un proceso de agrupamiento consiste en el particionamiento de datos en diferentes grupos o clusters de instancias de datos, de tal forma que primero, cada grupo contenga instancias que sean muy similares o cercanas entre sí, y segundo, las instancias en cada grupo sean muy diferentes o lejanas de las instancias en el resto de los grupos. Un algoritmo de agrupamiento debe maximizar la similaridad dentro del grupo y minimizarla entre diferentes grupos. Además, es importante lograr obtener un pequeÑo número de grupos, incrementando el número de instancias de datos asignado a un grupo. Se busca lograr un buen equilibrio entre la similaridad alta al interior de los grupos, similaridad baja entre los grupos y un número pequeÑo de grupos.

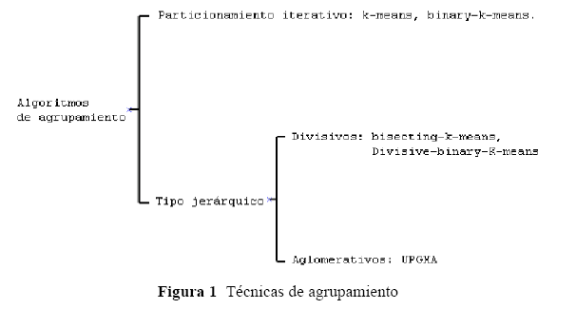
Dos de los tipos más populares de algoritmos de agrupamiento son: particionamiento iterativo y agrupamiento jerárquico (Ver Figura 1). Los algoritmos de tipo particionamiento iterativo, a su vez, se pueden subdividir en agrupamientos sin traslapo y con traslapo, mientras que los de tipo jerárquico se pueden subdividir en métodos aglomerativos y métodos divisivos. [3]

El algoritmo k-means es la técnica más empleada de particionamiento iterativo. El k-means particiona los datos dentro de K grupos, donde K es un parámetro que específica el usuario. Cada grupo se caracteriza por su centroide o centro que representa una media entre los elementos del grupo. El algoritmo comienza con K centroides, escogidos arbitrariamente, e iterativamente ejecuta los siguientes dos pasos: primero, asignar cada dato al grupo cuyo centroide sea más cercano al dato, y segundo, calcular los nuevos centroides de cada grupo. Los dos anteriores pasos se ejecutan hasta que ningún dato se mueva de un grupo a otro.

Dentro de las técnicas de agrupamiento de tipo jerárquico, las aglomerativas comienzan asignando cada instancia de datos a un grupo y entonces, iterativamente, mezclan los dos grupos más similares o cercanos entre sí, hasta que quede un solo grupo conteniendo todas las instancias de los datos que están siendo procesados. Este proceso se ejecuta iterativamente hasta que se obtiene un solo grupo que contiene todos los datos de partida. Este resultado se expresa en forma de un dendograma con su raíz en el tope, en otras palabras, una jerarquía. La única diferencia real entre los diferentes esquemas jerárquicos está en la forma cómo ellos escogen cuál de los grupos van a combinar, y esto depende de cómo se calcula la similaridad de los grupos. Por otra parte, las técnicas divisivas hacen el trabajo en forma inversa, es decir, comienzan asignando todos los datos a un grupo, entonces este grupo es subdividido iterativamente en grupos cada vez más pequeÑos, y a cada nuevo grupo se le hace nuevamente el proceso hasta que queden grupos de un solo elemento.

La efectividad de un algoritmo de agrupamiento depende de la forma y tamaÑo de los grupos naturales que están contenidos en los datos procesados. La mayoría de los métodos presupone alguna estructura de datos y no tratan de inferir la estructura de los datos. Por lo anterior, no se puede afirmar que un método es mejor que otro, o que un mismo método funcionará siempre bien, porque la calidad de los resultados que se obtengan dependerá tanto de las presunciones del método mismo como de los datos.

Para mirar la bondad de un agrupamiento se usan dos tipos de medidas. El primer tipo de medida permite comparar diferentes conjuntos de grupos sin referencia a un conocimiento externo, el cual se denomina medida de calidad interna del agrupamiento. El segundo tipo de medidas, las de calidad externa, permite evaluar qué tan buenos son los resultados de un algoritmo de agrupamiento con respecto a clases ya conocidas. Una medida de calidad externa es la entropía propuesta por Shannon en los inicios de la computación [16], la cual da una medida de la bondad de grupos no solapados. Sea C una solución de agrupamiento, para el grupo j la entropía se obtiene según la fórmula 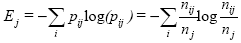, donde p _ij es la probabilidad de que un miembro del grupo j pertenezca a la clase i, i representa a cada una de las clases, n _ij es el número de miembros de la clase i en el grupo j y n_j y es el número de miembros del grupo j. La entropía total para un conjunto de grupos se calcula como la suma de las entropías de cada grupo, ponderada por el tamaÑo de cada grupo, según la fórmula 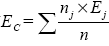, donde n_j es el tamaÑo del grupo j, m es el número de grupos y n el número total de puntos totales.

En el presente trabajo se establece que la representación de la frecuencia de términos en el modelo del vector espacial usará valores binarios con el fin de ahorrar almacenamiento y disminuir tiempo de cómputo. Se trata de considerar un método de agrupamiento que sea rápido y dé grupos de calidad aceptable. Inicialmente se propone el algoritmo binary-K-means, el cual es una variante del algoritmo k-means [3]. Nuestra propuesta es diferente a la de Neschen [12] porque permite definir como parámetro el grado de aceptación de términos en el centroide. Sea N el número de documentos, T el número total de términos o palabras de la colección, G el número de grupos deseados, P es el porcentaje de aceptación que permite decidir si un término será o no considerado en el centroide dependiendo de la relación entre el número de ocurrencias del término en los documentos del grupo y el número de documentos del grupo, M_KxN es la matriz binaria que contiene las instancias de datos que van a ser agrupadas, cada columna en M representa un documento particular y existirá una fila que corresponde a cada palabra de la colección total. Los pasos del algoritmo son:

1. Escoger los centroides iniciales. Sea , los vectores centroides, uno para cada grupo, inicialmente ellos se seleccionan al azar dentro de los documentos representados en M, esto es C_K=m_j, donde m_j es una columna de M escogida al azar, tal que m_j no haya sido generada como centroide inicial de otro grupo

2. Buscar el centroide más cercano a cada documento. Esto es, para todo m_j de M, asignar m_i al grupo más cercano, dado por máxima(similaridad 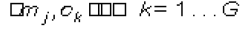. La similaridad se calcula con la fórmula 1.

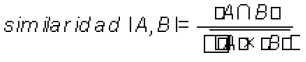
La similaridad es un valor entre 0 y 1; 0 indica que no hay similaridad y 1 indica que hay similaridad total entre los documentos comparados.

3. Obtener los nuevos centroides de cada grupo. Para todos los grupos, recalcular C_k de esta forma: sea 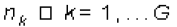el número de documentos en cada grupo.

Sea 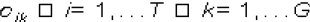el bit correspondiente en C_k para cada término i en el documento. Sea 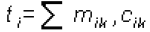será 1 si se cumple que 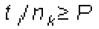, es decir, la relación entre número de términos con el mismo bit en 1 del grupo es mayor o igual que el porcentaje de aceptación, de lo contrario C_ik, será 0. Si algún 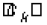es 0, seleccionar un nuevo centroide, tal como se hace en el paso 1.

Repetir los pasos 2 y 3, hasta que los centroides no cambien.

La principal ventaja del algoritmo de agrupamiento binary-K-means es que su complejidad computacional es lineal 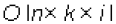donde n es el número de documentos, k es el número de grupos y i es el número de iteraciones. Los requerimientos de almacenamiento en memoria son muy bajos, sólo t_xn bits para la matriz M y t_xn bits para los centroides de los grupos. La principal desventaja del algoritmo binary-K-means es que, en algunos casos, el algoritmo puede no converger, esto es, permanece en una oscilación cíclica de tal forma que los centroides siempre cambian y nunca se llega a satisfacer la condición de terminación. Por otro lado, la selección de los centroides iniciales afecta la calidad del resultado de los agrupamientos. También se puede tender a que haya grupos con muchos documentos y a la vez que existan otros grupos de muy pocos documentos. Esto último es una característica poco deseable para un usuario final en un sistema de navegación de resultados obtenidos ante una consulta.

4.2 Algoritmo Divisive-Binary-K-means

Steinbach, en un estudio reciente [17], compara experimentalmente varias técnicas de agrupamiento y propone la variante Bisecting-k-means del algoritmo k-means, que consiste en partir en dos grupos un conjunto de documentos usando el algoritmo k-means; luego, con algún criterio, seleccionar uno de los grupos y partirlo igualmente, repitiendo estos pasos hasta alcanzar el número de grupos deseado. El algoritmo Bisecting-k-means es superior al algoritmo k-means debido a que obtiene unos grupos de tamaÑos más homogéneos y de mejor calidad respecto a la entropía; sus autores afirman también, que producen jerarquías de documentos ligeramente mejores que las obtenidas por técnicas tradicionalmente consideradas superiores, como el algoritmo UPGMA jerárquico. Por otra parte, la complejidad computacional del algoritmo Bisecting-K-means es O(n) comparada contra O(n2) de una técnica aglomerativa jerarquizada UPGMA según lo afirma Steinbach.

Se propone la variante Divisive-Binary-K-means, la cual aprovecha las ventajas del algoritmo Binary-K-means, junto con las ventajas del algoritmo Bisecting-K-means [17], es decir rapidez, dada la complejidad computacional del Bisecting-K-means y disminución significativa de los requerimientos de almacenamiento, pues en vez de requerirse el uso de variables float de, por ejemplo, 2 bytes, sólo se requieren variables binarias.

Sea N el número de documentos, T el número total de términos o palabras de la colección, G el número de grupos deseados, P es el porcentaje de aceptación que permite decidir si un término será o no considerado en el centroide dependiendo de la relación entre el número de ocurrencias del término en los documentos del grupo y el número de documentos del grupo, MTxN es la matriz binaria que contiene las instancias de datos que van a ser agrupadas, cada columna en M representa un documento particular y existirá una fila que corresponde a cada palabra de la colección total. Los pasos del algoritmo son:

1. Se parte de un único grupo en el cual se encuentran todos los documentos, se ejecuta el algoritmo binary-K-means para obtener dos grupos M₁ y M₂ es decir ,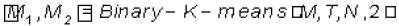 . Sea NGO = 2 una variable que representa el número de grupos obtenidos.

2. Repetir mientras NGO < G : seleccionar un grupo a dividir Mj y aplicarle 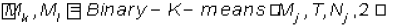donde Mj representa los documentos del grupo seleccionado, Nj es el número de documentos de dicho grupo, tal que,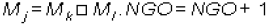

El criterio para seleccionar qué grupo dividir viene dado por la fórmula 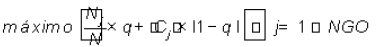, donde Nj es el número de documentos del grupo j, |Cj | es la magnitud del centroide del grupo j, q es un valor aleatorio real entre 0 y 1 obtenido para la iteración actual que evita que el algoritmo se quede iterando cíclicamente y no converja pues el algoritmo Binary - K - means puede generar uno de los grupos vacíos.

Con el fin de probar la aplicabilidad de los algoritmos presentados anteriormente sobre sistemas Opac, se desarrolló un prototipo de software. El software permite a un usuario final plantear una consulta general y obtener los resultados de su consulta en forma agrupada. El usuario define como parámetro de entrada adicional, el número de grupos que desea obtener. Cada grupo resultante consta de una identificación del grupo, una relación con los títulos pertenecientes al grupo y los términos principales que caracterizan al grupo. Cada título, a su vez, es un enlace al registro completo del título dentro de la colección o ficha bibliográfica.

Para el desarrollo del prototipo se utilizó la colección de datos del sistema de bibliotecas de la Universidad de Antioquia (http://biblioteca.udea.edu.co), el cual consta aproximadamente de un millón de títulos que incluyen libros, material audiovisual, revistas, entre otros.

Con el fin de tener la representación del modelo de espacio vectorial, cada título de la colección del sistema de bibliotecas se considera como un conjunto de términos que lo caracterizan. Dichos términos corresponden a las palabras encontradas en el título, los autores, los descriptores y, además, la descripción asociada a la codificación decimal o Dewey del título. Para reducir la cantidad de información generada, se eliminan los términos irrelevantes, conocidos también como stop-words, tales como los artículos y preposiciones, además, los términos se trabajan como raíces o prefijos, de tal forma que los singulares y los plurales se manejan como la misma palabra.

Cuando el usuario hace la consulta, entra los términos de búsqueda y el número de grupos que desea generar. El sistema extrae las raíces de los términos de búsqueda y elimina los términos irrelevantes, encuentra los títulos de la colección que contienen dichos términos de búsqueda y genera una matriz que representa el modelo de espacio vectorial en el cual las filas contendrán todos los términos asociados a los resultados obtenidos y en las columnas los títulos encontrados; en cada casilla habrá un 1 si el término pertenece a ese título o un 0 en caso contrario. Con dicha matriz y el número de grupos dado por el usuario, el sistema invoca el algoritmo Divisive-Binary-K-means, posteriormente, al usuario le son presentados los resultados en forma de grupos; para cada uno se presenta una identificación del grupo, los títulos que pertenecen al grupo y los términos que caracterizan al grupo; es decir, aquellos que pertenecen al centroide.

Consideramos que lo más útil para un usuario que plantea búsquedas muy generales, es que los términos que caracterizan a cada grupo puedan acercarlo a precisar lo que realmente busca y con estos nuevos términos el usuario los pueda utilizar en subsiguientes búsquedas y de esta manera pueda cambiar de su estrategia de búsqueda muy general a una estrategia de búsqueda más específica que evite el problema de la sobresaturación de resultados.

En la Figura 2 se muestran los resultados obtenidos ante la consulta televisión efectuada sobre el prototipo. El prototipo muestra la consulta efectuada, y una tabla con los resultados. En la primera columna, el número del grupo, en la segunda, los títulos de los registros que pertenecen al grupo, y en la tercera columna, las palabras que están presentes en el centroide que identifica al grupo. El usuario puede reformular su consulta incluyendo los términos presentes en el centroide que tal vez él no conocía, o puede seleccionar uno de los títulos de los registros encontrados y consultar la información.

Básicamente, el prototipo es una implementación del método que se propone usando como algoritmo de agrupamiento el Divisive-Binary-K-Means. El prototipo se desarrolló en el lenguaje de programación Java como un servlet, es decir, como una aplicación para la Web.

Hemos presentado un par de variantes nuevas de K-means para efectuar agrupamientos no supervisados, que permiten obtener grupos rápidamente con mínimos requerimientos de memoria, aplicables a casos de agrupamiento de resultados ante consultas de usuario en sistemas en línea o para agrupar síntesis breves de resultados de consultas en motores de búsqueda. Los métodos planteados disminuyen dramáticamente los requerimientos de memoria, y especialmente el algoritmo divisive-K-means ofrece grupos de tamaÑos relativamente homogéneos, dependiendo, por supuesto, de la naturaleza de los datos, lo cual resuelve algunos de los problemas presentes con el binary-K-means. Se requiere comparar estos resultados con otras técnicas orientadas a datos binarios, con el fin de obtener una evaluación de calidad de agrupamientos más justa que la hecha actualmente con técnicas convencionales.

El prototipo de software muestra la viabilidad de la incorporación de los agrupamientos a sistemas Opac's. Se plantea en el futuro incorporar un módulo de agrupamiento al sistema OpacUdea (http://OpacUdea.udea.edu.co), usado como catálogo de contingencia en el sistema de bibliotecas de la Universidad de Antioquia para luego tratar de medir el impacto del módulo.

Anexo A

Experimentos con los algoritmos de agrupamiento

A.1. Planteamiento del diseÑo experimental

Para evaluar el algoritmo propuesto, Divisive-Binary-K-means, se debe tener en cuenta que este algoritmo fue pensado para el caso de documentos con una representación binaria de términos; sin embargo, no existen algoritmos ya evaluados ni conjuntos de datos que se puedan usar para hacer una evaluación cuyos resultados sean completamente comparativos. Por esta razón se opta, de una parte, por hacer la comparación con técnicas de agrupamiento ya conocidas como el Bisecting-K-means y el algoritmo jerárquico UPGMA (Ver sección 4.2); y por otra parte, trabajar con los mismos conjuntos de datos usados en el estudio de Steinbach [17], disponibles a través de la documentación puesta en Internet del proyecto Cluto de la Universidad de Minnesota [6].

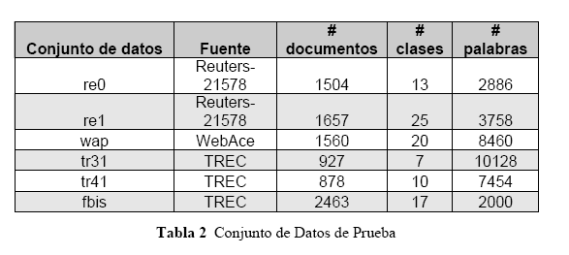
En la Tabla 2 se presenta un resumen de los documentos usados en la evaluación del método propuesto. Los conjuntos de datos tr31 y tr45 provienen de TREC-5, TREC-6 y TREC-7 [19]. Los conjuntos de datos fbis son datos del Foreign Broadcast Information Service del TREC-5 [19]. Los rótulos de clasificación de los documentos manualmente clasificados en los conjuntos de datos tr31 y tr45 se obtienen de los juicios de relevancia dados por 'qrels.1-243.part1', 'qrels.1-243.part2', 'qrels.251-300.part1', 'qrels.trec6.adhoc.part1', 'qrels.trec7.adhoc.part1', 'qrels.251-300.part3' y 'qrels.trec7.adhoc.part5' [18]. Los conjuntos de datos re0 y re1 provienen de la colección de textos Reuters- 21578 distribución 1.0 [7]. El conjunto de datos wap proviene del proyecto WebAce [4], cada documento corresponde a una página listada en la jerarquía de materias de Yahoo!. Los documentos seleccionados tienen un único juicio de relevancia.

A.2. Resultados

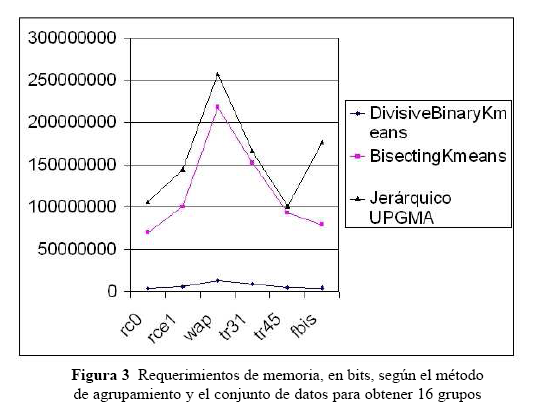
Para la determinación del consumo de memoria de los métodos de agrupamiento evaluados, se usaron estas fórmulas: para bisecting-K-means bits, para divisive-K-means bits y Jerárquico UPGMA , donde t es el número de términos, n es número de documentos, k es el número de grupos y B es el número de bits requeridos para almacenar cada elemento de la matriz de términos, matriz de similaridad y matriz de centroides donde aplique. Asumiendo para B un valor de 16 pensando en una variable tipo float, en la Figura 3 se presenta una comparación del consumo de memoria para cada método de agrupamiento y cada conjunto de datos para obtener 16 grupos.

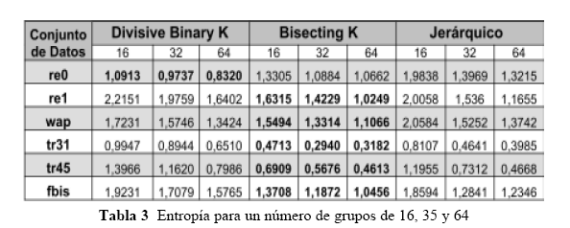
Con respecto a la evaluación del método de agrupamiento Divisive-Binary-K-means, en la Tabla 3 se presentan los resultados obtenidos de entropía, al efectuar corridas de los diferentes métodos de agrupamiento, generando grupos de 16, 32 y 64 documentos respectivamente; se compara con respecto a los métodos de agrupamiento Bisecting-k-means y Jerárquico UPGMA sobre los conjuntos de datos re0, re1, wap, fbis, tr31 y tr45.

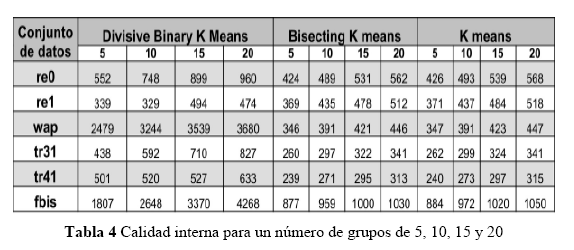
A.3. Análisis de resultados

De la Figura 3 se puede apreciar claramente que el algoritmo divisive-K-means reduce dramáticamente los requerimientos de memoria en todas las corridas, lo cual lo hace muy superior con respecto a los otros algoritmos comparados. Considerando que se requiere mover muchos menos datos, este algoritmo también mejora la velocidad en la obtención de grupos.

El Divisive-Binary-K-means es más rápido que Bisecting-K-means y Jerárquico UPGMA. Tanto Divisive-Binary-K-means como Bisecting-K-means tienen una complejidad computacional lineal donde n es el número de documentos, k es el número de grupos y i es el número de iteraciones, la cual es inferior a la complejidad computacional de método de agrupamiento Jerárquico UPGMA que es . El Divisive-Binary-K-means, debido a que hace operaciones a nivel de bits, es decir, usando operadores binarios, aprovecha las instrucciones de máquina básicas lo cual lo hace mas veloz que el Bisecting-K-means, el cual debe efectuar operaciones mas costosas de punto flotante, especialmente en los cálculos de similaridad entre documentos. Además, el Divisive-Binary-K-means requiere menos recursos para almacenamiento, dado que representa a los documentos en matrices binarias, las cuales se pueden implementar usando facilidades de clases de java o cualquier lenguaje que las permita implementar a nivel de bits. En este trabajo la implementación se hizo con arreglos de variables de 64 bits tipo long de java.

De acuerdo con los resultados presentados en la sesión anterior, obtenidos sobre conjuntos estándar de pruebas de categorías en investigaciones de recuperación de información como las colecciones TREC o Reuters, era de esperar que el desempeÑo en cuanto a calidad de los grupos con el algoritmo Divisive-Binary-K-means, sería inferior a los algoritmos Bisecting-K-means y Jerárquico UPGMA, debido precisamente a que la frecuencia de términos en el Divisive-Binary-K-means es binaria y no interesa si una palabra en particular es más importante que otras dentro de un documento o en la colección de documentos, dado que lo único que se almacena es si un término está o no está en un documento dado. Pero al mirar que precisamente este algoritmo se ha diseÑado para el caso de fichas bibliográficas o documentos efímeros, en donde no se está trabajando con documentos de texto completo sino con unos pocos atributos que describen un material bibliográfico, o párrafos que muestran el contexto donde se halló lo buscado, el asumir que todos los términos tienen igual importancia no es crítico, teniendo en cuenta que términos de alta frecuencia que no aportan (o stop words) como artículos, preposiciones, pronombres entre otras pueden ser filtrados en una etapa previa. Para mirar la calidad de los agrupamientos se usó la entropía porque los documentos de prueba cuentan con unas clasificaciones previamente efectuadas y la entropía permite medir la calidad externa de los agrupamientos; en tanto mas alta sea la entropía, la pureza del grupo es inferior y viceversa, es decir, un valor bajo de entropía indica alta pureza del grupo. El Divisive-Binary-K-means dio mejor resultados con el conjunto de datos re0; en el resto de los casos fue superior el Bisecting-K-means.

* Artículo derivado de la tesis de maestría Agrupamiento de resultados obtenidos de consultas distribuidas en sistemas de catálogos públicos en línea (OPAC). Programa de Maestría en Ingeniería de Sistemas, Universidad Nacional de Colombia sede Medellín, Colombia, 2005.

Referencias bibliográficas

1. BORGMAN, C. L. Why are online catalogs still hard to use?. Journal of the American Society for Information Sciences. 1996, no. 47, p. 493–503.        [ Links ]

2. CUTTING, Douglass R.; PEDERSEN, Jan O.; KARGER, David and TUKEY, John W. Scatter/ gather: A cluster-based approach to browsing large document collections. En: Proceedings of the Fifteenth Annual International ACM SIGIR Conference on Research and Development in Information Retrieval, 1992, p. 318–329.        [ Links ]

3. FREITAS,Alex A. Data Mining and Knowledge Discovery with Evolutionary Algorithms. Estados Unidos: Springer Verlag , 2002.        [ Links ]

4. HAN, Eui-Hong; BOLEY, Daniel; GINI, Maria; GROSS, Robert; HASHING, Kyle; KARYPIS, George; KUMAR, vipin; MOBASHER, B. and MOORE, Jerry. Webace: A web agent for document categorization and exploration. En: Proceedings of the 2nd Internationl conference on Autonomous Agents, 1998.        [ Links ]

5. HEARST, Marti A. y PEDERSEN, Jan O. Reexamining the cluster hypothesis: Scatter/gather on retrieval results. En:Proceedings of SIGIR-96, 19th ACM Internacional Conference on Research and Development in Information Retrieval, pages (76–84, Zurich, CH, 1996)        [ Links ]

6. KARYPIS, George. Cluto a clustering toolkit. [En línea]. 2003. Disponible en: http://www.cs.umn.edu/~karypis.[Consulta: enero 12 de 2005]        [ Links ]

7. LEWIS, D. Reuters-21578 text categorization text collection 1.0. [En línea] Disponible en: http://www.research.att.com/~lewis [Consulta: enero 12 de 2005]        [ Links ]

8. MAAREK, Yoelle S.; FAGIN, Ronald; BEN-SHAUL, Israel Z. and PELLEG, Dan. Ephemeral document clustering for web applications. Technical Report RJ 10186, IBM Research, 2000.        [ Links ]

9. MARCOS, Mari Carmen. Mejoras en la consulta y presentación de los resultados en catálogos de bibliotecas. En: IV Congreso de Interacción Persona-Ordenador IPO '03 (Vigo), (Junio 2003)        [ Links ]

10. MATTHEWS, Joseph R. Time for new opac initiatives: An overview of landmarks in the literature and introduction to wordfocus. Library Hi Tech. 1997, vol. 57-58, no. 5, p 111– 122.        [ Links ]

11. MURAMATSU, J. y PRATT, W. Transparent queries: Investigating user's mental models of search engines. In SIGIR-01. Proc of the Twenty fourth Internacional ACM Conference on Research and Depelopment in Information Retrieval. September 2001. New Orleans, LA. ACM.        [ Links ]

12. NESCHEN, Martin. Hierarchical binary vector quantisation classifiers for handwritten character recognition. In Sagerer, Gerhard; Posch, Stefan and Kummert, Franz, editors, DAGM-Symposium. Estados unidos: Springer,1995. p. 419–427.         [ Links ]

13. RIEKERT, Wolf-Fritz. The design of a multicatalog system for a public environmental information network. Technical report, GEIN: German Environmental Information Network, 1999.        [ Links ]

14. SALTON, G.; YANG, C. S.; and YU, C. T. A theory of term importance in automatic text analysis. Journal of the American Society for Information Science, 1975, vol. 26, no.1, p.33–44.        [ Links ]

15. SALTON, Gerald. Automatic Text Processing. New York: Addison-Wesley, 1989.        [ Links ]

16. SHANNON, C.E. A mathematical theory of communication. The Bell System Technical Journal, 1948, vol 27, pp 379–423,623–656.        [ Links ]

17. STEINBACH, Michael; KARYPIS, George and KUMAR, Vipin. A comparison od document clusterind techniques. Technical Report 00-034, Department of Computer Science and Engineering. University of Minesota, 2000.        [ Links ]

18. Trec. Text retrieva conference relevance judgments. [En línea]. Disponible en: http://trec.nist.gov/data/qrels-eng/index.html .[Consulta: enero 12 de 2005]        [ Links ]

19. Trec. Text retrieval conference. [En línea]. Disponible en: http://trec.nist.gov [Consulta: enero 12 de 2005]        [ Links ]

20. WARREN, P. Why thy still cannot use their library catalogues? In Conference on Information Technology in Tertiary Education. June 2000. CITTE 2000 Conference, Organising Committee,Attention: CJ Nel,IT Services,University of Port Elizabeth, PO Box 1600,Port Elizabeth, 6000. University of Port Elizabeth.         [ Links ]

21. WEISS, Dawid. Introduction to search results clustering. In Proceedings of the 6th International Conference on Soft Computing and Distributed Processing, Rzeszów. 2002. Poland.         [ Links ]

22. Zamir. ClusteringWeb Documents: A Phrase-Based Method for Grouping Search Engine Results. 1999. (PhD thesis, University of Washington).        [ Links ]

Artículo recibido: 11 de febrero de 2008. Aprobado: 3 de junio de 2008.