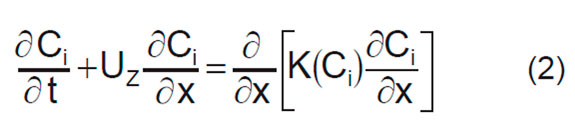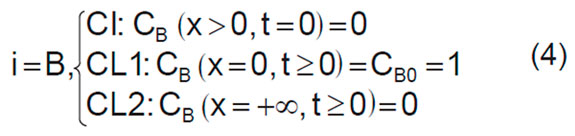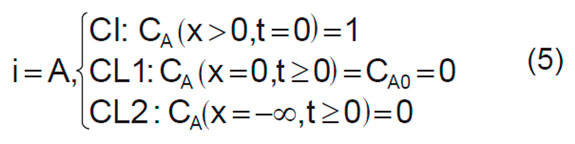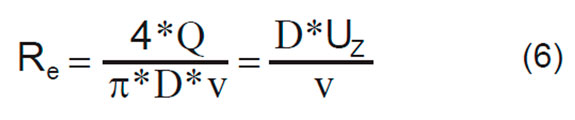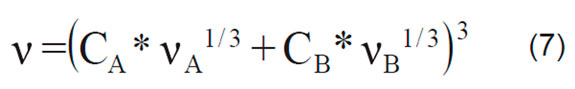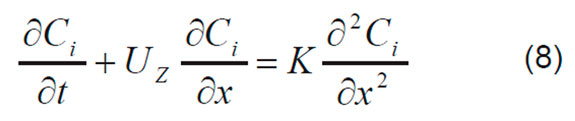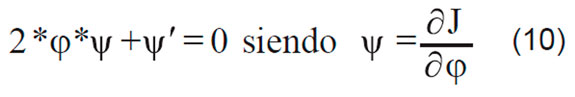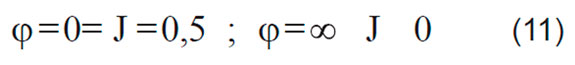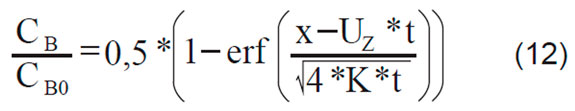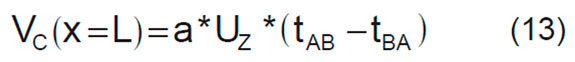Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Revista ION
Print version ISSN 0120-100X
Rev. ion vol.24 no.1 Bucaramanga Jan./June 2011
CONTAMINACIÓN GENERADO EN EL TRANSPORTE DE LOTES
SUCESIVOS DE HIDROCARBUROS A TRAVÉS DE POLIDUCTOS
JUAN CARLOS DÍAZ ALVAREZ1*; FERNANDO CORZO ALVAREZ1**;
ARIEL FLÓREZ GONZÁLEZ2; JULIO CÉSAR CARRILLO ESCOBAR2;
CRISÓSTOMO BARAJAS FERREIRA2; JOSÉ CARLOS CÁRDENAS MONTES1;
CÉSAR AUGUSTO GARCÍA CHINCHILLA3
1 Grupo de Investigación Campos Maduros, Universidad Industrial de Santander (UIS), Cra. 27 Calle 9, Bucaramanga, Colombia.
*jc.diaz.alvarez@hotmail.com, **fernando_corzoalvarez@hotmail.com
2 Universidad Industrial de Santander (UIS), Cra. 27 Calle 9, Bucaramanga, Colombia.
3 Ecopetrol S.A - Instituto Colombiano Del Petróleo (ICP), A.A. 4185 Bucaramanga, Santander, Colombia.
Fecha Recepción: 29 de julio de 2010
Fecha Aceptación: 4 de abril de 2011
El presente trabajo tiene como propósito predecir a diferentes concentraciones admisibles, el volumen de mezclado que se genera en el transporte de lotes sucesivos de los destilados gasolina y diesel a través de poliductos. Esto se realiza mediante la implementación de un modelo matemático reportado en la literatura, cuya solución consiste en el planteamiento de una metodología de cálculo basada en el desarrollo de un algoritmo numérico soportado en el software MATLAB y la introducción de un parámetro conocido como coeficiente de dispersión axial; el cual, dentro de las múltiples posibilidades existentes para su determinación, se encontró que la ecuación empírica propuesta por Sjenitzer, conlleva a un mejor ajuste con los datos experimentales. Obteniéndose de esta manera, las expresiones matemáticas que permiten estimar el tiempo de corte en función de la concentración admisible, generando así un significativo aporte en el establecimiento de los principios necesarios para realizar una posterior automatización del proceso de separación y respectivo almacenamiento de los fluidos que constituyen el sistema en cuestión. Finalmente, con la realización de un análisis estadístico se demostró que un cambio en el diámetro de la tubería, dado por un predominio de las fuerzas inerciales sobre las fuerzas viscosas en el número de Reynolds, ejerce un mayor efecto sobre el volumen de contaminación, en comparación con una variación en la longitud del poliducto y el caudal de flujo.
Palabras clave: modelo matemático, coeficiente de dispersión axial, tiempo de corte, concentración admisible
VOLUME GENERATED BY BATCHING TRANSPORT
OF HIDROCARBONS THROUGH PIPELINES
The purpose of this article is to determinate the mixing volumes in batching transfer of distilled fuel and diesel at different admissible concentrations trough multiproduct pipelines. The methodology employed to realize this work consists on both of an own numerical algorithm, which has been supported on MATLAB, and the introduction of a parameter called axial dispersion coefficient. In order to obtain a better coincidence between experimental data by using this methodology, we employed the empirical equation of Sjenitzer to determine the axial dispersion coefficient. This step allowed finding two mathematical expressions which allow obtain a relation between cut's times and the admissible concentrations; thus generating, a significant contribution to the necessary foundations to automatize the separation process and storage subsequent of the fluids which are part of the system in study. Finally, a change in the pipeline diameter given by a predominance of inertial forces over viscous forces in the Reynolds number, produces a higher effect over the contaminated volume in contrast with a pipeline length change or a flow change. These facts were demonstrated with a statistical analysis.
Keywords: mathematical model, axial dispersion coefficient, cut's times, admissible concentrations
El sistema de transporte de lotes sucesivos de hidrocarburos a través de poliductos, desde la refinería hasta los sitios de distribución, es ampliamente utilizado para enviar diferentes tipos de combustible tales como gasolina, queroseno, diesel, jet, etc. [1,2]. Por tanto, la conveniencia del uso de esta técnica se debe a que no sería económicamente viable utilizar tuberías paralelas dedicadas a transportar un solo tipo de fluido [3]. Sin embargo, realizar este proceso repercute en la calidad y especificaciones de los productos transportados, ya que se genera una zona de mezclado o volumen de contaminación en la interfase de las sustancias allí presentes debido a fenómenos de transferencia de masa; los cuales, van incrementando dicha zona a medida que transcurre el tiempo y se avanza a lo largo de la tubería [1, 2]. El modelamiento matemático del fenómeno de transferencia de masa presente en este tipo de transporte de fluidos ha sido presentado por diferentes autores considerando diversas suposiciones [2, 3,]; no obstante, la gran dificultad en la solución de este tipo de modelos, que combinan fenómenos de difusión por convección forzada y molecular, radica en el planteamiento de una solución ya sea numérica o analítica que permita establecer condiciones iniciales y de frontera adecuadas para la estimación del volumen de contaminación, de forma dinámica y eficaz mediante el cálculo de un perfil de concentración. Por tal razón este artículo presenta un procedimiento de cálculo alternativo para estimar el volumen de mezclado a diferentes concentraciones admisibles, así como la determinación de los tiempos de corte de los fluidos que componen el sistema, junto con la realización de un análisis estadístico enfocado en analizar la influencia que diferentes variables de operación y/o diseño, ejercen sobre el volumen de contaminación. De otra parte, ECOPETROL S.A., no cuenta con una ecuación matemática que permita modelar este tipo de sistemas, con el fin de estimar de forma segura el volumen de contaminación entre los hidrocarburos transportados a través de los poliductos y sus respectivos tiempos de corte, ya que las separaciones de los lotes de los fluidos deben realizarse mediante mediciones continuas de densidad [4].
Definición y descripción del proceso de mezclado en el sistema de transporte mediante flujo por lotes
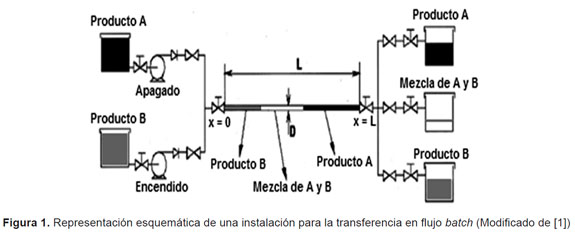
El transporte mediante flujo batch se realiza de la manera como se muestra en la Figura 1. Dicho sistema es usado para bombear secuencialmente dos productos miscibles y distintos denotados como A y B. La tubería tiene un diámetro D y una longitud L, la cual es medida desde la unión de la línea de descarga de la bomba hasta el punto de recepción al final de la tubería.
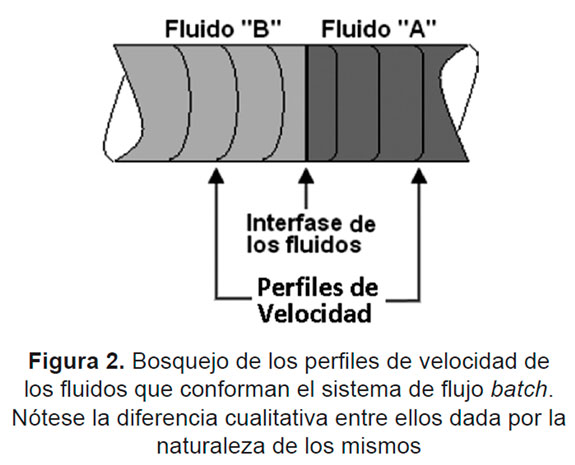
Mediante el uso de una válvula de desvío, en el instante de tiempo t=0, el bombeo de fluido A es interrumpido y en el mismo instante de tiempo inicia el bombeo del fluido B; de esta manera el fluido B empieza a desplazar el fluido A a lo largo de la tubería y así los dos fluidos son transportados uno seguido del otro. En el paso de productos a través de la tubería, una zona de mezcla es generada en las fronteras de los dos fluidos adyacentes (Fluidos A y B); la presencia de esta región, es consecuencia de la difusión convectiva, la cual depende en gran medida del cambio de la forma del perfil de velocidades que se presenta en la interfase de los fluidos [5] (Véase Figura 2).
Por consiguiente, cuanto más se aproxime el perfil de velocidad al de flujo tapón, la cantidad de mezcla axial es más pequeña [6, 7, 8]. Por último, cuando la zona de mezcla llega al final de la tubería es redireccionada a través de válvulas de desvío, de forma tal que pueda ser separada de los demás fluidos y de esta manera puedan ser almacenados el fluido A, el fluido B y la mezcla entre ellos en sus respectivos contenedores
Definición de variables. Considérese un sistema de flujo batch compuesto por dos productos denotados como A y B, siendo B el fluido desplazante y A el fluido desplazado. Además, defínase las siguientes variables como sigue [1, 2, 7]:
- t como la variable de tiempo (s).
- x es la coordenada axial de la línea que inicia en la zona de descarga de los fluidos x=0 y finaliza en el punto de recepción denotado como x=L, m.
- Ci(x,t) Є (0, 1) con i Є{A,B}, es la concentración media del fluido i dentro de la mezcla en la sección transversal de la tubería en un tiempo t y la coordenada axial x Є (0,L), (p/p).
- Xm(t) es el punto medio de la mezcla, el cual se refiere a la región de la mezcla en donde: CB (X=Xm(t), t) = CA (X=Xm(t), t) = 0,5, (m).
- Las concentraciones admisibles CBA y CAB corresponden respectivamente, a la concentración de producto B en A al inicio de la zona de mezcla, y la concentración de producto A en B al final de esta. Adicionalmente se tiene que: CBA + CAB = 1.
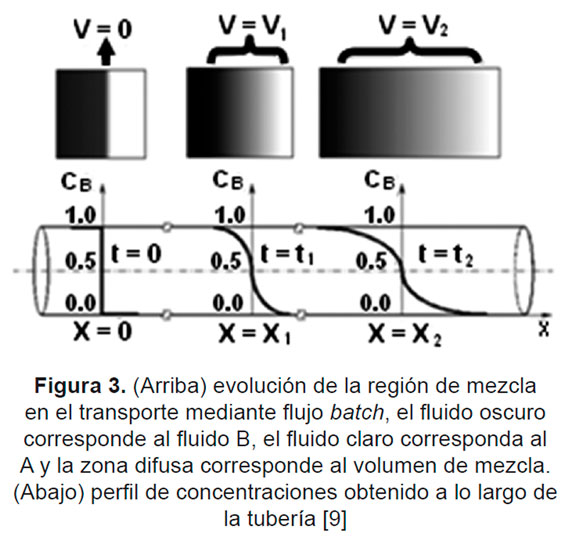
Ahora bien; cuando i=B, el perfil de concentración puede ser representado a lo largo de la tubería, como se ilustra en la Figura 3. En esta esquema se aprecia que al inicio de la transferencia de masa (x=0 y t=0), aún no se presenta una cantidad apreciable de volumen de mezclado y es por esto que en la interfase de los dos fluidos, el perfil de concentraciones presenta un cambio súbito de 1 a 0 (p/p); posteriormente, a medida que los fluidos se desplazan a lo largo de la tubería, el volumen de mezclado se va incrementando y con ello, el perfil de concentraciones se extiende cada vez más, tanto hacia adelante como hacia atrás del punto medio de la mezcla.
Desarrollo del modelo matemático. El modelo matemático desarrollado comprende las siguientes suposiciones [1, 2, 7]:
- La tubería es horizontal y de diámetro constante.
- La velocidad media de flujo es constante y el régimen de flujo es turbulento.
- La transferencia de masa ocurre sólo en dirección axial, debido al régimen de flujo.
- El sistema es isotérmico.
- Se considera que la tubería es lisa y que no posee accesorios tales como válvulas, codos y/o cualquier otro dispositivo que pueda generar pérdidas por fricción.
- No existen estaciones de bombeo intermedias a lo largo del poliducto.
- El peso específico de los fluidos no deben diferir significativamente uno del otro.
- Flujo estacionario y además el vector de velocidad en todos los puntos del sistema es idéntico tanto en magnitud como en dirección para un instante dado (flujo uniforme).
De acuerdo con lo expuesto en el proceso de mezclado para el sistema de transporte por flujo batch y las anteriores suposiciones, las ecuaciones que describen el fenómeno de mezclado son:
donde Q es el caudal (m3/s), a es el área de la sección transversal de la tubería (m2), Uz la velocidad media de los fluidos (m/s) y K(Ci) es el coeficiente de dispersión axial (m2/s); este último parámetro es el que determina la dispersión de una sustancia en otra bajo la acción combinada de la difusión molecular y la variación de la velocidad sobre la sección transversal de la tubería [7, 10, 11]. La expresión (1) para efectos prácticos, proviene de definir la velocidad media Uz en términos del caudal de fluido; y la Ecuación 2 proviene de un balance de masa en la interfase de los lotes de los fluidos a lo largo de la tubería. Considerando que los fluidos A y B son bombeados secuencialmente de tal manera que A es seguido por B y que la siguiente relación deber ser siempre sostenida [1, 2, 9]:

Las condiciones iniciales y de frontera para la ecuación (2) están dadas como sigue [12]:
Coeficiente de dispersión axial [K(Ci)]. Las ecuaciones semiempíricas mostradas en la Tabla 1 son las más utilizadas para determinar el coeficiente de dispersión axial. Cabe señalar que estas expresiones están en función del número de Reynolds (téngase en cuenta que este número adimensional se expresa como la razón entre las fuerzas inerciales y viscosas del fluido):
donde D es el diámetro de la tubería (m), Uz es la velocidad media de flujo (m/s), Q es el caudal (m3/s) y v es la viscosidad cinemática de la mezcla (m2/s), la cual es determinada mediante la siguiente correlación [13]:
Siendo vi (i = A o i = B) la viscosidad cinemática del fluido i (m2/s).
Por último, con el modelo matemático obtenido y las diferentes expresiones propuestas para calcular el coeficiente de dispersión axial, es posible determinar el perfil de concentraciones en la interfase de los dos fluidos a lo largo de la tubería en función del tiempo y la distancia.
Redefinición de las condiciones inicial y de frontera. Para la resolución del problema representado por (2) y (4) o (5), es necesario tener en cuenta que el flujo es estacionario y uniforme; así, el coeficiente de dispersión axial es constante y por consiguiente, la Ecuación 2 adopta la siguiente forma [12]:
Así mismo, la consideración de un coeficiente de dispersión axial constante, conlleva necesariamente a definir las concentraciones CA=CB=0,5 con el fin de considerar un aporte equitativo al valor de la viscosidad cinemática de la mezcla (Ecuación 7) por parte de los fluidos que conforman el sistema.
Para el caso en el que i=B, se toman las condiciones iniciales y de frontera dadas en (4). Además, mediante la sustitución de las siguientes variables adimensionales [3]:
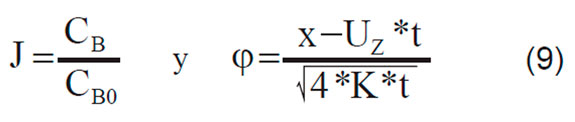
la ecuación (8) se convierte en:
De otra parte, resulta conveniente utilizar un punto de referencia que se mueva con la velocidad media de flujo en el punto medio de la mezcla (Xm(t)), ya que esto permite redefinir las condiciones límite dadas en (4) de la siguiente forma [7]:
Las nuevas condiciones límite dadas en (11) permiten acotar la variable φ de forma tal que la solución analítica de la ecuación (10) pueda ser evaluada mediante el reemplazo de las variables x y t, tomando como punto de partida la zona media del volumen de mezclado; así pues, dicha solución viene dada por la siguiente expresión:
La anterior ecuación presenta un bajo grado de complejidad en cuanto a su aplicación, ya que fijando la variable t es posible utilizar la variable x para recorrer una determinada zona de la tubería y de esta manera determinar el perfil de concentraciones. Cabe resaltar que el procedimiento de cálculo propuesto en este trabajo elimina el planteamiento de soluciones iniciales al problema junto con la asignación de los valores máximo y mínimo con más probabilidad de ocurrir en la variable φ; situación necesaria para modelar numéricamente la ecuación diferencial dada en (10), de acuerdo con lo planteado por [3].
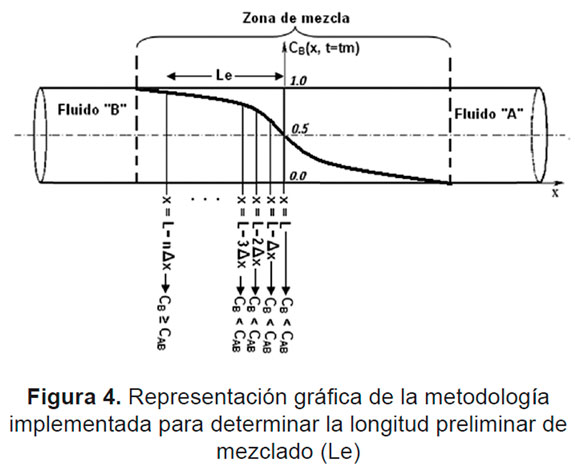
Metodología de cálculo para la determinación del volumen de mezcla. El procedimiento de cálculo se fundamenta en la suposición de que el sistema consta de un flujo permanente y uniforme. Este hecho permite determinar el tiempo en el que el punto medio de la mezcla (Xm(t)) se encuentra en el sitio de obtención de los datos experimentales (punto de medición) utilizando la relación tm=L/Uz, siendo tm el tiempo medio (s), L la distancia comprendida desde el punto donde inicia la transferencia de masa en el sistema hasta el punto de medición (m) y Uz la velocidad media de flujo (m/s). Una vez fija la variable t, se utiliza la ecuación (12) para recorrer la zona de mezclado desde el punto medio hacia atrás a distancias equidistantes del orden de 10-5 veces la distancia L mediante el uso de la variable x; de esta manera, se compara simultáneamente el valor de la concentración en dichos puntos con el valor de la concentración admisible, que en este caso sería CAB (véase Figura 4).
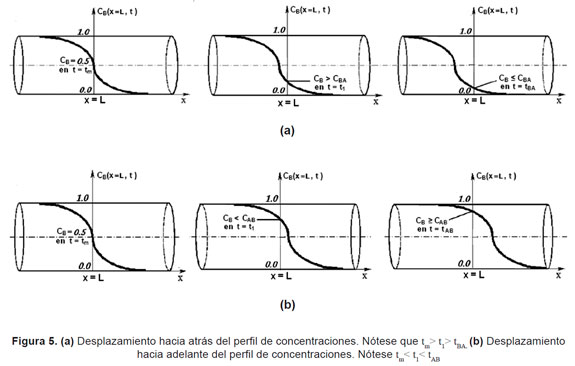
Este proceso se realiza n veces mientras el valor de la concentración dado en (12) sea menor que la concentración admisible CAB, obteniendo así una longitud de mezcla preliminar (Le en m), correspondiente a la distancia recorrida por la variable x; con esto, dicha variable es acotada como sigue: L - 3*Le ≤ x ≤ L. De acuerdo con lo anterior, se establece una región cercana al punto de medición, a la vez que se garantiza la existencia de todo el volumen de contaminación en dicha zona, reduciendo así el costo computacional en la determinación tanto del perfil de concentraciones como en la estimación del volumen de mezclado, ya que se establece una cota superior e inferior para la variable x. Luego de definirse la región de estimación, el proceso se inicia partiendo del tiempo medio en x=L, evaluando el perfil de concentraciones dado en (12) a lo largo de dicha zona y comparando el valor de la concentración de la sustancia B con la concentración admisible CBA en x=L; esta operación se detiene si en el punto en cuestión, la concentración de la sustancia B es menor o igual que el valor de CBA; si esto no es así, se fija un nuevo tiempo menor al establecido anteriormente con el fin de mover hacia atrás el perfil de concentraciones con respecto al punto de medición; este procedimiento se repite hasta que para un determinado tiempo en x=L la condición antes descrita sea satisfecha; así, el tiempo para cuando esto ocurre se denomina primer tiempo de corte tBA, el cual se define como el instante de tiempo asociado al arribo del inicio de la zona de mezcla con concentración admisible CBA en el punto de medición (Véase la Figura 5a). Para el cálculo del segundo tiempo de corte tAB, el cual corresponde al instante asociado con el arribo del final de la zona de mezcla con concentración admisible CAB en el punto de medición, se procede de manera análoga a la estimación del primero, con la diferencia de que en este caso el tiempo va en aumento con el fin de mover hacia adelante el perfil de concentraciones con respecto al punto de medición y el proceso finaliza hasta que la concentración de la sustancia B en x=L sea menor o igual que CAB (Véase la Figura 5b). Con la metodología anteriormente descrita, el volumen de mezcla puede ser estimado mediante la siguiente expresión [1, 2]:
en donde tBA y tAB son el primer y segundo tiempos de corte respectivamente (s), Uz es la velocidad media de flujo (m/s) y a es el área de la sección transversal de la tubería (m2).
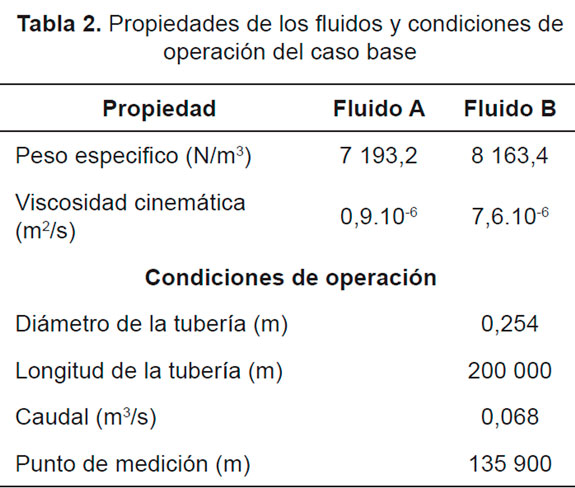
Con el propósito de evaluar los resultados obtenidos del modelo matemático enunciado, se estableció como fuente de datos experimentales el siguiente caso de estudio [1]: El sistema es un poliducto operado por Petrobras, en el cual, los fluidos transportados son gasolina y diesel, siendo el primero, el fluido desplazado (denominado fluido A) y el segundo, el fluido desplazante (denominado fluido B). Las condiciones de operación y propiedades de las sustancias implicadas en este sistema se encuentran en la Tabla 2.
Análisis del modelo fenomenológico
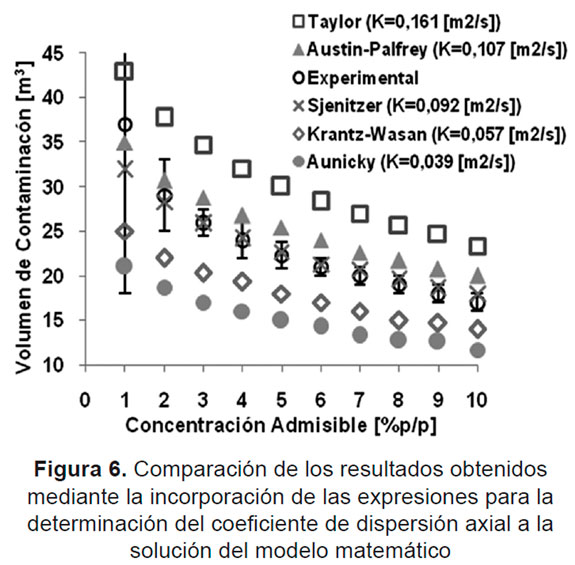
Con el objetivo de determinar el volumen de contaminación a diferentes concentraciones admisibles, se ensayó el modelo matemático anteriormente presentado con las diferentes expresiones para el coeficiente de dispersión axial dadas en la Tabla 1 para el caso anteriormente especificado (Véase la Figura 6).
En esta figura, se muestra que la incorporación de la expresión propuesta por Sjenitzer (ecuación dada en [10]) al modelo matemático en cuestión, conlleva a un mejor ajuste con los datos experimentales ya que los resultados obtenidos por la simulación numérica se encuentran dentro del intervalo de incertidumbre asociado a dichos valores y además presentan una discrepancia menor a 4,9%, en un rango de concentraciones admisibles del 2 a 10 (% en peso).
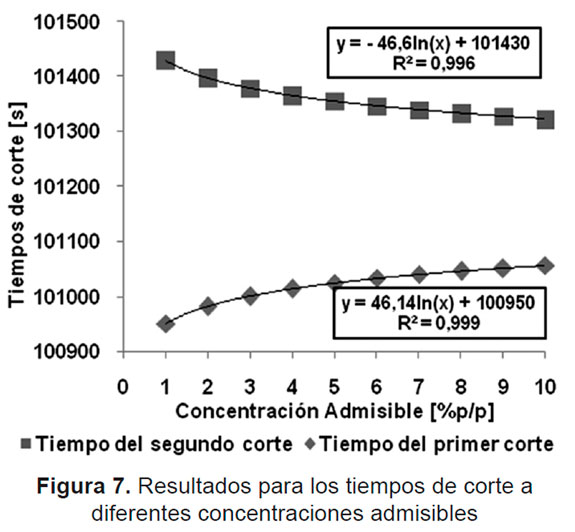
Tiempos de corte. En base a la estimación del volumen de mezcla a diferentes concentraciones admisibles se obtuvieron los respectivos tiempos de corte de la forma especificada así, teniendo en cuenta la necesidad de sentar las bases para realizar una posterior automatización del proceso, se considera necesario determinar los tiempos para los cuales la concentración en el punto de medición corresponde con la concentración admisible tanto al inicio de la zona de contaminación (primer tiempo de corte) como al final de esta (segundo tiempo de corte). Para tal fin se realizó una recopilación esquemática de dichos tiempos de corte de acuerdo con los datos obtenidos de la simulación numérica realizada (Véase la Figura 7).
Los resultados mostrados en la anterior figura son de gran importancia práctica ya que permite determinar de manera ágil y oportuna, los tiempos de corte de acuerdo a la concentración admisible necesaria para que los fluidos en cuestión sean almacenados con las especificacionas técnicas requeridas.
Análisis de los parámetros del sistema en el crecimiento del volumen de contaminación. Debido a la proximidad de los resultados obtenidos por el modelo matemático presentado y la metodología de cálculo propuesta con los datos experimentales, es deseable determinar la manera en que aumenta o disminuye el volumen de mezclado frente a la variación de parámetros como el caudal de flujo, el diámetro y la longitud de la tubería; ya que esto facilitaría la toma de desiciones al momento de realizar futuros cambios en infraestructura y/o variables de operación, que conlleven a optimizar el proceso de transporte de lotes sucesivos de fluidos a través de tuberías.
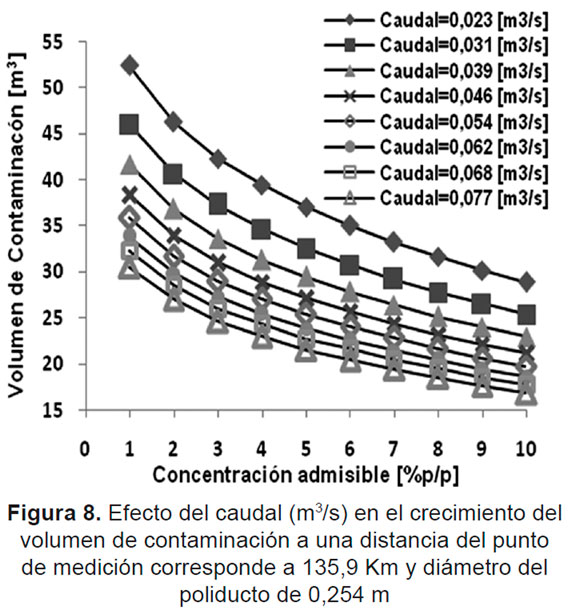
Variación del caudal de flujo con diámetro y longitud constante. La Figura 8 representa el perfil del volumen de contaminacion en función de la concentración adimisible para diferentes caudales de flujo definiendo el diámetro igual a 0,254 m (el tamaño de la tubería es escogido en base al caso de estudio).
En esta figura se aprecia que los efectos debido al cambio en el caudal de flujo, generan cambios apreciables en el volumen de contaminación dentro del rango de caudal que va desde 0,023 a 0,046 (m3/s) para una determinada concentracion admisible; por otro lado, las curvas obtenidas a caudales de flujo mayores que 0,046 m3/s, además de exhibir una disminución en el volumen de mezcla, muestran también que el efecto sobre dicha magnitud se hace menos notorio. En general, el hecho de que un aumento en el caudal de flujo disminuya el volumen de contaminación se debe principalmente a que las fuerzas inerciales predominan sobre las viscosas (pues esto se ve reflejado en el aumento del número de Reynolds, Ecuación 6); así, el régimen de flujo se hace más turbulento y con ello, la transferencia de masa de un fluido a otro se hace menos efectiva; resultando esto coherente de acuerdo con lo observado por otros autores [6, 7, 8] y por lo comprobado en la práctica.
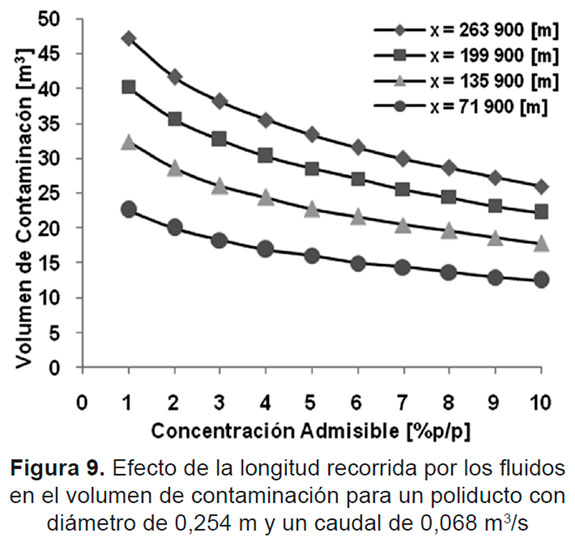
Longitud recorrida por los fluidos con caudal y diámetro constantes. El perfil del volumen de contaminación en función de la concentración admisible y la longitud recorrida por los fluidos, realizado para el caso de estudio se esquematiza en la Figura 9.
En la anterior figura se observa que al aumentar la longitud recorrida, el volumen de contaminación se incrementa para una concentración admisible determinada, debido a que los fluidos permanecen un mayor tiempo en contacto. También se puede observar que a medida que la longitud de la tubería recorrida por los fluidos se hace más grande, el cambio en el volumen de contaminación se hace más pequeño. Lo anterior, es consecuencia de la reducción en el cambio de la forma del perfil de velocidades de los fluidos puros hacia los puntos adyacentes de la mezcla (véase la Figura 2); este suceso, es atribuido principalmente a los cambios de concentración que resultan menos abruptos en dichos puntos a medida que transcurre el tiempo y se avanza en la tubería, lo cual concuerda con lo expuesto en [5, 7, 10, 11].
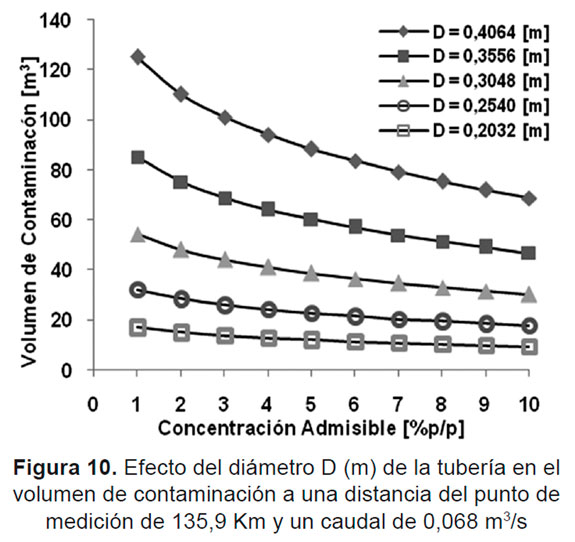
Variación del diámetro de la tubería con caudal y longitud constantes. El perfil del volumen de contaminación en función de la concentración admisible y el diámetro de la tubería realizado para el caso de estudio está dado en la Figura 10. En esta figura, se observa que al aumentar el diámetro de la tubería para una concentración admisible dada, se presentan cambios fuertes en el volumen de contaminación; esto se debe a que a medida que el diámetro crece, el área transversal disponible para la formación de los remolinos es mayor, facilitándose de esta manera el mezclado de los fluidos [3]. De acuerdo con esto, se obtiene que una disminución en el número de Reynolds (lo cual corresponde a que las fuerzas viscosas predominen sobre las inerciales), favorece un aumento en el volumen de contaminación.
Finalmente, mediante el análisis cualitativo anteriormente realizado se puede establecer que los cambios de diámetro de la tubería, generan efectos en el volumen de mezclado más grandes, en comparación al efecto que sobre este ejerce una disminución en el caudal y/o una reducción en la longitud recorrida por los fluidos. De otra parte, desde el punto de vista del régimen de flujo, se puede inferir para este tipo de sistemas, que si las fuerzas inerciales predominan sobre las viscosas, se obtiene una disminución en el volumen de contaminación; en tanto que si ocurre lo contrario, se favorece un aumento en el mismo; presentándose así, que el efecto sobre el volumen de contaminación generado por el predominio de cualquiera de las dos fuerzas mencionadas anteriormente es mayor al que ejerce el aumento o disminución de la longitud recorrida por los fluidos que componen el sistema.
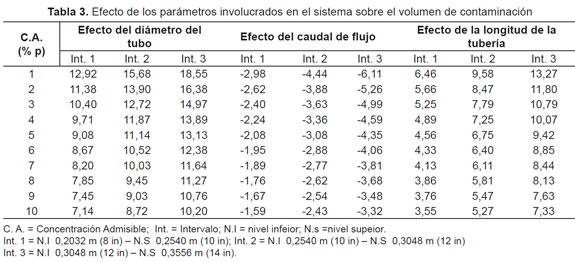
Cuantificación del efecto que los parámetros del sistema ejercen sobre el volumen de mezcla. Como se observó anteriormente, el parámetro del sistema que mayor efecto ejerce sobre el volumen de contaminación es el diámetro de la tubería; por tanto, para cuantificar sus efectos y facilitar la toma decisiones relacionadas con cambios en la infraestructura y/o condiciones de operación, se hizo necesario realizar un diseño experimental 23 ([16]), seleccionando como niveles inferior y superior del caudal de flujo los valores de 0,062 y 0,077 m3/s respectivamente; así como también, el valor de 135900 m para el nivel inferior y 199900 m para el nivel superior de la longitud de la tubería. Una vez hecho esto, se procedió a determinar el efecto que cada uno de estos ejercen sobre el volumen de mezclado a diferentes concentraciones admisibles para tres intervalos diferentes de diámetro (Véase Tabla 3). Los valores dados en la Tabla 3 corresponden a la magnitud del cambio en el volumen de contaminación a medida que cada uno de los parámetros pasa del nivel inferior al nivel superior; así por ejemplo en la tabla 3, para una concentración admisible de 1% en peso, se puede apreciar que cuando el diámetro de la tubería cambia de 0,2032 m (8 in) a 0,254 m (10 in), el volumen de contaminación aumenta en 12,92 m3; mientras que para el caudal de flujo se aprecia que en un cambio de 0,062 a 0,077 m3/s, el volumen de contaminación disminuye en 2,98 m3 como era de esperarse, de acuerdo con la sección anterior, el cambio en el diámetro de la tubería ejerce un mayor efecto sobre el volumen de contaminación en los intervalos descritos; así, de la Tabla 3 se obtiene que el efecto en el volumen de contaminación ejercido por el cambio del diámetro del nivel inferior al nivel superior es de entre 3,0 y 4,5 veces el efecto ejercido por el caudal de flujo; de la misma forma, el efecto ejercido por el diámetro en relación al efecto ejercido por la longitud de la tubería está entre 1,4 y 2,0 veces en magnitud sobre el volumen de mezclado; finalmente, el efecto ejercido por la longitud de la tubería sobre el efecto ejercido por el caudal de flujo se encuentra entre 2,1 y 2,3 veces en magnitud.
El empleo de la expresión dada por Sjenitzer para determinar un coeficiente de dispersión axial constante en la solución del modelo matemático expuesto, constituye junto con la metodología de cálculo planteada, una alternativa práctica y confiable en la determinación del volumen de contaminación en función de la concentración admisible, puesto que los datos arrojados por la simulación numérica se mantienen dentro del rango de incertidumbre asociado a la medición de los datos experimentales del sistema aquí analizado.
Mediante el uso de las correlaciones para los tiempos de corte dados en función de las concentraciones admisibles, obtenidas de la solución del modelo matemático presentado y la metodología de cálculo descrita en este trabajo, se propone una herramienta rápida y segura que puede ser aplicable, bajo las restricciones expuestas, como aporte en el establecimiento de los principios necesarios para realizar una posterior automatización del proceso de separación y respectivo almacenamiento de los fluidos del sistema gasolina-diesel al final de la línea.
En el análisis estadístico referente a la variación de los parámetros del sistema estudiado, se encontró que el parámetro de diseño que mayor efecto ejerce sobre el volumen de contaminación es el diámetro de la tubería, ya que este último determina en el número de Reynolds, el predominio entre las fuerzas, ya sea inerciales o viscosas, que se ejercen sobre el sistema de flujo, compuesto en este caso, por los fluidos gasolina-diesel y las respectivas restricciones de operación expuestas en el presente trabajo.
Los autores reconocen el apoyo de la UIS, ICP-ECOPETROL y GCM, por la gran oportunidad de realizar este trabajo de investigación.
[1] Freitas Rachid F. B.; Carneiro de Araujo J. H.; Basptista R. M. "Predicting Mixing Volumes in Serial Transport in Pipelines". Transactions of the ASME. Journal of Fluids Engineering., 124(2), 2002, 528-533. [ Links ]
[2] Baptista R. M.; Freitas Rachid F. B. "Estimating Mixing Volumes Between Batches in Multiproduct Pipelines". International Pipeline Conference ASME., 2, 2000, 1665-1170. [ Links ]
[3] Concha A.; Cruz H. Q.; Hernández P. N. "Modelamiento de la Propagación de los Frentes de Contaminación Generados por el Transporte de Combustibles por Poliductos". Dyna., 74 (152), 2007, 89-96. [ Links ]
[4] Ecopetrol (Empresa Colombiana de Petróleos), "Programa de control de calidad para combustibles transportados por poliducto". Bogotá D.C, Colombia, 1990. [ Links ]
[5] Levenspiel O. "How Much Mixing Occurs Between Batches". Pipe Line Industry., May, 1958, 51-54. [ Links ]
[6] Atsushi Hara; Hideo Hayashi; Masato Tsuchiya. "Mixing in Serial Flow in a Products Pipeline". Nippon Kokan Technical Report-Overseas., Dic, 1975, 51-55. [ Links ]
[7] Taylor G. I. "The Dispersion of Matter in Turbulent Flow Through a Pipe". Proceedings of Royal Society., Ser. A, 223, 1954, 446-468. [ Links ]
[8] Tichacek l. J.; Berkelew C. H.; Baron T. "Axial Mixing in Pipes". A.I.CH.E Journal., 3 (4), 1957, 439-442. [ Links ]
[9] Baptista R. M.; Freitas Rachid F. B.; Carneiro de Araujo J. H. "Mixing Volume Evaluation Under Pumping Shut-Down Conditions". Universidade Federal Fluminense, Octubre 20 de 2008, Disponible: http://www.psig.org/papers/2000/0111.pdf. [ Links ]
[10] Sjenitzer F. "How Much do Products Mix in a Pipeline". The Pipeline Engineer., Dic, 1958, d31-d34. [ Links ]
[11] Taylor G. I. "Dispersion of Soluble Matter in Solvent Flowing Slowing Through a Pipe". Proceedings of Royal Society., Ser. A, 219, 1953, 186-203. [ Links ]
[12] James W. Daily; Donald R. F. Harleman. Dinámica de fluidos con aplicaciones a la ingeniería. Editorial Tillas, México, 1975, 469- 493. [ Links ]
[13] Gambill Wallace R. "How to Estimate Mixture Viscosities". Chem. Eng., 66, 1959, 151-152. [ Links ]
[14] Victor L. Streeter. Mecánica de los fluidos. Editorial McGraw-Hill, México, 1972. 280. [ Links ]
[15] Aunicky Z. "The Longitudinal Mixing of Liquids Flowing Successively in Pipelines". Can. J. Chem. Eng., 48, 1970, 12-16. [ Links ]
[16] George E. Box; J. Stuart Hunter.; Willian G. Hunter. Estadística para investigadores. Editorial Reverté, S.A. España, 1989, 317-329. [ Links ]