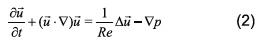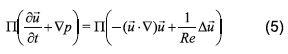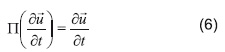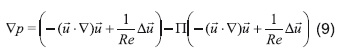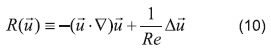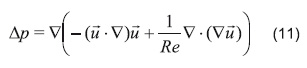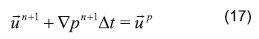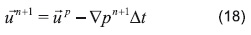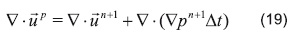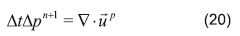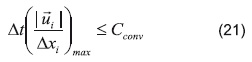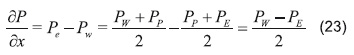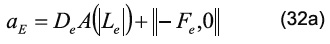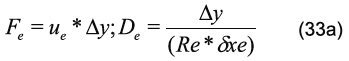Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Revista ION
Print version ISSN 0120-100X
Rev. ion vol.26 no.2 Bucaramanga July/Dec. 2013
incompresibles por el método de los volúmenes finitos
Karol Lizeth Cascavita Mellado1*; Julián Ernesto Jaramillo Ibarra2; Frank Rodolfo Fonseca
Fonseca3
1 Grupo de Modelado y Métodos Numéricos en Ingeniería (GNUM), Universidad Nacional de Colombia, Cra. 45 No 26-85 - Edificio Uriel Gutierrez Bogotá-Colombia
*klcascavitam@unal.edu.co
2 Grupo de Investigación en Energía y Medio Ambiente (GIEMA), Universidad Industrial de Santander (UIS), Cra. 27 calle 9, Bucaramanga, Colombia
3 Departamento de Física, Universidad Nacional de Colombia, Cra. 45 No 26-85 - Edificio Uriel Gutierrez Bogotá-Colombia
Fecha Recepción: 30 de mayo de 2013
Fecha Aceptación: 24 de octubre de 2013
El objetivo principal de este artículo es la resolución de las ecuaciones de conservación de cantidad de movimiento y de masa de Navier-Stokes, para un fluido incomprensible. Por esto, se presenta el planteamiento numérico con una discretización por medio de volúmenes finitos (MVF) y se hace uso del método de los pasos fraccionados, para la resolución del acoplamiento entre la velocidad y la presión. Con el propósito de validar el modelo matemático y verificar el código se resolvió un problema tipo "benchmark", el "Driven Cavity" en dos dimensiones. Se estudiaron dos números de Reynolds en régimen laminar: 100 y 1000. Los resultados obtenidos con la herramienta computacional desarrollada fueron similares a los esperados. Se usó un refinamiento del tipo h para la verificación.
Palabras clave: ecuaciones de Navier Stokes, volúmenes finitos, método de paso fraccional, driven cavity.
Stokes equations with finite volume method
The main goal of this paper is the numerical solution of the Navier-Stokes equations for an incompressible flow. A numerical approach with a finite volume discretization technique and using the method of fractional stepsare presented to solver the coupling between velocity and pressure. In order to validate the mathematical model and the code a the Driven Cavity problem in two dimensions for Reynolds numbers between 100 and 1000 was solved. The results given by the code are very similar to the expected. In order to verify the numerical results a h-refinement study is carried out.
Keywords: Navier Stokes equations, finite volumes, fractional step method, driven cavity.
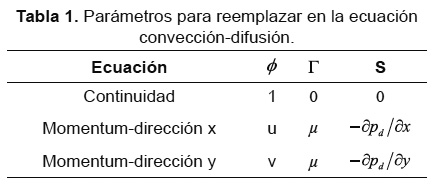
Las ecuaciones de conservación de masa y cantidad de movimiento se pueden escribir en forma general mediante la ecuación de convección difusión presentada a continuación
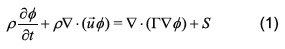
Para la obtención de las ecuaciones gobernantes mencionadas, referirse a la Tabla 1 y realizar la variación de los parámetros consignados allí.
El cálculo de las velocidades en la solución de las ecuaciones de conservación de cantidad de movimiento no presenta mayores inconvenientes cuando el campo de presiones es conocido. Caso contrario ocurre cuando debe calcularse, ya que no se tiene una ecuación explícita para la presión y se ha de derivar de la de conservación de la masa. Además, un gran inconveniente para la resolución y que hace más particular esta ecuación de conservación de cantidad de movimiento, es el acoplamiento entre las dos variables primitivas, ya que existe una interdependencia entre el campo de velocidades y el de presiones.
En general, existen tres tipos de métodos para resolver el sistema de ecuaciones de Navier-Stokes (NS) para flujo incomprensible: métodos basados en la ecuación de vorticidad donde se aplica la divergencia a la ecuación de NS, de forma que el vector de vorticidad se convierte en la nueva incógnita. Sin embargo, la ecuación resultante de vorticidad presenta cierta dificultad en el cálculo de la solución en las zonas cercanas a las paredes, siendo esta la principal desventaja, sin añadir el costo computacional adicional para problemas en 3D [1,2]. Métodos basados en compresibilidad artificial, adoptados de los métodos disponibles para flujo compresibles. Esta técnica relaja la ecuación de continuidad agregándole una derivada temporal artificial, obteniéndose así una ecuación análoga a la del flujo compresible. Por otra parte, son muy sencillos para la imposición de las condiciones de contorno, no obstante, el campo de velocidades se convierte en un campo libre de divergencia únicamente hasta que alcanza el régimen permanente [3,4]. De modo que para problemas no estacionarios, estos métodos tienden a ser más costosos en el cálculo computacional que los métodos de proyección de la presión [5,6]. Por último, métodos de iteración que resuelven el campo de presiones o aquellos de tipo predicción-corrección como son el Fractional Step Method (FSM)[7], el Semi-Implicid Method for Pressure-Linked-Equations (SIMPLE [8,9]) y sus modificaciones[1]: SIMPLER[10], SIMPLEC[11], PISO[12], entre otros. Estos métodos utilizan la ecuación de Poisson para la obtención de la presión, con la que se corrige la velocidad y se cumple así la condición de divergencia nula, impuesta por la ecuación de continuidad. Estos esquemas son también conocidos como esquemas de proyección [1].
El FSM, introducido por Chorin [7] y Temam [13], se basa en el uso de mallas centradas para las variables escalares y mallas desplazadas para cada componente del campo vectorial de la velocidad. Esta ubicación de las variables se realiza con el propósito de tener la presión exactamente en los contornos de los volúmenes de control, en la malla desplazada de las velocidades. Ya que estas fronteras representan los nodos de la malla colocada del campo escalar (Figura 3), en donde la variable es calculada por medio de la ecuación de Poisson, con lo cual se evita el problema del checkerd board [1]. También, se disminuye el número de interpolaciones, puesto que la presión no debe ser trasladada a las caras desde los nodos de los volúmenes de control. Sin embargo, aún se requieren algunas interpolaciones en los términos convectivos. En este trabajo se resuelve el problema de la cavidad con tapa movible mediante mallas estructuradas, por ser las que mejor se adaptan al dominio de estudio. Sin embargo, se advierte al lector que en la litertura científica puede encontrarlo resuelto con mallas no estructuradas, para lo cual se le remite a Boivina et al. [14].
En relación con el costo computacional en la resolución de ecuaciones dependientes del tiempo, la elección de un método iterativo es preferida respecto a un método directo, sobre todo en 3D por la capacidad computacional y de memoria demandados por este último. No obstante, puede implicar la necesidad de buenos precondicionadores, de acuerdo al problema a resolver [15]. En este contexto, los métodos fraccionados se presentan como una alternativa con partición del operador, que permite disminuir las restricciones sobre el paso del tiempo [15], haciéndo los métodos ampliamente utilizados debido a su notable eficiencia.
En cuanto a los métodos de discretización, el MVF presenta un uso más amplio en la dinámica de fluidos computacional (CFD, acrónimo en inglés) debido a que se mantiene la conservación de las variables discretizadas, inclusive en mallas no estructuradas para geometrías complejas. Este método captura discontinuidades y es sencillo de implementar [16]. Sin embargo, los métodos de elementos finitos (MEF), con mayor aplicabilidad en dinámica de sólidos, han ido incursionando en CFD hasta el punto que se emplea incluso para el diseño aerodinámico y el aeroespacial.
Inicialmente, el MEF se introdujo en CFD para resolver el flujo de Stokes, debido a su similitud con los problemas de elasticidad [17]. Posteriormente se aplicó a la resolución de las ecuaciones de Navier-Stokes [18-21]. Sin embargo, la formulación usual bajo la aproximación de Galerkin resultó ser inestable, a causa del mal condicionamiento del sistema por la naturaleza no autoadjunta del término advectivo [22]. Por tanto, para sobrepasar dicha dificultad se introdujeron los métodos mixtos [23], métodos de penalización, métodos de estabilización, el método de las líneas características y el método de los mínimos cuadrados.
El objetivo principal de este artículo es determinar la distribución de velocidades y presiones de un flujo incompresible mediante la resolución de las ecuaciones de Navier-Stokes. Las ecuaciones son discretizadas mediante la técnica de volúmenes finitos haciendo uso del FSM para resolver el acoplamiento entre la velocidad y la presión. Los autores pretenden que el documento sea una guía sencilla de implementación y que la metodología pueda ser usada para modelos más complejos. Es por esto que se introduce el FSM con un análisis detallado y paso a paso. Lo que es difícil de encontrar en la literatura, especialmente en el idioma español. Además, se aplica al problema de tipo benchmark de la cavidad debido a que a pesar de su geometría sencilla, el flujo presenta características complejas que lo convierten en un caso idóneo para la evaluación y validación de algoritmos o métodos numéricos.
Este documento se organiza de tal forma que inicialmente se presenta la teoría y la descripción del esquema FSM. Seguido por el modelo teórico y computacional para la solución del flujo dentro de una cavidad limitado a un caso bidimensional y de flujo incompresible, para luego pasar a los resultados y discusión del modelamiento para finalmente llegar a las conclusiones. Los casos estudiados son de flujos laminares con números de Reynolds igual a 100 e igual a 1000.
El Fractional Step Method
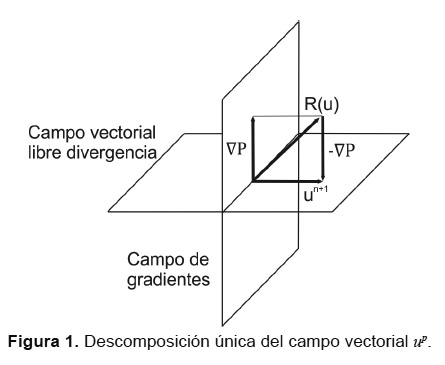
El FSM introducido por Chorin[7] fue más tarde modificado por Kim y Moin[24] extendiéndolo al método de los volúmenes finitos siendo desde entonces muy utilizado en la solución de las ecuaciones de Navier-Stokes en estado transitorio [25]. Esta técnica es de tipo predicción corrección, donde básicamente se descompone el campo vectorial de velocidades en dos campos ortogonales, uno de gradientes (presión) y un campo vectorial libre de divergencia. La velocidad esta formada por la única combinación lineal de estos dos anteriores, tal como se puede ver en la Figura 2. La presión se convierte en un operador que proyecta un vector arbitrario en un campo libre de divergencia [24]. Así, en primer lugar se obtiene la solución para el campo combinado, hallándose un mapa de velocidades intermedio, llamado el predictor de velocidades up. Este no cumple con la ecuación de continuidad para flujos incompresibles, por lo que se debe corregir proyectándolo sobre el plano que contiene todos los campos con divergencia cero (plano horizontal). Esta corrección la realiza mediante el gradiente de presiones y de esta forma se obtiene la solución real ut+dt.
Las siguientes secciones del documento se desarrollan con base en las ecuaciones adimensionales de conservación del momentum (2) y de la masa (3) de Navier-Stokes, para un fluido incompresible y Newtoniano, mostradas a continuación.

Planteamiento del método
En este apartado se presenta el planteamiento y discretización de las ecuaciones de NS mediante el FSM. El método del FSM se basa en el teorema de descomposición de Helmothz-Hodge [26]. El método inicia proyectando los términos de la Ecuación 2 en un campo libre de divergencia, donde el operador de proyección es П(·).
El término transitorio permanece invariante al ser proyectado puesto que el campo de velocidad es incompresible, de manera que ya se encuentra en el plano de proyección. Ortogonal a éste se tiene el plano de gradientes que contiene el gradiente de presiones, con lo que la proyección de este campo es nula.
Reemplazando las Ecuaciones 6 y 7 en la Ecuación 5 se llega a:
Ahora si se despeja el término de la presión de la Ecuación 2 y se reemplaza el término temporal por lo encontrado en la ecuación anterior se llega a:
De esta forma se ha obtenido una descomposición de la ecuación de Navier-Stokes en un campo vectorial libre de divergencia (Ecuación 8) y un gradiente de un campo escalar (Ecuación 9). Estos se pueden ver gráficamente en la Figura 1 donde los términos del primer paréntesis en la Ecuación 9 serán representados por el vector R(u):
y los términos del segundo paréntesis representan el vector proyectado un+1.
Si a la Ecuación 9 se le aplica el operador divergencia, se genera la conocida ecuación de Poisson, cuya importancia para este método está en generar la ecuación faltante para cerrar el sistema de ecuaciones.
Se puede notar como el término de viscosidad en la Ecuación 11 permanece incompresible, por lo que su proyección analíticamente es él mismo. Sin embargo, para una solución numérica, por ende discreta, es preferible corregir tantos los términos convectivos como los difusivos, asegurando el cumplimiento de la incompresibilidad del fluido. Los términos temporales se remueven debido a esta misma condición.
Discretización temporal
A continuación se presenta la discretización temporal de las ecuaciones diferenciales desarrolladas anteriormente. Para la aproximación del término temporal u:t se aplica el esquema de bajo orden CDS (Central Difference Squeme o Esquema de las Diferencias Centradas) [9], mientras que para los términos difusivos y convectivos agrupados en R(u), como se muestra en la Ecuación 10, se usa un esquema explícito de segundo orden conocido como el esquema Adams-Bashforth [27]. Así se obtiene el siguiente conjunto de ecuaciones discretizadas:
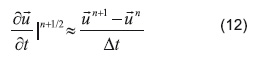
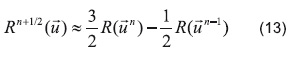
Cabe anotar que la ecuación de continuidad se cumple únicamente en el instante siguiente, lo que es lógico si se piensa que es un+1 la velocidad real del fluido y por ende es esta la única velocidad que debe cumplir con la restricción de incompresibilidad.

La Ecuación 2 queda escrita de manera discreta usando un esquema de primer orden hacia atrás de Euler para el término de presión, de la siguiente forma.

Reorganizando:
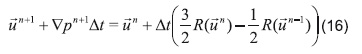
El término de la derecha de la ecuación anterior representa el predictor de velocidad up, reemplazándole se obtiene:
y finalmente se corrige la velocidad predictora con lo que se calcula la velocidad del instante siguiente:
La presión se obtiene de aplicar la divergencia a la Ecuación 17, produciendo la ecuación de Poisson en forma discreta (Ecuación 19):
Resultando la siguiente ecuación al aplicar la hipótesis de incompresibilidad:
Establecida la formulación matemática se procede a enumerar los pasos de resolución del FSM:
- Resolución de la ecuación de cantidad de movimiento sin el gradiente de presión: Primero evaluar R(un), y luego evaluar (up).
- Resolución de la ecuación de Poisson para obtener el campo de presiones: Esto requiere evaluar ∇.(up) y resolver la ecuación de Poisson discreta (20).
- Obtener el campo de velocidades en el instante n+1, haciendo la corrección con el campo de presiones de manera que se cumpla la continuidad: Evaluar Ecuación (18).
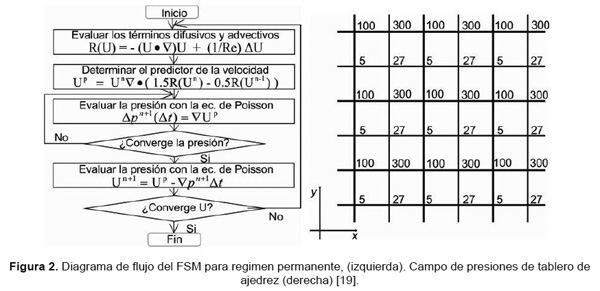
El diagrama de flujo de este método se presenta en la Figura 2 (panel izquierdo).
Criterio de estabilidad Debido a que el FSM es un método explícito, por razones de convergencia se deben especificar unos criterios de estabilidad para el Δt, los cuales vienen definidos por la Ecuación 21.

donde los valores de Cconv y Cvisc representan el criterio CFL (Courant-Friedrich-Levy), los cuales son tomados en este documento como 0,35 y 0,2 [28] respectivamente, para alcanzar una buena estabilidad del método.
Malla desplazada
El cálculo de las primeras derivadas de la presión en una malla colocada (es decir centrada en los nodos), acepta en las soluciones numéricas campos escalares sin significado físico, como el conocido tablero de ajedrez [9], en el cual los valores se van alternando tal como se ve en la Figura 2, (lado derecho). Esto se debe a que el gradiente de presiones no depende de la presión del nodo en el que se están realizando los cálculos, pero sí de la de los nodos adyacentes. Como lo muestran las Ecuaciones 23 y 24 la presión en el nodo Pp no aparece en la discretización final.
Una manera de solucionar este inconveniente es utilizar mallas desplazadas, para u y v, donde las velocidades se calculan exactamente en las caras. De ahí que no exista la necesidad de interpolar los valores de la presión hacia las caras desde los nodos para el cálculo del gradiente en las ecuaciones de conservación de cantidad de movimiento.
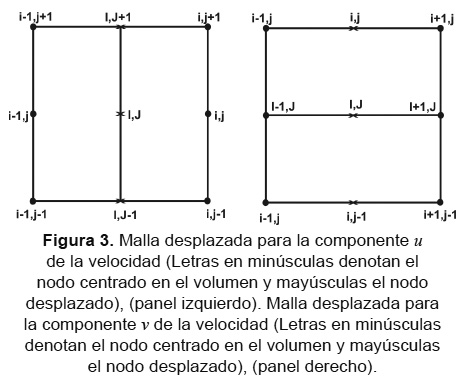
Este esquema requiere tres mallas diferentes, una malla colocada para presiones y temperaturas, una desplazada en dirección x para u (Figura 3 panel izquierdo), y una desplazada en dirección y para v (Figura 3 panel derecho) (las letras en mayúsculas indican los nodos de la malla colocada).
Las mallas se desplazan solo medio volumen de control, aquí únicamente se tienen en cuenta dos dimensiones, aunque para una tercera el procedimiento es análogo.
La notación de los subíndices se presenta gráficamente en la Figura 3.
Modelos teórico y computacional
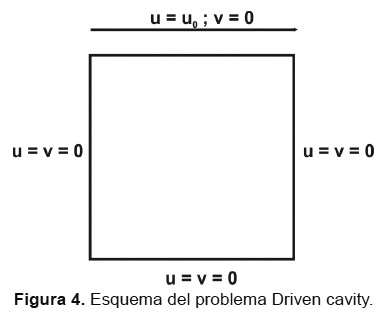
El problema estudiado conocido como "Driven Cavity" consiste en un flujo laminar e incompresible que se encuentra en una cavidad cuadrada, cuya pared superior se mueve con una velocidad uniforme en su mismo plano. Las demás paredes permanecen estáticas como se muestra en la Figura 4.
Esta configuración de flujo plantea un problema de convección forzada bidimensional, donde la fuerza motriz viene dada por la placa superior que se desplaza de manera constante. Así pues, no existen términos de flotación y por ende el campo de velocidades no se ve afectado por el de temperaturas, como ocurre en la convección natural.
Los flujos laminares con los que se evaluó la herramienta computacional desarrollada son Re=100 y Re=1000. Se procede a presentar el modelo matemático con su respectiva adimensionalización para el caso considerado en este trabajo.
Los parámetros de adimensionalización utilizados para este problema de convección forzada son los siguientes:

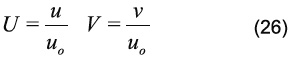

donde uo es la velocidad constante de la pared superior función del número de Reynolds impuesto por el problema (Figura 4). Las ecuaciones gobernantes adimensionalizadas de conservación de cantidad de movimiento (Ecuación 2) y de conservación de la masa (Ecuación 3) están sometidas a las siguientes condiciones de frontera:
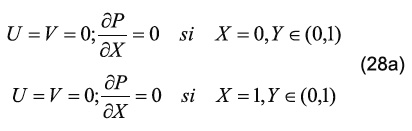
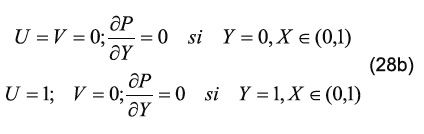
Vale la pena resaltar que el problema está en régimen permanente, por lo que la solución numérica es hallada con la estabilización del problema temporal.
Ecuaciones de discretización para la velocidad
En este apartado se introducen las ecuaciones discretas para el término R(ø), donde ø representa cada componente del vector velocidad u. Para esto primero se parte de la definición de R(u), dada anteriormente en la Ecuación 10, posteriormente se procede a integrarle espacialmente en las direcciones x y y.
<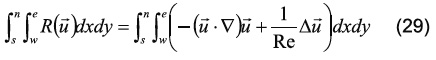
de forma discreta se tiene para cada componente:
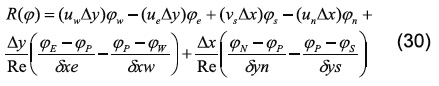
La cual puede expresarse de forma compacta así:
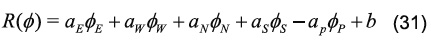
siendo los coeficientes:
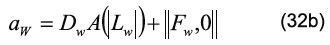
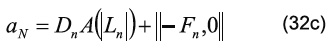
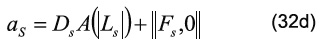
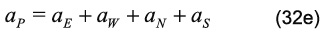

El término ƒ puede representar un término de flotación debido a las fuerzas másicas en la dirección del campo gravitatorio. Por otra parte, el símbolo ||°,*|| escoge el máximo de sus parámetros. Además, los coeficientes convectivos y difusivos están definidos como:
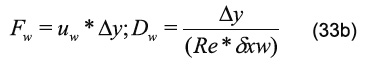
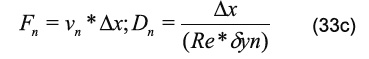
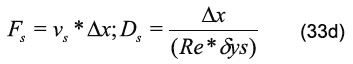
y los términos L como:

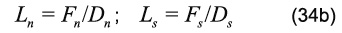
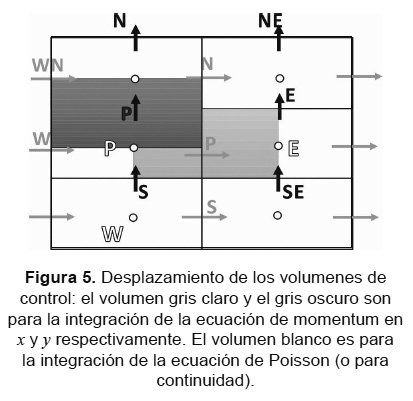
Las Tablas 2 y 3, listan los parámetros apropiados a reemplazar en la Ecuación 33, de manera que se obtengan las ecuaciones de discretización teniendo en cuenta las mallas desplazadas para las componentes de la velocidad, u y v.
Además, el desplazamiento de las mallas y por ende la notación de los subíndices se ha realizado de la forma como se presenta en la Figura 5.
Aproximación de los flujos
Los términos en las fronteras del volúmen de control (con subíndices en minúscula) provenientes de la discretización del fenómeno convectivo en este trabajo son aproximados mediante un esquema de bajo orden que admite una forma general como el de las Ecuaciones 32 y 33. Los métodos seleccionados son el CDS, el Upwind (UDS), el Híbrido (HDS) y el Power Law (PLDS) [9] (Tabla 4). También pueden ser aproximados por esquemas convencionales de alto orden conocidos como Quick [30] o Smart [31,32]. No obstante su implementación esta por fuera de los objetivos de este trabajo. Aquellos provenientes del término difusivo son aproximados con un CDS.
La precisión de los esquemas usados depende principalmente del número de Péclet en el que trabajan, ya que éste determina la relación entre los fenómenos de difusión y convección, expresando así el grado de predominancia para la convección con números altos de Reynolds y de la difusión en caso contrario. Así, por ejemplo, el CDS es especialmente útil en problemas donde los términos viscosos son los que dominan, siendo el flujo en el contorno calculado como un promedio aritmético:
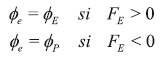
Por otro lado, el UDS es muy sencillo y se ajusta mejor cuando el fenómeno de convección predomina, puesto que toma en cuenta la dirección del flujo:

Como una combinación de ambos métodos se presenta el HDS, siendo ventajoso para amplios rangos de Pe, aunque muestra mayores errores en la aproximación con números de Péclet cercanos a ±2. Esto se debe principalmente a que desprecia muy rápidamente los términos difusivos conforme se aumenta su valor [9].
Por otra parte, el PDLS es un esquema de segundo orden, debido a que realiza una aproximación por medio de un polinomio de grado quinto de la solución exacta y de tipo exponencial, de la ecuación de conducción-convección en estado estable para 1D, con un término fuente igual a cero [9,33].
Debido a los números de Reynolds relativamente bajos en los que se desea aquí solucionar el problema driven cavity, se escoge el esquema CDS ya que posee el mismo orden de precisión del PDLS, pero exige un menor costo computacional debido a la ausencia del exponente a la 5.
Como una introducción a la simulación de problemas en la mecánica de fluidos el problema driven cavity presenta las ventajas de una geometría y condiciones de fronteras simples. Sin embargo, también induce cierta dificultad para los esquemas numéricos en la captación de los gradientes altos que se presentan en las zonas cercanas a las paredes. Otras ventajas son su solución laminar estable y por último pero no menos importante, la existencia de una gran literatura sobre el desarrollo de dicho ejercicio, puesto que es uno de los problemas de mayor interés en el modelamiento de fluidos permitiendo la validación de nuevos códigos para problemas más específicos.
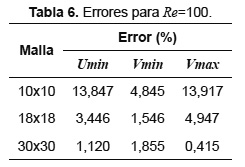
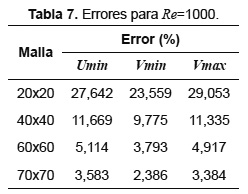
Con el propósito de verificar la independencia de la malla de las soluciones numéricas obtenidas, se toma primero una diferencia permisible del 5% en comparacíón con los datos presentados en la Tabla 5 y se evalúa con diferentes densidades de mallas. Los errores relativos asociados a las mallas empleadas teniendo en cuenta los valores mínimos de las componentes de la velocidad u y v, además del valor máximo de v, se encuentran tabulados en la Tabla 6 para Re=100 y en la Tabla 7 para Re=1000.
Conforme se incrementa el número de Reynolds la malla debe refinarse aún más para cumplir las especificaciones del error admisible, así mientras que para Re=100 es suficiente con una malla de 18x18, para Re=1000 la malla debe aumentarse hasta 70x70.
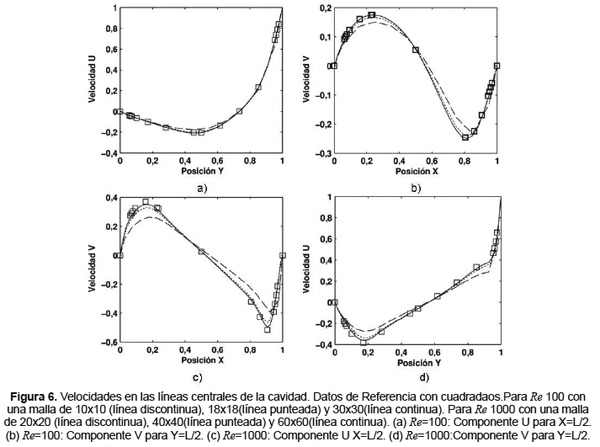
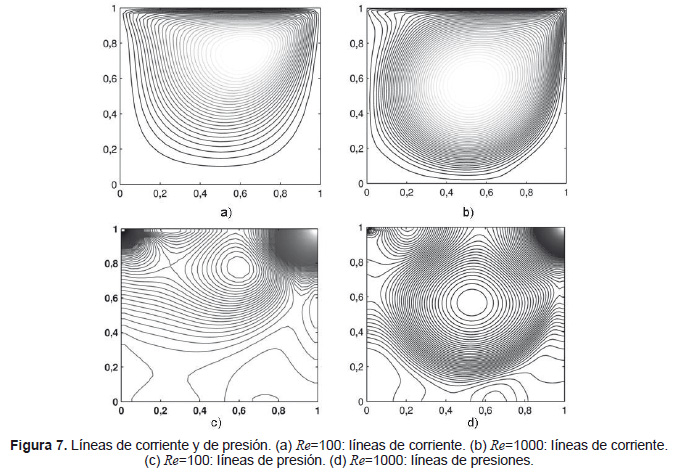
Los resultados obtenidos producto de la resolución de las ecuaciones de NS mediante el FSM se presentan en la Figura 6 (a, b, c y d). Se muestran las líneas de corriente en la Figura 7 (a y b), además el mapa de presiones en la Figura 7 (c y d) en la cavidad, con mallas uniformes de 30x30 (para una mejor resolución) para Re=100 y de 70x70 para Re=1000.
En la Figura 6 (a, b, c y d) se presentan las curvas de velocidades en las líneas que pasan por el centro geométrico de la cavidad, con los valores obtenidos y con los de referencia [34]. Conforme el número de Reynolds aumenta las fuerzas convectivas ejercen un mayor predominio sobre las fuerzas viscosas, haciendo que la transferencia de momento entre capas adyacentes del fluido sea cada vez menor. Sus implicaciones sobre los perfiles de velocidades de las gráficas mencionadas se explicarán a continuación.
Asumiendo que el fluido se encuentra inicialmente en reposo al comenzar a actuar la pared superior, éste fluirá hacia el dominio en sentido contrario al de las manecillas de reloj. Durante esta trayectoria el fluido irá progresivamente transfiriendo su momentum hacia capas adyacentes, con lo cual las velocidades mas altas se tendrán al inicio del trayecto, en las zonas cercanas a la pared superior y vertical derecha (Figura 6).
Las altas velocidades en zonas cercanas a las paredes generan grandes gradientes debido a que el fluido debe desacelerarse rápidamente para cumplir la condición de no deslizamiento (u=0, v=0) sobre dichos lugares. Por lo anterior, las curvas de la componente de la velocidad v, en la Figura 6 (b y d), muestran unas pendientes muy elevadas sobre el extremo derecho que representa la pared vertical derecha. Sin embargo, cabe notar que estos gradientes son mayores cuando Re=1000, debido a que los términos difusivos son menos relevantes y por tanto la transferencia de momentum entre capas es menor. De esta forma el fluido que viene acelerado por la pared móvil, no disminuirá en gran medida su velocidad, pero si debe hacerlo conforme se acerca a la pared, generándose gradientes más altos. Estos cambios tienen una implicación sobre la precisión de los resultados, ya que una malla muy basta no es capaz de capturar estos gradientes y por ende la solución pierde exactitud. En consecuencia, en el caso de números de Reynolds elevados se requiere de mallas muy finas en las paredes, siendo esto un inconveniente en la obtención de los resultados de este trabajo, debido al uso de mallas uniformes, que implicaron un mayor costo computacional por el refinamiento de zonas que no lo requerían. Por lo anterior, se recomienda el uso de mallas no uniformes concentradas hacia las paredes para la solución de este problema.
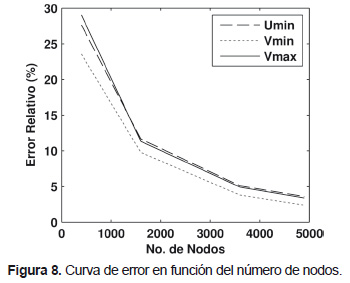
La Figura 8 muestra la curva de disminución del error al incrementar el número de nodos para Re=1000, en la cual se puede observar que el efecto del aumento de la densidad de la malla sobre la precisión es cada vez menor, ya que esta tiende a mostrar una forma exponencial en descenso.
Por otra parte, la dificultad en la implementación se encuentra principalmente en el uso de las tres mallas que se trabajan, llevando algunas veces a confusiones. Sin embargo, el hecho que las mallas escalonadas permitan la obtención de las velocidades justo en las caras de los volúmenes de control, omite la interpolación de los valores en los nodos de la malla colocada (usada para resolver las variables escalares) hacia los caras de los volúmenes, reduciendo los errores. También evita los valores irreales de la presión.
En este documento se estudió el comportamiento de las ecuaciones de NS con bajos números de Reynolds, haciendo uso del FSM y una discretización por el método de los vólumenes finitos. En primera instancia se presentó el procedimiento para la obtención del campo de velocidades que posteriormente fue corregido con el de presiones, cumplíendose así la condición de incompresibilidad. El modelo numérico aplicado usa esquemas numéricos tanto para la discretización espacial (CDS) como temporal (Adams-Bashforth) de segundo orden de aproximación.
El uso de un esquema temporal explicito conjuntamente con el FSM hacen que sólo sea necesario resolver la ecuación de Poisson para obtener la presión, en comparación con otros métodos más convencionales en los que se debe resolver también el campo de velocidades.
De las comparaciones de los resultados obtenidos en el driven cavity con las soluciones usadas como referencia, se puede deducir que la herramienta desarrollada es capaz de resolver las ecuaciones de NS para flujos laminares e incompresibles. De este modo, las pruebas numéricas corroboraron las hipótesis planteadas en la solución del modelo matemático y las aproximaciones de los métodos en la solución numérica.
Jaramillo JE y Cascavita KL desean agradecer al Centro Tecnológico de Transferencia de Calor (CTTC), Universidad Politécnica de Cataluña (UPC), por financiar parte del trabajo y al profesor Oliva A del CTTC por su soporte.
[1] Solution Methods for the Navier Stokes Equation (Sitio en internet). School of Civil and Enviromental Engineering. Georgia Tech. Disponible en: http://cfd.ce.gatech.edu/docs/CEE7751-7.pdf. Acceso el 5 de enero de 2012. [ Links ]
[2] Gatot B, Pranowo. Artificial compressibility method for steady circulation flow in a Lid Driven Cavity. J. Teknologi Industri. 2000;4(2):135-42. [ Links ]
[3] Green SI. Fluid Vortices. Netherlands: Springer Science+Business Media Dordrecht; 1995. [ Links ]
[4] Peyret R, Taylor TD. Computational methods for fluid flow. Nueva York: Springer-Verlag; 1983. [ Links ]
[5] Chan DC, Darian A, Sindir M. A comparison of artificial compressibility and fractional step methods for incompressible flow computations. NASA Goddard Space Flight Center. Washington D.C, Estados unidos;1992. [ Links ]
[6] Kwak D, Kiris C, Dacles-Mariani J. An assessment of artificial compressibility and pressure projection methods for incompressible flow simulations. En: Bruneau CH. 16th International Conference on Numerical Methods in Fluid Dynamics; 1998 jul 6-10; Arcachon, France. Berlin: Springer; 1998. p. 177-82. [ Links ]
[7] Chorin AJ. Numerical Solution of the Navier-Stokes Equations. J. Comput. Phys. 1968;22:745-62. [ Links ]
[8] Van Doormaal JP, Raithby GD. Enhancement of the SIMPLE method for predicting incompressible fluid flows. Numer. Heat Transfer. 1984;7:147-63. [ Links ]
[9] Patankar SV. Numerical Heat Transfer And Fluid Flow. Series in computational methods in mechanism and thermal sciences. Washington, D.C.: Hemisphere Publishing Corporation; 1980. [ Links ]
[10] Patankar SV. A calculation procedure for two-dimensional elliptic situations. Numer. Heat Transfer. 1981;4:409-25. [ Links ]
[11] Van Doormaal JP, Raithby GD. Enhancement of the SIMPLE method for predicting incompressible fluid flows. Numer. Heat Transfer. 1984;7:147-63. [ Links ]
[12] Issa RI. Solution of the implicitly discretized fluid flow equations by operator-splitting. J. Comput. Phys. 1985;62:40-65. [ Links ]
[13] Temam R. Sur l'approximation de la solution des équations de Navier-Stokes par la méthode des pas fractionnaires (II). Archive for Rational Mechanics and Analysis. 1969;33:377-85. [ Links ]
[14] Boivina S, Cayré,F Hérard JM. A finite volume method to solve the Navier-Stokes equations for incompressible flows on unstructured meses. J. Therm. Sci. 2000;39:806-25. [ Links ]
[15] Krotkiewski M, Dabrowski M, Podladchikov YY. Fractional Steps methods for transient problems on commodity computer architectures. Physics of the Earth and Planetary Interiors. 2008;171:122-36. [ Links ]
[16] Ferziger JH, Peric M. Computarional Methods for Fluid Dynamics. 3 ed. Berlín: Springer, 2002. [ Links ]
[17] Zienkiewicz OC, Taylor RL. The Finite Element Method: Volume 3: Fluid Dynamics. 5 ed. Barcelona: Butterworth-Heinemann; 2000. [ Links ]
[18] Crouziex M, Raviart PA. Conforming and nonconforming finite element methods for solving the stationary Stokes equations I. RAIRO. 1973;7(R-3):33-76. [ Links ]
[19] Girault V, Raviart PA. Finite element approximation of the Navier-Stokes equations. Nueva York: Springer, 1979. [ Links ]
[20] Temam R. Some finite element methods in fluid flow. Lecture Notes in Physics. 1979;90:34-55. [ Links ]
[21] Temam R. Navier-Stokes equations. Nueva York: North-Holland; 1984 [ Links ]
[22] Garzon DA. Aplicación del método Petrov-galerkin como técnica para la estabilización de la solución en problemas unidimensionales de convección-difusión-reacción. Revista Facultad de Ingeniería Universidad de Antioquia. 2009;47:73-90. [ Links ]
[23] Hermann IR. Elasticity equations for incompressible and nearly incompressible materials bye a variational theorem. AIAA Journal.1965;3(10):1986-1900. [ Links ]
[24] Kim J, Moin P. Application of a Fractional-Step Method to Incompressible Navier-Stokes Equations. J. Comput. Phys. 1985;59:308-23 . [ Links ]
[25] Armfield SW, Street R. Fractional step methods for the Navier-Stokes equations on non-staggered grids. ANZIAM J. 2000: 42(E):C134-C156. [ Links ]
[26] Arfken G, Weber H, Hans J. Mathematical Methods for Physicists. 6 ed. Londres: Academic Press; 2002. [ Links ]
[27] Butcher JC. Numerical methods for ordinary differential equations. 2 ed. Inglaterra, Chichester: John WileySons; 2008. [ Links ]
[28] Introduction to the Fractional Step Method. Universidad Politécnica de Cataluña, Terrasa (Barcelona), Instituto Tecnológico de Transferecia de Calor. [ Links ]
[29] Pantakar SV. Numerical Heat Transfer And Fluid Flow. London: Thaylor y Francis; 1980. p.116. [ Links ]
[30] Leonard BP. A stable and accurate convective modelling procedure based on quadratic upstream interpolation. Comput. Methods in Appl. Mech. Eng. 1979;19:59-98. [ Links ]
[31] Gaskell PH, Lau AKC. Curvature-compensated convective transport: SMART, a new boundedness preserving transport algorithm. Int. J. Numer. Methods Fluids. 1988;8:617-41. [ Links ]
[32] Zhu J. On the higher-order bounded discretization schemes for finite volume computations of incompressible flows. Comput. Methods in Appl. Mech. Eng. 1992;98:345-60. [ Links ]
[33] Numerical solution of convection. Universidad Politécnica de Cataluña, Terrasa (Barcelona), Instituto Tecnológico de Transferecia de Calor. [ Links ]
[34] Ghia U, Ghia KN, Shin CT. High-Re solutions for incompressible flow using the Navier-Stokes equations and a multigrid method. J. Comput. Phys. 1982;48:387-411. [ Links ]