Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Accesos
Accesos
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares en
SciELO
Similares en
SciELO -
 Similares en Google
Similares en Google
Compartir
Lecturas de Economía
versión impresa ISSN 0120-2596
Lect. Econ. n.68 Medellín ene./jun. 2008
Technological Integration and Income Gaps
Integración tecnológica y brecha del ingreso
Intégration technologique et écarts de revenu
Carlos Humberto Ortiz and Javier Andrés CastroI
I Carlos Humberto Ortiz: Professors at the Economics Departament of Universidad del Valle (Cali, Colombia). E-mails: ortizc@univalle.edu.co. Postal address: Departamento de Economía, Universidad del Valle, A.A. 25360, Cali, Colombia. Javier Andrés Castro: Professors at the Economics Departament of Universidad del Valle (Cali, Colombia). E-mails: jacastro@univalle.edu.co. Postal address: Departamento de Economía, Universidad del Valle, A.A. 25360, Cali, Colombia. Financial support from Universidad del Valle and Colciencias is gratefully acknowledged. Erika Badillo and Milena Valens were excellent research assistants. Douglas Laing provided invaluable advice. As usual, the authors are responsible for the whole text.
–Introduction. –I. The Model in Autarky. –II. Open Economy. –III. Some Empirical Support. –Concluding Comments. –References
Resumen: Leontief (1963) sostiene que los países subdesarrollados son pobres porque son en gran medida, económicamente menos diversificados. Este artículo muestra que un modelo de equilibrio general con una estructura de insumo-producto estable y con una externalidad de la productividad generada por diversificación de factores, puede ser consistente con la hipótesis de Leontief. Una versión del modelo en economía abierta permite la posibilidad de violar el teorema de la igualación del precio de los factores, permitiendo así que las economías desarrolladas obtengan una alta remuneración de capital y un alto nivel de ingreso. Se presenta alguna evidencia empírica sobre la relación entre la integración tecnológica y el ingreso real.
Palabras clave: Insumo-producto, integración tecnológica, brecha del ingreso, estructuras tecnológicas asimétricas, igualdad de los precios de los factores. Clasificación JEL: C67, D57, F11, L60, O14.
Abstract: Leontief (1963) claimed that underdeveloped countries are poor because they are by far less economically diversified. This paper shows that a general equilibrium model with a stable input-output structure and a productivity externality due to input diversification may be consistent with Leontief's hypothesis. An open economy version of the model yields the possibility of breaking the factor price equalization theorem so that developed economies enjoy higher capital remuneration and higher income level. Some empirical evidence on the relationship between technological integration and real income is provided.
Keywords: input-output, technological integration, income gaps, asymmetric technological structures, factor price equalization. JEL Classification: C67, D57, F11, L60, O14.
Résumé: Leontief (1963) soutient que les pays sous-développés sont pauvres parce qu'ils sont moins diversifiés. Cet article présente un modèle d'équilibre général avec une structure input-output stable et avec une externalité dans la productivité entrainée par la diversification dans les facteurs de production. Il s'agit d'un modèle qui peut être consistant avec l'hypothèse de Leontief. Une version de ce modèle en économie ouverte permet de rejeter le théorème de l'égalisation des prix des facteurs, permettant ainsi que les économies développées puissent obtenir une rémunération de capital élevée et un niveau de revenu également élevée. Nous présentons une évidence empirique sur la relation entre l'intégration technologique et le revenu réel.
Mots clef: structure input-output, intégration technologique, écarts de revenu, structures technologiques asymétriques, égalisation des prix des facteurs. Classification JEL: C67, D57, F11, L60, O14.
Introduction
The central issue of development economics is the prevalence of huge per capita income gaps across countries (World Bank's World Development Report, Union Bank of Switzerland's Prices and Earnings Around the Globe). In order to make a contribution to the explanation of these gaps, this paper rescues a hypothesis that was first proposed by Leontief (1963): underdeveloped countries are poor because they are by far less economically diversified and less tecnologically integrated.
This hypothesis was based on several empirical findings about "The Structure of Development" (Leontief, 1963). As the main main objective of this paper is to build a general equilibrium model that replicates these findings, it is convenient to start by describing them.
After a rigorous cross-country comparison of input-output matrices, Leontief found that the technologies are relatively invariable: each productive sector exhibits a relatively constant relationship between the inputs it receives from other sectors and its contribution to total product of the economy. According to Leontief, each technology is some kind of "recipe" that allows the transformation of some "ingredients" into the sector's product. consequently, the net of interindustry linkages is relatively stable.
Based on his structural analysis, Leontief revealed a common feature of underdeveloped countries: "Their input-output tables show that in addition to being smaller and poorer they have internal structures that are different because they are incomplete, compared with the developed economies" (Op. cit., p. 163).
Since a country's lack of development can be compensated by importing those goods that it does not produce but needs to consume, Leontief paid special attention to the countries' profile of international trade. He found that underdeveloped and developed countries are asymmetrically related in the world markets: underdeveloped countries are characterized by structural lacks and specialize in primary goods, whilst developed countries are characterized by structural completeness and specialize in manufacturing products.
Hence, Leontief showed that the more developed is the economy, the more economic activities it has, and the more complete and articulated is its economic structure. This pattern of structural change was later empirically recognized and validated by development economists: "As countries industrialize their productive structures become more `roundabout' in the sense that a higher proportion of output is sold to other producers rather than to final users" (Chenery, Robinson and Syrquin, 1986, p. 57).
Chenery and collaborators named this pattern of development as inputoutput deepening. Besides, Chenery et al also rediscovered that comparative advantages tend to change from primary to secondary activities along the process of structural change.
Leontief did not only discover input-output deepening, he also showed that this process follows some regular path:
"Displayed in the input-output table, the pattern of transactions between industries and other major sectors of the system shows that the more developed the economy, the more its internal structures resembles that of other developed economies" (Op. cit., p. 163).
In order to reach this conclusion, Leontief (1963) compared the inputoutput matrix of the United States with the input-output matrix of the advanced economies of Western Europe. Hence, a country's degree of economic development could be assessed by the relative completeness of its economic structure. Moreover, the most developed economies set the technological horizon for underdeveloped economies to reach.
As in Marx (1867), who believed that the more industrialized countries pointed out the path of development to the less progressive countries, Leontief claimed that, "Given the country mix of resources and the available technologies, the essence of the process of development [is] to create an economic system as similar as possible to the system of the most developed economies" (Op. cit., p. 164).
Therefore, Leontief's advice for economic development was to remain on the path of structural change.
When you read Leontief's paper, everything seems to be easy: just follow the path set by the old industrialized countries. Actually, by the time Leontief was writing his essay on the structure of development, some small countries from South-East Asia were following his advice without being aware of it. They became the famous group of the "Asian Tigers": Korea, Hong-Kong, Taiwan, Singapour and Malaysia. Just before them, Japan had made an impressive industrial take off. And nowadays continental China and India are also turning themselves into newly industrialized economies. However, most underdeveloped countries have been unable to follow suit.
In order to explain these few experiences of economic success and the many experiences of stagnation or mediocre performance, economic historians such as Amsden (1989) and Landes (1998) have pointed out that economic diversification is a public asset requiring a long sequence of efforts to be built. It seems that achieving a high degree of economic diversification calls for a strong long-run political commitment from the government and from the private sector. Investments in education and public infrastructure seem to be necessary complementary processes. Learning-by-doing and industrial policies seem also to be necessary conditions for consolidating an industrial base. Moreover, some development economists have claimed that failing to build a diversified economic structure and excessive reliance in static comparative advantages, especially those based on natural resources and unskilled labour, may lead to deindustrialization and inferior paths of economic growth (Lucas, 1988; Young, 1991; Matsuyama, 1992; Sachs and Warner, 1995; Landes, 1998).
Based on the above considerations, this paper aims at building a general equilibrium model with a stable input-output structure and a productivity externality due to input diversification (and increasing technological integration) that is consistent with Leontief's hypothesis: economic diversification and technological integration are directly related with productivity. Since this feature is a well-known result from general equilibrium models that embody input diversification in a closed economy context, this paper justification is twofold. First, it explicitly models input-output deepening as a technological feature; second, it extends the analysis to international trade: the open economy version of the model delivers the possibility that factor remunerations across countries are unequal, where the winners are the most diversified economies. According to this analysis, a country may find itself with lower factor remuneration if factor mobility is internationally restricted, and the country's factor supply is too high relative to its own degree of economic diversification. Hence, the inherited levels of economic diversification (and technological integration) across countries may help explain the income gaps between developed and underdeveloped countries.
The relationship between economic structure and income gaps has been explored previously by Ortiz (2001, 2002). This paper includes an explicit analytical solution to the gap of capital factor remuneration across countries in the context of a general equilibrium model of international trade. This paper also provides econometric evidence that the relationship between aggregate technological integration and income level is not rejected by the data.
The paper is organized as follows. The model under autarky is set up in the second section. The third section contains the analysis of international trade. The fourth section examines some empirical data that are consistent with the paper hypothesis. The fifth section ends up with some concluding comments.
Due to space constraints, appendices 1 to 8, and the the statistical data base are excluded from the text. They are available from the authors by request.
I. The Model in Autarky
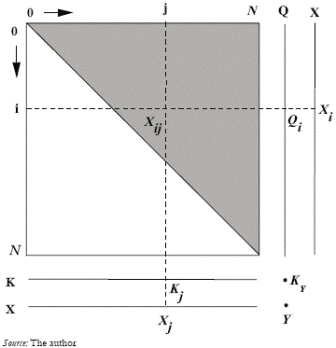
The economic structure is represented by an input-output matrix augmented with the vector of capital allocation (see figure 1). Capital in this model may be considered as an index of all forms of capital involved in the technology. All sectors are indexed according to its degree of backward technological integration between 0 and N. From now on N will be referred to as the number of intermediate goods. Thus, the economy is made up of N+1 productive activities: N intermediate-good sectors and the final-good sector. X represents the vector of intermediate goods produced in the period of analysis; and K represents the vector of capital. As figure 1 shows, backward technological integration –technological dependence on input suppliers– is assumed to increase linearly with the sector's index: the sector j only uses as intermediate inputs the goods with lower index. This feature guarantees that the input-output matrix is perfectly triangular.
Figure 1. Closed Economy Structure
The intermediate inputs of any sector can be read vertically off the inputoutput matrix. The vector Q, in particular, is the set of intermediate inputs of the final-good production activity. Notice that the final sector uses in its activity all available intermediate goods.
The technology of the j-th intermediate good is defined by the following production function:
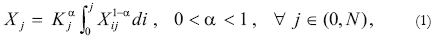
where Xj is the gross output of good j, Kj is the capital of sector j, and Xij is the intermediate consumption of good i in sector j (i ≥ j).
There are some important features of these technologies: 1) economic activities are characterized by constant returns to scale in capital and intermediate inputs; 2) intermediate inputs are good substitutes: the marginal rate of technical substitution between any pair of intermediate inputs is given by 1/α> 1 (Appendix 1); 3) all intermediate goods are produced with the same technology, the only difference comes from the range of intermediate inputs used by each sector. The final good technology is given by:

where Y is the final good output, KY is the capital of the sector, and Qi is the intermediate consumption of the i-th input in the final good sector. This technology is then identical to the technology of the N-th intermediate good. Notice that creation of new inputs –a larger diversification– implies a productivity externality: ∂Y/∂N = Kyα QN1-α > 0. Hence, an important characteristic of the model is the existence of productivity externalities derived from input diversification. As in the pin factory of Adam Smith (1776), productivity increases with division of activities.
The final good technology [equation (2)] embodies the well-known CES utility function of Dixit and Stiglitz (1977) thought of, as in Ethier (1982), as a composite intermediate input that increases with input variety. This specification has been used in well-known endogenous growth models with product diversification: Romer (1987, 1990), Rivera-Batiz and Romer (1991), Grossman and Helpman (1991), Aghion and Howitt (1992), among others. In these models, however, the technologies are assumed to be equal across intermediate-good sectors. This paper assumes, instead, a triangular structure of the input-output matrix. This feature is consistent with the hypothesis of input-output deepening. Returning to the model, it is assumed that capital in the period of analysis is given. In equilibrium, capital is allocated among the different sectors:

Each intermediate good is used in the production of those intermediate goods with higher technological integration. It is also used in the production of the final good. Thus:
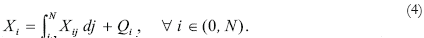
Firms in the j-th sector maximize profits which are given by the following expression
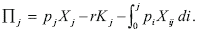
Competitive behaviour is assumed in all markets. Hence, given market prices, the demand for capital and intermediate goods satisfy the following first order conditions for profit maximization:

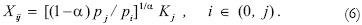
Appendix 2 shows the solution for the equilibrium price of the i-th good:
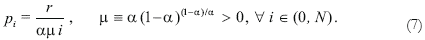
Notice that relative prices are fixed: pi/pj = j/i. Given the externalities from diversification, sectors with higher backward economic integration (higher i) enjoy higher productivity and thus produce cheaper goods. If the final good is taken as numeraire, pY = pN = 1, the factor price is determined as r = αμN, and the relative price structure is given by:
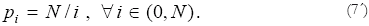
Combination of the price equations (7) and the first order conditions for maximization, equations (5) and (6), yields the optimal technical coefficients for capital and intermediate goods of the j-th sector:

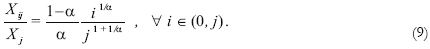
Note that technical coefficients in this economy are fixed. This characteristic is not due to the assumption of Leontief technologies (fixed technical coefficients); actually, intermediate goods are assumed to be good substitutes. The fixity of technical coefficients is due to the fixity of relative prices. And this feature, in turn, is due to the assumption of a fixed range of intermediate inputs for each sector.
Technical coefficients of the final good sector are deduced by symmetry:

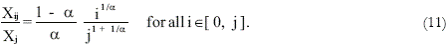
Given the price solutions and the technical coefficients, the gross demand of the i-th good is deduced (Appendix 3). The solution is the following:
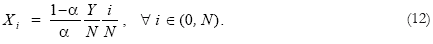
Finally, by substituting equations (8), (10) and (12) into equation (3), the capital market equilibrium, the economy's aggregate production function is deduced:
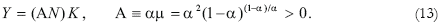
The aggregate production function of this economy exhibits constant returns to scale with respect to capital. To that extent, it gives a microeconomic foundation to the Rebelo's (1991) aggregate production function. Moreover, this production function embodies the Dixit-Stiglitz externalities from economic diversification: aggregate capital productivity, AN, increases linearly with input diversification, N . Hence, the more diversified is the economy, the more productive is the final goods production, and the higher is real income.
From the aggregate production function [equation (13)], and the technical coefficient of capital in the final goods sector [equation (10)], the capital allocation to the final good activity is deduced:

The remainder, (1–α)K, is evenly distributed among the intermediate-goods sectors. This result is obtained by substituting equations (12) and (13) into equation (8):

It is convenient to highlight the capital allocation among sectors. It will play an important role in the explanation of income gaps within an open economy context.
II. Open Economy
A. Assymetric Technological Structures
Two economic blocks, the South and the North, are initially in autarky and afterwards they are joined through international trade. Each block is made up of many small countries, so that good prices are competitively determined in the world markets. Some usual assumptions are made: transport costs for goods are assumed to be small (all goods are tradable), but international mobility of capital is forbidden. It is also assumed that the North has a more diversified economy; i.e. the North produces N* goods and the South produces N goods, such that N* > N > 0. The gap of technological diversification is measured by the ratio N*/N. From now on, all variables related to the North will be denoted with an asterisk.
Just before commercial integration, it must be the case that the South and the North exhibit compact input-output matrices: under autarky each country must produce all its inputs. As soon as trade is established, the South and the North are asymmetrically related. Whilst the North may be specialized in goods with higher backward integration (i ≥ N) it nevertheless could produce the goods with lower backward integration which the South produces. The South, however, cannot produce the highly backward-integrated goods because of its lack of structural diversification. Besides, even if transport costs are small, and the South imports the inputs it does not produce, the South could not produce cheaper the highly integrated goods. In addition, Southern economies as a whole give up producing the final good. The proof is straightforward if the factor price is equalized across countries. Since the maximum level of diversification is N*, and the final good is taken as numeraire, the relative price structure is given by pi = N*/i [see equation (7')]. By setting the Northern price of the final good to 1 (pY = pN* = 1), the South would be able to produce that good at the price N*/N > 1. Hence, the South is driven out of this market, Q.E.D. Equation (7) implies that capital remuneration in the world economy is equal to r = αμN*. If, on the other hand, factor price equalization does not hold, one should verify that the North should be able to drive the South out of the final good market. This condition is necessary for the North to be in command of the final good production.
Inherited structural assymetries leads the South, under an open economy regime, to specialize in intermediate goods up to the degree of technological integration given by the index N (once the South produces an intermediate good, there is no reason in this model to give up producing it). The North produces intermediate goods and the final good. Hence, the South supplies intermediate goods with low technological integration in exchange for the (highly integrated) final goods of the North. Since specialization is deepened under international trade, the compactness of the Southern input-output matrix is preserved.
In the context of an open economy with small transport costs, it might seem plausible that a country of low technological integration could produce a good of higher technological integration by importing those inputs the country does not produce. However, several reasons can be put forward for the compactness assumption of the Southern technologies as a whole.
First, the experience of economic development shows that underdeveloped countries follow quite diverse paths of development, but they are restricted to some patterns of structural change (Chenery et al., 1986). Typically, underdeveloped countries start their industrial take off by producing primary goods (Hirschman, 1958, 1986). Afterwards they diversify their economic structures by producing intermediate goods which are based mainly in agricultural goods and minerals. In the following stage they develop intermediate goods that use other industrial inputs. Finally, they produce capital goods and develop manufacturing goods based on scientific innovations. Hence, goods tend to be developed once their inputs are domestically produced. Otherwise, a temporary disequilibrium would induce the domestic supply of those inputs through import susbtitution; this is one of Hirchman's (1958) arguments of disequilibrium growth. In the long-run, thus, the compactness feature is restored.
Second, it is well known that technologically advanced productive activities require sophisticated skills. Using Leontief's simile, one can say that a longer list of available goods require "cooks" with a greater knowledge of "recipes" and "ingredients". Moreover, to master the advanced technologies one must go through the knowledge and practice of the less advanced ones –that is why models of economic catching-up through learning-by-doing and economic diversification are essential to understand the economic take-off of newly industrialized countries (Arrow, 1962; Lucas, 1988, 1993; Young, 1991; Matsuyama, 1992). Hence, it is sensible for developing economies to produce first those goods with a shallow use of intermediates, and advance, step by step, towards economic activities with a longer list of input requirements.
Third, it is well known that transport costs have historically played an important role in the process of industrialization through import substitution. Moreover, even if transport costs are negligible, a near input supplier may imply important strategic advantages for local producers in terms of availability, quickness of delivery and safety against shocks (wars, terms of trade fluctuations, and so on). The argument is advanced by Porter (1990). Hence, it is sensible as well to produce safely first those goods whose inputs are domestically supplied.
B. Factor Price Equalization Might Be Broken
Under conditions implying incomplete specialization, the competitive equilibrium of the world economy is analogous to the competitive solution of a closed economy. After all, the world economy is just a bigger closed economy. In this situation, the country blocks share some (Southern) economic activities and the factor price is equalized across countries.
The world capital is simply the sum of Southern and Northern capitals: K+K*. If the factor price equalization theorem holds, the allocation of the world capital follows the pattern determined by equations (14) and (15); i.e., the final good activity demands a fraction α of the world capital: KY = α (K+K*), and the remainder is evenly distributed among the intermediate-good sectors: Kj= (1– α) (K+K*)/N*, ∀j ∈ (0, N*).
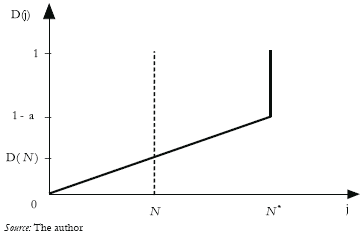
Figure 2 exhibits the cumulative world distribution of capital according to the index of technological integration, i. The fraction of capital demand for activities with backward technological integration from 0 to N is given by D(N) = NKj/(K+K*) = (1–α)N/N*. Hence, factor price equalization is sustained as long as the Southern fraction of the world capital, K /(K+K*), is lower than or equal to D(N), which implies N*/N ≥ (1–α)(1+K*/K). In this case the South and the North share the production of goods with technological integration lower than N; goods with higher technological integration, including the final good, are produced by the North.
Figure 2. Capital Distribution in the World Economy
Another situation arises if the Southern supply of capital is higher than D(N), which implies N*/N > (1–α)(1+K*/K). In this situation, some capital is redundant in the South: the Southern capital supply exceeds the demand for capital in the region. The South ends up completely specialized in those goods with backward technological integration from 0 to N; and the North is completely specialized in those goods with higher technological integration, including the final good. Redundant capital would flee to the North if it would be allowed, but it is not, by the assumption of strict international mobility barriers. In the short run some capital from the South may be unused, but in the long run prices tend to adjust, so that capital remuneration is set at a lower level in the South with respect to the Northern level. At this point an international factor remuneration gap emerges. Moreover, Southern prices are also downwardly adjusted because they are proportional to capital remuneration [see equation (7)]. Southern countries experience, therefore, a deterioration of their terms of trade.
It is important to determine whether this result is sustained if some factors are internationally mobile. In Appendix 4 the model is expanded, following Ortiz (1996), to consider two different types of capital. The expanded model reveals that, under the assumption of factor price equalization, both types of capital have a similar cumulative distribution to the allocation distribution of capital shown in figure 2. Hence, if one of these factors is immobile –let us say, human capital, and its relative supply in the South is higher than the required demand from activities with backward technological integration between 0 and N, the factor remuneration is lower in the South. Thus, the South experiences a deterioration of terms of trade, and an income gap appears between the North and the South. This result does not change if physical capital –the other form of capital– is perfectly mobile; in this case that mobility ensures the international equalization of physical capital remuneration, but human capital is underpaid in the South.
C. The Small Country Case with Factor Price Equalization
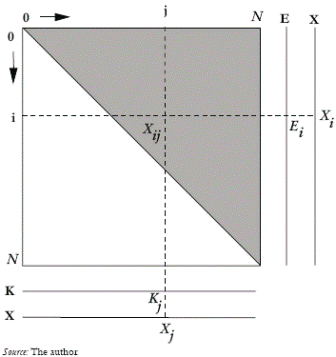
The case of a typical Southern country that opens its doors to the world markets when the diversification differential between the South and the North is not large, i.e. when factor price equalization holds, is analyzed in this section. Figure 3 depicts the situation of this country. It produces with a degree of economic diversification N. It does not produce the final good so that its whole productive capacity is used to produce intermediate goods within the range (0, N). The country produces its own intermediate inputs and the remainder is exported to the rest of the world in exchange for the final good. The export vector is denoted with the letter E.
Figure 3. Open Economy: The Small Country Case
Since the technology is analogous to the closed economy case, the country's capital is homogeneously distributed among the N sectors of activity: Kj = K/N. It is also easily deduced that factor and input coefficients are fixed. Hence, the gross output of good j is deduced by using the equivalent equation (8):

From the equivalent equation (9) the intermediate use of the i-th good in the j-th sector is deduced:
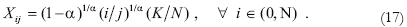
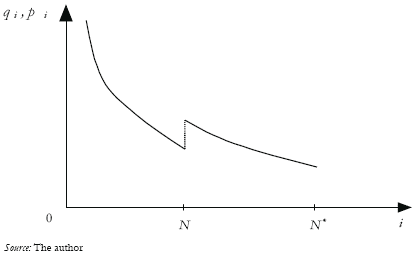
As figure 3 shows, the exports of the i-th good are defined as the difference between production and intermediate use:
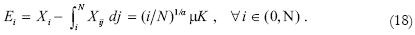
As shown above, in an integrated world market and with factor price equalization, the relative price structure is given by pi = N*/i. Thus, the export value of the Southern country is given by:

In this situation, international trade is convenient for the Southern country. Proof: under a closed economy regime, the production of the final good would be equal, as equation (13) shows, to (AN)K. Specialization in intermediate goods and assuming that factor price equalization holds internationally, delivers a welfare gain to the country which starts consuming (AN*)K units of the final good through imports. The welfare gain is proportional to the productivity gain of belonging to an international economic system characterized by higher economic diversification (N* > N). Q.E.D.
D. International Trade with Complete Specialization
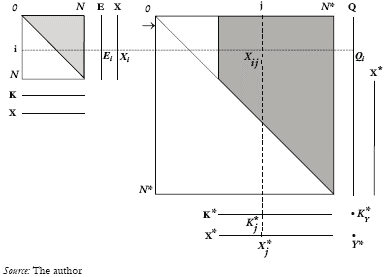
This situation is characterized by Figure 4. The South produces only intermediate goods with backward technological integration from 0 to N. The North produces those intermediate goods with backward technological integration above N; this region also produces the final good. Outputs from the North are denoted with asterisk.
Figure 4. World Economy: South and North Complete Specialization
The capital factor from the South is completely allocated to the production of intermediate goods indexed from 0 to N; and the capital from the North is completely allocated to the production of the activities of higher backward integration. Notice that goods with backward integration from 0 to N, which are used in the production activities of the North, are completely supplied by the South. The North exchanges the final good for the intermediate inputs of the South.
Let us examine now the technologies of the North. Equation (20) is the production function of the j-th good produced by the North (X* j), which uses as factors of production capital (K* j), the intermediate goods supplied by the South (those with backward technological integration from 0 to N), and the intermediate goods produced by the North itself (those with backward technological integration from N to j)
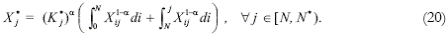
Equation (21) is the final good technology which is identical to the technology of the N*-th intermediate good
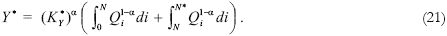
The equilibrium conditions of the goods markets are given by equations (22) and (23). Equation (22) is the equilibrium condition between the exports of the i-th good from the South and the imports of the same good from the North [i ∈ (0, N)]. These imports are divided between intermediate imports for production of intermediate goods, Xij, and imports for the final good activity, Qi,
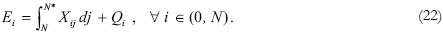
Equation (23) represents the equilibrium in the market of the i-th good produced in the North:
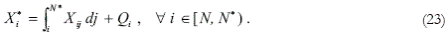
It means that supply of the i-th intermediate good is equated with the demand from the activity of production of intermediate goods and the demand from the final good activity.
The equilibrium condition of the capital market in the North is given by the following equation:

Capital is distributed among the production of N*-N intermediate goods, and the production of the final good.
The sector j maximizes profits which are given by:
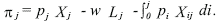
Note that the price of the i-th intermediate good from the South is denoted with qi for i ∈ (0, N); whilst the Northern prices are denoted with pi for i ∈ [N, N*).
Profit maximization determines that demand for capital, intermediate inputs of the South, and intermediate inputs of the North satisfy the following first order conditions:
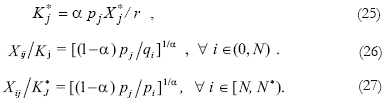
First order conditions for profit maximization in the final good activity are deduced by symmetry:
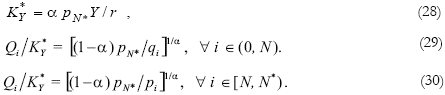
Southern prices are deduced as if the South were a closed economy. Hence, the relative prices of the South satisfy equation (7), with the difference that capital remuneration in the South is scaled down by the fraction θ with respect to capital remuneration in the North (r):
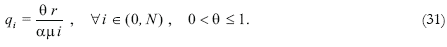
This fraction θ measures how much the Southern factor remuneration is reduced with respect to the Northern factor remuneration. It will be explicitly determined below.
The Northern prices are deduced in Appendix 5:
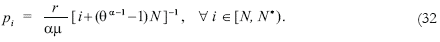
Note that price equations (31) and (32) collapse into equation (7) when the factor price, r, is equalized across countries, i.e. when θ = 1. It is convenient to define the expression between squared brackets in equation (32) as:
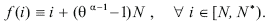
A comparison of the price equations (31) and (32) shows that the price structure is broken when the backward technological index is equal to N: qN= θ r/(αμN), pN = θ 1-α r/(αμN), and thus pN/qN = θ - α > 1. This feature is depicted in Figure 5. The smooth, continuous, price structure which is expressed by equation (7) when factor price equalization holds, is changed by a price structure where the whole set of Southern prices is lower due to a factor remuneration gap between the North and the South. The South experiences deterioration in terms of trade in order to equilibrate the goods markets and the factor markets. An "unequal exchange" takes place because the productive factor in the South is underpaid.
Figure 5. Price Structure under Complete Specialization
The next task is to determine the North output. The aggregate production function of the North is deduced in Appendix 6:
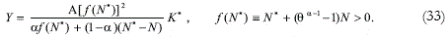
It is worth noting that specialization of the North increases its productivity and welfare. Proof: If the North had to produce all its required inputs, the aggregate production function would be Y = AN*K*. The above statement is true, then, if the following inequality holds:
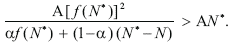
Using the definition of f(N*), the inequality is transformed as follows:
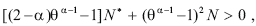
which is true because all the left-hand side terms are positive. Q.E.D.
The factor remuneration gap between the North and the South, θ, is found by explicitly considering the equilibrium of Southern exports with Northern imports. Appendix 7 yields the following expression:
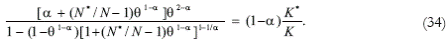
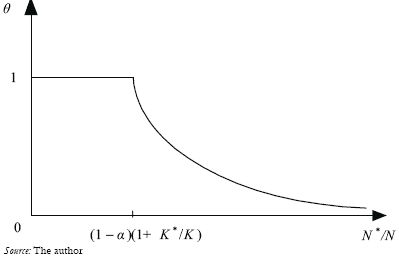
For the discount factor to be a positive fraction (0 < θ < 1), capital per (intermediate-good) sector in the South should be higher than the capital that an economically integrated world would assign to each intermediate-good sector: K/N > (1–α)(K+K*)/N* or N*/N > (1–α)(1+K*/K). This analysis is based on our knowledge of capital distribution across sectors in a closed economy [see equation (15)]. In other words, there should be an excess factor supply in the South relative to its own degree of industrialization for the existence of a remuneration gap. Equation (34) is consistent with this analysis because it delivers the limit condition for non-existence of excess supply in the South, i.e. N*/N = (1–α)(1+K*/K), when the discount factor, θ, is set equal to 1. Now, assuming that an excess factor supply does exist in the South, the discount factor diminishes with the industrialization ratio of the North, dθ /d(N*/N) < 0. Figure 6 depicts this behaviour: for an industrialization ratio of the North below or equal to the critical level, N*/N ≥ (1–α)(1+K*/K), the discount factor is 1 (the factor price equalization theorem holds); on the other hand, an industrialization ratio of the North above this critical level implies a gap in factor remuneration between the North and the South (the discount factor is lower than 1).
Figure 6. Factor Remuneration Gap between the North and the South
Given the determination of the factor remuneration gap, it is possible to determine the aggregate output of the South. By choosing the final good as numeraire,
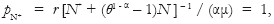
the Northern factor remuneration is determined as r = A[N* + (θ 1-α – 1) N], where A ≡ αμ. Hence, given the price structure of Southern goods [equation (31)], and the Southern exports function [equation (18)], it is possible to define the Southern purchasing power in terms of the final good:
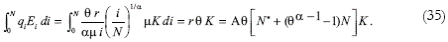
From this expression it is possible to conclude that trade also improves welfare in the South with respect to autarky. Proof: the aggregate production function of the South under a closed economy would be Y = ANK. Hence, the purchasing power in the South is higher under an open economy. For this statement to be true the following inequality should hold
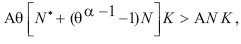
which implies N*/N > 1 + θ-1 (1 – θα). Is this inequality fulfilled under an open trade regime? The answer is positive. In order to completely control the final good production, the North should be able to produce the final good cheaper than the South: pN* < qN . Using the price equations (31) and (32), this price inequality also implies N*/N > 1 + θ-1 (1 – θα) > 1. Hence, it must hold. This feature implies a sufficiently large diversification gap between the North and the South.
Finally, the model shows that marginal productivity of capital measured in terms of the final good is higher in the North than in the South. Proof: from equations (33) and (35) one infers
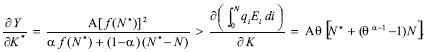
Using the definition of f(N*) the previous inequality becomes
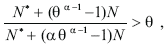
which is true as the left-hand side expression is higher than 1 (remind that α is a positive fraction), and θ is lower than 1, Q.E.D.
E. The Small Country Case with International Income Gaps
Consider the situation when the factor price equalization theorem does not hold and the world economy is characterized by an international gap in per capita real income. This is, of course, the most relevant case. The North is completely specialized in sectors with backward integration higher than N, and the South is completely specialized in sectors with backward integration from 0 up to N. In such a case the commercial openness of a small underdeveloped country generates two possibilities:
1. Low Industrialization
The country is characterized by a lower industrial diversification than the bulk of underdeveloped economies: No < N (< N*). From now on the small country is denoted with the superscript o. In this case, the commercial gains in productivity are at least diminished by the lower Southern prices. The factor remuneration is equalized with that of the Southern countries. Hence, it is not that evident that the small country benefits from a strategy of open markets. Moreover, as international prices are already given –a small country does not modify the given terms of trade, the country may suffer from a low demand for its domestic factor. This is the case when the relative factor endowment of this country is high even for Southern standards (Ko/No > K /N). This picture resembles the commercial experience of some Latin American countries.
2. High Industrialization.
The small country in this case is characterized by a higher industrial diversification than the remainder underdeveloped countries: N < No (< N*). This is what may be named the strategy of the "Asian Tigers": the small country opens its doors to the world market only when its own degree of economic diversification is higher than the Southern degree of diversification. Then, the small country produces some intermediate goods that the North produces, those with backward technological integration higher than N. This country is highly favoured by commercial openness: the country specializes in those goods with higher degree of technological integration, those with technological index between N and No. Therefore, its factor price is equalized with the Northern factor price. Moreover, the small country's profits become positive because it produces and exports at the high Northern prices, and buys intermediate goods from the South at low prices.
III. Some Empirical Support
A. A Small Panel Data
According to the analysis of structural change (Chenery et al., 1986), economic diversification is directly related to production "roundaboutness" or, in other words, interindustry dependence. In terms of the model, countries with more sectors characterized by larger sets of intermediate inputs are more technologically integrated. It is thus convenient to test the diversification effects on income using a measure of interindustry dependence as a proxy. In order to do that, a small panel data set containing such a measure is used.
Based on Kubo's work on cross-country comparisons of interindustry linkages (Kubo, 1985), Kubo, De Melo, Robinson and Syrquin (1986) calculated comparable indices of aggregate interindustry linkages using information from 30 input-output matrices of nine countries: Colombia, Mexico, Turkey, Yugoslavia, Japan, South Korea, Taiwan, Israel and Norway. Observations were taken for some years between 1950 and 1975. According to the authors, each country represented a different stage of structural change. To that extent, the sample may be thought of as representative of the experience of economic development.
The Statistical Appendix exhibits the data on the measures of interindustry linkages, overall linkages (OL) and domestic linkages (DL), for the panel of countries. The procedure to calculate the mentioned indices is indicated in Ortiz (1994). The Statistical Appendix also shows the corresponding data on real GDP per worker (YL), capital per worker (KL), the average schooling years in the total population over age 25 (EDU), and the ratio of imported intermediate inputs to real GDP (IMY).
B. Income Level Effects
As mentioned before, this paper contends that technological integration has income level effects. This hypothesis is tested using a small unbalanced panel (see the Statistical Appendix). The methodological approach consists in the assumption of an aggregate production function of a Cobb-Douglas type:
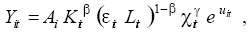
where Yit is output in the i-th country at time t, Ai is a fixed country effect, Kit is capital in the i-th country at time t, εitLit is the human capital level in the i-th country at time t (where ε is a measure of average schooling, and L is the labour force size), Χit is the degree of technological integration in the i-th country at time t, and exp(uit) is the error term. The coefficient β is assumed to be a constant positive fraction, and γ measures the output elasticity of technological integration on productivity.
In per worker terms and after taking logs, the above equation becomes:
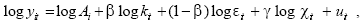
where yit ≡ Yit/Lit is output per worker, kit ≡ Kit /Lit is capital per worker, and uit, the error term, is assumed to be distributed with mean 0 and constant variance. Since this last condition is less likely to be satisfied in cross-country regressions, OLS estimates are corrected using White's consistent covariance matrix. The results are shown in table 1.
Table 1. Level Regressions from Panel Data (Sample=30, t-statistics in parentheses)
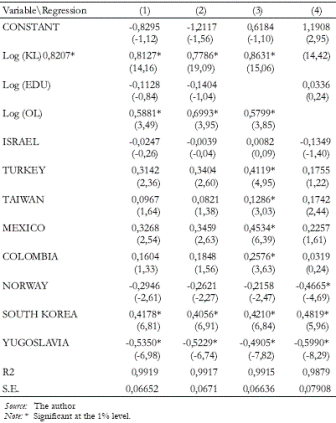
The dependent variable is the log of output per worker. Assuming the existente of contries's fixed effects on productivity, a set of country dummies are used in the regressions. An F-test yields that the whole set of country dummies is statistically significant at all levels; this result implies that local determinants of economic performance are still missing in the production function specification. Regression (1) yields that capital per worker (KL) and the measure of overall linkages (OL) are statistically significant variables. However, this regression does not address the likely problem of endogeneity between the measure of overall linkages and output per worker: the data set shows a clear time trend between per capita income level and structural change (as measured by the index of overall linkages, OL) at the country level. Regression (2) aims at correcting this problem by using two instrumental variables for the measure of overall linkages (OL): the domestic linkage measure (DL), and the ratio of imported intermediate inputs to real GDP (IMY). The first instrument captures the domestic component of interindustry linkages, and the second one captures the imported component. In Appendix 8 a regression is run in order to show that these variables are likely to be valid instruments. Thus, regression (2) confirms that capital per worker and overall linkages have positive and statistically significant effects on output per worker. It comes as no surprise that capital per worker is found to have an important and significant effect on real income level, but educational attainment is not significant either in regression (1) or regression (2). This last result is at odds with many production function estimations, where education plays an important role as human capital. Many reasons may explain this econometric result: function misspecification, smallness of the panel data, measurement error and collinearity. The latter is a likely possibility. In fact, the log of educational attainment [log(EDU)] is highly correlated with the log of overall linkages [log(OL)] and with the log of capital per worker (logKL): the respective correlation coefficients are 0.81 and 0.47. Measurement error may be another reason for the non significance of educational attainment: without ignoring the role of education, it seems that technological integration captures better the impact of education in output than the number of years of education itself. This apparent paradox may be explained if one considers that educational attainment (EDU) is a quantitative measure of education that completely neglects the impact of education quality on human capital. This argument is consistent with the viewpoint that economic development imposes some education requirements, and not the other way round. In fact, when the education measure is excluded from regression (2), as in regression (3), the coefficients associated to capital and technological integration experience a small negative bias, but the signs and the statistical significance of these variables are not affected. Finally, when the measure of overall linkages is excluded, as in regression (4), the coefficients associated to capital per worker and education attainment are upwardly biased. These results suggest that education is important as far as it goes together with industrialization, and that technological integration (and economic diversification) has important external effects on total factor productivity.
Concluding Comments
This paper aims at explaining the existence of factor remuneration gaps between developed countries and underdeveloped countries. In order to do that it is necessary to posit the existence of sufficiently high barriers to international mobility of the factor. The model is thus more appropriate when applied to factors such as labour and human capital, given that developed countries erect more barriers to immigration than they do to capital flows. In fact, whilst capital returns are quickly equalised through international capital markets, labour remunerations exhibit huge and persisting international disparities for similar jobs (Union Bank of Switzerland, yearly).
Nevertheless, barriers to migration are not a sufficient explanation for income inequalities because mobility of goods may act as a substitute for mobility of people –this is the factor price equalization theorem of the neoclassical theory of international trade. Hence, if international factor remuneration disparities are to be thought of as explanation of per capita real income gaps, one ought to build a model where the renowned theorem does not hold.
The paper thus builds a general equilibrium model for the world economy whose main features are the following: a stable input-output structure, a productivity externality due to input diversification with increasing technological integration and strong international restrictions to factor mobility. Under these conditions, and for sufficiently large differentials in economic diversification between the industrialized North and the underdeveloped South, the model delivers a factor price gap between North and South. The model construction was guided by Leontief's hypothesis that underdeveloped countries are poor because they are by far less economically diversified.
The factor price gap arises in the model if the South suffers from an excess of factor supply relative to its own degree of economic diversification. Given the South's low level of diversification, complete specialization occurs in a sub-set of goods characterized by a shallow use of intermediate goods. The limited international demand for Southern goods implies a limited demand for the Southern factor. In a competitive setting, general equilibrium is achieved with lower Southern prices and a lower remuneration for the Southern factor. Moreover, under these circumstances, the lower relative economic diversification of the South, the greater is the income gap between the North and the South, and the more deteriorated are the terms of trade for the South.
Under complete specialization, the Southern factor remuneration falls behind the Northern level, and thus the South endures a lower income. The model proves, however, that even under complete specialization, and with a factor remuneration gap in favour of the North, the gains of trade prevail for each block of countries, i.e. trade is preferred to autarky. Nevertheless, given the technological asymmetry between North and South, it is also proven that the Northern block of countries specializes completely in higher technologically integrated goods (including the final good activity), and has a larger productivity gain that Southern countries.
After solving the general equilibrium for a world economy, where the North enjoys a larger degree of economic diversification, the case of a small Southern country that takes the choice of opening to the world market is considered. The general conclusion from this analysis is that a less developed economy might be better off under a closed economy regime whilst it builds its economic structure –input diversification takes time, and then opens its doors to the world market and becomes an exporter of highly backward integrated goods. If this country opens its commercial doors before reaching a sufficiently high degree of economic diversification, its price factor converges to the lower Southern level. On the other hand, if the Southern country has reached a sufficiently high degree of diversification when it opens its doors to the world economy, the country specializes in the goods with a higher degree of technological integration. This specialization increases its national income since the factor remuneration converges to the Northern level. Besides, some profits are made because the country exports goods at the high Northern prices, and buys Southern intermediate goods at the low Southern prices. These possibilities help to understand both the failure of some Latin American trade strategies (early commercial openness), and the trade success of the newly industrialized countries (late commercial openness).
This paper shows theoretically that international asymmetries in the economic structure of nations are important and, to that extent, history matters: diversification gives productive advantages. Empirical analyses for a small but representative panel of countries show that aggregate technological integration, a variable closely related to input diversification, seems to be directly related to income level. A previous paper had proposed and tested the growth effects of technological integration (Ortiz, 1994). This variable seems to deliver both income level effects and growth effects. Therefore, to remain on the path of structural change does seem to be "the essence of the process of development".
References
1. Aghion, Philippe and Howitt, Peter (1992). "A Model of Growth through Creative Destruction", Econometrica, Vol. 60, No. 2 (March), pp. 323-351. [ Links ]
2. Amsden, Alice (1989). Asia's Next Giant, Oxford University Press. [ Links ]
3. Arrow, Keneth (1962). "The Economic Implications of Learning by Doing", Review of Economic Studies, Vol. 29, May, pp. 155-173. [ Links ]
4. Barro, Robert and Lee , Jong-Wha (1993). "International Comparisons of Educational Attainment", Journal of Monetary Economics, Vol. 32, No. 3 (December), pp. 363-394. [ Links ]
5. Chenery, Hollis B., Robinson, Sherman and Syrquin, Moshe (1986). Industrialization and Growth: A Comparative Study, Washington, World Bank. [ Links ]
6. Dixit, Avinash, and Stiglitz, Joseph E. (1977). "Monopolistic Competition and Optimum Product Diversity", American Economic Review, Vol. 67, pp. 297-308. [ Links ]
7. Ethier, Wilfred J. (1982). "National and International Returns To Scale In The Modern Theory of International Trade", American Economic Review, Vol. 72, pp. 389-405. [ Links ]
8. Grossman, Gene and Helpm an, Elhanan (1991). Innovation and Growth in the Global Economy, The MIT Press. [ Links ]
9. Heston, Alan; Summe rs, Robert and Bettina Aten (2002). Penn World Table Version 6.1, Center for International Comparisons at the University of Pennsylvania (CICUP), October. [ Links ]
10. Hirschman, Albert (1958). The Strategy of Economic Development, Yale University Press, Inc., New Haven. [ Links ]
11. Hirschman, Albert (1986). Rival Views of Market Society and Other Recent Essays, Elisabeth Sifton Books-Viking, New York. [ Links ]
12. Kubo, Yuji. (1985). "A Cross-Country Comparison of Interindustry Linkages and the Role of Imported Intermediate Inputs", World Development, Vol. 13, No. 12, pp. 1287-1298. [ Links ]
13. Kubo, Yuji; Robinson, Sherman and Syrquin, Moshe (1986). "Interdependence and Industrial Structure" in Chenery, H.B., S. Robinson and M. Syrquin (1986), Industrialization and Growth: A Comparative Study, Washington, World Bank.. [ Links ]
14. Landes, David (1998). The Wealth and Poverty of Nations, W.W. Norton and Company. [ Links ]
15. Leontief , Wassily (1963). "The Structure of Development", Chapter 8 in Leontief, Input-Output Economics, Second ed., Oxford University Press, 1986. [ Links ]
16. Lucas, Robert Jr. (1988). "On the Mechanics of Economic Development", Journal of Monetary Economics, Vol. 22, pp. 3-42. [ Links ]
17. Lucas, Robert Jr (1993). "Making a Miracle", Econometrica, Vol. 61, No. 2, pp. 251-272. [ Links ]
18. Matsuyama, Kiminori (1992). "Agricultural Productivity, Comparative Advantage and Economic Growth", Journal of Economic Theory, Vol. 58, pp. 317-334. [ Links ]
19. Marx, Karl (1867). The Capital, Vol. I, foreword to the first edition, London. [ Links ]
20. Ortiz, Carlos H. (1994). "Integración Tecnológica y Crecimiento Económico: Evidencia Empírica", Ensayos sobre Política Económica, No. 25, pp. 73-95, Banco de la República, Bogotá, Junio. [ Links ]
21. Ortiz, Carlos H. (1996). "Input-Output Deepening and Education in an Aggregative Model of Economic Growth", Revista de Análisis Económico, Vol. 11, No.1, pp. 23-41, Ilades/Georgetown University, Santiago, Chile. [ Links ]
22. Ortiz, Carlos H. (2001). "Estructura Económica, División Internacional del Trabajo y Brechas de Ingreso", Revista de Economía el Rosario, Vol. 4, No. 1, Junio, Universidad del rosario, Bogotá. [ Links ]
23. Ortiz, Carlos H. (2002). "Economic Structure, International Income Differentials and Long-Run Growth", Revista de Análisis Económico, Ilades/Georgetown University, Vol. 17, No. 1, pp. 45-70, Santiago de Chile, junio. [ Links ]
24. Porter, Michael (1990). The Competitive Advantage of Nations, The Free Press, New York. [ Links ]
25. Rebelo, Sergio (1991). "Long-Run Policy Analysis and Long-Run Growth", Journal of Political Economy, Vol. 99, No. 3, pp. 500-521. [ Links ]
26. Rivera-Batiz, Luis and Paul, Rome r (1991). "Economic Integration and Endogenous Growth", Quarterly Journal of Economics, Vol. 106, No. 2, pp. 56-72. [ Links ]
27. Romer, Paul (1987). "Growth Based on Increasing Returns Due to Specialization", American Economic Review, Papers and Proc. Vol. 77, No. 2, pp. 56-62. [ Links ]
28. Romer, Paul (1990). "Endogenous Technological Change", Journal of Political Economy, Vol. 98, S71-S102. [ Links ]
29. Sachs, Jeffrey, and Warner, Andrew (1995a). "Natural Resource Abundance and Economic Growth", NBER Working Paper, No. 5398. [ Links ]
30. Smith, Adam (1776). An Inquiry into the Nature and Causes of the Wealth of Nations, Oxford: Clarendon Press, 1976. [ Links ]
31. Summers, Robert and Heston, Alan (1991). "The Penn World Table (Mark 5): An Expanded Set of International Comparisons, 1950-1988", The Quarterly Journal of Economics, Vol. 106, May, pp. 327-368. [ Links ]
32. Union Bank Of Switzerland. Yearly. Prices and Earnings Around the Globe, Zurich. World Bank. Yearly. World Development Report, Oxford: Oxford University Press. [ Links ]
33. Young, Alwyn (1991). "Learning by Doing and the Dynamic Effects of International Trade", Quarterly Journal of Economics, Vol. 106 No. 2, pp. 369- 406. [ Links ]
Primera versión recibida en febrero de 2008; versión final aceptada en mayo de 2008