ARTÍCULOS

 

Efectos de las técnicas de filtrado en la evaluación de un modelo de ciclos económicos reales

 

Effects of Filter Techiniques on the Evaluation of a Model of Real Economic Cycles

 

Effets des techniques de filtration dans l'évaluation d'un modéle de cycles réels

 

 

Fredy Vásquez*; Sergio Restrepo**

* Fredy Vásquez Bedoya: profesor de la Facultad de Ciencias Económicas de la Universidad de Antioquia. Dirección electrónica: favasquez@economicas.udea.edu.co. Dirección postal: Universidad de Antioquia, Departamento de Matemáticas y Estadística, Oficina 13-110, Apartado1226, Medellín, Colombia.

** Sergio Restrepo Ochoa: Profesor de la Facultad de Ciencias Económicas de la Universidad de Antioquia. Dirección electrónica: siro@economicas.udea.edu.co. Dirección postal: Universidad de Antioquia, Departamento de Matemáticas y Estadística, Oficina 13-122, Apartado 1226, Medellín, Colombia. Este trabajo es resultado del proyecto: ''Estrategia para la sostenibilidad de grupos A y B 2007-2008'' realizado por el Grupo de Estudios Regionales y financiado por el Comité de apoyo a la investigación CODI de la Universidad de Antioquia.

 

–Introducción. –I. El modelo. –II. Comparaciones formales entre algunos momentos implicados por las técnicas de filtrado DT, HP y PB.–Conclusiones. –Bibliografía.

---

Resumen: Este trabajo emplea el filtro de Hodrick y Prescott (HP), el filtro Paso de Banda (PB) y una descomposición teórica (DT), para mostrar cómo las regularidades cíclicas caracterizadas por el modelo de crecimiento exógeno de King, Plosser y Rebelo (1988) dependen de la técnica de filtrado empleada. Este artículo exhibe diferencias estadísticamente significativas entre propiedades de los componentes cíclicos aislados con los filtros HP, PB y DT; en particular entre los filtros HP y PB, lo cual difiere de los resultados de Canova (1998). También se evidencia que el método de filtrado DT no es consistente con la definición del cíclico económico dada por la National Bureau of Economic Research (NBER).

Palabras Clave: Modelo de crecimiento neoclásico básico, técnicas de filtrado, contrastes estadísticos, análisis en el dominio de la frecuencia. Clasificación JEL: C14, C15, E32

---

Abstract: This work uses the Hodrick and Prescott filter (HP), the Band-Pass filter (BP), and a theoretical decomposition (TD), to show how the cyclical regularities characterized by the model of exogenous growth of King, Plosser and Rebelo (1988) depend on the filter technique used. This article exhibits statistically significant differences between properties of the cyclical components isolated with the HP, BP and TD filters; in particular between the HP and BP filters, which differs from the results of Canova (1998). It also shows that the TD filter technique is not consistent with the definition of economic cycle given by the National Bureau of Economic Research (NBER).

Key words: Basic Neoclassical Growth Model, Detrending Methods, Statistical Tests, Frequency- domain Analysis. JEL Classification: C14, C15, E32.

---

Résumé: Ce travail utilise le filtre Hodrick-Prescott (CV), le filtre passe bande (PB) et une décomposition théorique (DT) pour montrer comment les régularités cycliques du modèle de croissance exogène de King, Plosser et Rebelle (1988) dépendent de la technique de filtration employée. Cet article montre les différences statistiquement significatives existantes dans les propriétés de composantes cycliques isolées avec les filtres CV, PB et DT. Tout particulièrement nous soulignons les différences entre les filtres CV et PB, dont les résultats diffèrent de ceux présentés par Canova (1998). On démontre également que la méthode de filtration DT n'est pas consistante avec la définition de cyclique économique proposée par le National Bureau of Economic Research (NBER).

Mots Clé : Modèle néo-classique de croissance, techniques de filtration, contrastes statistiques, dominance de la fréquence. Classification JEL : C14, C15, E32

---

 

 

Introducción

''Las economías de mercado experimentan fluctuaciones en los ritmos de crecimiento de un conjunto amplio y diverso de series: producción, empleo, precios, consumo, inversión, etc.... Tales oscilaciones son recurrentes y sistemáticas aunque con patrones variables de amplitud y duración. Estos fenómenos se denominan ciclos económicos''.

National Bureau of Economic Research (NBER)

 

En muchos trabajos actuales de Ciclos Económicos Reales (CER), todavía se afronta el mismo problema básico al que se enfrentaron Burns y Mitchell (1950), a saber ¿cómo se debe aislar el componente cíclico de una serie de tiempo económica? En otras palabras ¿cuál es la técnica de filtrado más adecuada en el análisis de un modelo de crecimiento a la hora de estudiar el fenómeno del ciclo económico?

En el análisis de los modelos de CER se pueden distinguir, principalmente, dos formas alternativas de aislar el componente cíclico de las variables agregadas, tanto de las series temporales observadas como de las series temporales sintéticas.¹ Por un lado, Hodrick y Prescott (1980) sugirieron un filtro, en adelante filtro HP, de baja frecuencia capaz de aislar las fluctuaciones que persisten por periodos de tiempo entre ocho y 32 trimestres; esta caracterización del ciclo económico es consistente con la definición de ciclo de los negocios adoptada tradicionalmente por el National Bureau of Economic Research (NBER)

Por otro lado, King, Plosser y Rebelo (1988) consideran que la descomposición de las variables agregadas en ciclo y tendencia, debe tener en cuenta cómo el modelo caracteriza la tendencia para obtener una descomposición ciclo-tendencia que sea consistente con la teoría de crecimiento propuesta por el modelo analizado. Más concretamente, se define una descomposición ciclo-tendencia como (DT) cuando el componente cíclico obtenido mediante dicha descomposición preserva las propiedades de ortogonalidad impuestas por la hipótesis de expectativas racionales asumida por el modelo.

En este trabajo se analizan las consecuencias a la hora de evaluar las propiedades cíclicas del modelo, que tienen las dos formas de obtener los componentes cíclicos de las variables observadas y sintéticas. El análisis se realiza en el marco de un modelo de crecimiento estándar utilizado en la literatura de los CER, en particular se considera el modelo de crecimiento exógeno estudiado por King, Plosser y Rebelo (1988); se entiende que este tipo de análisis es importante ya que el uso de un filtro, como el filtro HP, puede distorsionar algunas de las propiedades cíclicas caracterizadas por el modelo; la causa de esta distorsión como demuestra Singleton (1988), radica en que la práctica habitual de filtrar los datos sintéticos implica, en general, la violación de las restricciones de expectativas racionales impuestas por el problema de optimización intertemporal de los agentes. Esta implicación resulta bastante preocupante porque los ciclos económicos reales se entienden como las respuestas óptimas de agentes racionales a perturbaciones aleatorias.

En palabras de Hansen ''(the real business cycle research program) has been devoted to modeling the business cycle as an equilibrium outcome of optimizing agents to random changes in technology'' ( Hansen, 1997, p. 1005). En consecuencia, si el componente cíclico extraído mediante un filtro no respeta las restricciones cruzadas de ortogonalidad impuestas por el supuesto de expectativas racionales, en las condiciones de primer orden que describe el comportamiento de los agentes, difícilmente se puede argumentar que las fluctuaciones agregadas son el resultado de las reacciones óptimas de los agentes ante cambios en la tecnología; más aún, estimar este tipo de modelos mediante el método generalizado de momentos, utilizando las series filtradas, no es apropiado debido a que las series previamente filtradas no van a satisfacer las restricciones de ortogonalidad impuestas por el modelo original y son precisamente estas restricciones las que se utilizan en el método generalizado de los momentos.

La literatura de los CER parece sugerir que el filtrado a través del filtro HP (en general, el filtrado de bajas frecuencias) no afecta sustancialmente las propiedades cíclicas que presentan los modelos económicos y que tampoco altera los resultados de la evaluación cuantitativa de los mismos. Sin embargo, los resultados obtenidos en este trabajo muestran la conclusión opuesta a algunos trabajos de la literatura de los CER y similar a la obtenida por King y Rebelo (1993), Park (1996) y Canova (1998): la práctica común del uso de filtros de bajas frecuencias tiene consecuencias, tanto sobre las propiedades cíclicas caracterizadas por el modelo, como sobre la evaluación cuantitativa del mismo, pero a diferencia de estos modelos, nuestro trabajo emplea contrastes estadísticos. Por otro lado, este trabajo muestra una conclusión opuesta a la de Canova (1998), al mostrar cómo las propiedades estadísticas del componente cíclico extraído con el filtro de Hodrick y Prescott y el filtro de Paso de Banda de Baxter y King (1999), presentan diferencias estadísticamente significativas.

En los trabajos de KPR y King y Rebelo (1993) se comparan los segundos momentos poblacionales de los componentes cíclicos de las series sintéticas de interés, con los momentos muestrales correspondientes del componente cíclico de las series observadas. En este trabajo se comparan momentos muestrales entre sí por dos razones: por un lado, la comparación entre momentos muestrales coincide con la práctica común seguida en la mayor parte de la literatura; por otro lado, como muestra Lucke (1996), cuando se trabaja con series temporales que incluyen pocas observaciones y si están próximas a tener una raíz unitaria,² los momentos muestrales pueden ser sustancialmente diferentes de los momentos poblacionales.³ Se incluye en el análisis, además del filtro HP, el filtro de Paso de Banda sugerido por Baxter y King (1999), denotado como el filtro PB, con el objeto de tener un mejor conocimiento acerca de la comparación del filtrado de bajas frecuencias con la descomposición ciclo-tendencia teórica al tratar de evaluar cuantitativamente el modelo.

En la primera sección de este trabajo se presenta el modelo de crecimiento exógeno de King, Plosser y Rebelo (1988) y el método de filtrado DT para aislar el componente cíclico, aplicando una descomposición teórica en ciclo-tendencia; ésta es consistente con la teoría de crecimiento determinista propuesta por el modelo de King, Plosser y Rebelo (1988). La descomposición DT deriva el componente cíclico al extraer de los datos la tendencia determinista propuesta por el modelo. En la segunda sección se emplean contrastes estadísticos que permiten comparar formalmente los métodos de filtrado DT, HP y PB; para ello se realiza un experimento de Monte Carlo que permite concluir, a un nivel de significancia que las técnicas de filtrado DT, HP y PB condicionan la evaluación cuantitativa del modelo; en esta sección también se calcula el periodograma del componente cíclico aislado con los filtros DT, HP y PB, con el fin de identificar la frecuencia de los componentes aislados en los datos a través de cada uno de los filtros, y así mostrar si generan o no ciclos con longitudes iguales.

 

I. El modelo

El modelo de crecimiento exógeno de King, Plosser y Rebelo (1988), es un modelo neoclásico unisectorial de acumulación de capital que frecuentemente ha sido empleado en el análisis de crecimiento económico. Este modelo a diferencia del modelo neoclásico simple, considera el trabajo como una variable de elección. Aquí se supone una economía conformada por un gran número de individuos idénticos que viven infinitamente y que derivan su utilidad del bien de consumo y del ocio. Las preferencias del agente representativo están descritas por la función (1).

 

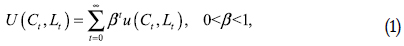
Donde C_t es el bien de consumo en el periodo t y L_t es el ocio en el mismo periodo. Se supone además que la utilidad es creciente en el bien de consumo y en el ocio. El parámetro β es la tasa subjetiva de descuento intertemporal.

El bien final de la economía se produce con una tecnología neoclásica de producción con rendimientos constantes a escala. En particular, se supone una tecnología descrita por una función de producción Cobb-Douglas, que expresada en términos per cápita se representa por la ecuación (2).

Y_t = Z_tK_t^α (X_tN_t)^{1 – α}, (2)

 

Donde K es el stock de capital predeterminado, N_t es el tiempo dedicado al trabajo en el período t, Z_t es una perturbación tecnológica que afecta a la productividad total de los factores. Por otro lado, las variaciones tecnológicas permanentes afectan sólo a la productividad marginal del trabajo vía X_t. La variable X_t está exógenamente determinada y evoluciona de acuerdo con el proceso X_t = θ X_t -1 , con θ > 1; y por tanto, la tendencia en el largo plazo es determinista. El parámetro θ coincide con la tasa de crecimiento bruta de la economía. Además, el término X_t N_t representa las unidades efectivas de trabajo.

En este modelo el bien final puede ser consumido o asignado a la inversión. La evolución del capital está descrita por la ecuación (3).

K_t+1 = (1 – δ)K_t + I_t,

 

Donde I_t es la inversión bruta y δ es la tasa (constante) de depreciación del capital.

En cada periodo un individuo afronta dos restricciones presupuestarias: primero, el tiempo total dedicado al trabajo y al ocio no debe exceder la dotación que se ha normalizado a la unidad, y segundo, el uso total del producto no debe exceder el producto total de la economía.

L_t + N_t ≤ 1, (4)

C_t + I_t ≤ Y_t. (5)

 

Naturalmente, también hay restricciones de no negatividad para algunas variables tales como L_t , N_t , C_t , K_t , Y_t , ≥ 0.

La función de utilidad considerada tiene la forma:

u(C_t, L_t) = log(C_t) + Alog(1 – N_t) (6)

 

Este tipo de función de utilidad garantiza la existencia de una sendade crecimiento equilibrada en la que las variables per cápita crecen a la misma tasa y en la que las fracciones de tiempo dedicadas a cada actividad permanecen constantes. Se supone que la perturbación tecnológica, Z_t evoluciona siguiendo el proceso expresado por la ecuación (7).

 

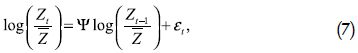
Donde ε es una variable aleatoria independiente e idénticamente distribuida con media 0 y varianza σ²_ε y donde Z es E (Z_t ).

Las condiciones que caracterizan el equilibrio competitivo se pueden obtener de las condiciones de primer orden que resuelve el planificador central:

 

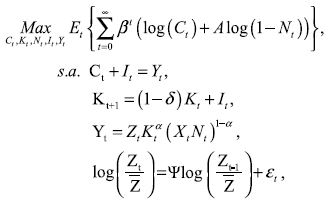
con K₀, Z₀ y X₀ dados y, como se indicó anteriormente, la X_t variable evoluciona de acuerdo al proceso X_t = θX_t-1

Sabemos que este modelo presenta crecimiento en el estado estacionario. Un método estándar para resolver esta clase de modelos consiste en transformarlo de tal forma que todas las nuevas variables sean estacionarias. En este caso, una posible transformación consiste en dividir todas las variables no estacionarias por el componente de crecimiento X_t Entonces, el modelo queda expresado en función de las variables y_t = Y_t / X_t , k_t = K_t / X _t , i_t = I_t / X _t y c_t = C_t / X _t que son estacionarias.

En función de las nuevas variables el problema de maximización que resuelve el planificador central está dado por:

 

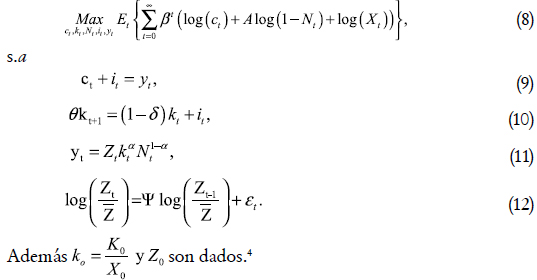
Las condiciones que caracterizan el equilibrio competitivo se pueden resumir en las ecuaciones derivadas de las condiciones de primer orden y las restricciones del problema de maximización, que en forma compacta estarían representadas por:

 

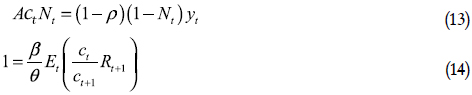
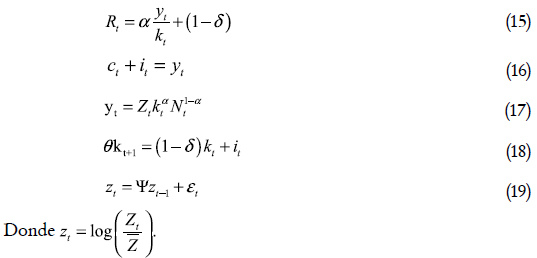
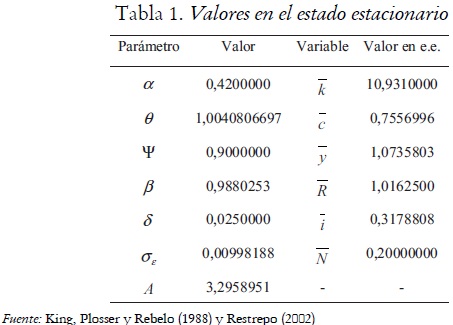
Restrepo (2002) utiliza el método de Uhlig (1999) para resolver y analizar modelos dinámicos y estocásticos no lineales. Este método le permite obtener las leyes de movimiento recursivas para las desviaciones logarítmicas de las variables de interés respecto al estado estacionario. La solución requiere un ejercicio de calibración, para lo cual se toman datos de la economía de Estados Unidos. Restrepo emplea la calibración realizada en el modelo King, Plosser y Rebelo (1988). Por tanto, a la participación del capital en la producción, se considera igual a 0,42. Suponiendo una tasa anual de crecimiento igual a 6,5%, se tiene una tasa de rendimiento trimestral 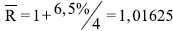. Se utiliza este valor porque la frecuencia de medición de los datos utilizados en la evaluación del modelo es trimestral. La tasa de depreciación del capital físico se fija en el 10% anual, lo que implica que δ = 0.025. El valor de la fracción de tiempo dedicado al trabajo N se fija igual a 0,2. El parámetro θ es igual a 1 más la tasa de crecimiento de la economía, que en este caso se fija igual a la tasa de crecimiento para la serie temporal del producto para los Estados Unidos durante el periodo 1955:3–1984:4, que es 0,0040806697, por tanto θ = 1, 0040806697. La tasa de crecimiento se obtiene al regresar la componente de crecimiento para la serie temporal del producto estadounidense obtenida con el filtro HP respecto a una constante y una tendencia determinista. Con respecto a los parámetros correspondientes a la perturbación tecnológica se selecciona ψ=0,9, y la varianza de la perturbación se escoge de tal forma que el modelo genere una volatilidad del producto similar a la observada en los datos estadounidenses; esta condición impone que σ_ε = 0,00998188. El valor de la constante A y el valor de las variables del modelo en el estado estacionario (y, k, c, i)se obtienen evaluando desde la ecuación (13) a la ecuación (18) en el estado estacionario (e.e.). Estos valores y los parámetros del modelo se presentan en la tabla 1.

 

Para este modelo el método de Uhlig proporciona las siguientes leyes de movimiento:

 

Además, se supone que la perturbación tecnológica sigue el proceso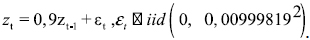

De las ecuaciones (20) usando un valor inicial para K_t y z_t se obtienen las series generadas por el modelo KPR, filtradas mediante la descomposición DT para las desviaciones logarítmicas del estado estacionario representadas por K_t , y_t , i_t y c_t. Teniendo presente que 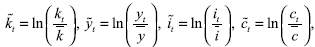se obtienen las series para los ratios 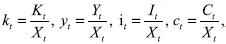y para los niveles N_t y R_t Además, dado que X_i = θX_t-1 basta tomar un valor inicial para X_t y recuperar las series en niveles para el capital, el producto, la inversión y el consumo (K_t , Y_t , I_t, C_t )⁵.

Para filtrar las series generadas por el modelo King, Plosser y Rebelo (1988) con los filtros HP y PB, y evaluar cuantitativamente el efecto de las técnicas de filtrado HP y PB, se emplean las series en niveles Y_t, C_t, I_t .

 

II. Comparaciones formales entre algunos momentos implica- dos por las técnicas de filtrado DT, HP y PB.

En los trabajos de Cogley y Nason (1995), Park (1996), Canova (1998), y Baxter y King (1999), se comparan las propiedades estadísticas del componente cíclico de una serie temporal, aislado con diferentes métodos de filtrado. Esta metodología permitió a los autores mostrar cómo varían las propiedades del componente cíclico de las series temporales dependiendo del filtro utilizado en la descomposición ciclo-tendencia. Desde un punto de vista riguroso se podría afirmar que, dicha metodología es más bien informal porque sólo contempla la comparación entre las magnitudes de estadísticos convencionales y no cuenta con un soporte estadístico que permita realizar inferencia estadística y así obtener conclusiones con un grado específico de confiabilidad. En este trabajo se realizan comparaciones más formales que permiten establecer diferencias significativas entre las propiedades del componte cíclico aislado con diferentes métodos de filtrado; en particular, se emplean contrastes para comparar la desviación estándar promedio del componente cíclico aislado con las técnicas de filtrado DT, HP y PB, y comparar su correlación contemporánea promedio con el producto.

Con el propósito de comparar formalmente los métodos de filtrado DT, HP⁶ y PB,⁷ bajo condiciones uniformes, se realiza un experimento de Monte Carlo. En cada réplica del experimento se generan 500 economías a través del modelo King, Plosser y Rebelo (1988) y de esta forma se obtienen 500 series de tamaño 115 para el producto, el consumo y la inversión. Al componente cíclico de cada variable simulada se le calcula la desviación estándar, y posteriormente se calcula la desviación estándar promedio correspondiente a las 500 realizaciones. El procedimiento se realiza para cada variable filtrada tanto con DT como con HP y PB. Este proceso se realiza 100 veces para crear vectores de tamaño 100 que contienen las desviaciones estándar promedio de las series filtradas generadas en la etapa anterior. De manera similar se construyen vectores de tamaño 100 para las correlaciones contemporáneas promedio del producto con el consumo y del producto con la inversión.

Con las comparaciones formales entre las distribuciones de desviaciones estándar promedio y las correlaciones contemporáneas con el producto el objetivo es establecer formalmente que los componentes cíclicos aislados con las técnicas de filtrado DT, HP y PB poseen propiedades estadísticas diferentes y que por tanto, las técnicas de filtrado condicionan la evaluación cuantitativa de un modelo económico al no tratar de igual forma las series temporales. Adicional a los contrastes formales se presenta un análisis basado en el dominio de la frecuencia, con el cual se muestra que los filtros mencionados aíslan componentes en los datos que se mueven con diferentes frecuencias.

A continuación se presenta un análisis descriptivo de las distribuciones de desviaciones estándar promedio y de las correlaciones contemporáneas promedio con el producto. Se realizan también contrastes de ajuste a una distribución teórica para verificar si las distribuciones estudiadas se ajustan a una distribución normal; de igual forma, se hacen contrastes de independencia.

 

A. Histogramas de frecuencia

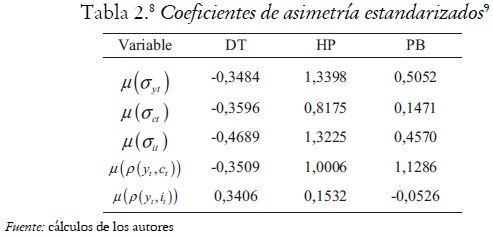
En esta sección se construyen los histogramas de frecuencia para los vectores de desviaciones estándar promedio de las series del producto, el consumo y la inversión filtradas con los tres filtros alternativos, al igual que los histogramas para las series de correlaciones contemporáneas promedio del producto con el consumo y del producto con la inversión. Estos muestran que las distribuciones de las desviaciones estándar promedio y de las correlaciones contemporáneas promedio con el producto son simétricas. Una prueba informal de ello son los coeficientes de asimetría estandarizados: si se encuentran dentro del intervalo se infiere que la distribución estudiada es simétrica (véase tabla 2).

 

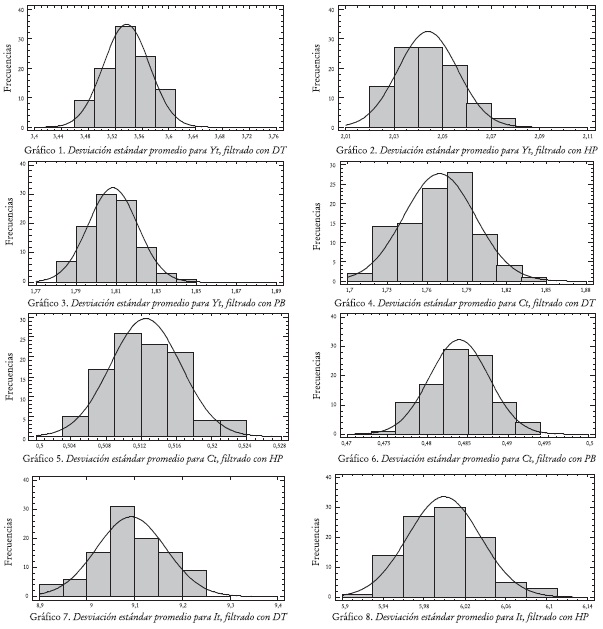
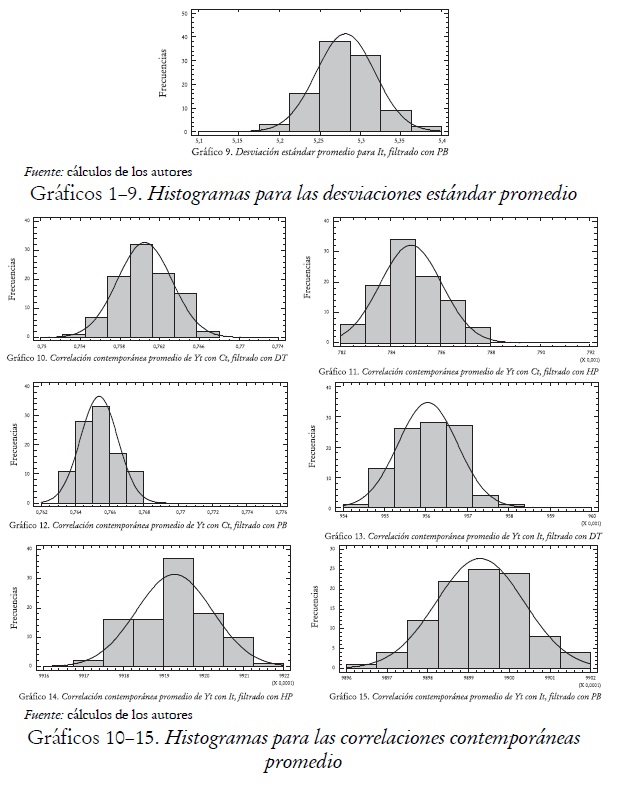
Los histogramas de frecuencias revelan que los filtros DT, HP y PB no generan las mismas distribuciones para las desviaciones estándar promedio de cada variable. Esta conclusión se extiende para las correlaciones contemporáneas del producto con el consumo y la inversión. Se observa que las distribuciones de desviaciones estándar promedio para las series del producto, el consumo y la inversión filtradas con DT, están a la derecha de las filtradas con HP y PB (véanse gráficos 1-9), esto nos indica que las series filtradas con DT son más volátiles que las filtradas con HP y PB. Las distribuciones de las correlaciones contemporáneas del producto con el consumo y la inversión filtradas con DT están a la izquierda de las filtradas con HP y PB; esto indica que el filtro DT reduce las correlaciones contemporáneas con el producto en relación con los filtros HP y PB (véanse gráficos 10-15). Los Histogramas sugieren que existen diferencias entre las propiedades del componente cíclico extraído con los filtros DT, HP y PB, por un lado entre volatilidades y por otro entre correlaciones contemporáneas con el producto, y que por tanto la evaluación de un modelo basado en estas propiedades estará condicionada por la técnica de filtrado empleada.

 

B. Contrastes de ajuste

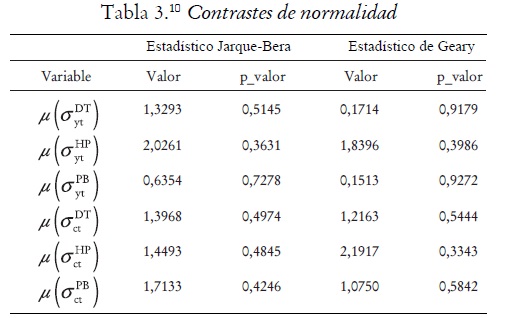
A continuación se emplea el contraste de normalidad Jarque-Bera (1987) y la prueba de normalidad de Geary (1947) para mostrar si las distribuciones de las desviaciones estándar promedio para las series del producto, el consumo, y la inversión se ajustan a una distribución normal. También se realizan estos contrastes para las distribuciones de las correlaciones contemporáneas del producto con el consumo y del producto con la inversión. La hipótesis contrastada tiene la forma:

H₀: La distribución es normal Vs. H₁: La distribución no es normal

Los contrastes de normalidad permiten concluir a los niveles de significancia estándar que, las distribuciones de las desviaciones estándar

promedio y las distribuciones de las correlaciones contemporáneas promedio con el producto que son implicadas por los filtros DT, HP y PB se ajustan a una distribución normal (véase tabla 3).

 

 

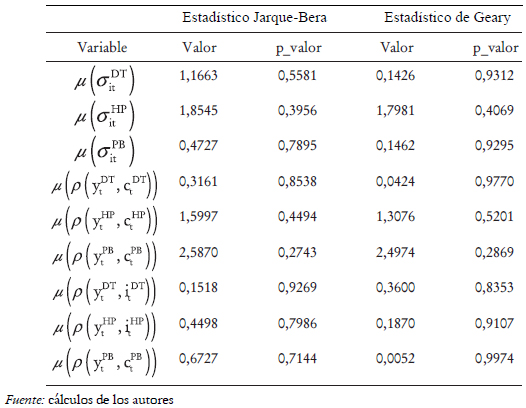
C. Contrastes de independencia

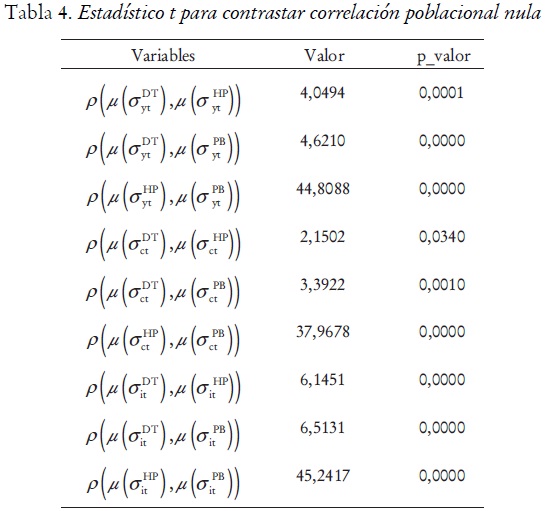
Ahora se exhibe el grado de asociación lineal entre las distribuciones de las desviaciones estándar promedio de cada una de las variables filtradas con los tres filtros alternativos, y entre las distribuciones de las correlaciones contemporáneas promedio de cada variable con el producto. Para ello se utiliza el contraste de correlación poblacional presentado en Newbold (1997). El contraste permite inferir cuán verosímil es encontrar correlaciones muestrales que difieran de cero en cierta magnitud, cuando realmente no existe ningún tipo de asociación lineal entre las variables aleatorias que se estudian. Dada la forma como se realizó el experimento, se presume que las distribuciones estudiadas son dependientes. La hipótesis contrastada tiene la forma: H₀: ρ = 0 Vs. H₁: ρ ≠ 0.

A los niveles de significancia estándar se rechazan las hipótesis de correlación población nula entre las desviaciones estándar promedio de las series del producto, filtradas con los filtros DT, HP y PB. La conclusión es la misma para las series del consumo y la inversión. También se rechaza la hipótesis de correlación poblacional nula entre las correlaciones contemporáneas promedio del producto con el consumo, al igual que del producto con la inversión, y de las series filtradas con los filtros alternativos HP y PB. A los niveles de significancia estándar, no es posible rechazar la hipótesis de correlación poblacional nula entre las correlaciones contemporáneas promedio del producto con el consumo, así como del producto con la inversión, implicadas por los filtros alternativos DT y HP, y DT y PB (véase tabla 4).

 

 

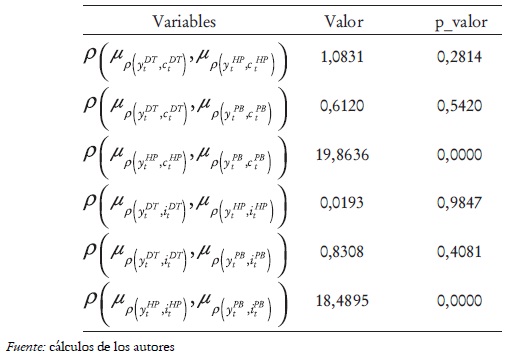
Los análisis realizados hasta el momento permiten concluir que las distribuciones de las desviaciones estándar promedio de las series del producto, el consumo y la inversión, filtradas con DT, HP y PB, al igual que las distribuciones de las correlaciones contemporáneas promedio del producto con el consumo y del producto con la inversión de las series filtradas con HP y PB, se ajustan a una distribución normal y son dependientes. También se concluye que las distribuciones de las correlaciones contemporáneas promedio del producto con el consumo y del producto con la inversión, provenientes de las series filtradas con los filtros DT y HP, y DT y PB, se ajustan a una distribución normal y son independientes.

 

D. Comparación entre las desviaciones estándar promedio

Con el fin de mostrar cómo las técnicas de filtrado condicionan las características cíclicas de las series temporales económicas, se han realizado investigaciones donde se comparan las propiedades estadísticas del componente cíclico, aislado con diferentes métodos de filtrado; estas comparaciones son de carácter informal, dado que no cuentan con un soporte estadístico riguroso. En este trabajo se emplean contrastes estadísticos para realizar comparaciones formales entre momentos relevantes de las series filtradas con los filtros alternativos; además se comparan las desviaciones estándar y las correlaciones contemporáneas con el producto; estos momentos miden respectivamente la volatilidad y los movimientos conjuntos con el producto para las series consideradas.

Se toma una réplica del experimento de Monte Carlo para comparar las desviaciones estándar de las variables filtradas y las correlaciones contemporáneas con el producto. Las quinientas series generadas por el modelo se filtran con DT, HP y PB, luego se les calcula la desviación estándar y por último se comparan entre sí las desviaciones estándar promedio. Esto es, se tienen tres vectores de tamaño 500 (X, Y, y Z) cuyas componentes son las desviaciones estándar de las series filtradas con DT, HP y PB respectivamente. Posteriormente, con base en X, Y, y Z que son las desviaciones estándar promedio, se comparan sus respectivas medias poblacionales μ_x, μ_y y μ_z . Un procedimiento similar se realiza para comparar las correlaciones contemporáneas del producto con el consumo y del producto con la inversión.

Dado que las distribuciones de las desviaciones estándar promedio siguen una distribución normal y son estadísticamente dependientes, se emplea un contraste estándar de comparación de medias para datos pareados. En los contrastes propuestos se comparan las desviaciones estándar promedio de una serie sometida a dos procesos alternativos de filtrado, lo que sugiere dependencia entre las observaciones, la cual es ratificada por los contrastes de independencia desarrollados previamente. La hipótesis nula para estos contrastes tiene la forma H₀: μ_D = μ_X - μ_y = 0, donde D es una variable aleatoria que representa la diferencia entre X e Y. No rechazar H0 permite concluir que la volatilidad de la serie implicada por los dos filtros es la misma; mientras que, al rechazar podemos concluir que la volatilidad implicada por los dos filtros es diferente, y así afirmar que los dos métodos de filtrado condicionan las propiedades estadísticas de una serie, en particular, su desviación estándar.

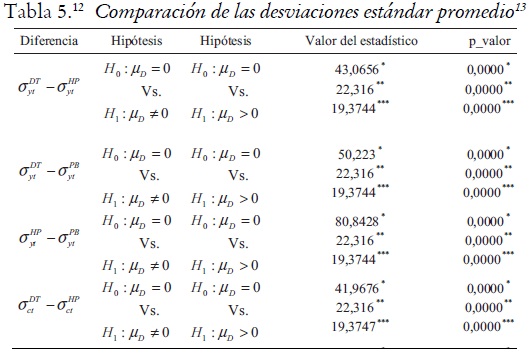
Para contrastar la hipótesis nula de que la diferencia de las medias poblacionales de las desviaciones estándar es cero, contra la alternativa de que es diferente de cero, se emplean contrastes paramétricos y no paramétricos tales como el contraste el contraste del signo y el contraste del rango con signo; estos permiten rechazar a los niveles de significancia estándar que la volatilidad promedio del producto, implicada por los filtros alternativos, es la misma. Una conclusión similar se obtiene en el caso del consumo y la inversión; además se infiere que los filtros HP y PB respecto al filtro DT, reducen significativamente la volatilidad promedio para cada serie, siendo mayor la reducción con el filtro PB que con el filtro HP (véase tabla 5).

 

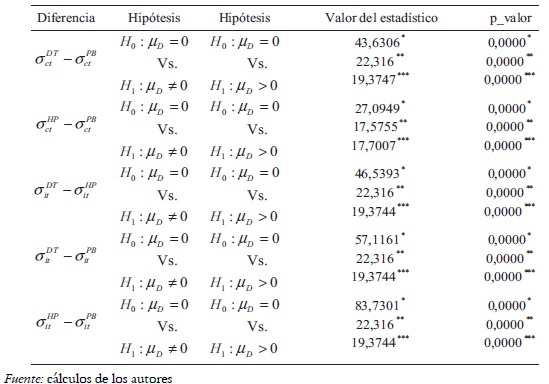
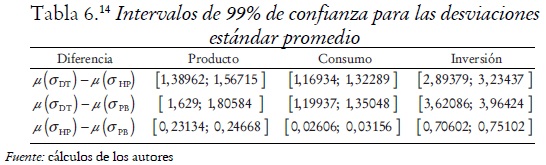
Para complementar el análisis anterior se construyen los intervalos de confianza para la diferencia entre las medias poblacionales; dado que los intervalos de confianza no incluyen el cero se infiere que la diferencia de las desviaciones estándar promedio para las series del producto implicadas por los filtros DT, HP y PB, es significativa a los niveles de confianza estándar; lo mismo se concluye para las desviaciones estándar promedio de las series del consumo y la inversión (véase tabla 6).

 

En resumen, a partir de los resultados anteriores se concluye que los filtros HP y PB reducen la volatilidad, en relación con la volatilidad obtenida mediante la descomposición DT para las series del producto, consumo e inversión. Además, la volatilidad que se obtiene para estas series cuando se filtra con HP es mayor que la volatilidad que se obtiene cuando se filtra con PB. Por lo tanto, se puede concluir que la evaluación de los modelos está condicionada en gran parte por la técnica de filtrado utilizada.

 

E. Comparación entre las correlaciones contemporáneas con el producto

Para comparar las correlaciones contemporáneas promedio del producto con el consumo, al igual que las del producto con la inversión, obtenidas al aplicar técnicas de filtrado alternativas, se deben tener en cuenta los resultados de independencia y normalidad desarrollados previamente. Dadas las características del problema, si las correlaciones contemporáneas con el producto son dependientes, el problema consiste en la comparación de la media de dos poblaciones cuando las observaciones son dependientes y están por pares. En caso contrario, el problema consiste en la comparación de la media de dos poblaciones normales e independientes.

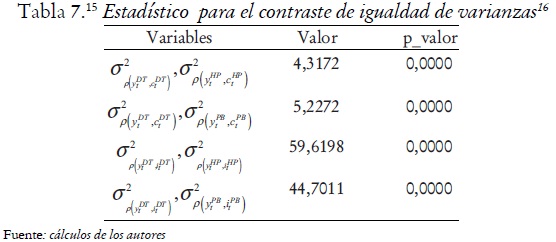
Para el caso de muestras independientes, antes de contrastar la igualdad de la media de las dos poblaciones se debe contrastar la igualdad de sus varianzas, para lo cual se emplea un contraste estándar de comparación de varianzas. Este contraste se debe hacer para las distribuciones de las correlaciones contemporáneas del producto con el consumo correspondiente y a las series filtradas con DT y HP y con DT y PB. Idénticamente para las distribuciones de las correlaciones contemporáneas del producto con la inversión de las series filtradas con DT y HP, y con DT y PB. La hipótesis contrastada tiene la forma:

 

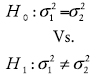
Al contrastar la hipótesis planteada, se rechaza a los niveles de significancia estándar que la varianza de las correlaciones contemporáneas del producto con el consumo procedentes de las series filtradas con DT y HP, al igual que con DT y PB, sean iguales. La misma conclusión se obtiene para correlaciones contemporáneas del producto con la inversión (véase tabla 7).

 

 

Por lo anterior, en las pruebas de hipótesis para comparar las correlaciones contemporáneas promedio con el producto, cuando las muestras son independientes, se asume que las varianzas poblacionales son desconocidas y diferentes. Estas pruebas se plantean de la siguiente forma:

 

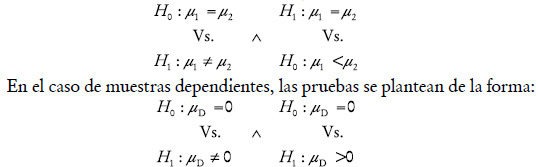
donde D es la variable aleatoria que representa la diferencia entre las correlaciones contemporáneas promedio del producto con el consumo o del producto con la inversión, filtradas con dos filtros alternativos, y μ_D representa la media poblacional de las diferencias.

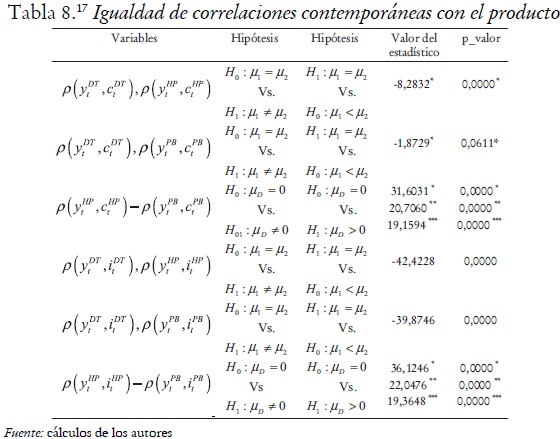
Al realizar las pruebas planteadas, empleando el contraste el contraste del signo y el contraste del rango con signo, se rechaza a los niveles de significancia estándar que las correlaciones contemporáneas promedio del producto con la inversión y de las series filtradas con HP y PB sean iguales. La misma conclusión se obtiene en el caso de las series filtradas con DT y HP y con DT y PB, pero empleando sólo el contraste. A partir del contraste no se rechaza al 5%, pero sí se rechaza al 10% de significancia la hipótesis nula de igualdad entre correlaciones contemporáneas promedio del producto con el consumo, proveniente de las series filtradas con DT y PB. El filtro DT con respecto a los filtros HP y PB reduce significativamente las correlaciones contemporáneas del producto con el consumo y del producto con la inversión. Además las correlaciones que se obtienen con el filtro HP son mayores a las que se obtienen con el filtro PB (véase tabla 8).

 

 

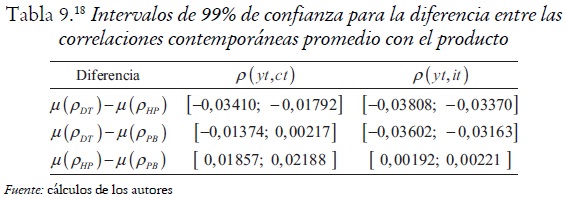
Finalmente, se construyen los intervalos de confianza del 99% para la diferencia entre las medias poblacionales de las correlaciones contemporáneas del producto con el consumo, al igual que para las diferencias del producto con la inversión; dado que estos intervalos no contienen al cero, se concluye que la diferencia entre las correlaciones contemporáneas promedio del producto con el consumo, lo mismo que las del producto con la inversión, es significativa, excepto en el caso de las correlaciones contemporáneas promedio del producto con el consumo de las series filtradas con DT y PB (véase tabla 9).

 

 

Los análisis realizados permiten concluir que las técnicas de filtrado DT, HP y PB condicionan las características cíclicas de las series filtradas. Los métodos de filtrado considerados no consideran de igual forma una serie de tiempo respecto a sus correlaciones contemporáneas con el producto. Por lo tanto, se puede concluir una vez más que la evaluación cuantitativa de los modelos de ciclos económicos reales está condicionada por la técnica de filtrado utilizada.

 

F. Análisis en el dominio de la frecuencia

El análisis espectral, herramienta básica para los análisis en el dominio de la frecuencia, permite descomponer la varianza de una variable en una gran cantidad de ciclos, y determinar la importancia relativa de cada uno de ellos. En el espectro y el periodograma, que es el resultado gráfico de este análisis, se determinan cuáles ciclos son cruciales para explicar la variable estudiada. Los ciclos importantes serán identificados por la altura del espectro y del periodograma en esa frecuencia, la cual representa la amplitud relativa del ciclo. Si el periodograma presenta un pico en una frecuencia, este pico indica que dicha frecuencia tiene mayor importancia en la serie que las otras frecuencias. La amplitud determina la importancia del ciclo.

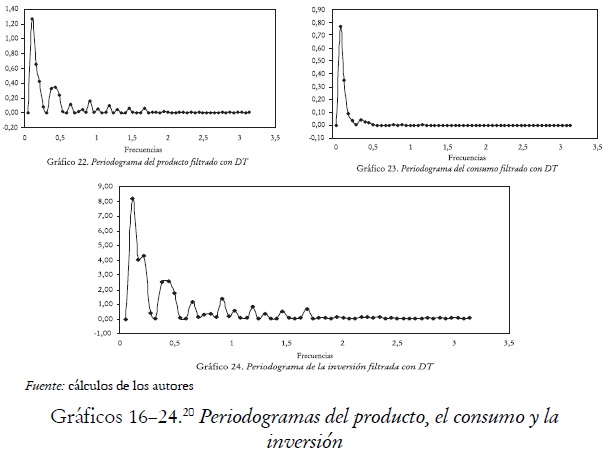
En economía el análisis espectral se usa principalmente para descomponer una serie de tiempo en sus componentes cíclicos. En este apartado se realiza un análisis en el dominio de la frecuencia con el fin de mostrar que una posible causa de las diferencias encontradas entre los filtros DT, HP y PB está relacionada con la frecuencia del tipo de componente que los filtros aíslan en los datos. Para ello se construyen los periodogramas del componente cíclico de las series del producto, el consumo y la inversión generadas por el modelo de crecimiento exógeno de King, Plosser y Rebelo (1988).

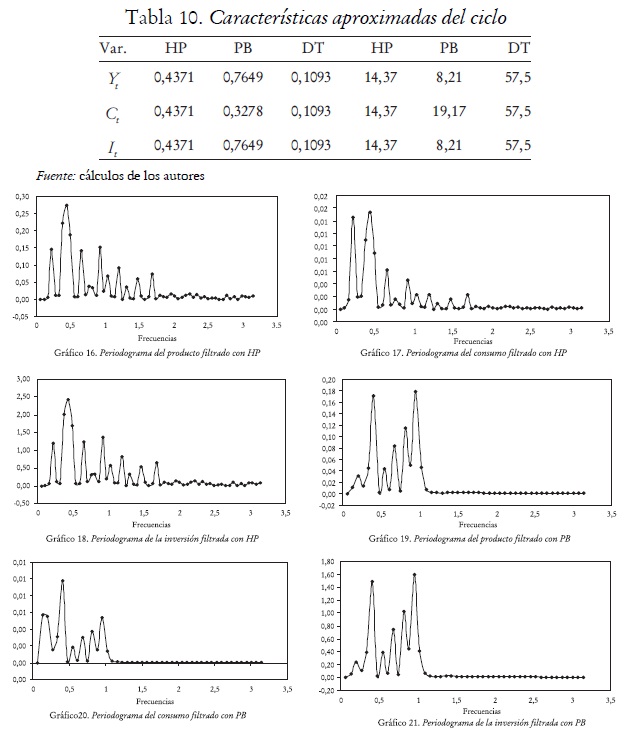
Los periodogramas estimados indican que los filtros HP, PB y DT retienen componentes en los datos que se mueven con diferentes frecuencias (véanse gráficos 16-24), generando ciclos de diferente longitud. Las componentes aisladas por el filtro PB, excepto en el caso del consumo, son más frecuentes que las aisladas con el filtro HP, por tanto la longitud o periodo del ciclo implicado por el filtro PB es de menor duración que el implicado por el filtro HP. Los periodogramas estimados para el componente cíclico aislado con el filtro DT, presentan su máximo pico en frecuencias cercanas a cero, lo cual indica que dicho filtro sólo retiene componentes que se mueven lento en los datos. Esto es, componentes que se producen con frecuencias relativamente bajas, eliminando, por lo tanto, componentes con frecuencias muy altas. Es de anotar que los filtros HP y PB aíslan fluctuaciones que persisten por periodos comprendidos entre ocho y 32 trimestres, que es la caracterización de ciclo económico consistente con la definición de ciclo de negocios adoptada tradicionalmente por la NBER, mientras que el filtro DT aísla fluctuaciones no consistentes con dicha definición (véase tabla 10).¹⁹ Las frecuencias y periodos se calculan empleando la metodología de Wei (1989).

 

 

Conclusiones

Algunos trabajos en la literatura de los CER han mostrado que la técnica de filtrado empleada para extraer el componente cíclico de las series de tiempo económicas es relevante en el momento de evaluar las características cíclicas de la serie. Una investigación representativa es la de Canova (1998), donde se utiliza un conjunto de técnicas de filtrado y se muestra cómo varían las propiedades cíclicas observadas en los datos, dependiendo del filtro utilizado en la descomposición ciclo-tendencia. En el trabajo realizado se reafirma dicha conclusión al mostrar que las propiedades del componente cíclico extraídas con los métodos de filtrado alternativos DT, HP y PB difieren significativamente, pero a diferencia de otros trabajos similares, éste lo hace empleando contrastes estadísticos.

Los contrastes realizados permiten concluir que los filtros HP y PB con respecto al filtro DT, reducen significativamente la volatilidad promedio para las series del producto, el consumo y la inversión. La volatilidad promedio obtenida con el filtro HP es mayor a la obtenida con el filtro PB. También se concluye que, con respecto a los filtros HP y PB, el filtro DT reduce la correlación contemporánea promedio del producto con el consumo y del producto con la inversión. La correlación contemporánea promedio con el producto, obtenida con el filtro HP, es mayor que la obtenida con el filtro PB. Las diferencias encontradas entre los filtros HP y PB con el filtro DT, puede darse porque la descomposición teórica preserva las propiedades de ortogonalidad impuestas por la hipótesis de expectativas racionales asumidas por el modelo de crecimiento exógeno de King, Plosser y Rebelo (1988), mientras que los filtros HP y PB no lo hacen. Por otro lado, a diferencia del trabajo de Canova (1998), los contrastes sugieren que existen diferencias estadísticamente significativas entre las propiedades del componente cíclico extraído con los filtros HP y PB, en particular entre las volatilidades implicadas por estos y las correlaciones contemporáneas con el producto.

Las afirmaciones previas permiten dilucidar que la evaluación del modelo de crecimiento exógeno de King, Plosser y Rebelo (1988) depende del método de filtrado empleado para extraer el componente cíclico de las series temporales. En otras palabras, los filtros DT, HP y PB condicionan la evaluación cuantitativa del modelo de King, Plosser y Rebelo (1988) cuando es comparado con las propiedades cíclicas de una economía observada. Dado que las características de un filtro aparecen reflejadas en el componente cíclico estimado de las series generadas por un modelo económico, o en el de las series observadas en una economía, se recomienda, en cualquier proceso que requiera de la utilización de técnicas de filtrado, especificar la técnica empleada con el fin de sopesar los resultados obtenidos.

Las comparaciones realizadas en el dominio de la frecuencia permiten concluir que los componentes cíclicos extraídos con los filtros DT, HP y PB, obedecen a diferentes rangos de frecuencia de los datos. Al analizar los periodogramas de los componentes aislados, se deduce que el filtro DT está asociado con componentes que se mueven lento en los datos (con frecuencia baja) o alternativamente de periodo alto. El filtro DT está asociado con la evolución en el largo plazo de la serie temporal.

A pesar de que la descomposición teórica es consistente con la teoría de crecimiento determinista propuesta por el modelo de crecimiento exógeno de King, Plosser y Rebelo (1988), que deriva el componente cíclico al extraer la tendencia determinista a los datos, este trabajo evidencia que el método de filtrado DT no es un método ideal para aislar el componente cíclico porque contradice la definición de ciclo económico dada por la NBER.

 

Bibliografía

1. BAXTER, Marianne y KING, Robert (1999). ''Measuring Business Cycles: Approximate ban-pass Filters for Economic Time Series'', The Review of Economics and Statatistics, Vol. 81, No. 4, pp. 575-593.        [ Links ]

2. BURNS, Arthur y MITCHELL, Wesley (1950). Measuring Business Cycles, National Bureau of Economic Research, Working Paper.        [ Links ]

3. CANOVA, Fabio (1998). ''Detrending and Business Cycles Facts'', Journal of Monetary Economics, Vol. 41, No. 3, pp. 475–512.        [ Links ]

4. COGLEY, Timothy y NASON, James (1995). ''Effects of Hodrick and Prescott Filter on Trend and Difference Stationary Time Series. Implication for Business Cycle Research'', Journal of Economic Dynamics and control, Vol. 19, No 1-2, pp. 253-278.        [ Links ]

5. GEARY, Roy Charles (1947). ''Testing for Normality'', Biometrika, Vol. 34, No. 3-4, pp. 209-242.        [ Links ]

6. HANSEN, Gary (1997). ''Technical progress and aggregate fluctuations'', Journal of Economic Dynamics and control, Vol. 21, No. 6, pp. 1005-1023.        [ Links ]

7. HODRICK, Robert y PRESCOTT, Edward (1980). ''Post-War U.S. Business Cycles: An Empirical Investigation'', working paper, Carnegie-Mellon University.        [ Links ]

8. HODRICK, Robert y PRESCOTT, Edward (1997). ''Business Cycles: Real Facts and a Monetary Myth'', Journal of Money, Credit and Banking, Vol. 29, No. 1, pp. 1-16.        [ Links ]

9. JARQUE, Carlos y BERA, Anil (1987). ''A Test for Normality of Observations and Regression Residuals'', International Statistical Review, Vol. 55, No. 2, pp. 163-172.        [ Links ]

10. KING, Robert; PLOSSER, Charles y REBELO, Sergio (1988). ''Production, Growth and Business Cycles: I and II'', Journal of Monetary Economics, Vol. 21, No 2-3, pp. 195-232 and 309-341.        [ Links ]

11. KING, Robert y REBELO, Sergio (1993). ''Low Frecuency Filtering and Real Business Cycles'', Journal of Economics Dynamics and Control, Vol. 17, No 1-2 207-231.        [ Links ]

12. LUCKE, Bernd (1996). ''Sampling Properties of Real Business Cycles Models'', Discussion Paper 3, Freie Universitat Berlin.        [ Links ]

13. NEWBOLD, Paul (1997). Estadística para los negocios y la economía, Madrid, Prentice Hall, 4ta edición.        [ Links ]

14. PARK, Gonyung (1996). ''The Role of Detrending Methods in a Model of Real Business Cycles'', Journal of Macroeconomics, Vol. 18, No. 3, pp. 479-501.        [ Links ]

15. RESTREPO OCHOA, Sergio Iván (2002). Análisis de las propiedades cíclicas y tendenciales en el marco de dos modelos estándar de crecimiento, Tesis doctoral, Universidad del País Vasco, pp. 15-80.        [ Links ]

16. SINGLETON, Kenneth (1988). ''Econometric Issues in the Analysis of Equilibrium Business Cycle Models'', Journal of Monetary Economics, Vol. 21, No. 2-3, pp. 361-386.        [ Links ]

17. UHLIG, Harald (1999). ''A Toolkit for Analyzing Nonlinear Dynamics Stochastic Models Easily'', Center for Economic Research University of Tilburg, and CEPR. Disponible en: http://www2.wiwi.hu-berlin.de/ wpol/html/toolkit/toolkit.pdf (1 de diciembre de 2009).        [ Links ]

18. WEI, William (1989). Time Series Analysis, Addison Wesley Publishing Company, INC.        [ Links ]

 

 

Primera versión recibida en octubre de 2009; versión final aceptada en diciembre de 2009

 

 

Notas

1. Las series temporales sintéticas son aquellas series generadas por un modelo económico.

2. Series con componentes cíclicas muy persistentes.

3. Se puede mostrar que las series que se generan en este modelo son bastante persistentes.

4. Para un análisis detallado de la solución del modelo véase Restrepo (2002).

5. Para una explicación más detallada ver Restrepo (2002).

6. Para el filtro HP, el parámetro de suavidad se seleccionó como se recomienda en la literatura para datos trimestrales, es decir, un valor

7. Para el filtro PB, el orden de la media móvil simétrica es el recomendado por Baxter y King (1999), es decir,

8. Los símbolosrepresentan las distribuciones de desviaciones estándar promedio del producto, el consumo, la inversión, las correlaciones contemporáneas promedio del producto con el consu- mo y del producto con la inversión, respectivamente

9. Todos los resultados de los apartados A-E se han obtenido usando el software Statgraphics bajo Windows, versión 5.1.

10. Los superíndices introducidos en la notación indican la técnica de filtrado empleada para extraer el componente cíclico: DT representa la descomposición teórica, HP el filtro de Hodrick y Prescott y PB el filtro Paso de Banda.

11. La expresión representa el coeficiente de correlación entre las distribuciones de desviaciones estándar promedio del producto filtrado con los filtros alternativos DT y HP. La expresión representa el coeficiente de correlación entre las distribuciones de las correlaciones contemporáneas promedio del producto con el consumo de series filtradas, por un lado con DT y por otro con HP; de manera similar para las otras expresiones.

12. Los símbolos representan respectivamente las distribuciones de desviaciones estándar del producto, el consumo y la inversión filtradas con DT. De manera análoga cuando los superíndices son HP y PB.

13. En las tablas 5 y 8 se emplea: * para el contraste t, ** para el contraste del signo y *** para el contraste del rango con signo.

14. Representa la media de las desviaciones estándar para las series de una variable filtrada con DT. De manera análoga cuando los subíndices son HP y PB.

15. Representa la varianza de la distribución de correlaciones contemporáneas del producto con el consumo, de series filtradas con DT. De manera similar si en lugar de DT es HP o PB.

16. El contraste se realiza con 499 grados de libertad en el numerador y en el denominador.

17. y representan respectivamente las distribuciones de las correlaciones contemporáneas del producto con el consumo, y del producto con la inversión de series filtradas con DT. De manera análoga si los superíndices son HP o PB.

18. representan la media de las distribuciones de correlaciones contemporáneas con el producto de series filtradas con DT. De manera análoga si los superíndices son HP o PB.

19. En la descomposición teórica correspondiente a los periodogramas analizados, se empleó la tasa de crecimiento del componente de tendencia del producto aislado con el filtro HP.

20. Todos los periodogramas se obtuvieron usando el software Stata/ Statistics/ Data Analysis, bajo Windows, versión 9.2.