Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Lecturas de Economía
Print version ISSN 0120-2596
Lect. Econ. no.73 Medellín July/Dec. 2010
ARTÍCULOS
Elementos para una teoría clásica de los precios de equilibrio y desequilibrio
Elements for a Classical Theory of Equilibrium and Disequilibrium Prices
Éléments pour une théorie classique des prix d'équilibre et de déséquilibre
Eduardo Bolaños*; Alexander Tobón**
* Profesor de la Universidad de Antioquia, miembro del Grupo de Macroeconomía Aplicada. Dirección electrónica: eabc@economicas.udea.edu.co. Dirección postal: Departamento de Economía, oficina 13-111, Universidad de Antioquia, calle 67 No. 53-108, Medellín 050010, Colombia.
** Profesor de la Universidad de Antioquia, miembro del Grupo de Macroeconomía Aplicada. Dirección electrónica: atobon@economicas.udea.edu.co. Dirección postal: Departamento de Economía, oficina 13-122, Universidad de Antioquia, calle 67 No. 53-108, Medellín 050010, Colombia.
Este artículo es un derivado de la investigación Un estudio sobre el capital en la teoría clásica de los precios de reproducción, la cual se encuentra inscrita en el sistema universitario de investigación de la Universidad de Antioquia, según el Acta CODI número 574 del 13 de abril de 2010.
–Introducción. I. El modelo clásico de Robert Torrens. –II. El modelo clásico de Benetti, Bidard y Klimovsky (modelo BBK). –III. La determinación de la tasa de beneficio en términos físicos. –IV. Algunos elementos de dinámica. –Conclusiones.–Anexos. –Bibliografía.
RESUMEN
El objetivo de este artículo es presentar una concepción no tradicional de la teoría clásica de los precios relativos a la luz de los desarrollos recientes y establecer el alcance de su contenido. Para llevar a cabo este objetivo se adopta como marco teórico de referencia la obra reciente de Carlo Benetti, Christian Bidard y Edith Klimovsky (Bidard y Klimovsky, 2006), cuyo propósito central es generalizar la teoría clásica de los precios de producción, de tal manera que la misma formulación dé cuenta de las situaciones de equilibrio y de desequilibrio. Se muestra así la ascendencia del nuevo modelo teórico, sus hipótesis de partida, su estructura, sus principales propiedades y su aptitud para explicar la dinámica económica.
Palabras clave: Precios relativos, beneficio, tasas de acumulación, reproducción del capital, desequilibrio clásico, equilibrio clásico.
Clasificación JEL: B24, B51, E11, E12.
ABSTRACT
This paper intends to present an unconventional approach to the classical theory of relative prices based on recent developments and current limitations. Using the work of Carlo Benetti, Christian Bidard y Edith Klimovsky (Bidard and Klimovsky, 2006) as a conceptual framework that generalizes the classical theory of production prices, this analysis provides explanations for both equilibrium and disequilibrium cases. Accordingly, this paper depicts the importance of this new theoretical model, its initial hypothesis, structure, main properties and proficiency for explaining economic dynamics.
Key words: Relative prices, benefit accrual rates, reproduction of capital, balance classic, classical balance.
JEL Classification: B24, B51, E11, E12.
RÉSUMÉ
L'objectif de cet article est de présenter une conception non traditionnelle de la théorie classique des prix relatifs à la lumière des développements récents et d'établir la portée de son contenu. Pour mener à bien cet objectif nous adoptons comme cadre théorique de référence l'ouvrage de Carlo Benetti, Christian Bidard et Edith Klimovsky (Bidard et Klimovsky, 2006), dont le but central est de généraliser la théorie classique des prix de production, de telle sorte que la même formulation puisse rende compte des situations d'équilibre et de déséquilibre. On montre ainsi la genèse du nouveau modèle théorique, ses hypothèses de départ, sa structure, ses principales propriétés et sa capacité pour expliquer la dynamique économique.
Mots clés : Prix relatifs, profit, taux d'accumulation, reproduction du capital, déséquilibre classique, équilibre classique.
Classification JEL : B24, B51, E11, E12.
Introducción
La obra Capital, salaire et crises (Bidard y Klimovsky, 2006) tiene que ver con los problemas de la reproducción del capital, de la distribución de los ingresos y del crecimiento económico de una economía no monetaria en el marco de la teoría económica clásica. Este libro constituye un gran esfuerzo en el progreso de esta teoría, pues, según Deleplace (2007), el texto representa una de las direcciones recientes de la heterodoxia neoricardiana, la cual ''busca reemplazar el método de Sraffa en la perspectiva de un desarrollo moderno de la teoría clásica antigua''. (Deleplace, 2007, p. 477). Mientras que Bellino (2008, p. 203) sostiene que ''The authors presents a framework [...] conceived as an alternative to the Ricardian approach and that can be applied to situations of equilibrium and disequilibrium''.
Los autores señalan claramente la novedad de su enfoque de la siguiente manera: ''Nuestro propósito está centrado en la presentación de una formulación común al desequilibrio y al equilibrio'' (Bidard y Klimovsky, 2006, 183). Su formulación apunta hacia una lógica diferente de aquella planteada por la teoría clásica antigua, en la cual la explicación de los precios naturales y de los precios de mercado está sustentada en dos modelos teóricos distintos: un modelo explica la determinación de los primeros; otro modelo, toma estos como referencia, sin explicarlos, para dar cuenta de la formación de los segundos y de su estabilidad.
La que consideramos gran contribución de Bidard y Klimovsky, plasmada en la última parte de su libro, y sobre la cual versará este escrito, consta de dos partes. En la primera, ellos proponen un modelo, perteneciente al enfoque clásico, que da cuenta tanto de las situaciones de equilibrio, como de las situaciones de desequilibrio del sistema económico (capítulo 11 de su libro). En la segunda, los autores utilizan el modelo anterior para iniciar un análisis dinámico del sistema, explorando las posibilidades de crisis e infiriendo trayectorias de las variables fundamentales, diferentes a aquellas de la tradición clásica antigua y moderna, que concibe la dinámica en términos de gravitación de los precios de mercado en torno a los precios naturales (capítulo 12 de su libro). La presentación de estas dos partes la hacen utilizando ejemplos numéricos bisectoriales, a partir de los cuales derivan densas argumentaciones teóricas, sin que resulte fácil captar su esencia. En Klimovsky (2006), aunque se centra la atención sólo en el análisis estático, se mejora la comprensión al poderse extender el análisis a una economía con n sectores productivos, representable simbólicamente.
En una primera aproximación, pueden considerarse los modelos de Sraffa y de Torrens como casos particulares extremos del modelo expuesto en Capital, salaire et crises, que en adelante denominaremos modelo BBK (modelo de Benetti, Bidard y Klimovsky). En efecto, en Sraffa se asume, implícitamente, que todo el excedente social o producto neto es consumido (Klimovsky, 2006), mientras que en Torrens todo el excedente es acumulado. En el modelo BBK se considera el caso general, según el cual una parte del producto neto es acumulada y la otra es consumida. La teoría de Torrens constituye el marco teórico de referencia de nuestros autores, pues, esta última pertenece al programa clásico de investigación que se interesa en la determinación de los precios y las tasas de beneficio, por medio de una formulación común al equilibrio y al desequilibrio.
Los objetivos que nos planteamos con este artículo son: proponer una generalización del modelo BBK formalizada matricialmente; mostrar el alcance y poder explicativo del modelo en la determinación de las configuraciones de equilibrio y desequilibrio; e indagar acerca de las condiciones bajo las cuales la dinámica del modelo BBK podría establecer una trayectoria que converja al equilibrio. Aunque se hace énfasis en la formalización del modelo, también recurriremos a algunos ejemplos numéricos que permitan captar mejor la operatividad de las relaciones esenciales.
El artículo está organizado como sigue: La primera sección presenta la teoría de Robert Torrens. La segunda, es consagrada a la exposición del modelo de estos autores según diferentes hipótesis sobre la acumulación y el consumo del excedente social. La tercera, se dedica a la explicación de una importante propiedad del modelo, tan preciada para clásicos antiguos y modernos: la determinación de la tasa de beneficio en términos físicos. En la cuarta sección, se hacen algunas apreciaciones sobre el problema de la dinámica económica, que se derivan cuando se considera el modelo en una perspectiva intertemporal. Finalmente, el lector encontrará las conclusiones de nuestro estudio y dos anexos.
I. El modelo clásico de Robert Torrens
A continuación presentamos una síntesis, formalizada matricialmente, de la interpretación que Benetti (1986), Bidard y Klimovsky (2006) hacen de la teoría de Robert Torrens (1821) sobre la reproducción de una economía capitalista. Se trata de un modelo de enfoque clásico que determina las tasas de acumulación, las tasas de beneficio y los precios relativos de los bienes de un sistema económico, en las situaciones de desequilibrio y equilibrio.
Sea un sistema económico en el cual los métodos de producción son invariables, los salarios reales hacen parte del capital físico, los bienes se utilizan como medios de producción estrictos o como bienes de subsistencia de los trabajadores, el capital es circulante y la producción de todos los bienes se efectúa en el mismo período. En este sistema, a partir de la matriz Y de consumos productivos se obtiene el vector y de productos totales1:

Donde ŷ es la matriz conformada por los productos en su diagonal principal y cuyas otras componentes son nulas. Además, se tiene que A = [aij] es la matriz de coeficientes técnicos tipo Leontief. Se supone que todo el excedente social es acumulado y totalmente invertido en el período siguiente (Ley de Say extrema en una economía no monetaria). En esta situación, las tasas de acumulación deben ser compatibles con las cantidades de bienes producidas, es decir, deben cumplir las siguientes condiciones de factibilidad, las cuales conforman un sistema de interdependencia general:

Donde g = [gi ] es el vector fila de tasas de acumulación posibles en la economía, con i = 1,2...n ; y u =[1 1 ... 1]. El lado derecho de este sistema representa las ''demandas efectivas'' de los diferentes bienes, dados los coeficientes técnicos y la estructura productiva; es decir, las demandas para la reposición del consumo productivo del período actual y las demandas para la ampliación de la escala de producción en el período siguiente. El vector g de tasas de acumulación, o de tasas de crecimiento del producto físico, está determinado endógenamente como solución de este sistema de ecuaciones.
Una vez conocido el vector g, los precios p estarán determinados por las siguientes ecuaciones de circulación o ecuaciones de gasto:

O, también, por las siguientes ecuaciones de producción:

Donde 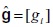 es la matriz conformada por las tasas de acumulación en la diagonal principal, siendo ceros los demás elementos, y
es la matriz conformada por las tasas de acumulación en la diagonal principal, siendo ceros los demás elementos, y 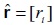 es la matriz constituida por las tasas de beneficio en la diagonal principal y ceros en las demás posiciones. Cualquiera de los dos sistemas anteriores determina el mismo vector p, puesto que al estar establecido que los beneficios de cada sector son totalmente invertidos, entonces,
es la matriz constituida por las tasas de beneficio en la diagonal principal y ceros en las demás posiciones. Cualquiera de los dos sistemas anteriores determina el mismo vector p, puesto que al estar establecido que los beneficios de cada sector son totalmente invertidos, entonces, 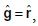 es decir, gi = ri , para todo i, aunque ocurra que
es decir, gi = ri , para todo i, aunque ocurra que 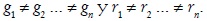
Las ecuaciones de circulación (2) expresan, para cada industria, la igualdad entre los ingresos que recibe y los gastos que hace en el mercado, para reponer las condiciones de producción del período actual y para ampliarlas en el período siguiente. Las condiciones de producción (3) representan las condiciones de rentabilidad, es decir, indican, para cada industria, la igualdad entre los ingresos y los costos de producción más las ganancias.
Los precios que satisfacen tanto las condiciones de circulación como las de producción son precios de reproducción, puesto que garantizan la reproducción con crecimiento del sistema productivo y, por consiguiente, la reproducción de los capitalistas como clase social con capacidad de conservar y ampliar su poder, es decir, de obtener ganancias positivas con posibilidad de aumentarlas en el futuro.
Los sistemas (1) y (2) sintetizan el modelo de Torrens para una economía que puede estar en situación de desequilibrio o de equilibrio. Si estos sistemas determinan tasas de acumulación diferentes 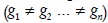 y tasas de beneficio diferentes
y tasas de beneficio diferentes 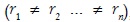 , entonces, están describiendo una situación de desequilibrio del sistema económico. Si los sistemas (1) y (2) determinan tasas de acumulación y de beneficio iguales
, entonces, están describiendo una situación de desequilibrio del sistema económico. Si los sistemas (1) y (2) determinan tasas de acumulación y de beneficio iguales 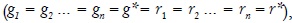 entonces, describen una situación de equilibrio del sistema económico.
entonces, describen una situación de equilibrio del sistema económico.
El equilibrio es una situación especial, denominada por Torrens ''posición natural'', que ocurre cuando los niveles de producción tienen unas ''buenas proporciones''. Se trata de un sistema de producción homotético cuya construcción y propiedades son similares a las del ''sistema patrón'' de Sraffa; pues, tanto en el sistema en ''buenas proporciones'' como en el ''sistema patrón'', las mercancías son producidas en las mismas proporciones en que ellas entran en el conjunto de los medios de producción de todo el sistema. La ''posición natural'' o situación de equilibrio del modelo de Torrens está descrita por los siguientes conjuntos de ecuaciones, que sintetizan las condiciones de reproducción del sistema económico:

Donde y* es el vector de producciones brutas en ''buenas proporciones'', las cuales pueden encontrarse; 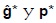 son, respectivamente, el vector de tasas de acumulación y de precios correspondientes a y*. Puesto que
son, respectivamente, el vector de tasas de acumulación y de precios correspondientes a y*. Puesto que 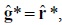 , las ecuaciones de circulación
, las ecuaciones de circulación 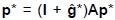 son equivalentes a las ecuaciones de producción
son equivalentes a las ecuaciones de producción 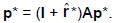
Según Torrens, en la ''posición natural'' se verifica que ''la demanda efectiva y la oferta están en relación de igualdad cuando los ingredientes del capital ofrecidos a cambio de las mercancías exceden en la tasa de beneficio normal a los ingredientes del capital gastados en su producción'' (Torrens, 1821, pp. 360, 361). Es decir, que en esta situación especial de equilibrio, la estructura de la producción permite obtener para cada uno de los bienes producidos, un excedente igual a la tasa de beneficio normal (r*) multiplicada por la cantidad empleada del bien como medio de producción y como subsistencia. Cuando esto ocurre, para cada bien, la oferta (cantidad producida en un período) es igual a la demanda (requerimientos del bien en todo el sistema para reponer el consumo productivo del período y para aumentarlo en el período siguiente). Esta situación de equilibrio es tal, que los valores que toman las variables económicas no cambian en los períodos sucesivos; la economía está en equilibrio dinámico, creciendo a la tasa g* y conservando la misma estructura productiva en todos los períodos sucesivos. En esta situación particular sería válida la Ley de Say e impensable una crisis de sobreproducción general.
Por el contrario, en una situación corriente en que el sistema no está en las ''buenas proporciones'', para cada uno de los bienes producidos el excedente no es igual a la tasa única de beneficio normal multiplicada por la cantidad empleada de cada bien. En estas condiciones, una vez determinadas las tasas de acumulación correspondientes a cada período, si estas se hacen efectivas en el período siguiente, el sistema crecerá desequilibradamente y no se corroborará la igualdad entre la oferta y la ''demanda efectiva''. Una situación como esta es de desequilibrio y se caracteriza porque los valores que toman las variables económicas en un período determinado son tales, que el mismo sistema genera fuerzas que los modifican; los sectores productivos crecen a diferentes tasas cambiantes en el tiempo y la economía crece, o decrece, sin conservar la misma estructura productiva en todos los períodos sucesivos.
Carlo Benetti ilustra con un ejemplo numérico (Benetti, 1986) la proposición de Torrens, según la cual en la situación de desequilibrio de su modelo el comportamiento dinámico de las variables es tal que al menos una mercancía resulta en estado de sobreproducción (oferta mayor que ''demanda efectiva''), ocasionando inevitablemente, en algún momento, la sobreproducción general. Esto puede entenderse de la siguiente manera: en algún período el vector g, determinado por el sistema (1), puede contener algún elemento gi = -1, digamos que esto ocurre en el período t, lo que implica que (1+gi) = 0 y, por el sistema (3), pi = 0. Esta última igualdad significa que no hay precio positivo al cual toda la producción de i pueda ser vendida, lo que implica que habrá un stock de i invendido o una sobreproducción del bien i. Que el factor de acumulación (1+gi) sea nulo significa que, en el período t+1, la producción de la mercancía i será nula, por lo cual la industria i no demandará el insumo j, ocasionando una sobreproducción del bien j. En el período t+2, la industria j disminuye la demanda del insumo m, dándose una sobreproducción del bien m. La continuación de este proceso llevará al sistema económico indefectiblemente a un estado de sobreproducción general. Luego, cuando el sistema de producción está en las proporciones corrientes (no es un sistema homotético) no se puede garantizar la Ley de Say y lo más probable (tesis de Malthus) es que en cualquier momento ocurra una crisis desencadenada por la sobreproducción de al menos un bien.
A partir de los sistemas (1) y (2) es posible iniciar el análisis del comportamiento dinámico de los tres conjuntos de variables; para lo cual habrá que empezar estableciendo un conjunto de relaciones que liguen las producciones de períodos consecutivos: de (1) se deduce: 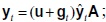 como
como 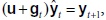 entonces
entonces
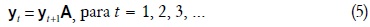
Este sistema de ecuaciones determina el vector yt + 1 de las cantidades de productos que se obtendrán en el período t +1 , dado el vector yt de los productos obtenidos por la economía en el período t, si estos son utilizados en el consumo productivo (y nada va al consumo final). La resolución repetitiva del sistema de ecuaciones (5) engendra una serie de vectores y1, y2... yt, yt + 1,..., cuyos componentes representan los diferentes niveles de productos y las diferentes proporciones entre ellos que se generan en el tiempo.
Así presentado, el modelo de Torrens constituye un aparato conceptual propicio para el objetivo de Bidard y Klimovsky, puesto que un mismo sistema de ecuaciones permite modelar tanto el equilibrio como el desequilibrio y determinar las variables fundamentales del sistema económico.
Ejemplo del modelo de Torrens
Sea un sistema concreto que produce los bienes trigo, identificado como el bien 1, y carbón, identificado como el bien 2:
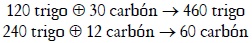
En este sistema la proporción entre los productos es y1/y2 = 7,66, el excedente social o producto neto es PN = [100 trigo 18 carbón] y las tasas de excedente de cada tipo de producto son: s1 = 0,277; s2 = 0,428 . La matriz de coeficientes técnicos es:
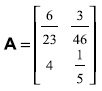
Con base en estos datos, la situación económica viene dada por los siguientes sistemas de ecuaciones:
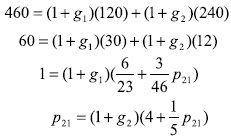
La solución de este conjunto de ecuaciones es secuencial: las dos primeras (ecuaciones de factibilidad) determinan los valores de las tasas de acumulación g1=54,16%, g2=14,58% y de las tasas de beneficio r1=54,16%, r2=14,58%; reemplazando estos valores en las dos siguientes (ecuaciones de circulación) se obtiene el precio relativo p21=5,946. Como puede observarse, el sistema concreto está en situación de desequilibrio dado que las tasas de acumulación son diferentes y también las tasas de beneficio, aunque para cada sector coincidan la tasa de acumulación y la de beneficio. En el siguiente período, si el sistema crece a las tasas de acumulación obtenidas, se tendrá un nuevo sistema de producción con unas proporciones diferentes a la proporción del período anterior. Este nuevo sistema determinará unos nuevos valores para todas las variables; así sucesivamente, en los períodos siguientes ocurrirá algo similar, trasladándose el sistema a través de una secuencia de situaciones de desequilibrio.
A partir del sistema concreto, puede obtenerse el sistema en equilibrio o en ''posición natural''. Primero, se calcula el valor propio dominante de la matriz A, el cual es α*=0,7421; luego, se calcula un vector propio a izquierda asociado al valor propio dominante, que para el caso es q =[1 0,1203]. Finalmente, se aplican los elementos de este vector a los datos iniciales del sistema concreto, obteniéndose el siguiente sistema homotético:
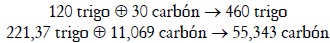
En este sistema, la proporción entre los productos es la ''buena proporción'': y*1/y*2 = 8,31; el producto neto es PN = [118,63 trigo 14,274 carbón] y las tasas de excedente de cada tipo de producto son: s1 = s2 = 0,347 . Con estos nuevos datos, ahora la situación de equilibrio viene dada por los siguientes sistemas de ecuaciones:
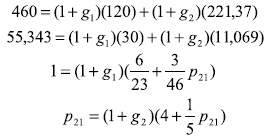
Al resolver secuencialmente este conjunto de ecuaciones, resulta la siguiente solución: g1 = r1 = 34,7%, g2 = r2 = 34,7%, p21 = 7,379. El sistema se encuentra en una situación de equilibrio, pues, en los siguientes períodos, si no hay un choque exógeno, los dos sectores pueden seguir creciendo indefinidamente a las mismas tasas y los productores seguir obteniendo indefinidamente las mismas tasas de ganancia. En estas condiciones, el sistema homotético inicial crece de tal manera que los sistemas de producción sucesivos seguirán siendo homotéticos, es decir, se conserva la misma proporción (y*1/y*2 = 8,31) entre los productos, y todas las variables endógenas correspondientes a esos sistemas seguirán teniendo los mismos valores.
II. El modelo clásico de Benetti, Bidard y Klimovsky (modelo BBK)
El modelo BBK se obtiene introduciendo en el modelo de Torrens la posibilidad de que una parte del producto neto no sea acumulada. Para ello es necesario que las tasas de acumulación, que se suponen positivas y viables, verifiquen las siguientes condiciones de factibilidad:

Ahora el vector g es exógeno, lo que significa que cada capitalista decide la tasa a la cual crecerá su producción para el siguiente período y, por tanto, la tasa a la cual deben crecer los componentes de su capital físico. Conocidos los elementos de g, se conocerán las cantidades de cada bien que los capitalistas acumularán e invertirán en el período siguiente, las cuales sólo serán viables si cumplen la condición (1a). Esta exogeneidad de las tasas de acumulación, concuerda con la característica del enfoque clásico de explicar las relaciones económicas a partir de las decisiones sobre la producción: el productor capitalista es el agente económico esencial, quien controla el proceso productivo y decide, entre otras cuestiones, el volumen de su producción.
Una de las hipótesis de los creadores del modelo consiste en asumir que la parte no acumulada de cada bien es consumida improductivamente por todos los capitalistas, de tal manera que estos resultan vendiendo toda su producción. Consecuentemente con esta hipótesis, el valor del consumo de los capitalistas de cada sector puede ser considerado de dos maneras: a) igual al valor de la parte no acumulada del excedente del bien producido por el sector, b) igual a una proporción uniforme de los beneficios de los capitalistas del sector. Cada modo de tratar el valor del consumo origina una variante de un único modelo:
A. El consumo del sector es igual al valor de la parte no acumulada del excedente del bien producido por el sector
Se parte de un sistema concreto de producción que verifica las mismas hipótesis del modelo de Torrens, excepto la correspondiente a la utilización de los bienes. En efecto, ahora se supone que los bienes pueden emplearse tanto productiva como improductivamente (consumo capitalista). Una vez fijado g, el vector F =[F1 F2 ... Fn ], de las cantidades de bienes disponibles para el consumo de los capitalistas, queda determinado por el siguiente sistema:

El i-ésimo elemento del vector F, Fi >0 , representa la parte del excedente de mercancía i destinada al consumo de los capitalistas. Sea el coeficiente de consumo fi = (Fi / yi), el cual expresa la parte de una unidad de mercancía i consumida por los capitalistas, y sea f = [f1 f2 ... fn ] el vector de todos los coeficientes de consumo. Ahora, las ecuaciones de circulación y las ecuaciones de producción se expresan, respectivamente, de la siguiente manera:

en donde 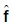 es la matriz conformada por los coeficientes de consumo en la diagonal principal, siendo ceros los otros elementos. En las ecuaciones de producción, los precios a los que se valora el consumo productivo no son los precios de compra o históricos, sino los precios de reposición, pues, es de las ganancias calculadas a los costos de reposición de las que dependen las decisiones de acumulación de los capitalistas. Con
es la matriz conformada por los coeficientes de consumo en la diagonal principal, siendo ceros los otros elementos. En las ecuaciones de producción, los precios a los que se valora el consumo productivo no son los precios de compra o históricos, sino los precios de reposición, pues, es de las ganancias calculadas a los costos de reposición de las que dependen las decisiones de acumulación de los capitalistas. Con 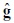 exógeno y
exógeno y 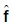 determinado por el sistema (1b), el sistema (2a) determina el vector p, el cual se reemplaza en el sistema (3) para obtener el vector
determinado por el sistema (1b), el sistema (2a) determina el vector p, el cual se reemplaza en el sistema (3) para obtener el vector 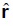 .
.
Los sistemas (2a) y (3) permiten describir una economía real, tanto en desequilibrio como en equilibrio. Sin embargo, hay una diferencia adicional respecto al modelo de Torrens: el desequilibrio y el equilibrio, ahora, son situaciones que se presentan tanto en el sistema de producción concreto como en el sistema de producción homotético. La razón de esta diferencia radica en que las tasas de acumulación son exógenas y la definición del desequilibrio y del equilibrio se establece respecto a ellas. Veamos en detalle.
Considerando, en primer lugar, el sistema concreto: si los capitalistas deciden tasas de acumulación diferentes, entonces los sistemas (2a) y (3) determinan tasas de beneficio diferentes, situación que se define como un desequilibrio. Por el contrario, si ellos deciden tasas de acumulación iguales, entonces los sistemas (2a) y (3) también determinan tasas de beneficio diferentes. Esta última situación es denominada, por los creadores del modelo BBK, ''equilibrio en la reproducción física'' o ''crecimiento regular''. Muestran igualmente, la existencia de otro equilibrio obtenido a partir del sistema concreto. Se trata del ''equilibrio en la rentabilidad'', el cual resulta cuando las tasas de beneficio son iguales, dadas unas proporciones particulares entre las tasas de acumulación exógenas2.
Razonando, en segundo lugar, a partir del sistema homotético o en ''buenas proporciones'': si los capitalistas deciden tasas de acumulación diferentes, entonces los sistemas, (2a) y (3) determinan tasas de beneficio diferentes, lo cual constituye un desequilibrio; es decir que, a diferencia del modelo de Torrens, cuando las tasas de acumulación no son endógenas, la existencia de un sistema de producción homotético no es condición suficiente para el equilibrio. Por el contrario, si ellos deciden tasas de acumulación iguales, entonces los sistemas (2a) y (3) determinan tasas de beneficio iguales, es decir, la condición g* = g1 = g2 = ... = gn garantiza el resultado r1 = r2 = ... = rn = r* , lo cual constituye, según nuestros autores, un ''equilibrio completo'', situación que, curiosamente, no es una situación de equilibrio en el modelo de Torrens.
El equilibrio completo está entonces descrito, a condición de que las tasas de acumulación sean iguales y verifiquen 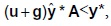 , por el siguiente sistema de ecuaciones:
, por el siguiente sistema de ecuaciones:

La diferencia más notoria respecto al equilibrio de Torrens es que las tasas de acumulación son exógenas o decididas por los capitalistas de acuerdo a su lógica de acumulación, sin embargo, esas tasas tienen que ser realizables o compatibles con la producción disponible.
A partir del sistema (1b) es posible iniciar una formulación dinámica para la reproducción física, similar a la descrita para el modelo de Torrens. El conjunto de relaciones que ligan las producciones de períodos consecutivos son del siguiente tipo:
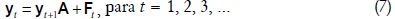
Dadas las producciones, yt, y los consumos improductivos, Ft, el sistema (7) determina las producciones del período t+1, yt+1; siempre y cuando las tasas de acumulación exógenas sean viables (que cumplan las condiciones (1a)).
La resolución repetitiva del sistema de ecuaciones (7) engendra una serie de vectores y1, y2...yt, yt+1,..., que representan los diferentes niveles de productos y las diferentes proporciones entre ellos que se generan en el tiempo.
Ejemplo para el primer modelo BBK
Consideremos el mismo sistema concreto del ejemplo de Torrens:
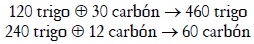
Supóngase que las tasas de acumulación decididas por los capitalistas son g1 = 25% y g2 = 6%, las cuales cumplen las condiciones de factibilidad (1a). Al reemplazarlas en el sistema (1b) quedan determinadas las cantidades no acumuladas del excedente:
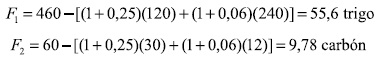
Una vez conocidas estas cantidades, destinadas al consumo improductivo, se pueden conocer los coeficientes de consumo por unidad de bien producida: f1 = 0,1208, f2 = 0,163.
La situación del sistema económico, de acuerdo con el primer modelo BBK, se representa por el siguiente sistema de ecuaciones de circulación y de producción:
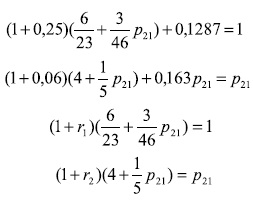
Las dos primeras ecuaciones de circulación determinan el precio relativo p21 = 6,784 . Luego, introduciendo este valor en las dos últimas ecuaciones de producción, quedan determinadas las tasas de beneficio r1 = 42,2%, r2 = 26,6%. Esta situación es de desequilibrio dado que a partir de tasas de acumulación exógenas diferentes se obtienen tasas de beneficio distintas. Sin embargo, el equilibrio de la reproducción física puede obtenerse si se consideran tasas de acumulación iguales. Por ejemplo, si g1 = g2 = 20%, se obtiene r1 = 27,7%, r2 = 42,8%.
A partir del sistema concreto, puede obtenerse un sistema homotético, el cual es el mismo encontrado en el ejemplo para el modelo de Torrens:
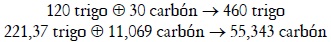
Si los capitalistas decidieran unas tasas de acumulación iguales, g1 = g2 = 20%, entonces, las partes del excedente social destinadas al consumo, serían:
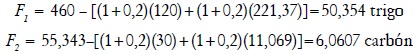
y los coeficientes de consumo serían los siguientes: f1 = f2 = 0,10949 . Con estos datos, el primer modelo BBK para el sistema en las ''buenas proporciones'', será el siguiente:
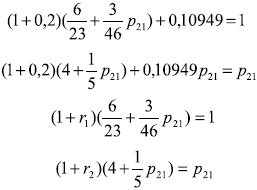
Este sistema homotético determina un equilibrio completo, pues al resolver las ecuaciones anteriores se tiene: p21 = 7,3788, r1 = r2 = 34,7%. Este mismo sistema homotético determinaría un desequilibrio si los capitalistas deciden tasas de acumulación diferentes; por ejemplo, si g1 = 25%, g2 = 6% se obtienen tasas de beneficio diferentes: r1 = 49,4%, r2 = 19,1% .
B. El consumo del sector es igual a una proporción uniforme de los beneficios
Se parte de un sistema concreto que verifica las mismas hipótesis del primer modelo BBK. Sin embargo, ahora se asume que los capitalistas consumen una proporción uniforme c de sus beneficios. Cuando g > 0 cumple la condición de factibilidad (1a), entonces F > 0 y 0 < c ≤1, pudiéndose escribir las ecuaciones de circulación y de producción, respectivamente, de la siguiente manera:

Estos dos sistemas conjuntamente determinan 2n variables endógenas: n-1 precios relativos (p), n tasas de beneficio ( ) y la proporción consumida del beneficio ( c ). Si de la i-ésima ecuación de (2b) y de la i-ésima ecuación de (3), se despeja la relación entre el valor del producto bruto y el valor del capital invertido y se igualan las expresiones obtenidas, para todo i =1, 2,... n, se obtiene el siguiente sistema de ecuaciones:
) y la proporción consumida del beneficio ( c ). Si de la i-ésima ecuación de (2b) y de la i-ésima ecuación de (3), se despeja la relación entre el valor del producto bruto y el valor del capital invertido y se igualan las expresiones obtenidas, para todo i =1, 2,... n, se obtiene el siguiente sistema de ecuaciones:

De este sistema se deduce la relación (gi / gj) = (ri / rj), para todo i, es decir, que las tasas de acumulación y las tasas de beneficio están en las mismas proporciones. Esta propiedad permite recurrir a otras maneras de resolver el sistema de ecuaciones del segundo modelo BBK: conocida la estructura de las tasas de ganancia ( gi / gj = ri / rj ), las ecuaciones (3) determinan los precios relativos y las tasas de beneficio, luego, una de las ecuaciones (1c) permite calcular la proporción consumida del beneficio. Otra manera de resolución, permitida por la lógica de deducción de (1c), consiste en agregar las ecuaciones (1c) a las ecuaciones (2b) y determinar simultáneamente todas las variables endógenas.
Las ecuaciones que constituyen el segundo modelo BBK permiten describir una economía real (no monetaria) tanto en desequilibrio como en equilibrio. Estos sistemas tienen las siguientes propiedades: a) debido al supuesto de rendimientos constantes de escala, un cambio en la estructura productiva no afecta los sistemas (2b) y (3) y, por lo tanto, a diferencia del primer modelo, una variación en los niveles de producción de las industrias no afecta ni a los precios ni a las tasas de beneficio; b) un aumento de las tasas de acumulación, que mantenga constante su estructura relativa, hace disminuir el consumo capitalista, pero no altera ni los precios ni las tasas de beneficio; c) un aumento de la tasa de acumulación relativa de un sector, tendrá como consecuencia el incremento de su precio relativo y de su tasa de beneficio.
El segundo modelo BBK describe una situación de desequilibrio cuando los capitalistas deciden tasas de acumulación distintas; en este caso, las tasas de ganancia también serán desiguales. A diferencia del primer modelo, en este el equilibrio de la reproducción física implica el equilibrio de la rentabilidad, puesto que, según (1c), la igualdad de las tasas de acumulación (no nulas) implica la igualdad de las tasas de beneficio. Este ''equilibrio completo'' es el mismo que se alcanzaría con el sistema homotético o en ''buenas proporciones'', pues, dada la constancia de los rendimientos, los sistemas (2b) y (3) son los mismos para el sistema concreto y para el sistema homotético.
La formalización dinámica de la reproducción física, según este segundo modelo, es igual a la descrita para el primer modelo BBK, a través del sistema (7).
Ejemplo para el segundo modelo BBK
Consideremos el mismo sistema concreto del ejemplo de Torrens:
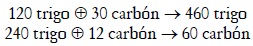
Si los capitalistas deciden las tasas, g1 = 25%, g2 = 6%, acordes con las condiciones de factibilidad (1a), al reemplazar estos datos en los sistemas (2b) y (3) se obtiene una situación de desequilibrio, representada por las siguientes ecuaciones:
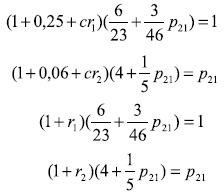
cuya solución es: p21 = 5,8611, r1 = 55,49%, r2 = 13,31%, c= 0,5495. Si los capitalistas deciden tasas de acumulación uniformes, se obtiene inmediatamente el ''equilibrio completo''; por ejemplo, cuando g1 = g2 = 20%, se obtiene p21 = 7,3788, r1 = r2 = 34,7%, c= 0,4245. La utilización del sistema homotético permite determinar estas mismas situaciones de equilibrio y de desequilibrio.
Una característica interesante de este segundo modelo tiene que ver con el equilibrio estacionario. En efecto, si suponemos tasas de acumulación nulas, el sistema de ecuaciones (1c) muestra que c = 1, lo que implica que los sistemas (2b) y (3) son idénticos. De esta manera, el sistema en su conjunto no puede resolverse por ninguno de los métodos propuestos arriba. Para sobrepasar esta dificultad, Klimovsky (2006) propone suponer conocidas (n – 1) tasas de beneficio o suponer conocida su estructura. Se obtiene un resultado interesante si se adopta un caso especial de la segunda posibilidad; así, si se supone que la estructura de las tasas de beneficio es igual a la unidad (tasas de beneficios uniformes), se obtiene la solución del modelo ricardiano. ''En definitiva, [la variante ricardiana d] el sistema de Sraffa es un caso particular del segundo modelo'' (Klimosvky, 2006, 54). En efecto, es el modelo ricardiano el que resulta ser un caso particular y no el modelo sraffiano puro (el cual considera la totalidad de los salarios pagados postfactum con una parte del excedente social).
Los autores del modelo BBK hacen una extensión interesante de su esquema teórico que permite considerar la tributación. En los dos modelos expuestos anteriormente, al introducir los impuestos pagados al Estado por parte de los capitalistas, respectivamente en términos físicos y en valor, pueden obtenerse dos nuevas versiones que conservan la mayor parte de las propiedades de los modelos básicos: en la primera, aparecen como variables adicionales las tasas de beneficio neto, y en la segunda, las tasas de beneficio neto y la tasa uniforme de impuestos sobre las ganancias (Bidard y Klimovsky, 2006).
III. La determinación de la tasa de beneficio en términos físicos
En Producción de mercancías por medio de mercancías (1960), se demuestra, utilizando el ''sistema patrón'', que la tasa de beneficio máximo del sistema concreto se puede determinar sin necesidad de conocer los precios, a partir de magnitudes físicas. Dado este resultado, Piero Sraffa sugiere que la tasa de beneficio del sistema ricardiano de los precios también es determinable en términos físicos. Esto puede demostrarse también para la tasa de beneficio, inferior a la máxima, del sistema sraffiano puro (Klimovsky, 2006); lo que autoriza establecer que, en general, en la teoría clásica hay una determinación física de la tasa de ganancia normal. Por consiguiente, en la teoría clásica del valor, a diferencia de la teoría neoclásica del equilibrio general, no necesariamente hay determinación simultánea de la tasa de ganancia natural y de los precios naturales (solución de un sistema de ecuaciones simultáneas), sino que la determinación de la primera es independiente de la determinación de los precios. En otras palabras, en la lógica clásica, las variables distributivas no obedecen a la misma ley que rige los valores de cambio de los bienes.
Un resultado relevante de los modelos BBK, es el demostrar que esta lógica es extensible a las tasas de beneficio correspondientes a las situaciones de desequilibrio descritas por esos modelos. Si en el sistema (3) puede demostrarse que  se obtiene sólo a partir de las magnitudes físicas de la producción de los bienes, entonces, ese solo sistema calcula el vector de precios relativos de los bienes en función de sus dificultades de producción físicas; la solución del primer modelo BBK deja de ser secuencial, puesto que el sistema (2a) ya no es necesario, y la solución simultánea del segundo pasa a ser secuencial: primero se resuelve el sistema (3) y luego el (2b). Lo interesante es que ahora, en los dos modelos, el vector
se obtiene sólo a partir de las magnitudes físicas de la producción de los bienes, entonces, ese solo sistema calcula el vector de precios relativos de los bienes en función de sus dificultades de producción físicas; la solución del primer modelo BBK deja de ser secuencial, puesto que el sistema (2a) ya no es necesario, y la solución simultánea del segundo pasa a ser secuencial: primero se resuelve el sistema (3) y luego el (2b). Lo interesante es que ahora, en los dos modelos, el vector 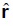 de tasas de ganancia de desequilibrio se puede conocer independientemente y antes que el vector p de precios de desequilibrio.
de tasas de ganancia de desequilibrio se puede conocer independientemente y antes que el vector p de precios de desequilibrio.
El procedimiento lógico para obtener tasas de beneficio físicas, en el marco del primer modelo BBK3, se presenta en el Anexo 2. Si rit es la tasa de beneficio de desequilibrio del sector i, en el período t, y si+ = si(t+1) es la tasa de excedente físico del bien i en el período t+1, este procedimiento permite demostrar que la tasa de beneficio se puede obtener a partir de la siguiente expresión del factor de excedente físico del bien i:
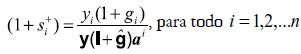
llegando al siguiente resultado:
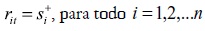
Esto puede comprobarse con el ejemplo que sirvió para ilustrar el primer modelo BBK, donde, al resolver los sistemas de (2a) y (3), se obtienen las tasas de beneficio r1t = 0,422 y r2t = 0,266 , las cuales dependen de los precios de desequilibrio. Sin embargo, es posible obtener estas mismas tasas independientemente de esos precios; para ello, se calculan las tasas de excedente si+ y se puede comprobar que son exactamente iguales a las tasas de beneficio calculadas con el sistema de precios:

La importancia de la determinación física de las tasas de beneficio está en que ellas, aunque son calculables a partir de relaciones entre valores, poseen un fundamento material en el sistema de producción. A su vez, los precios de desequilibrio, al depender de las tasas de ganancia físicas, pueden concebirse como la expresión de las dificultades de producción de las mercancías.
De esta manera puede concluirse que las propiedades de la teoría de David Ricardo (determinación física de la tasa de ganancia y principio de la dificultad de producción física), cuya generalidad pudo demostrarse con los aportes de Sraffa, se sostienen también para una teoría del desequilibrio de ascendencia ricardiana expresada por los modelos BBK4.
En la teoría sraffiana de los precios de producción también es válida la determinación de la tasa de beneficio en términos físicos, aunque no se cumple el principio de la dificultad de producción física5 , según el cual la tasa de beneficio y el precio dependen exclusivamente del costo de producción físico relativo. Bajo los supuestos de Sraffa sobre los salarios, puede demostrarse que la tasa de ganancia tiene una determinación física, pero dicha tasa no sólo depende del costo físico en que se incurrió para producir las mercancías sino también de un salario que, aunque puede expresarse en términos físicos, no hace parte del costo sino que es una fracción del excedente social. Como es bien sabido en la literatura sraffiana, esta fracción, variable y pagada post factum, depende de cómo se resuelva el conflicto de intereses socio-políticos entre capitalistas y trabajadores por la distribución del producto neto de la economía. Intuimos (pero habría que demostrarlo) que si en los modelos BBK se introdujeran las hipótesis de Sraffa sobre los salarios, podría concluirse también la independencia de la tasa de beneficio respecto a los precios, pero no el cumplimiento estricto del principio de la dificultad de producción física; lo cual no estaría acorde con el espíritu de la economía ricardiana.
IV. Algunos elementos de dinámica
Al observar la evolución de la reproducción física, se puede percibir que el estado actual del sistema económico está descrito por la producción actual, la cual depende de la producción y su utilización en los períodos pasados y esta, a su vez, depende de las tasas de acumulación pasadas (decididas por los productores de cada sector). Las producciones que surgirán en el futuro y sus correspondientes utilizaciones estarán subordinadas a la situación de la economía en el período presente y al comportamiento que adopten los capitalistas cuando deciden las tasas de acumulación que regirán en el próximo período.
La dinámica del modelo BBK da cuenta rigurosa de esta dependencia secuencial de los períodos productivos. Los estudios concernientes a este tema se encuentran condensados en el capítulo 12 de Capital, salaire et crises y en los artículos de Benetti et al. (2007 y 2007a). A partir de un estado de desequilibrio, como aquel descrito por los sistemas (2a) y (3), puede iniciarse un análisis de la dinámica del sistema económico, que permite seguir la evolución en el tiempo de las producciones (yt, yt+1 ,...) y de las variables económicas fundamentales, trazar sus posibles trayectorias y establecer algunas propiedades. Dentro de este contexto, nos hemos planteado la cuestión de la estabilidad del equilibrio en el modelo BBK (la posible solución del problema de Smith):
¿Partiendo de una situación cualquiera de desequilibrio, la economía converge hacia el equilibrio?
En la segunda sección del capítulo 12, que acabamos de mencionar, intitulada ''Reproduction physique et régionnement'', encontramos la herramienta teórica adecuada que nos ayuda a proponer una respuesta a esta pregunta. Desafortunadamente, la sección aludida es presentada en torno a una compleja gráfica difícil de entender, aunque no imposible. La complejidad del análisis gráfico no nos ha permitido expresar su contenido teórico en términos de la formalización matricial utilizada en las tres primeras partes de este artículo. Ante este impasse, hemos optado por aplicar la lógica del análisis gráfico al desarrollo de un ejercicio numérico que nos permita, en un primer intento, responder a la pregunta planteada.
Bidard y Klimovsky refieren su análisis a una economía bisectorial: a partir de los datos de un sistema productivo se puede generar un sistema de restricciones sobre las tasas de acumulación, el cual puede graficarse en el cuadrante positivo de un plano cartesiano, lográndose obtener una región en la cual las tasas de acumulación, decididas por los capitalistas, son realizables (positivas y menores o iguales a las tasas de acumulación máximas). En esta región distinguen tres subregiones (Bidard y Klimovsky, 2006), de las cuales dos son esenciales para el análisis; una de ellas, que denominan ''región A'', tiene esta particularidad: cuando las tasas de acumulación (exógenas) están en esta subregión, al hacerse efectivas, generan un nuevo sistema productivo en el cual la desviación, |S1(t) – S2(t)|, entre las dos tasas de excedente aumenta. Hay otra subregión, la ''región B'', en la cual sucede lo contrario que en la ''región A'' y, además, tiene una ''frontera especial'': cuando las tasas de acumulación están en ella, al hacerse efectivas, generan un nuevo sistema productivo cuya estructura garantiza el equilibrio completo del primer modelo BBK.
Nuestro ejercicio, referido al sistema concreto del ejemplo presentado en la sección II de este artículo, se sintetiza en la tabla 1, donde aparecen los valores secuenciales que van tomando los datos de la producción y las variables fundamentales, a medida que las tasas de acumulación se van haciendo variar de acuerdo con la lógica de las ''regiones'' de Bidard y Klymovsky.
La tabla 1 puede leerse de la siguiente manera:
Período 1 (desequilibrio): el sistema produce y1(1)= 460, y2(1) = 60 y está en situación de desequilibrio; los capitalistas deciden unas tasas de acumulación g1(1) = 0,25, g2(1) = 0,06, las cuales son realizables, menores a las tasas máximas6 y están en la ''región A''.
Período 2 (desequilibrio): al hacerse efectivas estas tasas y por pertenecer a la ''región A'', generan el sistema que produce y1(2) = 575, y2(2) = 63,6 y para el cual la desviación entre las dos tasas de excedente aumenta con respecto al período anterior; los productores fijan las tasas g1(2) = 0,16, g2(2)= 0,20, las cuales son realizables, menores a las máximas y están en la ''región B''. Por pertenecer a esta región, generarán, en el período 3, un sistema para el cual la desviación entre las tasas de excedente se reduce. Para los períodos siguientes, las tasas de acumulación serán mantenidas siempre en la ''región B'', con el fin de que la desviación entre las tasas de excedente tienda a cero (requisito para el equilibrio completo).
Período 3 (desequilibrio): al hacerse efectivas las tasas de acumulación decididas en el período 2, resulta el sistema que produce y1(3) = 667, y2(3) = 76,32; los capitalistas fijan la tasas g1(3)= 0,198, g2(3) = 0,26, que pertenecen a la ''frontera especial'' de la ''región B''.
Período 4 (equilibrio en rentabilidad): se hacen efectivas las tasas decididas en el período 3, y generan un sistema concreto que produce y1(4)* = 799,07, y2*(4) = 96,14. La proporción entre estos productos, y1*(4)/y2*(4) = 8,31, es la ''buena proporción'' del sistema homotético o en ''posición natural'' del modelo de Torrens. Como el sistema de producción del período 4 es homotético, las tasas de excedente son iguales: s1(4) = s2(4) = 0,347 y, también las tasas de beneficio, r*1(4) = r*2(4) = 0,347. En esta situación, suponemos que los capitalistas deciden tasas de acumulación iguales: g1(4) = g2(4) = 0,2.
Período 5 (equilibrio completo): al hacerse efectivas las tasas de acumulación iguales del período anterior, resulta un sistema que produce y*1(5) = 958,88, y*2(5)= 115,37, el cual es también homotético y tiene la misma proporción entre productos que el sistema del período anterior. En estas condiciones, el equilibrio, según el primer modelo BBK, es completo, pues, g1(4) = g2(4) = 0,2 y r*1(5) = r*2(5) = 0,347. Si en el período anterior los capitalistas hubieran decidido las tasas de acumulación máximas, entonces, en este período el equilibrio hubiera sido el ''equilibrio completo de Torrens'': g1(4) = g2(4) = r*1(5) = r*2(5) = 0,347. Si las tasas de acumulación decididas en el período t= 6 y posteriores, siguen siendo iguales y menores a las máximas, se seguirá repitiendo la ''situación de equilibrio completo de BBK'' con nuevos niveles de productos sectoriales, conservando la misma estructura productiva; la situación de crecimiento equilibrado se mantendrá indefinidamente.
Lo anterior nos muestra que la lógica del primer modelo BBK permite una trayectoria convergente hacia el equilibrio, si las tasas de acumulación exógenas están dentro de ciertos rangos de factibilidad (''región B''). Ahora bien, ¿se puede garantizar una secuencia de tasas de acumulación efectivas como la propuesta en este ejercicio? Parece que no, pues, para ello se requiere la adopción de hipótesis muy fuertes respecto a los comportamientos de los capitalistas y su armonización, las cuales son inconcebibles en una economía descentralizada. Tales hipótesis deberían ser: a) los capitalistas conocen la lógica que se deriva del modelo BBK (hipótesis de expectativas racionales) para poder adoptar unas tasas de acumulación coherentes y realizables; b) los capitalistas se ponen de acuerdo (¿decisiones centralizadas o estratégicas?) respecto al número de períodos en los cuales la convergencia se debe llevar a cabo7; c) quieren estar en situación de equilibrio (¿qué los motivaría a ello?, en la tabla 1 vemos que la tasa de beneficio del primer sector no aumenta progresivamente).
¿Y qué sucede por fuera de esta improbable trayectoria convergente? Al respecto Bidard y Klimovsky enfatizan que las posibles secuencias en el tiempo de las tasas de acumulación efectivas son múltiples y muy diversas, dependiendo de las hipótesis de comportamiento de los productores retenidas. En este sentido expresan: ''la dinámica depende, a la vez, de la especificación retenida para el modelo estático y de las hipótesis que permiten encadenar un período al otro. Esto explica la diversidad de trayectorias encontradas en el marco de una misma formalización general'' (Bidard y Klimovsky, 2006, p. 220). Estas trayectorias, explican, tienen que ver con dos procesos consecutivos: (i) el proceso de formación de las tasas deseadas o anticipadas (inversiones proyectadas) y (ii) el proceso de formación de las tasas efectivas (inversiones efectivas) a partir de las tasas anticipadas. Ambos procesos se pueden desarrollar de distintas maneras, según cuáles sean las hipótesis de comportamiento retenidas, las cuales pueden ser de muchos tipos.
Para efectos exploratorios Bidard y Klimovsky (2006) postulan para una economía de dos sectores, algunas hipótesis sencillas sobre el comportamiento de los capitalistas en el primer proceso (inversiones proyectadas), y adoptan una regla simple que asigna a todo conjunto de tasas de acumulación anticipadas un conjunto de tasas de acumulación efectivas8. Con base en estas hipótesis, razonando en el marco de sus dos modelos, ellos son capaces de describir algunas posibles dinámicas del sistema económico. De las correspondientes al primer modelo BBK, destacamos las siguientes características de los respectivos senderos descritos por la reproducción física del sistema: crecimiento regular, estado estacionario, permanencia en desequilibrio con crisis de la reproducción en algún momento, crisis de proporciones a mediano plazo (tasa de crecimiento negativa en un sector y sobreproducción en el otro) y crisis de largo plazo de contracción progresiva de la actividad económica.
Este análisis sobre dinámica lleva a Bidard y Klimovsky a afirmar que, a pesar de ser simples las hipótesis de comportamiento retenidas, aunque difíciles de justificar, ''la persistencia de un desequilibrio o la sub-optimalidad del equilibrio es un resultado significativo'' (Bidard y Klimovsky, 2006, p. 204). El hallazgo de estos economistas va en contra, una vez más, de la pretensión de las teorías canónicas de los precios, tanto clásicas como neoclásicas, de demostrar la estabilidad del equilibrio. Ubicándose en la perspectiva clásica, lo que por ahora se puede concluir, a partir del modelo BBK, es la posibilidad de una diversidad de trayectorias dinámicas compatibles con una misma formalización general, cuyas formas dependerán de los distintos comportamientos de los productores en el proceso descentralizado de toma de decisiones respecto a las tasas de acumulación. Ahora bien, la imposibilidad de la demostración de la estabilidad del equilibrio no vuelve árido e inoficioso el campo de investigación sobre la dinámica de una economía descentralizada; por el contrario, la investigación de las trayectorias efectivas de las economías en desequilibrio es de suma importancia teórica, así como también el estudio de su viabilidad (entendida como la estabilidad de la estructura dinámica fundamental de un sistema económico) y de la necesidad eventual de regulación. En estas cuestiones, los modelos BBK y el análisis dinámico derivado de ellos, tienen mucho que aportar.
Conclusiones
De acuerdo con Bellino (2008, 2004), ''todo el análisis presentado [...] es seguramente un intento interesante por guiar el análisis clásico en una nueva dirección''; y de esta manera ''el innovador marco desarrollado por los autores debería ser mirado con el más alto interés'' (p. 205). Nosotros compartimos esta apreciación; en efecto, la teoría clásica de los precios de reproducción presentada por Bidard y Klimovsky tiene el mérito de generalizar la teoría clásica de los precios de producción, haciendo aparecer, bajo ciertas hipótesis, a Ricardo, Sraffa y Torrens como casos particulares.
La generalidad se deriva de la posibilidad de que un mismo sistema de ecuaciones permita efectivamente describir un conjunto preciso de equilibrios y desequilibrios y de que en ese sistema aparezca el conjunto de decisiones individuales esenciales de los capitalistas, como el mecanismo cíclico impulsor del proceso económico. Tanto el equilibrio como el desequilibrio se encuentran definidos por los ''fundamentales'' de la economía: los precios de producción relativos y las tasas de beneficio, obtenidos a partir de la hipótesis según la cual los capitalistas pueden decidir sus tasas de acumulación. Se trata entonces de una teoría que estudia simultáneamente la distribución de los ingresos a través de los precios relativos y el fenómeno del crecimiento (exógeno), característica compartida también por los desarrollos teóricos de algunos economistas postkeynesianos.
Otro aspecto de la generalidad del modelo BBK tiene que ver con la posibilidad de determinar físicamente la tasa de beneficio, tanto en equilibrio como en desequilibrio. De acuerdo a la concepción tradicional de la teoría clásica, la tasa de ganancia es una proporción entre magnitudes en términos de valor y ''debe ser determinada a través del mismo mecanismo y al mismo tiempo que los precios de las mercancías'' (Sraffa 1960, p. 21). En el modelo BBK las tasas de beneficio cumplen con esta propiedad, sin embargo, allí es posible desvelar una propiedad oculta de las tasas de beneficio: su determinación a partir de magnitudes físicas. Esta propiedad dota a las tasas de beneficio de independencia respecto a los precios, y permite ver el contraste entre la teoría clásica de los precios y la teoría neoclásica, referidas a cualquier situación del sistema económico: en la primera hay una diferencia analítica entre la explicación de los precios de las mercancías y la de los ingresos de los agentes económicos; en la segunda, hay una sola explicación para los precios y la distribución.
Respecto al análisis dinámico que permite el modelo BBK, con base en los pocos elementos presentados en este escrito, puede concluirse que la dinámica económica está asociada a una multiplicidad de hipótesis sobre el comportamiento de los capitalistas, las cuales ocasionan infinidad de trayectorias de las variables fundamentales del modelo. Dentro de esa multiplicidad de hipótesis, algunas pueden conducir efectivamente al equilibrio (garantizan la estabilidad), sin embargo, como lo hemos visto, dichas hipótesis no se pueden justificar en una economía de mercado, tal y como ocurre también en la teoría neoclásica.
Dentro del contexto del análisis real (representación de una economía sin dinero), al cual pertenece el modelo BBK, la teoría de los precios de reproducción derivada de la contribución original de Bidard y Klimovsky (2006) constituye un punto de partida riguroso y un esquema teórico muy poderoso en la renovación del pensamiento clásico. No obstante, al no dar cuenta de una economía monetaria, esta teoría suscita la misma crítica dirigida a las teorías del valor tradicionales: no puede explicar satisfactoriamente el papel de los precios en los intercambios descentralizados9.
Bibliografía
1. Bellino, Enrico (2008). ''Review to C Bidard-E. Klimovsky, capital, salaire et crises-une approche classique, Paris, Dunod, 2006 (avec la collaboration de Carlo Benetti)'', Cahiers d'économie politique, No. 54, pp. 201-206. [ Links ]
2. Benetti, Carlo (1986). ''La théorie de la demande effective chez R. Torrens'', Cahiers d'Economie Politique, No. 12, pp. 3-39. [ Links ]
3. Benetti, Carlo; Bidard, Christian y KlimovsKy, Edith (2007). ''Classical dynamics of disequilibrium'', Cambridge Journal of Economics, Vol. 1, No. 31, pp. 41-54. [ Links ]
4. Benetti, Carlo; Bidard, Christian; Klimovsky, Edith y Rebeyrol, Antoine (2007a). Déséquilibre de marché et reproduction dans un modèle classique bisectoriel, Working Paper, Université Paris 10 Nanterre. [ Links ]
5. Bidard, Christian y Klimovsky, Edith (2006). Capital, salaire et crise: une approche classique, Dunod, Paris. [ Links ]
6. Deleplace, Ghislain (2007). Histoire de la pensée économique, Dunod, Paris. [ Links ]
7. Klimovsky, Edith Alicia (2006). ''Tasas de ganancia, acumulación, producción y circulación: Los conceptos básicos de la teoría clásica del valor'', Cuadernos de Economía, Vol. xxv, No. 44, pp. 33-55. [ Links ]
8. Klimovsky, Edith y Rosell, Olivier (2010). ''Salaire, prix et taux de profit dans un modèle classique en déséquilibre'', Cahiers d'économie politique, en edición. [ Links ]
9. Torrens, Robert (1821). An Essay on the Production of Wealth, A.M. Kelley, New York, 1956. [ Links ]
10. Sraffa, Piero (1960). Producción de mercancías por medio de mercancías, Oikos Tau, Barcelona, 1966. [ Links ]
Primera versión recibida en mayo de 2010; versión final aceptada en noviembre de 2010
Anexos
Anexo 2. Demostración de las tasas de beneficio en términos físicos, en el primer modelo BBK
Sea ki la tasa de reinversión del bien i con 0 ≤ ki ≤1, la cual indica la proporción de la producción del bien i que entra en los sectores en calidad de reposición de los medios de producción gastados en el período vigente y para aumentarlos en el período siguiente:

Del sistema concreto inicial se extrae un subsistema de producción K, denominado núcleo de acumulación, multiplicando los datos de la producción del sector i por ki, el sistema K se escribe así:
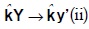
donde k es la matriz constituida por las tasas de reinversión de los bienes en la diagonal principal, siendo ceros los demás elementos. El sistema K produce las cantidades reinvertidas en el sistema concreto inicial. Las tasas de acumulación (gki ) del sistema K son endógenas y se obtienen resolviendo el siguiente sistema:
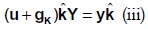
donde gk es el vector fila de las tasas de acumulación del sistema K. El sistema concreto del período siguiente se escribe:
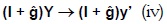
Por lo tanto, el sistema K del período siguiente es:
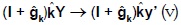
donde 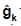 es la matriz constituida por las tasas de acumulación del sistema K en la diagonal principal, siendo ceros los demás elementos. Por equivalencia entre (iv) y (v), se tiene:
es la matriz constituida por las tasas de acumulación del sistema K en la diagonal principal, siendo ceros los demás elementos. Por equivalencia entre (iv) y (v), se tiene:
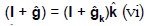
Sea (1 +si) el factor de excedente en bien i, en el período actual t:
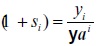
el factor de excedente en bien i en el próximo período t+1, será:
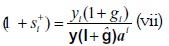
De (i) se tiene 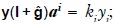 ; luego, reemplazando en (vii), se obtiene: (1+gi) = (1 + si+)ki, para todo i = 1,2,...n , o en forma matricial:
; luego, reemplazando en (vii), se obtiene: (1+gi) = (1 + si+)ki, para todo i = 1,2,...n , o en forma matricial:
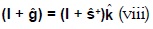
Donde s+ es la matriz diagonal constituida por las tasas de excedente del próximo período en la diagonal principal, siendo ceros los demás elementos. Por equivalencia entre (vi) y (viii) se tiene que:
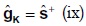
A partir de las ecuaciones (3) del primer modelo se tiene:
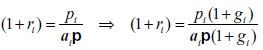
Utilizando las ecuaciones (2a) se puede escribir aip(1+gi ) = pi – fi pi ; por el sistema (1b) se tiene 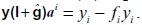 . Teniendo en cuenta estas dos igualdades, (1 +si+) y (1+ri) pueden ser reescritas de la siguiente manera:
. Teniendo en cuenta estas dos igualdades, (1 +si+) y (1+ri) pueden ser reescritas de la siguiente manera:
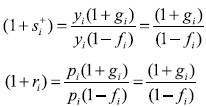
De donde, finalmente, se obtiene: ri = si+, para todo i = 1,2,...n , o en forma matricial:
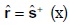
Finalmente de (ix) y (x) se obtiene:
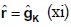
Según la expresión (x), en situación de desequilibrio, la tasa de beneficio (ri) de cada sector es independiente de los precios e igual a la tasa de excedente físico (si+) del bien correspondiente a ese sector en el siguiente período. De acuerdo con la expresión (xi), la tasa de beneficio (ri) de cada sector también es independiente de los precios e igual a la tasa de acumulación (gKi) del mismo sector perteneciente al subsistema K. Este subsistema, que produce y reproduce el capital del sistema concreto, cumple las condiciones del sistema de producción del modelo de Torrens, por lo cual sus condiciones de factibilidad (1) determinan endógenamente las tasas de acumulación (gKi) a partir de las cantidades físicas de bienes y de las condiciones técnicas de producción.
Notas
1 Para la definición de los símbolos matriciales y vectoriales, véase el Anexo 1.
2 Estas proporciones particulares pueden calcularse. Para el procedimiento que permite hacer este cálculo, véase Bidard y Klimovsky (2006, p. 190).
3 Con un método ligeramente diferente, es igualmente posible demostrar la determinación de las tasas de beneficio de desequilibrio en términos físicos para el segundo modelo. Véase Bidard y Klimovsky (2006, pp. 192-194) y Klimovsky (2006, pp. 49-50).
4 Klimovskey y Rosell (2010) hacen un estudio de los efectos de una variación del salario sobre los precios relativos y sobre las tasas de beneficio en los dos modelos de BBK.
5 Excepto en el caso extremo en que el salario es nulo (los trabajadores no participan del excedente social).
6 Las tasas de acumulación máximas de la Tabla 1 (git máxima) se calculan haciendo F = 0 en el sistema (1b) de cada período, lo que resulta equivalente a utilizar el sistema (1) del modelo de Torrens.
7 Podrían llegar al equilibrio en el período 2 si en el período 1 se ponen de acuerdo y deciden las tasas de acumulación g1(1) = 0,3476 y g2(1) = 0,428.
8 A esta regla simple la denominan ''regla del mínimo'', la cual asigna a todo conjunto de tasas de acumulación anticipadas (que pueden ser irrealizables, incompatibles con las cantidades disponibles en la economía) un conjunto de tasas de acumulación efectivas positivas (realizables, compatibles con las cantidades disponibles). También consideran el caso en que esta regla no funciona apropiadamente y puede ocasionar tasas de acumulación efectivas negativas. Ver al respecto Bidard y Klimovsky (2006, pp. 209-211).
9 Al respecto, Bidard y Klimovsky asumen la centralización de los intercambios a través de la caja de compensación de Debreu. Véase, Klimovsky (2006, 40).