ARTÍCULOS

 

Una estimación no paramétrica y robusta de la transformación Box-Cox para el modelo de regresión

 

A Non-Parametric Robust Estimation of the Box-Cox Transformation for Regression Models

 

Une estimation non paramétrique et robuste de la transformation de Box-Cox pour le modèle de régression

 

 

Elkin Castaño*

* Profesor asociado Universidad Nacional - Sede Medellín y profesor titular en la Unversidad de Antioquia. Miembro del Grupo de Econometría Aplicada. Dirección postal: Universidad Nacional Sede Medellín, calle 59A No. 63-20, oficina 43-216. Dirección Electrónica: elkincv@gmail.com.

 

–Introducción. –I. Metodología. –II. Experimiento Monte Carlo.–III. Aplicación de procedimiento a datos reales. –Conclusiones. –Bibliografía.

 

Primera versión recibida en mayo 2011; versión final aceptada en septiembre de 2011

 

---

RESUMEN

Frecuentemente en el análisis de regresión es necesario transformar la variable dependiente con el fin de obtener aditividad y errores normales y de varianza constante. Box y Cox (1964) proponen una transformación paramétrica de potencia basada en el supuesto de normalidad con el propósito de lograr los objetivos anteriores. Sin embargo, algunos autores tales como Carroll (1980, 1982b), Bickel and Doksum (1981), Powell (1991), Chamberlain (1994), Buchinsky (1995), Marazzi y Yohai (2004) y Fitzenberger et al. (2005) han señalado que dicha transformación no es robusta cuando existen observaciones atípicas en la muestra y proponen estimadores robustos para el parámetro de transformación, reemplazando la verosimilitud normal con una función objetivo que es menos sensible a observaciones atípicas. Este artículo presenta un procedimiento alternativo no paramétrico y robusto que permite obtener la transformación de potencia en la familia de transformaciones de Box-Cox cuando existen observaciones atípicas en la variable dependiente. El procedimiento es una extensión de la propuesta de Castaño (1994, 1995) para una transformación de simetría de un conjunto de datos.

Palabras clave: transformación Box-Cox, estimador robusto, estimador no paramétrico, observaciones atípicas.

Clasificación JEL: C14, C15, C51.

---

ABSTRACT

In regression analysis, it is frequently required to transform the dependent variable in order to obtain additivity and normal errors with constant variance. Box and Cox (1964) proposed a parametric power transformation based on the assumption of normality with the aim to achieve these goals. However, some authors such as Carroll (1980, 1982b), Bickel and Doksum (1981), Powell (1991), Chamberlain (1994), Buchinsky (1995), Marazzi and Yohai (2004) and Fitzenberger et al. (2005) have pointed out that this transformation is not robust to the presence of outliers, and propose robust estimators for the transformation parameter by replacing the normal likelihood with an objective function that is less sensitive to them. This paper presents a non-parametric alternative procedure for obtaining a power transformation within the Box-Cox family which is robust to the presence of outliers in the dependent variable. The procedure is an extension of the one proposed by Castaño (1994, 1995) for a symmetry transformation of a dataset.

Keywords: Box-Cox transformation, robust estimator, non-parametric estimator, outliers.

JEL Classification: C14, C15, C51.

---

RÉSUMÉ

Dans l'analyse de régression il est souvent nécessaire de transformer la variable dépendante afin d'obtenir l'additivité, des erreurs normaux et une variance constante. D'après Box et Cox (1964), ces mêmes objectifs peuvent être atteints à travers une transformation paramétrique de puissance, laquelle est basée sur l'hypothèse de normalité. Cependant, certains auteurs tels que Carroll (1980, 1982b), Bickel et Doksum (1981), Powell (1991), Chamberlain (1994), Buchinsky (1995), Marazzi et Yohai (2004) et Fitzenberger et al. (2005) ont montré que cette transformation n'est pas robuste lorsqu'il y a des valeurs atypiques dans l'échantillon. Ils proposent donc des estimateurs robustes pour le paramètre de transformation, tout en remplacement la verosomilité normale par une fonction objectif qui est moins sensible aux valeurs atypiques. Cet article présente une démarche non paramétrique et robuste alternative permettant d'obtenir la transformation de la puissance dans un ensemble de transformations du type Box-Cox, lorsque nous avons des valeurs atypiques dans la variable dépendante. La démarche est une extension de Castaño (1994, 1995) dans le cadre d'une transformation symétrique dans un ensemble de données.

Mots-clés : transformation de Box-Cox, estimateur robuste, estimateur non-paramétrique, valeurs atypiques.

Classification JEL: C14, C15, C51.

---

 

 

INTRODUCCIÓN

El análisis de regresión lineal clásico se basa en los supuestos de que el término de error es aditivo, sigue una distribución normal y tiene varianza constante. Cuando estas hipótesis son seriamente violadas, se sugieren diferentes alternativas a seguir (ver por ejemplo Sakia, 1992):

i) Ignorar la violación de los supuestos y proceder como si fueran válidos.

ii) Analizar cuál es el supuesto adecuado y usar un procedimiento válido que lo tenga en cuenta.

iii) Diseñar un nuevo modelo que tenga las características importantes del modelo original y satisfaga todos los supuestos, por medio de la aplicación de una transformación adecuada a los datos o filtrado algunos datos que parecen sospechosos de ser atípicos.

iv) Usar un procedimiento a distribución libre que sea válido aún cuando varios supuestos son violados.

La opción iii) es frecuentemente el camino elegido por muchos investigadores y generalmente la transformación de Box y Cox (1964) es utilizada con el objetivo de que los supuestos de aditividad, normalidad y varianza constante sean satisfechos aproximadamente. Sin embargo, dicho procedimiento no es robusto y puede verse afectado ante la existencia de observaciones atípicas en los datos. En esta situación, autores como Carroll (1980, 1982b), Bickel y Doksum (1981), Powell (1991), Chamberlain (1994), Buchinsky (1995), Marazzi y Yohai (2004) y Fitzenberger et al., (2005) proponen estimadores robustos para el parámetro de transformación, reemplazando la verosimilitud normal con una función objetivo que es menos sensible a las observaciones atípicas.

Este artículo presenta un procedimiento alternativo no paramétrico y robusto que permite obtener la transformación de potencia en la familia de transformaciones de Box y Cox cuando existen observaciones atípicas en la variable dependiente. El procedimiento es una extensión de la propuesta de Castaño (1994, 1995) de una transformación de simetría para un conjunto de datos.

El orden del documento es el siguiente. La sección 1 presenta la metodología propuesta. En la sección 2 se presenta un estudio Monte Carlo donde se compara el procedimiento propuesto con el método de Box y Cox y la estimación del parámetro de transformación por medio de búsqueda directa, usando la regresión robusta de mínima desviación absoluta LAD (Least Absolute Deviation). También se ilustra el cálculo del error estándar del estimador propuesto por medio de la técnica de bootstrap. En la sección 3 se presenta una aplicación del nuevo procedimiento a datos reales. Finalmente, se presentan las conclusiones.

 

1. Metodología

A. El procedimiento de Box y Cox

La transformación de Box y Cox (1964) trata de estimar el parámetro λ de una transformación potencial sobre la variable dependiente del modelo de regresión lineal

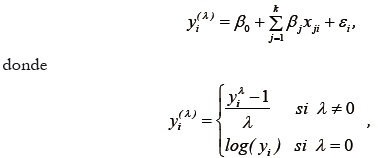
es la familia de transformaciones de potencia de Box y Cox. La transformación estimada se obtiene por medio de la maximización de la verosimilitud normal

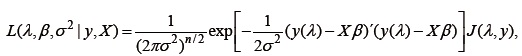
donde y es un vector de nx1 con las observaciones de la variable dependiente, y(λ) es un vector de nx1 con las observaciones de la variable dependiente transformadas por el parámetro λ, X es la matriz de nx(k+1) de diseño del modelo de regresión lineal, β es el vector de (k+1)x1 que contiene los parámetros del modelo, σ² es la varianza del término de error del modelo y es el Jacobiano de la transformación de Box y Cox.

Aunque la transformación estimada posee las propiedades de los estimadores máximo verosímiles, no es robusta a la presencia de observaciones atípicas en la variable dependiente.

Ejemplo. El Gráfico 1 presenta 250 datos simulados usando un modelo de regresión lineal simple, donde λ = 0,5, β₀ = 2 y β₁ = 5, ε ~ N(0, 1) y hay una contaminación de 5 datos procedentes de una N(0, 15).

Se observa que existe una relación no lineal entre las variables y la existencia de datos que no siguen este patrón de comportamiento.

El empleo de la transformación de Box-Cox proporciona 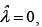lo cual sugiere que existe una relación lineal entre el logaritmo natural de y_i y x_i. La estimación por mínimos cuadrados produce . Los resultados muestran que la presencia de las observaciones atípicas afecta seriamente la estimación del parámetro λ y en consecuencia las estimaciones de β₀, β₁ y σ². El Gráfico 2 muestra que la transformación obtenida no linealiza la relación entre las variables y la regresión estimada no es adecuada, pues la nube de datos sugiere una relación no lineal entre log(y) y X.

Sin embargo, el Gráfico 3 muestra que si transformamos los datos usando la verdadera transformación λ = 0,5, la relación entre los datos transformados es lineal aunque se advierte la presencia de las observaciones atípicas, lo que sugiere una técnica de estimación robusta para los parámetros del modelo.

El ajuste del modelo usando la técnica de estimación robusta de la mínima desviación absoluta (LAD), produce 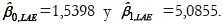El buen comportamiento de la regresión robusta estimada y el diagrama de dispersión de los datos transformados se presenta en el Gráfico 4.

Si se emplea la verdadera transformación λ = 0,5 sobre los datos, y la estimación de los parámetros se realiza usando máxima verosimiltud bajo normalidad, los estimadores obtenidos para β₀ y β₁ son, respectivamente 4,6641 y 0,3803. Este resultado muestra que aunque se use la verdadera transformación, la estimación máximo verosímil es sensible a la presencia de observaciones atípicas.

A diferencia de la regresión de mínimos cuadrados ordinarios (OLS), la cual es equivalente a la estimación máximo verosímil en el modelo clásico de regresión lineal

donde los estimadores de los parámetros se obtienen minimizando 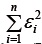con respecto a β_j, j = 0,1,2,..., k, la regresión de la mínima desviación absoluta (LAD) obtiene los estimadores minimizando . Esta función proporciona menos peso a grandes residuales, es decir, está menos influenciada por datos atípicos en la variable dependiente. En este caso, Bassett & Koenker (1978) muestran que la regresión LAD es robusta y desarrollaron la correspondiente teoría asintótica.

Dichos autores probaron que en el modelo lineal general con errores generados por la misma función de distribución F(ε ) , el estimador LAD es consistente y asintóticamente normal.

B. El procedimiento propuesto

El procedimiento que se propone trata de obtener una transformación λ en la familia de transformaciones de potencia de Box y Cox de forma tal que en el modelo

el error ε_i sea aditivo, homocedástico y con distribución simétrica.

El procedimiento de búsqueda del estimador de λ consta de las siguientes etapas:

i) Defina un conjunto de valores para λ . Generalmente el valor de λ se encuentra en el intervalo [-2, 2]. Para cada valor de λ elegido, estime el modelo (1) usando regresión LAD y calcule los residuales e_i(λ).

ii) Obtenga los residuales normalizados como 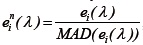, donde MAD=mediana{|e_i (λ) − mediana{e_i (λ)}|}. Este procedimiento elimina las diferentes unidades de medida en la función objetivo, introducidas al ir cambiando λ.

iii) Calcule los percentiles muestrales para varios valores de p, 0 < p < 1. Obtenga

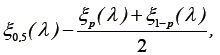
y defina la función

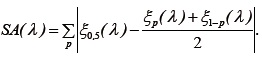
Bajo el supuesto de que la transformación λ simetriza la distribución de los errores,

Por tanto, el valor que minimiza a SA(λ) es la transformación de potencia en la familia de transformaciones de Box-Cox que simetriza la distribución de los errores. Para el caso de una muestra aleatoria, Castaño (1995) muestra es un estimador consistente.

C. Obtención del error estándar de la transformación estimada

Para el cálculo del error estándar se emplea la técnica del Bootstrap (ver, por ejemplo Efron y Tibshirani, 1986). El procedimiento es el siguiente.

i) Obtenga la transformación y calcule los residuales e_i, i=1,2,..., n, de la regresión estimada

ii) Obtenga una muestra aleatoria de tamaño n usando muestreo reemplazamiento de los residuales e_i. Sean e*_i los residuales obtenidos. Construya los pseudos datos para la variable dependiente y_i como

iii) Use el procedimiento descrito para estimar λ en el modelo con los pseudo datos

Regrese a ii) y repita este proceso B veces. Sea el estimador de λ obtenido en la iteración j = 1, 2,..., B.

Obtenga la desviación estándar de usando su distribución bootstrap. Es decir, el error estándar de es

donde .

 

2. Experimentos Monte Carlo

Se consideraron simulaciones con 100, 250 y 1.000 observaciones para la estimación de λ considerando la existencia o no de observaciones atípicas. El número de repeticiones empleado para cada experimento fue de 2.500.

Caso 1. No hay observaciones atípicas. Se generaron observaciones para el modelo

donde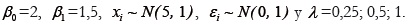

Caso 2. Hay observaciones atípicas. Se generaron observaciones para el mismo modelo anterior, pero en el término de error se generaron 5 observaciones atípicas usando la distribución N( 0,25 ) .

Los resultados reportados consisten de la raíz cuadrada del error cuadrático medio (RECM) dado por , el sesgo promedio (SESGO) definido como , y el sesgo absoluto (SESGOABS) medio dado por .

La función objetivo SA(λ) fue minimizada usando los percentiles para p = 0,10; 0,20; 0,30; 0,40; 0,50; 0,60; 0,70; 0,80 y 0,90. Los cálculos se realizaron usando el paquete quantreg de R.

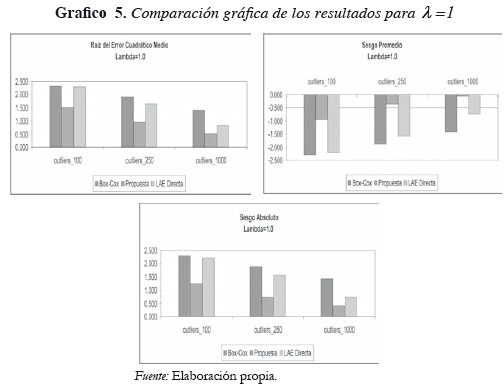
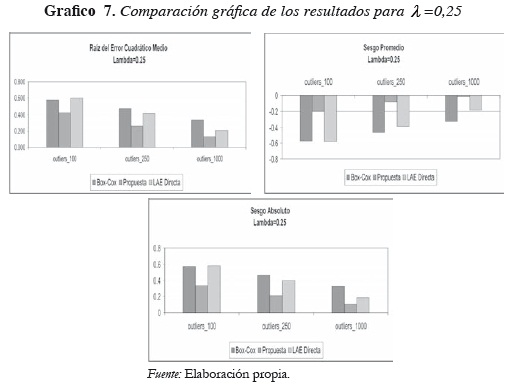
Las siguientes Tablas y Gráficos presentan los resultados de la estimación de λ por medio de transformación de Box y Cox (denominada Box-Cox en las tablas), usando la regresión LAD directamente (denominada LAD-Directa en las tablas) y usando el método propuesto (denominada Propuesta en las tablas). Para obtener los resultados de LAD-Directa, se empleó el método de búsqueda de λ en el intervalo [-2, 2] como aquel valor de λ que minimiza .

Para los experimentos realizados, los resultados muestran que cuando existen observaciones atípicas, en general, el método propuesto es más preciso y produce menos sesgos que el método de Box y Cox y que la búsqueda directa por medio de la regresión robusta LAD. También se observa que a medida que el tamaño muestral crece, los sesgos decrecen y estimador propuesto converge al parámetro desconocido, exhibiendo la propiedad de consistencia del nuevo estimador para λ . En muestras pequeñas, el procedimiento LAD tiene un comportamiento un poco más malo que el de Box y Cox, aunque es mejor a medida que el tamaño muestral crece.

 

 

 

 

 

 

 

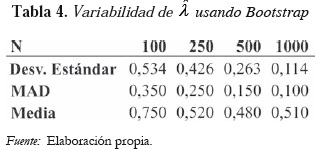
A. Cálculo del error estándar de

El cálculo del error estándar del estimador se realizó por medio del procedimiento bootstrap, explicado en la sección anterior, para el caso de contaminación por 5 observaciones atípicas. Para λ = 0,5, y cada tamaño muestral n = 250, 500, 1.000, se generó una simulación para estimar a λ en el modelo de regresión. Con los residuales se generaron 2.500 repeticiones de bootstrap. A continuación se presentan los resultados de la estimación del error estándar de , el MAD y las correspondientes distribuciones bootstrap.

 

Debido a la existencia de datos atípicos, el MAD parece una medida más adecuada para medir la variabilidad del estimador. Los resultados, presentados en el Gráfico 8, evidencian que el estimador parece no ser preciso en muestras pequeñas.

Los Gráficos de las distribuciones mencionadas, muestran empíricamente la propiedad de consistencia y de normalidad asintótica del estimador propuesto.

 

3. Aplicación del procedimiento a datos reales

A continuación se presenta la aplicación del nuevo procedimiento a la relación de producción de la industria metálica básica (SIC 33) de 27 establecimientos de Estados Unidos. Los datos contienen información sobre el producto (y_i), trabajo (x_1i) y capital(x_2i), y se encuentran en el conjunto de datos denominado Metal del paquete Ecdat de R. Usando estos datos, Vinod (2008), muestra que la función de producción de Cobb-Douglas parece ser un modelo adecuado para la relación de producción. Para esto muestra que la estimación de la transformación de Box y Cox en el modelo.

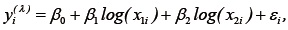
corresponde a = -0,1, pero el valor λ = 0 cae dentro del intervalo del 95% para λ, es decir, la transformación asociada al producto es log(y_i), lo cual define el modelo de producción de Cobb-Douglas.

Para observar el comportamiento del procedimiento propuesto, se procedió a contaminar dos observaciones aleatoriamente elegidas de la información original. Se asignaron observaciones atípicas considerando los siguientes tres casos:

Caso 1. Los datos contaminados fueron y₃ = 8.000 y y₂₀ = 0,5.

Caso 2. Los datos contaminados fueron y₅ =0,3 y y₂₅ = 1.

Caso 3. Los datos contaminados fueron y₈ =12.000 y y₂₆ = 10.000.

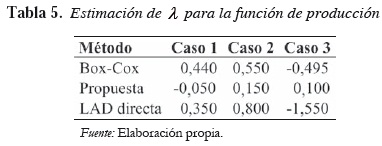
En la Tabla 5 se presentan los resultados de la estimación del parámetro λ usando la transformación de Box-Cox, la regresión LAD y el nuevo procedimiento. Con el nuevo procedimiento, como el número de datos es pequeño, es conveniente emplear un número menor de percentiles que los empleados en los experimentos anteriores. Se emplearon los percentiles para p = 0,2; 0,3 y 0,4 y sus complementos.

 

 

De la Tabla anterior se concluye que en todos los casos de contaminación, los estimadores de λ por los procedimientos de Box-Cox y LAD tienen grandes sesgos, mientras que el estimador propuesto presenta el mejor comportamiento.

 

Conclusiones

Para los casos estudiados se pueden extraer las siguientes conclusiones.

1. El procedimiento de Box-Cox es sensible a la presencia de observaciones atípicas en la variable respuesta. El procedimiento propuesto proporciona un estimador más eficiente que el procedimiento de Box-Cox y que el de la búsqueda directa empleando la regresión LAD.

2. Cuando no existen observaciones atípicas, como era de esperar, es más eficiente el procedimiento de Box-Cox, seguido de lejos por la búsqueda directa usando regresión LAD.

3. Para muestras pequeñas la regresión LAD y el procedimiento de Box- Cox obtienen resultados similares, con una ligera ventaja de Box-Cox. Sin embargo, a medida que el tamaño muestral crece, la regresión LAD presenta mejor comportamiento que el procedimiento de Box-Cox.

4. El nuevo procedimiento disminuye sesgos y aumenta precisión a medida que el tamaño muestral crece.

5. La nueva transformación parece ser útil en muestras moderadas y grandes.

 

Bibliografía

Bassett, Gilbert and Koenker, Roger (1978). ''Asymptotic Theory of Least Absolute Error Regression'', Journal of American Statistical Association, Vol. 73, pp. 618-622.        [ Links ]

Box, G.E.P. and Cox, D.R. (1964). ''An Analysis of Transformations'', Journal of the Royal Statistical Society, Series B, Vol. 26, pp. 211-252.        [ Links ]

Bickel, Peter and Doksum, Kjell (1981). ''An Analysis of Transformations Revisited'', Journal of the American Statistical Association, Vol. 76, pp. 296-311.        [ Links ]

Buchinsky, Moshe (1995). ''Quantile Regression, Box-Cox Transformation Model, and the U.S. Wage Structura, 1963-1987'', Journal of Econometrics, Vol. 65, pp.100-154.        [ Links ]

Carroll, Raymond (1980). ''A Robust Method for Testing Transformation to Achieve Normality'', Journal of the Royal Statistical Society, Series B, Vol. 42, pp. 71-78.        [ Links ]

Carroll, Raymond (1982b). ''Two Examples of Transformations When there are Possible Outliers'', Applied Statistics, Vol. 31, pp. 149-152.        [ Links ]

Castaño, Elkin (1994). ''Una transformación para simetrizar un conjunto de datos usando la familia de transformaciones potenciales'', Revista Colombiana de Estadística, No. 28, pp. 21-36.        [ Links ]

Castaño, Elkin (1995). ''Una transformación de simetría y la media retransformada'', Lecturas de Economía, No. 43, pp. 21-35.        [ Links ]

Chamberlain, Gary (1994). ''Quantile Regression, Censoring, and the Structure of Wages''. En: Sims, Christopher (ed.), Advances in Econometrics: Sixth World Congress, Vol. 1, Econometric Society Monograph.        [ Links ]

Efron, Bradley and Tibshirani, Robert (1986). ''Booststrap Methods for Standard Errors, Confidence Intervals, and Others Measures of Statistical Accuracy'', Statistical Science, Vol. 1, No. 1, pp. 57-77.        [ Links ]

FitzenberGer, Bernd; Wilke, Ralf and ZhanG, Xuan (2005). ''A Note on Implementing Box-Cox Quantile Regression'', ZEW Discussion Paper No.04-61.        [ Links ]

Marazzi, Alfio and Yohai, Victor (2004). ''Robust Box-Cox transformations for simple regression. Theory and Applications of Recent Robust Methods'', Series: Statistics for Industry and Technology, Birkhauser, Basel. Edited by M. Hubert, G. Pison, A. Struyf and S. Van Aelst. pp 173-182.        [ Links ]

Powell, James (1991). ''Estimation of Monotonic Regression Models Under Quantile Restrictions''. En: Barnett, William; Powell, James and Tauchen, George (eds.), Nonparametric and Semiparametric Methods in Econometrics, (pp. 357-384), Cambridge University Press, New York, NY.        [ Links ]

Sakia R.M. (1992). ''The Box-Cox Transformation Technique: A Review''. The Statistician, Vol. 41, pp. 169-178.        [ Links ]

Vinod, Hrishikes (2008). Hands-On Intermediate Econometrics Using R, World Scientific, New Jersey.        [ Links ]