Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Lecturas de Economía
Print version ISSN 0120-2596
Lect. Econ. no.78 Medellín Jan./June 2013
ARTÍCULOS
Economic growth consequences of structural stagnation: A two-sector model of productive diversification
Consecuencias para el crecimiento económico del estancamiento estructural: Un modelo de diversificación productiva de dos sectores
Implications pour la croissance économique de la stagnation structurelle: un modèle de diversification à deux secteurs
Carlos Humberto Ortíz1
1 Profesor titular, Universidad del Valle, Cali, Colombia. Address: Universidad del Valle, Departamento de Economía, A.A. 25369, Cali-Colombia. E-mail: carlos.ortiz@correounivalle.edu.co.
Financial support from Universidad del Valle and academic advise from Douglas Laing are gratefully acknowledged. An earlier version of this paper was presented to the XIII Latin-American Workshop in Economic Theory, Universidad de los Andes, 26th October 2012, Bogotá. The annexes referred herein can be found online in http://aprendeenlinea.udea.edu.co/revistas/index.php/lecturasdeeconomia/article/view/15711/13669
-Introduction. -I. Autarky. -II. International trade. -III. Concluding comments. -References
Primera versión recibida el 13 de diciembre de 2012; versión final aceptada el 2 de mayo de 2013
ABSTRACT
The role of manufacturing input diversification is addressed in a two-sector model of endogenous growth. The general economic equilibrium is solved for the world. It is also solved for a small country with scant capital accumulation, low input diversification and high agricultural productivity. In this set up, developed economies lead the world structural transformation and achieve increasing growth rates by carrying out processes of productive diversification. For each country, the model yields that specialization may enhance economic development if factor prices are internationally equalized. However, due to terms of trade deterioration, factor prices are lower in underdeveloped economies. Hence, specialization of the small country according to its comparative advantages -structural stagnation- generates an inferior path of economic development (lower income and slower growth).
Key words: Diversification, specialization, input-output deepening, structural stagnation, economic growth.JEL classification: O11, O12, O14, O24, O33, O41.
RESUMEN
El rol de la diversificación de insumos manufactureros se aborda en un modelo de crecimiento endógeno de dos sectores. El equilibrio económico general se resuelve para el mundo. También es resuelto para un país pequeño con escasa acumulación de capital, baja diversificación de insumos y alta productividad agrícola. En este marco, los países desarrollados lideran la transformación estructural del mundo y alcanzan tasas ascendentes de crecimiento llevando a cabo procesos de diversificación productiva. Para cada país, el modelo arroja que la especialización puede mejorar el desarrollo económico si los precios de los factores están igualados internacionalmente. Sin embargo, debido al deterioro de los términos de intercambio, los precios de los factores son más bajos en los países subdesarrollados. De ahí que la especialización del país pequeño según sus ventajas comparativas -estancamiento estructural- genere una trayectoria inferior de desarrollo económico (con menor ingreso y menor crecimiento).
Palabras clave : diversificación, especialización, profundización insumo-producto, estancamiento estructural, crecimiento económico.
Clasificación JEL: O11, O12, O14, O24, O33, O41.
RÉSUMÉ
Cet article étudie le rôle des inputs manufacturiers diversifiés dans un modèle de croissance endogène à deux secteurs. L'équilibre économique général est résolu pour une économie composé par un ensemble des pays (le monde). Il est également résolu pour un petit pays à faible accumulation de capital, à faible diversification dans l'approvisionnement et avec une productivité agricole élevé. Dans ce cadre, les pays développés conduisent à la transformation structurelle du monde, où les taux de croissance élevés entretiennent les processus de diversification. Pour chaque pays, le modèle montre que la spécialisation peut améliorer le développement économique si les prix des facteurs sont égalisés au niveau international. Toutefois, en raison de la dégradation des termes de l'échange, les prix des facteurs sont plus faibles dans les pays en développement. C'est ainsi que la spécialisation des petits pays en fonction de leurs avantages comparatifs -stagnation structurelle- entraîne une trajectoire de développement économique inférieure (avec un faible revenu et une croissance plus faible).
Mots clés: diversification, spécialisation, approfondissement des entrées-sorties, stagnation structurelle, croissance économique.
JEL Classification: O11, O12, O14, O24, O33, O41.
Introduction
Is it convenient for an underdeveloped country to diversify its economy? Or, should it be specialized according to the world division of labour? Underdeveloped economies face this dilemma: specialization or diversification.
Most analysts bet on the specialization option. From a static viewpoint there is not much discussion. The world as an integrated economic system increases its efficiency when each country engages in those productive activities for which it has comparative advantages -the gains from trade are well established in economic theory. In fact, this paper provides a theoretical support to the gains from specialization if factor prices just were internationally equalized.
On the other hand, a long tradition in economic development analysis has spoken in favour of the diversification option. The fundamental common idea is that comparative advantages are not static but dynamic. As a country diversifies, its economic structure reaches the production of more technologically integrated goods so that the economy as a whole gains efficiency. Productive diversification becomes a comparative advantage itself since the economic structure must be patiently built (Hirschman, 1958; Leontief, 1963; Landes, 1998). Besides, private capital and fixed social capital are accumulated along the process of productive diversification, so that comparative advantages change in favour of capital intensive goods (Hirschman, 1958; Chenery, Robinson and Syrquin, 1986).
According to this viewpoint, history matters. Early and late developers are not symmetrically related in the world markets. Late developers face technological disadvantages and political risks. They start with a lower aggregate productivity and have to solve coordination problems for further industrialization (Murphy, Shleifer and Vishny, 1989). Sometimes the thrust to industrialization finds a b opposition from already established industrial entrepreneurs who prefer foreign (instead of local) supplies for their own industries (Hirschman, 1958).
Given the existing asymmetries in the world economy, this paper provides theoretical support for the gains from productive diversification. It is argued that the bunch of countries that are unable to climb the ladder of industrialization contributes to world market disequilibria by exacerbating competition among them. As a result, countries whose productive activities require a shallow use of intermediate goods -a lower degree of interindustrial integration- experience terms of trade deterioration, perceive lower factor remunerations, earn lower real incomes, and achieve lower rates of economic growth. Moreover, in a world where technological innovation is monopolized by a few industrialized nations, this paper predicts that specialization leads to world-market disequilibria, international price gaps and differentiated paths of economic growth. Hence the specialization option may be good for the short run, but it is not good in the long run.
Is this perspective relevant? Yes. Neither prices nor earnings are internationally equalized (see any World Bank's World Development Report or any Union Bank of Switzerland's Prices and Earnings around the Globe). In fact, huge price gaps remain between developed and underdeveloped countries. Besides, rich countries have grown faster than poorer countries in the long run (Pritchett, 1997; Easterly and Levine, 2001; Perry et al., 2006).
In order to substantiate the above statements, a two-sector growth model is described and solved in this paper. The model rests on two bases: externalities from productive diversification, and a sectorally differentiated (triangular) economic structure. External effects from input diversification increase manufacturing productivity and enhance the growth rate of the economy. This is a contribution of endogenous growth models based on productive diversification (Romer, 1987, 1990; Grossman and Helpman, 1991; Aghion and Howitt, 1992) that, in turn, model the economic intuitions of Smith (1910), Marshall (1890) and Young (1928) on the circular growth effects of market extension, labour division of work and scale economies. From the structuralist view of economic development, this model incorporates the triangular, recursive structure of intermediate goods linkages. Some productive activities require a shorter list of intermediate goods and some others a longer list; when they are ordered in the input-output table according to its degree of backward technological integration a triangular pattern arises (Leontief, 1963).
The main implication from these technological features is that productive activities with a shallow use of intermediate inputs should develop before than more complex technological activities. Chenery et al. (1986) named this development pattern as input-output deepening. This is a key feature of economic development. Firstly, it has important income level effects. Both Chenery (1960, 1963) and Leontief (1963) found that real income increases across countries with input-output deepening. As Leontief put it, underdeveloped countries are poor because they are by far less economically diversified and less technologically integrated. Based on an empirical analysis of nine representative economies, Chenery et al. (1986) confirmed this pattern of economic development. A recent cross-country analysis could not reject the positive relationship between income level and input-output deepening (Ortiz and Castro, 2008). Secondly, input-output deepening also has important growth effects. It was Hirschman (1958) who first called attention to inter-temporal backward- and forward linkages of investments as important mechanisms of economic development -Hirschman envisaged an evolving input-output matrix through punctual investments which induce further investments in technologically linked productive activities. Kaldor (1961) pointed out the growth gaps across countries, and Kaldor (1966) related this phenomenon to the degree of industrialization. Chenery et al. (1986) confirmed this pattern of economic development. Another recent cross-country analysis could not reject the growth effects from input-output deepening (Ortiz, Castro and Badillo, 2009). They found that the rate of economic growth increases across countries with the input-output coefficient of the manufacturing sector -an indirect measure of the tightness of interindustrial transactions in the manufacturing sector; the relationship, however, is not linear: a manufacturing input-output coefficient threshold has to be surpassed in order to enjoy increasing rates of economic growth.
Thus input-output deepening seems to be a virtuous feature of economic development. Unfortunately, there exists no automatic mechanism to industrial diversification. It was Hirschman (1958), again, who first pointed out the risk of losing the industrialization thrust. His explanation was simple but blunt: as an underdeveloped economy ought to go step by step in the process of economic diversification, there always exists the risk of stopping the process at some intermediate level of the industrial ladder. Hirschman (1992) named this threat as structural stagnation. By resorting to world markets as main providers, an underdeveloped country could face structural stagnation. The main economic consequence is growth deceleration: by suspending the inter-temporal links between sequential investments, this country renounces one of its more important engines of economic development.
This paper is organized as follows. The second section solves for the general competitive equilibrium of an autarkic economy with and without manufacturing input diversification. The third section solves for the competitive equilibrium of a small, underdeveloped and open economy with and without factor price equalization. In both sections the static equilibrium is characterized first, and the path of economic growth is derived afterwards. Some concluding comments close this paper in the fourth section.
I. Autarky
A. Technologies
There are two sectors. The agricultural sector produces food. The manufacturing sector produces intermediate goods and a capital good. Food and intermediate goods are consumed in the period of analysis. Capital is thought of as a composite index of all forms of private capital.
The production function of food is represented by a Cobb-Douglas technology with constant returns to scale in capital and land
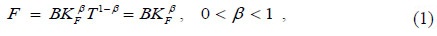
where F is the output of food in the period of analysis, B is the sector's constant productivity level, KF is the sector's capital, β is the sector's constant product-capital elasticity, and T is the sector's land. Land is exclusively used in agriculture; being a fixed factor, the land supply is normalized to 1 (T = 1). Therefore, agricultural activity is characterized by a decreasing marginal productivity of capital.
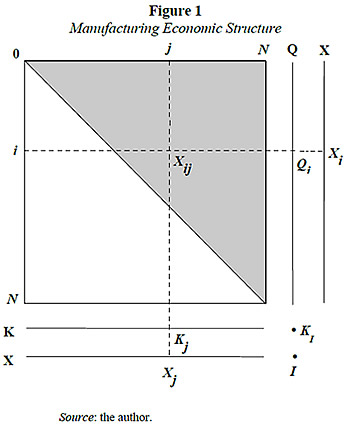
As Figure 1 shows, the manufacturing economic structure is represented by an input-output matrix augmented with the vector of capital allocation. With capital as main production factor, intermediate goods are used to produce themselves and the capital good. All sectors are indexed according to its degree of backward technological integration between 0 and N. From now on, N will be referred to as the number of intermediate goods. Thus, the manufacturing sector is made up of N + 1 productive activities: N intermediate-good sectors and the capital-goods sector. X represents the vector of intermediate goods produced in the period of analysis, and K represents the vector of capital. Backward technological integration -technological dependence on input suppliers- is assumed to increase linearly with the sector's index: sector j only uses as intermediate inputs those intermediate goods with lower index. This feature guarantees that the input-output matrix is perfectly triangular. The intermediate inputs of any sector can be read vertically off the input-output matrix. The vector Q, in particular, is the set of intermediate inputs of the final-good production activity.
The technology of the j-th intermediate good is defined by the following production function.
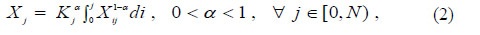
where Xj is the gross output of the j-th good, Kj is the capital of the j-th sector, and Xij is the intermediate consumption of the i-th good in the j-th sector (i < j).
The technology of the capital good is given by

where IS is the production of capital in the period of analysis (gross investment from the supply side), KI is the sector's capital, and Qi is the intermediate consumption of the i-th input in the capital-goods sector.This technology is then identical to the technology of the N-th intermediate good, so that the capital-good technology includes the whole range of available intermediate goods. Notice that creation of new inputs implies a productivity externality in the capital good activity: 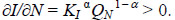 Hence, an important characteristic of the model is the existence of productivity externalities derived from input diversification. As in the pin factory of Adam Smith (1910), productivity of the capital sector increases with division of cooperative productive activities.
Hence, an important characteristic of the model is the existence of productivity externalities derived from input diversification. As in the pin factory of Adam Smith (1910), productivity of the capital sector increases with division of cooperative productive activities.
It is convenient to emphasize some other features of the manufacturing sector's technologies: 1) Manufacturing activities are characterized by constant returns to scale in capital and intermediate inputs; 2) All intermediate goods are produced with the same technology, the only difference comes from the range of intermediate inputs used by each sector; 3) Intermediate inputs are good substitutes: the marginal rate of technical substitution between any pair of intermediate inputs is given by 1/α > 1 (see Annex 1).
The manufacturing technologies as defined by equations (2) and (3) embody the effect of input variety on productivity. These equations are a variation of the CES utility function of Dixit and Stiglitz (1977) thought of, as in Ethier (1982), as a production function where the composite intermediate input increases with input variety. This specification has been used in well-known endogenous growth models with product diversification: Romer (1987, 1990), Rivera-Batiz and Romer (1991), Grossman and Helpman (1991), Aghion and Howitt (1992), among others. In these models, however, the technologies are assumed to be equal across intermediate-good sectors. This paper assumes, instead, a triangular structure of the input-output matrix. This technological feature is consistent with the development pattern of input-output deepening.
If K is the capital of this economy, a fraction z is assigned to the agricultural sector:

The remainder is allocated to the manufacturing sector. Within this sector, as Figure 1 shows, capital is distributed among the sectors producing intermediate goods and the capital-goods sector:
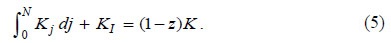
The input-output matrix in Figure 1 shows that each intermediate good is used in the production of those intermediate goods with higher technological integration. It is also used in the production of the capital good. Thus, the market equilibrium condition of the i-th intermediate good is given by:
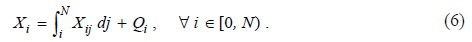
Firms in the j-th sector maximize profits which are given by the following expression:
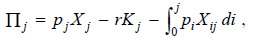
where pj is the price of the j-th intermediate good, r is the gross return on capital denominated in the capital good. The capital good is taken as numeraire (pI = 1). Competitive behaviour is assumed in all markets. Given market prices, the demand for capital and intermediate goods in the j-th intermediate-good sector satisfy the first order conditions for profit maximization:
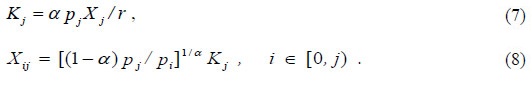
Substitution of equations (7) and (8) into equation (2) yields: 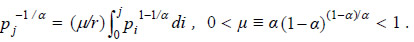 By differentiating this expression with respect to j, it is obtained that
By differentiating this expression with respect to j, it is obtained that 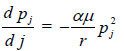 The equilibrium price of the i-th good is found by integrating this differential equation between 0 and i:
The equilibrium price of the i-th good is found by integrating this differential equation between 0 and i:
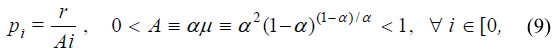
For this result to hold, it is necessary to put forward that the equilibrium price of good 0 is infinity. Given the technology, the production of an intermediate good that does not use inputs is zero; hence, its only meaningful price is infinity.
From equation (9) it is deduced that relative prices are fixed: pi /pj = j/i. There is another implication from equation (9): since the capital good is taken as numeraire (pI = pN = 1), the gross return on capital is determined as r = A N . Hence, the relative price structure is solved as follows:

Given the externalities from input diversification, sectors with higher backward economic integration (higher i) enjoy higher productivity and thus produce cheaper intermediate goods. Combination of the price equations (9) and the first order conditions for maximization, equations (7) and (8), yields the technical coefficients for capital and intermediate goods of the j-th sector

Note that technical coefficients in this economy are fixed. The fixity of technical coefficients is due to the fixity of relative prices. And this feature, in turn, is due to the assumption of a fixed range of intermediate inputs for each sector.
Technical coefficients of the capital-goods sector are deduced by symmetry
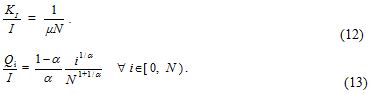
Given the price solutions and the technical coefficients, gross output of the i-th good is deduced. Substitution of the technical coefficients of the i-th good, equations (11) and (13), in the equilibrium condition of the i-th good market, equation (6), gives the following expression
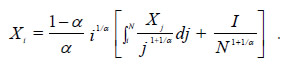
Differentiating with respect to i, it is deduced that (d Xi / d i)/(i/ Xi) = 1. Hence, Xi = ω i, where ω is a constant term to be determined. By substituting the generic solution into the above expression ω is identified, and the gross output of the i-th good is solved as
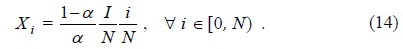
Finally, by substituting equations (10), (12) and (14) into equation (5), the capital market equilibrium, the net production function of capital is deduced:
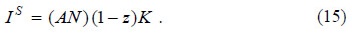
Net production functions are those whose intermediate inputs are net out and thus relate output directly with the sectors' main factors (Ortiz, 1995). For this result it is necessary to assume no joint production, constant returns to scale and competition (Samuelson, 1966). In this way, it is feasible to track down the direct and indirect main factor requirements for each output. The mentioned conditions are satisfied by this model. Hence, the net production function of the capital good, equation (15), embodies the whole structure of the manufacturing sector as depicted by Figure 1. And this net production function preserves the characteristics of the manufacturing sector technologies: constant returns to scale, and productive externalities from economic diversification.
B. Summary on Capital Allocation
It is convenient to highlight the capital allocation among sectors for future reference. As noted in equation (4), a fraction z of total capital is allocated to food production. Then, capital of the manufacturing sector, [(1-z)K], is distributed as follows: a fraction α is allocated to the capital-goods sector, and the remainder is evenly distributed among the intermediate good sectors. Taking into account the production of the intermediate-good sectors, equations (14), and the capital-good output, equation (15), the first result is obtained by substituting the technical coefficients of capital, equations (10) and (12), in the market equilibrium condition for the capital good, equation (5):

The second result is obtained by substituting equations (14) and (15) into equation (10):
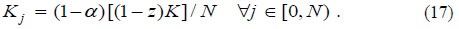
C. The Dynamics of the Closed Economy
1. The Key Differential Equation
This section solves for the dynamic behaviour of this economy under autarky. Since it is convenient to simplify notation, some conventions will be useful. To begin with, all Latin letters are assumed to be time variables; for instance, K ≡ K(t). The exceptions to this rule are the following: A, B, T, e, d, t, i and j. The first three (upper case) letters are assumed to be constant parameters; e is the mathematical constant; d is the mathematical symbol for derivative; and the last three (lower case) letters are count indexes. Greek letters always represent constant parameters.
As it was previously proved, a two-sector model is able to describe the entire economic activity. By combining equations (1) and (4), the food production function is deduced:
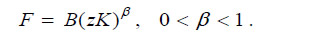
The capital good is produced with the following linear technology:
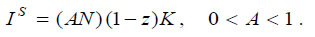
These two equations, F and IS, define the supply side of the model. Gross investment includes net capital accumulation and capital reposition:
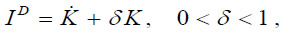
where δ is the constant depreciation rate. As it is usual in this kind of analyses, a variable with a dot on top denotes a time derivative. The market equilibrium condition, IS = ID, defines the capital growth rate:
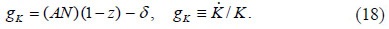
From now on, any growth rate is represented with the letter g.
Profits of the capital goods sector are linear in capital:
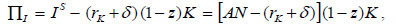
where rK is the net return on capital denominated in the capital good. The market equilibrium condition implies zero profits, which means that the gross return on capital equates the sector's productivity level:

Differentiating the food production function with respect to time yields the following dynamic relationship:

Profits of the agricultural sector are given by
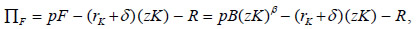
where p is the relative price of food, and R represents the land rents. The first order condition (FOC) for profit maximization is
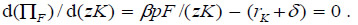
Given the concavity of the production function, β < 1, the second-order condition is satisfied:
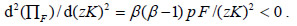
Using equation (19) and the production function for food [F = B(zK)β], the FOC can be rewritten as βpF/(zK) = AN, and also as βBp(zK)β-1 = AN. Differentiating the latter expression with respect to time yields the following dynamic relationship:
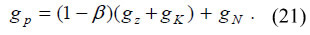
By setting profits in the food sector to nil -land owners extract the whole surplus of agricultural activity- and using the FOC, land rents are defined as follows:
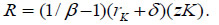
It is assumed that food is the only final consumption good. In a closed economy, market equilibrium requires food demand to be equated with food production. Hence, the representative household maximizes the discounted flow of utility from food consumption (production) along a time path with infinite horizon
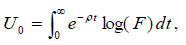
where ρ is the discount rate. This inter-temporal utility function is subject at any moment to the budget constraint, the equilibrium between expenditures and incomes. Expenditures are composed of the value of food consumption and gross investment, and incomes are made of returns on capital and land rents:
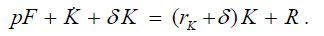
The Hamiltonian equation related to this problem is
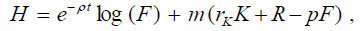
where m is the Lagrangian multiplier. The first-order conditions for inter-temporal utility maximization are the following:
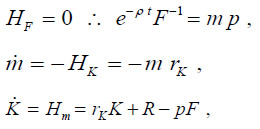
and
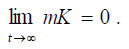
By differentiating the first FOC with respect to time, and using the second FOC, the growth rate of food production is defined as
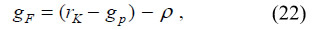
where rK - gp equates the interest rate denominated in the consumption good (food), rF. The equation rF = rK - gp is attained in a competitive environment as the arbitrage condition between assets denominated in the capital good and assets denominated in food.
By adding up equations (20) and (21) it is obtained that
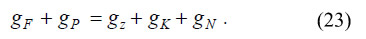
This expression is also deduced by differentiating the FOC for food profits, βpF/K = ANz, with respect to time.
Combination of equations (19) and (22) yields
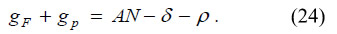
By combining equations (18), (23) and (24) it is finally deduced

This is the differential equation that commands the motion of capital allocation and thus the dynamics of the economic system. In order to be properly defined, some assumptions must be made about the growth rate of economic diversification, gN.
2. Economic Behaviour under Autarky and a Frozen Economic Structure
By a frozen economic structure, it is understood a situation whereby the range of intermediate inputs is fixed. This situation may arise because no private agent has the incentive to invest in input innovation: given that competitive conditions set prices at marginal costs, no margin is allowed to cover the initial fixed costs of technological innovation or technological adoption and adaptation. Hence, the rate of economic diversification is nil, gN = 0.
Under this assumption, equation (25) is reduced to
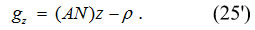
The corresponding phase-plane diagram is shown in Figure 2. Economic intertemporal stability is only assured for gz = 0, which in turn is satisfied if and only if z = ρ/(AN). Note that a minimum level of capital productivity is required for an interior solution, z < 1 ⇔ AN > ρ, which implies a minimum level of manufacturing diversification, N > ρ/A.
Given the capital allocation to the food sector, z = ρ/(AN), the capital growth rate is deduced from equation (18), gk = AN - ρ - δ.
Since the allocation of capital is defined from the beginning (gz = 0), equation (20) delivers the growth rate of food production gF = βgk. And equation (21) yields the growth rate of the relative price of food gp = (1 - β)gk.
The gross national product of this economy is defined from the supply side as GNP = I + p F. From the production function of the capital good, it is deduced that gross investment is linearly related to the capital stock, I = AN(1-z)K = (AN-ρ)K. Thus, the growth rate of gross investment equates the capital growth rate:
gI = gK.
Besides, the growth rate of the value of food is also equated to the capital growth rate:
gp + gF = (1-β)gK + βgK = gK.
Hence, the GNP growth rate equates the capital growth rate:
gGNP = gK.
Given the FOC for maximization of food profits, βpF/(zK) = AN, and the allocation of capital, z = ρ/(AN), it is deduced that the ratio of food value to capital is constant:
pF/K = ANz/β = ρ/β.
As shown above, gross investment as a fraction of capital is also solved as a constant ratio:
I/K = AN - ρ.
Hence, the economy's savings rate is constant as well:
s = I/(I + pF) = (AN - ρ)/(AN - ρ + ρ/β).
In the context of a closed economy and in a long-run perspective, investment is totally financed by savings, and so these variables are equalized.
Welfare Considerations under Autarky and a Frozen Economic Structure
If N is constant -no manufacturing diversification takes place in the economy, the growth rate of capital, gK (= AN - ρ - δ), is also constant, so that the time path of capital is given by K = K0ekgt where K0 is the initial stock of capital. Substitution of this expression in the production function of food solves for the time path of food consumption
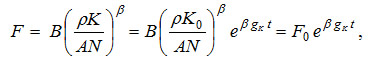
where F0 is the initial consumption of food. Thus, the intertemporal utility function may be analytically solved as a function of its determinants:
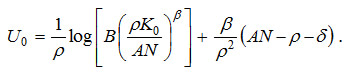
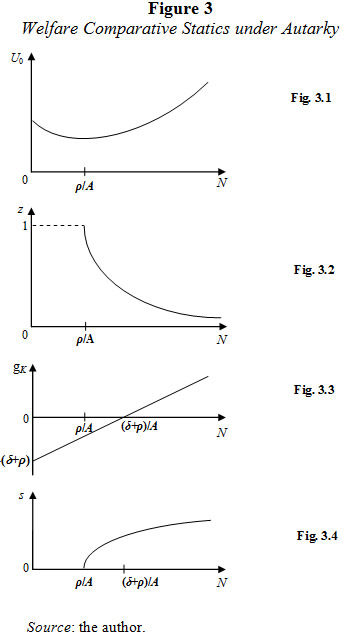
Figure 3 depicts some comparative static analyses for autonomous changes in manufacturing diversification (N). Figure 3.1 shows that the intertemporal utility value is convex in N; the minimum value of N for the intertemporal utility is ρ/A, which is also the minimum degree of manufacturing diversification required to allocate capital to manufacturing activities. As Figure 3.2 shows, if N ≤ ρ/A, z = 1: all capital is allocated to the food sector; hence, the economy would not be viable in the long run as capital is not produced. A further effort of productive diversification is required in order to improve social welfare (as shown by Figure 3.1) and induce manufacturing activity (as shown by Figure 3.2). Moreover, as Figure 3.3 shows, a higher degree of manufacturing diversification above the minimum is required for positive economic growth gK > 0 if and only if N > (δ+ρ)/A (> ρ/A). Therefore, efforts to diversify the economy must be made in advance in order to reap the benefits from positive economic growth. As Figure 3.4 illustrates, only for relatively high savings rates does the economy experience positive economic growth, but the relationship is spurious as both variables, s and gK, depend on the degree of manufacturing diversification, N.
Since the manufacturing sector's productivity is the key dynamic variable of the model, and it depends on the sector's diversification (N), some minimum degree of manufacturing diversification is required for the economy to take off. This minimum level is given by (δ+ρ)/A. This feature of the model coincides with an empirical finding: economic growth across countries increases with manufacturing technological integration only after some threshold is overcome (Ortiz, Castro and Badillo, 2009). Both the model and this empirical finding support to some extent the balanced growth theory related to the importance of an initial ''Big Push'' of multiple-sector investments for economic take off (Rosenstein-Rodan, 1943; Nurkse, 1953; Murphyet al.,1989).
3. Economic Behaviour under Autarky and an Evolving Economic Structure
Let us assume that the range of manufacturing inputs increases autonomously at a positive rate: gN > 0. Let us also define the following auxiliary variable: y ≡ Nz. Hence, the differential system that commands the model dynamics, equation (25), can be rewritten as follows

gZ + gN = 0.
This result provides a theoretical explanation for the change in capital distribution from primary activities towards manufacturing activities along the process of economic development: manufacturing diversification, gN > 0, leads to a lower allocation of capital to the food sector, gz < 0.
Substitution of the stability condition, Nz = ρ/A, in equation (18) delivers the same function that was found before for the capital growth rate: Note, however, that in this context -productive diversification- the growth rate of capital increases in time. This feature may help to explain the long-run pattern of accelerated economic growth under capitalism (Romer, 1986).
The ratio between the value of food production and capital remains constant, pF/K = ANz/β = ρ/β, and the ratio between gross investment and capital keeps its algebraic formI/K = (AN)(1 - z) = AN - ρ. From the above equations it is deduced that the value of food, pF, increases at the growth rate of capital. Investment, I, grows faster because of the diversification effect. Hence, the gross national product, GNP = I + pF = [AN + (1/β - 1)ρ]K, grows at a weighted growth rate and the following chain of inequalities holds: gK < gGNP < gI.
In the autarky context, this model helps to explain some of the main characteristics of structural economic change: 1) Along the path of development new manufacturing activities appear, the degree of intersectoral linkages increases and thus the input-output matrix of the economy becomes deeper (Chenery et al. 1986); 2) economic development induces a relative reallocation of capital from primary activities towards manufacturing activities (Chenery et al. 1986); 3) income increases as the economy unfolds and manufacturing diversification takes place (Chenery, 1963; Leontief, 1963; Chenery et al. 1986); 4) The growth rate of the economy accelerates in time and depends directly on the degree of manufacturing diversification (Kaldor, 1961, 1966; Romer, 1986). As the economy grows up it gets industrialized and more technologically integrated, it becomes richer and the pace of economic activity increases.
Endogenizing Manufacturing Diversification under Autarky
Since the private sector under competitive conditions would not invest in economic diversification, let us assume that the government taxes land rents in order to finance the creation of new intermediate good sectors. Since relative prices are not distorted, the general equilibrium that was characterized above remains valid.
Define the land rents in the economy's general equilibrium as R = (1/β - 1)(rK + δ)(zK) = (1/β - 1)(AN)(zK) = (1/β - 1) ρ K . For this result to be deduced, use was made of the stability condition Nz = ρ/A. The tax rate on land rents is defined by τ. Assume that each value unit allows the creation of an intermediate-good sector. Hence, the dynamics of this economy is determined by the following system of differential equations:
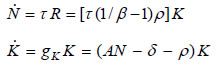
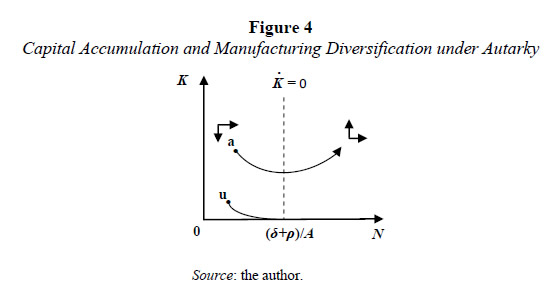
The corresponding phase-plane diagram is shown in Figure 4.
From Figure 4 it is deduced that there exists a possibility of sustained economic growth, as the dynamics of point a shows. The dashed line is the locus corresponding to nil capital accumulation. Given a low level of manufacturing diversification, capital growth may be negative whilst the economy reaches some minimum level of manufacturing diversification and productivity increases so as to sustain positive growth rates. That is why some minimum level of capital accumulation is required since the beginning; as the dynamics of point u shows, there is a possibility of growth traps.
The virtuous path of economic development -like the path starting at point a- shows that an active industrialist policy might be welfare enhancing, as it was in the Colombian development experience during the first seven decades of the XX century. By the way, besides the autonomous impulse to industrialization by entrepreneurs who took advantage of a growing domestic demand, high commercial protection and frequent disruptions of international trade (Hirschman, 1958; Poveda Ramos, 1976), the Colombian government also financed the industrialization process during the mentioned period by transferring rents from agriculture -especially from coffee exports- to the manufacturing sector.
4. Capital Demand across Sectors under Autarky
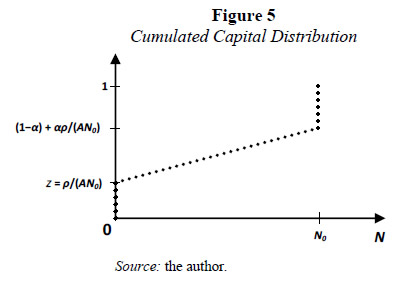
Given the dynamic stability condition of the economic system, Nz = ρ/A, it is now possible to define the cumulated allocation of capital across sectors. This is depicted by the dotted line in Figure 5.
The food sector is indexed by 0 because it does not require intermediate inputs. For a given level of manufacturing diversification, N0, the fraction of capital allocated to the agricultural sector is z = ρ/(AN0). The complement, 1-z, is distributed among the intermediate goods sectors and the capital good. Now, from equation (17) it is known that capital allocation among sectors producing intermediate goods is evenly distributed; hence, the cumulated fraction of capital increases linearly with the degree of backward technological integration, as shown by the dotted line of Figure 5 for the range 0 < N ≤ N0. From the same equation, it is also known that the fraction of capital for intermediate goods production is given by (1-α)(1-z); thus, at the higher degree of technological integration, N0, the cumulated allocation of capital (the dotted line) reaches the value z + (1-α)(1-z) = (1-α) + αρ/(AN0). Finally, as it is known from equation (16), the capital allocation to the capital-goods sector, α(1-z), completes the total allocation of capital across sectors (the dotted line jumps to 1 or 100%). Notice that the index of the capital goods sector is the same index of the last intermediate-good sector, N0.
Given that aggregate capital, K, is assumed to be inelastically provided, Figure 5 may be understood as the distribution of accumulated capital demand according to the degree of backward technological integration (N).
II. International trade
A. The World Representative Country
In this section it is analysed the case of a small country with some stylized characteristics in its technologies. Smallness ensures that its peculiar technological specifications do not affect the world economic equilibrium. Price flexibility holds everywhere. Circulation of goods and capital within each country is assumed to be free -prices are domestically equalized. At the international level goods also flow freely among countries, but international capital flows are forbidden or they are extremely expensive. This last feature may be explained by the fixed characteristics of capital, by complementarities among different forms of capital (human capital, physical capital, public infrastructure, etc.), and by migration barriers imposed by rich countries. Notwithstanding, as the factor price equalization theorem posits, international mobility of goods might be a good substitute for factor mobility (so that factor prices are also internationally equalized). On the other hand, this paper shows that high international differentials in manufacturing input diversification might break the factor price equalization theorem, so that factor prices are not internationally equalized.
As globalization implies a growing international commercial integration and a continuous trend to lower transport costs, the world market behaviour ought to converge to competition. This is the main reason to build this approach to product diversification under the assumption of strict competition (no room is allowed for prices to divert from marginal costs). Competition is the appropriate market environment to analyse the economic performance of a small underdeveloped country that ought to choose between specialization and diversification under an open economy regime in the context of globalization.
From now on, parameters and variables of the world representative country are identified with an asterisk, whilst parameters and variables of the specific country are free of marks. Some key parameters reflect the state of the representative country of the world: the degree of manufacturing diversification (N*), the accumulation of capital (K*), and the productivity of the food sector (B*). The corresponding variables for the specific country are N, K and B. Now, some asymmetries are included. To begin with, the world representative economy surpasses our specific country in capital accumulation (K* > K), and manufacturing diversification (N* > N). But, as in Matsuyama (1992), the productivity of food production in the world representative country is assumed to be lower than in the specific country (B* < B). This feature is explained because of abundance of land and/or higher land fertility in the specific country. It is also assumed that the world representative country increases manufacturing input diversification at the constant rate gN* = n (> 0), whilst the specific country does not make any effort to diversify its productive structure (N is given).
The following set of equations define the capital allocation, the growth rates of the main variables, and the prices of the world representative economy. The corresponding equations have the same reduced-form solutions that were found under the assumption of autarky -the world economy is just a closed economy at the planetary level- and manufacturing input diversification:
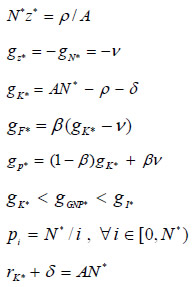
As it was seen before, this whole system of variables is determined once the stability condition of the world economy is defined, which is given by the first expression. The growth rates are just as defined in the case of an autarkic country with an evolving economic structure. In order to understand the last two price equations, it must be said that the capital good keeps its character of numeraire, thus pN* = 1. Hence, based on equation (9'), the relative prices of intermediate goods are determined by the penultimate equation. Based on equation (19), it is deduced that the gross rate of return on capital depends on the world degree of manufacturing diversification (N*), as shown by the last equation.
B. The Specific Country Economy
1. The Compactness Assumption
If the compactness assumption of the input-output matrix is preserved for the specific country under globalization, it is immediately deduced that the specific country is excluded from the production of intermediate goods with a higher degree of technological diversification and from the production of the capital good. Its lacking of economic integration does not allow the country to produce those goods at competitive prices; hence, this economy experiences a specialization in the production of food and the intermediate goods indexed in the range [0, N).
In the context of an open economy with small transport costs, it might seem plausible that a country of low technological integration could produce a good of higher technological integration by importing those inputs the country does not produce. However, several reasons can be put forward for the long run compactness assumption of the country technologies:
1. Underdeveloped countries follow quite diverse paths of development, but they are restricted to some patterns of structural change (Chenery et al, 1986). Typically, underdeveloped countries start their industrial take off by producing primary goods. Afterwards, they diversify their economic structures by producing intermediate goods which are based mainly in agricultural goods and minerals. In the following stage, they develop intermediate goods that use other industrial inputs. Finally, they produce capital goods and develop manufacturing goods based on scientific innovations. Hence, goods tend to be developed once their inputs are domestically produced. Otherwise, a temporary disequilibrium would induce the domestic supply of those inputs through import substitution; this is one of Hirchman's (1958) arguments of disequilibrium growth. In the long-run, thus, the compactness feature is restored.
2. Technologically advanced productive activities require sophisticated skills. It can be said that a longer list of available goods require ''cooks'' with a greater knowledge of ''recipes'' and ''ingredients'' (Leontief, 1963). Moreover, to master the advanced technologies one must go through the knowledge and practice of the less advanced ones. Hence, it is sensible for developing economies to produce first those goods with a shallow use of intermediates, and advance, step by step, towards economic activities with a longer list of input requirements.
3. It is also well known that transport costs have played an important role in the process of industrialization through import substitution. Moreover, even if transport costs are negligible, a near input supplier may imply important strategic advantages for local producers in terms of availability, quickness of delivery and safety against external shocks (Porter, 1990).
In the context of an open economy, relative prices are imposed by the world market. The terms of trade -the relative price of food in international markets- are given by p*. This feature implies that the domestic allocation of capital in the specific country is exogenously determined according to the specific country's comparative advantages.
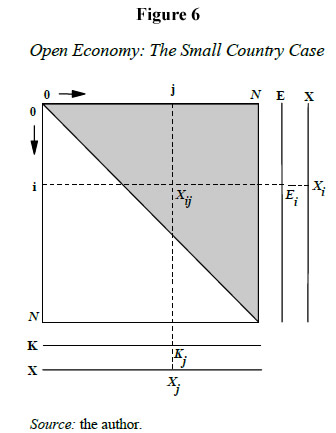
The manufacturing economic structure of the specific country is given by Figure 6. This country is constrained to produce food and the intermediate goods in the range [0, N). A fraction z of capital is allocated to the production of food, and the remainder 1-z is allocated to the production of intermediate goods. Since capital among the intermediate-good sectors is evenly distributed, the amount of capital in the j-th sector is given by kj = [(1-z)K]/K.
Based on the technical coefficient of capital [equation (10)], it is deduced the gross product of the j-th intermediate good: Xj=μjKj=μj(1-z)K/N Since there is no difference between sectors and activities, the counter j can be changed by i.
Based on equation (11), it is possible to define the input requirements of the i-th good for the production of one unit of the j-th good: Xij = (1-α)1/α(i/j)1/α(1-z)K/N
As Figure 6 shows, exports of the i-th good are given by the excess of output with respect to intermediate demands: 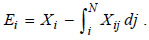 Hence, by combining the last three expressions the amount of exports of the i-th intermediate good is deduced:
Hence, by combining the last three expressions the amount of exports of the i-th intermediate good is deduced: 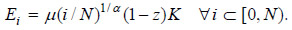
Now, the value of intermediate exports is given by 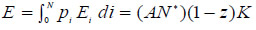 where the relative price of the i-th intermediate input is given by pi = N*/i.
where the relative price of the i-th intermediate input is given by pi = N*/i.
The intermediate exports function embodies three important features of the country's economic structure:
1) Prices are internationally equalized.
2) The compactness assumption of the input-output structure implies that openness to international trade automatically excludes the specific country from producing the higher level technologically integrated intermediate goods (activities whose indices are higher than N) and the capital good.
3) Even though the specific country is now restricted to produce intermediate goods in the range [0, N), the value of intermediate exports of the specific country, E, does not depend at all on its own degree of manufacturing diversification (N).
Hence, a two-sector model summarizes the whole productive structure of the small country under an open economy regime with international price equalization. The net production functions, F and E, define the respective technologies of food and intermediate exports:
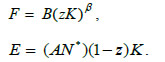
Therefore, a small underdeveloped country that opens its doors to international trade is favoured by a higher world level of productivity, AN* > AN, which corresponds to a higher gross return on capital (and a higher degree of the world manufacturing diversification, N* > N). Under autarky the country's food production function would be the same, but instead of the intermediate exports production function, E = (AN*)(1-z)K, the specific country would have the capital-good production function, I S = (AN)(1-z)K. The latter equation implies a lower productivity level, AN < AN*, because of the specific country's lower manufacturing diversification, N < N*. Hence, the system of net production functions under openness embodies the usual gains from international trade.
Notice that the country's GNP (= p* F + E) under an open economy regime and factor price equalization does not depend on its own degree of manufacturing diversification, N. Therefore, the government of a small, underdeveloped country that has opened its doors to international trade may conclude that manufacturing diversification is not worth the effort. It will be argued that the government is right in the short run, but it is completely mistaken in the very long run.
2. Capital Allocation in the Specific Country under Openness
Profits in the sectors exporting intermediate goods are given by
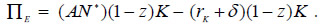
Since profits are linear in capital, market equilibrium requires that the gross rate of return equates the productivity of intermediate goods exports, rk + δ = AN* which is identical to the world gross rate of return on capital.
Profits of the food sector are given by
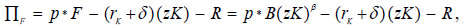
where p* are the terms of trade. The FOC for profit maximization implies
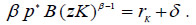
Hence, the first order conditions for profit maximization imply the equalization of the value of marginal product across sectors:
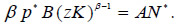
This equalization must also hold for the world representative economy:
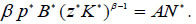
Using the last two equations in order to eliminate p*, the specific country allocation of capital, z, is deduced:
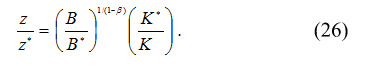
Notice that a higher productivity in primary activities of the specific country (B/B* > 1) and a lower level of capital accumulation in our specific country (K*/K > 1) imply a higher allocation of capital in the specific country to the food activity: z/z* > 1. Thus, openness implies an even higher level of specialization of the specific country. Moreover, if the structural differences in primary productivity and capital accumulation are big enough, the specific country may be completely specialized in food production (z = 1). This would imply to diminish the growth rate of the specific country to the growth rate of the food sector, which is a fraction of the capital growth. Since most underdeveloped countries produce some intermediate goods, the possibility of complete specialization in the primary activity is discarded from now on.
Equation (26) implies that a country's capital allocation under an open economy regime is determined by the strength of comparative advantages.
It is convenient to define the land rents of the specific economy under an open trade regime with price equalization across countries:
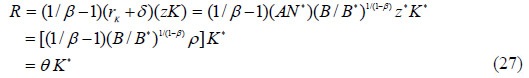
where θ ≡ (1/β-1)(B/B*)1/(1-β) ρ > 0. This result entails the country's capital allocation function [equation (26)], and the world economy's stability condition, N*z* = ρ/A.
With these section results, it is possible to define the specific country's GNP:
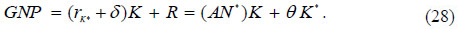
3. Small Country Dynamics under Capital Price Equalization
It is also possible to deduce the specific country's growth rate. The following set up is completely parallel to the analysis of optimal economic growth under autarky. The main difference comes from the fact that food demand under an open economy regime, represented by the letter D, is not necessarily equal to the production of food, F, as it was the case under autarky. Hence, it is unavoidable to distinguish these two variables.
The intertemporal utility function of the specific country is defined in terms of the current value flow of food demands in an infinite horizon:
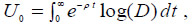
The instantaneous budget constraint of the representative consumer is given by
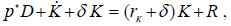
where p* represents the terms of trade (the relative price of food in the world market).
It will be assumed that the world representative economy enjoys a constant positive rate of input diversification, gN* = n > 0 , whilst the specific country is stuck to its own degree of input diversification, N. The rationale for this last assumption might be that, as it was analysed before, once the specific economy opens its doors to international trade the country's income shows no evident advantages from input diversification. Hence, the world degree of manufacturing diversification evolves according to the time path N * = N0* eνt, where N0* is the initial level of world manufacturing diversification. Thus, the growth rate of capital accumulation in the world is given at any time by gK* = AN * - ρ - δ = AN0*eνt - ρ - δ . And capital of the world representative economy expands according to the path K* = K0* exp [AN0*(eνt - 1)/ν - (ρ + δ)t], where K0* is the initial stock of capital of the world representative country.
The dynamic problem of the specific country is solved in Annex 2. It is found that the country's capital path is given by
K = K0 exp [AN0*(eνt - 1)/ν - (ρ + δ)t],
Hence, capital in the specific country is accumulated at the same speed of the more developed economies, gK = gK*. Notice as well that this growth rate accelerates over time.
This result seems to be good news for all economic analysts that advise free market economic policies. Under an open economy regime, this advice would imply that domestic capital allocation across sectors is defined by the country's comparative advantages. Given important resources of land, low availability of capital and low productive diversification, the specific country would be highly specialized in productive activities with a lower index of technological integration, but it would grow as fast as any developed economy.
This last result rests entirely on the assumption that the gross remuneration of capital is equalized across countries. As explained before, however, this is not realistic: huge gaps in prices and earnings are observed across countries, especially between developed and underdeveloped countries. How can this phenomenon be explained? In Annex 3, it is considered a hypothetical dualistic world where the gap between developed and underdeveloped economies in terms of industrial diversification is so big that a capital price gap arises between these economic blocks.
4. Small Country Dynamics under Unequal Capital Price
The analysis in Annex 3 reveals that any underdeveloped country may be subject to terms of trade deterioration and lower factor remuneration if its own degree of economic diversification is too low. Hence, let us assume that a specific underdeveloped country faces international input prices that are lowered by the constant fraction γ for those intermediate goods that the country produces:
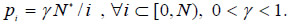
In this new situation, the country's production function of food is unchanged:
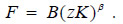
But the export function of intermediate goods in this country with low diversification changes because productivity is lowered by the same fraction:
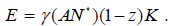
With lower input prices, the value of exports lowers by the same fraction. And also will be the gross capital return on capital of the low diversification countries. The export profits of the specific country are given now by 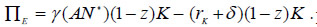 Because of the linearity in capital of this profit function, the market equilibrium condition imposes zero profits, so that the gross capital remuneration in the specific country satisfies
Because of the linearity in capital of this profit function, the market equilibrium condition imposes zero profits, so that the gross capital remuneration in the specific country satisfies 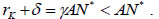 This new situation has implications for capital allocation in the specific country. Given the profits of the food sector,
This new situation has implications for capital allocation in the specific country. Given the profits of the food sector,
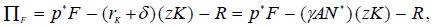
The first order condition for profit maximization yields the equalization of the value of marginal product between sectors:
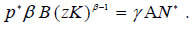
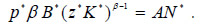
Thus, capital allocation in the specific country is defined as follows:
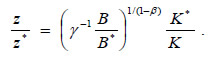
With terms of trade deterioration, 0 < γ < 1, or γ-1 > 1, and the same assumptions on the primary productivity gap B/B* > 1 and the capital accumulation gap K*/K > 1, the allocation of capital to the production of food is now even ber z >> z*.
In this situation, land rents in our specific country are now higher:
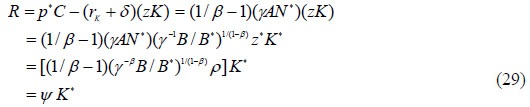
where ψ ≡ (1/β-1)( γ-β B/B*)1/(1-β)ρ (> 0). For this result, the international stability condition N*z* = ρ/A is used. Therefore, land rents increase under terms of trade deterioration. By comparing equations (27) and (29) it is found that
ψ ≡ (1/β-1)(γ-β B/B*)1/(1-β)ρ > θ = (1/β-1)( B/B*)1/(1-β)ρ .
Notice that γ < 1 (terms of trade deterioration) implies γ -β/(1 - β) > 1.
Thus, the specific country's GNP with deterioration of terms of trade is given by
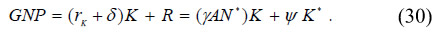
Deterioration of terms of trade changes income distribution in favour of land rents. By comparing equations (28) and (30) it is deduced that capital remuneration lowers (γAN* < AN*) and land rents increase (ψ > θ).
The intuition says that the dynamics of the price adjustment factor, γ, will depend on the dynamics of the diversification gap between underdeveloped and developed economies: N*/N. This is a task to be solved in the future. Hence, for simplicity suppose that N, N* and γ are fixed. Even in that favourable scenario, it could be proved that an underdeveloped country grows slower than fully developed economies. This proof is accomplished in Annex 4. There it is shown that capital accumulation in the specific country grows at the following rate:
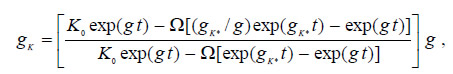
where Ω ≡ [-ψK0*]/[(1 - γ)AN* - ρ] > 0, g ≡ γAN* - δ - ρ, and gK* ≡ AN* - δ - ρ.
This last expression is the capital growth rate of the representative world economy. Notice that the following chain of inequalities holds: gK < g < gK*: since g < gK*, the expression in brackets above is lower than 1, then gK < g. Moreover, as time passes, the bracketed expression lowers. Hence, capital of the specific country with low manufacturing diversification that experiences terms of trade deterioration not only accumulates capital at a slower pace than the world economy, gK < gK*, but also its capital growth rate gK diminishes slowly along time.
Concluding comments
This model has been built to analyse the case of a small, underdeveloped and open economy that has abandoned the diversification policy to pledge itself to the mainstream vision of productive specialization. The analysis of the autarkic economy in the second section yields the tools to define the world economic equilibrium and its dynamic path. Given this economic world context, the third section solves for the general equilibrium of the specific country both in static and dynamic terms. As this economy is well endowed with natural resources but lacks capital -physical and human capital- and manufacturing input diversification, the specific country ends up producing primary goods (food) and some intermediate goods of low backward-technological integration. If the capital price is internationally equalized, the change from a closed economy to an open economy benefits the specific country. Moreover, the country's economic growth rate equates the growth rate of developed economies. However, in this situation, when the small economy works as a functional part of the world economic system, the underdeveloped country's government does not experience any need of keeping the economy along the track of diversification. That is why it is assumed that the small country abandons itself to the siren songs of the advantages of productive specialization.
This last assumption is quite realistic. Unlike Ulysses, who had his crew tie him to the ship's mast in order to resist the charming but dangerous siren songs, most underdeveloped economies have abandoned the structural transformation agenda and thus made real the risk of structural stagnation. Then life becomes difficult. This model yields that underdeveloped countries are more likely to experience terms of trade deterioration and lower capital remuneration -the factor price equalization theorem is broken- as all of them concentrate their economic activity in sectors whose relative demand falls as the world productive diversification grows. As a result, the international growth gaps increase: developed economies accelerate their long-run economic growth whilst underdeveloped economies suffer from economic deceleration.
These results fit with the Colombian experience of economic development: By the 1970s, the economic policy regime changed from a relatively closed environment and an active promotion of industrialization to an increasingly open economy without industrialization policies. As a result, the Colombian economy went from long-run economic acceleration to long-run economic deceleration, and economic activity as a whole increased its specialization in primary activities and intermediate-good activities highly intensive in natural resources (Ortiz, 2009).
In general, the model yields the following results: First, income levels and welfare are directly related to manufacturing input diversification (MID). Second, the economic growth rate increases with MID. This relationship is not linear, as the economy has to overcome some threshold of MID before the growth rate reacts positively. And third, structural transformation (the change of capital distribution from primary to manufacturing activities) is directly related to MID.
This paper suggests that government policies to keep the economy along the track of productive diversification enhance social welfare.
REFERENCES
Aghion , Philippe & Howitt, Peter (1992). ''A Model of Growth through Creative Destruction'', Econometrica, Vol. 60, No. 2, pp. 323-351. [ Links ]
Chenery, Hollis B. (1960). ''Patterns of Industrial Growth'', American Economic Review, Vol. 50, No. 4, pp. 624-654. [ Links ]
Chenery, Hollis B. (1963). ''The Use of Interindustrial Analysis in Development Programming''. In: Barna, Tibor (Ed.), Structural Interdependence and Economic Development (pp. 11-27). New York, St. Martin's. [ Links ]
Chenery, Hollis B.; Robinson, Sherman & Syrquin, Moshe (1986). Industrialization and Growth: A Comparative Study, Washington, World Bank, Oxford University Press. [ Links ]
Dixit, Avinash and STIGLITZ, Joseph (1977). ''Monopolistic Competition and Optimum Product Diversity'', The American Economic Review, Vol. 67, No. 3, pp. 297-308. [ Links ]
Easterly, William & Levine, Ross (2001). ''It's Not Factor Accumulation: Stylized Facts and Growth Models'', World Bank Economic Review, Vol. 15, No. 2, pp. 177-220. [ Links ]
Ethier, Wilfred (1982). ''National and International Returns to Scale in the Modern Theory of International Trade'', The American Economic Review, Vol. 72, No. 3, pp. 389-405. [ Links ]
Grossman, Gene and Helpman, Elhanan (1991). Innovation and Growth in the Global Economy, Cambridge, MA: MIT Press. [ Links ]
Hirschman, Albert O. (1958) The Strategy of Economic Development, New Haven, Yale University Press. [ Links ]
Hirschman, Albert O. (1992). ''The Case Against 'One Thing at a Time'''. In: Teitel, Simon (Ed.), Towards a New Development Strategy for Latin America: Pathways from Hirschman's Thought (pp. 15-22). Washington, Inter-American Development Bank. [ Links ]
Kaldor, Nicholas (1961). ''Capital Accumulation and Economic Growth''. In: F. Lutz and D. Hague (Eds.) The Theory of Capital (pp. 179-222). London, Palgrave Macmillan. [ Links ]
Kaldor, Nicholas (1966). Causes of the Slow Rate of Economic Growth of the United Kingdom, United Kindom, Cambridge University Press. [ Links ]
Landes, David (1998). The Wealth and Poverty of Nations, United States of America, W.W. Norton & Company. [ Links ]
Leontief, Wassily (1963). ''The Structure of Development'', Scientific American, Vol. 209, pp. 148-166. [ Links ]
Marshall, Alfred (1890). Principles of Economics, Library of Economics Liberty, available at: http://www.econlib.org/library/Marshall/marP.html (May 28th, 2013). [ Links ]
Matsuyama, Kiminori (1992) ''Agricultural Productivity, Comparative Advantage and Economic Growth'', Journal of Economic Theory, Vol. 58, pp. 317-334. [ Links ]
Murphy, Kevin; Shleifer Andrei & Vishny Robert (1989). ''Industrialization and the Big Push'', Journal of Political Economy, Vol. 27, No. 5, pp. l003-1026. [ Links ]
Nurkse, Ragnar (1953). Problems of Capital Formation in Underdeveloped Countries, Oxford, Basil Blackwell. [ Links ]
Ortiz, Carlos H. (1995). ''La Transformación de Funciones de Producción Bruta en Funciones de Producción Neta'', Boletín Socioeconómico, No. 29, pp. 83-92. [ Links ]
Ortiz, Carlos H. (2009). ''La Desaceleración Económica Colombiana: Se Cosecha lo que se Siembra'', Revista de Economía Institucional, Vol. II, No. 21, pp. 107-147. [ Links ]
Ortiz, Carlos H. & Castro Javier A. (2008). ''Technological Integration and Income Gaps'', Lecturas de Economía, No. 68, pp. 217-247. [ Links ]
Ortiz, Carlos H.; Castro, Javier Andrés & Badillo, Erika Raquel (2009). ''Industrialization and Growth: Threshold Effects of Technological Integration'', Cuadernos de Economía, Vol. 28, No. 51, pp. 75-97. [ Links ]
Perry, Guillermo; Arias, Omar; Maloney, William; López J. Humberto & Servén Luis (2006). Poverty Reduction and Growth: Virtuous and Vicious Circles, Washington, World Bank Latin American and Caribbean Studies. [ Links ]
Poveda Ramos, Gabriel (1976). Políticas Económicas, Desarrollo Industrial y Tecnología en Colombia, 1925-1975, Bogotá, Editora Guadalupe. [ Links ]
Porter, Michael (1990). The Competitive Advantage of Nations, New York, The Free Press, [ Links ]
Pritchett, Lant (1997). ''Divergence, Big Time'', Journal of Economic Perspectives, Vol. 11, No. 3, pp. 3-17. [ Links ]
Rivera-Batiz Luis A. & Romer Paul (1991). ''Economic Integration and Endogenous Growth'', Quarterly Journal of Economics, Vol. 106, pp. 531-555. [ Links ]
Rosenstein-Rodan, P. (1943). ''Problems of Industrialization in Eastern and South-Eastern Europe'', The Economic Journal, 53, No. 210/211, pp. 202-211. [ Links ]
Romer, Paul (1986). ''Increasing Returns and Long-Run Growth'', Journal of Political Economy, Vol. 94, No. 6, pp. 1002-1037. [ Links ]
Romer, Paul (1987). ''Growth Based on Increasing Returns Due to Specialization'', The American Economic Review, Papers and Proc. Vol. 77, Issue. 2, pp. 56-62. [ Links ]
Romer, Paul (1990). ''Endogenous Technological Change'', Journal of Political Economy, Vol. 98, No. 5, Part. 2, pp. S71-S102. [ Links ]
Samuelson, Paul A. (1966). ''The Fundamental Singularity Theorem for Non-Joint Production'', International Economic Review, Vol.7 No. 1, pp. 34-41. [ Links ]
Smith, Adam (1910). An Inquiry into the Nature and Causes of the Wealth of Nations, London and Toronto, published by J. M. Dent and Sons Ltd, and in New York by E. P. Dutton, based on Smith's publication of 1776. [ Links ]
Union Bank of Switzerland (2009). Prices and Earnings Around the Globe, Zurich, Autor. [ Links ]
Young, Allyn. 1928, ''Increasing Returns and Economic Progress'', Economic Journal, Vol. 38, No. 152, pp. 527-542. [ Links ]