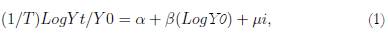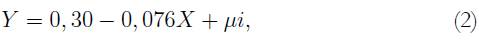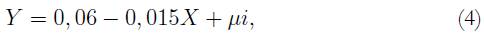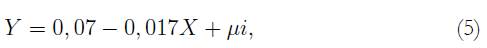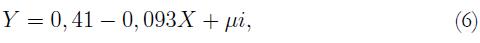Introducción
La convergencia regional es una teoría del desarrollo que sostiene que las regiones pobres crecen más que las ricas, llegando así al punto de alcanzarlas reducir la desigualdad. Por tal motivo, es importante para los gobiernos conocer el grado de desarrollo de su territorio para así determinar la existencia de convergencia regional y formular políticas públicas focalizadas.
Esta teoría, desarrollada por Xavier Sala i Martin y Robert Barro, parte de los supuestos de modelos neoclásicos de crecimiento como el de Solow, en el que existe movilidad de factores estimulada por el comercio y el rendimiento marginal del capital decreciente, el cual migra de las regiones ricas a las pobres estimulando su crecimiento, haciendo que se acerque al estado estacionario y favoreciendo el desarrollo regional.
Diversos estudios se han realizado demostrando la existencia de la convergencia regional, pero dichos estudios tradicionalmente se han realizado utilizando el PIB per cápita sin tener en cuenta variables sociales que permitan conocer el bienestar y la calidad de vida de las personas, si éstas tienen acceso a servicios básicos y desarrollan libremente sus capacidades. Por el contrario, el modelo del desarrollo humano propone medir el grado de desarrollo teniendo en cuenta, además, del ingreso, variables de educación y salud.
En este contexto, en Colombia se han realizado estudios que utilizan variables sociales, pero la mayoría de ellos lo hacen a nivel departamental, y son muy escasos los que miden el desarrollo desde las dinámicas municipales.
I. Fundamentación teórica
La convergencia regional, según Murillo y Gaviria (2008), “se refiere a la posibilidad de que a corto plazo las economías pobres logren crecer más que las ricas” (p. 94 ), esto implica que el rendimiento marginal del capital de las regiones pobres sea más alto que el rendimiento marginal del capital de las regiones ricas, llegando a un punto donde las regiones que tenían niveles iniciales de ingresos per cápita altos crezcan tan poco que sean alcanzadas por las regiones que tenían niveles iniciales de ingresos per cápita bajos, lo que, como señalan Ramírez y Ayala (2014), reduce la desigualdad entre regiones (2014).
Existen dos tipos de convergencia: la beta y la sigma. La primera es una relación inversamente proporcional entre el nivel inicial de los ingresos per cápita y su tasa de crecimiento, la cual puede ser absoluta (si todas las regiones convergen a un mismo estado estacionario) o condicional (si cada región converge a su propio estado estacionario). La convergencia sigma es, en palabras de Gómez (2006), “[…] la reducción de las disparidades del PIB per cápita de un grupo de economías en un periodo de tiempo y se vincula a la evolución de una medida de dispersión. Esta convergencia depende, además de la convergencia beta, de la varianza de las perturbaciones de la ecuación de convergencia, la cual puede disminuir (aumentar) si la misma está sobre (debajo) de la dispersión del estado estacionario sin importar la evolución del beta” (p. 7).
De acuerdo con Leon y Ríos (2013) “el concepto de convergencia fue desarrollado por Robert Barro y Xavier Sala I Martin” (p. 108). Sus investigaciones pioneras fueron los modelos de convergencia regional (Barro, 1989; Barro & Sala I Martin, 1990 y 1991), donde analizaron las economías de los estados de Estados Unidos, Europa y 100 países en el mundo, y encontraron evidencia empírica de convergencia regional en el PIB per cápita, con una beta equivalente al 2% anual.
El primer trabajo en Colombia en este campo fue el realizado por Mauricio Cárdenas en 1993, quien realizó un modelo con el PIB per cápita departamental entre 1950 y 1989, y encontró convergencia regional a una tasa de 4% por año (Bonet & Meisel, 1999).
A partir de la investigación pionera de Cárdenas, se han realizado diversas investigaciones en convergencia regional. Se destaca, por ejemplo, la de González (2007), quien encontró convergencia beta absoluta, condicional y convergencia sigma del PIB per cápita departamental en Colombia entre 1980 y 2004.
Birchenall y Murcia (1997), quienes no encontraron evidencias de convergencia regional, afirman que “Colombia no es un caso de convergencia” (p. 305) y que, al contrario, se incrementa la distancia de los ingresos per cápita de los departamentos colombianos.
Barón (2003) tampoco encontró convergencia del PIB per cápita departamental en la década de 1990, pero sí en la década de 1980, y afirma que a partir de 1990 las disparidades tendieron a crecer.
Por su lado, Bonet y Meisel (1999) utilizaron los depósitos bancarios departamentales per cápita como proxy del PIB per cápita departamental para el periodo 1926-1960, y encontraron convergencia regional beta a una velocidad del 2,5%, además de encontrar convergencia tipo sigma.
Utilizando el ingreso per cápita departamental de 1980 al 2000, Acevedo (2003) encontró convergencia regional en la década del 80 y divergencia en la década de los 90, similar a los resultados obtenidos por Barón (2003).
La convergencia regional es una teoría del desarrollo que tradicionalmente se ha medido con el PIB per cápita, pues se entiende que ésta es la variable que permite conocer el grado de desarrollo de una región, y se considera que el crecimiento del PIB es suficiente para realizar dicha medición. Sin embargo, este indicador no tiene en cuenta los problemas de distribución del ingreso nacional, y la desigualdad que ésta conlleva.
Como teoría alternativa al desarrollo neoclásico, aparece la teoría del desarrollo humano, el cual concibe el desarrollo de una economía en términos de calidad de vida de las personas. Como lo explica el teórico Mahbub Ul Haq (1995) “el objetivo del desarrollo es crear un ambiente para las personas que les permita disfrutar larga, saludable y creativamente sus vidas” (p. 14). Para él, esa fue siempre la preocupación de la economía.
Martha Nussbaum (2010) también critica el modelo de desarrollo que solo se basa en la medición del crecimiento del PIB. La autora explica que “según ese modelo de desarrollo, la meta de toda nación debería ser el crecimiento económico. No importan la distribución de la riqueza ni la igualdad social […]” (p. 34). Precisamente por eso, los autores del modelo de desarrollo humano abogan para que en la literatura económica se comprenda la importancia de que el desarrollo de las regiones se haga desde las dimensiones del ser humano.
Para Sen (2000) concibe “el desarrollo como un proceso de expansión de las libertades reales que disfrutan los individuos” (p. 55). Es decir, el desarrollo y el crecimiento económico sirven como medios para conseguir las libertades, que son el fin que se pretende alcanzar.
Martha Nussbaum (2005) desarrolla la teoría de Sen sobre las capacidades, entendidas éstas como el poder ser y hacer del hombre, y como aquellas que permiten dimensionar la dignidad humana. Desde esta perspectiva, el papel del Estado debe ser el de garantizar las titulaciones fundamentales que le permitan al individuo alcanzar su plena libertad y permitir que se disponga todo lo necesario para el efectivo goce de las libertades humanas. La autora propone una lista de 10 “capacidades humanas básicas” que pueden aplicarse a cualquier sociedad. Estas son: vida; salud corporal; integridad corporal; sentidos, imaginación y pensamiento; emociones; razón práctica; afiliación; otras especies; recreación; y control sobre el propio entorno. Cada capacidad tiene su definición y unos mínimos alcances para la satisfacción plena del ser.
Es así como los autores del modelo del desarrollo humano proponen medir el desarrollo desde distintas variables sociales que permitan conocer la calidad de vida de los habitantes de determinada zona, y no solo medirlo con la variable del PIB, aunque no se oponen a su medición. En este contexto nace el Índice de Desarrollo Humano (IDH). Como lo explica Mahbub Ul Haq (1995), este indicador surgió cuando le fue presentado al administrador del Programa de las Naciones Unidas para el Desarrollo, con el fin de elaborar un informe anual, desde 1990, sobre la situación de los países en términos de desarrollo humano, según 3 dimensiones del aspecto socioeconómico de las personas: el conocimiento o la educación, la salud o la longevidad y los ingresos, medidos en una escala que va desde 0 hasta 1.
Sobre el IDH Mahbub Ul Haq explica que “La longevidad es medida por la esperanza de vida al nacer como un indicador, el conocimiento es medido por dos variables, alfabetización de adultos y los años de escolaridad, con un peso de dos tercios para el primero y un tercio para el segundo y los ingresos medidos en dólares en paridad del poder adquisitivo” (p. 49). Así el IDH mide el desarrollo de las regiones en términos de ingreso, salud y educación, los cuales para Sen (2000) “han arrojado de manera sistemática alguna luz sobre la vida real de los individuos, en especial de los relativamente desfavorecidos” (pp. 97-98).
Conocer el desarrollo en Colombia desde la teoría del desarrollo humano permite entender el estado de las regiones, la calidad de vida de los habitantes de su territorio, y si éstas convergen en sus variables sociales.
En ese sentido se han encontrado algunas investigaciones que vale la pena destacar. Entre ellas se encuentra la de Aguirre (2005), quien, utilizando la metodología tradicional y los Kerneles de densidad con variables sociales como la esperanza de vida al nacer, la tasa de analfabetismo y la tasa de mortalidad infantil, encontró convergencia departamental en la primera variable, ya que los departamentos que tenían una menor esperanza de vida al nacer en 1985 fueron los que más crecieron hasta el 2001. Igualmente, encontró convergencia en la tasa de mortalidad infantil, pero no en la tasa de analfabetismo.
León y Ríos (2013) trabajaron con el IDH organizado como datos panel y, para el periodo 1990 al 2010, encontraron divergencia regional en el PIB per cápita, también en la esperanza de vida al nacer por departamentos y en la tasa de matrícula educativa.
De otro lado, Meisel y Vega (2004) trabajaron con la estatura de hombres y mujeres en Colombia en el periodo de 1910 a 1984 utilizando los registros de las cédulas de ciudadanía. Ellos encontraron convergencia beta y sigma, y destacaron como razones de dichas convergencias el mejoramiento de las condiciones laborales de las mujeres y también el “continuo mejoramiento en la nutrición de los colombianos a lo largo del siglo debido al crecimiento económico sostenido” (p. 32).
Las investigaciones citadas han trabajado con variables sociales en Colombia, lo cual aporta luces a la teoría del desarrollo humano; sin embargo, estas investigaciones se han hecho a nivel departamental, sin tener en cuenta que dentro de un mismo departamento pueden existir dinámicas diferentes. Hay pocas investigaciones que utilizan variables a nivel municipal, dentro de las que vale la pena destacar las siguientes: Galvis y Meisel (2000), Jaramillo (2013) y Galvis y Hahn (2015).
Estos últimos autores anotan que “para el caso colombiano muy pocos trabajos han analizado las dinámicas que existen por municipios” (p. 17) y mencionan dos investigaciones: una en la que se trabajó con la proporción municipal de hogares con electricidad y la calidad de vías; y la segunda investigación, perteneciente a Galvis y Meisel (2000), en la que se midió, para 20 ciudades del país, el porcentaje de viviendas con servicios públicos básicos de 1993, las líneas telefónicas por cada 100 habitantes de 1998, la tasa de homicidio 1973-1998, la población municipal en 1998, el porcentaje de población con estudios universitarios 1973, la tasa de crecimiento de los depósitos bancarios reales 1973-1998, entre otros sin encontrar evidencia de convergencia beta ni sigma.
Galvis y Hahn (2015) realizaron un análisis espacial de datos teniendo en cuenta el capital humano y físico de los municipios colombianos, de 1993 al 2012, y encontraron que los municipios más pobres crecieron más que los ricos. Sin embargo, también encontraron que existe un segundo efecto, el cual consiste en que los municipios que se hallan en vecindarios más pobres crecieron menos que sus vecinos. Por consiguiente, los municipios más pobres que limitan con otros municipios pobres crean zonas del territorio pobres, y por ese motivo no hay evidencias de convergencia regional.
En su investigación, Jaramillo (2013) analizó el valor del impuesto de industria y comercio per cápita para 787 municipios colombianos como variable proxy de los ingresos per cápita municipales, utilizando técnicas de econometría espacial, los kerneles estocásticos y el uso de matrices de Markov, y no encontró convergencia regional.
Dado lo anterior, se pretende analizar la convergencia regional desde la teoría del desarrollo humano aportada por Mahbub Ul Haq, Amartya Sen y Martha Nussbaum en la dinámica municipal en el departamento del Meta.
II. Metodología
A. Fuentes de información
El presente estudio mide el desarrollo en 3 indicadores: salud, ingresos y educación. De estos, el primero hace parte de la capacidad “salud corporal” y el tercero de la capacidad de “sentidos, imaginación y pensamiento”, según listado de capacidades de Martha Nussbaum. La elección de dichos indicadores se realizó según la disponibilidad de información de las variables que lo conforman a nivel municipal y según el marco teórico explicado por los exponentes del modelo de desarrollo humano.
Para el indicador de ingresos, se utilizó como variable el ingreso per cápita a nivel municipal. Dicha variable fue construida como proxy de los ingresos municipales (los cuales se tomaron de las ejecuciones presupuestales municipales de la página web del Departamento Nacional de Planeación −DNP−) y divididos en la población de acuerdo con las proyecciones de población del Departamento Administrativo Nacional de Estadísticas (DANE), toda vez que no existe un PIB municipal. El indicador se construyó desde 1985 a 2012 deflactado a pesos del 2012.
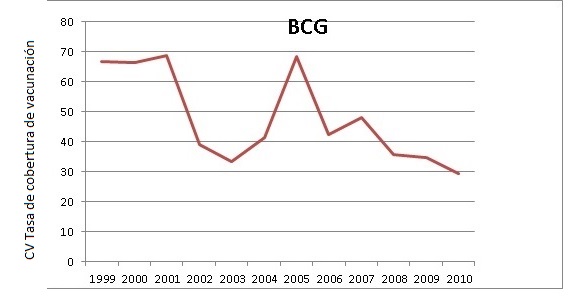
Como dimensiones sociales se tienen los indicadores de salud y educación. En el indicador de salud se utilizó la cobertura de vacunación contra el Bacilos de Calmette y Guérin (BCG) desde 1999 a 2010; esta información fue descargada de la página web del Ministerio de Salud y la Protección Social. Como indicadores de educación se tienen 2 variables: el porcentaje de estudiantes aprobados (serie disponible del 2004-2013 en el DANE), variable que hace parte del indicador de Eficiencia Educativa, y el promedio de los resultados de matemáticas de las pruebas Icfes (también conocido como Saber 11) (serie disponible del 2000-2015 de manera semestral en la base de datos del Instituto Colombiano para el Fomento de la Educación Superior −Icfes−); se tuvo en cuenta el municipio donde se encuentra la Institución Educativa en la cual estaba matriculado cada estudiante que presentó la prueba para el segundo semestre de los años 2000 al 2015.
B. Técnica
La metodología usada contiene 3 partes. Primero se realiza un análisis exploratorio espacial de datos (AEED), con el fin de ubicar a nivel municipal en quintiles, las variables de estudio, clasificándose en municipios muy altos, altos, medios, bajos y muy bajos según los valores que toma la variable por grupo de municipios.
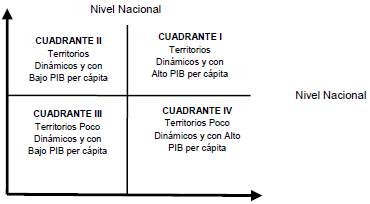
El segundo paso consiste en aplicar el modelo de regresión para determinar si existe convergencia beta absoluta, se estima la regresión y luego se genera el gráfico para analizar el ajuste de los datos al modelo. Posteriormente se completa con el análisis por cuadrantes de desempeño, tal como lo realizaron Carreño y Portilla (s.f.) y Betancourt y Sarmiento (2014), quienes realizan gráficos del modelo separándolo por cuadrantes, como se muestra en el Gráfico 1, el cual relaciona la variable PIB per cápita.
Este análisis puede realizarse para cualquier variable, permitiendo de manera visual confirmar si hay convergencia, tal como lo indica Acevedo (2003): “la forma más elemental de evaluar la beta convergencia absoluta es por medio de la construcción de un diagrama de dispersión entre las tasas medias de crecimiento anual per cápita y el logaritmo del nivel inicial de renta per cápita” (p. 58)
Fuente: Carreño y Portilla (s.f.), rediseñado por los autores
Gráfico 1 Esquema para el análisis por cuadrantes de desempeño económico
En el gráfico, la línea vertical representa la media del logaritmo del nivel inicial de la variable que se esté examinando, y la línea horizontal representa la media de la tasa de crecimiento del periodo de la variable estudiada. Cuando se cruzan la línea vertical y la línea horizontal en el gráfico se forman 4 cuadrantes. Así, el cuadrante I representa las regiones prósperas, ya que superan la media del nivel inicial y la media de la tasa de crecimiento; el cuadrante II es uno de los cuadrantes convergentes, porque relaciona las regiones con niveles iniciales bajos pero que crecieron mucho por encima de la media del periodo; el cuadrante III representa las regiones rezagadas porque iniciaron niveles inferiores de la variable estudiada y durante todo el periodo crecieron muy poco, es decir, por debajo de la media departamental; y el cuadrante IV es una región convergente, porque allí se ubican las regiones que tuvieron niveles iniciales muy altos pero que crecieron por debajo de la media departamental.
En un modelo de regresión, al explorarse los datos mediante gráfico se espera que estos estén cerca de la recta de regresión, si la relación entre las variables es inversa, como lo indica la teoría de la convergencia regional, los datos ajustados a la recta pasarían por los cuadrantes II y IV.
Para Meisel y Vega (2004) “hay convergencia beta cuando el departamento que estaba más rezagado crece más rápido en la variable analizada” (p. 27). Es decir, los rezagados que crecen más rápido se ubicarían en el cuadrante II, y viceversa, los “adelantados” que crecen más lento se ubicarían en el cuadrante IV.
Una vez realizado el análisis gráfico que acompaña las ecuaciones del modelo, el último paso es analizar la convergencia sigma.
Para el AEED se utilizó el software GEODA que permitió localizar a los municipios por quintiles según los datos. Para todas las variables se generan los gráficos del año inicial y del año final.
Al terminar el gráfico de quintiles de cada variable se complementa el análisis con el gráfico condicional, el cual evalúa los cambios dados entre el momento inicial y el momento final de cada variable. Este tipo de gráficos permite analizar si existe convergencia, si hay pocos municipios sobre los 3 mapas ubicados en la diagonal que va desde la esquina inferior izquierda hasta la esquina superior derecha; en otras palabras, permite analizar si hay municipios para la mayoría de los 9 mapas.
En cuanto al modelo de convergencia, es una ecuación que evalúa dos momentos en el tiempo (T1 y T0). Existe convergencia si el beta es negativo y significativo. La variable dependiente es la tasa de crecimiento de la variable de interés Yt/Y0 expresado en logaritmos y dividido entre el número de años transcurridos entre la medición inicial (año 0) y la final (año t). La variable independiente es el logaritmo de la variable en el año cero, por ende, su coeficiente, el Beta, debe ser negativo para indicar convergencia. La ecuación de convergencia absoluta es la siguiente:
donde T es el número de años transcurridos entre el momento t y el momento 0, Y es la variable de interés (cualquiera de las anteriormente descritas), la expresión Yt/Y0 se refiere a una tasa de crecimiento, y μi son los errores del modelo.
La convergencia sigma se trabajará con el coeficiente de variación (una de las medidas de dispersión utilizadas en estadística), el cual se verifica que disminuya en el tiempo, en concordancia con Barón (2003), quien lo utilizó para su estudio.
III. Resultados
A. Análisis exploratorio espacial de datos
Según el quintil en el que se ubiquen, el mapa de quintiles organiza los 29 municipios del departamento del Meta por colores, en tonalidades que van del oscuro al claro: en oscuro se encuentra el quintil superior que contiene los mayores valores de la variable estudiada y en color claro los menores valores, según la variable.
El análisis de cada variable concluye con un mapa condicional (el cual se representa en un gráfico que contiene 9 mapas) que mide en el eje X el año inicial de cada variable por niveles: los 3 mapas ubicados en la columna izquierda representan los municipios de nivel inferior, es decir, los de menores valores según la variable; la columna intermedia refleja valores medios; y la columna derecha refleja los más altos valores de la variable. En el eje Y se mide el año final de cada variable: así, la fila superior representa los de mayor valor, la fila intermedia los de valores medio y la fila inferior los de menor valor; de esta manera cada uno de los 9 mapas representa un nivel para el año inicial y otro nivel en el año final, lo que permite analizar los municipios que cambiaron de niveles en el periodo estudiado.
En los mapas condicionales, los cambios que ocurrieron en los municipios se reflejan en los 9 mapas. Así, se puede trazar una diagonal a lo largo de 3 mapas: el que se encuentra ubicado en el extremo inferior izquierdo, el de la mitad y el del extremo superior derecho; estos representan los municipios que no cambiaron durante el periodo estudiado, debido a que en el año inicial y final registraron niveles bajos de cada variable (mapa del extremo inferior izquierdo), niveles intermedios (mapa de la mitad) y niveles altos (mapa del extremo superior derecho).
Los otros 3 mapas ubicados por encima de la diagonal reflejan los que incrementaron de nivel durante el periodo, y los 3 mapas que se encuentran debajo, los que disminuyeron durante el periodo. Dado lo anterior, se procede a realizar los gráficos analizando los indicadores de salud, ingresos y educación.
1. Indicador de salud
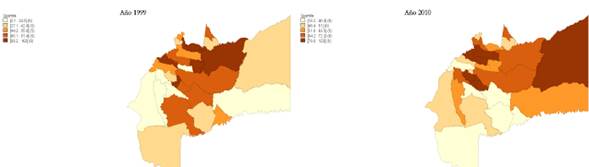
Como indicador de salud se cuenta con la cobertura de vacunación del BCG en el periodo 1999-2010 a nivel municipal en el departamento del Meta. El Gráfico 2 muestra los mapas de quintiles de la Cobertura de Vacunación del BCG a nivel municipal del Meta, el mapa de la izquierda representa la cobertura del año 1999 y el mapa de la derecha la cobertura del año 2010.
Fuente: elaboración propia con base en datos del Ministerio de Salud y la Protección Social
Gráfico 2 Cobertura municipal de vacunación del BCG, 1999 y 2010
En el gráfico se observa una distribución uniforme de la cobertura de vacunación, con mayor concentración de cobertura de vacunación en el norte del departamento que en el sur, situación que cambia para el año 2010, en el cual la cobertura es más homogénea.
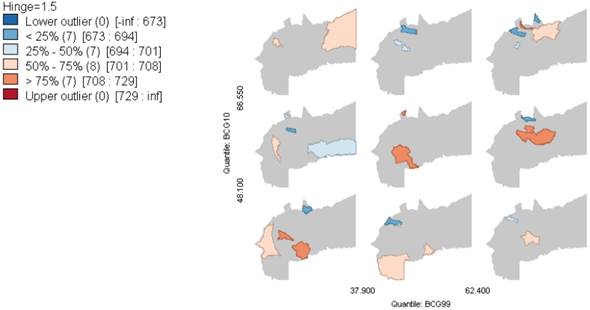
En el Gráfico 3 se observan 9 mapas condicionales que comparan la cobertura de vacunación del BCG de los años 1999 y 2010. En general se observa que los municipios se distribuyen de manera uniforme en los 9 mapas. 11 de los 29 municipios se encuentran ubicados en la diagonal, y los 18 restantes cambiaron de nivel durante el periodo, sin observarse algún patrón de distribución espacial en el departamento.
2. Ingresos per cápita a precios del 2012
En esta sección se observan los mapas de quintiles y condicionales de los ingresos per cápita a precios del 2012, con el fin de ilustrar espacialmente la distribución del ingreso de los 29 municipios del Meta.
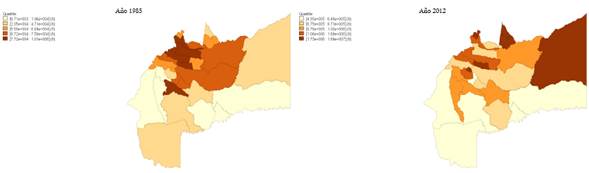
El Gráfico 4 muestra los mapas de quintiles de los ingresos per cápita a precios del año 2012 a nivel municipal del Meta: el mapa de la izquierda representa los ingresos per cápita del año 1985 y el de la derecha los del 2012.
El gráfico muestra que para el año 1985 los municipios con mayores ingresos se encontraban en Villavicencio y sus alrededores, mientras que los municipios más alejados de la capital eran los de menores ingresos per cápita, pero para el año 2012 la situación cambia y se observa que Villavicencio y sus alrededores se ubican en quintil intermedio e inferior, mientras que los municipios del quintil superior en ingresos se encuentran en el norte, centro y oriente del departamento.
Fuente: elaboración propia con base en datos del DNP
Gráfico 4 Ingresos per cápita municipales, 1985 y 2012
En ambos mapas se observa que el sur del departamento se ubicó en los quintiles inferiores de ingreso per cápita durante los años analizados.
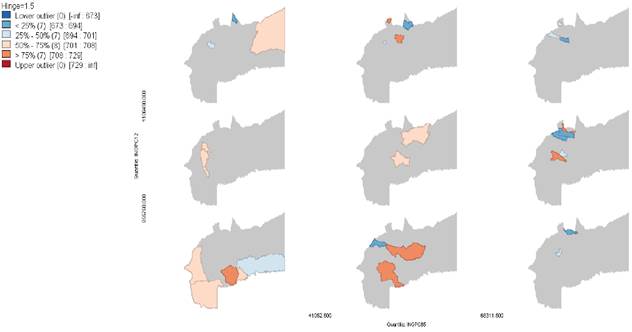
En el Gráfico 5 se observan 9 mapas condicionales en los que se compara el ingreso per cápita municipal de los años 1985 y 2012. En general, se observa que los municipios se distribuyen de manera uniforme en los 9 mapas. De los 29 municipios, 10 se ubican en la diagonal, arriba de ésta se encuentran los municipios que se ubicaron en niveles altos en el último periodo, principalmente, los del norte del departamento, mientras que debajo de la diagonal se encuentran municipios como Villavicencio y sus alrededores, los cuales se ubicaron al final del 2012 con niveles de ingreso per cápita bajo.
3. Indicadores educativos
En esta sección se presentan los resultados de las pruebas Icfes y el porcentaje de alumnos aprobados, variables que componen el indicador.
El Gráfico 6 muestra los mapas de quintiles de los resultados de las pruebas Icfes a nivel municipal del Meta, el mapa de la izquierda representa los resultados de las pruebas Icfes del año 2000 y el de la izquierda los resultados del 2015.
En el gráfico se observa que para el año 2000 no existía una distribución espacial definida de los resultados de las pruebas Icfes, pero para el año 2015 los municipios con altos promedios en estas pruebas tienden a concentrarse en Villavicencio y sus alrededores, mientras que los municipios alejados tienen bajos promedios en las pruebas Icfes.
Fuente: elaboración propia con en datos del DNP
Gráfico 5 Mapa condicional de ingresos per cápita municipales, 1985 y 2012
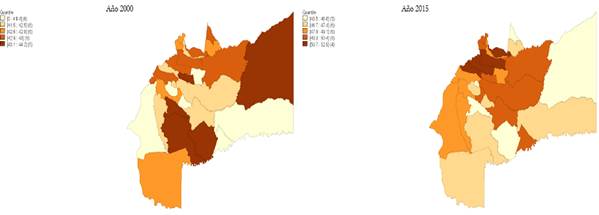
Fuente: elaboración propia con base en datos del Icfes
Gráfico 6 Resultados municipales de las pruebas Icfes, 2000 y 2015
En el Gráfico 7 se observan los 9 mapas donde el eje X mide los resultados de las pruebas Icfes del año 2000 y el eje Y mide los del año 2015. Aquí se puede observar que, de los 29 municipios, 6 se encuentran en la diagonal, mientras que los 23 municipios restantes tuvieron cambios durante el periodo 2000 al 2015, en los que se observa mayor crecimiento en los municipios del norte y centro del departamento, ubicados en los 3 mapas arriba de la diagonal
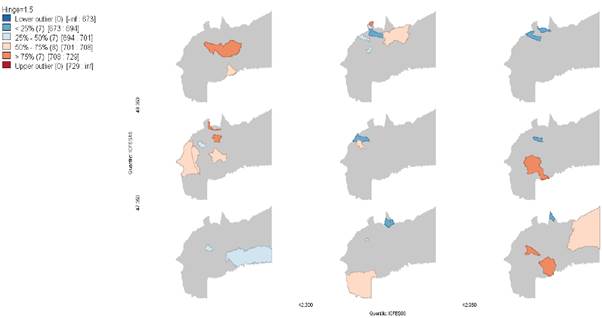
Fuente: elaboración propia con base en datos del Icfes
Gráfico 7 Mapa condicional de los resultados de las pruebas Icfes, 2000 y 2015
El Gráfico 8 muestra los mapas de quintiles del porcentaje de estudiantes del Meta aprobados a nivel municipal. El mapa de la izquierda representa los resultados de los porcentajes de estudiantes aprobados en el año 2004 y el de la derecha los aprobados en el 2013.
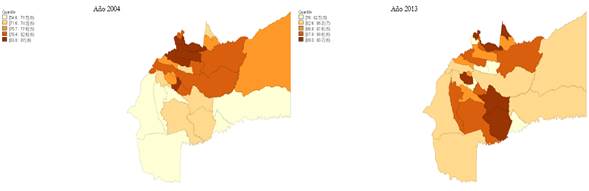
Fuente: elaboración propia con base en datos del DANE
Gráfico 8 Porcentaje municipal de estudiantes aprobados, 2004 y 2013
En el gráfico se observa que para el año 2004 los municipios con mayor porcentaje de alumnos aprobados se encontraban en Villavicencio y sus alrededores, siendo los municipios más alejados de la capital los de menor porcentaje de alumnos aprobados, pero para el año 2013 la situación cambia y no se encuentra una concentración espacial en la distribución de ingresos.
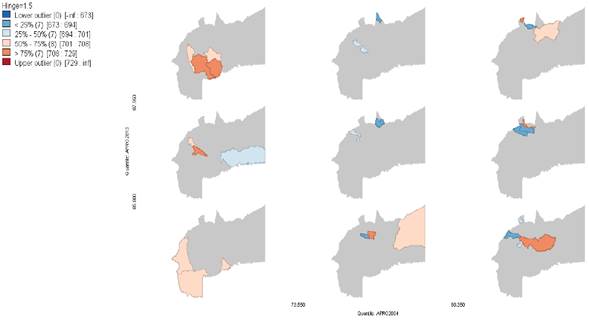
En el Gráfico 9 se observan 9 mapas en los cuales el eje X mide el porcentaje de alumnos aprobados en el año 2004 y el eje Y mide el del 2013. El Gráfico muestra 9 municipios ubicados en la diagonal, los cuales no cambiaron durante todo el periodo. Arriba de la diagonal, en los 3 mapas, se observan los municipios que aumentaron en el periodo, algunos ubicados en el centro y sur del departamento, mientras que los municipios pertenecientes a los mapas de abajo de la diagonal disminuyeron de quintiles en los años indicados, entre los cuales se reconocen los alrededores de Villavicencio y algunos del centro del departamento.
B. Modelo de convergencia regional
Se procede a estimar la regresión con las variables estudiadas, utilizando el software STATA con el fin de hallar y analizar la convergencia beta. Luego se genera el gráfico del modelo estimado y, por último, se realiza el gráfico con el análisis de la convergencia sigma de cada variable.
1. Indicadores de salud
En la Tabla 1 Se presenta la estimación del modelo de convergencia con la variable Cobertura del BCG para el periodo 1999-2010 como se muestra a continuación.
En la Tabla 1 se observa que el estadístico F es significativo, el R2 es alto, el beta es negativo y significativo, lo cual indica convergencia regional. El modelo queda entonces especificado de la siguiente forma:
donde: Y = varBCG, X = LnBCG99 y μi = residuos del modelo.
Leyenda: varBCG (variación o tasa de crecimiento de la cobertura del BCG 1999-2010), LnBCG99 (Logaritmo natural de la cobertura del BCG del año 1999).
En el Gráfico 10 se observa la relación entre el logaritmo de la cobertura de vacunación del BCG del año 1999 en el eje X y su tasa de crecimiento en el eje Y. También se observa que los datos municipales se encuentran cercanos a la línea de tendencia y que la mayoría de los municipios del Meta se encuentran en los cuadrantes II y IV, lo cual corrobora la convergencia regional en el indicador. Como se explicó en la metodología, el cuadrante I representa las regiones prósperas, en las que se encuentra Granada, Barranca de Upía, Acacías y El Castillo. El cuadrante III se representa las regiones rezagadas, como Puerto Concordia.
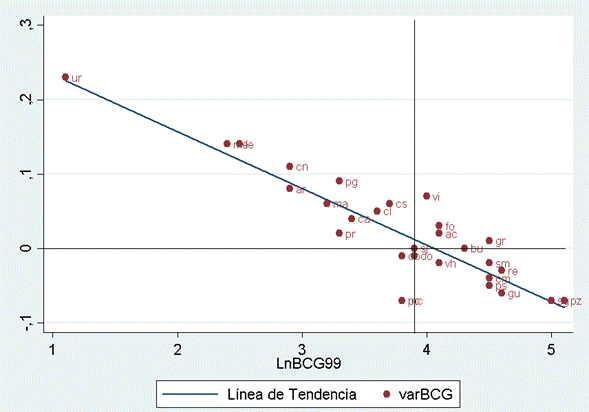
Nota: Las abreviaturas corresponden a los municipios de: Villavicencio (vi), Acacias (ac), Barranca de Upía (bu), Cabuyaro (ca), Castilla la Nueva (cn), Cubarral (cb), Cumaral (cm), El Calvario (cl), El Castillo (cs), El Dorado (do), Fuente de Oro (fo), Granada (gr), Guamal (gu), Mapiripán (ma) Mesetas (me), Macarena (mc), Uribe (ur), Lejanías (le), Puerto Concordia (pc), Puerto Gaitán (pg), Puerto López (pz), Puerto Lleras (ps), Puerto Rico (pr), Restrepo (re), San Carlos de Guaroa (sg), San Juan de Arama (ar), San Juanito (sj), San Martín (sm), Villa Hermosa (vh). Fuente: elaboración propia
Gráfico 10 Modelo estimado de la convergencia de la cobertura BCG, 1999-2010
El Gráfico 11 muestra el coeficiente de variación (cv) de la tasa de la cobertura de vacunación del BCG de 1999 al 2010. Se observa que la disparidad entre municipios del Meta tiende a disminuir en el tiempo, por lo cual se evidencia convergencia sigma para la variable.
2. Indicador de ingresos
En la Tabla 2 Se presenta la estimación del modelo de convergencia con el Ingreso per cápita para el periodo 1985-2012 como se muestra a continuación.
En los ingresos se observa que el estadístico F es significativo y el R2 es bueno, en la estimación, el beta es negativo y significativo, lo que denota una convergencia. El modelo queda especificado de la siguiente manera:
donde: Y = varingpc, X = Lningpc85 y μi = residuos del modelo.
Leyenda: varingpc (variación o tasa de crecimiento del ingreso per cápita 1985-2012), Lningpc85 (Logaritmo natural del ingreso per cápita del año 1985).
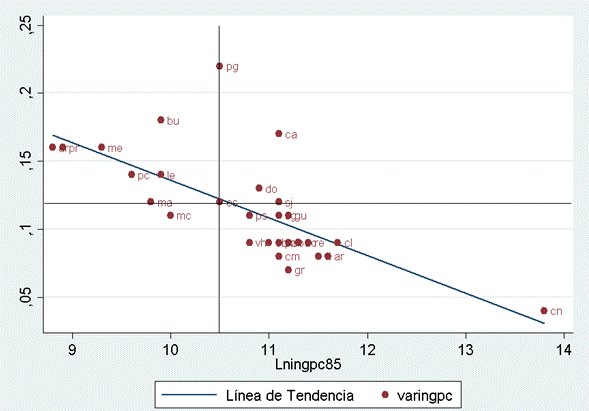
En el Gráfico 12 se observa la relación entre el logaritmo del ingreso per cápita del año 1985 en el eje X y su tasa de crecimiento en el eje Y. También se observa que los datos municipales se encuentran cercanos a la línea de tendencia, y la mayoría de los municipios del Meta se encuentran en los cuadrantes II y IV, lo cual corrobora la convergencia regional en el indicador. Como se explicó en la sección de la metodología, el cuadrante I representa las regiones prósperas, en las que se encuentra Cabuyaro y El Dorado, y el cuadrante III las regiones rezagadas, como La Macarena.
Nota: Las abreviaturas corresponden a los municipios de: Villavicencio (vi), Acacias (ac), Barranca de Upía (bu), Cabuyaro (ca), Castilla la Nueva (cn), Cubarral (cb), Cumaral (cm), El Calvario (cl), El Castillo (cs), El Dorado (do), Fuente de Oro (fo), Granada (gr), Guamal (gu), Mapiripán (ma) Mesetas (me), Macarena (mc), Uribe (ur), Lejanías (le), Puerto Concordia (pc), Puerto Gaitán (pg), Puerto López (pz), Puerto Lleras (ps), Puerto Rico (pr), Restrepo (re), San Carlos de Guaroa (sg), San Juan de Arama (ar), San Juanito (sj), San Martín (sm), Villa Hermosa (vh).
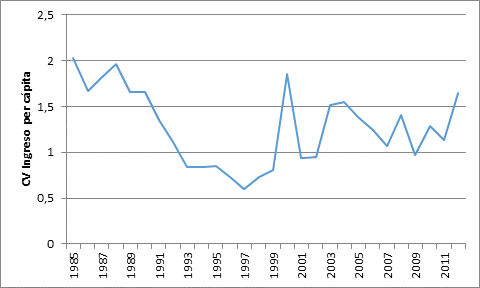
El Gráfico 13 muestra el coeficiente de variación (cv) del ingreso per cápita de 1985 al 2012. Se observa que la disparidad entre los municipios del Meta se redujo entre 1985 y 1997, pero luego comenzó a aumentar hasta el 2012. Se evidencia convergencia sigma hasta 1997 a nivel municipal en el Meta.
3. Indicadores de educación
En la Tabla 3 Se presenta la estimación del modelo de convergencia con los resultados de las pruebas Icfes para el periodo 2000-2015 como se muestra a continuación.
En el indicador de los resultados de las pruebas Icfes del periodo 2000-2015 se observa que el estadístico F no es significativo, el R2 es muy bajo y el beta, aunque tiene signo negativo, no es significativo, lo cual no se puede concluir como un proceso de convergencia. Sin embargo, para el año 2000 no se cuentan con datos de Mapiripán, La Uribe y Puerto Concordia, los cuales tienen datos a partir del 2004. Por lo anterior, para examinar si existe un proceso de convergencia regional se procede en la tabla 4 a realizar la regresión entre el 2004 y el 2015. Este modelo queda especificado de la siguiente forma:
donde: Y = varicfes0015, X = Lnicfes00 y μi = residuos del modelo.
Leyenda: varicfes0015 (variación o tasa de crecimiento del promedio de las pruebas Icfes 2000-2015), Lnicfes00 (Logaritmo natural de las pruebas Icfes del año 2000).
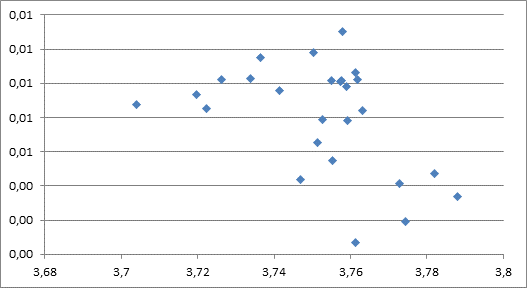
En el Gráfico 14 se observa la relación entre el logaritmo de los resultados de las pruebas Icfes del año 2000 en el eje X y su tasa de crecimiento promedio entre 2000 y 2015 en el eje Y. En el gráfico se puede observar que los datos se encuentran alejados entre sí y no se evidencia ninguna línea de tendencia, así mismo, presentan forma de nube de puntos, lo cual evidencia que no hay relación entre ambas variables.
Fuente: elaboración propia
Gráfico 14 Modelo estimado de los resultados de las pruebas Icfes, 2000-2015
En la Tabla 4 se observa la salida de la estimación de los resultados de las pruebas Icfes del 2004 al 2015.
En la anterior tabla el estadístico F sigue siendo no significativo, el R2 es bajo y el coeficiente beta sigue siendo negativo, pero sin ser significativo, lo cual no evidencia resultado de convergencia regional. El modelo queda especificado de la siguiente forma:
donde: Y = varicfes0415, X = Lnicfes04 y μi = residuos del modelo.
Leyenda: varicfes0415 (variación o tasa de crecimiento del promedio de las pruebas Icfes 2004-2015), Lnicfes04 (Logaritmo natural de las pruebas Icfes del año 2004).
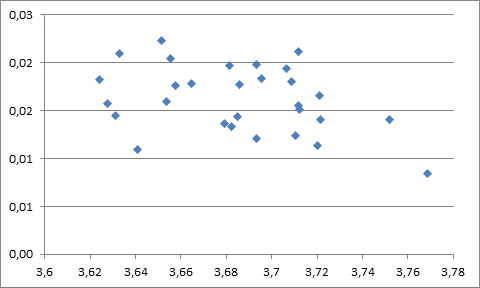
En el Gráfico 15, se relaciona en el eje X el nivel inicial de los resultados de las pruebas Icfes en el año 2004 en logaritmos, y en el eje Y la tasa de variación de dichos resultados del 2004 al 2015. Se observa una ligera relación inversa entre ambas variables, pero no se alcanza a evidenciar convergencia regional en el indicador.
Fuente: elaboración propia
Gráfico 15 Modelo estimado de los resultados de las pruebas Icfes, 2004-2015
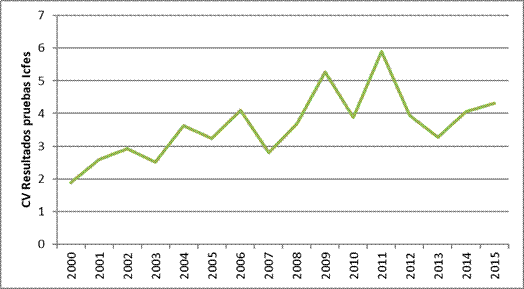
El Gráfico 16 muestra el coeficiente de variación (cv) de los resultados de las pruebas Icfes de los años 2000 al 2015. Se observa que la disparidad entre municipios del Meta tiende a aumentar en el tiempo, por lo que no se evidencia convergencia sigma.
En la Tabla 5 se observa la salida de la estimación de los estudiantes aprobados en el periodo 2004-2013.
En la anterior tabla, el estadístico F, que es la prueba conjunta, muestra ser significativo, el R2 es alto y representa un 67,23%, el coeficiente de la regresión es negativo y significativo, lo cual evidencia convergencia regional. El modelo queda especificado de la siguiente forma:
donde: Y = varaprobados, X = Lnaprobados04 y μi = residuos del modelo.
Leyenda: varaprobados (variación o tasa de crecimiento del porcentaje de alumnos aprobados 2004-2013), Lnaprobados04 (Logaritmo natural del porcentaje de alumnos aprobados del año 2004).
En el Gráfico 17 se observa la relación entre el logaritmo del porcentaje de alumnos aprobados en el año 2004 en el eje X y su tasa de crecimiento en el eje Y. También se observa que los datos municipales se encuentran cercanos a la línea de tendencia y que la mayoría de los municipios del Meta se encuentran en los cuadrantes II y IV, lo cual corrobora la convergencia regional en el indicador. Como se explicó en la sección de la metodología, el cuadrante I representa las regiones prósperas, en las que se encuentran los municipios del Cabuyaro y El Dorado. No se observan datos en el cuadrante III del gráfico.
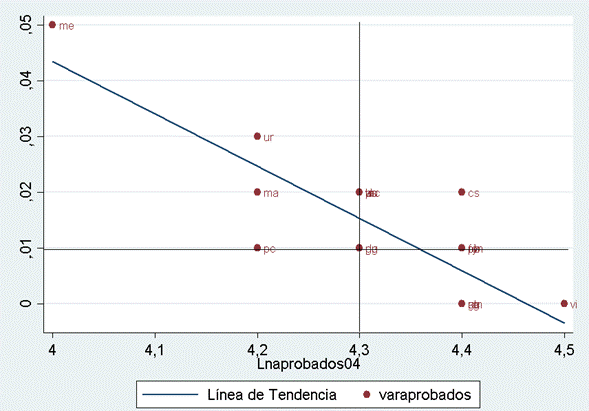
Nota: Las abreviaturas corresponden a los municipios de: Villavicencio (vi), Acacias (ac), Barranca de Upía (bu), Cabuyaro (ca), Castilla la Nueva (cn), Cubarral (cb), Cumaral (cm), El Calvario (cl), El Castillo (cs), El Dorado (do), Fuente de Oro (fo), Granada (gr), Guamal (gu), Mapiripán (ma) Mesetas (me), Macarena (mc), Uribe (ur), Lejanías (le), Puerto Concordia (pc), Puerto Gaitán (pg), Puerto López (pz), Puerto Lleras (ps), Puerto Rico (pr), Restrepo (re), San Carlos de Guaroa (sg), San Juan de Arama (ar), San Juanito (sj), San Martín (sm), Villa Hermosa (vh). Fuente: elaboración propia
Gráfico 17 Modelo estimado del porcentaje de alumnos aprobados, 2004-2013
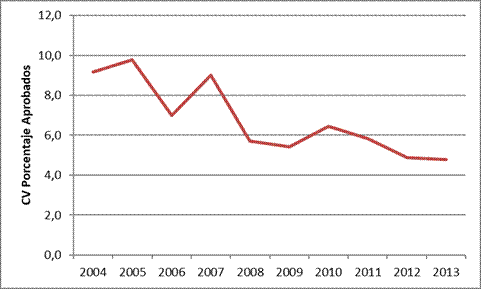
El Gráfico 18 muestra el coeficiente de variación (cv) del porcentaje de alumnos aprobados el 2004 y el 2013. Se observa que la disparidad entre municipios del Meta tiende a reducirse en el tiempo, por lo que se evidencia convergencia tipo sigma.
Discusiones y conclusiones
El análisis exploratorio espacial de datos (AEED) mostró que en los años 1999 y 2010 los municipios del Meta en el indicador de salud tenían una distribución más o menos uniforme, con una ligera mayor cobertura de vacunación en el norte del departamento que en el sur, situación que disminuye para el último año. Por otro lado, el modelo de regresión mostró que existe convergencia regional para la cobertura de vacunación, lo que significa que los municipios que tenían niveles iniciales de cobertura bajo (año 2004), fueron los que más aumentaron en cobertura con respecto a los que tenían niveles iniciales altos.
Respecto a los ingresos, el análisis espacial mostró cómo los municipios cercanos a Villavicencio en 1985 eran los de más altos ingresos per cápita, y los que estaban al sur y al oriente del departamento eran los más pobres. Sin embargo, para el 2012, cambió la situación y varios municipios ubicados lejos de Villavicencio tuvieron los ingresos per cápita más altos, aunque se encontraron algunas excepciones, en especial al suroriente, donde estos municipios se mantuvieron con bajos ingresos. En el análisis de regresión se observa que existió convergencia regional en el periodo estudiado, lo que significa que los municipios con niveles iniciales de ingresos per cápita bajos fueron los que más crecieron, respecto a los que tuvieron niveles iniciales de ingresos per cápita altos.
En el indicador educativo, el análisis espacial de los resultados de las pruebas Icfes mostró que para el año 2000 los promedios eran más o menos homogéneos en el departamento, pero para el año 2015 los promedios altos tienden a concentrarse en Villavicencio y sus alrededores. Aunque no se evidencia convergencia regional en el modelo, sí se tiene un signo negativo en el coeficiente, y la convergencia sigma aumenta en el periodo.
Para la variable de porcentaje de alumnos aprobados, el análisis espacial mostró cómo en el año 2004 los municipios con mayor porcentaje eran los cercanos a Villavicencio, pero para el año 2013, esta situación cambia y se encuentra que en diferentes zonas del departamento hay municipios con porcentajes altos. El modelo de regresión evidenció convergencia regional en el indicador, en el cual los municipios que inicialmente tenían porcentajes bajos de alumnos aprobados fueron los que más aumentaron en dicho porcentaje, en comparación con los municipios con porcentajes iniciales altos.
Los resultados obtenidos en materia de salud, ingresos y educación permiten responder la pregunta de investigación, pues se evidencia convergencia regional desde el enfoque del desarrollo humano; la única variable que no registró convergencia regional fueron los resultados en las pruebas Icfes, que tuvo el signo negativo esperado por la teoría, pero no fue significativo.
También se observa que el departamento del Meta ha tenido avances en materia de desarrollo humano, pues algunas regiones anteriormente pobres pudieron crecer más rápido y los municipios que tuvieron niveles bajos en salud y educación mejoraron.
Lo anterior lleva a concluir que se han generado avances en las capacidades de los habitantes del departamento del Meta, pues de manera general ha llegado el desarrollo incluso a las zonas alejadas de la capital y ha mejorado la calidad de vida de su población. No obstante, también se observa que este desarrollo no es homogéneo y algunos municipios como La Uribe, La Macarena, Vistahermosa y sus alrededores no mejoraron mucho en desarrollo humano, lo cual deberá permitir a los hacedores de política dar un tratamiento especial a esta zona para lograr avances en materia de salud, ingresos y educación.