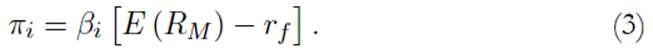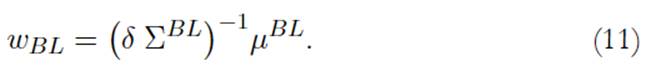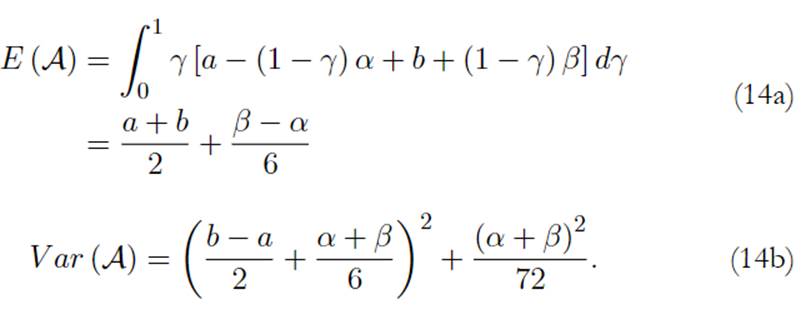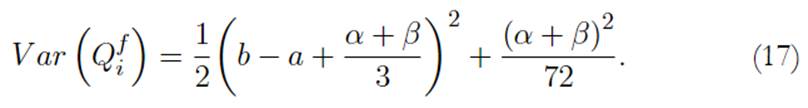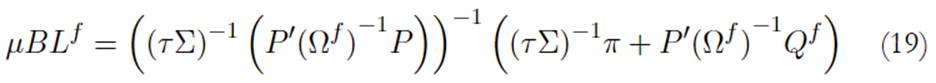Spanish (pdf)
Article in xml format
Article references
Automatic translation
Send this article by e-mail
Cited by SciELO 
Cited by Google 
Similars in
SciELO 
Similars in Google 
Permalink
Introducción
El modelo Black-Litterman (BL) proporciona un marco bayesiano intuitivo para la selección de portafolios de inversión al combinar las opiniones subjetivas (views) con la solución del modelo de valoración de activos de capital (CAPM) o modelo de equilibrio y del modelo media- varianza (MV). Esta novedad del modelo BL, les permite a los inversionistas gestionar los portafolios de inversión de forma prospectiva (Kolm et al., 2014). Para ello, se incorporan las views de los inversionistas como una entrada en el proceso de optimización del portafolio, lo cual permite romper con la dependencia exclusiva a los datos históricos que tiene el portafolio MV1 2, como fue señalado por Black y Litterman (1990, 1991, 1992).
Este enfoque bayesiano ha presentado un crecimiento notable en las últimas dos décadas. También se encuentran contribuciones importantes en los trabajos de He y Litterman (1999, 2002), Idzorek (2007), Meucci (2008, 2009), entre otros. Sin embargo, aún persisten limitaciones en el enfoque para la selección óptima de portafolios, sobre todo en el tratamiento de la incertidumbre de los retornos esperados, dados los supuestos de normalidad y linealidad como señalan Kolm et al. (2021). En la formulación original del modelo BL, se asume que la distribución de los retornos de los activos es normal multivariante, mientras que las views se asumen lineales. En este ámbito, los autores encuentran algunos avances que se han dado en los campos de la “optimización robusta” y la lógica difusa y, su incorporación al modelo BL. En ambos casos se busca mitigar el impacto de la especificación de los parámetros en la construcción del portafolio óptimo.
Este artículo se centra en la incorporación de lógica difusa al modelo BL. Algunas contribuciones importantes en este campo se identifican en Gharakhani y Sadjadi (2013) y Fang et al. (2018). Cabe resaltar que, aunque es amplia la literatura de lógica difusa aplicada al portafolio MV, son escasos los trabajos donde se realiza una implementación de esta al contexto del modelo de BL, como señalan Fang et al. (2018). En el ámbito de aplicaciones de lógica difusa en teoría de portafolio MV, se encuentran los trabajos de Tanaka y Guo (1999), Tanaka et al. (2000), Arenas et al. (2001), Wang y Zhu (2002), Lin et al. (2005), Bilbao et al. (2006), Fang et al. (2006), Lacagnina y Pecorella (2006), Huang (2006), Gupta et al. (2008), Lawrence et al. (2009), Li et al. (2010), Zhang et al. (2014), Li y Yi (2019), Yang et al. (2021) y Pahade y Jha (2021), entre otros.
De igual forma, algunos trabajos han empleado la lógica difusa en un marco de programación multiobjetivo. En este campo se resaltan los desarrollos de Gupta et al. (2021), Gong et al. (2021) y Franco (2020). Estos desarrollos han llevado a la consolidación de un nuevo campo de investigación en la teoría de portafolio conocido como selección difusa de portafolios, como señalan Li y Yi (2019). Además, Franco (2020) incorpora la lógica difusa en un ejercicio comparativo para los modelos MV y BL, al desarrollar una extensión del trabajo de Gharakhani y Sadjadi (2013), quienes cuantificaron las views del modelo BL mediante una representación canónica de números difusos. Los autores implementaron un modelo de optimización mediante programación lineal multiobjetivo que toma como referencia diferentes criterios de desempeño e índices de mercado, y permite superar la incertidumbre asociada a la especificación de las views en el modelo.
En esta misma línea, Fang et al. (2018) desarrollan una implementación del modelo BL con views difusas en dos aplicaciones diferentes para el mercado financiero de China. En esta implementación redefinen la estimación de los retornos esperados y la matriz de incertidumbre, y proponen una formulación de las views del inversionista mediante conjuntos difusos usando una función de pertenencia triangular. Los resultados muestran una ventaja notable de este enfoque frente al modelo BL tradicional ya que, mediante esta formulación, las views incorporan más información y se logra medir mejor la incertidumbre.
El presente artículo realiza una implementación del modelo BL con views difusas. Para ello, los retornos esperados, las views y la matriz de incertidumbre del modelo BL se redefinen al usar una función de pertenencia trapezoidal. De esta forma, no solo se implementa un modelo robusto para la selección óptima de portafolios de inversión, siguiendo el enfoque bayesiano en el marco del modelo BL, sino que se pueden superar algunas de las limitaciones al usar la lógica difusa que incorpora información adicional en las views y en la matriz de incertidumbre. Esta formulación contribuye a superar los hechos latentes de subjetividad que recaen sobre el modelo BL, así como las limitaciones del modelo MV. La aplicación se realiza para un portafolio conformado por las acciones del índice colombiano MSCI COLCAP3. Los resultados muestran una mejora en el desempeño -fuera muestra- del portafolio, en comparación con el modelo BL tradicional y el portafolio MV.
El artículo está organizado en cinco secciones que incluyen esta introducción. En la primera sección se presentan las formulaciones teóricas para la construcción de un portafolio óptimo siguiendo los desarrollos del modelo media-varianza y el modelo BL. En la sección II se presenta la incorporación de la lógica difusa en su formulación. En la tercera sección se desarrolla una aplicación que incorpora tanto el ejercicio de optimización como la evaluación de desempeño. Finalmente, se presentan las conclusiones del trabajo.
I. Revisión de literatura
La teoría moderna de portafolio (TMP) representa uno de los desarrollos más importantes de la ciencia financiera al aportar soluciones óptimas y diversificadas para inversiones conformadas por activos riesgosos. Al contemplar la naturaleza estocástica de los retornos de los activos financieros, Markowitz (1952, 1959) formula una solución de equilibrio para la selección de un portafolio óptimo al considerar el retorno esperado de los activos financieros -por ejemplo, acciones- y su medida de riesgo, bajo la presunción de normalidad en los retornos (Romero, 2010).
La formulación de Markowitz representa el inicio de un campo de investigación que extiende a la valoración de activos financieros, donde se identifican los trabajos seminales de Sharpe (1964), Lintner (1965) y Mossin (1966). En este marco, la solución óptima de portafolio se vincula al portafolio tangente, el cual representa la mejor asignación de activos riesgosos en presencia del activo libre de riesgo. Todo este desarrollo se conoce como el enfoque media-varianza (MV). En términos generales, el problema de optimización MV puede ser descrito mediante la maximización de una relación trade-off entre el retorno esperado del portafolio: E (R P ) = µ ′ w y su varianza: σ 2 = w ′ Σw.
donde λ se define como la medida de aversión al riesgo, w es el vector (n x 1) de pesos de los activos que componen el portafolio, µ es el vector (n x 1) de retornos esperados de los activos (E (R i )), Σ es la matriz (n x n) de covarianzas y 1 denota un vector (n x 1) de unos. Un supuesto importante del enfoque MV es que asume que µ y Σ son conocidos.
Una formulación adicional del problema descrito en la ecuación (1), es el que incorpora restricciones en el signo de los pesos. Por ejemplo, si las ventas en corto están prohibidas en el mercado, se puede agregar la restricción w >= 0. Además, la formulación de optimización del portafolio MV se resuelvecomo un problema determinístico (Kolm et al., 2021) utilizando programación cuadrática -QP, por las siglas en inglés-. La solución óptima de este problema, que es equivalente a la optimización del coeficiente de Sharpe (ϑ), comprende el insumo para la construcción del modelo de valoración de activos de capital -CAPM, por sus siglas en inglés-, el cual viene determinado por la ecuación (2).
donde, E (R i ) es el retorno esperado del activo i, E (R M ) es el retorno esperado del portafolio de mercado y r f es la tasa de interés libre de riesgo.
Además,
es la medida de riesgo sistemático de cada activo i, donde σ
2
M es la varianza del portafolio de mercado. Si se define π
i
como el
retorno de equilibrio del activo i, expresado como el exceso respecto a la tasa
r f , la ecuación (2) puede expresarse como:
Al reemplazar los componentes de la medida de riesgo β i , se tiene:
Ahora, como E (R
M
) se obtiene al ponderar los n activos de mercado teniendo en cuenta su peso w
i
, es decir,
entonces la ecuación (4) puede ser escrita como:
En forma matricial, la ecuación (5) se expresa como sigue:
donde,
. De esta forma, se obtienen los retornos esperados de equilibrio o retornos implícitos. Al despejar el vector w de la ecuación (6), se encuentra la solución para el portafolio MV: w
MV
= (δΣ)
−1
π
i
. Una formulación alternativa para esta solución de equilibrio, también conocida como optimización inversa, se encuentra en Bertsimas et al. (2012).
El modelo BL, introducido por Black y Litterman (1990,1991, 1992), parte de esta solución del modelo MV o solución de equilibrio e incorpora información exógena, tal como las creencias o puntos de vista (views) subjetivas del inversionista o del gestor del portafolio. Estas views representan aquellas expectativas que tiene el inversionista sobre el desempeño futuro del activo. De esta forma, el modelo BL proporciona mayor flexibilidad al combinar el equilibrio del mercado con las views del inversor.
El supuesto subyacente del modelo BL es que el retorno esperado del activo i debe ser consistente con la solución de equilibrio del mercado, salvo que el inversionista tenga una view específica para el retorno esperado. La incorporación de esta información, a través de las views junto con la incertidumbre, representa un marco de actualización bayesiana que permite corregir limitaciones del modelo MV, dada la dependencia exclusiva de este a la información histórica.
Black y Litterman (1990, 1991) asumen que la distribución de los retornos esperados de los activos viene dada por: E (E) ∼N (π, τ Σ), donde µ es el vector (n x 1) de retornos esperados que, a diferencia del enfoque MV, se asume desconocido.
Las views del inversionista pueden expresarse como P µ ∼ N (Q, Ω) donde P ∈ Rk×n asocia al activo i involucrado por la view k, Q ∈ Rk describe el retorno esperado de la view y Ω ∈ Rk×k es su matriz de covarianzas. Además, la matriz Ω puede ser estimada como sigue:
De esta forma, las views del inversionista pueden expresarse como sigue:
donde, ε ∈ Rk×1 es un vector de los errores con media cero y varianza Ω, tal que ε∼N (0, Ω). Si los inversionistas tienen confianza total en sus creencias, entonces cada view queda expresada como PE (R) = Q, de lo contrario debe representarse como indica la ecuación (8). De acuerdo con lo anterior, los retornos esperados en el modelo BL vienen dados por:
con matriz de covarianzas igual a:
Además, los pesos óptimos del portafolio BL vienen dados por:
De esta forma, a partir de la creación un portafolio de equilibrio inicial y, mediante la incorporación de las views, se obtiene un portafolio óptimo que considera no solo la información histórica, sino las expectativas sobre el desempeño futuro de los activos. Sin embargo, como señalan Kolm et al. (2021), la incertidumbre en las views representa el elemento más abstracto y difícil de especificar del modelo BL. Además, como afirman Fang et al. (2018), el modelo BL representa una solución simple de este problema ya que trata la incertidumbre solo como un parámetro, lo cual genera pérdida de información. Para superar esta limitación, se propone una extensión del trabajo de Fang et al. (2018) para incorporar views difusas. Este desarrollo se presenta a continuación.
II. Metodología
La formulación del problema de selección de portafolio en el enfoque MV requiere la estimación de los retornos esperados de los activos y de sus covarianzas. Estas estimaciones representan la “mejor” estimación sobre el desempeño futuro de los activos y presentan el insumo para la construcción del portafolio óptimo. Desde el enfoque bayesiano, el modelo BL incorpora una actualización subjetiva de esta estimación para el inversionista, teniendo en cuenta el conjunto de información disponible al momento de toma de decisión. Sin embargo, como afirman Gupta et al. (2008) y Fang et al. (2018), este conjunto de información puede ser interpretado de manera diferente por todos los inversionistas en el mercado. Por ello, la construcción del portafolio óptimo se convierte en una elección de un conjunto difuso con interpretaciones subjetivas, tanto en la formulación de la función objetivo - a optimizar- como en las restricciones.
Esta reformulación del problema se da gracias a los desarrollos de la lógica difusa4. En este ámbito, Fang et al. (2018) plantearon conjuntos difusos para las views que pueden tratar de manera eficiente el problema de la incertidumbre. Aunque existen diferentes clases de conjuntos -o números- difusos dependiendo de su función de pertenencia, los más comunes son aquellos asociados a las funciones de pertenencia triangular y trapezoidal (Gupta et al., 2008).
Para cualquier conjunto clásico A se define su función de pertenencia, también llamada función característica o función de discriminación, como:
Es decir, esta función relaciona cada elemento del conjunto de referencia X con el conjunto {0, 1} , µ A : X → {0, 1} , y muestra la pertenecía o no del elemento x al conjunto A. En el caso de un conjunto difuso B, la función de pertenencia es de la forma µ B : X → [0, 1] e indica que la frontera de un conjunto difuso es vaga, comparada con la de un conjunto clásico. El soporte de un conjunto difuso B es el conjunto { x ∈ X | µ B (x) > 0 } y los α- cortes del conjunto se definen como A α = { x ∈ X | µ B (x) ≥ α } con α [0, 1]. Además, un conjunto difuso se dice convexo si todos los α-cortes son conjuntos convexos.
Un número difuso es un conjunto difuso convexo y normalizado -con máximo valor de la función de pertenencia igual a 1-, cuya función de pertenencia se define sobre los reales. Para efectos de este artículo, se adopta la función de pertenencia trapezoidal como sugieren Li y Yi (2019), teniendo en cuenta que la función de pertenencia triangular puede verse como un caso particular de la función de pertenencia trapezoidal. Además, la función trapezoidal permite la inclusión de un conjunto de valores en el soporte con el mismo nivel de pertenencia.
En este contexto, se define la view del inversionista como un número difuso trapezoidal representado como A = (a, b, α, β) con función de pertenencia:
donde, [a, b] es el intervalo de tolerancia, con ancho izquierdo de tamaño a − α > 0 y ancho derecho de tamaño β − b > 0, como muestra la Figura 1.
Si A es un número difuso, el conjunto difuso de nivel γ de A es definido por [A]y = {x ∈ R | A (x) ≥ γ}, donde:
Carlsson et al. (2002) muestran que el valor esperado y la varianza -en el sentido clásico- del número trapezoidal A vienen dado por:
Por tanto, el retorno esperado del portafolio, E (R p ), puede ser estimado como5:
Y su varianza, σ 2 , por:
De forma análoga y, extendiendo el desarrollo de Fang et al. (2018), para una función de pertenencia trapezoidal se encuentra que el inversionista puede expresar una view relativa de que el retorno esperado de la acción A superara el retorno esperado de la acción B, la cual viene determinada por
. De esta forma, se obtiene:
Entonces, la matriz diagonal de la ecuación (7), puede ajustarse mediante la expresión:
Como resultado, el retorno esperado y las covarianzas del modelo BL se ajustan al tomar views difusas. De esta forma, las fórmulas (9) y (10) vienen dadas ahora por:
Finalmente, el problema de optimización del modelo BL con views difusas (BL f ), puede resolverse mediante programación cuadrática, como sugiere Fang et al. (2018). Por tanto, de forma análoga a la ecuación (11) se tiene:
En la siguiente sección, se propone una aplicación de este desarrollo del modelo BL f para el mercado de valores colombiano.
III. Aplicación y discusión de resultados
En esta sección se implementa el desarrollo propuesto del modelo BL f para la selección de un portafolio óptimo tomando el mercado de valores colombiano. El desempeño -dentro y fuera de muestra- de este portafolio se compara con los resultados del modelo BL tradicional y con el portafolio MV. Además, se toma como índice bursátil de referencia el COLCAP, el cual está conformado por las 25 acciones con mayor volumen de negociación en la Bolsa de Valores de Colombia (BVC). El periodo de análisis dentro de muestra comprende desde enero de 2015 hasta diciembre de 2019, mientras que el periodo fuera de muestra6 se toma para enero de 2020 a diciembre de 2020. La muestra de datos se construye tomando los precios de cierre ajustados de las acciones y del índice de referencia con periodicidad mensual. Además, del total de acciones del índice se realiza un filtrado de estas tomando los siguientes criterios:
Si la empresa emite acciones ordinarias y preferenciales, solo se toma una de ellas considerando la de mejor retorno promedio
Se omiten aquellas acciones que no registran precios para número mayor de 3 días
De esta forma, no solo se consideran aquellas acciones de mayor volumen de negociación, sino que se evita tomar dos acciones del mismo emisor. A partir de este filtrado se obtienen un total de 10 acciones con un total de 600 observaciones con periodicidad mensual para el periodo dentro de muestra y 120 observaciones para el periodo fuera de muestra. Para el periodo de análisis se encuentra una r f = 0,044. Cabe señalar que todas las tasas de retorno, incluida la r f se toman como tasas continuas. La Tabla 1 presenta la información resumen de la muestra.
Tabla 1 Información de la muestra de acciones seleccionadas (datos anualizados)
| Periodo dentro de muestra | Periodo fuera de muestra | ||||
| Acción | Retorno promedio | Desviación estándar | Acción | Retorno promedio | Desviación estándar |
| BCB | -0,0493 | 0,2988 | BCB | 0,042 | 0,2039 |
| ECO | -0,1315 | 0,3761 | ECO | 0,6037 | 0,2761 |
| SIS | 0,1181 | 0,3113 | SIS | -0,0719 | 0,2552 |
| ARG | 0,1018 | 0,2556 | ARG | 0,0958 | 0,2557 |
| DVI | -0,0531 | 0,2804 | DVI | 0,0513 | 0,2779 |
| CCB | 0,1583 | 0,2509 | CCB | -0,1071 | 0,1486 |
| EXI | 0,006 | 0,2605 | EXI | 0,5536 | 0,4901 |
| ANC | 0,0042 | 0,1911 | ANC | -0,0017 | 0,2654 |
| ETB | 0,1812 | 0,3233 | ETB | -0,1689 | 0,2528 |
| ISA | -0,2193 | 0,22 | ISA | 0,0077 | 0,2137 |
| COLCAP | 0,0188 | 0,1423 | COLCAP | -0,1451 | 0,3936 |
Fuente: elaboración propia con datos de Bloomberg.
Aunque el retorno esperado es positivo para la mayor parte de las acciones seleccionadas durante los periodos de análisis dentro y fuera de muestra, el desempeño del COLCAP fue negativo. Para el 2020, se encuentra una fuerte caída en el retorno del portafolio (-0,1451) y un aumento considerable de la volatilidad (0,3936).
Ahora, para la formulación del modelo BL, se consideran las siguientes views -absolutas y relativas- que involucran a las acciones: SIS, ARG, CCB, EXI, ANC, ETB e ISA. Para la formulación de estas views se consideran aquellas medidas y estrategias de fortalecimiento y mayor presencia en el mercado (SIS, EXI, ANC, ETB), así como los resultados de aquellos proyectos de expansión que estas tienen (ARG, CCB, ISA) a cierre del año 2019.
Views absolutas:
ISA: Retorno de 0,21
Views relativas:
Se espera un retorno de CCB superior a ETB en 0,05 Se espera un retorno de EXI superior a ARG en 0,07 Se espera un retorno de ANC superior a SIS en 0,04
La formulación de estas views se consolida en las matrices P y Q, como se muestra a continuación:
Además, se toma como parámetro τ = 0, 05, el cual representa el nivel de confianza en las views que se han formulado. Con esta información se obtiene la matriz Ω como indica la ecuación (7).
Cabe señalar que la formulación de estas views difiere bastante del resultado observado en el periodo fuera de muestra. Aunque las expectativas de desempeño futuro son positivas para estas acciones, se encuentran fuertes caídas, especialmente en las acciones CCB y ETB.
Finalmente, se definen las views difusas para el modelo BL (BL f ) tomando la función de pertenencia trapezoidal.
Todas las views difusas se toman con valores positivos entre los límites inferior y superior, aunque estas no son simétricas. Para esta formulación, se toma β i − b i > a i− α i . Además, se asume que todas ellas no son correlacionadas.
A. Comparación de los portafolios óptimos: MV, BL y BL con views difusas
El portafolio óptimo MV se construye a partir del problema indicado en la ecuación (1), donde se incorpora la restricción de cortos (pesos negativos). De igual forma, se implementa la formulación para los modelos BL y BL f , como se indica entre las ecuaciones (9) a (11) y (19) a (21). Los resultados de estos portafolios óptimos se presentan en las Tablas 2 y 3.
Tabla 2. Pesos óptimos
| Acción | MV (w MV ) | BL (w BL ) | BL f (wBLf ) |
| BCB | 0,0000 | 0,0000 | 0,0000 |
| ECO | 0,0000 | 0,0000 | 0,0000 |
| SIS | 0,0000 | 0,0000 | 0,0000 |
| ARG | 0,0000 | 0,0000 | 0,0000 |
| DVI | 0,0000 | 0,0000 | 0,0000 |
| CCB | 0,6053 | 0,3679 | 0,3121 |
| EXI | 0,0000 | 0,0787 | 0,1107 |
| ANC | 0,0000 | 0,3975 | 0,3925 |
| ETB | 0,3947 | 0,0000 | 0,0000 |
| ISA | 0,0000 | 0,1559 | 0,1848 |
Fuente: elaboración propia.
Tabla 3. Resultados de los portafolios
| Periodo dentro de la muestra | Periodo fuera de la muestra | ||||||
| MV | BL | BL f | MV | BL | BL f | ||
| E (R P ): | 0,1673 | 0,0262 | 0,0112 | E (R P ): | -0,1315 | 0,0047 | 0,0286 |
| σ P : | 0,1685 | 0,1892 | 0,1987 | σ P : | 0,2356 | 0,1862 | 0,183 |
| ϑ: | 0,5234 | 0,1408 | 0,0613 | ϑ: | -1,0417 | 0,0251 | 0,1440 |
Fuente: elaboración propia.
Los resultados confirman no solo los problemas del modelo MV, respecto a la alta concentración del portafolio en pocos activos. En el portafolio MV solo las acciones CCB y ETB quedan con participaciones, las cuales -además- son elevadas. Esta situación cambia para los portafolios BL y BL f , al aumentar el número de activos (CCB, EXI, ANC, ISA). Asimismo, se encuentra una mejora notable en las medias de riesgo (σ P ) de estos dos portafolios, aunque se identifica una caída importante en el coeficiente de Sharpe (ϑ) de 0,5234 a 0,1408 y 0,0613, respectivamente.
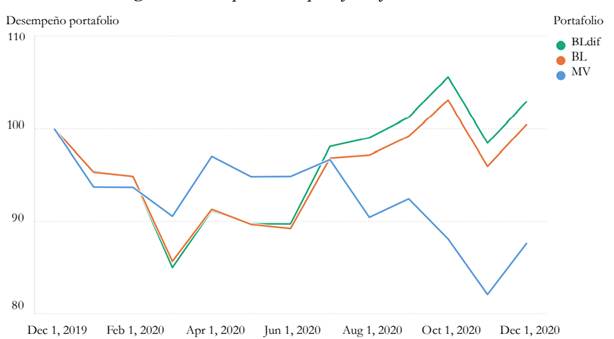
Aunque estos resultados son desfavorables para los portafolios BL y BL f en las medidas de retorno esperado y en el coeficiente de Sharpe (ϑ), los resultados cambian completamente para la evaluación de desempeño en el periodo fuera de muestra. Para este ejercicio se toma un portafolio hipotético con valor inicial de 100 millones. Mientras el portafolio MV presenta una caída del -13,15 %, similar al desempeño del índice COLCAP para este periodo -como muestra la Figura 2-, los portafolios BL y BL f alcanzan resultados positivos.
Si se tiene en cuenta la coyuntura presentada para el año 2020, producto de la enfermedad infecciosa provocada por el virus SARS-CoV-2 -también conocido como la Covid-19- los resultados muestran un buen desempeño para el portafolio BL f (Bldif en la Figura 2), y confirman que las views difusas se ajustan mejor al modelo BL e incorporan más información, convirtiéndolo en un enfoque adecuado para la construcción de portafolios óptimos.
Conclusiones
Este artículo presentó una implementación novedosa para la formulación de las views del inversionista sobre los retornos esperados de los activos en el modelo BL mediante la lógica difusa. Para ello, se redefinen las views del modelo BL usando una función de pertenencia trapezoidal. En este ámbito, se superan los criterios de subjetividad y abstracción que estas representan al incorporar más información en la matriz de incertidumbre. Los resultados obtenidos para el mercado de valores colombiano muestran que el modelo BL con views difusas (BL f ) alcanza un mejor desempeño para el periodo fuera de muestra, en comparación con la formulación tradicional del modelo BL y del mismo modelo MV.
Esta evaluación se realizó para un periodo de alta incertidumbre y fuertes caídas en los activos e índices de mercado, como lo fue el año 2020, producto de la crisis originada por la pandemia de la Covid-19. Aunque, para el periodo dentro de muestra, el modelo MV presentó una ventaja importante, tanto en las medidas de retorno esperado como en el coeficiente de Sharpe, los resultados fuera de muestra confirman las fallas que usualmente presenta el modelo MV en la creación de portafolios óptimos, como fue señalado al inicio del trabajo. Además, si bien los resultados resaltan las ventajas del modelo BL f , al incorporar información adicional en las views, estas no están completamente libres de sesgos cuando se incorporan a posteriori.
