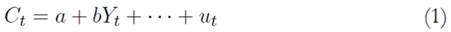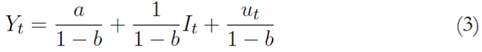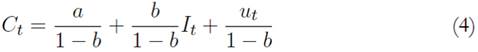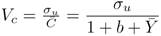Introduction
In the 1957 February issue of the Journal of Political Economy, Milton Fried man and Gary S. Becker published their paper “A Statistical Illusion in judging Keynesian Models”. In this work, their purpose was to question Keynesian macroeconometric models for their inappropriate treatment of the consumption function, and for their inability to yield accurate predictions of income. Friedman and Becker (1957, p. 64) claimed that in replacing “the ultimate objective of predicting income [...] by the proximate objective of predicting consumption”, Keynesian modelers had fallen into a statistical illusion. According to them, the illusion resulted from the adoption of the relative error in predicting consumption as a criterion to judge the performance of macroeconometric models. In a nutshell, Friedman and Becker’s (1957) criticism of the “statistical illusion” in judging Keynesian models consisted of two points. While their first point focused on how to correctly evaluate model performance, their second point was related to the specification of the consumption function itself.
In the 1957 February issue of the Journal of Political Economy, Milton Fried man and Gary S. Becker published their paper “A Statistical Illusion in judging Keynesian Models”. In this work, their purpose was to question Keynesian macroeconometric models for their inappropriate treatment of the consumption function, and for their inability to yield accurate predictions of income. Friedman and Becker (1957, p. 64) claimed that in replacing “the ultimate objective of predicting income [...] by the proximate objective of predicting consumption”, Keynesian modelers had fallen into a statistical illusion. According to them, the illusion resulted from the adoption of the relative error in predicting consumption as a criterion to judge the performance of macroeconometric models. In a nutshell, Friedman and Becker’s (1957) criticism of the “statistical illusion” in judging Keynesian models consisted of two points. While their first point focused on how to correctly evaluate model performance, their second point was related to the specification of the consumption function itself.
Surprisingly enough, Friedman and Becker (1957) made an important contribution to large-scale macroeconometric modelling, anticipating both the dissemination of a method to evaluate model performance and the important role that dynamics would play in the construction of these models.
This method was full model simulation, later routinized as computer dynamic simulation.1 Through their insistence on the use of the relative error in the prediction of aggregate income as the adequate criterion to evaluate model performance (instead of the relative error in prediction of aggregate consumption), Friedman and Becker advocated for the evaluation of structural equations to rely on full model simulations and not on predictions based on single equations. Accordingly, in order to evaluate their models, macroeconometricians should emphasize the simultaneous equation characteristics of structural equations (in particular on the accuracy of their predictions) rather than on their single equation characteristics (Bodkin 1995, pp. 53-54).
Yet, by the 1950s, macroeconometricians were not necessarily convinced about the requirement of this criterion nor did they have the computational power to bring about the burdensome calculations that would allow them to meet this criterion. Some considered, instead, that out-of-sample predictions or extrapolations (even when performed on single equation bases) would be more adequate to evaluate models than sample predictions (even if performed as full model simulations). While macroeconometricians’ idea of prediction focused on what Klein (1958, p. 543) called the “painful [test] of experience” (i.e., the comparison between observed values (ex-ante or ex-post) and out of-sample “concrete forecasting results” of alternative models), full model simulation could be understood as a sort of Turing test, or as an “imitation game” (Turing, 1950).
The increasing availability and improvement of computational methods, as well as the expansion of large-scale macroeconometric modelling in general, provided some of the necessary conditions for the dissemination of full model simulations (Ando & Modigliani, 1969; Bodkin, 1995; Bodkin et al., 1991). The successful application of this kind of simulations was also an important push in this direction. The particular case of Irma and Frank Adelman’s (1959) simulation of the Klein-Goldberger (1955) model certainly exerted an important effect on the establishment of this method as a standard criterion to evaluate model performance.
Although simultaneous equations characteristics represent only some among a whole battery of criteria used to judge models’ performance, this controversy illustrates the way macroeconometricians discussed, developed, and adopted standards to judge (and improve) the performance of their models. My main claim is that independently of Friedman and Becker’s critical claims and clear methodological differences regarding the Keynesian modelers, a common background of general principles turned this controversy (and the larger debate) into a fruitful and revealing episode of the history of macroeconomics. This common background consisted of the belief of three points by contemporary macroeconomists: (1) that they should adopt an empirical approach to economics, (2) that macroeconometric modelling was the way to go if they wanted to integrate rigorous thinking to economics, and (3) that statistical techniques were considered necessary to provide rigorous criteria to judge model performance.2
In this paper, I give an account of the early discussions on the evaluation of the performance of macroeconometric models and on the way ideas about dynamics entered the discussion of this, by the time, novel scientific practice. I begin by revisiting a fundamental difference between two modelling strate gies in macroeconomics: the Marshallian approach adopted by Friedman and the Walrasian approach adopted by Klein. Then, I describe the common back ground shared by contemporary macroeconomists who saw their discipline already in the late 1950s necessarily as an empirical discipline that should be based on modelling and on the use of the latest statistical techniques. In the next two sections I describe in detail the Controversy on Statistical Illusions, I revisit the three Keynesian responses to Friedman and Becker’s critique, before going into the details of one of the Keynesians’ counterattacks which consisted on Klein’s claim that Friedman’s Permanent Income Hypothesis had been anticipated by T.M. Brown in the early 1950s. The last two sections of the paper, I emphasize on Klein’s response that the most important feature of his macroeconometric models consisted in their capacity to perform policy evaluation, and on their ability to mimic the economy, its movements, and predict turning points. Given the important role that macroeconometric modelling played in the spread of the use of the computer in economics, I suggest that the scale to which full model simulation of macroeconometric models was compared was an idea similar to the Turing Test, in which the model should be able to imitate reality. I present the conclusions in the last section of the paper.
The Controversy’s milieu: Marshallian and Walrasian approaches to macroeconomic modelling
The controversy on statistical illusions was embedded within a larger me thodological debate confronting two empirical approaches to economics: the “statistical economics” and the “econometrics program”. While the NBER appeared as the most visible and important stronghold of the statistical eco nomics approach, the Cowles Commission, during its years in Chicago (1939 1955), constituted the bastion of the econometrics program.3 Since at least the mid-1940s, Friedman had sustained longstanding discussions with various members of Cowles in which he had expressed his concern about the neces sity of finding a sound and rigorous criterion to evaluate model performance.4 In fact, this was one of the main arguments in his 1946 debate with Oskar Lange (Friedman, 1946).
Departing from a situation of involuntary unemployment, Lange’s Price Flexibility and Employment (1944) investigated whether a decrease in money wages could re-establish full employment using, according to Friedman (1946, p. 613), an “unreal and artificial” approach. Friedman’s claim was not so much against abstraction, but rather about the way Lange used abstraction. According to Friedman, Lange attributed too much importance to the con formity of the model structure with the cannons of logic, ignoring the model’s “empirical application or test”. Lange’s use of “casual observation” (p. 618) as his only method to evaluate his model was not a sufficiently rigorous criterion to evaluate the relevance of the proposed functions, and it resulted in systems with no “solid basis on observed facts”, yielding “few if any conclusions sus ceptible of empirical contradiction” (p. 619). Friedman’s concern, again, was about Lange’s (and the Commission’s) lack of a rigorous method to evaluate model performance based on a sound empirical approach.5
Some important methodological works published during this period re sulted, partly, because of the exchanges between Friedman and the Cowles’s members. Friedman’s criticisms ultimately led, even if unwittingly, to the strengthening of the Cowles’s effort to provide a solid empirical approach to macroeconometric modeling.6 A recurrent subject in these works, notably in the case of Friedman’s, related to the ancient Walras-Marshall divide. To Friedman, the important element of this divide did not consist of the classical opposition of general and partial equilibrium attributed to Léon Walras and Alfred Marshall. The ulterior motive of this divide relied on a more pro found methodological question. Both Walras and Marshall understood that the economic system was fundamentally complex and that all its parts were interdependent. Thus, given this interdependency, the question was whether the economist, interested in finding concrete solutions relative to some parts of the economy, should take the entire system into consideration (as Walras suggested) or focus only on a few parts of it (as Marshall proposed).
Friedman’s response to this question pointed clearly in Marshall’s direc tion. His Marshallian approach was based on the idea that economic theories
or models should be perceived as a way to construct systems of thought or “engine[s] for the discovery of concrete truth” (Marshall, 1885, p. 159). Since both the economist’s knowledge and his capacity to observe the world were partial, these systems should be constructed through the rigorous observation of specific parts of the economy and of the “real” world and not through elegant but empty abstractions of the entire system. In brief, these systems should provide “generalizations of the real world” instead of “formal models of imaginary worlds” (Friedman, 1946, p. 618). This approach, however, recognized that the economy was a complex system with interdependent re lations, which had nothing to do with the notion of partial equilibrium.
Klein’s Walrasian approach, on the contrary, was based on the idea that the economy should be considered as a whole despite the economist’s inability to observe or understand the system in all its complexity. Independently of the economist’s capacity to build a simple (or complex) model, his point of departure to build macroeconomic models should be the entire economic system. Klein’s claim was that the combination of a mathematized frame work of general equilibrium with statistical theory and with rigorous empirical work, would be useful to provide a tool of reasoning for understanding and intervening in the economy.7
It is worth noting that neither Friedman nor Klein explicitly alluded to the Walras Marshall opposition during the controversy on statistical illusions. The larger methodological debate, however, was the background and the pillar of the controversy on statistical illusions and has to be born in mind at all times in the study of this controversy.
To be clear, I believe that there are two different levels in this controversy. The first level, again, goes up to the larger debate (and to the opposition) between two alternative empirical approaches in macroeconomics: the “statistical economics approach” and the “econometric program”. At this level, given the nature of Friedman and Becker’s paper, there is no doubt that the authors insisted on the abandonment of the “econometric program”, even if they did so in a somewhat subtle way.8 It is at this first level, too, that Friedman would pick up his later debates with the Keynesian approach, in particular in Friedman and Meiselman (1963), and in Friedman and Schwartz (1963).9 At the second level, it seems as if Friedman and Becker had accepted to play within the rules of the “macroeconometricians’ game”, which was on its way to becoming the dominant approach in macroeconomics (see Bodkin et al. 1991). At this level, their critique could be qualified as constructive, for it sought to establish a criterion to evaluate model performance and improve model specification.
Economics as an empirical and modelling science: A common background
In his review of the controversy on statistical illusions, Ronald G. Bodkin (1995, p. 45) contended that any commentator on this discussion should “take into account [...] whether there was [...] a genuine disagreement, or whether the issues among the participants were principally semantic”.10 Perhaps this contention should be reformulated in a somewhat different way. There is no doubt that there were issues of substantial disagreement between the participants, as Bodkin recognized at the end of his paper.11 More importantly, there was also a certain degree of agreement on fundamental points that allowed the participants to actually engage in a productive conversation. I claim that, in order to make a contribution to the history of macroeconometrics, anyone commenting on this controversy should take these points of agreement seriously into account, for these points allowed the participants to engage in a discussion in the first place.
It is clear that for any scientific controversy to take place and for it to be fruitful, some agreement must exist between its participants. This agreement, reflected in some general, but fundamental points, can be understood as a sort of “common background”. Without this common background, fertile scientific controversies would simply become fruitless and meaningless at tacks or semantic misunderstandings at best. Thus, a brief characterization of this background is useful for at least two reasons: First, it sheds light on some of the important issues at stake, making them more visible; second, it provides the possibility of historicizing the controversy, putting some flesh on the methodological skeleton of the discussion.
In the particular case of the controversy on statistical illusions, no less than three fundamental points of agreement built the common background between Friedman and Klein (and the other participants). Both factions considered that:
Economics was a science whose foundations should be grounded on an empirical approach.
A way of integrating a rigorous empirical approach in economics was through the practice of econometric modelling (in a broad sense).12
Statistical techniques could help economists to develop rigorous criteria to judge the performance of their models, helping them in the discovery and further specification of the underlying economic mechanisms.
These general principles established the point of departure of the controversy between Friedman and Becker, and Klein. There are, of course, important (and sometimes irreconcilable) differences between the methodological positions of these authors concerning the way to tackle each of these principles. Yet, the important point here is that this common background was not exclusive to Friedman, Becker, and Klein, but was part of the economists’ scientific community, and that discussions, criticisms, and controversies based on this common background contributed, even if unwittingly, to the devising and determination of empirical criteria to judge the performance of large-scale macroeconometric models.
The “Simple Keynesian Model” and the Controversy on statistical illusions
To illustrate their criticism, Friedman and Becker (1957, p. 64) used a Keynesian model “in its simplest form”, specified according to the absolute income hypothesis.13 This simple model contained a consumption function (1) and a national income accounting identity (2). Investment was considered autonomous:
with Ct and Yt the aggregate consumption and income in a given year, while a and b are parameters, ut is the stochastic perturbation of the consumption function, and It is realized investment, which, by definition, is also realized savings.
The common forecasting practice consisted of the use of the reduced forms of the model. In this case, the reduced form equations (3) and (4) are obtained by replacing the structural equation (1) in the accounting identity (2):
Forecasts of the level of consumption obtained through the reduced form equation (4), would present a small relative error of prediction Vc (see the first column of Table 1), according to which macroeconometricians (under the statistical illusion) tended to consider that their model, as a whole, would perform well.14 This, however, was a misleading consideration, since conclu sions on the performance of the whole model were drawn based on single equation characteristics. This procedure, of course, was not necessarily con sistent and entailed misleading results. For instance, Friedman and Becker (1957) showed that, if macroeconometricians kept this (incorrectly) specified model structure, forecasts of the level of income would present dramatically higher relative errors of prediction, revealing that the model, as a whole, did not perform well. This was a relevant point, since the ultimate objective of macroeconometricians was, indeed, to forecast the level of income, while forecasting the level of consumption was only a secondary objective.
Table 1 Errors in the Prediction of Consumption and Income from Different Consumption Functions.
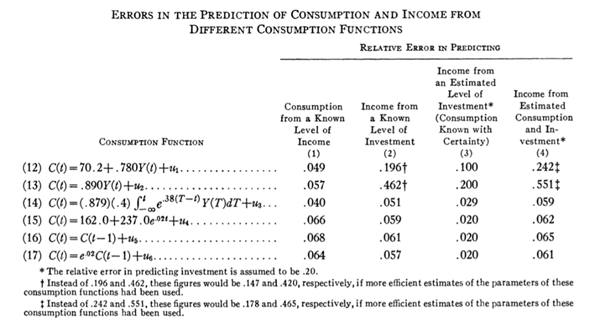
Source: Friedman and Becker (1957, p. 67).
Based on the data published in Raymond Goldsmith’s A Study of Savings (1955), Friedman and Becker performed a numerical exercise to illustrate their point and to compare the performance of six different consumption equations following four distinct procedures of prediction.15 Table 1 describes the relative error in prediction of these consumption functions.
In predicting consumption from income (column 1) the Keynesian functions, equations (12) and (13), presented a small relative error of prediction (0.49 and 0.57, respectively), showing superior results (in terms of smaller relative errors) compared to all the other consumption functions, except for (14), whose relative error is the smallest of all (0.40). This was the source of the statistical illusion that would misleadingly justify the maintenance of the Keynesian consumption function.
As opposed to the conclusions that could derive from the evidence that was first visible (the small relative error in predicting consumption), the simple Keynesian model actually presented important flaws in its consumption func tion. These flaws were translated into misspecifications that led the model to perform poorly in its forecasts of the level of income (see column 2 of Table 1) and was the result of the interaction of single equation random errors. “[A] given error in predicting consumption [was] magnified by the multiplier process into a much larger error in predicting income” (Friedman and Becker 1957, p. 66). This was so, because “the accuracy of the estimate of income depends not only on the accuracy of the estimate of consumption but also on the form of the consumption function in particular, on the fraction of consumption which [the consumption function] designates as ‘autonomous”’ (p. 64, my emphasis). The problem was that the statistical illusion would hide the misspecification of the whole model and that small relative errors obtained from the single equations built up to produce even larger relative errors in predicting other variables of the model. The presence of multipliers in the Keynesian models made these errors even more important.
This argument set the basis for Friedman and Becker (1957, p. 75) to conclude that “improvement in the consumption function [...] may [...] make a greater contribution to our ability to predict income than improvement in the estimates of investment”. The problem of Keynesian models was not one of statistical or mathematical adequacy, but one of “the structure [these mod els] attribute to the economic system” (p. 73). Since Keynesian modelers did not apply the correct criterion for judging model performance, they fell into a statistical illusion that led them to accept a misleading model specification, hence the wrong structure. Friedman and Becker did not limit their claim to this already important point but went further to claim the general principles to be taken into account to specify a correct consumption function. These principles, which were, of course, related to Friedman’s (1957) A Theory of the Consumption Function, his Marshallian approach, and his “rule of parsimony”, (Klein, 1958, p. 545) were put forward in order to build macroeconometric models.
It is worth noting, that even if the particularly simple Keynesian system used in the critique constituted a pedagogical tool only, the predicting pro cedure denounced by Friedman and Becker was a common practice among Keynesian macroeconometricians during the 1950s (Bodkin 1995, p. 46).
Friedman and Becker were then correct both in criticizing this practice and in raising this important methodological concern. Indeed, the fact that the relative errors in predicting the level of consumption were small, was not a sufficient condition to consider the whole model accurate in predicting income. Statistical adequacy based on the prediction of a single equation did not immediately mean that the complete model would perform well.
Keynesian Responses to Friedman and Becker
Johnston (1958), Kuh (1958), and Klein (1958) provided three separate responses to Friedman and Becker (1957). Although each one referred to different important aspects of the controversy, four common claims were made. The first reflected a shared feeling that the macroeconometric ap proach had been unfairly criticized. Indeed, given the obsolete nature of the functions and the time period (1905-1951), to which the simple model had been fitted in the critique, Johnston (1958) declared that it was “hardly [...] surprising to read the final conclusion that these simple functions give an inadequate specification of dynamic characteristics of the economic structure” (pp. 296-297). According to Johnston (Kuh, and Klein), and this was the second common argument, the type of functions used in the critique had been abandoned in actual practice at least since the last ten years, and in particular after the publication of Franco Modigliani’s (1949) paper, “Fluctuations in the Saving-Income Ratio: A Problem in Economic Forecasting”.
In this paper, Modigliani criticized Jacob Mosak (1945) and Arthur Smithies’s (1945) forecasting methods because they relied on simple Keynesian functions similar to the one used by Friedman and Becker (1957) to illustrate the Keynesian approach. Modigliani highlighted the difficulties related to the use of these “simple” functions in economic forecasting. Indeed, economists faced a complex task in their forecasting objective, given the “pronounced discrepancy between the cyclical, or short-run, and the secular, or long-run” forms of economic relations in a period of “violent cyclical fluctuations” like the first half of the twentieth century (particularly in the US). Notably, Modigliani suggested a method “by which it seem[ed] possible to estimate” both the secular and the cyclical forms of economic relations (p. 371). Based on Modigliani (1949), Johnston (1958) estimated two consumption functions that allowed for the differentiation of (a) the short-run or cyclical marginal propensity to save, and (b) the long-run average and marginal propensity.
where Y 𝑡 0 is the highest income experienced before time t.
Judged according to Friedman and Becker’s (1957) criteria, both equations (5) and (6) presented a well predicting performance. The relative error in predicting consumption and income from equation (5) was VC = 0.0304, and VY = 0.053, respectively. In the case of equation (5), these relative errors were of VC = 0.53, and VY = 0.0485. With this estimation, Johnston not only made his point that the simple model used by Friedman and Becker as an illus tration of the Keynesian model was no longer used in actual practice but also that alternative consumption functions that could easily improve the results obtained by Friedman and Becker existed (this was the third common claim of the three respondents). This improvement of the consumption functions did not consist of envisaging a future possibility of refining existing functions. In fact, far more sophisticated consumption functions which yielded more adequate results, even according to Friedman and Becker’s criteria, had already been in use. In this respect, Klein (1958, p. 540) asserted that in the actual practice, those “who have seriously attempted forecasting from Keynesian models had used much more complicated systems in which the reduced-form equation for consumption is vastly different from and [...] superior to [Fried man and Becker’s]”.
The fourth common claim consisted of the macroeconometricians’ con sideration that there had been no statistical illusion. The three respondents did recognize, however, the existence of simultaneous equations biases in the forecasts obtained from reduced form equations. Yet, these problems were already known to econometricians and, according to the respondents, Fried man and Becker had discovered nothing new. Klein, for instance, claimed that “when Friedman and Becker showed that the variance of
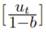 in the multiplier equation is much larger than the variance of [ut] in the consumption equation (both expressed as a percentage of average consumption or income), [Friedman and Becker] are not proving the general inadequacy of Keynesian models or even of the consumption function”. To Klein, they were “simply giving a laborious demonstration of the fact, already well known, that the simple multiplier model is not suitable for more than pedagogical use in the classroom” (p. 540) and acknowledging relative errors in prediction would accumulate in models presenting important multiplier effects.
in the multiplier equation is much larger than the variance of [ut] in the consumption equation (both expressed as a percentage of average consumption or income), [Friedman and Becker] are not proving the general inadequacy of Keynesian models or even of the consumption function”. To Klein, they were “simply giving a laborious demonstration of the fact, already well known, that the simple multiplier model is not suitable for more than pedagogical use in the classroom” (p. 540) and acknowledging relative errors in prediction would accumulate in models presenting important multiplier effects.
Although this would concede the argument to Friedman and Becker if seen from a purely methodological perspective, in his response, Klein seemed to intentionally deviate attention from it by providing a different interpretation of what the critique actually meant. Referring to Haavelmo (1947, pp. 539-540), Klein claimed that “the appropriate way to estimate the structural parameters of equations in a complete system is to regard the whole set of equations simultaneously from a statistical point of view”. In the case of the consumption function, this meant that “the propensity to consume should be estimated from the reduced forms and not by direct reference to the consumption function, to the neglect of the accounting definition”. Since Klein’s response seems to accept Friedman and Becker’s criticism, one understands why Friedman and Becker (1958, p. 545) considered the macroeconometricians’ responses (and especially Klein’s) as a “supplement” of their article. Still, the problem raised was that, although Klein was probably right in evocating the strength of his models, he focused too much on the ability of his reduced forms to yield accurate extrapolations of the economy. Klein, however, misses the point that this criterion does not always constitute a sufficient measure of the accuracy of model performance.
Brown’s Anticipation of the Permanent Income Hypothesis
Another important point of the controversy has to do with Klein’s (1958, p. 541) claim that “Brown’s work on lags in consumer behavior is truly a complete anticipation of the Friedman-Becker article”.16 T. M. Brown (1952) had developed his “habit persistence theory”, where, contrarily to Modigliani (1949), previous real consumption, and not previous income played an im portant role in the determination of the level of consumption. Brown (1952) claimed that:
[The] lag effect in consumer demand was produced by the con sumption habits which people formed as a result of past consump tion. The habits, customs, standards, and levels associated with real consumption previously enjoyed become ‘impressed’ on the human physiological and psychological systems and this produces an inertia or ‘hysteresis’ in consumer behaviour (p. 539).
A similar feature between Brown (1952) and Modigliani (1949) was that both approaches allowed for distinguishing between short-run and log-run marginal propensities to consume.
In his “supplementary comment”, Friedman (1958) actually conceded this point to Klein (1958, p. 549) by stating that he “did not recognize that [his] procedure was equivalent to Brown’s use of the consumption of the preceding year, and [that] Klein [was] quite right in criticizing [him] for this error of omission”. As noted by Bodkin (1995, p. 55), Friedman might have hastened too much in conceding this point of the controversy to Klein. Years later, Balvir Singh and Aman Ullah (1976, pp. 101-102) showed that “Brown’s model [was] by no means ‘truly a complete anticipation of Friedman”’. In fact, “even though the Friedman model [...] looks quite similar to the one suggested by Brown, the models differ in terms of the nature of the regressors, interpretation of the error term, and the nonlinearity in parameters”.
In my opinion, the essential point here is not whether Brown anticipated Friedman. The truly important point is whether the Keynesian and the non Keynesian models present specifications close enough to be considered simi lar. This is important in order to understand the extent to which other criteria to judge model performance and model relevance, apart from the method ological approach itself, play a role in moulding and shaping economic mod els. Economists, like other scientists, rely on a battery of criteria to choose among different model specifications and to shape their models or theories.
This battery of criteria is not completely rigid and might be composed of a variety of elements such as statistical tests, adequacy of mathematical forms and procedures, the nature of data, political convictions, or even particular material and historical conditions like the existence and availability of digital computers, or the access to funding. Indeed, this battery of criteria belongs to the common background shared by macroeconomists at the time, whether Keynesians or not in their methodological approach. In this sense, these criteria to judge model performance are defined by the common background of the community, by their common practices and beliefs, rather than by their affiliation to a particular methodological or theoretical approach.
Differences in the Concepts of Prediction
In terms of methodology, the most important point discussed in the con troversy was about how to adequately evaluate model performance. Macroe conometricians considered that ex-ante or ex-post forecasts or extrapolations from the reduced form equations were an adequate way to evaluate model perfor mance. As discussed above, both the critics and the econometricians knew that this procedure could produce biased results. Keynesians thought of these biases as the result of a statistical problem, particularly simultaneous equations biases. Friedman and Becker (1957), however, insisted that the biases were caused by a poor model specification, considering them a result of an economic theoretic problem. According to the Keynesians, the best way to avoid these problems was through painstaking tinkering, re-estimation, and actualization of the model, and through the inclusion of more explanatory variables in each equation. Klein (1958, 545) for instance, claimed that “re searchers [had] sought improvement in the Keynesian consumption function through the introduction of new variables” and that there were “great limits to the extent to which one can come upon radically improved results by juggling about the same old variables in a different form”:
Instead of adhering to the “rule of parsimony”, we should accept as a sound principle of scientific inquiry the trite belief that con sumer economics, like most branches of our subject, deals with complicated phenomena that are not likely to be given a simple explanation [...] The addition of extra predetermined variables (not lagged incomes) that are not correlated with income or that do increase the multiplier are likely to improve the fit of the multiplier equation at the same time that they are improving the fit of the consumption equation. I venture to predict that much good work will be done in the years to come on adding new variables to the consumption function and that it will not be illusory.
Friedman and Becker (1957), on the contrary, made a plea for econome tricians to adopt a different economic structure, based on a consumption function specified according to the permanent income hypothesis. Their plea, nonetheless, was also directed towards the development of parsimonious models that would explain more through simpler equations. In this particular case, both critics and respondents were exclusively focusing on how to solve the problem of obtaining biased results. However, none of them actually attempted to identify if the origin of the problem was statistical or economic.
To detect and define the nature of the problem, Keynesians and critics had to find an adequate measure, allowing for the understanding of the kind of problem they were facing. In this case as well, they still could not agree on what an adequate criterion would be since they valued different kinds of predictions. On the one hand, the Keynesians thought that extrapolation or out-of-sample predictions were a more important kind of prediction in that it constituted the more adequate criterion to judge model performance. Extrapolation meant that one should test the model’s theoretical and statistical whole structure not only to fit the observed data but also to predict values that were outside the observed sample. Yet, by the 1950s, these extrapolations were performed only on the bases of reduced form equations and not on the bases of whole model simulations, partly because computers were still not available for economists in general, but more importantly, because macroeconometri cians believed that reduced forms forecasts were adequate criteria to judge model performance.
On the other hand, Friedman and Becker (1957) suggested that predicting did not necessarily mean extrapolating. To them, retrodiction and extrapolation were equivalent in evaluating model performance, and the truly important criterion was to find out whether extrapolation or retrodiction was performed on the basis of reduced form equations or on the basis of full model simulations., Once again, to them, only full model simulations would provide adequate ways of evaluating model performance.
Klein’s Emphasis on Extrapolation
A somewhat surprising way of interpreting Friedman and Becker’s (1957) paper is to consider it as an important contribution to large-scale macroecono metric modelling. In fact, their critique can be understood as an anticipation of full model simulation as an important method to evaluate model performance. In this sense, again, the evaluation of the simultaneous equations characteristics of structural functions would be a better criterion to judge model performance compared to single equations characteristics.
Although Klein later adopted this criterion as the rest of the discipline did (Klein, 1969), in the 1950s, he was skeptical about Friedman and Becker’s proposition. His skepticism relied on his different views on the nature of predictions. To Klein, Friedman and Becker’s proposition put too much emphasis on the goodness-of-fit measures obtained for sample period predictions or retrodictions. Instead, Klein appraised other criteria like out-of-sample predictions or extrapolations, like the model’s capacity to predict turning points in the economy. Making a clear reference to Friedman (1953), Klein considered that Friedman and Becker’s (1957) proposition was rather “strange”, since “Friedman [had], on many occasions, stressed the criterion of predictive ability as a suitable test of theory”. And yet, in his defensive effort, Klein disregarded the fact that full model simulation provided also a kind of prediction. Only, this was a different kind of prediction.17
Klein’s idea of prediction focused on the “painful [test] of experience”, i.e., the comparison between observed values and ex-ante or ex-post out-of-sample “concrete forecasting results” (p. 543) of alternative models. For instance, to Klein and Goldberger (1955, p. 72):
The severest test of any theory is that of its ability to predict. Our equation system presents a theory of economic behavior in the aggregate. We have fitted the model to the sample, and although it may be an achievement to find a structural system which does fit the observed facts, we cannot be satisfied with the performance of the system solely with reference to the sample data [...] In a broad sense, we mean, by prediction, the ability of the equations to explain aggregate economic behavior for sets of observations outside the sample.
Klein considered both ex-ante and ex-post extrapolations as important constituents of his predictions. These were complementary types of predictions, and both had to be conducted in order to evaluate model performance. Yet, between ex-ante extrapolations, Klein considered that policy simulation was more useful than mere forecasts of the level of particular endogenous variables. Klein and Goldberger, for instance, explained this procedure in the following way (1955, p. 72):
We have approached this problem empirically from two points of view. In an ex post sense we may insert observed and essentially correct values of predetermined variables in the model and solve it algebraically for the values of endogenous variables in the forecast period. One interested in the degree to which our model represents a true picture of behavior should base this judgement of performance on this ex-post type of extrapolation. This is a case of testing the model outside the confines of the sample and determining how well it fits actual observations when there is no statistical forcing towards conformity [...] If the ex-post extrapolations have shown a system to give a good explanation of economic behavior, we can then place a measure of reliance on the use of this system to show what would happen if exogenous variables were to be placed at particular assumed levels. We might show, for example, the sensitivity of aggregate activity to variations in government tax-expenditure plans. This is a form of ex-ante forecasting and may be a more useful econometric application than pure forecasts of the levels of endogenous variables (emphasis in the original).
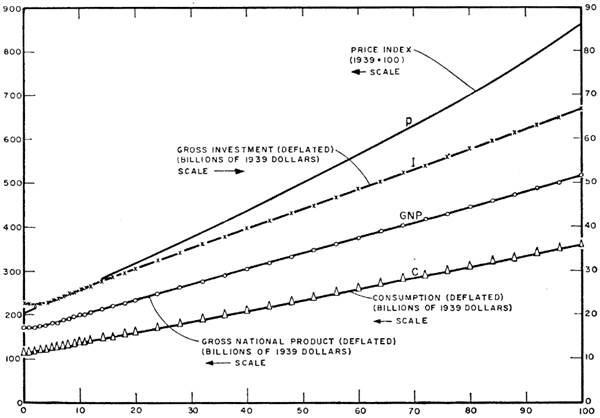
Figure 1 is an illustration of the type of ex-post forecasts performed by Klein and Goldberger (1955). Klein and Goldberger presented ten figures of this type, where they examined the behaviour of the ten most impor tant equations of their model individually. Each graph consisted of a first chart (at the top of the figure) where the observed and forecasted trends of the endogenous variable for the whole period (1929-1952) were presented. The remaining lower charts presented the individual contributions of the exogenous variables and the errors in explaining the behaviour of the en dogenous variable. Figure 1 reproduces the example of the consumption function. These variables were examined individually, in part, because of the computational burden that a full model simulation would mean for the time. However, with the advent of the digital compute, by 1959 it was possible to conduct dynamic or full model simulation of the Klein-Goldberger (1955) model. In this sense, this model was not only a pedagogical reference on how to build large scale models or a tool to carry on policy evaluation, but it also became an example of how to use the digital computer in macroeconomics, as well as how to develop a test that would measure model performance in its full form and not just through reduced form equations.
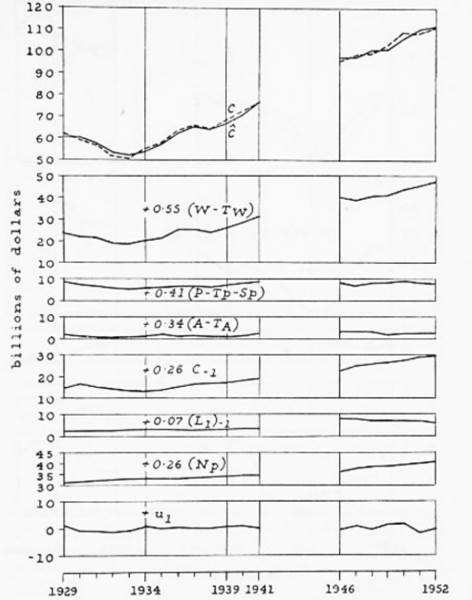
Source: Klein and Goldberger (1955, 93).
Figure 1 Errors in the Prediction of Consumption and Income from Different Consumption Functions.
Full Model Simulations as a Turing Test
Full model simulation could be understood as a sort of Turing test, or as an imitation game (Turing, 1950).18 In order to pass the Turing test, the model should be able to generate data series that are indistinguishable from the data actually observed in the economy. In other words, the model should be able to imitate reality. If the model-generated data produced a pattern that was comparable (although not necessarily equal) to the “real-world” data, then the model would fulfil this test.
This was, in fact, the objective of the Adelmans’ (1959) simulation of the Klein Goldberger (1955) model. In particular, Adelman and Adelman (1959) examined whether the model “really [offered] an endogenous explanation of a persistent cyclical process [...] whether the system [was] stable when subjected to single exogenous shocks, what oscillations (if any) accompany the return to the equilibrium path, and what is the [response] of the model to repeated external and internal shocks”. (p. 597) To do this, the Adelmans simplified the 22 simultaneous equations model through algebraic substitutions, into a “set of four simultaneous equations in four unknowns” (600). This allowed them to significantly reduce the computational time of the model. The Adelmans performed at least four different simulations in which they asked different questions. The first simulation dealt with the deterministic form of the model and showed that in absence of external shocks, the system was monotonic and essentially linear. Figure 2 presents the results of the first simulation:
The other simulations included different types of shocks. First, they simulated the behaviour of the system when “shocks of type I” were introduced.
This type of shocks consisted in the introduction of a severe and sudden shock in terms of the reduction of government expenditures. As this simulation produced cycles that were “unrealistically small” (p. 609), another type of shocks was introduced.
Shocks of type II transformed the deterministic system into a stochastic system through the introduction of errors into each of the estimated equations. This time (Figure 3), the model appeared to be more realistic since it not only produced three to four-year cycles, but most importantly, the magnitudes of the cycles “here compare[d] favourably in magnitude with those experienced by the United States economy after World War II” (p. 611).
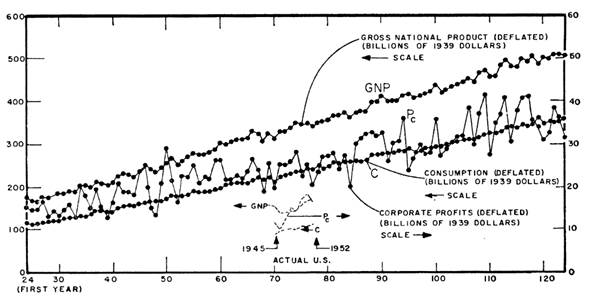
Source: Adelman and Adelman (1959, 611).
Figure 3 Klein-Goldberger Selected Time Paths under Type II Impulses
The importance of the Adelmans’ simulations, especially of those of the stochastic Klein-Goldberger system, resided on its resemblance to the behaviour of the US economy. This resemblance, however, was not only qualitative in nature but also quantitative.
All in all, it would appear that there is a remarkable correspondence between the characteristics of fluctuations generated by the super position of random shocks upon the Klein-Goldberger system and those of the business cycles which actually occur in the United States economy. The resemblance is not restricted to qualitative parallelism, but is, indeed, quantitative, in the sense that the dura tion of the cycle, the relative length of the expansion and contraction phases, and the degree of clustering of peaks and troughs are all in numerical agreement (within the accuracy of measurement) with empirical evidence (Adelman and Adelman 1959, p. 614).
Full model simulations such as that performed by the Adelmans’ (1959) allowed macroeconometricians to judge models’ performance, taking into account simultaneous equations characteristics that Friedman and Becker (1957) had been missing in Keynesian models. These full model simulations would become increasingly important for the practice of macroeconometric modelling, becoming an important and concrete way in which ideas about dynamics entered this scientific practice.
Conclusions
In a nutshell, Friedman and Becker’s (1957) criticism of the “statistical illu sion” in judging Keynesian models consisted of two points. The first focused on how to correctly evaluate model performance. According to Friedman and Becker, the performance of the entire macroeconometric model should not be evaluated on the basis of the “apparently” good performance in prediction of the consumption function alone. Implicitly, this point was directed towards the idea that the single equation characteristics are not sufficient to evaluate the performance of the whole model. Instead, to make a sound evaluation of the performance of their models, econometricians should focus on the structural equations characteristics, and undertake whole model simulations. This argument would become common ground in the subsequent years among macroeconometricians, but, at the time, some confusion still existed about the necessity of this criterion. Adelman and Adelman’s (1959) simulation of the Klein Goldberger (1955) model contributed to the establishment of whole model simulation as a criterion of model performance evaluation. Other important contributions in this direction were the further development of the digital computer and the dissemination and further development of the macroeconometric modelling approach.
Friedman and Becker’s (1957) second point of criticism was related to the specification of the consumption function itself. In this respect, they insisted that the Keynesian function had to be changed and improved. The important points here are that Friedman and Becker proposed not only two statistical criteria to guide the specification of the new consumption function (the relative error in predicting income from the reduced form equations and the “naive models”), but they also advanced another argument in favour of the permanent income hypothesis proposed by Friedman (1957).
These points, however, have to be understood at two different levels. First, as a claim inscribed within a larger debate between two empirical approaches to macroeconomics, and thus as a claim directed towards the abandonment of the large-scale macroeconometric approach. More importantly to my purpose here is the other level, which interprets Friedman and Becker’s (1957) claim as a constructive critique and as precursor of a criterion to evalu ate model performance that would become common ground around macroeconometricians: full model simulations or dynamic model simulations.