Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO  Similars in Google
Similars in Google
Share
Revista Colombiana de Química
Print version ISSN 0120-2804On-line version ISSN 2357-3791
Rev.Colomb.Quim. vol.35 no.1 Bogotá June 2006
Carlos Ariel Cardona1Iván Ricardo Navarro1Luis Gerónimo Matallana1
1Departamento de Ingeniería química Universidad Nacional de Colombia - Sede Manizales
E-mail:ccardonaal@unal.edu.co
RESUMEN
En este trabajo se midió experimentalmente el equilibrio líquido vapor para el sistema binario Metanol - Acetato de Metilo a 580 mmHg. Las mediciones experimentales fueron realizadas utilizando un equipo con recirculación tipo Cottrell. Los datos obtenidos fueron comparados con los resultados adquiridos de la simulación del equilibrio líquido vapor del sistema bajo estudio. En la simulación se empleó el modelo de actividad NRTL para representar la no idealidad de la fase líquida (con parámetros encontrados en la literatura), y la ecuación de estado de Hayden O´Connel para la no idealidad de la fase vapor. De igual manera, se correlacionaron los datos para encontrar nuevos parámetros del modelo de actividad en NRTL. Además, a partir de datos experimentales medidos a 760 mmHg encontrados en la literatura para el sistema estudiado, se verificó la ley de Vresky, la cual permite sin necesidad de cálculos rigurosos predecir la dirección de desplazamiento de un azeótropo binario cunado se varía la presión del sistema.
Palabras Claves:Equilibrio líquido vapor, Ley de Vrevsky, metanol, acetato de metilo.
ABSTRAC
In this work the liquid - vapor binary equilibrium for the system Methanol - Methyl Acetate was measured at 580 mmHg using equipment with recirculation that also can be employed for reactive mixtures. The obtained data was compared with liquid vapor equilibrium prediction employing NRTL activity model for the liquid phase (using parameters found in the literature) and the Hayden O´Connel's equation of state for the non ideality of vapor phase. New parameters of NRTL activity model were obtained. The Vresky law that permits without rigorous calculations to predict qualitatively the displacement of binary azeotropes by pressure changes was confirmed, using various experimental data that is reported in the literature for this system at 760 mm Hg.
Keywords:Vapor-Liquid equilibrium, Vrevsky´s Law, Methyl acetate, Methanol.
INTRODUCCIÓN
Un aspecto importante del diseño de procesos químicos es el entendimiento adecuado del comportamiento termodinámico del sistema analizado. Este comportamiento debe alcanzar un estado de equilibrio bajo ciertas condiciones fisicoquímicas denominado equilibrio de fases. Es importante resaltar que la predicción del equilibrio de fases es la base fundamental para el diseño de los principales equipos de separación en la industria de procesos.
Así mismo se ha demostrado en los últimos años que la exactitud en la medición y predicción del equilibrio de fases de sistemas reactivos son la base de un buen diseño para procesos simultáneos como la destilación reactiva (1, 2).
Actualmente se encuentran disponibles una gran variedad de modelos que pueden predecir de forma precisa el equilibrio de fases para sistemas binarios o incluso para sistemas multicomponentes. Estos modelos se han desarrollado dependiendo de la naturaleza química de las sustancias que intervienen y de las interacciones que presentan entre si. No obstante, la obtención de datos experimentales de equilibrio es de suma importancia para verificar la confiabilidad de dichos modelos y de esta manera poderlos aplicar. A esto se le suma la necesidad de examinar muchos datos de la literatura que se obtuvieron a presión atmosférica y que se utilizan deliberadamente a cualquier presión utilizando correlaciones.
En el calculo de algunos equilibrios de fases, es común encontrar sistemas que tengan puntos estacionarios (azeótropos) que dificultan la separación de mezclas multicomponentes. Estos azeótropos son limitantes termodinámicas presentes en estos sistemas. Por tal razón es de vital importancia conocer profundamente el comportamiento de estas mezclas para que dichas limitaciones no afecten de manera considerable la separación. Este artículo además de presentar el equilibrio de fases para la mezcla acetato de metilo - metanol estudia el desplazamiento de su azeótropo con la presión. De este desplazamiento dependen las regiones de separación por destilación y por ende las posibilidades de separación en este sistema. Todo esto es la base para poder modelar el respectivo proceso de obtención de acetato de metilo por esterificación del ácido acético con metanol (3).
Desplazamiento del Azeótropo con la Presión.La destilación de mezclas azeotrópicas a diferentes presiones se basa en que la composición del azeótropo generalmente se desplaza al variar la presión. Esto fue suficientemente explicado por Vrevsky, Storonkin y Morochevsky (4, 5). En general la ecuación de estado termodinámica para una mezcla azeotrópica se expresa en función de la ecuación de Clapeiron Claussius:
Donde P: presión de vapor, T: temperatura del sistema, Q: calor molar parcial de vaporización, V: delta de volumen. La forma de esta ecuación debido a la igualdad xi = yi parece ser una ecuación de estado de un componente. Lo anterior permite suponer que con respecto a la dependencia de la temperatura y la presión, la mezcla azeotrópica tiene un comportamiento parecido al de una sustancia pura.
La relación entre la temperatura y la presión según la ecuación 1, se define por los efectos de transición de fase volumétrico V(12) y energético o calorífico Q(12). A presiones subcríticas el V(12) y el Q(12) tienen el mismo signo, lo que significa que un aumento de presión conlleva a un aumento de la temperatura de ebullición de la mezcla azeotrópica. Debido a que entre estos parámetros de estado existe una relación sencilla (ecuación 1) en vez de la influencia de la presión sobre la composición de la mezcla azeotrópica se puede tomar la influencia de la temperatura.
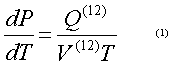
En el presente caso, los azeótropos binarios son los de mayor interés para un análisis de cambio de composición por presiones ya que, los azeótropos ternarios y cuaternarios generalmente pertenecen a una separatriz de primer grado (dentro del simplex concentracional) y por ende el desplazamiento de la separatriz por la presión debe ser modelado en la etapa de la síntesis del diagrama de destilación o también llamado mapa de curvas de residuo. De tal manera se aplica la segunda ley de Vrevsky (6).
Donde x: Composición molar de la fase líquida, T: temperatura, P: presión, V: volumen molar, L1,L2: Calores normales de vaporización de los componentes, xaz: composición molar del azeótropo,y: coeficiente de actividad.
Al observar las ecuaciones 2 y 3 queda claro que el signo de las derivadas (dx/dT)az y (dx/dP)az se define por el signo de la derivada parcial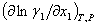 y también por el signo de la diferencia L1 -L2 . El análisis realizado por Kogan (6) demostró que para sistemas con desviaciones positivas de la idealidad en el punto extremo de temperatura y presión,
y también por el signo de la diferencia L1 -L2 . El análisis realizado por Kogan (6) demostró que para sistemas con desviaciones positivas de la idealidad en el punto extremo de temperatura y presión,
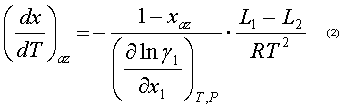
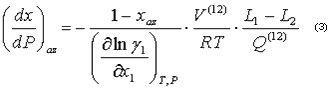
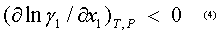
Y para los sistemas con desviaciones negativas de la idealidad
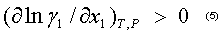
Por lo anterior, para los azeótropos binarios positivos (con temperatura de ebullición mínima)
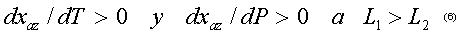
y para los azeótropos binarios negativos (con máxima temperatura de ebullición)
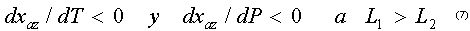
Las anteriores desigualdades se conocen popularmente como una aplicación de la segunda ley de Vrevsky, y permiten sin necesidad de cálculos rigurosos predecir la dirección del desplazamiento de un azeótropo binario al variar la presión. De tal manera que si tenemos por ejemplo un azeótropo con mínima temperatura de ebullición, el aumentar la presión generará un enriquecimiento del componente 1 en la composición del azeótropo si el calor molar parcial de evaporación del componente 1 es mayor que el componente 2. En el caso en que el calor molar parcial de evaporación del componente 2 sea mayor que el del componente 1, la composición del azeótropo se enriquecerá en el componente 2.
Para entender mejor lo anteriormente descrito se realizó el análisis del sistema binario metanol y acetato de metilo los cuales hacen parte del sistema de obtención del acetato de metilo por esterificación del ácido acético con metanol. Para realizar el análisis, es necesario llevar a cabo la simulación del sistema binario y corroborarlo a partir de resultados experimentales. Con este fin se dispone de datos experimentales a 760 mmHg (7) y a 580 mm de Hg obtenidos en este trabajo.
PARTE EXPERIMENTAL
Para la determinación experimental del equilibrio de fases del sistema binario metanol y acetato de metilo se ha utilizado un equipo con sistema de recirculación diseñado y modificado por los profesores Moszhukhin y Cardona (8); dicho equipo también es empleado para el estudio de equilibrio de fases en sistemas con reacción química, (ver Figura 1).
En este equipo la muestra alimentada es constantemente recirculada por medio de un sistema tipo Cottrell (sistema que consiste de un tubo con una resistencia que vaporiza la mezcla, este tubo va conectado a otro tubo de diámetro menor que permite una intensa recirculación en todo el sistema) para asegurar que las fases están en contacto intimo entre si; después de la primera hora de operación se extraen muestras para análisis cada 15 minutos hasta alcanzar la estabilización del sistema (la cual siempre estuvo cercana a las dos horas de funcionamiento para este sistema binario).
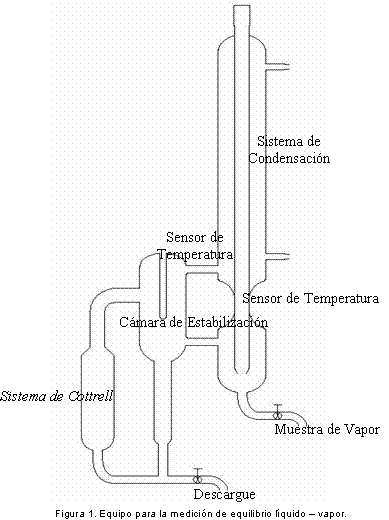
El procedimiento experimental empleado inicia con la carga del equipo con la mezcla binaria a una composición conocida, luego de alcanzar el estado de equilibro se tomaron muestra y contra muestra por punto, la contra muestra permitía verificar posteriormente los resultados obtenidos en la muestra. Con el ánimo de comprobar la reproducibilidad del procedimiento y del equipo experimental cada experimento se repitió 2 veces. Cabe adicionar que las condiciones de equilibrio se alcanzaban cuando las composiciones y temperaturas de las fases no cambiaban en el tiempo. Por esta razón fue necesario tomar datos de temperatura cada 15 minutos hasta que la condición de equilibrio fuera alcanzada.
MATERIALES Y EQUIPOS DE MEDIDA
Los reactivos utilizados en el desarrollo experimental fueron: a) Metanol Grado reactivo marca Fischer, b) Acetato de Metilo Grado Reactivo marca Carlo-Erba. Las temperaturas del experimento fueron medidas con termómetros digitales con una tolerancia de ±0.05 °C conectados con una interfase de computador donde se podía verl el alcance del equilibrio en el tiempo. La presión al inicio de los experimentos se midió con un barómetro marca CASIO 1160 DW6500.
Las muestras obtenidas fueron analizadas por medio de índice de refracción y cromatografía de gases; el cromatógrafo utilizado fue PERKIN ELMER Autosystem XL con detector FID, gas de arrastre He con velocidad de 2 ml por minuto, la temperatura de inyección fue 40 °C y temperatura de detección 250 °C; la columna de identificación PE-WAX de 30m X 0.32 mm, la cual identifica correctamente los compuestos analizados. La medida de las composiciones de las muestras experimentales fue realizada principalmente utilizando el índice de refracción. Es importante resaltar que la correlación obtenida entre la composición de la mezcla binaria y el índice de refracción fue verificada utilizando el cromatógrafo de gases, corroborando que los datos (12 en total) de composición dados por esta técnica correspondían de forma directa a los entregados por la técnica instrumental.
RESULTADOS Y DISCUSIONES
Para verificar la validez de los datos obtenidos experimentalmente se realizo una simulación del equilibrio liquido-vapor utilizando como modelo de fugacidad la ecuación de Hayden O´Connel (9) y para la no idealidad de la fase liquida se utilizo el modelo de actividad de NRTL; ambos modelos fueron seleccionados por su alto grado de confiabilidad para el sistema analizado.
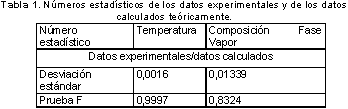
Los datos experimentales y los datos calculados por los modelos mencionados, fueron sometidos a análisis estadísticos que incluían la desviación estándar y la prueba F. La tabla 1 muestra que los datos experimentales comparados con los obtenidos teóricamente presentan una baja desviación estándar, lo que indica que los valores experimentales concuerdan en gran medida con los calculados teóricamente. Aún así, para corroborar de forma más eficaz el resultado obtenido por la desviación estándar se aplicó la prueba F. La prueba F, permite determinar la probabilidad de que las varianzas de dos grupos de datos no presenten diferencias significativas. Para el caso bajo estudio la prueba F se aplicó a los grupos de datos experimentales temperatura y composición fase vapor.
Estos grupos experimentales fueron confrontados con sus homólogos calculados teóricamente obteniéndose los valores de la prueba F mostrados en la tabla 1. Se nota que la probabilidad de que los datos experimentales concuerden con los calculados es superior al 83% para el caso del conjunto de datos pertenecientes a la composición de la fase vapor y del 99% para el caso de los datos que pertenecen al grupo de la composición de la fase líquida, la temperatura es la que tiene la mayor probabilidad de concordancia con un 99.9% de probabilidad. Estos resultados indican que los datos experimentales y los calculados teóricamente son confiables y que la probabilidad de que esa confiabilidad sea cierta es del 83.24% (valor de menor probabilidad para el caso de la fase vapor).
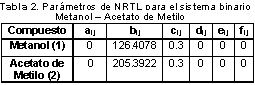
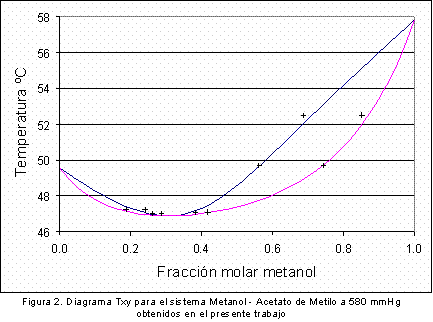
La Figura 2 y la Figura 3 muestran los puntos obtenidos experimentalmente a una presión de 580 mmHg confrontados con la simulación realizada previamente mediante los diagramas Txy y xy respectivamente. Como puede observarse, los resultados obtenidos se acercan adecuadamente a la curva de equilibrio obtenida en la simulación, de esta manera se puede concluir que los resultados obtenidos en este equipo presentan una elevada confiabilidad. La Tabla 2 muestra los parámetros de interacción binaria calculados para el sistema binario metanol acetato de metilo a 580 mm Hg a partir de los datos experimentales mostrados en las figuras 2 y 3
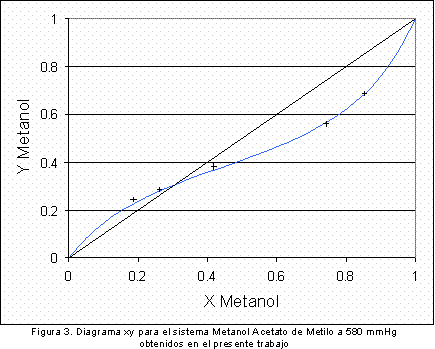
Vista la concordancia de los datos experimentales y teóricos, se procedió a verificar la ley de Vrevsky. Para aplicar esta Ley es necesario contar con los datos del calor normal de vaporización de los compuestos puros ( Tabla 3 ) e introducirlos dentro de las ecuaciones 2 y 3 para obtener los valores que se listan en la tabla 3.

De la tabla anterior se deduce que en vista de que el calor de vaporización del metanol es mayor que el del acetato de metilo, al disminuir la presión el azeótropo se desplazará hacia un aumento en la composición del acetato. Para lograr establecer la veracidad de esta conclusión fue necesario encontrar la composición del azeótropo metanol-acetato de metilo a dos presiones diferentes a 580 mm Hg y a 760 mm de Hg. A condiciones de presión de 760 mmHg se utilizaron los valores experimentales reportados por Dovroserdov (7); los resultados de este estudio se presentan en la Figura 4 y la Figura 5 .
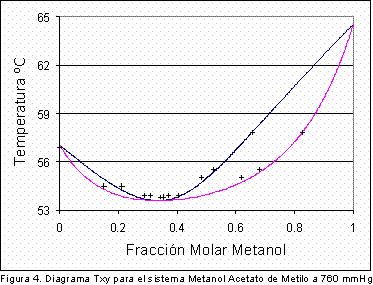
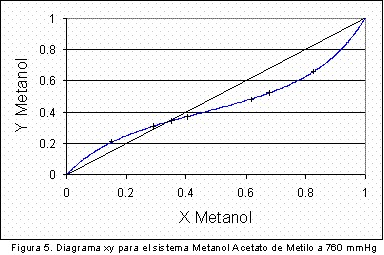
En la Tabla 4 se presentan los datos de composición y temperatura del azeótropo binario metanol/acetato de metilo obtenidos en las simulaciones realizadas a 760 y 580 mmHg.

Observando los resultados de los datos experimentales a 580 y 760 mm de Hg es posible aseverar que la ley de Vrevsky es válida para el azeótropo binario metanol acetato de metilo. Para verificar la validez general de la ley de Vrevsky es necesario realizar estudios en otros sistemas.
CONCLUSIONES
Según los resultados presentados en los análisis estadísticos es posible asegurar que el equipo experimental y los análisis instrumentales utilizados en el presente trabajo son confiables para el sistema bajo estudio. No obstante, es importante verificar la confiabilidad del equipo testeando otros sistemas e incorporando otros modelos termodinámicos. La ecuación NRTL está prevista de parámetros de interacción binaria ajustables para permitir mejorar la correlación de los datos experimentales con el modelo. Se observó además que los datos experimentales con menor probabilidad de concordancia son los que pertenecen a la fase vapor, esto puede ser debido a que le equipo tiene una pequeña zona donde no se realiza una mezcla homogénea de los componentes de la fase vapor cuando éstos son condensados, de tal manera que para mejorar el equipo es posible incluir un agitador magnético para asegurar la perfecta mezcla de los condensados.
En cuento a la ley de Vrevsky se demostró que es valida como planteamiento termodinámico para el azeótropo binario metanol-acetato de metilo y que es una poderosa herramienta para permitir sin necesidad de cálculos rigurosos conocer cualitativamente el desplazamiento del azeótropo. Esta ley debe ser corroborada para otros sistemas en otros rangos de presión para así poder determinar el verdadero alcance de la ecuación. El potencial que demuestra esto es de alta importancia para predecir también el desplazamiento de separatrices en destilación de sistemas multicomponentes, pues al tener claro el sentido del desplazamiento del azeotropo, también queda claro el desplazamiento que tendrá la separatriz termodinámica que lo incluye en su fronteras y separa las regiones de destilación. De estos análisis dependen las estructuras de destilación con cambio de presión y de procesos de destilación reactiva (1) donde la escogencia de la presión puede determinar la eficiencia del sistema.
BIBLIOGRAFÍA
1. Pisarenko, Yu.; Serafimov, L.; Cardona, C.; Efremov, D.; Shumalov, A. (2001). Reactive Distillation Design: Analysis of the Process Statics. En: Reviews In Chemical Engineering - Freund Publishing House Israel-England, Vol. 17, No 4, p.76. [ Links ]
2. Cardona, C. (2004). Aplicación de la Destilación Reactiva en Colombia para la Obtención de Acetatos y Aditivos Oxigenantes. Informe final, proyecto de investigación DIMA - Universidad Nacional de Colombia sede Manizales. [ Links ]
3. Cardona, C.; Matallana, L.; Gómez, P.; Cortes, L.; Pisarenko Y. (2002). Phase equilibrium and residue curve analysis in DIPE production by reactive distillation. VI Conferencia Iberoamericana sobre equilibrio de fases para el diseño de procesos. Foz de Iguazú, Brasil. [ Links ]
4. Vrevsky, M, S. (1953). Works in Solutions Theory. Academia de la Ciencia URSS, [ Links ]
5. Storonkin, A.; Morochevsky, A. (1957). Journal of Physical Chemistry. Vol. 31. N. 32. [ Links ]
6. Kogan, V, B. Azeotropía y destilación Extractiva. Khimia, Moscow 1971. [ Links ]
7. Dovroserdov, L. P.; Bagrov, I. V. (1967) Journal of applied Chemistry. Vol. 40, No 4, 875-879. [ Links ]
8. Cardona, C. A. (2001). Diseño de Procesos de Destilación Reactiva para la Producción de Alkil Acetatos a Partir de Anhídrido Acético. Tesis PhD. Lomonosov Academy of Fine Chemical Engineering. Moscow. [ Links ]
9. Hayden, J. G.; O'Connell, J. P. (1975). A generalized method for predicting second virial coefficients. Ind. Eng. Chem. Process Des. Dev., 14 (3), 209-216. [ Links ]














