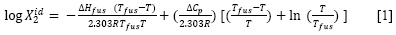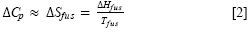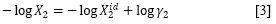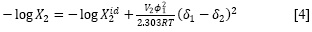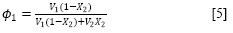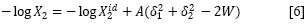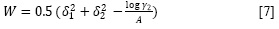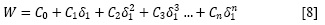Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Revista Colombiana de Química
Print version ISSN 0120-2804
Rev.Colomb.Quim. vol.45 no.1 Bogotá Jan./Apr- 2016
https://doi.org/10.15446/rev.colomb.quim.v45n1.57201
DOI: http://dx.doi.org/10.15446/rev.colomb.quim.v45n1.57201
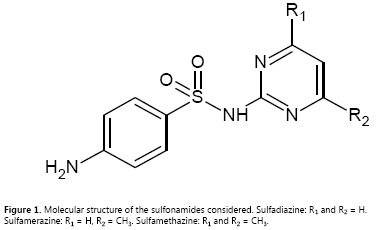
Extended Hildebrand solubility approach applied to some structurally related sulfonamides in ethanol + water mixtures
Método extendido de Hildebrand en la estimación de la solubilidad de algunas sulfonamidas estructuralmente relacionadas en mezclas etanol + agua
Método ampliado de Hildebrand na estimação da solubilidade da algumas sulfamidas estruturalmente relacionadas em misturas do etanol + agua
Daniel R. Delgado1, María Á. Peña2, Fleming Martínez3*
1 Programa de Ingeniería Industrial, Facultad de Ingeniería, c Universidad Cooperativa de Colombia. Neiva, Colombia.
2 Departamento de Ciencias Biomédicas, Facultad de Farmacia, Universidad de Alcalá, Alcalá de Henares. Madrid, Spain.
3 Grupo de Investigaciones Farmacéutico Fisicoquímicas, Departamento de Farmacia, Facultad de Ciencias, Universidad Nacional de Colombia - Sede Bogotá, Cra. 30 No. 45-03. Bogotá D.C., Colombia.
* Corresponding Author: fmartinezr@unal.edu.co
Article citation: Delgado, D. R; Peña, M. Á; Martínez, F. Extended Hildebrand solubility approach applied to some structurally related sulfonamides in ethanol + water mixtures. Rev. Colomb. Quim. 2016, 45(1), 34-43. DOI: http://dx.doi.org/10.15446/rev.colomb.quim.v45n1.57201
Recibido: 15 de Febrero de 2016. Aceptado: 29 de Marzo de 2016.
Abstract
Extended Hildebrand Solubility Approach (EHSA) was applied to evaluate the solubility of sulfadiazine, sulfamerazine, and sulfamethazine in some ethanol + water mixtures at 298.15 K. Reported experimental equilibrium solubilities and some fusion properties of these drugs were used for the calculations. In particular, a good predictive character of EHSA (with mean deviations lower than 3.0%) were found by using regular polynomials in order four correlating the interaction parameter W with the Hildebrand solubility parameter of solvent mixtures without drug. The predictive character of EHSA was the same as that obtained by direct correlation of drug solubilities with the same descriptor of polarity of the cosolvent mixtures.
Keywords: Sulfonamides, ethanol, binary mixtures, extended Hildebrand solubility approach, Hildebrand solubility parameter.
Resumen
Se aplicó el Método Extendido de Solubilidad de Hildebrand (MESH) al estudio de la solubilidad de sulfadiazina, sulfamerazina y sulfametazina en mezclas binarias etanol + agua a 298,15 K. Se utilizaron valores reportados de solubilidad en equilibrio y algunas propiedades fisicoquímicas de fusión de estos compuestos. Se obtuvo una adecuada capacidad predictiva del MESH (con desviaciones promedio menores del 3,0%) al utilizar modelos polinómicos regulares de cuarto orden relacionando el parámetro de interacción W con el parámetro de solubilidad de Hildebrand de las mezclas solventes. El carácter predictivo del MESH fue de magnitud semejante al que se obtuvo calculando esta propiedad directamente, donde se utilizó una regresión empírica regular de cuarto orden de la solubilidad experimental logarítmica de los fármacos en función del parámetro de solubilidad de las mezclas disolventes.
Palabras clave: Sulfonamidas, etanol, mezclas binarias, método extendido de solubilidad de Hildebrand, parámetro de solubilidad de Hildebrand.
Resumo
Na presente investigação, aplicou-se o Método Estendido de Solubilidade do Hildebrand (MESH) ao estudo da solubilidade da sulfadiazina, sulfamerazina e sulfametazina em misturas binárias etanol + agua a 298,15 K. Obteve-se uma adequada capacidade preditiva (com menor desvio padrão de 3,0%) do MESH ao utilizar modelos polinomiais regulares de quarta ordem relacionando o parámetro de interação W com o parâmetro de solubilidade do Hildebrand das misturas de solventes. O caráter preditivo do MESH foi semelhante ao obtido pelo cálculo utilizando uma regressão empírica regular da quarta ordem, da solubilidade experimental logarítmica dos fármacos em função do parâmetro de solubilidade das misturas dissolventes.
Palavras-Chave: Sulfamidas, etanol, misturas binárias, método estendido de solubilidade do Hildebrand, parâmetro de solubilidade do Hildebrand.
Introduction
Sulfonamides are synthetic drugs used to treat certain infections caused by a wide group of microorganisms in human and veterinary medicine practice (1-3). Nevertheless, the physicochemical properties of these drugs in aqueous solutions have not yet been studied completely (4). Regarding their aqueous solubilities, it is well known that they are very low, being considered as very slightly soluble or even practically insoluble (5). In this way, it has been reported that the cosolvency is the best technique used in pharmacy for increasing the drugs equilibrium solubility (6-8).
Moreover, it is clear that predictive methods of physicochemical properties of drugs, in particular those intended to estimate their solubilities, are very important for pharmaceutical and chemical industry. This is because these methods allow the optimization of several design and development processes (4) In this regard, some recent examples of these developments about the solubility prediction of drugs are described in the literature as follows: in neat water (9), in simulated gastrointestinal fluids (10), in organic solvents (11) and in mixed solvents (12-14). In addition, some attempts to estimate the solubility of sulfonamides in different aqueous or organic media have been reported in the literature (15-17).
For this reason, this research presents a physicochemical study about the solubility prediction of three structurally related sulfonamides, namely, sulfadiazine (SDZ, Fig. 1), sulfamerazine (SMR, Fig. 1) and sulfamethazine (SMT, Fig. 1), in binary mixtures conformed by ethanol (EtOH) and water at 298.15 K. The study was performed based on the Extended Hildebrand Solubility Approach (EHSA) (8, 18) by using reported experimental equilibrium solubility values and some thermal properties relative to the fusion of these drugs (19-21). Thus, this communication is similar to those developed previously for other drugs in the same cosolvent mixtures (22-26), and also to that developed about the behavior of other sulfonamides in propylene glycol + water mixtures (27).
It is crucial to note that EHSA method has been widely used to study the solubility of many pharmaceutical compounds as has been exposed previously (28). Furthermore, it is still employed to analyze the behavior of several drugs in different cosolvent mixtures (29-32). On the other hand, it is remarkable that EtOH and its aqueous mixtures are the most employed solvent systems to develop liquid pharmaceutical dosage forms owing its solubilizing and antimicrobial properties (33, 34).
Theoretical background
In a first approach, based on the Henry's law, the ideal solubility (X2id) of a solid solute could be calculated by means of the following expression:
whereΔH fus is the molar enthalpy of fusion of the pure solute (at the melting point), Tfus is the absolute melting point, T is the absolute solution temperature, R is the constant gas (8.314 J/mol-K) and ΔCp is the difference between the molar heat capacity ofthe crystalline form and the molar heat capacity of the hypothetical supercooled liquid form, both at the solution temperature. Since ΔCp values are not commonly reported, they may be approximated to the entropy of fusion, ΔSfus calculated as follows:
Ideal solubility depends on the physicochemical properties of the solid compound without considering the properties of the solvent. In this way, the ideal solubility would be higher if the solute-solute interactions are lower (35). Accordingly, compounds with high values of melting point and enthalpy of fusion have lower ideal solubilities.
On the other hand, the real solubility (X2) of a solid solute in a liquid solution is analyzed by means of the following expression (25-27):
Her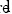 og γ2 is the non-ideality term with ½ as the solute activity coefficient defined on asymmetric basis. This property is determined experimentally from real and ideal solubilities. Nevertheless, a classical method of Y2 calculations is based on the regular solutions model as:
og γ2 is the non-ideality term with ½ as the solute activity coefficient defined on asymmetric basis. This property is determined experimentally from real and ideal solubilities. Nevertheless, a classical method of Y2 calculations is based on the regular solutions model as:
where, V2 is the partial molar volume of the solute, Φ1 is the volume fraction of the solvent in the saturated solution and δ1 and δ2 are the Hildebrand solubility parameters of solvent and solute, respectively. Φ1 is calculated as:
where V1 is the molar volume of the solvent.
However, all the pharmaceutical aqueous dissolutions deviate significantly from that predicted by the regular solutions theory. For this reason, Martin et al. (36-42) developed the EHSA method. Thereby, if the A term (defined as V2Φ21 /(2.303RT)) is introduced in the equation [4], the real solubility of drugs can be calculated from the expression:
Here, the W term is equal to 2Kδ1δ2 (where, K is the Walker parameter (18)). The W factor can be calculated from experimental data by means of:
where, y2 is the activity coefficient of the solute in the saturated solution and it is calculated as: X2id /X2. The experimental values of the W parameter can be correlated by means of regression analysis by using regular polynomials as a function of δ1 as follows:
These empiric models can be used to estimate the drug solubility by means of back-calculation, resolving this property from the specific W value obtained in the respective polynomial regression (25, 26).
Results and discussion
The required properties about the sulfonamides studied such as ideal solubility, molar volume, and Hildebrand solubility parameter are presented in Table 1 (5, 21, 22). The volumetric behavior and polarity of EtOH + water mixtures, as a function of the composition, is shown in Table 2. Volume fractions and Hildebrand solubility parameters were calculated assuming additive behavior (8, 43). Table 2 also summarizes the experimental solubility of the sulfonamides expressed in molarity and mole fraction reported in the literature (20, 21).
In all cases the relative standard deviations in reported solubilities were lower than 2.0% (20, 21). It is important to note that by using the inverse Kirkwood-Buff integrals (44-46) these drugs are preferentially solvated by water in water-rich and EtOH-rich mixtures but preferentially solvated by EtOH in mixtures with similar proportions of both solvent components (47). These results were interpreted as a consequence of hydrophobic hydration around the non-polar moieties of these sulfonamides in aqueous-rich mixtures and by polarity effects in those mixtures of similar proportions.
Similar considerations about the aqueous behavior have been reported from the temperature-dependence of their octanol-water partition coefficients (48). Moreover, these sulfonamides are acting as Lewis acids with ethanol molecules, because this cosolvent is more basic than water based on their Kamlet-Taft hydrogen bond acceptor parameters reported (as β = 0.75 for ethanol and 0.47 for water) (49). Furthermore, in EtOH-rich mixtures, where these drugs are preferentially solvated by water again, these results were analyzed by considering that the sulfonamides are acting mainly as Lewis bases with water based on the Kamlet-Taft hydrogen bond donor parameters of the solvents, i.e. α = 1.17 for water and 0.86 for EtOH, respectively (50, 51).
Figure 2 shows the ideal and experimental solubility, as well as those calculated by using the regular solution model (equation [4]), as a function of the Hildebrand solubility parameter of the solvent mixtures, i.e. from 26.5 to 47.8 MPa½. In order to use equation [4] the molar volume and Hildebrand solubility parameter of the sulfonamides were taken from the literature as shown in Table 1 (20, 21). These values were calculated by using the groups' contribution method proposed by Fedors (52).
Regarding Fig. 2, it is noteworthy that the regular solutions model predicts that the maximum solubility value corresponds to the ideal solubility and this is obtained when both the Hildebrand solubility parameters of drug and solvent mixture are coincident. In a similar way, according to the literature the maximum experimental solubility values are found when the Hildebrand solubility parameters of both solute and solvent are also coincident (8, 18), despite they can be very different regarding the ideal solubility.
The Φ1 values for all these sulfonamides, calculated according to equation [5], are almost equal to 1.000 because the solubility of these sulfonamides is very low in all the solvent system considered (Table 3). The activity coefficients of these sulfonamides expressed as decimal logarithms are also shown in Table 3. Analysis of these activity coefficients has been reported previously in the literature (20, 21). Briefly, based on the activity coefficients magnitudes it follows that the solvent-solvent interactions are higher in neat water (with Hildebrand solubility parameter δ = 47.8 MPa½) and they are smaller in ethanol (with δ = 26.5 MPa½) (50).
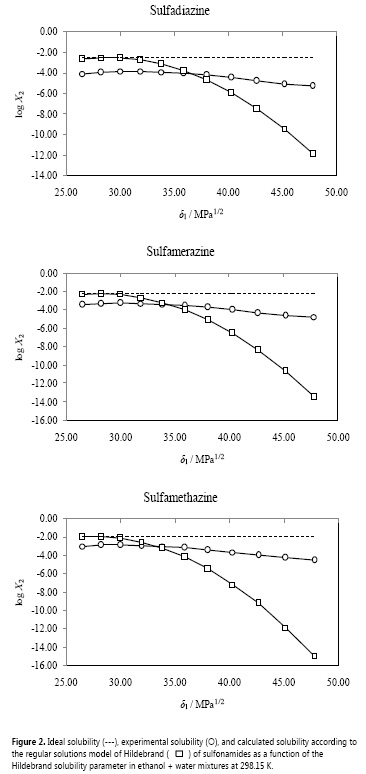
Pure water and water-rich mixtures exhibiting larger log y2 values (even higher than 2.80) would imply high solvent-solvent interactions and low solvent-solute interactions. On the other hand, in ethanol-rich mixtures (exhibiting log y2 values between 0.90 and 1.30), the solvent-solvent interactions are comparatively low and the solvent-solute interactions would relatively be high. Accordingly, the solvation of these sulfonamides would be just higher in ethanol-rich mixtures. Table 3 also summarizes the calculated parameters A, K, and W of the sulfonamides in EtOH + water mixtures.
Figure 3 shows that the W parameter of all sulfonamides exhibits some deviation from the linear behavior with respect to the Hildebrand solubility parameter of the solvent mixtures. This behavior is expectable because the W term implies the summation of two quadratic (δ21and δ22 ) and one non-constant-quotient (-log y2/A) terms (equation [7]).
W values were adjusted to regular polynomials in orders from 2 to 5 (equation [8]) (53). As comparison the linear equation was also considered. Table 4 summarizes the coefficients obtained in all the regular polynomials for these sulfonamides.
Searching for the best adjust, the first criterion used to define the best polynomial order of W term as function of δ1 was the fitting standard error (Table 4). As another comparison criterion, the difference percentages between the experimental solubilities and those calculated by using EHSA were also calculated as shown in Table 5.
It is observed that as more complex is the polynomial used, there is a better correlation between experimental and calculated solubility. Accordingly, the most important increment, in concordance, is obtained by passing from linear equation to polynomial in order 2. The concordances also increase significantly from orders 2 to 3 and 3 to 4.
Nevertheless, from order 4 to 5 the concordance increment is not so much relevant, because in the last case the mean uncertainties obtained are in the same order or lower than those reported experimentally (20, 21). It is important to know that uncertainties lower than 5% are useful for pharmaceutical purposes, but better agreements are required for academic and theoretical purposes.
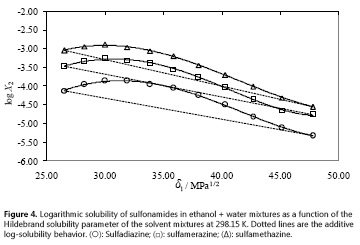
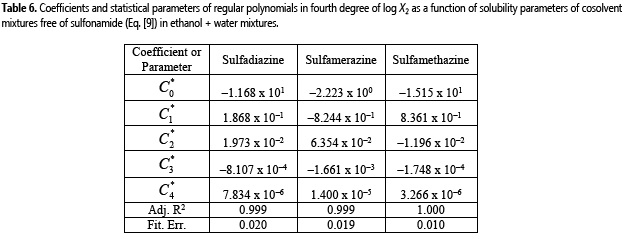
As it has already been described, regarding the practical usefulness of the EHSA, a very important consideration is about the complex calculations involving other experimental variables of solute and solvents, instead of the simple empirical regression of the experimental solubility values as a function of the Hildebrand solubility parameters of solvent mixtures as shown in Fig. 4 (18). For this reason, Table 6 shows the coefficients of regular polynomials in order 4 of log X2 vs. δ1 values (equation [9]) (18), whereas Table 7 shows the calculated values of solubility by using equation [9] and also the respective deviation percentages in front of the experimental ones.
It is noteworthy that empirical regular polynomials, as shown in equation [9], are commonly referred as Bustamante's Equation and are widely used in pharmaceutical sciences owing its simplicity, as has been described in the literature (4).
By using both calculation methods, the same mean deviation percentages were obtained as shown in Tables 5 and 7, i.e. 2.65%, 2.82% and 1.41% for sulfadiazine, sulfamerazine, and sulfamethazine, respectively. This behavior is similar to those described earlier for other drugs in different cosolvent mixtures (22-28). Thereby, the results for these sulfonamides could indicate a non-significant usefulness of EHSA method for practical and academic purposes. Nevertheless, it is necessary to know that this correlative method considers the drug solubility from a complete thermodynamic viewpoint.
In this way, the main point about these calculations is about to find an effective method for the Walker K parameter estimation to calcúlate the W term as 2Kδ1δ2. Because the δ1 and δ2 terms would be known, the drug experimental solubility could be calculated in any mixture (18).
Conclusion
In this research, the extended Hildebrand solubility approach was adequately used to analyze the solubility of sulfadiazine, sulfamerazine, and sulfamethazine in EtOH + water mixtures at 298.15 K. A good predictive character within 3.0% were observed by using regular polynomials in orders four by correlating the interaction parameter W with the Hildebrand solubility parameter of the solvent mixtures without drugs. Nevertheless, the predictive character of EHSA method is the same as the one obtained by direct correlation of the sulfonamides solubility and the same descriptor of polarity of the cosolvent mixtures. Ultimately, it is noteworthy that this research expands the analyses developed previously based on classical dissolution thermodynamic properties as well as the preferential solvation of the drugs by the solvent components (20, 21, 47).
References
1. Korolkovas, A. Essentials of Medicinal chemistry 2nd ed.; John Wiley & Sons, Inc.: New York (NY), 1988; pp. 699-716. [ Links ]
2. Gelone, S.; O'Donnell, J. A. Anti-infectives. In Remington: The Science and Practice of Pharmacy, 21st ed; Gennaro A. Ed.; Lippincott Williams & Wilkins: Philadelphia (PA), 2005; pp. 1630-1633. [ Links ]
3. Delgado, D. R.; Rodríguez, G. A.; Martínez, J. A.; Rojas, J. H.; Martínez, F. Validación de una metodología analítica empleando espectrofotometría UV/vis para el estudio de la solubilidad de algunas sulfonamidas en mezclas cosolventes alcohol ' agua. Rev. Colomb. Quim. 2013, 42 (3), 31-40. [ Links ]
4. Jouyban, A. Handbook of Solubility Data for Pharmaceuticals. CRC Press: Boca Raton (FL), 2010; pp. 453-461. [ Links ]
5. Budavari, S.; O'Neil, M. J.; Smith, A.; Heckelman, P. E.; Obenchain, J. R., Jr.; Gallipeau, J. A. R.; D'Arecea, M. A. The Merck index, an encyclopedia of chemicals, drugs, and biologicals, 13th ed; Merck & Co. Inc.: Whitehouse Station, NJ, 2001; pp. 1585-1595. [ Links ]
6. Rubino, J. T. Cosolvents and cosolvency. In Encyclopedia of Pharmaceutical Technology; Swarbrick J., Boylan J. C. Eds.; Marcel Dekker, Inc.: New York (NY), 1988; vol. 3, pp. 375-398. [ Links ]
7. Yalkowsky, S. H. Solubility and Solubilization in Aqueous Media. American Chemical Society and Oxford University Press: New York (NY), 1999; pp. 180-235. [ Links ]
8. Martin, A.; Bustamante, P.; Chun, A. H. C. Physical chemical Principles in the Pharmaceutical Sciences 4th ed.; Lea & Febiger: Philadelphia (PA), 1993; pp. 227-229. [ Links ]
9. Wang, J.; Hou, T. Recent advances on aqueous solubility prediction. comb. chem. High Throughput Screen. 2011, 14 (5), 328-338. DOI: http://dx.doi.org/10.2174/138620711795508331. [ Links ]
10. Jonas H. Fagerberg, J. H.; Karlsson, E.; Ulander, J.; Hanisch, G.; Bergstróm, Ch. A. S. Computational prediction of drug solubility in fasted simulated and aspirated human intestinal fluid. Pharm. Res. 2015, 32 (2), 578-589. DOI: http://dx.doi.org/10.1007/s11095-014-1487-z. [ Links ]
11. Abraham, M. H.; Smith, R. E.; Luchtefeld, R.; Boorem, A. J.; Luo, R.; Acree, W. E. Jr. Prediction of solubility of drugs and other compounds in organic solvents. J. Pharm. Sci. 2010, 99 (3), 1500-1515. DOI: http://dx.doi.org/10.1002/jps.21922. [ Links ]
12. Keramatnia, F.; Shayanfar, A.; Bozorgi, A. H.; Mottaghi, M.; Jouyban, A. Prediction of drug solubility data in polyethylene glycols + water mixtures at various temperatures. Lat. Am. J. Pharm. 2015, 34 (8), 1614-1621. [ Links ]
13. Jouyban, A.; Shayanfar, A.; Panahi-Azar, V.; Soleymani, J.; Yousefi, B. H.; Aeree, W. E. Jr.; York, P. Solubility prediction of drugs in mixed solvents using partial solubility parameters J Pharm. Sci. 2011, 100 (10), 4368-4382. DOI: http://dx.doi.org/10.1002/jps.22589. [ Links ]
14. Fujisawa, M.; Tsutsumi, H.; Kimura, T. Prediction of solubility of practically insoluble drugs in water/ethanol solvents using nonempirical methods. J. Chem. Pharm. Res. 2011, 3 (3), 750-758. [ Links ]
15. Regosz, A.; Pelpliñska, T.; Kowalski, P.; Thiel, Z. Prediction of solubility of sulfonamides in water and organic solvents based on the extended regular solution theory. Int. J. Pharm . 1992, 88, 437-442. DOI: http://dx.doi.org/10.1016/0378-5173(92)90344-2. [ Links ]
16. Martínez, F.; Gómez, A. Estimation of the solubility of some sulfonamides in aqueous media from partition coefficients and entropies of fusion. Phys. Chem. Liq. 2002, 40, 411-420. DOI: http://dx.doi.org/10.1080/0031910021000017735. [ Links ]
17. Hanaee, J.; Jouyban, A.; Dastmalchi, S.; Adibkia, K.; Mirzazadeh, A; Barzegarjalali, M Solubility prediction of sulfonamides at various temperatures using a single determination. DARU 2005, 13, 37-45. [ Links ]
18. Martin, A.; Bustamante, P. El parámetro de solubilidad en las ciencias farmacéuticas. Anal. RealAcad. Farm. 1989, 55, 175-202. [ Links ]
19. Martínez, F.; Gómez, A. Thermodynamic study of the solubility of some sulfonamides in octanol, water, and the mutually saturated solvents. J. Solution Chem. 2001, 30, 909-923. DOI: http://dx.doi.org/10.1023/A:1012723731104. [ Links ]
20. Delgado, D. R.; Martinez, F. Solution thermodynamics of sulfadiazine in ethanol + water mixtures. J. Mol. Liq. 2013, 187, 99-105. DOI: http://dx.doi.org/10.1016/j.molliq.2013.06.011. [ Links ]
21. Delgado, D. R.; Martínez, F. Solubility and solution thermodynamics of sulfamerazine and sulfamethazine in some ethanol + water mixtures. Fluid Phase Equilib. 2013, 360, 88-96. DOI: http://dx.doi.org/10.1016/j.fluid.2013.09.018. [ Links ]
22. Aragón, D. M.; Pacheco, D. P.; Ruidiaz, M. A.; Sosnik, A. D.; Martínez, F. Método extendido de Hildebrand en la predicción de la solubilidad de naproxeno en mezclas cosolventes etanol + agua. Vitae, Rev. Fac. Quím. Farm. 2008,15, 113-122. [ Links ]
23. Gantiva, M.; Martínez, F. Método extendido de Hildebrand en la predicción de la solubilidad del ketoprofeno en mezclas cosolventes etanol + agua. Quím. Nova 2010, 33, 370-376. DOI: http://dx.doi.org/10.1590/S0100-40422010000200025. [ Links ]
24. Ruidiaz, M. A.; Delgado, D. R.; Mora, C. P.; Yurquina, A.; Martínez, F. Estimation of the indomethacin solubility in ethanol + water mixtures by the extended Hildebrand solubility approach. Rev. Colomb. Cienc. Quím. Farm. 2010, 39, 79-95. [ Links ]
25. Sotomayor, R. G.; Holguín, A. R.; Cristancho, D. M.; Delgado, D., Martínez F. Extended Hildebrand Solubility Approach applied to the piroxicam solubility in ethanol + water mixtures. J Mol Liq. 2013, 180, 34-38. DOI: http://dx.doi.org/10.1016/j.molliq.2012.12.028. [ Links ]
26. Cristancho, D. M.; Delgado, D. R.; Martínez, F. Meloxicam solubility in ethanol + water mixtures according to the extended Hildebrand solubility approach. J. Solution Chem. 2013, 42, 1706-1716. DOI: http://dx.doi.org/10.1007/s10953-013-0058-y. [ Links ]
27. Cárdenas, Z. J.; Jiménez, D. M.; Delgado, D. R.; Peña, M. Á.; Martínez, F. Extended Hildebrand solubility approach applied to some sulphonamides in propylene glycol + water mixtures. Phys Chem Liq 2015, 53, 763-775. DOI: http://dx.doi.org/10.1080/00319104.2015.1048247. [ Links ]
28. Holguín, A. R.; Delgado, D. R.; Martínez, F. Indomethacin solubility in propylene glycol + water mixtures according to the extended Hildebrand solubility approach Lat Am J Pharm 2012, 31, 720-726. [ Links ]
29 Rathi, P B Solubility prediction of satranidazole in propylene glycol-water mixtures using extended Hildebrand solubility approach. Indian J. Pharm. Sci. 2011, 73, 670-674. DOI: http://dx.doi.org/10.4103/0250-474X.100243. [ Links ]
30. Deshpande, K. V.; Panzade, P. S.; Rathi, P. B. Prediction of nabumetone solubility in propylene glycol-water mixtures using extended Hildebrand solubility approach. Inn Pharm Pharmacother. 2013, 1, 117-127. [ Links ]
31. Gómez, J. L.; Rodríguez, G. A.; Cristancho, D. M.; Delgado, D. R.; Mora, C. P.; Yurquina, A.; Martínez, F. Extended Hildebrand solubility approach applied to nimodipine in PEG 400 + ethanol mixtures. Rev Colomb Cienc Quím Farm. 2013, 42, 103-121. [ Links ]
32. Rathi, P. B.; Deshpande, K. V. Extended Hildebrand Approach: An empirical model for solubility prediction of etodolac in 1,4-dioxane and water mixtures. J. Solution Chem. 2014, 43, 1886-1903. DOI: http://dx.doi.org/10.1007/s10953-014-0251-7. [ Links ]
33. Rowe, R. C.; Sheskey, P. J.; Owen, S. C. (Eds). Handbook of pharmaceutical excipients, 5th ed; Pharmaceutical Press and American Pharmacists Association: Grayslake, IL, 2006; pp. 18-20. [ Links ]
34. Billany, M. Solutions. In Pharmaceutics, The Science of Dosage Forms Design, 2nd ed; Aulton, M. E. (Ed); Churchill Livingstone: London, 2002; pp. 309-322. [ Links ]
35. Delgado, D. R.; Martínez, F. Solution thermodynamics and preferential solvation of sulfamerazine in some methanol + water mixtures. J. Solution Chem. 2015, 44, 360-377. DOI: http://dx.doi.org/10.1007/s10953-015-0317-1. [ Links ]
36. Martin, A.; Newburger, J.; Adjei, A. Extended Hildebrand approach: Solubility of caffeine in dioxane-water mixtures. J Pharm. Sci. 1980, 69, 659-661. DOI: http://dx.doi.org/10.1002/jps.2600690613. [ Links ]
37. Martin, A.; Carstensen, J. Extended solubility approach: Solubility parameters for crystalline solid compounds. J Pharm Sci. 1981, 70, 170-172. DOI: http://dx.doi.org/10.1002/jps.2600700214. [ Links ]
38. Martin, A.; Wu, P. L. Extended Hildebrand solubility approach: p-Hydroxybenzoic acid in mixtures of dioxane and water. J Pharm Sci 1981, 72, 587-592. DOI: http://dx.doi.org/10.1002/jps.2600720603. [ Links ]
39. Martin, A.; Paruta, A. N.; Adjei, A. Extended Hildebrand Solubility Approach: Methylxanthines in mixed solvents. J Pharm Sci 1981, 70, 1115-1115. DOI: http://dx.doi.org/10.1002/jps.2600701007. [ Links ]
40. Martin, A.; Miralles, M. J. Extended Hildebrand solubility approach: Solubility of tolbutamide, acetohexamide, and sulfisomidine in binary solvent mixtures. J Pharm Sci 1982, 71, 439-442. DOI: http://dx.doi.org/10.1002/jps.2600710416. [ Links ]
41. Martin, A.; Wu, P. L.; Adjei, A.; Mehdizadeh, M.; James, K. C.; Metzler, C. Extended Hildebrand solubility approach: testosterone and testosterone propionate in binary solvents. J Pharm Sci 1982, 71, 1334-1340. DOI: http://dx.doi.org/10.1002/jps.2600711207. [ Links ]
42. Martin, A.; Wu, P. L.; Velasquez, T. Extended Hildebrand solubility approach: sulfonamides in binary and ternary solvents. J. Pharm. Sci. 1985, 74, 277-282. DOI: http://dx.doi.org/10.1002/jps.2600740311. [ Links ]
43. Connors, K. A. Thermodynamics of Pharmaceutical Systems: An Introduction for Students of Pharmacy. Wiley-Interscience: Hoboken (NJ), 2002; pp. 62-63. [ Links ]
44. Marcus, Y. Solvent Mixtures: Properties and Selective Solvation. Marcel Dekker, Inc.: New York (NY), 2002; pp. 180-238. [ Links ]
45. Marcus, Y. On the preferential solvation of drugs and PAHs in binary solvent mixtures. J. Mol Liq. 2008, 740, 61-67. DOI: http://dx.doi.org/10.1016/j.molliq.2008.01.005. [ Links ]
46. Marcus, Y. Preferential solvation in mixed solvents. In Fluctuation Theory of Solutions: Applications in Chemistry, Chemical Engineering, and Biophysics; Smith P. E., Matteoli E., O'Connell J. P. (Eds); CRC Press, Taylor & Francis Group: Boca Raton (FL),,2013; pp. 65-92. [ Links ]
47. Delgado, D. R.; Martínez, F. Preferential solvation of sulfadiazine, sulfamerazine and sulfamethazine in ethanol + water solvent mixtures according to the IKBI method. J. Mol. Liq. 2014, 193, 152-159. DOI: http://dx.doi.org/10.1016/j.molliq.2013.12.021. [ Links ]
48. Martínez, F.; Gómez, A. Thermodynamics of partitioning of some sulfonamides in 1-octanol/buffer and liposome systems. J Phys Org. Chem. 2002, 15, 874-880. DOI: http://dx.doi.org/10.1002/poc.564. [ Links ]
49. Kamlet, M. J.; Taft, R. W. The solvatochromic comparison method I The beta-scale of solvent hydrogen-bond acceptor (HBA) basicities. J. Am. Chem. Soc. 1976, 98, 377-383. DOI: http://dx.doi.org/10.1021/ja00418a009. [ Links ]
50. Marcus, Y. The Properties of Solvents. John Wiley & Sons: Chichester (UK), 1998: pp. 145-152. [ Links ]
51. Taft, R. W.; Kamlet, M. J. The solvatochromic comparison method II The alpha-scale of solvent hydrogen-bond donor (HBD) acidities J Am Chem Soc 1976, 98, 2886-2894 DOI: http://dx.doi.org/10.1021/ja00426a036. [ Links ]
52. Fedors, R F A method for estimating both the solubility parameters and molar volumes of liquids Polym Eng Sci 1974, 14, 147-154. DOI: http://dx.doi.org/10.1002/pen.760140211. [ Links ]
53. Bevington, P. R.; Robinson, D. K. Data Reduction and Error Analysis for the Physical Sciences, 3rd ed; McGraw-Hill Book Co.:NewYork(NY),2003;pp. 116-141. [ Links ]