Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Acta Agronómica
Print version ISSN 0120-2812
Acta Agron. vol.60 no.3 Palmira July/Sep. 2011
Artículo científico
1,2 Departamento de Ingeniería, Grupo de Investigación en Materiales y Medio Ambiente, Facultad de Ingeniería y Administración, Universidad Nacional de Colombia Sede Palmira, 3 Profesor Adjunto, Departamento de Matemática, Universidad Nacional de Tucumán, Avenida Independencia 1800, San Miguel de Tucumán, Tucumán, Argentina.
*Autor para correspondencia: logonzalezsa@unal.edu.co
Las redes neuronales artificiales, simuladoras del proceso de aprendizaje de las neuronas biológicas, han sido utilizadas con éxito en el cálculo de parámetros en diversos problemas de ingeniería en que las variables involucradas tienen una alta relación no lineal entre sí y la modelación no permite representar el problema mediante una función matemática de fácil deducción. En la ciencia del suelo la predicción de algunas propiedades involucra diversas variables que hacen de su estimación por medio de modelos matemáticos un proceso complejo, y trasladan la solución del problema al campo de la inteligencia artificial. En el presente artículo se reporta la elaboración de redes neuronales artificiales para la estimación de la resistencia a la penetración a diferentes profundidades de un suelo; se consideran como variables influyentes el contenido de humedad, la densidad, la carga estática y la presión de inflado. Los resultados muestran una mejor estimación para profundidades entre 20 cm y 30 cm.
Palabra clave: Suelo, compactación del suelo, inteligencia artificial, redes neuronales artificiales, resistencia a la penetración.
Artificial Neural Networks simulate the learning process of biological neurons, and these have been successfully used in the computation of parameters on several engineering problems where exist a strong nonlinear relation among the variables. In soil science, estimation of some properties involves variables that are complicated to estimate using mathematical models, so the solution for the problems fall into the field of Artificial Intelligence. The present paper reports the elaboration of an Artificial Neural Network for the estimation of penetration resistance of soil at different depths, considering as influential variables humidity, density, static load, and inflate pressure. The best estimation results were obtained at a depth of 20-30 cm.
Key words: Artificial intelligence, artificial neural networks, soils, soil compaction, soil penetration strength.
La compresión del suelo consiste en la disminución de su volumen por aplicación de una carga alta. Se denomina consolidación cuando el proceso ocurre en suelos saturados y hay exclusión del agua, y compactación cuando ocurre en suelos secos y hay exclusión del aire (Bradford y Gupta, 1986; Pinzón y Amézquita, 1991). La compactación causa cambios en el contenido de humedad y en el intercambio de gases entre el suelo y la atmósfera e impide el desarrollo de las raíces (Horn et al., 1995; Colmer, 2003; Foloni et al., 2003; Alliaume y Hill, 2008) (Foto 1) y en el horizonte superior ocasiona cambios físicos y pedogenéticos (Pinzón y Amézquita, 1991).
Se considera que la compactación por tránsito está asociada con un serio deterioro de la estructura de los suelos debido a la pérdida de su porosidad, que lleva a la impedancia mecánica generada por dicha carga (Gerster y Bacigaluppo, 2004). Como alternativa para reducir la impedancia se ha sugerido la descompactación mecánica; sin embargo, los resultados de esta experiencia han sido contradictorios (Balbuena, 2009). En estudios realizados se ha sugerido la resistencia mecánica a la penetración como un indicador para determinar el grado de impedancias físicas en el suelo, en razón de que muestra, a partir de un valor determinado, una disminución en los rendimientos de cultivo (Díaz-Zorita, 2004). En consecuencia, la resistencia mecánica a la penetración puede ser un indicador sensible para estudiar los efectos de la descompactación mecánica y de la secuencia de preparación del suelo para cultivo sobre el rendimiento (Gerster et al., 2010).
La amplia utilización de la resistencia mecánica a la penetración en suelos como un procedimiento para identificar y caracterizar capas densificadas por efectos del laboreo ha llevado a que sus resultados se correlacionen con el crecimiento de las raíces y la productividad de los cultivos (Ehlers et al., 1983), con el contenido hídrico en horizontes (Cerana et al., 2005) y con la humedad del suelo y la densidad aparente como indicadores de la calidad del suelo (Díaz et al., 2010). No obstante, aún no han sido exploradas otras variables involucradas en la caracterización del suelo cuando se mide la resistencia a la penetración, y no todas las variables son relacionadas en un solo modelo matemático que permita mostrar una relación compleja entre ellas. Una causa de este desconocimiento científico es la alta relación no-lineal y la dinámica de las variables en la estimación de parámetros relacionados con problemas en la ciencia del suelo (Valdés, 2010).
La inteligencia artificial es un área de la investigación que reúne una serie de técnicas que se aplican en el ordenador con el objeto de desarrollar su capacidad para realizar funciones de aprendizaje y autocorrección usando algoritmos o códigos de programación computacional para realizar tareas en la resolución de diversos problemas, de una forma similar a como pensaría el ser humano en busca de dicha solución. Los principales paradigmas de la inteligencia artificial son las Redes Neuronales Artificiales, los Algoritmos Evolutivos, y la Lógica Difusa (Trujillo y Gómez, 2007; Ponce-Cruz, 2010).
En el campo de la modelación las redes neuronales artificiales son modelos de caja negra, desarrollados para resolver problemas en los que las relaciones de los diferentes componentes son complejas, las variables o reglas de relación no son fáciles de obtener, existe escaso conocimiento pero sí existe la experiencia de una serie de datos (López y Caicedo, 2006). Estas redes son una similitud del funcionamiento de una red conformada por neuronas biológicas, y desde este punto de vista funcional son procesadores de información con un canal de entrada de información y un canal de salida, con alta capacidad de comunicarse y unirse entre sí, cuya unión es denominada sinapsis (Trujillo y Gómez, 2007; Ponce-Cruz 2010).
Las redes neuronales artificiales han sido utilizadas en la estimación de parámetros de diversos problemas de la ciencia del suelo, como la predicción de la cobertura vegetal (Kimes et al., 1998; Buendía et al., 2002; Mena y Montecinos, 2006; Bocco et al., 2007), la hidrodinámica del suelo (Maneta y Schnabel, 2003; Rubio, 2005), la dinámica de la erosión del suelo (Mas et al., 2002), y la contaminación de aguas subterráneas (Rebolledo et al., 2002; Rodríguez, 2009; García et al., 2010), aunque no se ha reportado aún la predicción de variables relacionadas con propiedades mecánicas del suelo. El estado del arte muestra, entonces, que es de interés estimar la resistencia a la penetración a partir de una red neuronal artificial. En este sentido, en el presente documento se presenta una primera aproximación en la estimación de dicho parámetro a partir de diversas redes neuronales artificiales, elaboradas para este objetivo.
Base de datos
Se empleó una base de datos elaborada por Valdés (2010) a partir de información disponible en reportes de ensayos de resistencia mecánica a la penetración en diversos tipos de suelos (Pérez, 1997; Gómez y Torres, 1997; Vidal, 1997; Bonilla, 1998; Viveros y Jaramillo, 2003), localizados en diferentes pisos térmicos y condiciones climáticas. La base de datos es utilizada para enseñanza, entrenamiento y validación en programas computacionales de las redes neuronales artificiales, y se encuentra conformada por 192 registros que constituyen los vectores de información completa del arreglo matricial de la base de datos para las variables involucradas. El ensayo de resistencia mecánica a la penetración está basado en la metodología del ensayo estandarizado del índice de cono usando el penetrómetro de impacto (Saravia, 1997; Rangeon et al., 2008), en el cual se mide la profundidad por golpe y número de golpes, que posteriormente son convertidos en unidades de presión (KPa).
Las variables contenidas en la base de datos corresponden a contenido de humedad (H) en %, masa de suelo en estado húmedo (MSH) en g, masa de suelo en estado seco (MSS) en g, densidad aparente (Da) en g/ cm3, carga estática aplicada al suelo (Ce) en KN, presión de inflado de las llantas (Prin) en psi, porosidad (poros) en %, relación de vacíos (Rel_Vacios) en %, y el índice de cono para la resistencia a la penetración, medido a profundidades de 0 - 0 cm (IC-H0), 10-20 cm (IC-H10), 20-30 cm (IC-H20), y 30-40 cm (IC-H30) en KPa.
Elaboración de las redes neuronales artificiales
En el Laboratorio del Departamento de Matemáticas de la Universidad Nacional de Tucumán se elaboró un programa de ordenador con el algoritmo para la red neuronal artificial usada en la estimación del índice de cono para la resistencia a la penetración en el suelo. La información recopilada en una base de datos general fue arreglada para conformar seis subconjuntos, con 192 vectores de información los tres primeros y 64 vectores de información los tres restantes, que a su vez constituyeron seis nuevas bases de datos específicas y que relacionan como información de interés para su estimación los valores de resistencia a la penetración en las profundidades mencionadas (IC-H10, IC-H20, y ICH30). Como lenguaje de programación para la escritura del algoritmo de la red neuronal artificial se usó Matlab®. La red neuronal se creó usando la caja de herramientas de redes neuronales del lenguaje mencionado (neural network tool box) (The Math Works Inc., 2000) y los vectores de información fueron leídos por fichero usando una hoja de cálculo en Excel® (The Math Works Inc., 2002). La tipología de la red neuronal artificial usada corresponde a una red multicapa (feedforward') y se usó una metodología de educación o aprendizaje de propagación hacia atrás (backpropagation); se utilizó para ello una técnica de división de datos para enseñanza-entrenamientovalidación denominada validación cruzada (K-Fold Cross Validation) con k = 3.
Arquitectura de la red neuronal artificial
De acuerdo con el teorema de Kolmogorov (Kurkova, 1992; Haykin, 1999) cualquier función continua creciente en n variables puede ser analizada usando sólo sumas lineales y una función no-lineal continua y creciente en una variable; esto demuestra que el conjunto de redes neuronales a partir de tres capas (de entrada, oculta y de salida) es denso en el espacio de todas las funciones continuas en n variables, y por tanto, la red multicapa con una única capa oculta puede aproximar hasta el nivel deseado cualquier función continua en un intervalo, siendo éstas apropiadoras universales de funciones.
La tipología feedforward con aprendizaje backpropagation, definida por Rumelhart et al. (1986), corresponde a un tipo de estructura de computación paralela donde muchas pequeñas unidades de cálculo llamadas neuronas están masivamente interconectadas con la capa anterior de donde reciben información y con la capa posterior hacia donde la transmiten. Las redes de este tipo están constituidas por una primera capa de entrada con variables seleccionadas –denominadas neuronas perceptoras o de entrada–, que influyen en el resultado del problema; esta capa de entrada está conectada normalmente a una o más capas ocultas, donde se realizan los cálculos, y finalmente la información transformada llega a una capa de salida, de donde se obtienen los resultados, que corresponden a las variables de salida –denominadas neuronas de salida–, que interpretan el comportamiento del problema de acuerdo con las variables de entrada. En la estimación usando redes neuronales entrenadas la neurona de salida corresponde a la variable de estimación. Sus capas ocultas poseen una función de activación que limita la salida a un rango cercano y en ésta la capa de salida puede producir todos los valores de estimación. La salida de cada capa es representada como
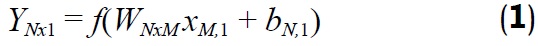
donde Y es un vector que contiene la salida desde cada una de las N neuronas en una capa dada, W es la matriz que contiene los pesos sinápticos (importancia) para cada una de las M salidas para todas las N neuronas, X es el vector que contiene las entradas, b es el vector que contiene los sesgos (biases), y f es la función de activación. Para la red neuronal artificial elaborada la función de activación no-lineal corresponde a una función sigmoidea expresada como:

siendo Z la expresión contenida dentro del paréntesis de la ecuación 1.
Para la tipología de la red la elección del número de neuronas de la capa oculta depende de factores como la naturaleza del problema o el tamaño y la calidad de los datos; una cantidad pequeña simplifica demasiado la red y no tiene una suficiente capacidad para aprender, y una cantidad alta da lugar a un sobreaprendizaje, lo que significa un buen ajuste con escaso poder predictivo para nuevos datos (Tam y Kiang, 1992; Brockett et al., 1997).
En redes multicapas la práctica sugiere para las capas ocultas un número de neuronas en una relación 10:1 en cuanto al número de neuronas de la capa de entrada, con resultados aceptables en el proceso de entrenamiento y de validación de la red neuronal artificial, tomando como indicador el valor del error calculado. Esta relación se determina con pruebas preliminares que se inician con una cantidad mínima de neuronas y se aumentan gradualmente hasta una cantidad máxima. La cantidad adecuada de ellas en las capas ocultas es aquella en la cual se consigue el menor error posible (Buendía et al., 2002). La cantidad mínima de neuronas (Noculta) se obtiene como un valor comprendido entre el número de neuronas de la capa de entrada (Nentrada) y de la capa de salida (Nsalida) (Fritz, 1999; Kimes et al., 1998):
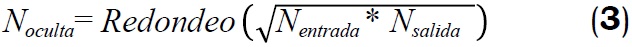
Para el caso de este estudio, Valdés (2010) realizó pruebas de entrenamiento en una de las redes conformadas, para lo cual usó en la capa oculta entre 5 y 80 neuronas, y repitió el procedimiento para 50, 60, 80 y 100 generaciones; encontró que los mejores resultados se logran para 100 generaciones y que antes de 50 neuronas se consigue el menor error. Al aumentar, a partir de este número, la cantidad de neuronas no se consiguieron mejores aproximaciones, con un incremento continuo del error. En el presente trabajo se eligió una capa oculta con 40 neuronas.
Aprendizaje y entrenamiento de la red neuronal artificial
La técnica de aprendizaje de backpropagation consiste en utilizar una optimización basada en derivadas, en que el error es derivable no solamente en función de los pesos de la capa de salida, sino también en función de los pesos de la capa oculta, utilizando la regla de la cadena (Hinton, 1989), que permite minimizar el error de entrenamiento de la red neuronal –la diferencia entre los valores calculados por la red neuronal utilizando un determinado conjunto de pesos y los valores originales–. El error y las correcciones efectuadas a los pesos se trasladan desde la capa de salida hacia atrás hasta la capa de entrada, de donde surge su nombre de propagación hacia atrás'. En este caso se eligió como forma de entrenamiento el método de descenso por gradiente o gradiente conjugado, correspondiente al gradiente conjugado con escalamiento SCG (Scale Conjugate Gradient).
El SCG ha sido definido por Moller (1993) y sustituye la búsqueda lineal por un escalamiento del paso, que depende del éxito en la reducción del error y buen desempeño de la aproximación cuadrática de éste. Esto es motivado para acelerar la típica baja convergencia asociada con el método del gradiente descendiente mientras se admiten los requerimientos de información asociados con la evaluación, almacenamiento e inversión de la matriz Hessiana, como es requerida en el método de Newton. El SCG es considerado más rápido que otros métodos existentes (Moghassem et al., 2010).
Evaluación del desempeño de la red neuronal artificial
El desempeño de una red neuronal artificial en las fases de entrenamiento y validación se puede evaluar usando diversas técnicas, entre ellas la raíz del error promedio cuadrado RMSE (RootMean Square Error), el total de los cuadrados de los errores SSE (Sum of Squares of Error), el error relativo promedio MER (Mean Error Ratio), el error promedio cuadrado MSE (Mean Square Error), el factor de correlación R2 (R2 Correlation Factor) (Goyal y Goyal, 2011). En el presente trabajo para el proceso de entrenamiento se utilizó el MSE, mientras que para la fase de validación se usaron el RMSE y el MRE (este último usado como reporte final del error), que fueron calculados como:
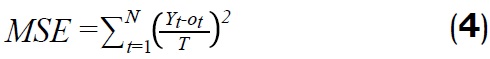
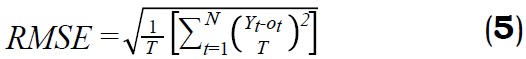
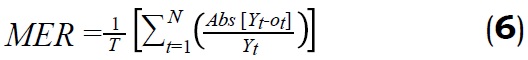
donde, Yt es la salida deseada, Ot es la salida obtenida, T es el número de registros en la base de datos, y N es el número de neuronas en la capa oculta.
División aleatoria de la base de datos
La técnica de división de datos K-Fold Cross Validation' con k = 3 divide cada base de datos específica en tres grupos de igual extensión con vectores de información escogidos al azar, usando alternativamente dos grupos como conjunto de educación de la red (aprendizaje y entrenamiento) y el tercero como validación (Refaeilzadeh et al., 2008). La técnica, que utiliza adicionalmente una regulación estadística bayesiana, elimina los sesgos de elección y da una mejor idea de los errores de validación y de la existencia de valores extremos o atípicos (outliers), que normalmente quedan ocultos por la división de datos y otros efectos (Varmuza y Filzmoser, 2009).
Conformación de las redes neuronales artificiales
Para el caso en estudio se elaboraron y se entrenaron seis redes neuronales artificiales, con tipología multicapa conformada por una capa de entrada, una oculta con 40 neuronas, y una de salida con una única neurona correspondiente al valor de la resistencia mecánica a la penetración en una profundidad de referencia (IC-H10, IC-H20, y IC-H30). Las variables (neuronas) de entrada y salida en cada red neuronal artificial elaborada y entrenada aparecen en el Cuadro 1.
Las seis redes neuronales artificiales para estimación de la resistencia a la penetración del suelo a diferentes profundidades (Cuadro 1) fueron elaboradas y entrenadas siguiendo el procedimiento antes mencionado. Como indicador de desempeño de estas redes artificiales se analizó el comportamiento computacional de los datos en la fase de entrenamiento y validación y el error reportado para la fase de validación.
El mejor comportamiento de los datos en la fase de validación se presentó en la red RNA_2, en la cual se estima la resistencia a la penetración a una profundidad entre 20 cm y 30 cm (IC-H20), cuyas características específicas de la red se incluyen en el Cuadro 2. En la Figura 2 aparece el comportamiento de los resultados en la fase de validación para las redes RNA_1, RNA_3, RNA_4 y RNA_6. Como se puede observar, y comparando con el comportamiento de los datos en la misma fase para la red RNA_2 (Figura 3a), las aproximaciones de las redes mencionadas alrededor de la línea de correlación (R2 = 1) son bastante dispersas. Con el objeto de ayudar a una mejor comprensión del resultado de estimación de la red neuronal entrenada para el fin propuesto, se muestra en forma gráfica este indicador de desempeño.
Para la red de mejor desempeño, RNA_2, se incluye en la Figura 3a la comparación del comportamiento como dato real vs dato estimado en las fases de entrenamiento y validación computacional. Se observa la presencia de datos que se salen de un patrón de comportamiento, aunque no se afirma que sean anómalos o erróneos en la experimentación original, y que pueden ser identificados para su exclusión en las bases de datos, permitiendo la repetición del proceso de simulación y la reducción del error. Es importante mencionar que en la base de datos de entrenamiento utilizada es posible eliminar los registros que contienen estos datos, mediante la aplicación de otras técnicas diseñadas para tal fin en la herramienta computacional de las redes neuronales artificiales, e incluirlas en el algoritmo elaborado (Valdés y González 2011).
Para analizar el tipo de relación (lineal o no-lineal) entre las variables se entrenó y validó computacionalmente la red de mejor desempeño (RNA_2) usando una función de activación lineal, expresada como

siendo Z la expresión que aparece dentro del paréntesis de la ecuación (1). La fase de entrenamiento y de validación usando una función de activación lineal aparece en la Figura 3b, donde se observa un comportamiento similar cuando la función de activación es lineal, con lo cual se puede concluir que en este caso específico de predicción las variables se interrelacionan entre sí con una dependencia lineal, y dicha estimación no se afecta si las variables se interrelacionan de una manera no-lineal.
- La posibilidad del acercamiento con redes neuronales artificiales fue explorada para predecir la resistencia a la penetración a diferentes profundidades de un suelo. Las redes neuronales artificiales con tipología feedforward con aprendizaje backpropagation y arquitectura multicapa fueron elaboradas y evaluadas usando como indicadores de desempeño el error relativo en la fase de validación. De acuerdo con el indicador mencionado, la red neuronal artificial para predecir la resistencia a la penetración en la profundidad entre 20 cm y 30 cm es la de mejor desempeño.
- A pesar del error obtenido en la estimación, es importante notar que la mejor estimación para una de las mayores profundidades (20 cm - 30 cm), donde se ha tomado en adición como variables de entrada la resistencia a la penetración a profundidades menores (0 cm - 0 cm y 10 cm - 20 cm), sugiere la realización del ensayo a menores profundidades, lo cual permitiría un ahorro significativo en el recurso tiempo y de costos.
- Los resultados en el presente trabajo muestran que mediante nuevas redes neuronales artificiales con mejores estimaciones se hace un aporte importante en la aplicación investigativa y profesional en la ciencia del suelo, debido a (1) La resistencia mecánica a la penetración, obtenida mediante el ensayo estandarizado del índice de cono, es usada como un indicador confiable para la correlación de productividad o rendimiento del cultivo y el suelo; sin embargo, debe realizarse con una amplia cobertura en las zonas de laboreo y a cuatro diferentes profundidades. La disponibilidad de una herramienta de estimación permite un ahorro importante en el tiempo y en el costo de la realización de los ensayos. (2) La profundidad de arraigamiento es definida como el espesor de la zona más apta para el desarrollo de raíces (Alliaume y Hill, 2008), clasificada en tres grupos: superficial (0 cm - 15 cm), media (15 cm - 30 cm) y profunda (> 30 cm). Es significativo, entonces, que la herramienta pueda reportar predicciones confiables de la resistencia a la penetración mecánica a mayores profundidades, puesto que permite conocer las condiciones del suelo para un desarrollo adecuado en aquellas especies vegetales de importancia económica que requieran estratos por encima de los 30 cm para su crecimiento radicular.
- Se sugiere que las nuevas redes neuronales artificiales desarrolladas para tal fin involucren adicionalmente como variables de entrada el tipo de suelo, la localización en un piso térmico, el tipo de labranza, las condiciones climáticas, entre otras. Aunque algunas de estas variables corresponden a variables cualitativas, el tratamiento como variables de clase permite que las redes neuronales artificiales las reconozcan y las asocien a un patrón de comportamiento.
Alliaume, F. y Hill, M. 2008. Propiedades físicas ¿en qué influyen?: dinámica del aire, dinámica del agua, crecimiento radicular. Presentación, Curso de Física de Suelos, Universidad Nacional de Colombia sede Palmira (Palmira – Colombia). (manuscrito). [ Links ]
Balbuena, R. 2009. Alternativas para la descompactación mecánica de los suelos. Taller Física de Suelos. Rio cuarto, Argentina. Actas III. [ Links ]
Bocco, M; Obando, G.; Sayago, S.; y Willington, E. 2007. Neural network models for land cover classification from satellite images. Agric. Téc. 67(4):414 - 421. [ Links ]
Bonilla, A. B.-H. 1998. Evaluación de la compactación de dos tipos de suelos causados por el tráfico del tractor en función de la presión de inflado de las llantas y del contenido de humedad del suelo. Tesis, Ingeniero Agrícola. Universidad Nacional de Colombia sede Palmira. [ Links ]
Bradford, J. M. y Gupta, S. C. 1986. Soil compressibility, methods of soil analysis. Madison. p. 479 – 492. [ Links ]
Brockett, P. L.; Cooper, W. W.; Golden, L. L.; y Xia, X. 1997. A case study in applying networks to predicting insolvency for property and casualty insurers. J. Operat. Res. Soc. 48:1153 - 1162. [ Links ]
Buendía, E.; Vargas, E.; Leyva, A.; y Terrazas, S. 2002. Aplicación de redes neuronales artificiales y técnicas SIG para la predicción de coberturas forestales. Serie Ciencias Forestales y del Medio Ambiente. Rev. Chapingo 8 (1):31 - 37. [ Links ]
Cerana, J.; Wilson, M.; Pozzolo, O.; De Battista, J. J.; Rivarola, S.; y Díaz, E. 2005. Relaciones matemáticas entre la resistencia mecánica a la penetración y el contenido hídrico en un Vertisol. Estudios de la Zona no Saturada del Suelo 7:159 - 163. [ Links ]
Colmer, T. D. 2003. Long-distance transport of gases in plants: a perspective on internal aeration and radial oxygen loss form roots. Plant, Cell Environ. 26:17 - 36. [ Links ]
Díaz, C. G.; Osinaga, R.; y Arzeno, J. 2010. Resistencia a la penetración, humedad del suelo y densidad aparente como indicadores de calidad de suelos en parcelas de largo plazo. XXII Congreso Argentino de la Ciencia del Suelo, Rosario, Argentina. [ Links ]
Díaz-Zorita, M. 2004. Effects of subsurface soil compaction of a typic hapludol on sunflower (Helianthus annus L.) Production. Ciencia del Suelo 22:40 - 43. [ Links ]
Ehlers, W.; Köpke, U.; Hesse, F.; y Bohm, W. 1983. Penetration resistance and root growth of oats in tilled and untilled loess soil. Soil Tillage Res. 3:261 - 275. [ Links ]
Foloni, J.; Calonego, J.; y De Lima, S. 2003. Efeito da compactação do solo no desenvolvimento aéreo e radicular de cultivares de milho. Pesqu. Agropec. Brasil. 38(8):947 - 953. [ Links ]
Fritz, L. W. 1999. High resolution commercial remote sensing satellites and spatial information systems. ISPRS Highligths 4(2). [ Links ]
García, I.; Rodríguez, J. G.; López, F.; y Tenorio, Y. M. 2010. Transporte de contaminantes en aguas subterráneas mediante redes neuronales artificiales. Inf. Tecnol. 21(5):79 - 86. [ Links ]
Gerster, G. y Bacigaluppo, S. 2004. Consecuencias de la densificación por tránsito en argisoles del sur de Santa Fe. Actas XIX Congreso Argentino de la Ciencia del Suelo, Paraná, Argentina. [ Links ]
Gerster, G.; Bacigaluppo, S.; Bodrero, M.; y Salvagiotti, F. 2010. Secuencia de cultivos, descompactación mecánica y rendimiento de soja en un suelo degradado de la región pampeana. Para Mejorar La Producción 45:59 - 61. [ Links ]
Gómez, O. Y. y Torres V. D. 1997. Efecto de la carga estática y presión de inflado en el grado de compactación del suelo. Tesis Ingeniero Agrícola. Universidad Nacional de Colombia sede Palmira. [ Links ]
Goyal, S. y Goyal, G. K. 2011. Cascade and feedforward backpropagation artificial neural network models for prediction of sensory quality of instant coffee flavoured sterilized drink. Can. J. Artif. Intell. Machine Learn. Pattern Recog. 2 (6):78 - 82. [ Links ]
Haykin, S. 1999. Neural networks: a comprehensive foundation. 2nd edition. Prentice Hall. [ Links ]
Hinton, G. 1989. Connectionist learning procedures. University Toronto. [ Links ]
Horn, R.; Domzal, H.; Slowinska-Jurkiewickz, A.; y Van Ouwerkerk, C. 1995. Soil compaction processes and their effects on the structure of arable soils and the environment. Soil Till. Res. 35:23 - 36. [ Links ]
Kimes, D. S.; Nelson, R. F.; Manry, M. T.; y Funk, A. K. 1998. Attributes of neural networks for extracting continuous vegetation variables from optical and radar measurements. Intern. J. Remote Sensing 19(14): 639 - 2663. [ Links ]
Kurkova, V. 1992. Kolmogorov theorem and multilayer neural networks. IEEE.ASSP Magazine 1:4 - 22. [ Links ]
López, J. A. y Caicedo, E. 2006. Una aproximación práctica a las redes neuronales artificiales. Conferencias. Curso de Redes Neuronales Artificiales, Universidad del Valle, Cali, Colombia. (manuscrito). [ Links ]
Maneta, M. y Schnabel, S. 2003. Aplicación de redes neuronales artificiales para determinar la distribución espacial de la humedad del suelo en una pequeña cuenca de drenaje: estudios preliminares. Estudios de la Zona no Saturada del Suelo 6:295 - 304. [ Links ]
Mas, J. F.; Puig, H.; Palacio, J. L.; y Sosa, A. 2002. Modelado del proceso de deforestación en una región del sureste de México. Memorias del II Seminario Latinoamericano de Geografía Física, Maracaibo, Venezuela, Julio 24-27. CD. [ Links ]
Mena, C. y Montecinos, R. 2006. Comparación de redes neuronales y regresión lineal para estimar productividad de sitio en plantaciones forestales, utilizando geomática. Bosque 27(1):35 - 43. [ Links ]
Moghassem, A. R.; Gharehaghaji, A. A.; Shaikhzadeh, S.; Palhang, M.; y Shanbeh, M. 2010. Application of artficial neural nets in carpet thickness loss prediction. World Appl. Sci. J. 9(2):167 - 177. [ Links ]
Moller, M. 1993. Efficient training of feed-forward neural networks. Ph.D. tesis. Arhus Univ. Daimi, Iran. [ Links ]
Pérez, V., S. 1997. Efecto de la carga estática del tractor en la compactación de un suelo franco y arcilloso. Tesis Ingeniero Agrícola. Universidad Nacional de Colombia sede Palmira. [ Links ]
Pinzón, A. y Amézquita, E. 1991. Compactación de suelos por el pisoteo de animales en pastoreo en el piedemonte amazónico de Colombia. Pasturas Tropicales 13(2):21 - 26. [ Links ]
Ponce-Cruz, P. 2010. Inteligencia artificial con aplicaciones a la ingeniería. Alfaomega, México. [ Links ]
Rangeon, N. I.; Aciar, L. M.; Osinaga, R.; Arzeno, J. L.; y Sánchez, C. 2008. Análisis de la resistencia a la penetración y humedad de suelo como indicadores de calidad en distintos sistemas de labranza. Actas XXI Congreso Argentino de la Ciencia del Suelo. Potrero de Los Funes, Argentina. [ Links ]
Rebolledo M., F. J.; Obregón N., N.; y Duarte, C. 2002. Ecohidroinformática: un nuevo paradigma para la gestión inteligente de los recursos hídricos. XXVIII Congreso Internacional de Ingeniería Sanitaria y Ambiental, Cancún, México, Octubre 27-31. [ Links ]
Refaeilzadeh, P.; Tang, L.; y Liu, H. 2008. Cross- Validation. Arizona State University. Tempe, USA. [ Links ]
Rodríguez O., J. G. 2009. Pronóstico de la migración de contaminantes en aguas subterráneas mediante redes neuronales artificiales. Tesis MSc. en Ingeniería Ambiental). Instituto Politécnico Nacional. México. [ Links ]
Rubio, C. 2005. Hidrodinámica de los suelos de un área de montaña media mediterránea sometida a cambios de uso y cubierta. Tesis Ph.D. en Ciencias del Suelo. Universidad Autónoma de Barcelona, Barcelona, España. [ Links ]
Rumelhart, D. E.; Hinton, G. E.; y Williams, R. J. 1986. Learning internal representations by error propagation. D.E. Rumelhart y J.L. McClelland (eds.). Parallel distributed processing, 1. MIT Press, Cambridge. [ Links ]
Saravia, S. 1997. Evaluación de las propiedades físicas del suelo en lo referente a la resistencia a la penetración y densidad aparente en distintos manejos de suelo. Universidad Nacional de Salta. Salta, Argentina). [ Links ]
Tam, K. Y. y Kiang, M. Y. 1992. Managerial applications of neural networks: The case of bank failure predictions. Manag. Sci. 38(7):926 -9 47. [ Links ]
The Math Works Inc. 2000. Neural Networks Toolbox. Version 4.0. User's Guide. Natick, USA. [ Links ]
The Math Works Inc. 2002. Excel Link for use with Matlab®. Version 2.0. User's Guide. Natick, USA. [ Links ]
Trujillo H., A. D. y Gómez A., L. E. 2007. Inteligencia artificial: emulación de mecanismos. TecnoIntelecto 4(2):116 - 120. [ Links ]
Valdés, N. J. 2010. Exploración y elaboración de una red neuronal artificial para determinar propiedades específicas en los suelos. Tesis Ingeniera Agrícola.Universidad Nacional de Colombia sede Palmira. [ Links ]
Valdés H., N. J. y González S., L. O. 2011. Una aplicación de redes neuronales artificiales en la estimación de la resistencia a la penetración en suelos. Castro, L.R.; Maciel, M.C.; y Castro, S.M. (eds.). Anales del III Congreso de Matemática Aplicada, Computacional e Industrial –MACI, Bahía Blanca, Argentina, Mayo 9-11. 3:227 - 230. [ Links ]
Varmuza, K. y Filzmoser, P. 2009. Introduction to multivariate statistics in chemometrics. (CRC Press). [ Links ]
Vidal, F. J. 1997. Efecto del contenido de humedad del suelo en la compactación causado por el tráfico de máquinas. Tesis Ingeniero Agrícola. Universidad Nacional de Colombia sede Palmira. [ Links ]
Viveros A., R. A.; y Jaramillo O., R. 2003. Caracterización e impacto físico en un Vertisol bajo uso intensivo del CIAT. Tesis Ingeniero Agrícola. Universidad Nacional de Colombia sede Palmira. [ Links ]














