Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Acta Agronómica
Print version ISSN 0120-2812
Acta Agron. vol.62 no.1 Palmira Jan./Mar. 2013
1Centro de Investigación en Ciencias y Recursos GeoAgroAmbientales – CENIGAA, A.A. 385, Neiva, Huila, Colombia. 2 Departamento de Ingeniería Agrícola, Facultad de Ingeniería, Universidad Surcolombiana, A.A. 385, Neiva, Huila, Colombia. 3 Grupo de Investigación Ciencia e Ingeniería del Agua y del Ambiente, Facultad de Ingeniería, Pontificia Universidad Javeriana, A.A. 56710, Bogotá D.C., Colombia. *Autor para correspondencia: j.romero@usco.edu.co
En la actualidad se desconocen las respuestas de los cultivos en términos de balances hídrico y energético frente al aumento de gases efecto invernadero y cambio climático. El objetivo de este trabajo fue formular y evaluar un modelo acoplado de fotosíntesis, conductancia estomática y transpiración para el cultivo de maracuyá (Passiflora edulis) en condiciones de clima tropical por medio de la combinación de submodelos ampliamente aceptados. Como caso de estudio se utilizó el protocolo de modelación matemática aplicado al cultivo en el departamento del Huila, Colombia. La transpiración real estimada por el modelo fue evaluada usando un lisímetro de tipo gravimétrico. Los resultados del estudio indicaron que el modelo propuesto fue capaz de estimar la transpiración del cultivo de maracuyá bajo condiciones de clima templado con una buena validación de 0.30. La transpiración media diaria para el cultivo en las condiciones de clima templado del departamento del Huila durante el periodo de estudio fue de 1.36 mm/día. Por análisis de sensibilidad se identificó el parámetro m siendo altamente sensible para el caso de estudio; por el contrario, los parámetros Vm25, Kc25, Jm25, Ko25, f, Bs mostraron escasa sensibilidad e identificación.
Palabra clave: Análisis de sensibilidad, clima templado, maracuyá, MCAT, modelamiento matemático.
At present, crop behavior due to climate change is not well known, in particular those responses related to water and energy balances. The aim of this work was to propose and implement a model aimed to evaluate interactions among photosynthesis, stomatal conductance and transpiration phenomenon under both crop growing process and tropic climate conditions. A passion fruit crop located in Colombia (Huila Department) is taken as a study case. The actual transpiration estimated by the model was evaluated using a gravimetric type lysimeter. The results indicated that the proposed model was able to estimate the passion fruit crop transpiration under conditions in the tropic climate with a good validation of 0.30. The mean daily transpiration rate under wet weather conditions during the study period was 1.36 mm d-1.Sensitivity analysis indicated that the parameter m is identified and is highly sensitive for the case study, however, VM25, KC25, JM25, Ko25, f, B parameters showed poor sensitivity and identification.
Key words: Mathematical modeling, MCAT, Passion fruit, Sensitivity analysis, temperature weather.
El uso eficiente del recurso hídrico, especialmente en el sector agrícola, es un desafío heredado desde la época antigua. Sin embargo, este desafío se ve agravado por problemáticas actuales como el aumento descontrolado de la población (UN, 2012; Chen et al., 2012), aumento de la frontera agrícola (Yu et al., 2012), efectos adversos del cambio climático y falta de una gestión integrada del territorio (Pandey et al., 2003). Una de las formas de ayudar a resolver el desafío del uso eficiente de agua consiste en estimar adecuadamente los requerimientos hídricos de los cultivos (Villalobos et al., 2000).
De acuerdo con las proyecciones de la segunda comunicación de cambio climático del IDEAM, el departamento del Huila será 30% más seco que lo que es hoy en día (Escenario A2), por el cambio en el régimen de las precipitaciones (Ruiz, 2010). En este contexto, las condiciones futuras del clima serán más secas y el Huila tendrá que adaptarse a las nuevas condiciones de clima mejorando sus estrategias de gestión y manejo del recurso hídrico (Ruiz, 2010). Brouder y Volenec (2008) consideran que el manejo de los cultivos, teniendo en cuenta el aumento de los gases efecto invernadero y los cambios del clima (escenarios de cambio climático), debe ser diferente debido a la influencia interactiva entre el dióxido de carbono, la temperatura, la humedad, la eficiencia fisiológica, la absorción de nutrientes y el uso eficiente del agua. En este sentido es necesario conocer cuál será la respuesta de las plantas en términos de balance hídrico y energético ante los posibles cambios de clima. La pregunta de investigación planteada en el párrafo anterior cobra especial importancia en el departamento del Huila, principalmente porque es productor de alimentos, entre ellos del cultivo de maracuyá. En 2009 este cultivo generó uno de los mayores aportes en el producto interno bruto (1.36%) del departamento (Garay, 2009).
En ciencias agrarias se utiliza y se acepta internacionalmente el método de FAO Penman- Monteith para estimar los requerimientos hídricos de los cultivos (Allen et al., 1998). Este método es interesante porque su implementación es de forma práctica y sencilla, pero lamentablemente tiene fuertes suposiciones teóricas (Orgaz et al., 2007). Por otro lado existen herramientas como el acople de modelos de fotosíntesis, conductancia estomática y el balance de energía que permiten estimar adecuadamente la transpiración de los cultivos y además analizar las respuestas productivas de los cultivos en escenarios de cambio climático, no obstante, este enfoque requiere de la evaluación bajo condiciones locales de las zonas tropicales (Orgaz et al., 2007). Yu et al. (2004) hicieron mejoras al modelo de fotosíntesis-transpiración propuesto por Yu (1999). Posteriormente, la aplicabilidad del modelo fue probada en condiciones de estrés ambiental, relacionado en particular con los contenidos de agua y nutrientes en el suelo (Yu et al., 2012). Sin embargo este modelo fue probado para cultivos de maíz y soya durante el verano de 1998 en Matsudo (Japón), en condiciones de zona climática templada. Los estudios antes mencionados pusieron en evidencia la necesidad de tener en cuenta variables fisiológicas, en particular relacionadas con el comportamiento estomático, cuya respuesta al estrés ambiental es diferente para cada especie. En la literatura se encuentran modelos estomáticos multiplicativos (Li et al., 2012) y modelos que combinan comportamiento estomático y procesos de fotosíntesis (Uddling et al., 2005); varios de ellos desarrollados para representar estrés hídrico de algunas plantaciones particulares en climas no-tropicales (Keenan et al., 2010; Egea et al., 2011), siendo más escasos los modelos que acoplan las variables fisiológicas y las actividades fotosintéticas y de transpiración de las plantas y menos que hayan sido probados en plantaciones en clima tropical para diferentes escenarios de cambio climático.
El objetivo de la presente investigación fue formular y evaluar un modelo acoplado de fotosíntesis, conductancia estomática y transpiración para el cultivo de maracuyá en condiciones de clima templado, por medio de la combinación de submodelos ampliamente aceptados. El modelo acoplado puede ser usado para estimar de forma precisa la transpiración del cultivo de maracuyá, con el fin de apoyar la toma de decisiones en el manejo adecuado del agua de riego y de esta forma, mejorar la calidad de los cultivos, e incrementar la competitividad y la calidad de vida de los agricultores.
Sitio experimental
La zona experimental está localizada en la región sur-occidente de Colombia, municipio de La Plata, vereda Fátima, en el departamento del Huila. El sitio experimental se encuentra a 2° 23' 19.9" N y 75° 54' 54.5" O, a 1134 m.s.n.m., la temperatura promedio es 24 °C, la humedad relativa de 72%, la precipitación de 1600 mm/año, la evaporación de 1180 mm/año y la velocidad del viento varía entre 0.8 y 1.6 m/s. El cultivo tiene un área total de 0.25 ha y se estableció en espaldera con riego por goteo (descarga de gotero 4 l/h) y un distancia de siembra de 2.5 m x 4 m entre plantas y calles, respectivamente.
Manejo del cultivo
La operación del sistema de riego se programó según lectura diaria (7 a.m.) de las baterías tensiométricas, considerando 20 centibares (cb) y valores superiores como punto crítico para la apertura de los sectores de riego, ya que muestran la existencia de déficit hídrico en la zona de raíces de la plantación.
En el perfil del suelo se identificaron tres horizontes bien definidos: el primero (0 - 25 cm) es de textura franco-arcillosa (FAr) a diferencia de los horizontes profundos con textura arcillosa (25 - 65 cm y 65 - X) que presentan la mayor retención de humedad el horizonte FAr con 25% de agua aprovechable.
Lisímetro utilizado
El lisímetro ubicado en la zona experimental era de tipo gravimétrico. Se trata de un recipiente de acrílico que contiene una matriz de suelo característico del sitio y un sistema de drenaje. Este equipo sirve para calcular las evapotranspiraciones potenciales y del cultivo. Sus dimensiones son de 1 x 1 x 0.6 m. Adicionalmente se utilizó el modelo de Ritchie (1972) para separar la evaporación del suelo y la transpiración de la planta. Las mediciones con el lisímetro se registraron durante 6 meses, para un total de 181 datos de transpiración diaria. Se utilizaron los primeros 127 datos para la calibración del modelo y los siguientes 54 para la validación.
Datos meteorológicos
Los datos meteorológicos que soportan la información de entrada del modelo (temperatura ambiente °C, velocidad del viento m/s, radiación solar W/m2 y humedad relativa %) provienen de una estación automatizada marca Weatherhawk. El periodo de información analizada corresponde del 20 de enero al 29 de diciembre de 2011. El equipo se programó para el registro de lecturas cada minuto y el promedio horario, para un total de 8160 datos disponibles. Al analizar la Figura 1 se observa que los máximos de temperatura se presentan un tiempo después de la incidencia de máxima energía radiante. Este tipo de retraso es común en sistemas con almacenamiento y resistencia (Campbell y Norman, 1997). Adicionalmente se representa un ambiente húmedo, especialmente en horas de la mañana y la noche, donde se observan condiciones de saturación de vapor de agua, esta condición ambiental puede propiciar el crecimiento de hongos y plagas perjudiciales para el cultivo de maracuyá (Figura 1).
Relación de las variables de entrada con los procesos representados
La temperatura del ambiente es un insumo importante para el cálculo de la presión de vapor del ambiente, así como la presión de vapor del agua saturada. Con estas variables se estima el déficit de presión de vapor. Además, la temperatura del ambiente se utiliza para calcular la curva de presión de vapor y es fundamental, junto con la radiación neta, para el cierre del balance de energía, lo que permite calcular la temperatura de la hoja, variable importante en la estimación de las tasas de transpiración del cultivo.
Por otro lado, la velocidad del viento es fundamental en la representación de los procesos terrestres como el cálculo de la capa límite en la hoja, el CO2 en la superficie de la hoja y la conductancia estomática. Las mayores remociones de vapor de agua en la hoja por efectos del viento ocurren a bajas velocidades, ya que a velocidades altas tiene lugar el cierre estomático, bien por efectos mecánicos o por posible deshidratación. De igual forma, la humedad relativa tiene una fuerte influencia sobre la estimación de la conductancia estomática y la presión de vapor en el ambiente.
Protocolo de modelación matemática
El protocolo de modelación usado fue el de Domínguez (2000). Se utilizó la herramienta MCAT (The Monte-Carlo Analysis Toolbox) Wagener y Kollat (2007) para calibrar el modelo. Esta herramienta permite analizar la estructura paramétrica del modelo y la bondad de ajuste. Se realizaron 10,000 simulaciones para estimar el rango de acción de los parámetros y el análisis de sensibilidad.
De igual forma, la calibración se llevó a cabo minimizando una función objetivo. Para efectos de la investigación se utilizó el coeficiente de determinación de Nash (R2) (Nash y Sutcliffe, 1970) como función objetivo, el cual a su vez es un indicador del ajuste de los datos modelados a la serie de tiempo observada (Ecuación 1). En este sentido, los datos observados de la transpiración del cultivo de maracuyá en el departamento del Huila se representan como ETr [mm/día] y la variable simulada se representa como ETheat [mm/día].
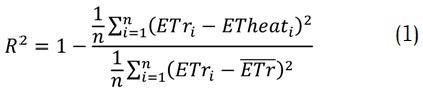
Es necesario tener en cuenta que n es el número de simulaciones y (ETr) es la media de los datos observados y en la medida que R2 tienda a cero la simulación es más adecuada, siendo aceptable un máximo de 0.4.
Finalmente la validación del modelo se realizó utilizando el criterio del Centro Hidrometeorológico de Rusia (S/sD) (Domínguez, 2000), el cual consiste en el cálculo de la desviación estándar del incremento de los valores reales:
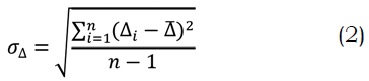
Donde, n es el número de pronósticos evaluados, Di es el incremento de los valores reales y D es el incremento medio. Además, la desviación estándar de los pronósticos de los errores se establece como:

Al observar las ecuaciones 2 y 3 se deduce que el criterio relaciona la desviación estándar de los incrementos de la magnitud pronosticada con la desviación de los errores de pronóstico, exigiendo que la variabilidad de los errores cometidos en los pronósticos no supere la variabilidad de los incrementos de las afluencias (Domínguez, 2000). Para determinar si un modelo matemático está validado se exige que S/sD< 0.8.
Descripción del modelo
El modelo representa procesos ecofisiológicos acoplados a nivel de hoja –fotosíntesis y conductancia estomática– con procesos físicos –balance de energía y conductancia de la capa límite–, procesos que determinan el flujo de CO2, el vapor de agua y el intercambio de calor entre las hojas y el ambiente. La interdependencia natural de los procesos a nivel de hoja y de follaje producen un conjunto acoplado de estrechas relaciones físicas y biológicas, que controlan los flujos entre las plantas y la atmósfera (Drewry et al., 2010).
Además, las respuestas de las hojas son determinadas por la interacción entre las reacciones bioquímicas, la transferencia de masa a través de los estomas y la capa límite de las hojas, así como un intercambio de radiación (Nikolov et al. 1995). En ese orden de ideas los tres modelos (fotosíntesis, conductancia estomática y balance de energía en la hoja) son interdependientes. Por esta razón se implementó un procedimiento iterativo anidado para resolver el sistema numéricamente a través del método de Newton-Raphson. A continuación se presenta la ecuación principal de cada uno de los submodelos utilizados, siendo el submodelo de fotosíntesis para plantas tipo C3 el correspondiente al propuesto por Farquhar et al. (1980).
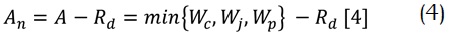
donde An es la tasa de asimilación neta de CO2(µmol/m2 por segundo); A es la tasa bruta de adsorción de CO2 (también llamada fotosíntesis bruta) y Rd es la respiración oscura, es decir producto de procesos como la fotorrespiración; Wc es la tasa de asimilación de CO2 restringida solamente por la activación y las propiedades cinéticas de la enzima rubisco y representa el mecanismo de carboxilación; Wj es igualmente la tasa de asimilación, pero limitada solamente por la regeneración del sustrato de la enzima, es decir, la capacidad de regeneración de la ribulosabifosfato (RuBP) dependiente del flujo de electrones; y Wp limita la tasa de asimilación por la capacidad para utilizar los productos de la fotosíntesis, por ejemplo, la síntesis desde la triosafosfato en el ciclo de Calvin.
Adicionalmente, se hizo uso del modelo propuesto por Ball y Berry (1982), el cual es de origen empírico basado en experimentos con intercambio de gases, pero que demuestra robustez al momento de capturar las respuestas de la conductancia estomática al vapor de agua (gsv) para diferentes condiciones ambientales.
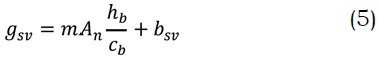
El modelo relaciona (gsv) con la asimilación de CO2 neta (An), la humedad relativa en la superficie de la hoja (hb) y la concentración de CO2 en la superficie de la hoja (cb). En esta ecuación, m es un parámetro adimensional específico de cada especie que determina la sensibilidad de gsv con An y bsv es un parámetro que representa el mínimo de conductancia estomática al vapor de agua.
Finalmente, el balance de energía en las hojas determina Tl, por tanto, la partición de energía en calor latente y sensible proporciona un control sobre la fotosíntesis de las hojas (Drewry et al. 2010). De hecho, en el caso de estado estable (temperatura de la hoja constante), la energía absorbida por ambas caras de las hojas se disipa a través de los flujos de calor latente y sensible, la radiación de onda corta y el almacenamiento metabólico (Nikolov et al., 1995).
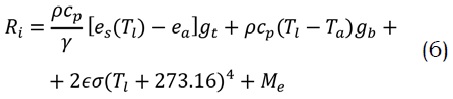
donde, Ri es la energía absorbida desde ambos lados de la hoja (radiación de onda corta y larga (W/m2), cp es el calor específico del aire seco (1010 J/kg °K), l es la constante sicrométrica (Pa/K), gt es la conductancia total de la hoja al vapor de agua (m/s), Ta es la temperatura ambiente (°C), Î es la emisividad térmica de la hoja (alrededor de 0.975), s es la constante de Stefan-Boltzmann (5.67*10-8 W/m2 °K-4) y Me es la energía almacenada por efectos de reacciones bioquímicas la cual representa una fracción muy pequeña de Ri (0.506 J (µmol/CO2) y puede ser ignorada (Nikolov et al., 1995).
Exploración del espacio paramétrico del modelo implementado
Utilizando 10,000 simulaciones se exploró el espacio paramétrico, lo que permitió seleccionar el conjunto de parámetros que mejor representan los datos observados. En la Figura 2 se observan los resultados obtenidos al explorar el espacio paramétrico factible del modelo con los gráficos de puntos generados a partir de 10,000 simulaciones de Monte- Carlo. En la Figura la superficie cóncava en un único vértice del parámetro (m) y es sinónimo de una alta identificabilidad; por el contrario, los demás parámetros presentan superficies muy planas a lo largo del eje x, lo cual sugiere problemas de interacción paramétrica y por tanto baja identificabilidad. No obstante, a pesar de la poca identificabilidad de los parámetros Vm25, Kc25, Jm25, Ko25, f y Bs la función objetivo 1-R2 es minimizada cercana a cero (0). En el Cuadro 1 se incluyen los parámetros identificados para el cultivo de maracuyá.
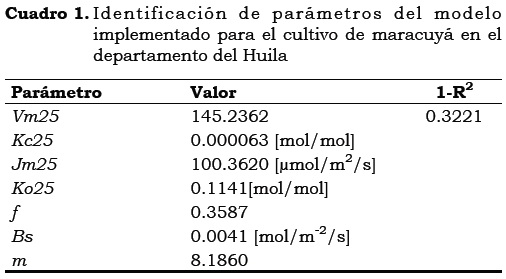
Nikolov et al. (1995) a 2600 m.s.n.m. al sureste de Wyoming (EE.UU.) encontraron para especies de pinos los valores del parámetro m siguientes: Pinus contorta m = 9.75; P. flexilis, m = 8.7; Populus tremuloides, m = 13.5. La identificación del parámetro m es importante ya que es característico de la actividad estomática de cada especie.
Análisis de sensibilidad regional
El análisis de sensibilidad del modelo tiene como objetivo evaluar el impacto generado por el cambio de los parámetros o los datos de entrada en las respuestas de un modelo matemático. Por tanto esta metodología permite determinar qué parámetro domina la respuesta y cuál podría ser eliminado por su baja sensibilidad o influencia en los resultados obtenidos en la simulación (Figura 3). El parámetro m en esta Figura sugiere una alta sensibilidad en la explicación de los fenómenos. Nótese que a medida que las probabilidades acumuladas varían con mayor gradiente, el parámetro analizado m es más sensible en un determinado rango; por el contrario, los demás parámetros son poco sensibles y por tanto se podría evitar su calibración.
Validación
En la Figura 4 se presenta la comparación de las series simulada y observada de la transpiración del cultivo de maracuyá, de acuerdo con el criterio del Centro Hidrometeorológico de Rusia el modelo cuenta con una buena validación (S/sD) de 0.30.
Simulación
Las fases de prefloración, floración, formación y llenado de frutos, así como de maduración de la planta están directamente relacionadas. Cuando la planta tiene un sistema radicular bien desarrollado se garantiza la absorción de agua y nutrientes, indispensables para la transpiración y otros procesos fisiológicos. Por otro lado, en las hojas se lleva a cabo la fotosíntesis, proceso por el cual se fabrican varios sólidos solubles totales que hacen parte del 80% de la masa seca del fruto (Shao et al., 2008), estos sólidos son translocados desde las hojas y vainas foliares hacia el fruto en formación (Taiz et al., 2006), haciendo que en éste se acumule una mayor masa.
La transpiración del cultivo de maracuyá durante el periodo de evaluación y el ciclo fenológico previo a floración hasta el final de la fase de llenado de fruto presentó variaciones entre 0.2 y 2.8 mm/día, con oscilación regulada por la apertura estomática de la plantación sometida a condiciones de clima altamente variables, tanto diario como mensual. En la zona, tanto la alta nubosidad como la limitada radiación solar directa inciden de manera importante en el estímulo de apertura y cierre de estomas, lo que finalmente controla el intercambio de vapor con la atmósfera circundante y la transpiración del cultivo de maracuyá (Figura 5).
El cultivo de maracuyá es una pasiflora semiperenne, cuya mayor demanda de agua se presenta parcialmente en la fase de floración y se acentúa durante la fase de formación y llenado de fruto. El llenado y formación de fruto es diferencial y escalonado, es decir, permite la obtención de cosechas sucesivas que se prolongan en el tiempo espaciando la recolección del fruto para el abastecimiento al mercado.
- Los resultados del estudio indican que con el modelo propuesto es posible estimar la transpiración del cultivo de maracuyá bajo condiciones de clima templado con una adecuada calibración (S/sD) de 0.30.
- Se identificó el parámetro m siendo altamente sensible para el caso de estudio en cultivo de maracuyá, a diferencia de los parámetros Vm25, Kc25, Jm25, Ko25, f, Bs que muestran escasa sensibilidad e identificabilidad. Por tanto, el parámetro m es clave durante el proceso de calibración.
- La transpiración media diaria para el cultivo de maracuyá en las condiciones de clima templado del departamento del Huila durante el periodo de investigación es de 1.36 mm/día.
- El modelo propuesto es una alternativa al método estándar FAO Penman - Monteith, y puede ser asociado con escenarios de cambio climático y seguridad alimentaria para trabajos futuros. Adicionalmente, este modelo podría integrarse a modelos hidrológicos, considerando la vegetación como agente modulador de los efectos de la variabilidad climática a través de las interacciones suelo-vegetación-atmósfera (García y Barros, 2005), lo cual será abordado en futuros trabajos.
Especial agradecimiento al Departamento Administrativo de Ciencia, Tecnología e Innovación –Colciencias- por la beca-pasantía de Joven Investigador, al Grupo de Investigación Hidroingenieria y Desarrollo Agropecuario –GHIDA- de la Universidad Surcolombiana, al Grupo Ciencia e Ingeniería del Agua y del Ambiente de la Pontificia Universidad Javeriana y a la Corporación Centro de Investigación para la Gestión Tecnológica de Passiflora, del departamento del Huila.
Allen, R. G.; Pereira, L. S.; Raes, D.; y Smith, M. 1998. Crop evapotranspiration-Guidelines for computing crop water requirements-FAO Irrigation and drainage paper 56. FAO, Roma. 300 p. [ Links ]
Ball, J. y Berry, J. 1982. The ci/cs ratio: a basis for predicting stomatal control of photosynthesis. Carnegie Institute of Washington Yearbook 81. p. 88 - 92. [ Links ]
Brouder, S. M.; y Volenec, J. J. 2008. Impact of climate change on crop nutrient and water use efficiencies. Physiol. Plant. 133:705 - 724. [ Links ]
Campbell, G. S. y Norman, J. M. 1997. An introduction to environmental biophysics, 2nd ed. Springer, EE.UU. [ Links ]
Chen, A. S.; Evans, B.; Djordjevic, S.; y Savic, D. A. 2012. Multi-layered coarse grid modelling in 2D urban flood simulations. J. Hydrol. 470 - 471:1 - 11. [ Links ]
Domínguez, C. E. 2000. Protocolo de modelación matemática de procesos hidrológicos. Meteorol. Col. 2:33 - 38. [ Links ]
Drewry, D.; Kumar, P.; Long, S.; Bernacchi, C.; Liang, X.; y Sivapalan, M. 2010. Ecohydrological responses of dense canopies to environmental variability: 2. Role of acclimation under elevated CO2. J. Geophys. Res. 115. G04022. [ Links ]
Egea, G.; Verhoef, A.; Vidale, P.L. (2011). Towards an improved and more flexible representation of water stress in coupled photosynthesis-stomatal conductance models. Agr. Forest. Meteorol. 151 (10), 1370-1384. [ Links ]
Farquhar, G. D.; Caemmerer, S.; y Berry, J. A. 1980. A biochemical model of photosynthetic CO2 assimilation in leaves of C3 species. Planta 149(1):78 - 90. [ Links ]
Garcia, J. F. y Barros, A. 2005. Incorporating canopy physiology into a hydrological model: photosynthesis, dynamic respiration, and stomatal sensitivity, Ecol. Model. 185(1):29 - 49. [ Links ]
Garay, S. J. 2009. Anuario estadístico agropecuario año 2009, Neiva – Huila: Gobernación del Huila. Secretaría de Agricultura y Minería. Disponible en: http://www.huila.gov.co/documentos/A/ANUARIO%20ESTAD%C3%8DSTICO%20AGROPECUARIO%20DEL%20HUILA%202009.pdf [Fecha revisión: Julio 19 de 2013] [ Links ]
Keenan, T.; Garcia, R.; Friend, AD.; Zaehle, S.; Garcia, C.; Sebaste, S. 2009. Improved under-standing of drought controls on seasonal variation in Mediterranean foresty canopy CO2 and water flux thoroug combined in situ measurements and ecosystem modelling. Biogeosciences. 6, 1423-1444. [ Links ]
Li, G. L.; Yongyi-Dong, L.; Dongsheng, A.; Yongxiu, L.; Weihong, L.; Xinyou, Y.; Wenwen, L.; Jingqing, S.; Yanbao, Z.; Jianfeng, D.; Weiping, C.; y Chunjiang, Z. 2012. Testing two models for the estimation of leaf stomatal conductance in four greenhouse crops cucumber, chrysanthemum, tulip and lilium, Agr. Forest. Meteorol. 165:92 - 103. [ Links ]
Nash, J. E.; y Sutcliffe, J. V. 1970. River flow forecasting through conceptual models. part IA discussion of principles. J. Hydrol, 10(3):282 - 290. [ Links ]
Nikolov, N. T.; Massman, W. J.; y Schoettle, A. W. 1995. Coupling biochemical and biophysical processes at the leaf level: an equilibrium photosynthesis model for leaves of C3 plants. Ecol. Model. 80(2 - 3):205 - 235. [ Links ]
Orgaz, F.; Villalobos, F. J.; Testi, L.; Fereres, E. 2007. A model of daily mean canopy conductance for calculating transpiration of olive canopies. Funct. Plant Biol. 34(3):178 - 188. [ Links ]
Pandey D. N.; Gupta A. K.; y Anderson, D. M. 2003. Rainwater harvesting as an adaptation to climate change. Curr. Sci. 85(1):46 - 59) [ Links ]
Ritchie, J. T. 1972. Model for predicting evaporation from a row crop with incomplete cover. Water Resour. Res. 8:1204 - 1213. [ Links ]
Ruiz, J. F. 2010. Cambio climático en temperatura, precipitación y humedad relativa para Colombia usando modelos meteorológicos de alta resolución. Panorama 2011 - 2100. Nota técnica 005/2010 del IDEAM. Bogotá. Colombia. [ Links ]
Shao, H. B.; Chu, L. Y.; Jaleel, C. A.; y Zhao, C. X. 2008. Water-deficit stress-induced anatomical changes in higher plants. Comptes Rendus Biologies 331(3):215 - 225. [ Links ]
Taiz, L. y Zeiger, E. 2006. Plant Physiology: Sinaver Associates, Inc. 700 p. [ Links ]
Trevor, K.; Santi, S.; y Gracia, C. 2010. Soil water stress and coupled photosynthesis–conductance models: Bridging the gap between conflicting reports on the relative roles of stomatal, mesophyll conductance and biochemical limitations to photosynthesis, Agr. Forest. Meteorol. 150(3):443 - 453. [ Links ]
Uddling, J.; Hall, M.; Wallin, G.; Karlsson, P. 2005. Measuring and modelling stomatal conductance andphotosynthesis in mature birch in Sweden. Agr. Forest. Meteorol. 132(1):115-131. [ Links ]
UN (United Nations). 2012. World urbanization prospects: The 2011 revision. Disponible en: http://esa.un.org/unpd/wup/index.htm [Fecha revisión: Julio 19 de 2013] [ Links ]
Villalobos, F.; Orgaz, F.; Testi, L.; y Fereres, E. 2000. Measurement and modeling of evapotranspiration of olive (Olea europaea L.) orchards. Eur. J. Agron. 13(2-3):155 – 163. [ Links ]
Wagener, T. y Kollat, J. 2007.Numerical and visual evaluation of hydrological and environmental models using the Monte Carlo analysis toolbox. Environ. Model. Softw. 22(7):1021 – 1033. [ Links ]
Yu, G. R. 1999. A study on modeling stomatal conductance of maize (Zea mays L.) leaves. Tech. Bull Fac. Hort. Chiba Univ. 53:145 - 239. [ Links ]
Yu, D.; Shi, P.; Liu, Y.; y Xun, B. 2012. Detecting land use-water quality relationships from the viewpoint of ecological restoration in an urban area. Ecol. Eng. 53:205 - 216. [ Links ]
Yu, Q.; Liu, Y.; Shi, P. 2004. Simulation of the Stomatal Conductance of Winter Wheat in Response to Light, Temperature and CO2 Change. Annals of Botany. 93: 435-441 [ Links ]













