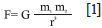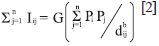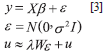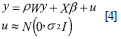INTRODUCTION
There is a myriad of technical analysis dealing with agricultural sector coming from academic and technical institutions and also pullulate policy documents emanated from national and regional governments, which diagnose the situation of rural sector. There the central topic gravitates around productivity, competitiveness, regional and local development and planning of territory. In this article we try to apply some quantitative techniques to identify economic and spatial trends of agriculture in Boyacá and we consider that by its methodology and approach, the article contributes to the discussion of productive and spatial conditions of agricultural output and remarks the fundamental drawbacks that hamper the productive and social development of provinces within the state.
As showed in Figure 1, it is clear that the geographical conditions of the state suggest a predominant presence of high lands and cold climates that propitiate the development of agricultural crops, adequately adapted to such conditions. In spite of the importance of cold climate production, we can also find a broad variety of climates and natural environments that stimulate the production of other commodities. So, from the outset we can presume the remarkable role of agriculture in the state's economy.
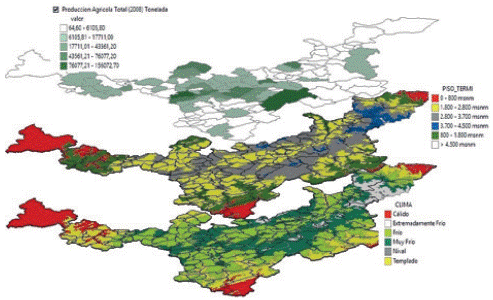
Source: Own elaboration based on Instituto Geográfico Agustín Codazzi, DANE, Ministerio de Agricultura y Desarrollo Rural
Figure 1 Map: Boyacá: Agricultural Production, Highness and Weather.
This article tries to identify the behavior in the spatial distribution of agricultural production in Boyacá state. Provided the remarkable role of its rural sector at a national scale, this article tries to analyze in detail the productive role of municipalities in the agricultural output and the implication of dependence in the spatial distribution of output. In order to deal with such topics the article is organized as follows: after this introduction, we present a short description of the main agricultural products in Boyacá. Secondly, a summary of theoretical and methodological approaches on gravity models are checked. Later, empirical strategy is developed and spatial econometric model is performed. At the end, some conclusions are proposed.
From the outset we highlight the spatial dimension of production either for theoretical analysis as for empirical methodologies. In fact, spatial distance becomes an important determinant in relationships and economic flows across territories. Commercial exchanges, mobility factor, capital movements, migrations, etc., can be prompted by closeness between countries and regions, and geographic proximity fosters specialization. The problematic of space have been treated before in the context of location theory (mainly Lõsch and Christaller) and more recently by New Economic Geography theorists, who incorporated transport costs as a crucial parameter in models of location and spatial distribution of manufacturing activity. At international level, the new international trade theory underlines the upsurge of intra industry exchanges between neighbor countries as the main feature of actual trade between advanced economies. In this kind of exchanges, differentiated goods classified in the same statistical category are traded between commercial partners who take advantages of increasing returns and scale economies (Krugman, 1992, 2008).
In spite of the evidence that spatial interactions make up an underlying phenomena in economic relationships, they have not been acknowledged or embodied in economic theory's hard core. In fact, in the conventional international trade theory, countries are assumed as points without spatial meaning (Krugman, 1992) and on this basis, conventional theories define commodities as perfectly traded and factors completely immobile assuming null transport cost. Quoting Leamer and Levinsohn, Anderson asserts that in academic context there is no "explicit reference to distance, but with the very strange implicit assumption that countries are both infinitely far apart and infinitely close, the former referring to factors, and the latter to commodities" (Anderson, 2010, p. 1).
So, in order to analyze geographical concentration of production and specialization of countries and regions, new economic geography integrates in analysis concepts as: transport cost, increasing returns and mobility of manufacturing labor (Krugman, 1991, 2008). So, in the context of theories and empirical works that highlight space, distance and spatial influences emerge as powerful forces that prod economic processes up.
According to new approaches, it is interesting to tackle a regional analysis about behavior of agricultural production and its spatial determinants, conditioned to market size and distance to consumer places. In doing so, we apply a gravity approach to identify municipalities that reveal different degrees of spatial interaction with neighboring markets, taking into account the magnitude of own agricultural output and the proximity to main regional centers. Boyacá state is an optimal case of study due to its key role in Colombian agricultural production, and its idiosyncratic productive organization, based on small scale peasantry and by the specific mechanism of harvest commercialization. So, using as basic unity of analysis the municipalities, all ingredients for gravitation analysis come up: distance between farms and markets, size of agricultural production and regional urban markets.
SPATIAL DESCRIPTION OF AGRICULTURE IN BOYACÁ
The role of Boyacá in national agricultural landscape is marked by specialization and by natural condition. Jointly with Cundinamarca, Boyacá leads the cold climate supply for central zone of Colombia, and beyond, its production reaches further markets in mild zones at north of the country.
Boyacá state is one of the most remarkable agricultural producers in Colombia, where the economic process is surrounded by a rural context of peasantry and small farms (DNP, 2007). According to Proexport (2014), this region stands out as the first vegetables and tomatoes producer. In the same way, it is ranked as the first supplier in eleven varieties of fruit and shares with Cundinamarca and Nariño the first places in the production of potatoes.
Also in onion crops the state is an active protagonist. Boyacá concentrates the half of onion production in Colombia, followed by Norte de Santander and Cundinamarca. At local level some towns have an important role. Production in Tibasosa and Samacá represents 16 % and 5 % of national production, respectively (Asohofrucol, 2013).
Natural diversity responds to complexity in weather conditions and climate areas in a reduced space. According to Plan Frutícola Nacional (PFN, 2006), the region has all climate areas. As we will show below, topographical conditions are a significant determinant of rural production provided that average highness in the towns of the department of Boyacá rises to 2066 m.
Broad climatic variety and diversity in environment conditions explain the productive vocation in Boyacá. Recent statistical information gives an idea of the dimension of volumes in agricultural output, as Table 1 shows:
Table 1 Boyacá: Main agricultural production (thousands of tons).
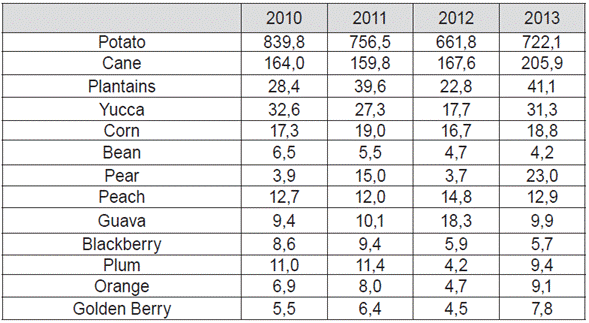
Source: Secretaría de Fomento Agropecuario de Boyacá.
In fact, it is used that small peasants alternate crops of potato with others of corn, beans, peas, wheat and barley (Rodríguez & Bermúdez, 1997). Such multi crop system reduces the economic risk for small farmers and offers food for self-consumption of peasant's family. On the other hand, the main fruit crops are: guava, orange, pear and plum. Moreover, the region is the leading producer of deciduous fruits due to its aptitude in plain lands, mainly in towns as Nuevo Colón.
A crucial aspect in agricultural production is the market orientation of commodities and the projection to nearby consumers looking for local demand. In terms of population Boyacá exhibits a few urban centers, meanwhile rural features predominates in less populated towns.
Most of the towns in Boyacá have a relevant rural predominance, and cities concentrate urban activities. Figure 2 shows more populated municipalities. Tunja represents the administrative and urban center of the whole region and concentrates bureaucratic, administrative, educational and financial activities. Secondly, other cities of a smaller size are, namely: Sogamoso, Duitama, Chiquinquirá and Puerto Boyacá.
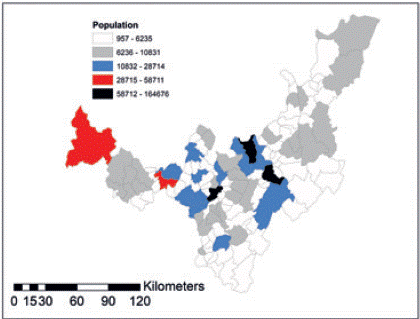
Source: Own elaboration based on Instituto Geográfico Agustín Codazzi and DANE
Figure 2 Map: Boyacá: population per municipalities.
In Duitama and Sogamoso farmers markets are opened several days in the week, in particular for fruits. In this condition, some intermediaries can trade in different points of the state during a week, forging an oligopsony structure taking information of prices from Bogotá's market: Corabastos (Plan Frutícola Nacional, 2006). Regional government plans to promote local farmers markets to guarantee food security and to match the productive cycle with local needs of consumers (Gobernación de Boyacá, 2012).
Intermediation chains and markets location are crucial for understanding the dynamics of agricultural system in Boyacá. A part of the output is carried out to markets from farms and huge quantities have as destination Bogotá, the national main city, Santander state and the Northern Coast. On the other hand, due to relatively short distances, production can be distributed to main markets within the state, where there are daily local transactions, according to the organization of farmer markets in each jurisdiction.
In general terms, peasant economy in agricultural exploitations has serious profitability and productivity drawbacks due to lags in technological and productive procedures and lack of credit sources. Regional authorities (Secretaría de Fomento Agropecuario) identified all the problems affecting the small parcel of production. Features of peasant economies are tiny size of farms, lagged infrastructures intended for storing and transformation of commodities, high cost of production, scarcity of labor, emigration of young workers, not remunerative prices for production and high climatological and business risks. Moreover, there are not sufficient coverage instruments for guarantee eventual losses associated to climatological and market uncertainty.
Potato is a basic commodity in nutritive habits of Colombian household and has a big weight in Colombian Consumer Price Index. Harvest has diverse destination: 8 % is used as input for manufacturing, processing, 10 % goes to self-consumption, 64 % is sold in wholesale markets and the remaining quantity is used as seed (Superintendencia de Industria y Comercio [SIC], s.f.).
The potato production system is dominated by a myriad of small dispersed farms. Technologies of production are very traditional and barely mechanized (DNP, 2007). Small size of parcels and irregular terrain hamper an intensive use of capital and machinery. Geographically, potato crops require adequate highness and specific climate conditions. In general crops are located at more than 2.600 meters over the sea level, in temperature conditions of 11 °C or 14 °C. Suitable places to cultivate potato includes central region of Boyacá in towns as: Tunja, Siachoque, Boyacá, Chivatá, Toca, Oicatá, Motavita, Cómbita, Paipa, Tuta, Duitama, Santa Rosa, Cerinza, Belén, Gámeza, Pesca, Aquitania and Sogamoso (Rodríguez & Bermúdez, 1997). Indeed, some of those towns appear henceforth with intense spatial interaction in the gravitation model and some of them are promptly connected, overlapping with an area very well connected by highways1 (see Figure 3).
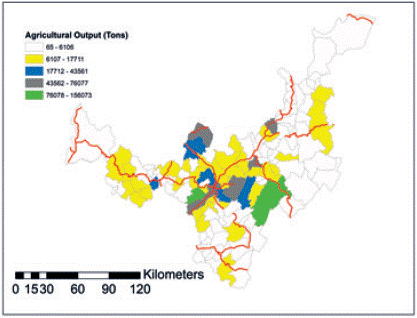
Source: Own elaboration based on Instituto Geográfico Agustín Codazzi -Ministerio de Agricultura y Desarrollo Rural - Ministerio de Transporte
Figure 3 Map: Department of Boyacá: Agricultural Output per Municipalities (Tons) vs. Main Highways (Primary net).
The system of commercialization of potato output at a national scale operates as an oligopoly mechanism. Indeed, to convey output into consumption centers a key figure emerges in landscape: the collector. This agent picks up the production from farms, transports potatoes in trucks and finally puts the product in wholesale markets. In fact, the whole -sale market is the main link between producers and consumers because it concentrates a larger quantity of potato traded.
In terms of symmetry of information and efficiency of markets, a small peasant operates with a big handicap because has no exact data on prevailing prices neither an integral perspective of the situation in wholesale markets. System of commercialization bestows huge market power on those intermediaries that collect harvest from peasant with full awareness of general market conditions and who are agents that know the conditions of final markets and the final prices of commodities. In general, small peasant ignores the prevalent circumstances of highly segmented market as potatoes (Rodríguez & Bermúdez, 1997).
On the other hand, fruits crops have an increasing importance in state's agricultural activities, particularly in mild climates. According to the National Fruit Plan (2006), the productive potential of the state could be increased in specific municipalities namely: Blackberry in Arcabuco, Gachantivá, Jenesano and Nuevo Colón; strawberry: Arcabuco, Villa de Leiva, Paipa, Tuta, Tunja and Duitama; guava: Moniquirá and Miraflores; orange: Muzo, Otanche, Santa María, Moniquirá, Miraflores, Páez, Berbeo and Campohermoso; grape: Villa de Leiva, Sutamarchán and Sogamoso; golden berry: Arcabuco, Úmbita, Santa Sofía and Miraflores (PFN, 2006).
According to PFN, there are three channels to sell the fruit output. Part of the output is traded through wholesale markets and neighborhood markets, aimed to the final consumption of a household. Part of the output is sold through large retailing stores. Finally, fruits can be used as input for manufacturing and processing (PFN, 2006). Nevertheless, the bulk of output is absorbed by a consumer through small farmers markets in towns and neighborhoods.
Deficiencies in commercialization chain and marketing deprive peasant, hinder the generation of added value and restrict the formation of remunerating prices. Many tasks must be done for improving stuff commercialization, as well as optimizing the quality, selection, packing and storing and incorporating any basic transformation. Regional policy suggests reinforcing the storage centers intended for selecting, sorting and packing, in particular for commodities as vegetables, potato, carrot, onion, fruits, cacao, coffee and milk (Secretaría de Fomento Agropecuario, s.f.).
But all public policies with long term goals, must aim to promote the effective insertion of peasant in market economy reaching remunerative prices covering the cost of production. All public efforts must contribute to improve competitiveness of peasant economy, pursuing a successful and sustainable expansion of rural production. In other places of the world similar goals has been proposed:
farmers have slowly acquired a deeper understanding of the importance of commercial channels and marketing mechanism for the whole process of agricultural and rural development. The role of national policy makers became crucial to speed up this process and facilitate the way farmers should learn to organize themselves around common interest. (De Noronha & De Noronha, 2010, p. 125).
GRAVITATION MODEL
Gravitation models are used to estimate statistically the relationship between variables that are supposed to be influenced by distance and spatial factors, when economic flows appear. From the beginning models have been applied mainly in the field of international trade, in order to detect the importance of distances and size of markets in exchange of commodities. Anderson (2010) evokes the works of Ravenstein in 19th century, analyzing migration patterns in Britain, and those of Jan Tinbergen about trade in 1962. Also, this kind of models has an enormous advantage provided that conventional theories of trade only puts in scene two countries, conversely gravitation models collect interaction among several trade partners (Anderson, 2010). Other gravity models have been applied to migration as in case of Tobler (1975).
As Isard points out: "Since 1960, a very large array of gravity and spatial interaction models has evolved. They relate to a different kind of interactions, some purely theoretical, but much more frequently interaction concerned with everyday problems" (Isard et al., 1998, p. 249).
In regional studies the gravitation approach has also been implemented successfully. In this context, regions are assumed as masses, in such a way that flows between regions can be understood as the interaction between masses (Isard et al., 1998), in consequence, the bigger their dimension, the strong interactions between them.
According to De Noronha and De Noronha (2010), in essence the model applies the same principle as the universal gravitation theory of physics as follows:
F being: the force of attraction between two objects, m two masses and r the distance. In these terms the spatial interaction between regions is strongly influenced by the size of two masses, acting as diminishing force the distance.
In Isard's version of gravity principles, analysis is applied to migration between the place i and j. In these terms the model can be presented as:
Where: I corresponds to interaction, Pi is population in I, Pj is population in j, G is gravitation constant and d is distance (Isard et al., 1998).
Moreover, gravitation models detect friction forces that lead the forces of the model in an opposite direction.
In spite of simplicity in the concept of gravitation, a key aspect must be outlined. In practice, trade and economic phenomena are influenced by forces outside the model that divert flows from multiple origins and diverse destination. Taking into account the definition of the model, people or goods can come from several origins different to i, and can have as destination diverse places excluding j. This circumstance inserts into model forces of friction that must be analyzed.
Results of Gravitation
For developing this section we will apply the formula that appears in [1]. For this calculation we will use agricultural output, population and crossed distances across towns.
In our exercise, gravitation principles are used to model the interaction throughout agricultural towns, consulting data on agricultural production and potential markets represented by the local population. Gravitation space is constrained to jurisdiction of Boyacá in order to control gravitation movements. At this point a caveat is worthy. Outward markets such as Bogotá, Bucaramanga or further points, in practice, are important market niches for Boyaca's production. Even few products as golden berry are sold in international markets. So, in spite of their potential relevance, outside markets are not included in the analysis because it would imply geo-statistical complications. In these terms, disposable data for Boyacá will be used at the state level for 119 municipalities.
To calculate gravitation forces in this exercise, two masses are assumed for the launching process. Firstly, agricultural production measured in ton interacts by interacts with population of towns, as a proxy for dimension of local markets. On the other hand, the distance between the masses is determined by geo-statistical tools. Geo-referenced and geo-statistical processes were carried out in software ARC GIS. Data were collected from the webpage of Colombian geographical office (IGAC), from Colombian statistical office (DANE) and from Ministerio de Agricultura y Desarrollo Rural (1997), including 119 municipalities.
Figure 4 summarizes the forces that interact in the model, and has a similar rendering as appears in De Noronha and De Noronha (2010). According to gravitational dynamics, surrounding Tunja cold climate agriculture predominates, pushing neighbor towns to supplying urban needs with agricultural commodities. In fact, in short distance to the main city, a system of fertile towns produces potato and vegetables, taking advantage of spatial proximity and working as a crossroad in the state receiving the main regional highways (see Figure 3).
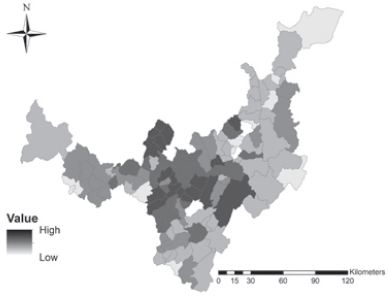
Source: Own elaboration based on Instituto Geográfico Agustín Codazzi & DANE
Figure 4 Map: Boyacá: Intensity of Spatial Interaction according to Gravitation Model.
Results of gravitation model depict concrete spatial zones located near to urban centers that spur agricultural output. The intensity of spatial dynamics reveals that urban markets and important producers of agricultural commodities are located in short distances and are connected by relatively well paved roads.
In productive terms, close towns, such as Samacá, Ventaquemada, Motavita, Chíquiza, Cómbita, harvest commodities of cold climate that are attracted to Bogotá (national main city). Also in this central zone, towns as Toca, Siachoque and Viracachá confirm their specialization in potato crops. Tunja itself appears in statistics either as a producer and important consumer for regional output. In previous research, Arias and Antosova (2015) identified a similar central zone in this state describing a spatial pattern of high agricultural activity, suggesting potential spatial autocorrelation. A relevant feature is the fluent communication that has this central zone, provided that an important highway crosses longitudinally those municipalities and connects quickly with the national main city (as shown in Figure 3).
With the purpose to mix the whole information offered by the gravitational model and basic data in mass variables (population and output), a cartographic superposition of layers will be built, in order to compare the spatial behavior of points of production and consumption with the spatial intensity of their interrelation.
A combination of three layers displayed previously is rendered now in Figure 5. Higher and lower maps render the local values for agricultural output and population, respectively. But the interesting information is rendered in the intermediate map, because it represents the outcomes turned out from the gravitation formula [1]. There can be appreciated more clearly the influence of the masses (output and population) on the results of gravitation model, and there also appear some insights about the distance between municipalities. It is exhibited there the most important zone in terms of spatial interaction around Boyacás main city. According to the results, important agricultural points are concentrated geographically in the state looking for supplying strong outer demand.
Source: Own elaboration based on Instituto Geográfico Agustín Codazzi, DANE and Ministerio de Agricultura y Desarrollo Rural
Figure 5 Map: Boyacá: Agricultural Production, The Gravitational Model and Population.
On the Figure 5, moving to east, Aquitania and Tibasosa emerge as leading producers of onion at national level, but nearby we find an important center namely: Sogamoso. Consequently, those towns show intense spatial interaction as agricultural producers. Although, Aquitania and Tibasosa are widely known as prominent producers of onion at a national level, and a big share of their output is sold in Bogotá and outside of Boyacá.
In the Northern Province of Ricaurte, warmer conditions allow to harvest commodities of mild climate. In the gravitational model Chitaraque appears having an intense spatial interaction as a producer and showing closeness to populate towns located towards east. Neighbors as Moniquirá and San José de Pare have an important share in production, but are located far away from cities as Duitama, Sogamoso, and even Tunja.
The geographical extremes of the department show a weaker intensity in spatial relationships, as can be appreciated at Provinces of Gutiérrez and Occidente. In the former, towns as Cubará, Chiscas, El Espino, Panqueba, Guacamayas, El Cocuy and Guicán are very remote places, barely communicated with the state's main centers. Consequently, gravitation models detect an important influence of geographical distance that inhibits spatial interaction in those cases. In regard to the Province of Occidente, it has two populated places: Chiquinquirá and Puerto Boyacá, but its mining vocation relegates agriculture activities to a second place.
Nevertheless, powerful friction forces intervene through the operation of commercialization systems. In fact, there are strong flows carrying out products outside the state, in particular to Bogotá, Bucaramanga, and other areas beyond state's frontiers. The well shaped connectivity built around potato towns helps to communicate quickly with Bogotá and projects the bulk of production of the national main city. Recentlly improved highway from Briceño to Sogamoso allows the connection of agricultural place as Samacá and Ventaquemada with Bogotá in a journey lasting roughly two hours (as shown in Figure 3).
In consequence, this geographical closeness to the national main city drives a large part of production into Bogotá and reinforces some frictional forces, it involves that there is commercial flows and spatial interactions there are getting out from our model centered in the geographical jurisdictions of Boyacá.
It could be concluded with Isard that: "the more clearly the gravitational interaction is discerned, the fewer the differences among the elements of each mass and the larger the masses involved" (Isard et al., 1998, p. 252).
EMPIRICAL STRATEGY
In this section, for performing geo-statistics and spatial econometrics our sources of information are DANE, IGAC and Ministerio de Agricultura y Desarrollo Rural with data available for 119 municipalities and distances to Tunja are calculated by means of geo-statistical tools. The cartographical, geo-statistical and econometric strategies were performed in ARC MAP and R software.
Analyzing 119 municipalities, we generated a spatial weight matrix (W) defining the kind of spatial interaction as queen. So the direction of spatial association flow is similar to the queen movement in chess.
Gravitation model highlights the enormous importance of markets, transport cost, distances, and connectivity in stimulating agricultural market output. A huge drawback comes up from the isolation of some towns in remote regions of Boyacá, affecting output and producer's productivity. In such conditions, farmers limit their potential markets, and output is sold once in a week at own local farmers markets. Only high competitive products can overcome geographical obstacles and can be sold at competitive prices that cover the high transport cost.
Moreover, it is normal that geographical conditions and climatological influence can explain clearly defined clusters of municipalities producing the similar kind of products as: potato, fruits, coffee, guava and cane. These reasons convey important assertions about localization of production. A worthy contribution to set out an analysis of agricultural sector is to inquire the economic and spatial aspects related to the volume of output at a local level. In doing so, spatial econometrics offers tools to figure out the spatial factors that affect spatial distribution of economic variables, e.g. distance, proximity and spatial dependence across geographical entities.
A crucial aspect to consider in spatial analysis of agriculture is that basic data captured are not independent, because there is a clear relationship between observations and neighboring places (Bongiovanni, 2009). The fact that there is effectively a strong influence across points in space drives to the concept of spatial autocorrelation. This is a regularity that occurs when the basic unities are geographically arranged.
This phenomenon is due to the presence of variables systematically correlated in space or by the evidence of dependence in the residuals (Moreno & Vayá, 2002). Spatial autocorrelation may be originated in omitted variables in the specified model and consequently, the error term will include this kind of spatial influence. It happens because there is dependence between the values of the endogenous variable in neighboring areas, independent of influence of exogenous variables. In other cases, political division of data has no economic significance because does not reflect the economic interaction across agents, and economic relations go beyond artificial borders (Helsen, 2008). Some theorists have defined such situation in terms of an administrative split of territory with no economic relevance as has been recognized by Krugman (1992) and Duranton and Overman (2005).
In technical terms, spatial autocorrelation comes up if residual terms of different geographical areas are correlated. It obligates to submit data to correction of spatial autocorrelation because results can be distorted and inference becomes inaccurate.
But this situation is normally ubiquitous if data have a spatial nature or if the location is a fundamental criterion. Once spatial autocorrelation is detected, a careful treatment must be implemented. The evidence of spatial autocorrelation conveys a difficulty for estimation of the classical OLS model because results can turn out biased and the estimators inefficient. Moreover, the variance of estimators can be biased as well (Dubin, 1998).
According to this, the process of correcting spatial autocorrelation helps to get accurate estimates and to improve the reliability of the hypothesis test. Once the identification of autocorrelation is achieved, its information is included in prediction contributing to improve precision. Afterwards, maximum likelihood techniques are commonly applied to model the autocorrelation parameters and estimations of regression (Dubin, 1998).
For correcting spatial correlation two possibilities have been defined. Firstly, a model of spatial lag can be estimated where a lag of the dependent variable is included in the matrix form Wy. Here it is assumed that spatial dependence is linked to the spatial model and both are used when the purpose is to assess the degree of intensity in spatial correlation. Arfa, Rodríguez, Daniel and Shonkwiler (2010) interpret the inclusion of spatial lag as a way to incorporate the local economies of location. In these cases, the presence of spatial autocorrelation of substantive class entails that estimations will be biased and inconsistent, even if error term is not correlated (Moreno & Vayá, 2002).
A second model assumes a structure of dependence in the error term (E[εiεj]≠0) and it is understood as a nuisance dependence, and is another useful strategy for correcting the biasing influence of spatial autocorrelation (Anselin, 2001). In these terms, correction for spatial autocorrelation conveys an additional advantage represented by an improvement in the fit of the model (Bernat, 1996).
On the other hand, in the error model if there is nuisance autocorrelation, estimators are inefficient and, in consequence, statistical inference is invalid although it could be unbiased (Helsen, 2008).
In consideration of the rising importance of spatial econometrics and its widespread application, in this article a model of agricultural output is run in order to detect the spatial structure of the endogenous variable.
Spatial Analysis and Geo-statistics
In order to apply the geo-statistical and econometric methodology, municipalities of Boyacá have been chosen as primary geographical unities of analysis. Data proceed from Colombian geographical office (Instituto Geográfico Agustín Codazzi) and Ministerio de Agricultura y Desarrollo Rural, using information adequately geo-referenced. Agricultural output is measured in tons and is available for all municipalities.
Exogenous variables have a close relationship with agricultural output and all of them are significant. Rural population shows an important explanatory capacity because commodities are offered at the local level, mainly if towns are barely communicated. A geographical variable is represented by distance regarding Tunja, the main city of Boyacá, and shows the projection to urban markets. According to Arfa et al. (2010) a topographic variables can represent local relief.
Global and Local Spatial Analysis
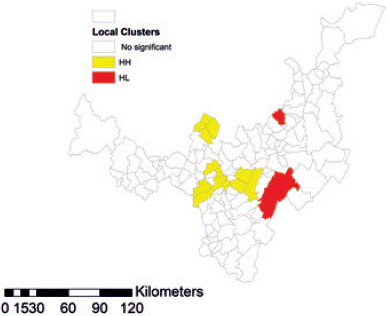
Figure 6 renders an additional statistical contrast intended to capture the local spatial dependence, known as LISA. For that purpose, at each spatial entity a significant contrast is applied, having as a null hypothesis of the absence of local spatial association. As a consequence, each spatial entity can be surrounded by different or similar values of the same variable.
Source: Own elaboration using ARC MAP, based on IGAC and Ministerio de Agricultura y Desarrollo Rural
Figure 6 Map: Boyacá's Agricultural Output in tons: Local Indicator of Spatial Association.
Concomitantly, the LISA map exhibits some clusters, indicating the behavior of values of variable for those places depending on the case. Our results corroborate the existence of a cluster of variable high values in the central corridor of the state and in peripheral zones of municipalities with low agricultural production, which are surrounded by others with similar features.
According with basic data and provided that we suppose spatial interaction only within the state borders, the process reports the case of municipalities having the lesser spatial contact with neighbors, so we find 4 cases connected only with one neighbor: Coper, Covarachía, La Capilla and Pisba.
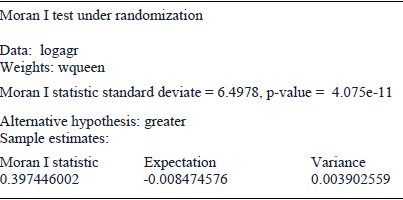
The Moran test of spatial autocorrelation makes up a very standard contrast for verifying spatial dependence. For such purpose the null hypothesis is defined in terms of absence of spatial autocorrelation and in case of rejection, there would be evidence that values prevalent in a specific geographical entity depend on the behavior of variable in neighboring spaces. For our purposes, the Moran test rejects the hypothesis of the no existence of spatial dependence in our endogenous variable agricultural production.
In spatial analysis any variable spatially lagged are defined as the weighted average of the neighboring values. This concept casts light on the possible existence of spatial dependence in values of variable distributed across different polygons in space. In such case we suppose that for diverse geographical entities the values of analyzed variable must be similar if they are located sufficiently close, suggesting that the economic phenomena behaves in a similar way across neighboring spaces. For our purposes, we are interested to bear out that agricultural production has similar values across close municipalities in order to confirm the existence of a contagion effect across towns.
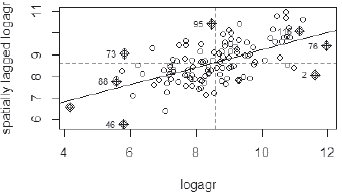
In Figure 7 is showed the Moran Dispersion Diagram representing in two axes the values of the logarithm of agricultural production and in the other hand, the spatially lagged value of the same variable. The diagram shows a positive relationship, suggesting the existence of spatial autocorrelation in our variable of interest. According to Chasco (2003), the slope of regression line corresponds to statistic of Moran, concomitantly, more open the angle formed with the abscise, highest degree of spatial autocorrelation.
Econometric Strategy
For empirical procedures hence we will use as endogenous variable the agricultural output in tons for 119 municipalities during 2005, and as exogenous the rural population in the year 2005 and the distance to Tunja in kilometers.
In terms of econometric procedures and as it is commonly used, the first step is to estimate an OLS regression assuming null values for autocorrelation parameters (p=λ=0). With such assumption the contrast of spatial autocorrelation is performed, and in case of finding evidence of this phenomenon, a Lagrange Multiplier test must be applied in order to choose the most suitable structure for spatial dependence (Helsen, 2008). Precisely OLS estimation is useful as benchmark and Lagrange Multiplier tests offer the criteria if the model requires to be extended for estimating spatial interaction effects (Elhorst, 2010).
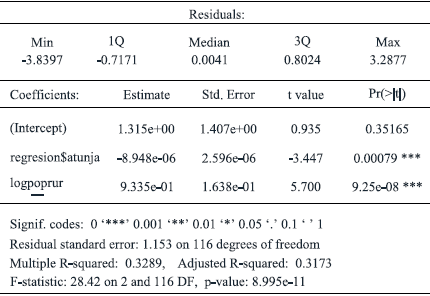
In this case the regression equation is similar to the conventional technique by OLS and results are shown in Table 4, which indicate the basic behavior of the model. Value of adjusted R2 0.328 suggests that the fit of model not jet includes relevant information about some explicative variables on model, but it is an acceptable value in cases of models with cross section or data panel arrangement. Both exogenous variables turn out significant.
Mathematical sign of the coefficient of relative distance to Tunja means that the central towns as important producers are located at short distances regarding regional main city where cold climate predominates. The other coefficient indicates that for small scale production, the preferential market is the local market and that the bulk of output produced with larger scales is conducted to Bogotá.
The next step consists in applying standard Lagrange Multiplicator contrasts for corroborating the presence of spatial autocorrelation, and to determine criteria for evaluating the pertinence of a spatial lag or spatial error patterns in order to define the kind of spatial dependence. In case of dubitation, robust Lagrange Multiplicator contrast is promptly performed.
The Table 6 shows the contrasts commonly used for choosing the correct structure of spatial dependence. In doing so, two additional tests help to understand the character of spatial dependence: LMlag and LMerr tests which indicate the significant results in the case of spatial lag model. The right choice of spatial dependence is crucial for analysis provided that this decision could conduct to diverse interpretation of the spatial dependence.
Table 6 shows the results of Lagrange Multiplier tests as definitive criteria for choosing the best description of the spatial dependence. Elhorst (2010) summarizes diverse approaches for tackling the estimation of spatial models, applying three possible strategies: Keleijan and Prucha, Lesage and Pace and Anselin. Accordingly, with the suggestion we choose Anselin's approach composed by several steps. Firstly, we estimate the OLS model and afterwards in concordance with contrasts of La-grange Multiplier (and for a definitive decision Robust LM), the disjunctive is to add or not spatial terms to regression and finally to decide if this spatial term must correspond to spatial error or spatial lag.
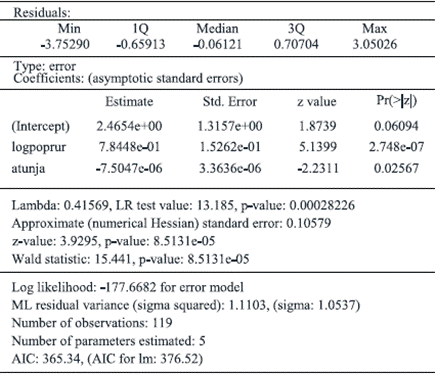
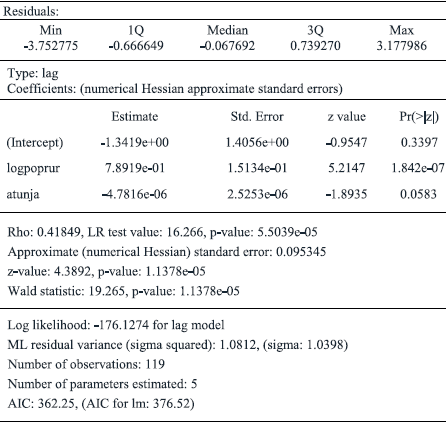
In fact, according to Table 6, Lagrange Multiplicator indicates significance either for the error model as for the lag model, so we are forced to interpret the Robust LM contrasts. Now, following the last test, the contrast of error model loses significance and in consequence, we consider that the best approach for describing the true data-generation process corresponds to spatial lag approach.
SPATIAL LAG AND SPATIAL ERROR MODELS
In tables 7 and 8 are presented two results of models, the first one corresponding to the case of the spatial error model and the second reports spatial lag model.
If the spatial autocorrelation is present only during error term, the model to estimate corresponds to:
Where: u is a withe noise term and λ becomes the autoregressive parameter.
In the model [3] if there is no omission of lag in endogenous variable of model, it corresponds to the case of residual spatial autocorrelation, then a scheme of spatial dependence in error term must be included (Moreno & Vayá, 2002).
The standard treatment of econometrics in the presence of spatial autocorrelation consists in performing a regression via Maximum Likelihood. As it is known, in this technique estimator is calculated maximizing the logarithm of a function of likelihood associated with a spatial model (Moreno & Vayá, 2002).
In the case of spatial lag it is necessary to specify the following model:
Where: y is a vector (Nx1), Wy is a spatial lag of variable, X is the exogenous variables matrix, u is a white noise error term, N is the number of observations and p is a autoregressive parameter.
In equation [4] can be observed that if spatial lag is omitted in exogenous or endogenous variables, the feature of spatial dependence will be transmitted to error term, in a case quoted as substantive spatial autocorrelation. To handle this case, it is necessary to include a spatial lag of dependent variable with spatial autocorrelation (Moreno & Vayá, 2002).
This kind of models is named also as Models of Communication or Contagion and integrates all autocorrelation structure into spatial lag, as an explicative argument of the endogenous variable. In the case of omission of weight matrix in this kind of model, estimation commits a specification error that biases estimators and drives to invalid inference.
Comparing tables 4, 7 and 8, the significance of estimators is maintained between OLS regression and two modes of correction of spatial autocorrelation, but Bernat warns about such situation in the presence of spatial autocorrelation because that effect invalidates the standard test when OLS regression are estimated, in a similar way as do serial autocorrelation or heteroskedasticity (Bernat, 1996). In lag model (Table 7), the rho parameter indicates the magnitude of effect originated in neighbor municipalities on an endogenous variable defined as agricultural output.
According to the results of both models for correcting spatial autocorrelation, the adequate specification for describing the spatial dependence of the model is the lag model, so the influence of neighboring areas on local manufacturing presence requires a special interpretation. In these cases, the spatial lag model indicates that agricultural output at each municipality is directly influenced by the size of agricultural production in neighboring localities and moreover, such spatial effect is independent regarding the set of exogenous variables. When rho parameter is high, the model has a substantial spatial dependence and municipalities show strong interest in the performance of agricultural output in neighboring places (Bernat, 1996). So, evidence indicates that an important and positive impact on the size of the agricultural production exists in municipalities if neighboring towns are prominent producers of agricultural commodities.
As can be appreciated in Table 8, coefficient rho is significant and has a high magnitude, reinforcing the influence of neighbor agricultural towns on the tons of local agricultural output. The magnitude of rho is neatly higher than the coefficients of relative distance to Tunja and rural population, suggesting that the influence of neighboring places is superior to exogenous variables. This is an additional argument for the presumption that lag model is the most adequate for our analysis.
In the presence of spatial autocorrelation the criteria derived from r squared regarding to fitness of the model, cannot be applied trustfully, so it is necessary to use other criteria for evaluating the good fit of the model. In this exercise, we check the result offered by Robust Lagrange Multiplicator criteria, and the elements offered by test conducted to choose the spatial lag model.
CONCLUSIONS
Both gravitational and econometrical exercises suggest several interesting conclusions. The gravitation model showed an important productive zone in the core of the state where municipalities share some common features. They are located in high cold lands and commodities correspond to cold climate products. But according to econometric and gravitation principles the destination of output could be quoted as bimodal. Cold climate production performed with high scales is conducted to larger national markets as Bogotá and Bucaramanga. Larger productive towns have quick geographical and logistical connection with those markets using important paved highways (as shown in Figure 3). Higher prices in larger cities attract strongly the output from Boyacá.
All gravitation principles admit some friction forces that exert outward pressure. According to econometric parameters, distance to Tunja has a negative impact on agricultural production. Consequently, if we combine all information from gravitational results and econometrics, we can assert that Bogotá and diverse markets beyond regional borders of Boyacá attract a substantial part of output produced in this state to municipalities located in central areas very close to Tunja.
In fact, the bulk of agricultural production in tons is concentrated in cold lands in the center of the state, located at high geographical positions. Cold lands are located at high geographical points, so highness is a strong factor affecting positively the agricultural production in Boyacá. Some of the important towns having a preponderant role in potato production are: Samacá (2604 m), Toca (2750 m), Siachoque (2760 m), Ventaquemada (2630 m) y Jenesano (2075 m).
A clear interaction is specially established in the central zone of the state where the cold climate crops mainly potato predominate. Moving to east, strong interaction is detected in towns as Aquitania and Tibasosa, typical producers of onion. It is possible that weak spatial intensity detected around Duitama and Sogamoso could be explained by the presence of dominant mining, manufacturing and commercial activities and less influential agricultural activities.
Farther towns in the Provinces of Occident and Gutiérrez show weak spatial interaction. Firstly, distance from the big cities and scarcity of connectivity hamper commercial flows with big markets, in consequence, small production with reduced scales are sold in weak local markets. Secondly, in some points agricultural production performs a secondary role in the local economy.
Peripheral zones in the state face an enormous market constraint. Precarious conditions of communication with important markets compel peasants to put production in local markets that, by small size, inhibit the development of sectorial scale economies. In fact, in the vast territories of Boyacá, local markets are insufficient in size for developing a broad scale of production. Spatial interaction could be intensified trough transportation, communication and associations across farmers and peasants.
Regarding commercialization of output, collectors and intermediates accomplish a role of arbitrage in agricultural markets. Relative close position across urban centers in Boyacá bestows upon them a privileged position for getting full information on prices, so they can take advantage of information and play an arbitrage function. Hiking prices and high population density attract the bulk of production.
The spatial econometric model indicated what kind of spatial dependence exists when agricultural output is used as an endogenous variable. The evidence of spatial autocorrelation confirmed that local agricultural output is strongly influenced by the size of sectorial output in neighboring localities.
This kind of spatial dependence is easy to understand for agricultural commodities because climatic and natural conditions are shared by nearby municipalities, so there must be coincidence in the productive profile between municipalities and other places located in proximity.
According to results of spatial econometric the most appropriated interpretation of spatial dependence deployed by the variables of model is concordant whit spatial lag.
Exogenous variables in model are also useful to understand the agricultural output and its spatial distribution. Municipal rural population is important because small peasant's output is sold in his own town. In fact, for tiny producers local weekly farmers markets and local demand can be strongly influential. Distance to the main city, Tunja, has a negative coefficient indicating that the closer cold lands are the relatively most productive area and emerge as a relevant agricultural cluster well connected by fluent paved highways.
An overwhelming conclusion that emerges throughout the analysis is the enormous negative impact of the high transport cost of the state's economic performance. Figure 3 shows that the main highway system has a radial design structure having as a central point Tunja and in consequence, in surrounding areas highly productive crops developed. But in further zones of peripheries we can find agricultural production, although with scarce productivity and with reduced scale economies.