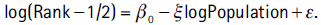Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Desarrollo y Sociedad
Print version ISSN 0120-3584
Desarro. soc. no.75 Bogotá Jan./June 2015
https://doi.org/10.13043/DYS.75.6
DOI: 10.13043/DYS.75.6
A Proposal to Delineate Metropolitan Areas in Colombia
Propuesta para la definición de áreas metropolitanas en Colombia
Gilles Duranton1
1 Wharton School, University of Pennsylvania, 3620 Locust Walk, Philadelphia, PA 19104, USA (e-mail: duranton@wharton.upenn.edu; website: https://real-estate.wharton.upenn.edu/profile/21470/). Also affiliated with the Centre for Economic Policy Research, the Rimini Centre for Economic Analysis, and the Spatial Economic Centre at the London School of Economics.
Este artículo fue recibido el 5 de junio de 2014, revisado el 10 de septiembre de 2014 y finalmente aceptado el 4 de marzo de 2015.Abstract
This paper discusses the need to delineate metropolitan areas and current practice in several countries. It argues for the use of a simple algorithm that examines cross-municipality commuting patterns. Municipalities are aggregated iteratively provided they send a share of their commuters, above a given threshold, to the rest of a metropolitan area. The algorithm is implemented on Colombian data and its robustness is assessed. Finally, the properties of the resulting spatial labor market networks are explored.
Key words: Delineation of metropolitan areas, municipal aggregation, Colombian cities, Zipf's Law.
JEL classification: R11, R12, R14.
Resumen
Este artículo analiza la necesidad de definir las áreas metropolitanas y su actual implementación en diversos países. Plantea el uso de un algoritmo sencillo que examina los patrones de los desplazamientos intermunicipales de las personas a su sitio de trabajo. Los municipios son agregados de forma iterativa siempre y cuando envíen un número de personas de un área metropolitana a otra que supere un umbral determinado. Este algoritmo es implementado utilizando datos colombianos y su eficacia es evaluada. Por último, se estudian las propiedades de las redes de mercados laborales espaciales que surgen como resultado del análisis.
Palabras clave: Definición de áreas metropolitanas, agregación municipal, ciudades colombianas, Ley de Zipf.
Clasificación JEL: R11, R12, R14.
Introduction
This paper proposes a methodology for delineating metropolitan areas by way of iterative aggregation of spatial units according to daily commuting flows between them. In essence, spatial unit A is aggregated to another spatial unit, B, if the share of the workers that reside in A and work in B is above a given threshold. Similarly, another spatial unit, C, may next be aggregated to the union of A and B if it sends a fraction of its commuters that is greater than the same threshold to the newly formed unit, A+B, even though it might not have been possible to aggregate C directly to either A or B in an initial round. This process of aggregation is repeated until no further unit can be added.
The algorithm is implemented using data for Colombian municipalities and a threshold of 10% of commuters (i.e. at least 10% of the municipal population commutes) to delineate metropolitan areas for the country, whose metropolitan areas are not currently well-defined. Although aggregating spatial units iteratively using a minimum commuting threshold is not novel, our approach is novel in two respects. First, we show that a careful implementation of an aggregation algorithm that relies solely on a minimum commuting threshold criterion is enough to delineate meaningful metropolitan areas and generate metropolitan cores endogenously. This practice differs from that used by many statistical institutes, which usually predefine metropolitan cores and use a minimum commuting rule in conjunction with several other criteria. Second, we assess the robustness of the set of resulting metropolitan areas to changes in the minimum commuting threshold for aggregation.
Delineating metropolitan areas is important for several reasons. Historically, as cities grew both in population and spatially, they would directly annex surrounding municipalities. In many countries, this process has now stopped; richer municipalities resist fiscal integration with their poorer neighbors; mayors attempt to retain their jobs; or -as in Colombia- there may be significant constitutional and administrative barriers to merging municipalities. As a result, administratively defined cities are typically restricted to an urban core and no longer represent their broader metropolitan environments.
Related to this, existing administrative units such as municipalities do not generally constitute functionally autonomous units. Instead, neighboring municipalities are often economically integrated in all sorts of ways. This implies that an economic shock or a policy intervention in one municipality may have important spillover effects on its neighbors. Given the difficulty of keeping track of spillover effects, it is easier (and typically more efficient) for policies to target functionally consistent units.
An ability to deal with functionally consistent units is also important for research. For instance, cities tend to grow geographically by spreading outwards, beyond the boundaries of the core municipality. An examination of patterns of urban growth based on municipal data may lead to the conclusion that large cities grow slowly. This is often far from being the case however. Core municipalities frequently become 'full' and their metropolitan area typically grow at their extensive margins via peripheral municipalities. Hence, urban growth is often most appropriately measured at the metropolitan level.
Finally, cities constitute interesting spatial networks of commuting workers, transacting firms, or interacting individuals. To be able to study these networks meaningfully it is fundamentally important to be able, first, to describe them.
The rest of this paper is organized as follows. Section I provides background information on the situation in Colombia, current practice in other countries, and prior academic literature. Section II presents the data and our aggregation algorithm. Section III provides our list of metropolitan areas and metropolitan regions for Colombia. The robustness of the results is assessed in section IV. Finally, section V concludes.
I. Background, Current Practice and the Literature
A. The Current Situation in Colombia
Although an official set of 'metropolitan areas' exists in Colombia, they are mostly administrative units, constituted on a voluntary basis (Congreso de Colombia, 2013; Senado de la República, 2012). Law 1625 of 2013 provides a formal framework for these bottom-up associations. Official metropolitan areas are formed as autonomous institutions to which specific powers are delegated voluntarily by the municipalities that belong to them. In practice, these powers vary widely. The official metropolitan area of Barranquilla simply assumes a coordination role in terms of planning and facilitates the mutualization of some public services. On the other hand, the official metropolitan area of Medellín (the Área Metropolitana del Valle de Aburrá, or 'Metropolitan Area of the Aburrá Valley') aims at much deeper integration. Among other things, it has jurisdiction over environmental matters and is directly responsible for operating an extensive public transit system.
While there is certainly a strong case for associations of neighboring municipalities forming broader formal institutions, these 'political' metropolitan areas are usually not appropriate for analysis and decision-making by higher levels of government. The frameworks for local cooperation should not conflict with metropolitan areas defined for economic and statistical purposes. For instance, in France the official statistical institute (the INSEE) is responsible for defining 'statistical' metropolitan areas. Simultaneously, many 'urban communities' exist which, as in Colombia, are voluntary unions of neighboring municipalities, i.e., political metropolitan areas. The two differ, sometimes considerably, but coexist as they serve dramatically different purposes.2
For historical reasons and, perhaps, because of institutional rivalry, Bogotá, the largest municipality in Colombia, does not form part of any officially constituted metropolitan area even though there is no observable discontinuity between Bogotá and, for instance, its Southern neighbor Soacha. Neither is Cali, the third largest city in Colombia, part of a constituted institutional arrangement with any of its neighbors. Barranquilla is a less extreme case. Its official metropolitan area is composed of only five municipalities, whereas our method yields a metropolitan area of nine municipalities even with an extremely conservative commuting threshold of 30% was applied (which is three times as large as our preferred threshold of 10%). On the other hand, for Medellín, the second largest city, the 'metropolitan area of the Aburrá Valley' corresponds exactly to the one generated by our algorithm with our preferred commuting threshold of 10%. However, Medellín is the exception, not the rule. Colombia needs a systematic and consistent set of metropolitan areas. Those defined here using commuting patterns are further compared with existing official metropolitan areas below.
B. Current Practice Around the World
While details vary, there are two features that are common to most ordinarily used definitions of metropolitan areas.
The first is the preponderant role given to commuting patterns, with the consequence that metropolitan areas are viewed as integrated labor markets. There are good reasons for this. Since Marshall (1890), economists usually think of cities as generating benefits in terms of 'thick' labor markets, greater diversity of available final and intermediate goods, and more intense individual interactions conducive to knowledge spillovers. It makes sense to focus on the first series of these benefits that accrue from local labor markets for two reasons. The first is that commuting patterns are easily tracked. The census and many other sources of labor market data usually record both place of residence and place of work. The variety of final and intermediate goods, input-output linkages and knowledge spillovers are much more complicated to track (Charlot and Duranton, 2004; Handbury and Weinstein, 2015; Holmes, 1999). There is also a broad consensus among economists interested in cities that commuting patterns generally take place over distances that we naturally recognize as being 'metropolitan'. Instead, knowledge spillovers might take place over much shorter distances, while input-output links often take place on a scale broader than the metropolitan area (see, for example, Krugman, 1991).
In addition, other criteria exist that could be used to define metropolitan areas, including non-economic criteria such as the sense of belonging to a place, etc. In practice, however, because they are easier to track and because their scale seems right, commuting patterns play an overwhelming role in the delineation of metropolitan areas.
The second key feature of most official definitions of metropolitan areas is the use of an iterative approach to aggregating municipalities (or other basic geographical units, such as counties in the US) into metropolitan areas. More specifically, a minimum threshold of commuters is chosen. As soon as the share of commuting flows from an originating municipality to a destination municipality exceeds this threshold, the originating municipality is aggregated to the destination municipality. We refer to the aggregated municipality as a 'satellite' municipality and the one to which it is aggregated as its 'core'. The two municipalities become part of the same metropolitan area. This procedure is then repeated until no municipality remains that can be aggregated.
If employment in metropolitan areas were fully centralized in a unique central business district there would be no need to use an iterative approach. All relevant municipalities would be aggregated in the first round. However, in reality only a small proportion of jobs is concentrated in the center of metropolitan areas. Glaeser and Kahn (2001) argue that less than 10% of employment in US cities is concentrated within 5 kilometers of their centers. This is far from the idealized description of monocentric cities where all the jobs are located in a central business district (Alonso, 1964; Mills, 1967; Muth, 1969). As a result, and given the gravitational nature of commuting where the number of commutes decreases with distance, an iterative aggregation procedure is needed. Imagine a core municipality, A, a 'first-ring' municipality, B, and a 'second-ring' municipality, C. Municipality C may send lots of commuters to A and B but not enough to warrant immediate aggregation to A. As a result, B may be aggregated to A during the first round while C is aggregated to the union of A and B during the second.
Note that commuting thresholds are defined relative to the number of workers in the municipality at hand. This is because municipalities differ vastly in terms of their resident labor force. Using a relative threshold is important because it allows the aggregation of a small satellite municipality that sends all its residents to the core. Using an absolute threshold would not allow for this. Worse, on Colombian data it would lead to very misleading outcomes since there are many 'commuters' (in absolute terms) between the largest cities, including for instance the pair composed of Bogotá and Barranquilla, which are located several hundred kilometers apart. Looking at absolute numbers of commuters is an interesting measure of the 'links' between municipalities and might be instrumental in the circulation of knowledge. It does not, however, help aggregate nearby municipalities into metropolitan areas.
Aside from these two features, which are used by most countries that delineate metropolitan areas, there are several other features which are common to many different circumstances.
The first of these (which is used for instance in the US) is the pre-determination of a 'core'. That is, the authority in charge of defining metropolitan areas aggregates satellite units (counties in the case of the US) only around particular 'core' units which satisfy, ex ante, some particular properties in terms of population size and density. Put differently, a city needs to be 'big enough' and 'dense enough' to be considered as a potential nucleus for a metropolitan area. For instance, in the US, the core county must "(a) Have at least 50 percent of [its] population in urban areas of at least 10,000 population; or (b) Have within [its] boundaries a population of at least 5,000 located in a single urban area of at least 10,000 population". (US Office of Management and Budget, 2010).
While this type of criterion seems intuitive, our results for the Colombian case show that it is not needed in practice. In addition, pre-defined cores might be arbitrary. Instead, the algorithm used to define metropolitan areas should also pick the cores endogenously. Then, given the absence of ex ante cores, issues surrounding the minimum criteria that a core should satisfy become moot, which is desirable. As will become clear below, it is best to avoid criteria that are either unnecessary or that can be manipulated, as this leaves open the opportunity of defing metropolitan areas whimsically.
It is possible to imagine that some mostly rural municipalities could attract a significant fraction of commuters from other, larger, municipalities. These rural municipalities would then be perversely tagged as 'metropolitan cores'. One could also imagine large groups of rural municipalities with lots of crosscommuting giving rise to 'metropolitan areas'. These would obviously be missing 'urban character'. While such pathological situations are theoretically possible in the absence of pre-defined cores, the Colombian example shows that, in all cases, aggregation into metropolitan areas occurs around the largest municipality and there are very few cases of aggregation involving municipal cores with a small population. As argued below, these areas can always be selected out ex post by imposing a minimum population size for metropolitan areas.
Geographical contiguity could also be added as a criterion for defining metropolitan areas. This seems natural. A highly integrated area is expected to be geographically continuous (sometimes referred to as coterminous). While there might be esthetic reasons for imposing geographical continuity, there is no strong economic justification. Two municipalities separated by inhospitable terrain may form one economically integrated area, with the area in between remaining mostly rural. It is not clear why this in-between area should be forcibly integrated when it is not interacting with the other two municipalities. In any case, this is again a moot point because the algorithm used below to delineate metropolitan areas only aggregates contiguous municipalities when our preferred threshold of 10% is used. Again, the gravitational nature of commuting implies that a municipality completely surrounded by a metropolitan area is unlikely to remain untouched when all of its neighbors have been aggregated. In any case, rather than imposing a contiguity constraint ex ante it is better to check for exceptions ex post and attempt to understand them.
Statistical authorities also sometimes add further criteria including, in the US, asking for 'local opinions'. A related issue is whether the algorithm used to delineate metropolitan areas should be applied in a strict fashion or be used more 'flexibly'. Conceptually, these two questions are separate. One may want to use a complicated algorithm to delineate metropolitan areas and apply it in a strict manner. Alternatively, it is possible to think of a simple algorithm subject to some 'operational adjustments' ex post. In practice, the issues of the number of criteria included in the algorithm and whether it is applied flexibly or not are deeply intertwined. The use of many criteria (including fairly subjective ones that rely on local opinions) is probably a way to have some flexibility in the delineation of metropolitan areas. To make things worse, countries that use a large number of criteria do not provide public information on the precise algorithm used or on the nature of the inputs fed into it.
There are two reasons why a unique, simple and transparent algorithm, strictly applied, should be used to delineate metropolitan areas. The first is that it really makes no sense to develop a methodology that then has to be renegotiated ex post at the whim of a statistician or in response to political pressure. The second reason is that metropolitan areas are included in the economic policies of some countries. Hence, their delineation affects the allocation of resources. It is therefore easy to see how and why the process can become politicized. Policies that allocate resources to metropolitan areas according to criteria that have been meddled with are by definition biased and policy outcomes are likely to have been inadequately evaluated, less efficient and potentially unfair. To avoid political interference, it is crucial that the definition of metropolitan areas remain as simple as possible and that decision-making powers be given to an independent statistical institute. The advantages of this approach are overwhelming when compared to the possible inconvenience of one or two 'awkward' cases appearing in the final list of metropolitan areas.
Statistical institutes also sometimes impose an ex post minimum population size criterion for the delineation of metropolitan areas. This may not be needed if, for instance, the original criteria include some minimum population level for the core municipality. For policy purposes it is obvious that such a minimum size threshold often needs to be considered. The threshold chosen will likely depend on the type of policy under consideration. Looking at the provision of university education, for which the metropolitan area is arguably the relevant spatial scale, it is clear that a relatively high population threshold needs to be considered as it is not reasonable to expect 'metropolitan areas' with only a few thousand inhabitants to be provided with universities. Likewise, when looking at environmental issues, such as the disposal of solid residuals, it is probably best to consider all metropolitan areas including small 'lone' municipalities. It is also the case that imposing a stringent minimum population threshold on the entire list of metropolitan areas suppresses useful information. It is therefore usually best to generate a complete list of municipalities and metropolitan areas. A cutoff can then be imposed for a particular analysis or for a specific policy or set of policies. This procedure has the added benefit of allowing for more relevant cutoffs to be considered and of forcing policy-makers to justify the cutoff they have chosen in a clear and transparent manner.
For the same reason, the threshold used for deciding whether satellite municipalities should be attached to a core needs to be clearly justified and should be a 'round number', like our preferred threshold for Colombia of 10%. A clear binding threshold may, in theory, lead to some awkward cases such as the inclusion of a remote municipality whose 'commuters' are in fact students who attend university in a distant city, or the non-inclusion of some municipalities that seem well-integrated with the nearby core on many other measures. Despite this, it is better to retain such awkward cases rather than permit more flexibility, and thus leave the way open to political interference. Furthermore, as the results discussed below make clear, awkward cases occur only in tiny numbers and when a low aggregation threshold of 5% is used. With the preferred 10% threshold, no such awkward case seems to occur. As our results also make clear, the population of metropolitan areas in Colombia is not sensitive to the chosen aggregation threshold of 10%, thought their physical extent does of course respond to the presence (or absence) of one or two municipalities with low population but large area.
Another interesting feature of the definition of metropolitan areas in many countries is the fact that several definitions are frequently used. For instance, France delineates both 'urban areas' and 'urban units'. The latter are typically organized around a single core whereas the former are more standard (and broadly defined) metropolitan areas. The same situation is encountered in the US where there is a list of 'consolidated' metropolitan areas and another of 'primary' metropolitan areas. Consolidated metropolitan areas are the union of several adjacent primary metropolitan areas. To give a concrete example, Washington DC and Baltimore form two separate primary metropolitan areas but also belong to the same consolidated metropolitan area. Again, as in France, the primary metropolitan areas appear to be core-based and to correspond to integrated labor markets. Consolidated metropolitan areas, by contrast, capture broader spatial units, and perhaps other forms of economic integration. Baltimore and Washington DC are certainly part of the same 'economic region' even though the proportion of workers that commute to DC from the northern suburbs of Baltimore is probably quite low. There is a clear tradeoff here. Having multiple definitions allows policy-makers and analysts to capture different dimensions of economically integrated areas. At the same time, a multiplicity of definitions opens the door to arbitrary decisions and political interference. There is also the issue of how to proceed when working with several delineations and whether they should be based on different thresholds for commuting or delineated using different principles. While we return to these issues in our discussion of the Colombian case below, we believe that two different definitions for two different spatial scales is attractive.
We draw a range of conclusions from this discussion. The case for defining metropolitan areas based on commuting flows and for using an iterative procedure is extremely strong. The case for using two definitions to capture two different scales is also strong. On the other hand, the justification for many other practices routinely used by statistical institutes appears weak. Defining 'cores' ex-ante appears to be unnecessary, prevents useful checks on the algorithm, and opens the door to political interference. The same arguments apply with respect to the use of other (i.e., non-commuting) criteria to define metropolitan areas. Finally, a simple and transparent algorithm that can be replicated (or used by others) allows for a number of useful checks. The usual practice followed by statistical institutes, of proposing a 'list' of metropolitan areas without presenting the raw data and the details of the algorithm used is clearly unsatisfactory.
C. Existing Literature
The need to delineate urban areas first became clear in the US during the 1950s. Powerful urban expansion and suburbanization ceased to be accompanied by municipal annexation. This led to a divergence between the political boundaries of the urban cores and the economic boundaries of their metropolitan areas. To resolve the problem, the US Census Bureau defined Standard Metropolitan Statistical Areas (SMSAS) in the early 1950s. Early discussions in Berry (1960) and Fox and Kumar (1965) were very much focused on defining metropolitan areas using a framework derived from central place theory. Later, Berry, Goheen and Goldstein (1969) offered a remarkable early discussion that echoes many of the points made here, suggesting that metropolitan areas should be delineated based solely on commuting patterns towards a predetermined urban core. Following the US, other developed countries also started defining their own metropolitan areas without much obvious academic input. Their choices came under scrutiny in Hall and Hay (1980) and Cheshire and Hay (1989), who attempted to develop a broader perspective on European cities and argued that it was necessary to use a consistent set of units.
More recently, Kanemoto and Kurima (2005) have proposed an algorithm for Japan that has been widely used by subsequent researchers in the absence of an official definition of metropolitan areas for the country. There is also a small stream of research that assesses how a range of local economic outcomes autocorrelates across small spatial units to aggregate them into larger ones (see Cörvers, Hensen and Bongaerts, 2009, for a recent example). In this spirit, a particularly interesting variable -land prices- is used by Bode (2008). He first detects some centers, defined as statistically significant spikes of land prices before estimating the part of urban land prices at each location that may be attributed to these centers and then aggregating satellite areas accordingly. His approach is interesting, as land prices are believed to reflect many different types of interactions between places, going well beyond commuting. The main drawback is that a lot of structure is imposed, minor aspects of which may affect the results. Finally, geographers often propose lists of metropolitan areas, but the delineations they propose are usually ad-hoc (see for instance Molina, 2001, for Colombia).
We also note that extant research sometimes defines its own zoning (Briant, Combes and Lafourcade, 2010; Rozenfeld, Rybski, Gabaix and Makse, 2011). The delineations currently used by researchers differ considerably. Using different zonings for policy purposes may be an issue because it is well known that the zoning that is adopted may drive some of the results.3 At the same time, as has already been argued, there is nothing intrinsically wrong with using different zonings for different purposes since some problems may require a focus on diverse spatial scales. There is also a strand of literature (e.g. Duranton and Overman, 2005) that attempts to measure economic phenomena in continuous space, doing away with spatial units altogether. This is not an option here, given our perspective.4
II. A Simple Aggregation Algorithm
Consistent with the arguments presented above, our proposed algorithm is as simple as possible. It aggregates a spatial unit to another if the former sends a high enough fraction of its commuters to the latter. Subsequently, a third spatial unit is aggregated to the union of the first two, provided it sends a high enough fraction of its commuters to the newly formed unit, even though it might not have been possible to aggregate this third spatial unit to either of the first two before they were aggregated. This process is repeated until no spatial unit remains to be aggregated.
A. Preliminary Issues
Before going into more detail on the algorithm and its implementation to the Colombian case, it is useful to discuss the choice of commuting threshold. This was fundamentally arbitrary; theory offers no reliable guidance, because the degree of economic integration between places evolves along a continuum. However, as the point of the exercise was to delineate discrete units there was no way to dispense with a threshold. Choosing a high threshold leads to the aggregation of very few satellite municipalities to urban cores, whereas a low threshold produces extremely large metropolitan areas. At the extreme, if each municipality were to send at least one commuter to each of its neighbors an arbitrarily low threshold would imply only one metropolitan area covering the entire country. This is not helpful.
In addition, the choice of threshold is likely to depend on the size of the underlying units to be aggregated. Colombian municipalities are fairly large (on average more than 100 square kilometers). The gravitational nature of commuting implies that large municipalities will send on average only a small proportion of their commuters to work elsewhere. By contrast, France has more than 35,000 municipalities (and their average land area is only about 15 square kilometers). We would thus expect much higher commuting flows between French municipalities. Unsurprisingly, the threshold used by the French statistical institute is high, at 40%.
Commuting distances also depend on levels of development. In developed countries, where a large fraction of workers can commute by car or using welldeveloped public transportation systems, a large proportion of workers may be able to commute over long distances. In Colombia car ownership is still limited and public transportation underdeveloped, so the fraction of commuters able to commute over long distances is much lower than in Europe or North America. Hence, it may be advisable to use different thresholds in developed and developing countries. That being said, we also need to keep in mind that it is desirable to retain some consistency in the way metropolitan areas are defined as a country develops.
A related problem associated with the choice of commuting threshold is the sensitivity of the delineation of metropolitan areas to small changes that may be made to it. This can occur because of the iterative nature of the algorithm. Think of the following hypothetical example. Municipality D sends 12% of its workers to municipality C and 10% to B. Municipality C sends 12% of its workers to B and 10% to A. Finally, municipality B sends 19% of its workers to A. With a commuting threshold of 20%, all four municipalities remain isolated, since there is no flow above this threshold. For a threshold below 19%, however, B gets aggregated to A during the first round. Then C, which sends 10% + 12% = 22% to the union of A and B, gets aggregated during the second round. During the third round, D is also aggregated and we end up with a metropolitan area made up of all four municipalities. In this example, a small change in the threshold from 20% to 19% leads to a radically different zoning.
There are two possible responses to the possibility of perverse cases such as the one suggested by this example. The first, already mentioned above, is to choose a 'natural' threshold (typically a round number) to avoid any suspicion of interference. The second is to assess the sensitivity of the delineation of metropolitan areas with respect to the choice of threshold by comparing outcomes for different values. Robustness checks of this kind are carried out below.
B. Data
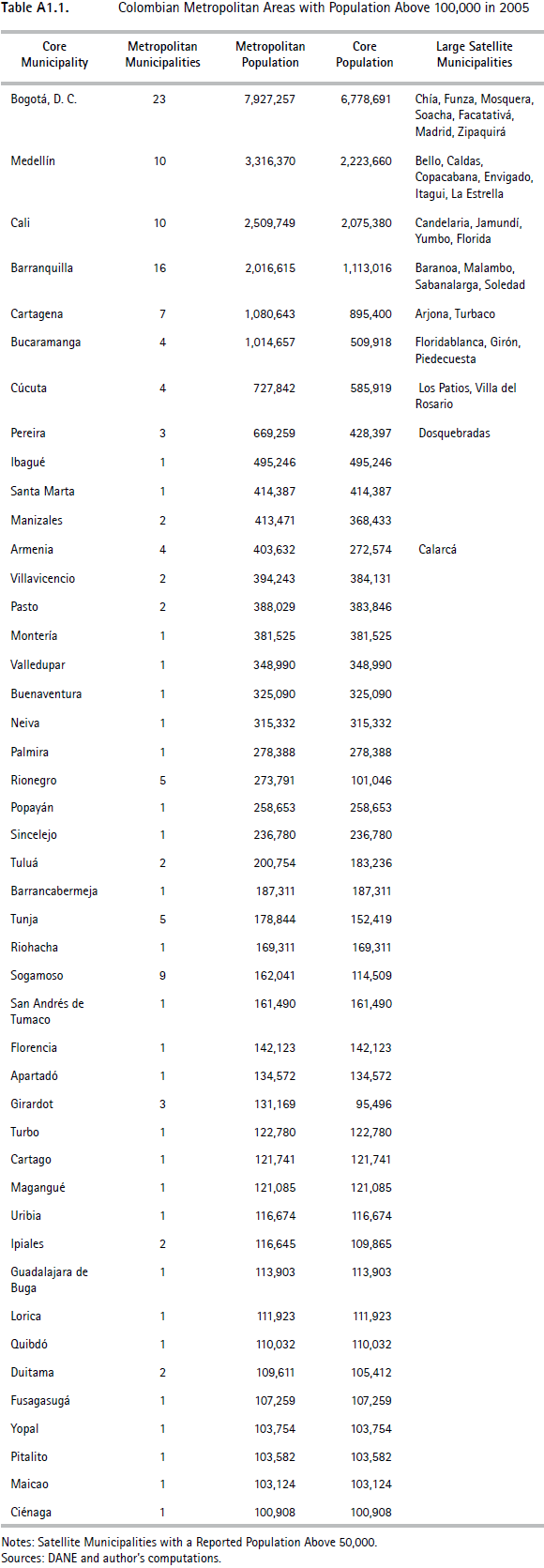
To delineate metropolitan areas for Colombia, a period of study had to be defined. There were two conflicting constraints: ensuring that consistent data was used (preferably from the same year) and that it was the most recent available. The most recent matrix of commuting flows comes from the 2005 census. Population data are also available for this year. More recent population estimates are also available from the Colombian statistical institute, DANE , for 2010. As it is probably preferable to offer the most up-to-date population numbers, our principal results are reported using 2010 population estimates. A list of metropolitan areas for the 2005 population is also reported, in Appendix 1.
The entire population of each municipality was considered. Colombian statistics typically distinguish between an urban (cabecera or 'head') part and a rural part. Taking the entire population has the obvious drawback of aggregating rural populations to metropolitan areas. However, this shortcoming is minor in practice since the populations of municipalities that form large metropolitan areas are overwhelmingly 'urban'. Since data for commuting flows are only available for entire municipalities, discarding rural populations would also lead to some awkward choices having to be made about how to compute commuting shares.
In most countries, including Colombia, census populations or population estimates based on censuses provide the best available population data. Commuting flows are measured from only a subsample of the population surveyed by the Colombian census.
This follows common practice in most countries where commuting questions (together with many others) are usually administered through the 'long forms' of the census given only to a fraction of the population for reasons of cost. In our case, this suggests some minor imprecisions resulting from mis-measured commuting flows. The lack of precision becomes more important as lower commuting thresholds are considered, since for smaller municipalities, using a low threshold of, say, 1% might well produce results that are well below the statistical margin of error. Results for low thresholds are reported below, but some care is needed in their interpretation given this reliability issue.
To delineate metropolitan areas for Colombia, we propose a commuting threshold of 10% which, to repeat, appears reasonable given that Colombian municipalities are fairly large.
C. The Algorithm
The algorithm is available upon request. It was programmed in Stata. After cleaning up the original matrix of cross-municipality commuting flows and creating a number of working files, each loop of aggregation works as follows. For all pairs of originating and destination municipalities the algorithm flags those where the share of commuters from the originating municipality is above the chosen commuting threshold. Before the municipality is aggregated to a destination, the algorithm verifies that in cases where a municipality could be aggregated to several destinations, it is in fact uniquely added to the one to which it sends the greatest number of workers. When commuting flows between two municipalities are above the threshold in both directions, the algorithm also ensures that the smaller municipality is aggregated to the larger.
At the aggregation stage, the name of the originating municipality is appended behind the name of the destination municipality and the populations of the two are added together. As explained above, the matrix of commuting flows is also appropriately aggregated and redefined. For instance, if municipality C sends 8% of its workers to municipality B and 9% to municipality A, and if B is appended to A, then the commuting flows from C to B and C to A are aggregated into a unique flow of 17% from municipality C into the metropolitan area A+B. The process is then repeated until no municipality or group of municipalities remains to be aggregated to a metropolitan area.
As a final output, the algorithm produces a list of metropolitan areas with their component municipalities (a 'core' and its 'satellites') and of single municipalities. For verification purposes, the algorithm keeps track, in addition, of all originating municipalities which were aggregated during the process and the destination municipalities they were aggregated to.
The algorithm generates a list of metropolitan areas and municipalities associated with a given commuting threshold. In Spanish, the acronym CAMA could be used to describe these constructs, standing for ciudades y áreas metropolitanas agregadas (cities and aggregated metropolitan areas). Cama is also the Spanish word for 'bed', a word that captures the notion of large residential areas unified around a common labor market.
We further propose delineating broader units, which we call 'urban regions'. As argued above, this is in keeping with existing practice in many countries. Recall that, for instance, the US metropolitan areas of Washington DC and Baltimore are separate but that they are also part of the same 'consolidated' metropolitan area. We propose a Spanish language acronym, CARA, standing for ciudades y áreas regionales agregadas (cities and aggregated metropolitan regions). 'Cara' is Spanish for the '[human] face'. To delineate these broader urban regions a natural approach would be to employ the same principle used for metropolitan areas but to adopt a lower commuting threshold. For these urban regions, we use a threshold of 5%. But note that this change alone does not lead to dramatically larger units, and clearly falls short of the notion of 'urban region'. The tempting response would be to lower the threshold even further. This would not, however, be a good idea since, as argued above, the aggregation exercise becomes fragile with very low commuting thresholds.
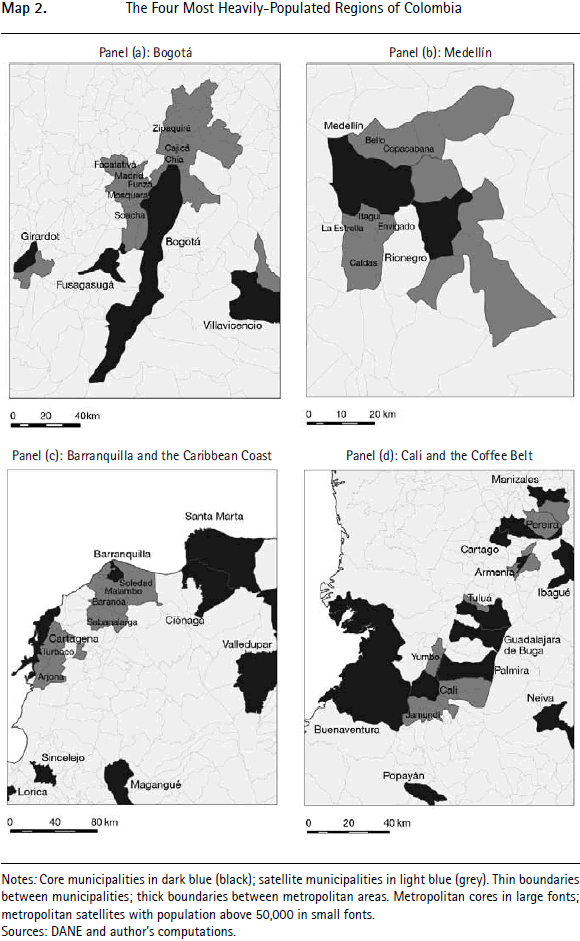
There is a deeper reason why even extremely low aggregation thresholds do not lead to urban regions. This is due to the self-reinforcing nature of the iterative aggregation process used to delineate metropolitan areas. To understand this subtle point, it is best to take a concrete example from Colombia. The country's 'Coffee Belt' is a confined to a region of high land in the Central Cordillera of the Andes. It has three major cities which are fairly close one to the other. The municipality of Pereira has around 450,000 inhabitants, Manizales is slightly smaller with a population under 400,000, while Armenia is smaller again at 300,000. As small neighboring satellite municipalities become aggregated to these three core municipalities, the three metropolitan areas that they form get more 'entrenched'. The municipalities that are located between these three principal cities may see a fair amount of cross-commuting. But, as aggregation proceeds, these 'in-between' municipalities are aggregated, together with more peripheral municipalities, to one of the three cores. Given the gravitational nature of commuting, the aggregation of these peripheral municipalities lowers the tendency of their inhabitants to commute to other peripheral municipalities. As a result, the metropolitan areas do not merge into a large single urban region even for a commuting threshold as low as 1%.5 However, it is interesting to observe that in many cases metropolitan areas are obtained that are contiguous with each other. Hence to delineate metropolitan regions, we propose aggregating metropolitan areas that are contiguous with each other using a commuting threshold of 5%. As a result, the three separate areas aggregated around Pereira, Manizales and Armenia, which are contiguous, also constitute the principal centers of the larger urban region of Pereira-Manizales-Armenia.
III. Results
A. Metropolitan Areas
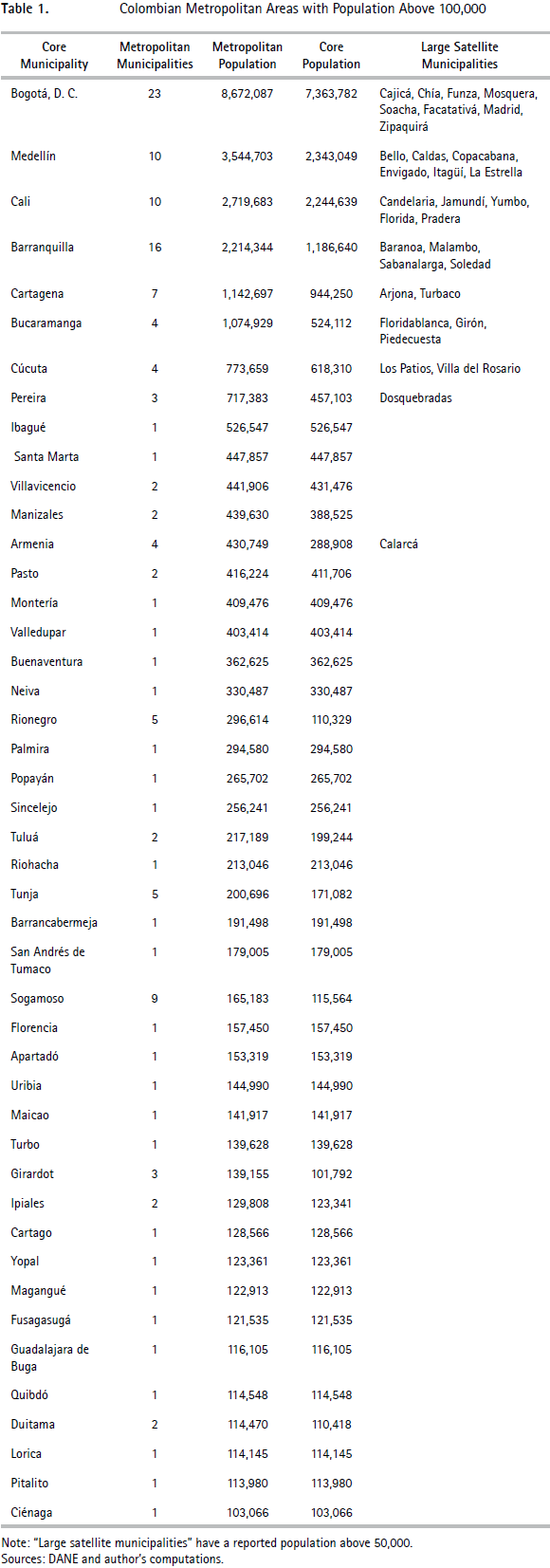
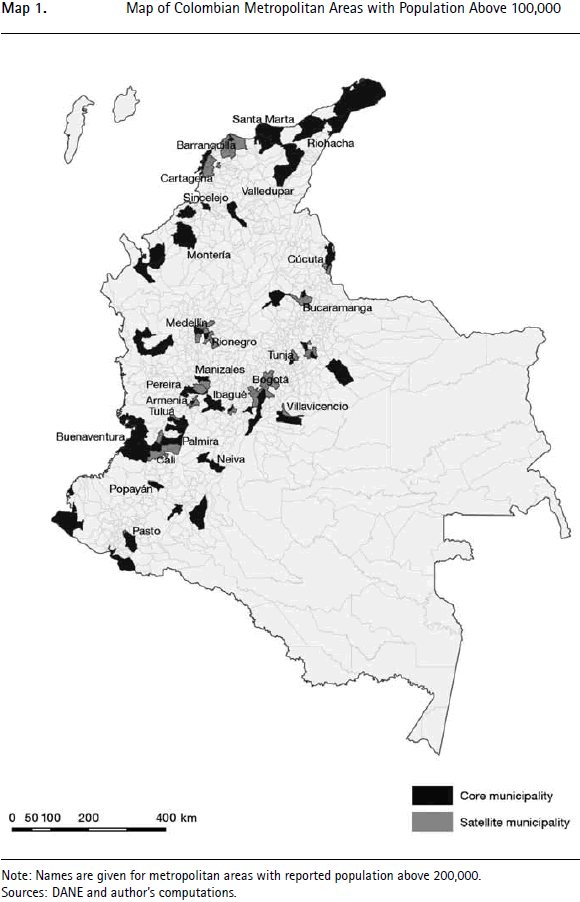
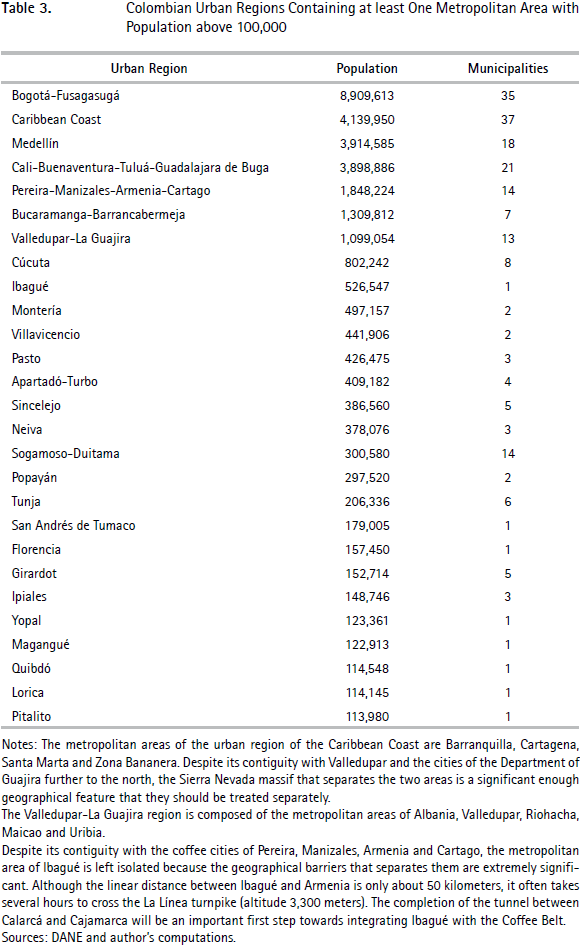
For the preferred commuting threshold of 10%, the list of the 45 resulting metropolitan areas with more than 100,000 inhabitants in 2010 is provided in Table 1. There are a further 39 metropolitan areas with populations above 50,000. In total, 99 satellite municipalities are aggregated to 22 cores, 19 of which have a population above 100,000. All the other urban centers remain as stand-alone municipalities. Metropolitan areas with a population above 100,000 are also depicted on the Map 1. While the results discussed here are for 2010 populations, Table A1.1 in Appendix 1 reproduces Table 1 using 2005 populations instead. The differences between the two tables are minimal and will not be discussed further.
Before commenting further the list of metropolitan areas in Table 1, a few important features related to the algorithm need to be discussed. First, its iterative nature is fundamental. With a 10% threshold, the algorithm goes through 7 rounds of aggregations before converging. In the case of the largest metropolitan area, composed of Bogotá and 22 neighboring satellite municipalities, only nine were added during the first round of aggregation.
It is also interesting to note that the algorithm always picks the largest urban center of the metropolitan area as core municipality. This demonstrates that the ex ante definition of cores is unnecessary in practice. As may be verified on the Map 1, the metropolitan areas generated by the algorithm are also composed of contiguous municipalities. This shows that it is not necessary to impose contiguity either. Finally, there is no set of small and rural municipalities that is aggregated into much larger 'metropolitan' areas. It is clear from the list given in Table 1 that the aggregation of peripheral municipalities into broader metropolitan units occurs mostly for the largest municipalities.
The list of the 84 largest metropolitan areas contains 180 municipalities (of a total of about 1,100 in the entire country). These 84 metropolitan areas host 32.1 million people, or about 71% of the overall population. We note that peripheral municipalities are concentrated around the largest four cities. 55 of the 99 satellite municipalities are aggregated to one of the four largest Colombian municipalities. We also note that only 4 satellite municipalities are aggregated to core municipalities to form metropolitan areas with fewer than 50,000 inhabitants. There is a strong rank correlation between the ordering of metropolitan areas in terms of population and the corresponding ranking of their core municipalities. For metropolitan areas with a population above 100,000, the correlation of the log population between the metropolitan area and the core municipality is 0.98. That said, there is some variation. The municipality of Medellín, the second largest in the country, has a population only 4% larger than that of the municipality of Cali, the third largest. However the population of the metropolitan area of Medellín is 30% larger than that of metropolitan Cali.
Viewed differently, our aggregation into metropolitan areas corrects for the idiosyncrasies of the official delineation of Colombian municipalities. Geographically, the municipality of Medellín is relatively small whereas that of Cali is large. At one extreme, in the cases of Barranquilla or Bucaramanga, the metropolitan area has a population that is twice that of the core municipality. At the other, some large municipalities like Santa Marta, Ibagué, or Villavicencio either remain isolated or only receive tiny satellite municipalities so that their metropolitan population roughly coincides with the number of their inhabitants. The near-absence of satellites for these municipalities is unsurprising. Santa Marta is a declining coastal city and residents of neighboring municipalities will be more easily lured to work in Barranquilla, which is fairly close. Ibagué and Villavicencio are fairly large isolated cities located close to major geographical 'ruptures' (i.e. they are relatively isolated from other urban centers by topography).
The four panels of Map 2 provide magnified maps of the four most important concentrations of urban population, where 16 of the biggest 20 metropolitan areas are located, including the largest five. The maps illustrate cases of contiguous metropolitan area such as Medellín and neighboring Rionegro or the main cities of the Coffee Belt. These cases suggest that it is indeed interesting to consider a regional level of aggregation larger than metropolitan areas, as is done below.
Overall, the output generated by the algorithm appears to be highly consistent with both the underlying principles discussed above and with the qualitative features of the Colombia's urban geography.
B. Comparison with Official Metropolitan Areas
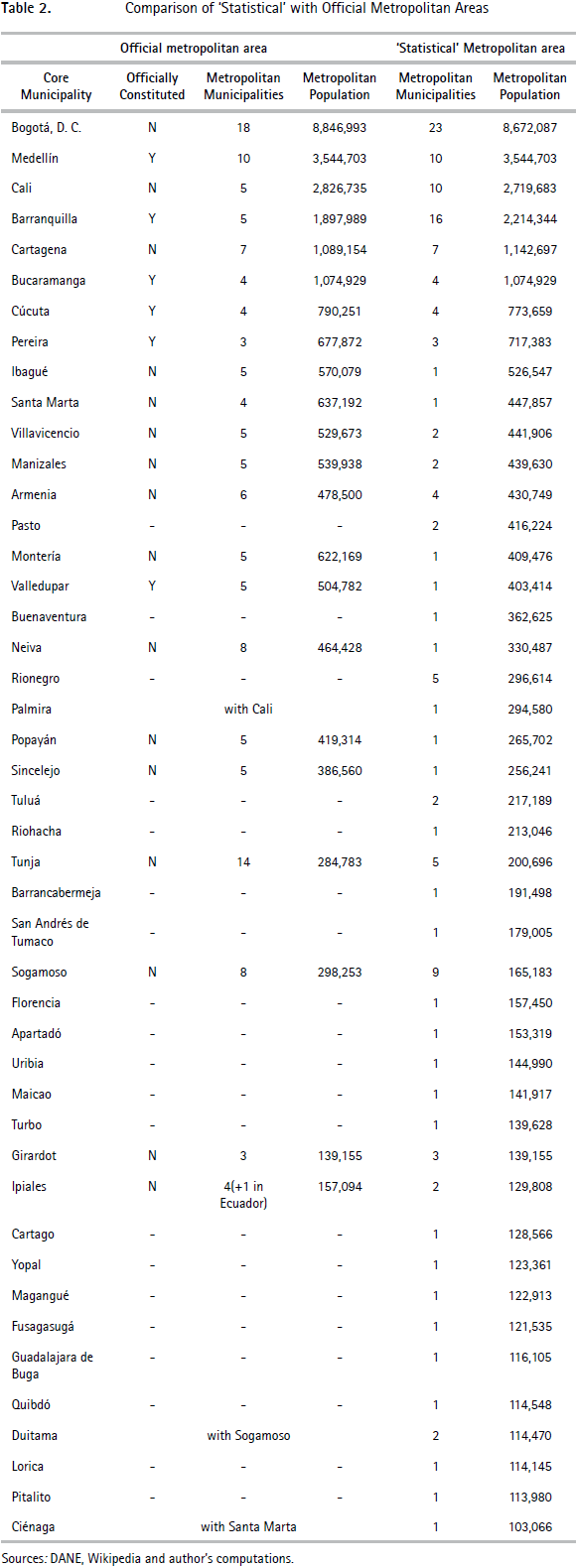
Before considering the robustness of our delineation and looking at alternative forms of aggregation, we are now in a position to compare the 'statistical' metropolitan areas defined here with the current 'official' metropolitan areas in greater depth. To reiterate, 'official' metropolitan areas are institutions that are formed voluntarily by participating municipalities in an effort to coordinate policies, mutualize some services, or provide certain public goods jointly. Their object differs from what is sought here. The purpose of the present work is to propose an operational definition that could be applied to the whole country by central government for statistical and national policy purposes. Despite these differences, it is interesting to compare the two approaches. There are currently only six officially constituted metropolitan areas in Colombia. Another 15 are recognized by central government but are not officially constituted. Finally, there are three bi- or tri-national metropolitan areas.6
Table 2 provides a detailed comparison between the 'statistical' metropolitan areas defined by us using commuting patterns and the official metropolitan areas. For the largest cities, the number of satellites in the official metropolitan area is lower or the same as in ours. For smaller cores, the opposite holds, and there is a tendency for more satellites to be aggregated to the official metropolitan areas and for these to be larger than those defined by us.
In part, these differences may be explained by the inclusion of small peripheral municipalities that get aggregated to their core when metropolitan areas are defined using commuting patterns but that remain separate according to official delineations. For instance, the commuting rule used here aggregates five more municipalities to Bogotá than the official delineation, but the largest of these municipalities has only about 20,000 inhabitants, and all are located at the periphery of the metropolitan area. There are also cases where the opposite occurs and small municipalities are aggregated to an urban core by the official delineation but not by the commuting rule.
While there are many such cases, they do not explain the larger differences between official metropolitan areas and those delineated by us. For instance, the official metropolitan area built around Sogamoso (the metropolitan area of Alto Chicamocha) has a population nearly twice as large as the corresponding statistical metropolitan area. Such large differences have two different sources. The first is the addition of fairly large but close neighbors as satellites to a given core. In the case of Sogamoso, the definition of the official metropolitan area treats Duitama as a satellite of Sogamoso, whereas the commuting rule identifies Duitama as a separate core. To take another interesting example, Ciénaga is part of the official metropolitan area of Santa Marta on the Caribbean Coast, whereas the commuting-based delineation treats Ciénaga as separate, since it only sends 2.3% of its workers to Santa Marta. Because the sample of workers is large, this proportion, well below the threshold of 10%, is unlikely to be caused by sampling error. This low level of commuting occurs because Ciénaga is a large labor market in its own right and thus sends few workers elsewhere, while Santa Marta is a city currently facing considerable economic challenges. However, it is true that Santa Marta is located only about an hour away from Ciénaga, which may justify some form of institutional cooperation. Again, it is not surprising that the approach developed here and the demands for inter-municipal cooperation that lead to the designation of official metropolitan areas should differ.
Other differences are, nonetheless, harder to justify. For instance, the official delineation of the metropolitan area of Cali includes Palmira, which is located about 3 hours away. While this may be an extreme case, official delineations of metropolitan areas often attach sizeable municipalities to existing urban cores that are located two hours away or more.
C. Urban Regions
We now turn to the delineation of broader urban regions. To delineate these regions we take a lower commuting threshold of 5% and aggregate the resulting adjacent metropolitan areas into urban regions.
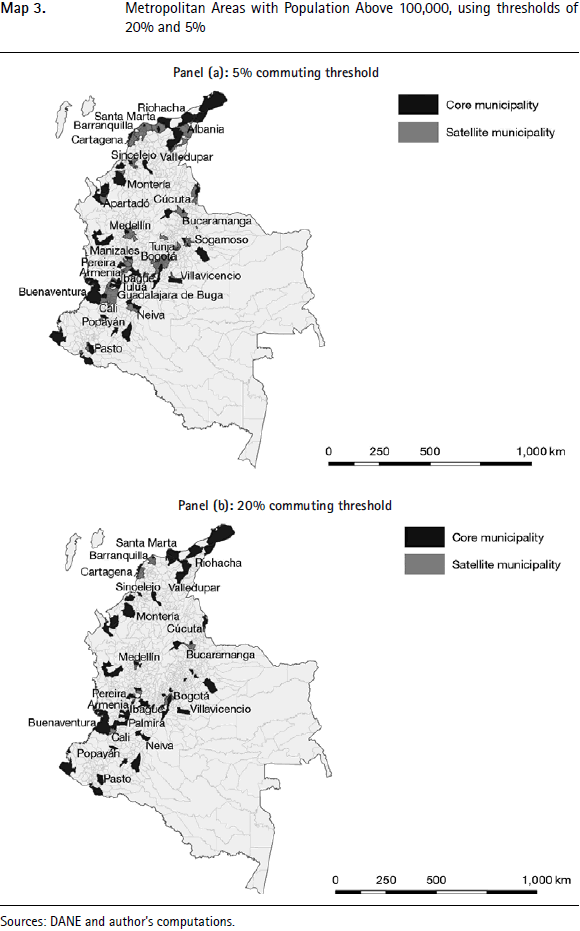
The list of the 27 urban regions produced by the exercise and composed of at least one metropolitan area of more 100,000 inhabitants is provided in Table 3. These urban regions are also depicted on the Map 3, panel (a).
Several features stand out from Table 3 and from the Map 3 (a). The most important is the emergence of several significant urban regions composed of a number of metropolitan areas. The Caribbean Coast along the Cartagena- Santa Marta axis appears as the country's second most important urban region, with more than four million inhabitants.7 There is also significant consolidation around Cali, Medellín, and the principal cities of the Coffee Belt: Pereira, Manizales and Armenia. A smaller urban region also exists around Bucaramanga and Barrancabermeja. The urban region of Bogotá contains 12 more municipalities than the city's previously delineated metropolitan area, but its population of 8.9 million is only marginally larger than that of metropolitan Bogotá, at 8.7 million.
The second important finding that comes out of Table 3 is that, altogether, about 21 million people live in the four largest urban regions. This is just below half the population of the country.
We also note some interesting microfeatures of Colombian urban regions. Some, such as those around Bogotá or Medellín, are highly compact while the urban regions that encompass the cities of the Coffee Belt and around Cali are less neatly structured and exhibit some 'holes'. These holes are even more apparent in the urban region of the Caribbean Coast. We could choose to aggregate the unattached municipalities that make up the holes to the urban region that surrounds them but that would disguise some interesting aspects. The holes reveal that these urban regions are still undergoing a process of formation. The regions around Bogotá or Medellín may be thought of as already-mature urban regions organized around one dominant pole, whereas the region around Cali remains in a process of consolidation. The same is the case for the urban regions of the Coffee Belt and the Caribbean, which display the further complication of containing several cores of relatively even population size. Other potential urban regions, still under formation, may also be detected. For instance, in the Department of Boyacá, Duitama and Sogamoso are already integrated, while Tunja, the region's largest metropolitan area, remains isolated. These two areas will eventually be integrated, perhaps into a much larger region with Bogotá. It is also possible to perceive the basis of a future urban region around Montería in the Southern part of the Caribbean region, stretching from Magangué in the north east to Turbo on the Gulf of Urabá to the south west.
IV. Robustness
To demonstrate the robustness of our approach, we duplicated our main analysis for a broad range of thresholds: 1%, 2%, 5%, 15%, 20%, 25%, and 30%. The two panels of Map 3 replicate the Map 1 for commuting thresholds of 5% and 20%. For most large Colombian cities, a higher threshold of 20% only produces minor differences. Using our preferred threshold of 10%, of the 20 largest metropolitan areas, 19 remain in the top 20, while using a commuting threshold of 20% the ordering of the top 10 is unchanged. Although the metropolitan area of Bogotá loses 15 municipalities out of 23 with the higher threshold of 20%, its population remains very similar, at 8.16 million instead of 8.72 million. The differences between these two rankings for the other core municipalities are even less important.
Moving to a lower threshold of 5% also makes little difference. The ordering of the largest nine cities is unchanged. The two most important changes are the disappearance of Rionegro and Palmira, which ranked 19 and 20 respectively with a threshold of 10%. Rionegro becomes aggregated to its neighbor Medellín, as is Palmira to Cali. Interestingly, there are no other changes among the largest metropolitan areas: the three main cities of the Coffee Belt remain separate metropolitan areas despite their proximity. Similarly, the three main cities of the Caribbean Coast, Barranquilla, Cartagena and Santa Marta, also remain separate.8 These features persist even when an extremely low threshold of 1% is chosen.
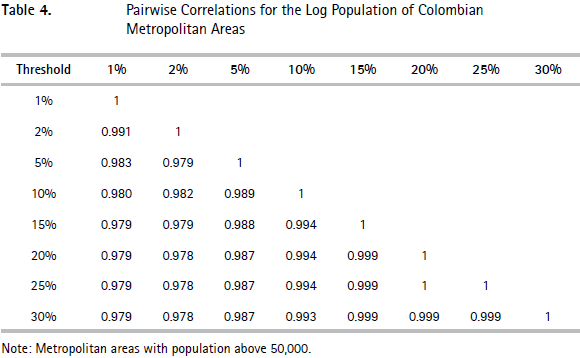
More generally, Table 4 reports log population size correlations for Colombian metropolitan areas defined according to the entire range of thresholds mentioned above. Among metropolitan areas that can be compared across thresholds (not all can, as, for instance, Rionegro disappears when the threshold is lowered from 10 to 5%), the correlations reported in Table 4 are extremely high, at 0.97 or more. The correlation using our 10% reference threshold is at least 0.98. Even higher correlations are produced when the table is repeated using absolute population numbers or ranks rather than the log population.
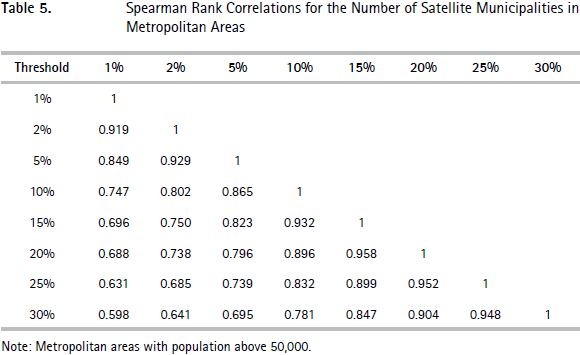
Next, we assessed how sensitive the number of municipalities in metropolitan areas is with respect to the chosen commuting thresholds. Obviously the number of satellite municipalities is sensitive to this threshold. Recall that with our reference threshold of 10%, 99 municipalities were defined as satellites of an urban core. With higher thresholds of 20% and 30%, this number falls to 41 and 25, respectively, while with lower thresholds of 5% and 1%, the number of satellite municipalities increases to 180 and 616. With a threshold of 30%, the metropolitan area of Bogotá has only three municipalities, instead of 208 when a low threshold of 1% is used, even though population is only 27% less.9 To implicitly control for the large changes in the total number of satellite municipalities, in Table 5 we applied Spearman's rank correlation for the number of satellite municipalities, as the commuting threshold varies. Except for the highest thresholds, under which very few metropolitan areas have satellites (only nine using a threshold of 30%), the correlations are generally high. For instance, Spearman's rank correlations between our preferred 10% threshold and the two alternative thresholds of 5% and 20% are 0.86 and 0.90, respectively.
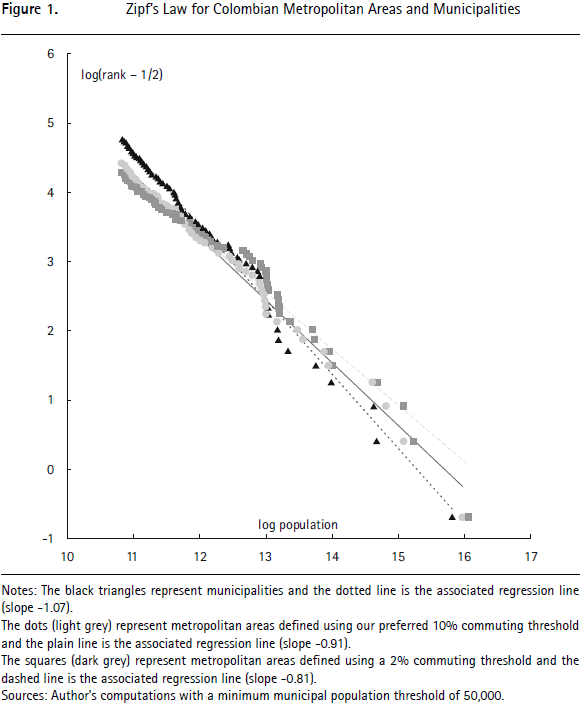
Another way to assess the robustness of our findings is to look at them in the light of Zipf's Law. This allows the effect of the commuting threshold on the number of metropolitan areas to be highlighted. Such an exploration is also of independent interest because Zipf's Law is the subject of intense academic interest. See for instance Duranton and Puga (2014) for a recent review and Pérez and Meisel Roca (2013) for a contribution focused on Colombian cities.
Ever since Auerbach (1913), the distribution of city sizes has often been approximated by a Pareto distribution. A popular way to do this is to rank cities in a country from the largest to the smallest and to regress log rank on log city population. Gabaix and Ibragimov (2011) highlight a possible small sample bias in the estimation of the coefficient on log city population and suggest instead using the log of the rank minus one half as the dependent variable:
The estimated coefficient, ξ, is the shape parameter of the Pareto distribution. Zipf's Law (after Zipf, 1949) corresponds to the statement that ξ = 1. This implies that the second largest city is expected to be half the size of the largest, the third largest a third of the size, etc.
Figure 1 provides a plot of the underlying data for Colombian municipalities, for metropolitan areas delineated according to our preferred commuting threshold of 10%, and to others using a lower threshold of 2%.
For all Colombian municipalities in 2010, the estimated value of ξ is 0.85 suggesting a distribution that is more uneven than Zipf's Law. We note, however, that this coefficient of 0.85 is mostly driven by a thin lower tail of small municipalities. It is reasonable to ignore extremely small municipalities since they are overwhelmingly rural. They are also exceptional, as Colombian municipalities were designed to avoid extremely low population levels. Considering only municipalities with a population above 5,000 (84% of the total, hosting 98.7% of the population) yields a value for ξ of 1.02 and a higher R2 of 98% instead of 92% for all municipalities. To make consistent comparisons with metropolitan areas, we can restrict our attention further to large municipalities with a population above 50,000. In this case, the estimated value of ξ is 1.07 with an R2 of 0.99. This value of 1.07 implies fewer disparities in population than implied by Zipf's Law. However, a relatively large standard error of 0.14 makes it impossible to reject a unit coefficient and Zipf's Law entirely.10
For Colombian metropolitan areas defined using our preferred commuting threshold of 10% and a minimum population size of 50,000, our estimate for ξ is 0.91, suggesting a distribution that is more uneven than implied by Zipf's Law. More generally, the estimate for ξ falls as lower commuting thresholds are considered. For a threshold of 30%, we estimate 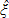 30 = 1.00 ; for 20% we get
30 = 1.00 ; for 20% we get 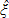 20 = 0.95; for 5%,
20 = 0.95; for 5%, 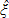 5 = 0.88; for 2%,
5 = 0.88; for 2%, 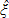 2 = 0.81; and, finally, for 1%,
2 = 0.81; and, finally, for 1%, 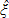 1 = 0.76. Visual inspection of Figure 1 confirms this trend.
1 = 0.76. Visual inspection of Figure 1 confirms this trend.
The counterclockwise rotation of the Zipf line as lower thresholds are considered in Figure 1 is easy to understand. On the one hand, a lower commuting threshold increases the size of the largest metropolitan areas. On the other hand, there are more satellite municipalities so that the number of metropolitan areas decreases. In turn, this means that the smallest areas, just above the population threshold of 50,000, are ranked lower. Hence, when lower commuting thresholds are used to delineate metropolitan areas there is a downward shift of the left tail of the Zipf regression line. A combination of a shift rightwards for the largest areas and a shift downwards for the smallest obviously implies a flatter curve and a lower regression coefficient. We note that this would be observed even without censoring our observations at a population threshold of 50,000 since municipal aggregation overwhelmingly benefits large core municipalities and reduces the number of municipalities of a lower size.
This decline of ξ from 1.07 to 0.75 as lower commuting thresholds are considered shows that the estimates of the Pareto shape parameters for city populations are sensitive to the in which metropolitan areas are defined. Zipf's Law is obtained exactly for a threshold of 30%, but this is arguably too high a threshold for defining meaningful metropolitan areas in Colombia. This result contrasts with older findings of Rosen and Resnick (1980) that the size distribution of cities conforms better with Zipf's Law when economically more meaningful definitions of cities are used. It contrasts also with the more recent results of Rozenfeld et al. (2011) for the US and UK, who find robust evidence for Zipf's Law after defining cities using an aggregation criterion based on the geographical continuity of development.
To summarize, our findings suggest that the population of Colombian metropolitan areas is fairly insensitive to the chosen commuting threshold. As lower thresholds are considered, all the remaining metropolitan areas gain population, but these increases tend to be small. Relative populations are even more stable, since lower thresholds lead to population gains for all metropolitan areas. By contrast, the number of satellite municipalities is more sensitive to the chosen commuting threshold. As lower thresholds are considered, the number of satellite municipalities increases dramatically. Although lower thresholds lead to the identification of more satellite municipalities for most metropolitan areas, heterogeneity also grows, with some metropolitan areas gaining a large number of satellites and some very few. In turn, the findings suggest that the physical extent of metropolitan areas is sensitive to the chosen commuting threshold. In turn, the aggregation of municipalities also affects estimates of the size distribution of cities. Finally, we note that the stability both of population levels and of the number of satellite municipalities is more marked around our reference commuting threshold of 10%.
V. Conclusions
In this paper we have proposed a simple way to define metropolitan areas that relies exclusively on commuting patterns. We have gone on to implement the method using Colombian data. In addition to its simplicity, our approach offers two further advantages. First, it is fully transparent, which matters as soon as definitions of metropolitan areas come to affect policy interventions. Second, the population of metropolitan areas is also highly robust to the details of the chosen threshold.
Acknowledments
I am grateful to Rafael Cubillos for giving me data without which this project would have been impossible. James Bernard, Matthew Degagne, and Hongmou Zhang provided very able research assistance. I also thank Paul Cheshire and Yoshi Kanemoto for very useful conversations and for getting me interested in this subject many years ago. Feedback from an anonymous referee and from Álvaro Pachón, Rafael Cubillos, Xavier Gabaix, José Salazar and other seminar participants at the Colombian Departamento Nacional de Planeación (DNP) is also gratefully acknowledged. This research was initially developed while the author was working as a consultant for the urban division of the DNP. The collaboration of the entire division, of Alejandro Bayona and of Carolina Barco was greatly appreciated. This paper reflects the author's views, not the DNP's.
The research carried out for this article had no institutional funding.
_____________________________
Foot notes
2 The parallels between the two countries run even deeper. As in the case of Bogotá, the metropolitan area around the largest city, Paris, is only minimally organized and faces a similar issue of a giant municipality surrounded by much smaller ones with a history of fractious relations. On the other hand, France's second largest metropolitan area, Lyon, has a fairly small core relative to its overall metropolitan population and boasts a long tradition of fruitful and deep cooperation. This is obviously not unlike Medellín.
3 See for example the well-known 'Modifiable Areal Unit Problem' (MAUP). See Cressie (1993) for a presentation and a discussion.
4 For instance, it is obvious that policies that allocate money to 'places' need discrete spatial units if they are to do so.
5 This phenomenon is not unique to the Coffee Belt. The same is observed in the region of the Caribbean Coast where three of the main cities - Barranquilla, Cartagena and Santa Marta - do not merge even for a low commuting threshold of 1%.
6 As of January 2015 (http://es.wikipedia.org/wiki/Áreas_metropolitanas_de_Colombia). Only one ofthese three areas is listed below. The other two are too small to make it to this list.
7 This region is technically contiguous with the Valledupar-La Guajira region to its north-east. However, the real contiguity is minimal, as the Sierra Nevada massif separates the two regions, which are probably best treated as separate. It takes five hours to drive from Santa Marta to 'neighboring' Valledupar. Were these two regions to be treated as one it would have 5.3 million inhabitants living in over 50 municipalities.
8 We also begin to see satellite municipalities which are not geographically adjacent to the rest of their metropolitan areas. There are two such cases. The first is the municipality of Sucre (Santander Department) which becomes attached to Bucaramanga though it is more than 200 kilometers distant. Given that this municipality is not negligibly small and sends about 7% of its commuters to Bucaramanga, this corresponds to real flows - perhaps mainly students who are counted together with workers. The other case is Guacamayas, a tiny municipality to the north of the Department of Boyacá, which becomes attached to Bogotá, nearly 400 kilometers away. Given that this case is driven by only 17 'commuters', this may be a statistical glitch.
9 While in general, municipalities that are aggregated to a core for a given threshold are also aggregated to this same core- or to a larger one- for a lower threshold, this need not always be the case. Although an exceptional case, the municipality of Sutatausa provides an interesting illustration which shows the potential pitfalls of iterative aggregation. This small municipality located to the north of Bogotá sends 6% of its workforce north to San Diego de Ubaté, 5% to Tausa, 4% to Nemocón, and 1% to Bogotá. At a 10% threshold, Sutatausa gets aggregated to Bogotá after Tausa and Nemocón have themselves been aggregated to it. However, with a 5% threshold, Sutatausa is immediately aggregated to San Diego de Ubaté. Since the latter is much larger and barely sends any workers to its south, it remains an independent core, with Sutatausa as satellite. This municipality of 5,000 inhabitants is the only case of a satellite of Bogotá at a 10% threshold which disappears with a 5% threshold.
10 First, because the dependent variable is computed directly from the explanatory variable, measurement error on the 'true' population also affects the rank and thus leads to a downward bias for the standard errors with OLS. Gabaix and Ibragimov (2011) show that the standard error on ξ is asymptotically 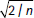 ξ where n is the number of observations. With our data, this implies a standard error of 0.14. The values of the standard errors for the other estimates of ξ reported here are of the same magnitude.
ξ where n is the number of observations. With our data, this implies a standard error of 0.14. The values of the standard errors for the other estimates of ξ reported here are of the same magnitude.
References
1. ALONSO, W. (1964). Location and land use; Toward a general theory of land rent. Cambridge, MA: Harvard University Press. [ Links ]
2. AUERBACH, F. (1913). "Das Gesetz der Bevólkerungskonzentration", Petermanns Geographische Mitteilungen, 59:73-76. [ Links ]
3. BERRY, B. L. J., GOHEEN, P. G., AND GOLDSTEIN, H. (1969). Metropolitan area definition: A re-evaluation of concept and statistical practice. Washington, D. C.: Bureau of the Census. [ Links ]
4. BERRY, B. J. L. (1960). "The impact of expanding metropolitan communities upon the central place hierarchy", Annals of the Association of American Geographers, 50(2):112-116. [ Links ]
5. BODE, E. (2008). "Delineating metropolitan areas using land prices", Journal of Regional Science, 48(1):131-163. [ Links ]
6. BRIANT, A., COMBES, P.-P., AND LAFOURCADE, M. (2010). "Does the size and shape of geographical units jeopardize economic geography estimations?", Journal of Urban Economics, 67(3):287-302. [ Links ]
7. CHARLOT, S., AND DURANTON, G. (2004). "Communication externalities in cities", Journal of Urban Economics, 56(3):581-613. [ Links ]
8. CHESHIRE, P. C., AND HAY, D. G. (1989). Urban problems in Western Europe: An economic analysis. London: Unwin Hyman. [ Links ]
9. CONGRESO DE COLOMBIA (2013). Por la cual se deroga la Ley orgánica 128 de 1994 y se expide el régimen para las áreas metropolitanas. Ley número 1625. [ Links ]
10. CRESSIE, N. A. C. (1993). Statistics for spatial data. New York: John Wiley. [ Links ]
11. CÖRVERS, F., HENSEN, M., AND BONGAERTS, D. (2009). "Delimitation and coherence of functional and administrative regions", Regional Studies, 43(1):19-31. [ Links ]
12. DURANTON, G., AND OVERMAN, H. G. (2005). "Testing for localization using micro-geographic data", Review of Economic Studies, 72(4): 1077-1106. [ Links ]
13. DURANTON, G., AND PUGA. D. (2014). "The growth of cities", in P. Aghion and S. Durlauf (Eds.), Handbook of Economic Growth (vol. 2, pp. 781-853). Amsterdam: North-Holland. [ Links ]
14. FOX, K. A., AND KUMAR, T. K. (1965). "The functional economic area: Delineation and implications for economic analysis and policy", Papers of the Regional Science Association, 15(1):57-85. [ Links ]
15. GABAIX, X., AND IBRAGIMOV, R. (2011). "Rank-1/2: A simple way to improve the OLS estimation of tail exponents", Journal of Business Economics and Statistics, 29(1):24-39. [ Links ]
16. GLAESER, E. L., AND KAHN, M. (2001). "Decentralized employment and the transformation of the American city", Brookings-Wharton Papers on Urban Affairs, 1-47. [ Links ]
17. HALL, P. G., AND HAY, D. (1980). Growth centres in the European urban system. London: Heinemann Educational Books. [ Links ]
18. HANDBURY, J., AND WEINSTEIN, D. E. (2015). "Goods prices and availability in cities", Review of Economic Studies, 82(1):258-296. [ Links ]
19. HOLMES, T. J. (1999). "Localisation of industry and vertical disintegration", Review of Economics and Statistics, 81(2):314-325. [ Links ]
20. KANEMOTO, Y., AND KURIMA, R. (2005). "Urban employment areas: Defining Japanese metropolitan areas and constructing the statistical database for them", in A. Okabe (Ed.), GIS-Based studies in the humanities and social sciences (pp. 85-97). Boca Raton: Taylor & Francis. [ Links ]
21. KRUGMAN, P. R. (1991). Geography and trade. Cambridge (MA): MIT Press. [ Links ]
22. MARSHALL, A. (1890). Principles of economics. London: MacMillan. [ Links ]
23. MILLS, E. S. (1967). "An aggregative model of resource allocation in a metropolitan area", American Economic Review (Papers and Proceedings), 57(2):197-210. [ Links ]
24. MOLINA, H. (2001). Análisis del sistema nacional de ciudades. Aportes para una nueva regionalización del territorio colombiano. New York and Bogotá, D. C.: UNDP and Ministerio de Desarrollo Económico. [ Links ]
25. MUTH, R. F. (1969). Cities and housing. Chicago: University of Chicago Press. [ Links ]
26. PÉREZ, G. J., AND MEISEL ROCA, A. (2013). Ley de Zipf y de Gibrat para Colombia y sus regiones: 1835-2005 (Documentos de Trabajo sobre Economía Regional 192). Banco de la República. [ Links ]
27. ROSEN, K., AND RESNICK, M. (1980). "The size distribution of cities: An examination of the Pareto law and primacy", Journal of Urban Economics, 8(2):165-186. [ Links ]
28. ROZENFELD, H. D., RYBSKI, D., GABAIX, X., AND MAKSE, H. A. (2011). "The area and population of cities: New insights from a different perspective on cities", American Economic Review, 101(5):2205-2225. [ Links ]
29. SENADO DE LA REPÚBLICA. (2012). "Informe de ponencia para segundo debate al proyecto de Ley número 141 de 2011", Gaceta del Congreso, 137(21). [ Links ]
30. US OFFICE OF MANAGEMENT AND BUDGET. (2010). 2010 standards for delineating metropolitan and micropolitan statistical areas; Notice. Washington, D. C.: Federal Register. [ Links ]
31. ZIPF, G. K. (1949). Human behavior and the principle of least effort: An introduction to human ecology. Cambridge (MA): Addison Wesley. [ Links ]