INTRODUCCIÓN
Durante las décadas más recientes se han procesado cambios demográficos y de las estructuras familiares en los países de América Latina, que tuvieron lugar juntamente con un marcado aumento en la participación laboral femenina. A partir de mediados de la década del 2000 se evidencia una desaceleración en la tasa de crecimiento de esta, aun cuando los principales determinantes de la actividad favorecerían mayores tasas de participación: las mujeres están más educadas, tienen menos hijos y viven menos en pareja (Gasparini, Marchionni, Badaracco y Serrano, 2015). Paralelamente, se mantienen en la región importantes diferencias en los ingresos promedio mensuales que perciben las mujeres y hombres ocupados, en especial en los países en los que la participación laboral de las mujeres es alta. Parte de esta diferencia se debe a que las mujeres trabajan menos horas en promedio que los hombres, aunque la brecha de ingresos por hora también resulta significativa en la mayoría de los países de la región (Cepal, 2014a).
Los efectos de estas desigualdades van más allá de la esfera individual. La incorporación de las mujeres al mercado de trabajo tiene efectos en el ingreso de sus hogares y, por lo tanto, en la pobreza y distribución del ingreso de toda la sociedad. Los impactos a escala nacional dependerán de quiénes son las mujeres que participen en el mercado laboral y de la correlación entre el ingreso de las mujeres y el de sus cónyuges (Atkinson, 2015). En este sentido, su incorporación puede atenuar o potenciar la desigualdad. Por ejemplo, en la posguerra en Estados Unidos las mejoras de la desigualdad antes de 1970 surgieron de la relativamente alta participación de mujeres casadas con hombres de bajos salarios. Luego de 1970 el aumento de la participación se dio entre mujeres con ingresos por encima del promedio, casadas con hombres de ingresos altos, presionando al alza a la desigualdad (Maxwell, 1990). Analizando evidencia más reciente, Harkness (2013) encuentra que el empleo femenino es un factor importante en la reducción de la desigualdad de ingresos1. Sus resultados indican que el aumento del empleo femenino y el cierre de la brecha salarial generarían reducciones de la desigualdad, aunque en el segundo caso los efectos son menores e incluso negativos en dos de los países estudiados.
A escala regional, dos estudios recientes buscan dimensionar el impacto que el aumento de la participación laboral de las mujeres tuvo sobre los indicadores de pobreza y desigualdad. El Banco Mundial (2012) encuentra que entre el 2000 y el 2010 los ingresos de las mujeres contribuyeron a un 30% de la reducción observada en la pobreza extrema, mientras que los masculinos explican un 39% y los no laborales un 31%. Los resultados son similares para la pobreza moderada, mientras que el aporte de las mujeres a la reducción de la desigualdad es algo menor (28%). Por otro lado, Gasparini y Marchionni (2015) concluyen que entre principios de la década de 1990 y el entorno del 2012 la fuerte incorporación de las mujeres al mercado laboral, en especial las más vulnerables, permitió a sus hogares salir de la pobreza y reducir la brecha entre estos hogares y los más favorecidos. Utilizando microsimulaciones, se encuentra que el empleo de las mujeres contribuyó con uno de los 14 puntos en los que se reduce la pobreza en el período, mientras que representa aproximadamente el 10% de la caída de la desigualdad. Otro estudio relevante, pero de una naturaleza prospectiva y no explicativa, es el de Cepal (2014a) que estima los impactos en pobreza y desigualdad de ingresos que tendría el cierre de las brechas de género en la participación laboral e ingresos laborales para 18 países de América Latina. A diferencia de los anteriores y en la misma línea del estudio de Harkness (2013), este trabajo no busca entender qué ha sucedido en la región en la última década sino dimensionar hasta dónde se podría avanzar en términos de reducción de la pobreza y la desigualdad, en caso de que desaparecieran las diferencias de género en el mercado laboral. Los resultados señalan que los indicadores de pobreza y desigualdad mejorarían, aunque las magnitudes del cambio dependen significativamente del punto de partida.
En este marco, este artículo se plantea analizar cómo afecta el empleo femenino al ingreso de los hogares y su distribución, estimando el efecto que el cierre de las brechas de género en la participación e ingresos laborales tendría en la pobreza y en la desigualdad de ingresos de los hogares. Trabajando con base en cuatro países de América Latina se realizan tres ejercicios: cierre de la brecha en el ingreso por hora, cierre de la brecha de participación y cierre de ambas brechas conjuntamente.
En primer lugar, se estudia el efecto que tendría el cierre de la brecha de ingresos, manteniendo las diferencias que se observan en la participación laboral. El segundo ejercicio consiste en la eliminación de las diferencias entre mujeres y hombres en la participación laboral, tanto en la decisión de participar como en las horas trabajadas, manteniendo las diferencias observadas en los ingresos por hora. Por último, se realizan ambos ejercicios de forma conjunta. En los tres escenarios se aplican los ingresos laborales u horas trabajadas de los hombres, según corresponda, a mujeres de características similares. La metodología utilizada se basa en una técnica de imputación múltiple de datos faltantes (Rubin, 1987) aplicada a ejercicios de construcción de contrafactuales.
Este análisis constituye una profundización y un avance sustantivo en relación con el presentado en Cepal (2014a). En primer lugar, este estudio se concentra en cuatro países, lo que permite profundizar en los resultados obtenidos y en los factores asociados a las modificaciones que se simulan. En segundo lugar, a diferencia de Cepal (2014a), se consideran brechas en ingresos por hora (en vez de mensuales), para poder modelizar los posibles efectos de cambios en el margen intensivo y extensivo de la oferta laboral. Por último, se utiliza una técnica más robusta y refinada de microsimulación que brinda resultados más ajustados. Este aspecto resulta innovador, ya que se aplica de la metodología de imputación múltiple a la simulación de un problema distributivo, lo que permite mejorar la calidad de la simulación, así como estimar de forma más ajustada la varianza.
Se opta por trabajar con países con alta participación laboral femenina debido a que son los que presentan con más claridad y conjuntamente los dos problemas que se quieren analizar: la brecha de participación laboral y la de ingresos2. Se selecciona a Brasil y Uruguay, donde la principal preocupación se centra en la brecha de participación, pero en los que las brechas de ingresos son menores, y a Bolivia y Perú, donde la brecha de ingresos es muy grande, manteniendo niveles altos en la brecha de participación. Adicionalmente, los diferenciales entre hombres y mujeres en las variables de interés a lo largo de la distribución del ingreso son diferentes entre los dos pares de países analizados.
El artículo continúa un dimensionamiento de las brechas de género en el mercado laboral para los cuatro países analizados (sección 1), presentando luego los aspectos metodológicos relevantes para realizar los ejercicios de simulación (sección 2). En la sección 3 se discuten los principales resultados y en la sección 4 se realizan los comentarios finales.
I. DESCRIPCIÓN DE LOS DATOS Y DE LAS BRECHAS DE GÉNERO OBSERVADAS EN EL MERCADO LABORAL
Los datos surgen de las encuestas de hogares de cada país, relevadas por la autoridad estadística nacional, Instituto Nacional de Estadística o equivalente. Se utiliza la información de horas e ingresos laborales de la ocupación primaria, secundaria, y la de otras ocupaciones en caso de contar con esa información. Se consideran tanto los ingresos que surjan de una relación de dependencia como las ganancias obtenidas por los independientes y se indaga por los ingresos en efectivo y en especie. Respecto a las horas, se consideran las horas trabajadas semanalmente3. Se eliminan los ocupados con horas trabajadas igual a cero dado que no se les puede calcular el ingreso laboral por hora, y se truncan en 90 las horas trabajadas por semana4.
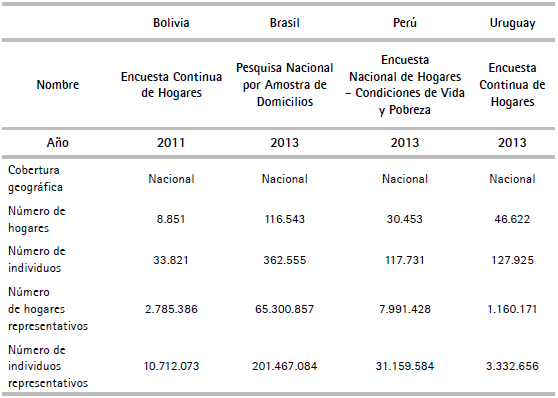
El cuadro A.1 resume las principales características de las encuestas utilizadas.
El cuadro 1 resume los principales indicadores del mercado laboral para los cuatro países analizados en este artículo.
Cuadro 1 Principales indicadores del mercado de trabajo. Personas de 15 a 65 años
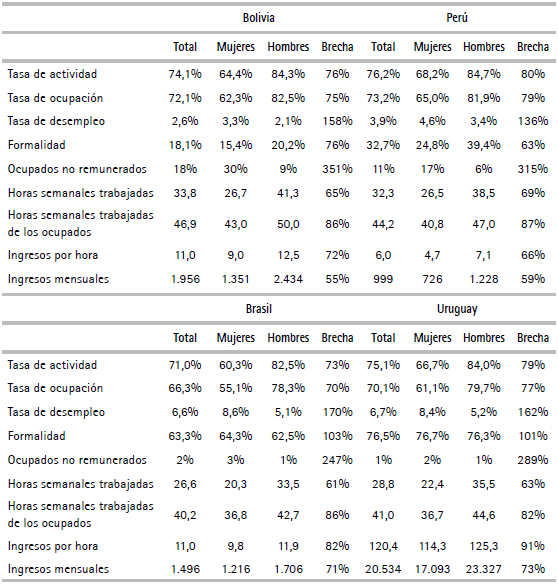
Nota: la brecha es calculada como el porcentaje del indicador de los hombres que representa el de las mujeres.
Fuente: elaboración propia sobre la base de las encuestas de hogares de los respectivos países.
Bolivia y Perú presentan mercados laborales con características similares: alta tasa de participación laboral masculina y femenina y altos niveles de ocupación, con bajo desempleo. La brecha de género en participación es del 76% en Bolivia y del 80% en Perú. Presentan diferencias algo mayores en los niveles de formalidad, aunque en ambos casos los valores de registro son relativamente bajos5. Una característica distintiva de estos mercados es la alta proporción de mujeres que se desempeñan como trabajadoras no remuneradas. Se entiende por trabajador no remunerado a quienes realizan un trabajo en el ámbito del mercado, aun cuando no obtengan ingresos por ello. En Bolivia, el 30% de las ocupadas pertenecen a esta categoría mientras que en Perú representan el 17%. El trabajo no remunerado está asociado al medio rural: la proporción mayoritaria de trabajadores no remunerados pertenecen a este medio (el 72% de los trabajadores no remunerados son trabajadores rurales en Bolivia y el 61% en Perú). A su vez, dentro de los trabajadores no remunerados el peso de la población indígena es superior que en el resto. Esto es muy relevante en el análisis de las brechas de ingresos laborales entre mujeres y hombres, dado que una proporción importante de las mujeres ocupadas presentan ingresos laborales iguales a cero.
Por su parte, Uruguay y Brasil presentan tasas de actividad y ocupación que son altas para la región. La brecha de participación entre mujeres y hombres se mantiene en valores altos: la tasa de actividad femenina es del 73% y el 79% de la masculina en Brasil y Uruguay, respectivamente. La tasa de formalidad de los ocupados es sensiblemente mayor que para los países andinos, en especial en Uruguay. A diferencia de Bolivia y Perú, el peso del empleo no remunerado entre los ocupados no es significativo en ninguno de los dos casos (2,2% en Brasil y 1,0% en Uruguay).
En los países andinos las horas trabajadas son sensiblemente superiores que las de Brasil y Uruguay, aunque las diferencias entre sexos son relativamente similares. Sin embargo, la brecha de ingresos laborales presenta importantes diferencias entre países, aunque en todos los casos la brecha es mayor para los ingresos laborales mensuales que para los horarios. En los países del Cono Sur los ingresos laborales por hora de las mujeres son siempre superiores al 80% del ingreso laboral de los hombres, mientras que en los países andinos no supera el 72%.
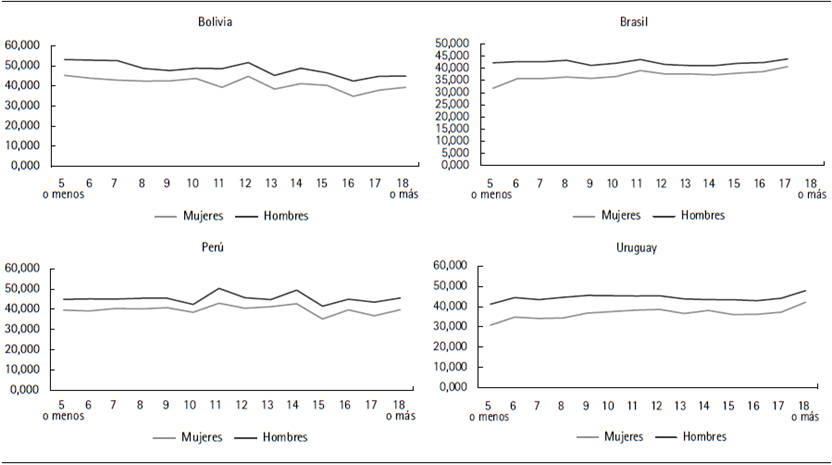
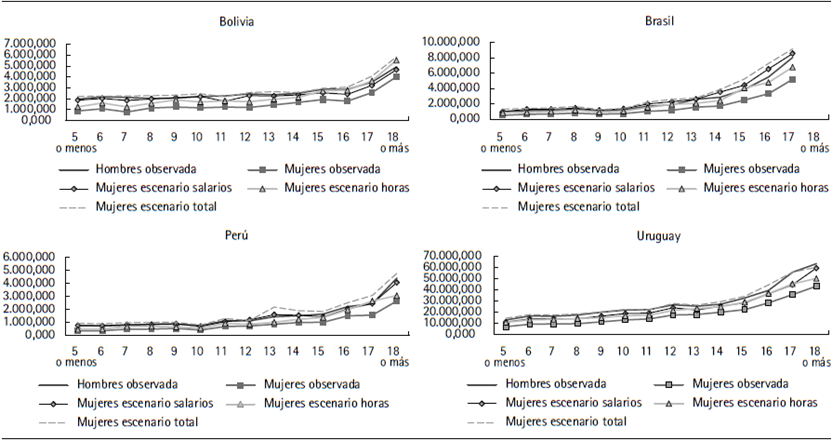
Resulta de interés analizar las brechas por nivel educativo dado que es un buen indicador de los ingresos esperados y por lo tanto del lugar que ocupan en la distribución del ingreso. Las figuras 1 y 2 presentan las brechas de ocupación e ingresos laborales por años de educación. En el anexo se presenta la brecha de horas trabajadas de los ocupados (figura A.1).
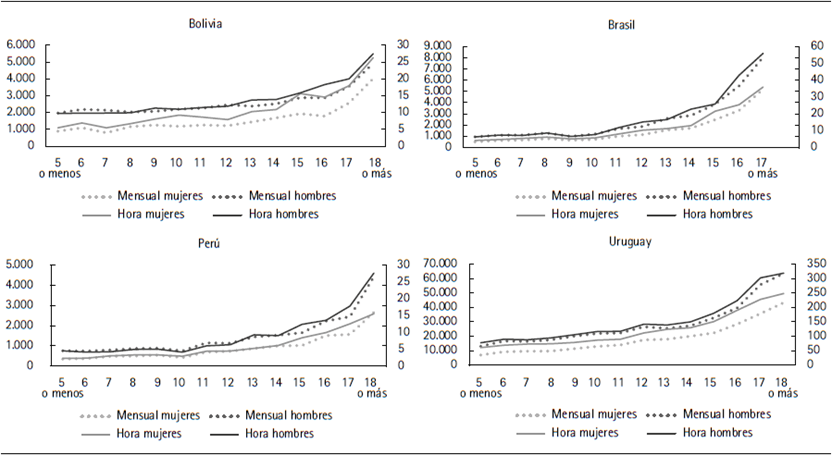
Fuente: elaboración propia sobre la base de las encuestas de hogares de los respectivos países.
Figura 1 Ingresos laborales mensuales y horarios por años de educación y sexo. Personas de 15 a 65 años

Fuente: elaboración propia sobre la base de las encuestas de hogares de los respectivos países.
Figura 2 Tasa de ocupación por años de educación y sexo. Personas de 15 a 65 años
Tanto los ingresos mensuales como los horarios aumentan a medida que crece el capital humano, mientras que, salvo en Bolivia, la brecha absoluta aumenta con el nivel educativo. La diferencia por sexo respecto a la ocupación presenta importantes variaciones entre países. En Brasil y Uruguay la tasa de ocupación es creciente con los años de educación en tanto que Bolivia y Perú tiene forma de U. Esto puede explicarse por la importancia que tiene en los países andinos el trabajo rural que se refleja en altas tasas de ocupación entre los menos educados. En países más urbanos, como Brasil y especialmente Uruguay, la tasa de ocupación de las menos educadas es muy baja. Entre los ocupados, las mujeres siempre trabajan una cantidad de horas menor que los hombres, con la mayor brecha en Uruguay. Tanto en Brasil como en Uruguay, la brecha disminuye a medida que aumenta el nivel educativo, mientras en los países andinos no presenta importantes diferencias (figura A.1).
II. ASPECTOS METODOLÓGICOS
Para realizar las microsimulaciones se utilizan imputaciones múltiples, considerando la construcción de contrafactuales como un problema de datos faltantes6. Esta técnica se encuentra ampliamente difundida y validada para la imputación de datos faltantes en varias disciplinas, en especial, entre las ciencias sociales y médicas. En economía se han utilizado también para la imputación de los ingresos en las fuentes de datos en las que los altos ingresos son censurados para preservar la identidad (An y Little, 2007; Gartner y Rässler, 2005; Jenkins, Burkhauser, Feng y Larrimore, 2011). Por otro lado, Piesse, Álvarez-Rojas, Judkins y Shadish (2010) utilizan esta técnica para la construcción de contrafactuales en la evaluación de impacto de un programa educativo cuyo diseño no es aleatorio.
La técnica de imputación múltiple, propuesta por Rubin (1987), consta de tres etapas: imputación, en la que se generan K > 1 bases de datos completas (simuladas), a partir de un modelo de imputación dado; análisis con datos completos, calculando los indicadores de interés en cada una de las K bases construidas, y agregación de los indicadores calculados en cada una de las K bases para obtener una estimación puntal, siguiendo las reglas de Rubin7. De este modo se refleja la incertidumbre adicional que surge de los datos faltantes. En el caso de la construcción de contrafactuales, este error es de particular relevancia dado que se cuenta con una proporción importante de datos faltantes (Piesse et al., 2011).
En este artículo se escoge el predictive mean matching como modelo de imputación, dado que permite replicar de forma muy ajustada la distribución de los datos observados. Además, es el método sugerido cuando la normalidad del modelo es cuestionable. Es un método parcialmente paramétrico que asimila cada valor faltante con el valor observado que sea más cercano a su predicción lineal.
Para clarificar la metodología se detalla la estrategia de imputación múltiple univariada. Y es la variable con datos faltantes y X un conjunto de variables que permiten la imputación. El primer paso consiste en estimar una regresión lineal de Y sobre X:
Se utiliza la técnica de bootstrap para la obtención de los parámetros dado que la normalidad del modelo no está asegurada, obteniendo las estimaciones 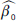 ,
, 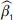 ,
, 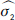 y los correspondientes residuos
y los correspondientes residuos 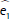 .
.
El segundo paso consiste en tomar k valores de 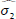 , considerando su distribución estimada en la muestra (obtenida a través de bootstrap), y se obtienen valores de los parámetros,
, considerando su distribución estimada en la muestra (obtenida a través de bootstrap), y se obtienen valores de los parámetros, 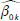 ,
, 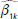 correspondientes. Con estos valores se realizan las k predicciones lineales de Y:
correspondientes. Con estos valores se realizan las k predicciones lineales de Y:
Para cada una de las observaciones que presentan el dato faltante se identifican las j observaciones completas cuya predicción, 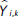 , sea más cercana a la de la observación faltante. La imputación se toma aleatoriamente del conjunto j de las observaciones más cercanas, imputando el valor observado de Y. En este trabajo se utilizan las cinco observaciones más cercanas para seleccionar la imputación (j = 5).
, sea más cercana a la de la observación faltante. La imputación se toma aleatoriamente del conjunto j de las observaciones más cercanas, imputando el valor observado de Y. En este trabajo se utilizan las cinco observaciones más cercanas para seleccionar la imputación (j = 5).
Una vez que se obtienen las K bases imputadas se trabaja en cada una de ellas como si fueran bases completas realizando las estimaciones necesarias. Luego se agregan los resultados obtenidos siguiendo las reglas sugeridas por Rubin.
Para aplicar esta técnica se debe especificar la estructura que tienen los datos faltantes, dado que modifica la cantidad de información que debe incluirse en la imputación. Rubin (1976) establece tres posibles estructuras de los datos faltantes: completamente aleatorios (missing completly at random [MCAR]), aleatorios (missing at random [MAR]) y no aleatorios (missing not at random [MNAR]). Estas estructuras dependen del problema que se esté analizando, no de los datos en sí mismos.
Por lo general, se asume MAR, lo que implica que la distribución de probabilidad de los datos faltantes, condicional en la información observada, no depende de la información no observada (Rubin, 1976)8. Esto permite estimar el modelo de imputación a partir de una regresión multivariada de la información parcialmente observada sobre la completamente observada, o procedimientos equivalentes. Para hacer inferencia bajo MNAR es necesario contar con una especificación explícita del mecanismo de selección o conocer cómo cambian las distribuciones de probabilidad de las variables parcialmente observadas, dadas las variables completamente observadas, entre individuos que tienen observaciones completas y aquellos que no.
Las imputaciones multivariadas realizadas en este trabajo (escenarios dos y tres) presentan un patrón conjunto de los datos faltantes monótono, es decir, la variable Y 1 solo presenta valores faltantes cuando la variable Y 2 también lo hace. En estos casos, la estimación se puede realizar de forma secuencial: la imputación multivariada se realiza como una secuencia de imputaciones univariadas. Esto es posible porque las variables se pueden ordenar de modo tal que las observaciones no faltantes de la variable que se está imputando también están completas en todas las variables usadas para predecirla9.
En este trabajo se utilizan 20 imputaciones, cantidad superior a la sugerencia de Rubin (1987) de un mínimo de 5. Se selecciona un número mayor a la recomendación mínima porque los indicadores de desigualdad estimados no tienen varianza en cada imputación, por lo que se requiere un conjunto alto de imputaciones para estimar correctamente su varianza entre imputaciones. Las imputaciones son consistentes y estables, lo que confirma que la cantidad de imputaciones realizadas no debe aumentarse (véase subsección A, de la sección III).
A lo largo de los tres escenarios estimados se opera con las horas trabajadas y los ingresos laborales por hora de las mujeres. Se trabaja con personas entre 15 y 65 años, tramo etario en el que la participación laboral es mayoritaria. Los nuevos vectores de horas trabajadas e ingresos laborales por hora para las mujeres se basan en la estructura de trabajo de los hombres, recalculando con ellos los ingresos laborales mensuales de las mujeres. Se construye un vector contrafactual de ingresos del hogar que incorpore el ingreso laboral mensual simulado de las mujeres y se recalculan los indicadores de pobreza y desigualdad. A continuación se describe en detalle cada uno de los escenarios y los procedimientos necesarios para la aplicación de las imputaciones.
En el primer escenario (denominado igualdad de ingresos) se cierra la brecha en el ingreso laboral existente entre mujeres y hombres, dadas sus características observables. Solamente se modifica el vector de ingresos laborales, imputando el ingreso por hora de las mujeres ocupadas con base en el de los hombres ocupados con similares características. El vector de horas trabajadas permanece incambiado. Se opera exclusivamente con las mujeres ocupadas.
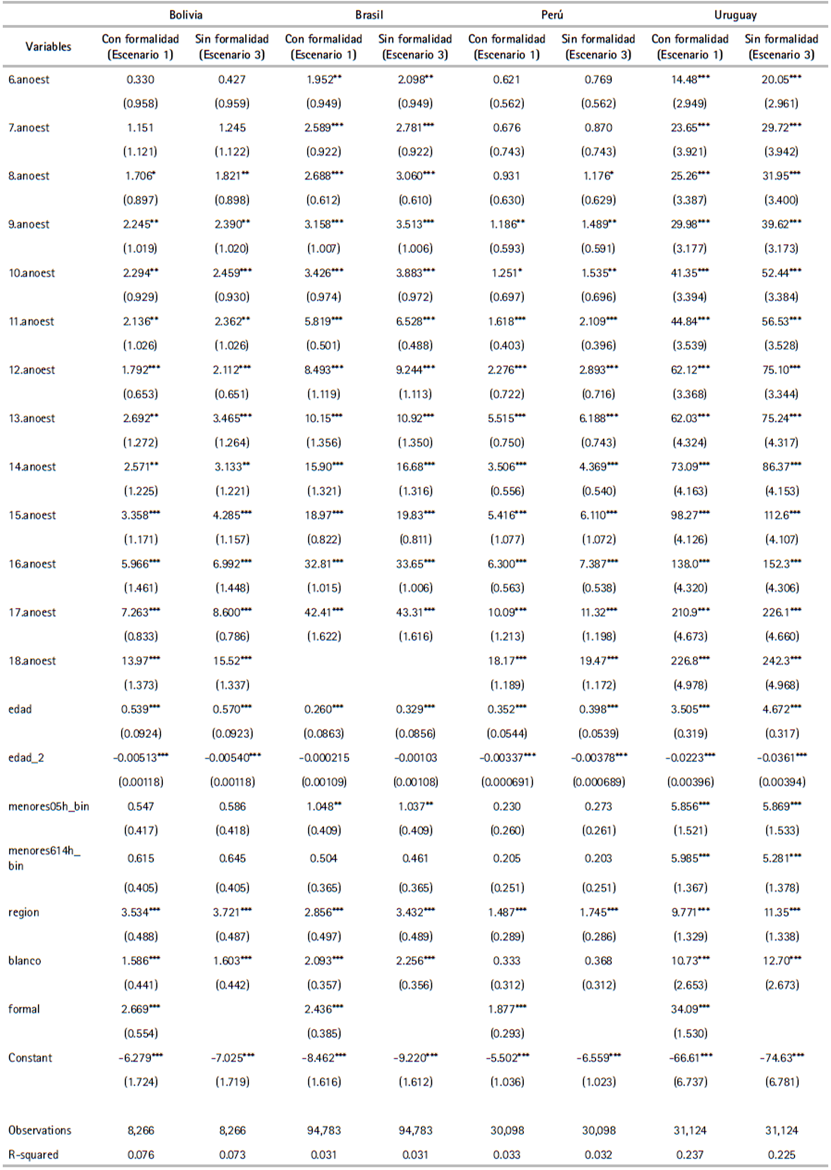
Se trabaja con un vector de ingresos laborales de los ocupados donde se codifica como faltante el ingreso laboral de todas las mujeres. Las variables utilizadas en el modelo de imputación son: edad, edad al cuadrado, años de educación, presencia de niños de 0 a 5 años en el hogar, presencia de niños de 6 a 14 en el hogar, región10, ascendencia blanca y formalidad en la ocupación. En el anexo se presenta el resultado de la estimación de los determinantes del ingreso laboral de los hombres para cada país (cuadro A.2).
Es ampliamente discutida en la literatura la existencia de un sesgo de selección al empleo en las mujeres, sesgo casi inexistente entre los hombres. Solo las mujeres con características más favorables, aquellas que serán mejor remuneradas en el mercado laboral, deciden trabajar mientras que entre los hombres la participación es prácticamente universal. Esto implica que, aun condicional a las características observables, los inobservables que determinan el ingreso laboral de mujeres y hombres difieren, lo que equivale a considerar que el patrón de datos faltantes es MNAR11. Sin embargo, el objetivo de este escenario es simular que, condicional en las características observables, los ingresos laborales de hombres (observados) y mujeres (faltantes) tienen la misma distribución de probabilidad, que los retornos tanto de los observables como de los inobservables sean iguales. Esto es equivalente a asumir que el patrón de datos faltantes es MAR.
Otro elemento para tener en cuenta es que no se incluyen en el modelo de imputación las variables asociadas a las características de la ocupación de la persona como por ejemplo la rama y el tipo de ocupación. Esto implica que al cerrar la brecha de ingresos laborales también se está eliminando la segregación laboral, tanto vertical como horizontal, que no dependa de las características de las personas12.
El segundo escenario (denominado igualdad de participación) simula el cierre de la brecha de horas trabajadas entre hombres y mujeres, operando sobre la participación laboral en el margen extensivo e intensivo simultáneamente. Se imputan las horas trabajadas de las mujeres, tanto ocupadas como no ocupadas, de modo que se asemejen a las que trabajan los hombres. Esto implica, por un lado, que más mujeres participen en el mercado laboral y, por otro, que las mujeres que ya trabajaban lo hagan una mayor cantidad de horas. Se construye un vector de horas en el que se codifican como faltantes las observaciones de todas las mujeres y se mantienen las observaciones de los hombres, identificando con horas trabajadas iguales a 0 a los que no trabajan; este es uno de los vectores que se imputa.
Para obtener el ingreso de las mujeres se debe, además, imputar el salario de las mujeres que cambian de condición de actividad. Dado que se pretende aislar el efecto de las horas trabajadas, el ingreso laboral se imputa con base en el de las mujeres ocupadas. Esto implica que esta imputación es condicional a ser mujer. Puesto que los ingresos laborales solo son faltantes si las horas lo son, se considera que el patrón de datos faltantes es monótono y se procede a una imputación bivariada secuencial de horas trabajadas e ingresos laborales.
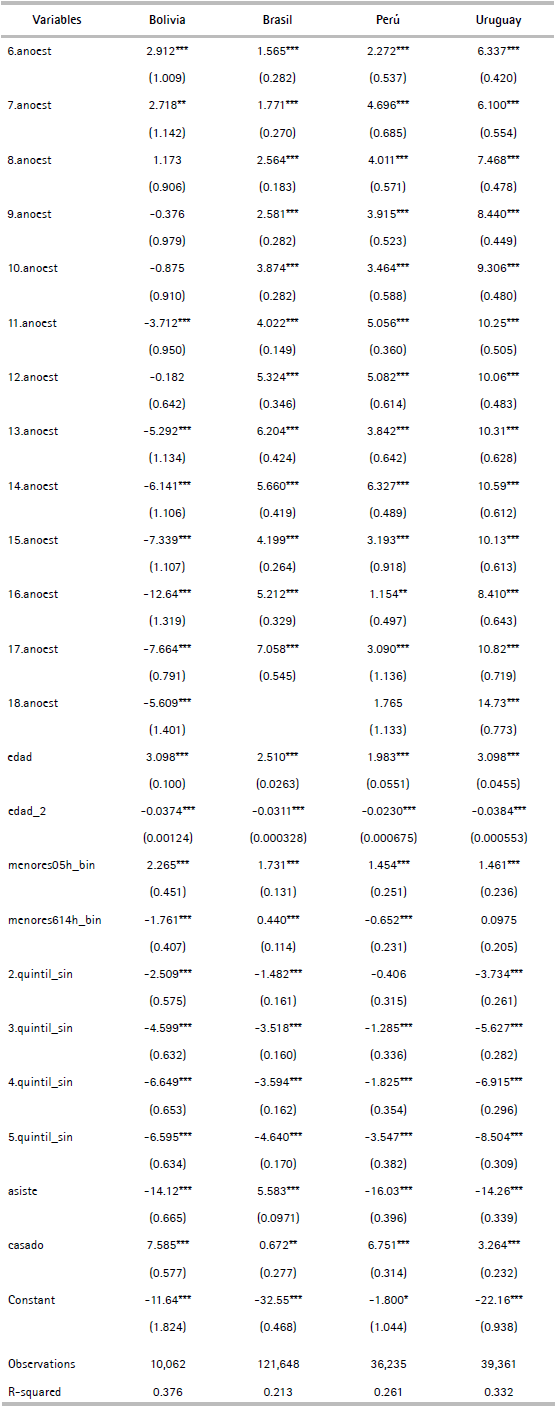
Las variables utilizadas para la imputación de las horas son edad, edad al cuadrado, años de educación, asistencia a un centro educativo, presencia de niños de 0 a 5 años en el hogar, presencia de niños de 6 a 14 en el hogar, quintil de ingreso del hogar sin considerar el ingreso de la persona. Para el modelo de ingresos laborales se utiliza edad, edad al cuadrado, años de educación, presencia de niños de 0 a 5 años en el hogar, presencia de niños de 6 a 14 en el hogar, región y ascendencia blanca. En el anexo se presenta el resultado de la estimación para cada país (cuadro A.3 para las horas de los hombres y A.4 para los ingresos laborales de las mujeres).
En este escenario se presenta un problema respecto a la estructura de los datos faltantes en la variable de ingresos laborales. El sesgo de selección en el empleo en las mujeres permite predecir que los ingresos laborales de aquellas que no trabajan serán más bajos que los de las que lo hacen. Sin embargo, en este escenario se simulan los ingresos laborales de las mujeres que no trabajan con base en los ingresos laborales observados para aquellas que sí lo hacen, introduciendo un potencial sesgo al alza. La estrategia de darle una estructura a la imputación, asumiendo una estructura de datos faltantes MNAR, implicaría acercarse a modelos como los de corrección de sesgo de selección de Heckman. Sin embargo, estos modelos tienen la gran dificultad de encontrar una variable de exclusión que determine la participación en el mercado laboral pero no los ingresos laborales percibidos. En la práctica es muy complejo encontrar una variable que cumpla con estas condiciones, por lo que los resultados no se diferencian de los que se obtienen si no se controla por el sesgo de selección (véase, por ejemplo, Lee, 2009). Debido a estas observaciones, se decide mantener la imputación asumiendo MAR, aun cuando se reconoce que el supuesto no se ajusta a los datos.
Para el caso de las horas trabajadas, la argumentación es similar a la planteada para los ingresos laborales en el primer escenario. Aun cuando la estructura de datos faltantes no sea MAR, el ejercicio que se quiere realizar implica asumir que lo es, dado que se quiere simular que las horas trabajadas de las mujeres se rijan por los mismos patrones que las de los hombres, dadas similares características observables.
Por último, el tercer escenario (denominado igualdad de género considera conjuntamente el cierre de las dos brechas: la de ingresos laborales y la de horas trabajadas. Para ello, se imputan las horas trabajadas del mismo modo que se realiza en el escenario dos. El vector de ingresos laborales por hora de todas las mujeres que resultan ocupadas del paso anterior se imputa con base en el ingreso laboral por hora de los hombres ocupados.
El último escenario busca considerar de forma simultánea los dos anteriores, al cerrar conjuntamente la brecha de ingresos laborales y la de horas trabajadas. Esto implica que tanto los ingresos laborales como las horas trabajadas de mujeres y hombres sean similares, dadas las características observables.
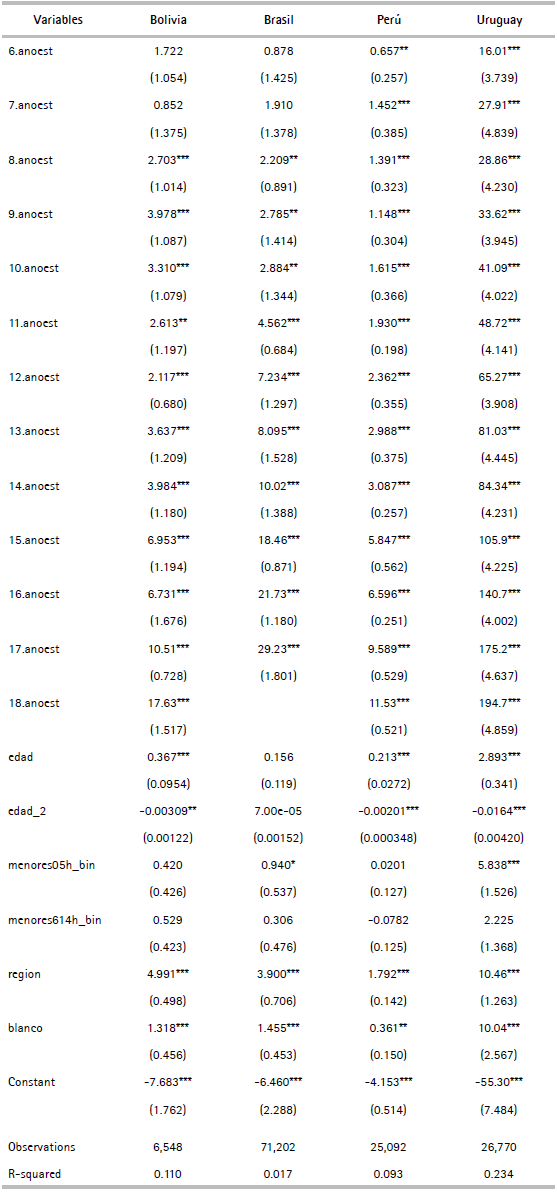
Para realizar la imputación se construye un vector de horas trabajadas igual al del segundo escenario, codificando como faltante las horas trabajadas de las mujeres, manteniendo las horas de los hombres. Para los ingresos laborales por hora se opera de forma similar al primer escenario, pero para toda la población, codificando como faltante el ingreso laboral para las mujeres y manteniendo el de los hombres. Para aquellos hombres que no trabajan se codifica un ingreso laboral de 0. Así como en el segundo escenario, el patrón de datos faltantes es monótono y se utiliza una imputación bivariada secuencial. El modelo para la imputación de las horas es el mismo que el utilizado en el escenario 2 (cuadro A.3). Para el ingreso laboral por hora la única diferencia con el modelo del escenario uno es que no se utiliza la variable formal dado que esta variable no es conocida para quienes no están ocupadas. La estimación del modelo se presenta en el anexo (cuadro A.2).
En este caso, las justificaciones del supuesto de estructura de datos faltantes MAR surgen de lo argumentado para los dos escenarios anteriores.
Se debe tener en cuenta que no se consideran efectos de equilibrio general, lo que podría modificar los resultados de forma significativa. La participación más equitativa de las mujeres y hombres en el mercado laboral requiere ajustes para mujeres y hombres simultáneamente. Es esperable que los ingresos laborales de los hombres reaccionen también al aumento de la oferta laboral de las mujeres. Asimismo, gran parte de las mujeres que no se encuentran en el mercado laboral realizan una proporción importante de las tareas no remuneradas del hogar, que deberían redistribuirse si las mujeres trabajaran igual que los hombres. Esto implica que las horas trabajadas de los hombres también podrían reaccionar frente a un aumento de las de las mujeres. Es por ello por lo que este ejercicio debe interpretarse como una cota superior de los posibles efectos que podrían observarse13.
III. RESULTADOS
En esta sección se presentan los principales resultados de la simulación del cierre de brechas de género en el mercado laboral para los cuatro países. Se informa primero de los resultados del ajuste de las imputaciones para luego analizar el efecto que el cierre de las brechas tendría sobre los indicadores de pobreza, la desigualdad de ingresos laborales y la desigualdad de ingreso de los hogares en cada uno de los tres escenarios.
A. Ajuste de las imputaciones
Un primer aspecto que es necesario destacar es que las imputaciones resultan altamente satisfactorias, ya que son al mismo tiempo estables y replican adecuadamente las distribuciones de referencia en cada caso. Por razones de simplicidad en la presentación de los resultados, no se reportan en el cuerpo de texto los intervalos de confianza14.
Se debe tener en cuenta que la metodología aplicada para la construcción de los contrafactuales se apoya (parcialmente) en la existencia de un soporte común para las características observables de mujeres y hombres15. Puesto que se utiliza como mecanismo para el emparejamiento el valor predicho de un modelo lineal, este problema se resuelve parcialmente. De todos modos, se podrían observar diferencias en las habilidades de las personas por sexo que no están consideradas en las variables y que, por lo tanto, no se tienen en cuenta.
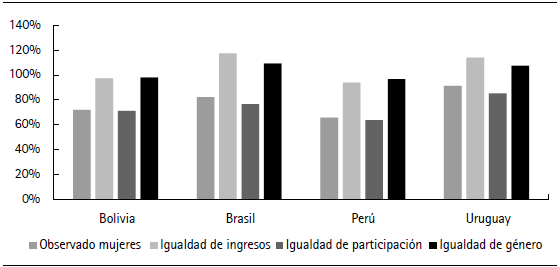
En la figura 3 se muestran los ingresos laborales promedio por hora de las mujeres en relación con el ingreso observado de los hombres, y se indican las variaciones importantes entre los escenarios. Estas diferencias se basan en la construcción de estos: a quién se utiliza como referencia para la imputación y a quiénes se incluye.
Fuente: elaboración propia sobre la base de las encuestas de hogares de los respectivos países.
Figura 3 Ingresos laborales de las mujeres según escenario, como porcentaje de los ingresos de los hombres ocupados
Cuando se imputan los ingresos siguiendo los determinantes de los hombres, es decir cuando se cierra la brecha de ingresos (escenarios igualdad de ingresos e igualdad de género), se obtienen ingresos mayores que el observado para las mujeres. En estos casos, el ingreso femenino promedio alcanza o supera el de los hombres. Esto se debe a que las mujeres tienen iguales (Bolivia y Perú) o mejores (Brasil y Uruguay) características observables que los hombres, en particular, la educación. Este es especialmente el caso entre las mujeres ocupadas, lo que se refleja en el hecho de que el ingreso laboral por hora en el escenario de igualdad de ingresos resulta mayor que el del escenario de igualdad de género. En el caso del escenario de igualdad de participación, se cierra la brecha de participación, pero no la de ingresos, por lo que se imputan los ingresos de las mujeres que ingresan al mercado laboral siguiendo el patrón de ingresos de las mujeres ocupadas. Dado que las mujeres que ingresarían al mercado laboral presentan peores características en promedio que las mujeres ocupadas, su ingreso laboral promedio es menor. Esto también sucede en el escenario igualdad de género, pero es compensando por el hecho de que se cierra la brecha de ingresos, calculando sus ingresos laborales siguiendo los de los hombres.
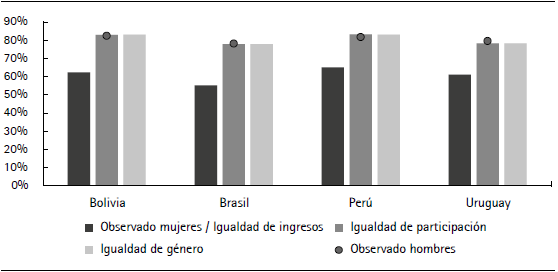
En el caso de las horas trabajadas, también se logran replicar los resultados observados para los hombres. Cuando se cierra la brecha de participación (escenarios de igualdad de participación e igualdad de género) se obtienen resultados promedio similares para mujeres y hombres en la tasa de ocupación (figura 4) y las horas trabajadas de los ocupados (figura 5). Se logra una variación significativa de la tasa de ocupación de las mujeres16. En el escenario de igualdad de ingresos solo se cierra la brecha de ingresos, manteniendo la participación incambiada. Por lo tanto, las horas trabajadas y tasa de ocupación son iguales a las observadas para las mujeres por construcción.
Fuente: elaboración propia sobre la base de las encuestas de hogares de los respectivos países.
Figura 4 Tasa de ocupación de las mujeres según escenario y observada para hombres y mujeres
Fuente: elaboración propia sobre la base de las encuestas de hogares de los respectivos países.
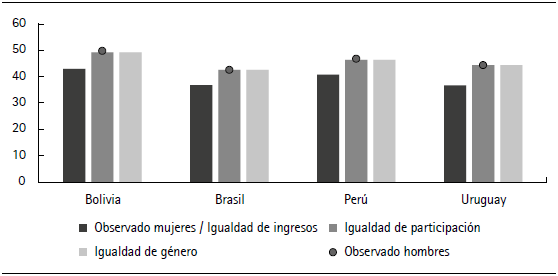
Figura 5 Horas trabajadas de las mujeres ocupadas según escenario y observadas de hombres y mujeres
En la figura 5 se presentan las horas trabajadas por los ocupados en cada escenario. Se observa que las horas trabajadas por las ocupadas aumentan significativamente al cerrar la brecha de participación, tanto en el escenario de igualdad de participación como en el de igualdad de género. El stock de horas trabajadas en la economía aumentaría de forma significativa en los dos escenarios. En este artículo no se analiza la demanda de trabajo, manteniéndose constante la tasa de desempleo. Pero resulta evidente que la absorción de esta oferta incrementada en el margen extensivo e intensivo sería un desafío para los cuatro países. Es probable que tanto el desempleo, como los ingresos laborales reaccionen frente a este aumento de la oferta laboral. Más aún, también sería esperable que se modifique la tasa de ocupación de los hombres.
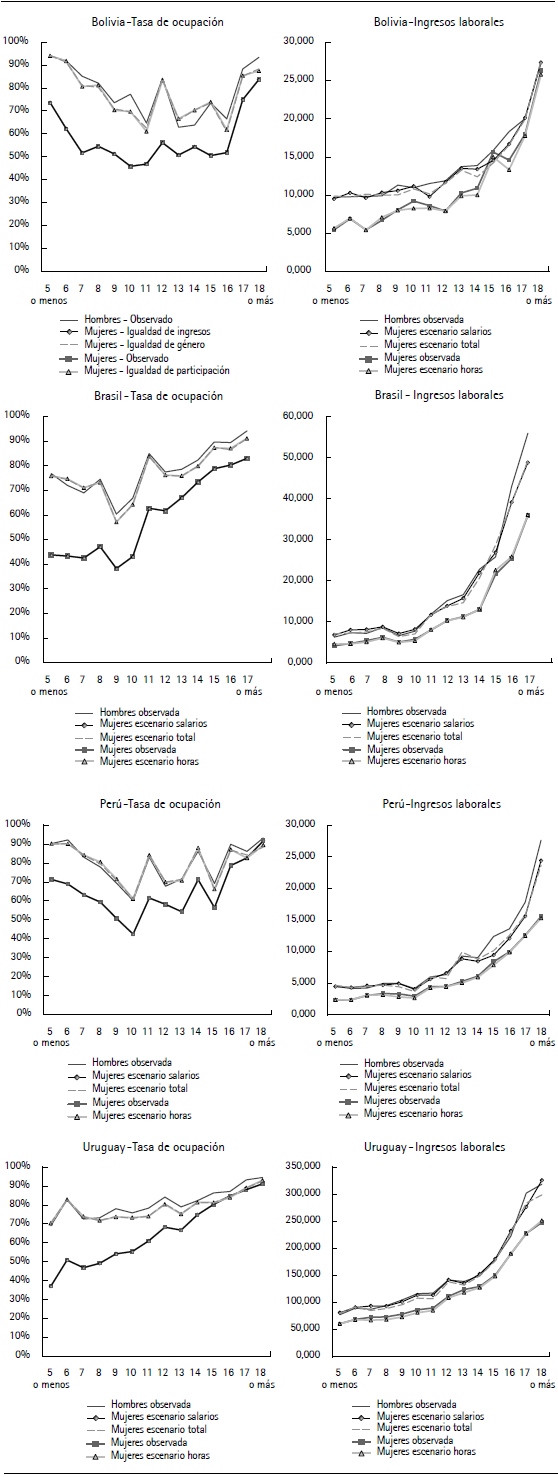
La figura 6 presenta las principales variables (tasa de ocupación e ingresos laborales por hora) observadas para hombres y mujeres, y las imputadas para mujeres en cada escenario por años de educación. El ingreso laboral mensual surge de la multiplicación de las variables anteriores y se presenta en la figura A.2 del anexo. Se presenta un panel para cada uno de los países. Por construcción, la tasa de ocupación de las mujeres en el escenario de igualdad de ingresos es exactamente igual a la observada, dado que esta variable no se modifica en ese escenario. En el caso del ingreso laboral por hora en el escenario de igualdad de participación, se logra seguir el patrón de las mujeres ocupadas utilizado como base en la imputación. En los otros casos, la curva se acerca a la observada para los hombres, cerrando la brecha de género en la variable de interés. En términos generales, el ajuste es mejor para los menos educados, tanto en la tasa de ocupación como en los ingresos laborales por hora.
Fuente: elaboración propia sobre la base de las encuestas de hogares de los respectivos países.
Figura 6 Ingresos laborales por hora y tasa de ocupación de las mujeres según escenario y observado para mujeres y hombres, por nivel educativo
En suma, se considera que las imputaciones fueron satisfactorias dado que son estables y replican razonablemente la distribución condicional de las variables tomadas como referencia. Esto implica que se logra simular el cierre de las brechas de género en el mercado laboral y que las pequeñas diferencias que permanecen se explican por las diferencias en las características observadas entre mujeres y hombres o por problemas menores en la modelización.
B. Resultados de pobreza y desigualdad
Para el cálculo de la pobreza se utiliza el método absoluto, usando las líneas de pobreza oficiales de los países, salvo en el caso de Brasil que se aplica la línea calculada por Cepal17. El ingreso utilizado es el ingreso del hogar con valor locativo para la pobreza dado que las líneas incorporan el gasto en servicios de vivienda, pero sin valor locativo para el cálculo de los indicadores de desigualdad.
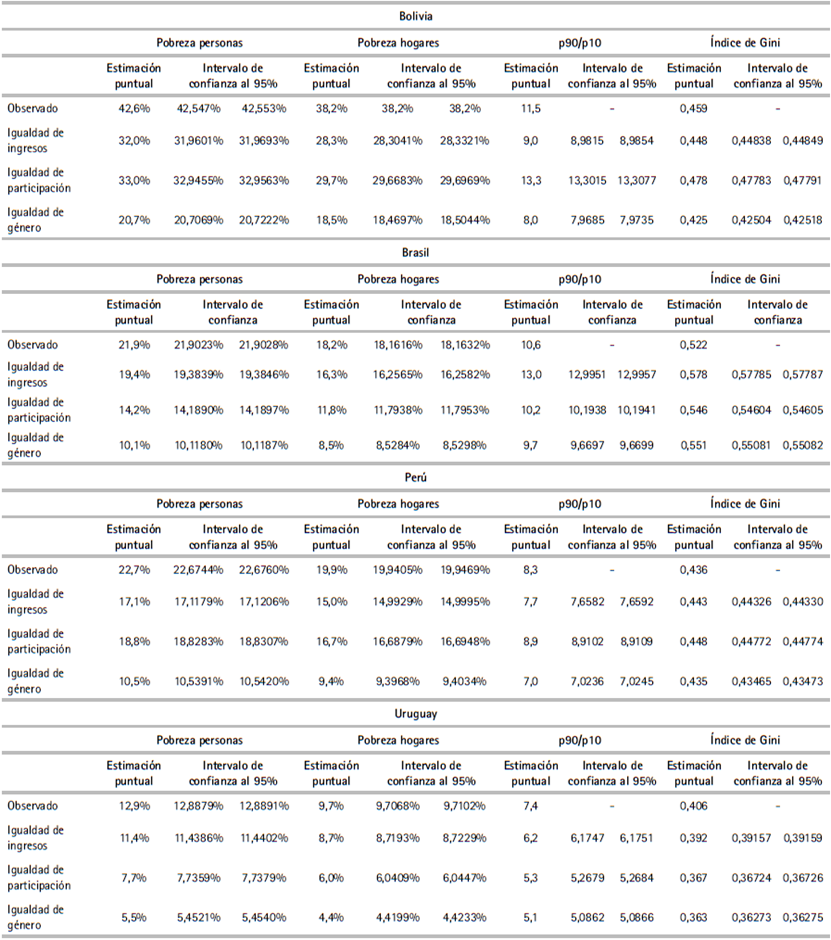
Se analiza el indicador de pobreza y los principales indicadores de desigualdad considerando a toda la población. A diferencia de la subsección anterior en la que se analizaban indicadores de personas de 15 a 65 años, en este caso se analiza el ingreso per cápita de los hogares y a la población total buscando reflejar el efecto macro de los cambios. Asímismo, se presenta el indicador de desigualdad de ingresos laborales, que se calcula para las personas ocupadas de entre 15 y 65 años y que contribuye a comprender los cambios en los indicadores de los hogares. Los resultados de los principales indicadores se presentan en el cuadro A.5 del anexo.
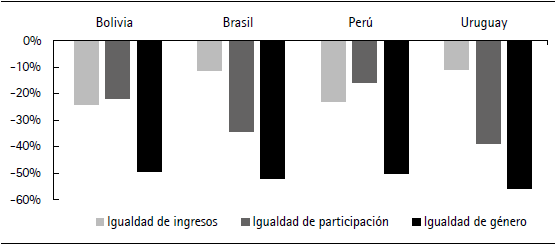
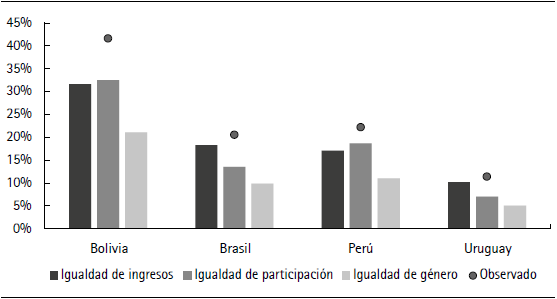
La pobreza cae en los tres escenarios para los cuatro países. La figura 7 muestra las variaciones porcentuales de la pobreza y la figura 8 muestra el porcentaje de personas pobres por escenario en comparación con la pobreza observada correspondiente al escenario base.
Fuente: elaboración propia sobre la base de las encuestas de hogares de los respectivos países.
Figura 7 Variación porcentual del porcentaje de personas pobres según escenario
Fuente: elaboración propia sobre la base de las encuestas de hogares de los respectivos países.
Figura 8 Porcentaje de personas pobres según escenario y observado
Los mejores resultados se obtienen en el escenario igualdad de género, cuando se cierran conjuntamente la brecha de ingresos y la de participación, con reducciones del entorno de entre el 49% y el 56% en la incidencia de la pobreza. En los cuatro países la suma de la reducción de cada escenario parcial es menor que el resultado obtenido en el de igualdad de género, lo que muestra que el cierre de la brecha de participación y horas trabajadas, y de ingresos se potencian mutuamente. Sin embargo, se observa un patrón diferenciado entre Bolivia y Perú, y Brasil y Uruguay. Mientras que en los primeros la mayor reducción se observa al cerrar la brecha de ingresos, en los últimos la mayor variación se presenta al cerrar la de participación. Esto responde a dónde se concentra la mayor desigualdad entre mujeres y hombres en el mercado laboral de cada país. De todos modos, en Bolivia y Perú las diferencias entre los escenarios de igualdad de ingresos e igualdad de participación son pequeñas en comparación con las de Brasil y Uruguay. La reducción de la pobreza en el escenario de igualdad de ingresos en los últimos es de aproximadamente el 11% y en el escenario de igualdad de participación es de más del 30%, mientras que en los primeros se ubica cerca del 20% para los dos escenarios. En otras palabras, Bolivia y Perú obtienen ganancias similares por el cierre de cada una de las brechas, mientras que Brasil y Uruguay tienen más para ganar en políticas de incremento de la participación femenina.
Respecto a los niveles, la situación también es diferente para los dos grupos de países. En Uruguay el cierre de las brechas de género en el mercado laboral permitiría niveles de pobreza razonablemente bajos (menores al 15%), más aún si se considera que se establecen umbrales absolutos. En Brasil, se logra ese objetivo con el escenario de igualdad de participación, aunque no con el de igualdad de ingresos. Sin embargo, en Bolivia y Perú los niveles de pobreza continúan siendo altos, con la excepción del escenario de igualdad de género en Perú. La situación de Bolivia es particularmente alarmante: cerrando las brechas de ingresos y participación entre mujeres y hombres en el mercado laboral la pobreza se mantiene en más del 20%. Los ingresos laborales percibidos por los hombres son tan bajos que no alcanza con una participación igualitaria en el mercado laboral para atenuar de forma significativa el problema de la pobreza, aun cuando se reduzca en casi el 50%.
Respecto a la desigualdad la comprensión de los resultados resulta más compleja, aunque se mantiene la relación entre los escenarios similar a la señalada para la pobreza: en Bolivia y Perú el escenario de igualdad de ingresos presenta mejores resultados que el de igualdad de participación y lo contrario sucede en Brasil y Uruguay. Sin embargo, del mismo modo que sucede en los países desarrollados analizados por Harkness (2013), el cierre de las brechas de género en el mercado laboral tiene efectos en la desigualdad que pueden ir en diferentes sentidos, dependiendo de los puntos de partida de cada país.
Para analizar los efectos en desigualdad del cierre de la brecha de género en el mercado laboral se construye un set de indicadores que sea capaz de informar sobre los movimientos que se producen en toda la distribución del ingreso.
Para entender el canal a través del que se procesan los cambios se presenta el efecto de los diferentes escenarios analizados en la distribución de los ingresos laborales horarios y mensuales, medido a través de la variación del índice de Gini. Para la distribución del ingreso de los hogares se calcula un conjunto amplio de indicadores: cocientes de percentiles (p90/p10, p75/p25, p25/p50, p10/p50, p90/p50 y p75/p50) e indicadores sintéticos (índice de Gini, familia de indicadores de Atkinson, con parámetro 0,5, 1 y 2, y familia de indicadores basados en la entropía, con parámetro -1, 0 y 1).
En primer lugar, se analizan los indicadores de desigualdad del ingreso laboral, que refieren a diferencias entre ingresos de las personas y no entre ingresos de los hogares. Se considera exclusivamente a los ocupados para realizar los cálculos, aunque se debe notar que los ocupados varían entre escenarios, dado que en dos escenarios se cierra la brecha de participación.
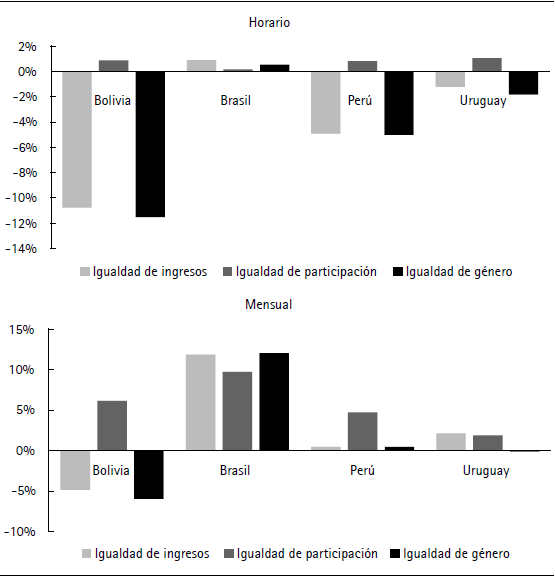
La figura 9 muestra la variación porcentual del índice de Gini de los ingresos laborales en cada escenario, en el panel de la izquierda los ingresos horarios y en el de la derecha los mensuales. En el cuadro A.6 del anexo se presentan los valores que toman los índices en cada caso. Tres elementos entran en juego: cómo es la brecha de ingresos observada a lo largo de la distribución del ingreso, quiénes son las mujeres que ingresan al mercado laboral al cerrar la brecha de participación y cómo se distribuyen las horas trabajadas respecto al ingreso, tanto de hombres como de mujeres.
Fuente: elaboración propia sobre la base de las encuestas de hogares de los respectivos países.
Figura 9 Variación porcentual del índice de Gini de los ingresos laborales de los ocupados por escenario
La desigualdad de ingresos laborales por hora disminuye cuando se cierra la brecha de ingresos, tanto en el escenario de igualdad de ingresos como en el de igualdad de género, excepto en Brasil. Esto puede deberse, por un lado, a que las mujeres y los hombres tendrían ingresos similares, por sus características observables, reduciendo la desigualdad entre grupos. Por otro lado, debe analizarse cómo era la brecha de ingresos en la distribución del ingreso. Bolivia y Perú presentan una brecha mayor en la parte baja de la distribución (Carrillo, Gandelman y Robano, 2014; Ñopo, 2009) lo que implica que el cierre de la brecha debería tener efectos igualadores. En Uruguay, la evidencia muestra que la brecha aumenta con el nivel de ingresos, lo que presionaría al aumento de la desigualdad. Sin embargo, el peso que tienen las diferencias de ingresos laborales en los tramos medios explicaría la pequeña caída observada.
Brasil es el único país analizado para el que aumenta la desigualdad de ingresos laborales por hora al cerrar la brecha de ingresos. La brecha de género en los ingresos laborales de Brasil es creciente con el nivel de ingresos (véase Madalozzo, 2010; Madalozzo y Martins, 2007; Santos y Ribeiro, 2006), lo que lleva a que el cierre de esta afecte en mayor medida a las mujeres ocupadas más ricas. Esto explicaría al leve aumento en la desigualdad del ingreso laboral que se observa, dado que aumenta el ingreso de las mujeres de mayor ingreso.
La desigualdad de ingresos laborales por hora apenas aumenta en el escenario en el que solo se cierra la brecha de participación. Esto puede explicarse entendiendo quiénes son las mujeres que ingresarían al mercado laboral en este escenario. Es esperable que las mujeres de menores ingresos esperados sean las que no participan en el mercado laboral, dado que sus retornos esperados son muy bajos. Su ingreso al mercado laboral, con ingresos que responden a los de las mujeres ocupadas implica que más personas tengan ingresos bajos, lo que aumentaría la desigualdad de ingresos laborales por hora. Cuando se cierran ambas brechas conjuntamente este efecto es neutralizado por el cierre de la brecha de ingresos dado que los efectos distributivos son mayores en el escenario de igualdad de género que en el de igualdad de ingresos.
Cuando se consideran los ingresos mensuales, los resultados empeoran en todos los países y escenarios. Esto implica que la distribución de las horas trabajadas tiene efectos desigualadores en el mercado laboral.
Por último, se presentan los efectos del cierre de las brechas de género en el mercado laboral en los indicadores de desigualdad del ingreso per cápita de los hogares. Así como señala Atkinson (2015), el efecto de la incorporación de las mujeres al mercado laboral en la desigualdad depende de quiénes se incorporen y de la correlación entre sus ingresos y los de sus cónyuges. Al respecto, en Cepal (2014a) se muestra que en la región la correlación entre los ingresos de los cónyuges es muy variable entre países, pero se evidencia una fuerte homogamia educativa, medida a través del coeficiente de correlación entre los años de educación de las parejas. Esto podría llevar a que el cierre de las brechas de género en el mercado laboral tenga efectos negativos sobre la desigualdad. Asímismo, los efectos en la desigualdad dependerán de la desigualdad de ingresos laborales estudiada previamente.
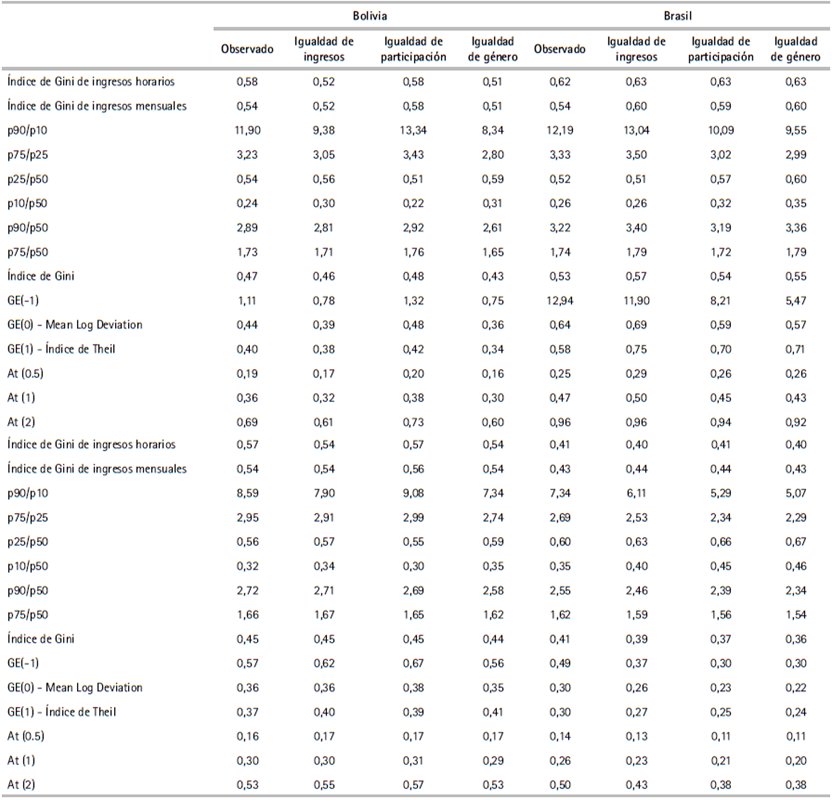
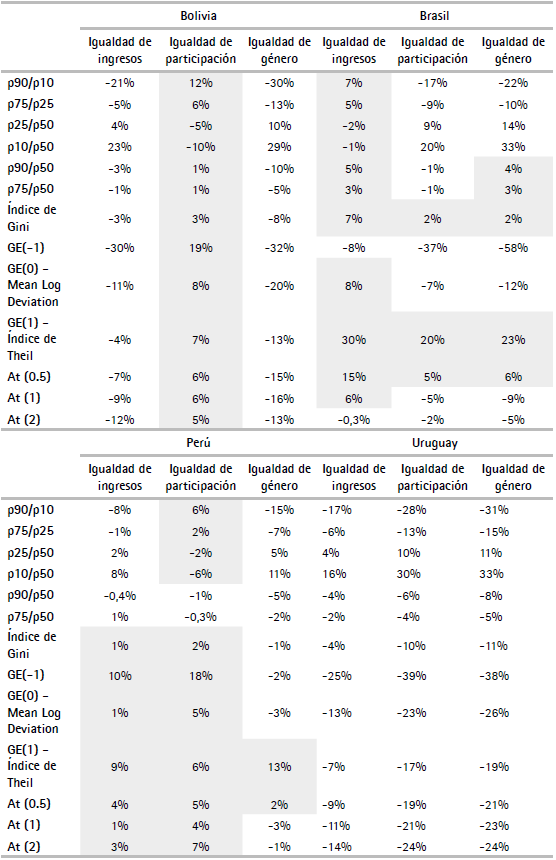
El set completo de indicadores para los cuatro países y los tres escenarios se presenta en el cuadro A.6 del anexo mientras que el cuadro 2 presenta las variaciones porcentuales de los indicadores. Las celdas destacadas en gris implican que la variación del indicador señala una distribución del ingreso menos equitativa. La evidencia de los efectos distributivos es inequívoca en Bolivia y Uruguay, con todos los indicadores mostrando efectos en la misma dirección. En Brasil y Perú los indicadores muestran movimientos discordantes. En lo que sigue se analizan los resultados por país.
Cuadro 2 Variación porcentual de los indicadores de desigualdad según escenario
Fuente: elaboración propia sobre la base de las encuestas de hogares de los respectivos países.
En el caso de Bolivia, el escenario de igualdad de participación es menos equitativo que la situación observada, mientras que los otros dos presentan mejoras distributivas. Esto puede explicarse por los cambios en la desigualdad de ingresos laborales. Bolivia es el único país en el que se observa que los ingresos laborales mensuales tienen una distribución más equitativa cuando se cierra la brecha de ingresos y cuando se cierran ambas brechas, lo que podría explicar los efectos de estos dos escenarios al considerar el ingreso del hogar. Sin embargo, cuando se cierra la brecha de participación empeora el índice de Gini de los ingresos laborales (véase figura 9) debido a que participan en el mercado laboral mujeres con ingresos laborales muy bajos o nulos. También, es probable que las mujeres que ingresan al mercado laboral estén en pareja con hombres de ingresos también bajos lo que refuerza el efecto de la desigualdad de ingresos laborales.
Para Brasil se observa que el escenario de igualdad de ingresos es el que tiene los peores resultados distributivos: todos los indicadores resultan negativos salvo el GE(-1) que da menor peso a los ingresos más altos y el At(2) que presenta variaciones muy pequeñas. Esto puede deberse a que solo impacta a los hogares que presentan mujeres ocupadas y al efecto desigualador de los ingresos laborales. En el caso del escenario de igualdad de participación sucede lo contrario: las variaciones son positivas salvo en los indicadores que ponderan más la parte alta de la distribución. El escenario de igualdad de género indica algo similar, con un empeoramiento de la distribución después de la mediana del ingreso, medido a través del aumento de los cocientes p90/p50 y p75/p90. Esto estaría indicando que en Brasil el cierre de las brechas de género en el mercado laboral tiene efectos diversos en la distribución del ingreso, mostrando efectos negativos en los indicadores que dan más importancia a la parte alta de la distribución mientras que mejoran los que ponderan más a la parte baja, en especial, en cuanto se cierra la brecha de participación.
Respecto a Perú, solo se logran resultados que mejoran claramente la distribución del ingreso en el escenario de igualdad de género; el cierre de la brecha de participación empeora la distribución del ingreso y se observan resultados ambiguos en el escenario de igualdad de ingresos. En este último caso solo mejoran los indicadores que hacen referencia al primer cuartil de la distribución, pero los indicadores que ponderan más la parte baja de la distribución igual empeoran. De todos modos, cabe resaltar que las variaciones son de baja magnitud. Se observa también que la distribución en la parte alta empeora en los tres escenarios.
En Uruguay, los tres escenarios presentan mejoras en la distribución del ingreso. El escenario de igualdad de participación tiene resultados más fuertes que el de igualdad de ingresos. Esto implica que la ubicación de las mujeres no ocupadas en la distribución y la composición de los hogares logran revertir el efecto desigualador que tienen los ingresos laborales mensuales. En los tres escenarios las variaciones más fuertes se producen en los indicadores que dan más importancia a la parte baja de la distribución: la variación de los indicadores de entropía se reduce a medida que aumenta el parámetro y la de los de Atkinson aumenta con la aversión a la desigualdad.
Más allá de los matices, el cierre de ambas brechas conjuntamente logra mejoras en la distribución del ingreso en Bolivia, Perú y Uruguay, y tiene resultados ambiguos en Brasil. Sin embargo, se mantienen niveles altos de desigualdad: el percentil 90 gana entre 5 (Uruguay) y 10 (Brasil) veces más que el 10 en el escenario de igualdad de género (véase cuadro A.6).
Las diferencias entre los escenarios de igualdad de participación y de igualdad de ingresos entre estos dos pares de países (Bolivia y Perú, por un lado, y Brasil y Uruguay, por el otro) tienen que ver con cómo se distribuyen las mujeres ocupadas, cómo son sus ingresos laborales y sus diferencias con los ingresos masculinos a lo largo de la distribución del ingreso. Mientras que en Brasil y Uruguay las mujeres de menor nivel educativo tienen tasas de ocupación bajas, en Bolivia y Perú están mayormente ocupadas, pero con ingresos laborales muy bajos o cero. Esto implica que cuando las mujeres de los países andinos equiparan sus ingresos a los de los hombres, las que viven en hogares de menores recursos son las que presentan las mayores variaciones de ingreso, produciendo mejoras en la distribución del ingreso. Esto va en la línea de la regularidad observada por Carrillo et al. (2014) respecto a la brecha salarial y la riqueza y desigualdad de los países: los países más pobres y más desiguales tienen mayores brechas salariales en el percentil 10 mientras que entre los más ricos y menos desiguales la brecha es mayor en el percentil 90 de la distribución salarial.
En suma, mientras que los efectos en pobreza son inequívocos y siempre positivos, los efectos del cierre de brechas de género en el mercado laboral en la desigualdad no pueden ser generalizados, dependerán del país y del escenario, dado que se generan modificaciones en diferentes partes de la distribución del ingreso. En términos generales, se puede concluir que los efectos son mejores en la parte baja de la distribución y que se mantiene la diferenciación observada en los efectos de pobreza de países respecto a los escenarios. Para Brasil y Uruguay los mejores resultados se obtienen a través del cierre de la brecha de participación mientras que en Bolivia y Perú se logran mejores resultados con el cierre de la brecha de ingresos. Esto se explica por la diferencia en las situaciones de partida de cada país, en especial, por la dimensión de las brechas a lo largo de la distribución.
IV. COMENTARIOS FINALES
La región presenta importantes diferencias respecto al nivel de las brechas de género en el mercado laboral, así como en la importancia relativa de la brecha de ingresos laborales y la de participación (véase Cepal, 2014a). Los países seleccionados para este estudio presentan un nivel relativamente alto de participación laboral entre las mujeres, aunque muestran dos tipologías diferentes en relación con la brecha de ingresos y de participación. Por un lado, se encuentran Brasil y Uruguay, que tienen una brecha importante de participación, pero cuya brecha de ingresos laborales es menor; por otro, Bolivia y Perú, donde la brecha de ingresos es muy grande, debido en parte a la gran cantidad de ocupadas que no reciben remuneración, aunque la brecha de participación se mantiene en niveles similares a los de Brasil y Uruguay. Asímismo, se encuentran diferencias entre los dos grupos de países en cuanto a cómo se distribuyen estas brechas por nivel educativo. Mientras que en Brasil y Uruguay las mayores diferencias de participación se dan entre las menos educadas, en Bolivia y Perú la relación entre la participación y los años de educación presenta una forma de U. Además, estudios previos señalan que la brecha de ingresos en Perú y Bolivia es mayor en la parte más baja de la distribución, mientras que entre Brasil y Uruguay es mayor para los ingresos más altos.
El análisis de las diferencias entre las dos tipologías sugiere que podría mejorar el ingreso de los hogares si se avanza hacia la equidad entre mujeres y hombres en el mercado laboral, y que la importancia del efecto del cierre de la brecha de ingresos y de la de participación podría ser diferencial en cada una. Esto inspiró los tres ejercicios que se realizaron: cierre de la brecha de ingresos por hora, manteniendo las diferencias que se observan en la participación laboral; eliminación de las diferencias entre mujeres y hombres en la participación laboral, tanto en la decisión de participar como en las horas trabajadas, manteniendo las diferencias observadas en los ingresos por hora, y ambos ejercicios de forma conjunta, cerrando la brecha de ingresos y la de participación.
Los resultados obtenidos deben interpretarse con cautela, dado que tienen varias limitaciones. En primer lugar, se debe tener en cuenta que los ejercicios realizados en este trabajo no consideran los efectos de equilibrio general, lo que podría modificar los resultados de forma significativa. La participación más equitativa de las mujeres y hombres en el mercado laboral requiere de ajustes para mujeres y hombres simultáneamente.
En este mismo sentido, la modificación de los ingresos de los hogares en la parte baja de la distribución podría cambiar su elegibilidad para ciertas políticas públicas, en especial, las transferencias condicionadas. Esto implicaría una pérdida de ingresos por parte del hogar y podría modificar las decisiones de ocupación de las mujeres.
Por otro lado, el estudio no analiza las políticas necesarias para lograr el cierre de la brecha de género en el mercado laboral. Las experiencias de los países más exitosos muestran la necesidad de un papel activo del Estado (véase Cepal, 2014a, para una reseña del caso de Noruega). Se requiere tanto de políticas específicas en el mercado laboral como de políticas de cuidado para incidir conjuntamente en ambas brechas y hacerlo de forma sostenible. En este sentido, cuáles sean las políticas que se implementen determinará el camino hacia el cierre de las brechas, dado que diferentes mujeres (y hogares) serán sensibles a diferentes políticas, modificando los efectos en el bienestar social, pobreza y desigualdad.
También, debe discutirse si los escenarios de participación laboral presentados son deseables desde un punto de vista social. No es claro que un patrón de trabajo similar al de los hombres sea el objetivo a conseguir, en particular, si se pone en consideración que superan las 40 horas semanales de trabajo promedio, llegando a las 50 en Bolivia.
Los resultados indican que los efectos en pobreza son inequívocos y siempre positivos, mientras que los efectos del cierre de brechas de género en el mercado laboral en la desigualdad no pueden ser generalizados, dependerán del país y del escenario, puesto que se generan modificaciones en diferentes partes de la distribución del ingreso. En términos generales, se puede concluir que los efectos distributivos son mejores en la parte baja de la distribución y que Bolivia y Perú presentan mejores resultados al cerrar la brecha de ingresos respecto a los del cierre de la brecha de participación, mientras que se observa lo opuesto en Brasil y Uruguay. Esto se explica por la diferencia en las situaciones de partida de cada país, principalmente, por la dimensión de las brechas a lo largo de la distribución.