Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Accesos
Accesos
Links relacionados
 Citado por Google
Citado por Google -
 Similares en
SciELO
Similares en
SciELO  Similares en Google
Similares en Google
Compartir
Cuadernos de Administración
versión impresa ISSN 0120-3592
Cuad. Adm. v.18 n.29 Bogotá jun. 2005
y los modelos GARCH*
* Este artículo es resultado del proyecto de investigación: Cálculo del VaR mediante el filtro de Kalman, financiado por el DIME de la Universidad Nacional de Colombia, sede Medellín. Contrato No. 030802656, durante el período 2003-2004. El autor agradece al DIME por el apoyo prestado y a uno de los evaluadores por las sugerencias hechas. Este artículo se recibió el 28-02-2005 y se aprobó el 29-05-2005.
** Magíster en Matemáticas, Universidad Nacional de Colombia, 1989; Matemático, Universidad Nacional de Colombia, 1982. Profesor asociado a la Escuela de Estadística, Universidad Nacional de Colombia, Medellín, Colombia. Correo electrónico: ndgirald@unalmed.edu.co.
RESUMEN
En este trabajo se estudió el desempeño de un estimador del VaR de portafolios de acciones basado en el cálculo de los coeficientes beta de las acciones que lo conforman, conocido como el VaR factorial. Para ello se proyectaron tales betas recursivamente, por medio del filtro de Kalman y modelando el término, que depende de la volatilidad de los rendimientos del mercado, de acuerdo con modelos condicionalmente heterocedásticos del tipo GARCH, EGARCH y GJR. A partir de simulaciones basadas en un modelo de baja oscilación para las betas, se compararon (con la metodología media-varianza de RiskMetrics) los resultados de estos modelos con el VaR calculado y se introdujeron dos pruebas de hipótesis para realizar tal comparación. La conclusión es que tanto el estimador propuesto como el de RiskMetrics pronostican correctamente el número de casos en los cuales los rendimientos extremos negativos de un portafolio superan el margen del VaR. No obstante, el estimador propuesto calcula de forma más precisa que el método de RiskMetrics el valor mediante el cual se supera tal margen.
Palabras clave: CAPM, valor en riesgo, filtro de Kalman, betas, heterocedasticidad, GARCH.
ABSTRACT
This paper studies the performance of an estimator used to calculate VaR for a stock portfolio using stock Beta coefficients. Such coefficients are recursively projected using Kalman's filter and modelling the market-volatility restrained term according to conditionally heteroscedastic GARCH, EGARCH and GJR models. A low Beta oscillation model is used to carry out diverse simulations and the results are compared with RiskMetrics mean-variance. Two hypothesis tests were introduced. We conclude that the new estimator is as effective as the one used by RiskMetrics to foresee those cases in which extremely negative yields overflow the VaR margin. However, our estimator is a better predictor of the excess amount on VaR margin than the one used by RiskMetrics.
Key words: CAPM, value at risk, Kalman's filter, betas, heterocedasticity, GARCH.
La metodología difundida por RiskMetrics (1996) para la estimación del valor en riesgo (VaR) de un portafolio en el período [t, t+1], con un índice de confianza 100(1-a), se define por la expresión:
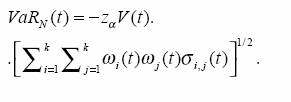
El VaR factorial es un método alterno, basado en las betas de las acciones que conforman el portafolio, y se define como:

De acuerdo con la ecuación anterior σ2m = Var(rm(t)) es la varianza del rendimiento del portafolio de mercado, asumida constante, al igual que las betas (Vilariño, 2001). Varios modelos para la estimación de las betas mediante el filtro de Kalman los ha desarrollado Wells (1994 y 1996), en una línea de trabajos que examina la validez de la hipótesis de estabilidad de las betas en el contexto de la teoría del Capital Asset Pricing Model (CAPM), mediante modelos econométricos con coeficientes variables.
El método de cálculo del VaR con el modelo factorial en que se incorporan betas variables y su proyección mediante el filtro de Kalman lo desarrollaron Berardi, Corradin y Sommacampagna (2003). Hurtado (2004) realizó un estudio con acciones de la Bolsa de Colombia, donde incorporó modelos tipo GARCH en la formula del estimador VaR factorial. Shah y Moonis (2003) utilizan una variante del filtro de Kalman con errores GARCH, propuesta por Harvey, Ruiz y Sentana (1992) para la estimación del VaR. Por su parte, Nelson y Kim (1999) tratan con profundidad esta variante.
El debate sobre si las betas de acciones son variables o no es extenso, aunque un resumen se puede encontrar en Brooks, Faff y McKenzie (1998), así como en los trabajos de Wells (1994 y 1996). Hurtado (2004) confirma la variabilidad de las betas del mercado colombiano aplicando diez pruebas estadísticas especiales. Debe tenerse en cuenta, sin embargo, que las betas son variables no observables, y esto dificulta justificar un método de cálculo particular y probar la hipótesis de variabilidad. Por lo tanto, todas las pruebas de esta autora se basan en mínimos cuadrados ordinarios, método sobre el cual también hay estudios cuyos resultados no siempre son satisfactorios.
En la bibliografía sobre cálculo de modelos de regresión con parámetros variables se han propuesto, al menos, cuatro modelos para el caso de las betas variables de la teoría CAPM: (1) con coeficientes aleatorios, (2) con régimen variable, (3) con parámetros que siguen un modelo markoviano (filtro de Kalman) y (4) con variación sistemática en los parámetros (véase Fabozzi y Francis, 1978). El tercer modelo asume un modelo autorregresivo de orden 1, AR(1) para las betas, que puede exhibir trayectorias muy oscilantes, a menos que exista una raíz unitaria; sin embargo, este caso no estacionario es poco realista.
A nuestro juicio, es más aceptable asumir que las betas fluctúan entre límites fijos durante plazos muy largos, pues cambios fuertes solamente se presentarían cuando el emisor se fusiona o se divide o cuando hay fuertes variaciones macroeconómicas. En este trabajo se propone un modelo estocástico con oscilaciones lentas, sin saltos, para las betas, compatible con un cálculo diario, aunque la frecuencia diaria no es común en la estimación de las betas.
Para este modelo estocástico se prefieren frecuencias mensuales o semanales, con períodos de, por lo menos, cinco años. Pero si se piensan aplicar las betas para calcular el VaR de un portafolio, necesariamente habría que utilizar frecuencias diarias o semanales -no es extraño pensar en proyecciones en tiempo real-. Las betas son estadísticas importantes en econometría financiera. Por ejemplo, se utilizan en la estimación de la cobertura para portafolios mediante futuros y opciones sobre índices bursátiles. Sin embargo, asumir que las betas varían en el tiempo, sugiere un problema de cálculo complejo, pues la estimación equivocada de las betas puede tener consecuencias graves. Gyshels (1998) presenta una discusión sobre los riesgos de asumir betas variables y realizar un cálculo erróneo, frente al supuesto de betas constantes.
El aporte de este trabajo consiste en definir un modelo con oscilaciones lentas para betas, que permite simular los rendimientos de las acciones de acuerdo con el modelo CAPM, incorporando efectos de heterocedasticidad y asimetría, o leverage, del mercado, mediante tres tipos de modelos para la varianza del rendimiento del índice del mercado, σ2m(t) = Var(rm(t)), GARCH, EGARCH y GJR.
Además, se propone un estimador del VaR, basado en la fórmula del VaR factorial, pero que calcula de manera recursiva las betas y proyecta la varianza del rendimiento del índice del mercado mediante cada uno de los tres modelos propuestos. De esta forma se conocen las betas a priori y se puede comprobar que el método produce cálculos y pronósticos (a un paso) bastante aceptables. Igualmente, se puede comparar el desempeño del método RiskMetrics con el método propuesto, sabiendo de antemano que los rendimientos de las acciones y del mercado tienen efectos heterocedásticos y de leverage.
Por lo tanto, se introduce una prueba de suma de rangos de Wilcoxon-Mann-Whitney para comparar el desempeño de los pronósticos del VaR. Los resultados muestran que el estimador sugerido captura mejor la volatilidad de los rendimientos del portafolio y produce valores menos sesgados de los extremos negativos que superan el VaR, que los que produce el VaR de RiskMetrics.
El artículo está organizado de la siguiente manera: en la sección 1 se establece la notación básica y los supuestos del modelo CAPM estándar. En la 2 se define el modelo de variables de estado y se introduce el estimador para este modelo (filtro de Kalman). En la sección 3 se desarrolla el modelo de variables de estado para el modelo CAPM. En la 4 se presenta el estimador propuesto. En la 5 se define el modelo de simulación utilizado, y en la 6 se presentan los resultados de los cálculos y las pruebas de hipótesis. Por último, se dan las conclusiones del estudio.
1. El Modelo CAPM
El modelo CAPM estándar es el marco teórico de este trabajo. Para su definición se introducen las siguientes variables. Se asumen n acciones transadas en la Bolsa. El precio de cierre de la j-ésima acción, al final del período [t-1,t], se denota por el proceso estocástico PJ(t) > 0, t = 1, 2,… El rendimiento logarítmico de la acción j-ésima en el período [t,t+1] se define como:
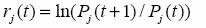
El portafolio de mercado consiste en el total de todas las n acciones. Su rendimiento está dado por:
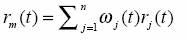
De acuerdo con la ecuación, wj(t) es el cociente entre el valor total de las unidades de la j-ésima acción y el valor total del portafolio de mercado en el tiempo t, y dado que no es un valor controlable, se asume que es aleatorio. La tasa sin riesgo de crédito del mercado, efectiva para el período [t,t+1], se indica por i(t), y la correspondiente tasa continua se expresa por r(t) = ln(1+i(t)). Asumimos que r(t) es un proceso estocástico con valores en (-∞, ∞). El CAPM establece que para la acción j-ésima, si se ajusta el modelo de regresión lineal, es:

Para t = 1, 2,…, donde las εj(t) son variables aleatorias normales independientes e idénticamente distribuidas, con E(εj(t)) = 0 y Var (εj(t)) = v2j Entonces se debe cumplir:
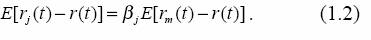
Es decir, no rechaza la hipótesis nula H0:aj = 0 . El coeficiente beta (ßj) establece la relación entre la prima de riesgo para el inversionista en la acción j-ésima y la prima de riesgo del mercado, entendidas ambas como la diferencia entre la rentabilidad esperada y la rentabilidad sin riesgo del mercado.
Estudios con datos de mercados de diferentes países han mostrado que los coeficientes beta, para acciones individuales o de portafolios, no son estables en el tiempo. Por ejemplo, Fabozzi y Francis (1978), Bos y Newbold (1984) y Brooks, Faff y McKenzie (1998). En este estudio se asume que las betas dependen de t, y escribimos ßj(t), y que los n betas del portafolio de mercado conforman un proceso aleatorio multivariado ß(t) = (ß 1(t),…, ß n(t)), t = 1, 2,… El modelo de la dinámica del vector ß(t), para portafolios de inversionistas, no para el del mercado, se define a partir del filtro de Kalman, el cual se describe a continuación.
2. Filtro de Kalman
El filtro de Kalman es un procedimiento para calcular y pronosticar, de manera recursiva, un proceso estocástico no observable, basándose en la información de otro proceso observable. En las definiciones que siguen, los vectores se asumen como vectores columna y una comilla sencilla indica el vector transpuesto. Suponga que los procesos n dimensionales:

Éstos son tales que E(ß2j(t)) < ∞ y E(y2j(t)) para j = 1, 2,…, n, i = 1, 2,…, n, t = 1, 2,…, y satisfacen el siguiente sistema de ecuaciones, denominado sistema de ecuaciones de estado:
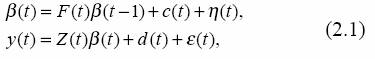
Donde F(t) y Z(t) son matrices cuadradas de dimensión n, conocidas para todo t, y c(t), d(t) son vectores i dimensionales, conocidos para todo t, al igual que el valor inicial b(t). Se asume que los vectores aleatorios n dimensionales h(t), e(t) forman una sucesión de variables normales multivariadas independientes, con:

En las ecuaciones R(t) y Q(t) son matrices nxn, definidas positivas, conocidas para todo t. Además, se asume, en primer lugar, que E(η(t)ε(s)') = 0, para todos t y s, y, en segundo lugar, que el proceso y(t) es observable pero el b(t) no. El objetivo es calcular b(t) basándose en la información disponible de y(t). Desde el supuesto de normalidad de los errores, en el modelo 2.1 se definen a continuación los estimadores de interés.
Definición 2.1. El valor calculado de b(t) se define como la esperanza condicional
b(t) = E(ß(t)| y(s), s = 1, 2,…, t). Por otra parte, el valor de pronóstico de ß(t) se define como la esperanza condicional
b(t | t-1) = E(ß(t)| y(s), s = 1, 2, …, t-1).
Además, se definen las matrices:
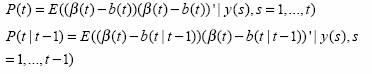
Tales matrices se interpretan como las matrices de varianzas y covarianzas de los errores de cálculo.
Definición 2.2. El filtro de Kalman consiste en un conjunto de ecuaciones que actualizan los valores de b(t), b(t|t-1), P(t) y P(t|t-1), t = 1, 2,…, basándose en los valores observados del proceso y(t), y a partir de los valores iniciales b(1|0) y P(1|0). Las ecuaciones son:

Tanto en Harvey (1989) como en Nelson y Kim (1999) se encuentran las definiciones y detalles sobre el filtro de Kalman.
Propiedades del filtro de Kalman. A fin de poder establecer conclusiones en el estudio, se requieren algunas propiedades del filtro:
• Bajo el supuesto de normalidad de ß(t), b(t) es el estimador de menor error cuadrático medio de ß(t). Entre tanto, P(t) es la matriz de varianzas covarianza del error ß(t)-b(t). Si no se cumple el supuesto de normalidad b(t), calculado con las ecuaciones 2.2, proporciona todavía un estimador que es el estimador lineal con menor error cuadrático medio entre todos los estimadores lineales de ß(t), basados en la información y(s), s = 1,…, t.
• Para que el filtro tenga un desempeño óptimo se requiere especificar los parámetros correctamente, es decir, las matrices R y Q deben estar cerca de los valores reales, al igual que las condiciones iniciales b(1|0) y P(1|0).
• Aquellas matrices R y Q con números condicionales muy altos pueden deteriorar los estimadores b(t), si y(t) presenta valores extremos.
• El filtro no es robusto. En la ecuación 2.2, b(t) depende linealmente de la nueva observación y(t). Existen versiones robustas del filtro de Kalman. Pero requieren una estimación a priori de la magnitud de las desviaciones de y(t) o de Z(t), para limitar el efecto de errores e incertidumbres en los estimadores.
• También se afectan los estimadores si las matrices F(t) y Z(t) presentan algún tipo de inestabilidad, por ejemplo, un número condicional alto.
• El filtro no requiere que los procesos involucrados sean estacionarios en covarianza, aunque es una propiedad deseable. Por ejemplo, la matriz F(t) puede tener algún valor propio fuera del círculo unitario. El filtro utiliza mínimos cuadrados en cada actualización de b(t), pero no minimiza una función de pérdida sobre toda la muestra. Por lo tanto, utilizar modelos no estacionarios no entra en conflicto con la estimación por mínimos cuadrados. Sobre este punto se puede consultar Sayed (2001).
A continuación se replantea el modelo CAPM como un sistema de ecuaciones de estado (2.1) para aplicar el filtro de Kalman (2.2) y obtener los estimadores de las betas.
3. Modelos para las betas
Tomamos como el proceso no observado el vector de los coeficientes betas del modelo 1.1, ß1(t),…, = (ßk(t)). El número k de acciones es menor que n (total de acciones del mercado). Como el proceso observado tomamos al vector y(t), de tal forma que su componente j-ésimo es:

Entonces, definimos la matriz Z(t) como la matriz diagonal,
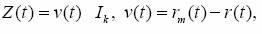
En la ecuación, Ik es la matriz identidad de dimensión kxk. El vector d(t) se toma como cero, y el vector c(t), constante. La definición de los errores η(t),ε(t) es igual a la dada en la sección 1, excepto que las matrices R(t) y Q(t) se toman constantes e iguales a R y Q, respectivamente. La matriz F(t) se toma diagonal y constante, F = Diag (ø1,…,øk). Así, cada ßj(t) se modela como un proceso autorregresivo de orden 1 [AR(1)]: ßj(t)=cj+øjßj(t-1)+ηj(t). Por lo tanto, el sistema de variables de estados (2.1) queda de la forma:

Los parámetros que se van a calcular antes de poner en uso el filtro de Kalman en el sistema 3.1 son: las matrices R y Q, el vector c y el vector ø=(øj,…,øk)'. Además, deben proporcionarse los valores iniciales b(1|0) y P(1|0). En la sección 5 se discute el problema de la implementación de estos valores y otros aspectos del cálculo con el filtro.
4. Cálculo del VaR
Consideremos nuevamente un portafolio de acciones, como en la sección 1. A diferencia del portafolio del mercado, éste contiene sólo k > 1 del total de acciones transadas en la Bolsa. Como en esa sección, el rendimiento de este portafolio está dado por:
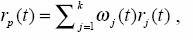
donde wj(t) es el cociente entre el valor total de las unidades de la j-ésima acción y el valor total del portafolio en el tiempo t. A diferencia del portafolio de mercado, las wj(t) se asumen ahora definidas al inicio de cada período [t,t+1] y, por lo tanto, no se consideran aleatorias. Además, se define el valor de este portafolio en t como:

donde Nj(t) > 0 es una sucesión no aleatoria que representa el número de unidades de la acción j-ésima. Se asume la posibilidad de cambiar Nj(t) al inicio de cada período [t,t+1] y que para todo t al menos una Nj(t) es positiva. Luego, ωj(t) = Nj(t)Pj(t) / V(t). El cambio porcentual de V(t) en el período [t,t+1] se puede aproximar con rendimiento en t. Es decir,
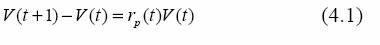
Supuesto 1. El supuesto utilizado en Risk Metrics para definir el VaR radica en que el vector r(t) = r1(t),…,rk(t)' se distribuye normal multivariado con media cero y matriz de varianzas covarianzas, dada por:
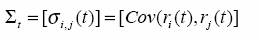
Esta ecuación se asume como definida positiva para todo t = 1, 2,… Luego, rp(t) se distribuye normal con media cero y varianza:

Si se reemplaza en la ecuación 4.1 el valor de rp(t) por el de un percentil suyo, asociado con una probabilidad muy baja ß, por ejemplo, 5%, el miembro de la derecha en 4.1 representaría una pérdida extrema en el portafolio, en el período [t,t+1], con una probabilidad a. Tal pérdida extrema define el VaR en t.
Definición 4.1. El VaR media-varianza del portafolio en el período [t,t+1], con un índice de confianza 100(1-α), basándose en el supuesto de normalidad multivariada del vector R(t), se define como:
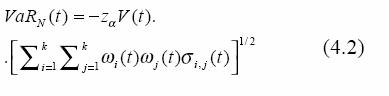
Su valor proyectado se obtiene reemplazando σi,j(t) en 4.2 por un estimador ởij(t), basándose en la información hasta t de los rendimientos. Es el estimador usual de una matriz de covarianzas -más detalles de este proceso se pueden encontrar Dowd (1998), capítulo 3-.
Definición 4.2. El VaR factorial, calculado en función de las betas del portafolio, con varianza heterocedástica, se define como:

Nótese que en el modelo CAPM de la ecuación 1.1 la varianza del error es Var(εj(t)9 = v2j. Al modelar con variables de estado, se introduce la matriz Q, tal que Qj,j = v2j. Además, σ2m(t) = Vart(rm(t)) es la varianza del rendimiento del portafolio de mercado, y rm(t) se modela con uno de tres modelos siguientes.
En las siguientes definiciones se utilizó la notación del Toolbox GARCH de Matlab (páginas 2-3 a 2-6). Sobre la teoría al respecto sugerimos remitirse a Frances y Van Dijk (1999), a Nelson (1991) y a Glosten, Jagannatham y Runkle (1993).
Primero: modelo r(t) = AR(r)-GARCH(p,q). Se define como el sistema de ecuaciones:

Para t = 1, 2,…, t, y donde a(t) es una sucesión iid, normal (0,1) o t-student con v ≥ 2 grados de libertad. Se requieren las siguientes restricciones: que r(t) sea estacionario en covarianza y que:
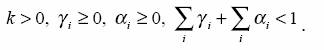
Segundo: modelo r(t) = AR(r)-EGARCH(p,q). En este caso se toman las expresiones para r(t) y e(t) en el sistema de ecuaciones 4.4, y la última se reemplaza por:
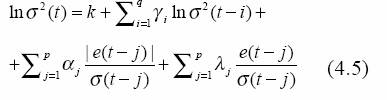
A diferencia de los otros dos modelos, el EGARCH no necesita restricciones sobre los parámetros, excepto que las raíces de la ecuación 1-y1z-…-yq zq = 0 sean en módulo mayores de 1, para garantizar que el proceso lnσ(t) sea estacionario en covarianza. Los parámetros αj son responsables de la asimetría.
Tercero: modelo r(t) = AR(r)-GJR(p,q). Como en el caso anterior, se toman las dos primeras expresiones del sistema de ecuaciones 4.4, y la última se reemplaza por:

En ésta I(A) = 1, si la condición A es cierta, y cero en otro caso. Las restricciones son:

La fórmula del VaR factorial (4.3) aparece en Vilariño (2001), con ωj, ßj y σ2M, independientes de t. Como se mencionó en la introducción, el aporte de este trabajo consiste en introducir modelos GARCH, EGARCH y GJR para la varianza de los rendimientos del mercado, después de extraer de éstos una componente autorregresiva de orden 1. Los dos últimos modelos capturan posibles efectos de asimetría o leverage del mercado. Esto es, se dice que un mercado, portafolio o acción presenta efectos de asimetría si al ajustar un modelo EGARCH, al menos uno de los parámetros aj es significativo, o si al ajustar un modelo GJR, al menos uno de los parámetros λj es significativo. En la sección 5 se definen el modelo de simulación y el procedimiento para implementar el filtro de Kalman.
5. Modelo de simulación
5.1 Definición del modelo para simulación
El objetivo de esta sección es definir un modelo para simular el sistema 3.1, es decir, el modelo CAPM con betas aleatorias. La dimensión de los vectores se toma como k = 8, ß(t),y(t)ε R8.
Por lo tanto, definimos la matriz Z(t) en la ecuación 3.1, tomando r(t) = 0, luego Z(t) = rm(t) I8, donde rm(t) es el rendimiento del portafolio de mercado. Entonces, se modela de acuerdo con uno de los tres modelos de la sección anterior. Las distribuciones de los errores en 3.1 toman normales multivariadas de la forma ε(t) ~ i.i.d N (0,Q), η(t) ~ i.i.d N (0,R), donde las matrices Q y R, 8x8, se toman como definidas positivas. El proceso ß(t)ε R8, t = 0,1,…, se define de forma que cada componente ßj(t) está descrito por un proceso gaussiano estacionario en covarianza, poco oscilante, de media cero y función de autocovarianza R(τ), dada por:

Es decir, la correlación entre ß(t) y ß(t-τ) está dada por R(τ). Para valores de t pequeños R(τ) se mantiene cercano a 1, siempre que α sea pequeño. Con ello se logra que el proceso oscile lentamente.1 Finalmente las betas se escalan para que su rango estén entre 0,1 y 1,3, que se asume en este estudio como un rango típico para betas de acciones.
Es preciso observar que no se está cumpliendo exactamente con el sistema 3.1, porque el proceso b(t) simulado como gaussiano no corresponde necesariamente a un modelo AR(1), markoviano, como en la primera ecuación del sistema 3.1. Sin embargo, esto es conveniente para examinar la capacidad del filtro de Kalman de estimar b(t) cuándo no se cumple el supuesto de proceso AR(1) para las betas. El Cuadro 1 muestra los parámetros utilizados para simular el modelo en cada uno de los tres casos.
Los parámetros del Cuadro 1 corresponden a los que se obtienen, en cada caso, mediante la estimación por máxima verosimilitud de la serie de rendimientos logarítmicos del índice IBOMED-IGBC diario para el período 01-02-2001 a 12-30-2003. El 7 de marzo de 2001 el IBOMED desaparece para dar lugar al IGBC. Aunque se trata de dos series, se tomó como una sola, para obtener valores realistas de los parámetros de simulación. El portafolio considerado, basándose en estas ocho acciones simuladas, se conformó según la teoría de Markovitz, en que se asume un rendimiento medio. No se profundiza esta parte, porque es una metodología bien conocida.

5.2 Justificación de este modelo
En el modelo simulado, las betas tienen trayectorias poco oscilatorias. Con ello se busca reproducir una dinámica que no varía significativamente en períodos cortos. La matriz Z(t) depende del valor simulado de rm(t); de un proceso AR(1) con varianza heterocedástica y asimetría (leverage), para proveer el efecto de valores extremos en los rendimientos de las acciones (no normalidad); así como de los efectos de asimetría y de agrupamiento (clúster) de datos extremos (períodos de inestabilidad en los precios de Bolsa). El Gráfico 1 muestra una trayectoria simulada de una de las betas (línea continua sin oscilaciones), contra el valor calculado mediante el filtro de Kalman —valor de b(t)—, para el caso en el cual rm(t) es un AR(1)-GJR(1,1).

5.3 Cálculo de los parámetros del filtro de Kalman
Los parámetros que se van a calcular son las matrices Q, R y F, y las condiciones iniciales b(1|0), P(1|0). Este punto es reconocido como particularmente difícil en la implementación del filtro de Kalman. Un método consiste en la aplicación del algoritmo EM en series de tiempo según Shumway y Stoffer (Shumway, 1988). Hurtado (2004) implementó este método para una versión univariada del CAPM, es decir, acción por acción.
En este trabajo se realizó un cálculo previo de las betas mediante un modelo de regresión dinámica o de coeficientes variables para la segunda ecuación de 3.1. Este método se diferencia del filtro en que no da pronósticos; solamente, valores estimados (Young, 2000). Con los residuos calculados multivariados se proyecta la matriz Q, y con las betas previas se ajusta un modelo AR(1) multivariado y se estima la matriz de transición F y la matriz de covarianza R. El método usual para proyectar betas mediante una regresión lineal sobre una ventana móvil (rolling regression) da proyecciones muy sesgadas de las betas simuladas desde el modelo propuesto.
5.4 Procedimientos para comparar el desempeño de los estimadores
Para comparar los estimadores propuestos (4.2 y 4.3) utilizamos dos pruebas de hipótesis: una que determina si el estimador es el adecuado y otra que compara dos distribuciones no normales.
5.4.1 Prueba de hipótesis para determinar si el estimador es adecuado
Para determinar si el estimador es adecuado, utilizamos una prueba de hipótesis clásica que compara una frecuencia empírica con una teórica. Por lo tanto, definimos la probabilidad:
De acuerdo con la ecuación, es el VaRα(t) estimado con uno de los dos métodos, para un índice de confianza 100(1-a)%, y la hipótesis, Ho = pa = α.. Para cada estimador del VaR se calcula, a la vez, el estimador de máxima verosimilitud de pa:
y un intervalo de confianza para Pα de 95%, IC = [p^1, p^2]. No se rechaza Ho, a un índice de significación de 5% si αε[p^1, p^2]. (Johnson, Kotz y Kemp, 1992, pp. 124-130). En caso de no rechazar H0, el estimador del VaR se considera adecuado, e inversamente. En la bibliografía acerca del VaR esta prueba se conoce como el test de Kupiec.
5.4.2 Prueba de hipótesis para comparar dos distribuciones no normales
En caso de que los estimadores presentados en las ecuaciones 4.2 y 4.3 resulten adecuados según la prueba anterior, proponemos utilizar la prueba de suma de rangos de Wilcoxon para compararlos. Por ende, definimos las variables condicionales no negativas:
X(t) y Y(t) son las diferencias entre el cociente VaR(t)/V(t) y el rendimiento extremo, en el caso de que tal rendimiento haya sido menor que este cociente, para los modelos 4.2 y 4.3, respectivamente. Estas variables son errores en la predicción del rendimiento extremo. Los valores de t se toman tal que cumpla, en cada caso:
La prueba de suma de rangos de Wilcoxon-Mann-Whitney se utiliza para decidir si los valores X(t) son mayores que los Y(t). Asumimos que las muestras son independientes. Las hipótesis son:
En caso de rechazar H0, con un índice de 5% se concluiría que los errores con el método propuesto del VaR factorial son menores que los del método del VaR media-varianza.
6. Resultados
Las pruebas de hipótesis anteriores se realizaron 100 veces, basándose en simulaciones de T = 500 datos, cada una. Los resultados de la prueba de hipótesis HoPα = α están en el Cuadro 2. Entre tanto, el Cuadro 3 muestra los resultados del criterio 5.4.2.


En la columna 3 del Cuadro 2, la sigla MV corresponde al modelo media-varianza de RiskMetrics, implementado en el estimador 4.2. De 100 repeticiones, el número de veces que no rechaza H0, utilizando el estimador propuesto, es mayor que la cantidad de veces en que se usa el de RiskMetrics, en los tres casos considerados. A partir de estos datos, consideramos que tanto el estimador 4.2 como el propuesto 4.3 presentan resultados satisfactorios. En conclusión, ambos son estimadores aceptables del VaR, en cuanto la proporción de eventos que sobrepasan el límite del VaR se calcula correctamente (5% en este caso).
Con la prueba de suma de rangos, los resultados fueron más concluyentes. Como mínimo, en 90% de los casos el estimador propuesto origina estimadores del VaR menos sesgados que los correspondientes al método de media-varianza. Este resultado corresponde a todo cuanto se puede apreciar en los gráficos 2, 3 y 4. El VaR media-varianza aparece graficado con la línea más gruesa. Como se utilizaron los primeros n = 50 datos para iniciar la matriz de covarianzas en este método, este intervalo aparece como cero en cada uno de los gráficos. El VaR con el método propuesto aparece indicado como una línea más fina y con una trayectoria más variable, que captura la volatilidad de los rendimientos del portafolio considerado.



Conclusiones
Para el estudio se definió un estimador del VaR de portafolios de acciones, que combina la definición de VaR factorial con la estimación de las betas mediante el filtro de Kalman y con la estimación de la volatilidad de los rendimientos del índice de bolsa. Además, se comparó su desempeño con el estimador estándar en la práctica financiera: la media-varianza, introducida por RiskMetrics.
Para realizar tal comparación se utilizaron simulaciones de los rendimientos de las acciones, las cuales se basan en un modelo estocástico para las betas, incorporado al modelo CAPM. Con esta estrategia se pudo comprobar que el filtro reproducía con exactitud las betas simuladas, algo que no puede hacerse en la práctica, debido a que éstas no son observables. Además, al simular el modelo CAPM, en que se incorporaban los efectos heterocedásticos y asimetría en los rendimientos del índice de la bolsa, se adicionó la no normalidad en los rendimientos de las acciones. Finalmente, con estos datos simulados, se ajustaron los mismos modelos para la volatilidad, se calculó el VaR factorial modificado (mencionado al comienzo) y se comparó con el VaR media-varianza.
Dos fueron los resultados obtenidos: primero, ambos estimadores cumplen con fijar un límite por debajo del cual solamente cae una fracción pequeña de los rendimientos del portafolio (5% para este trabajo). Segundo, el VaR propuesto calcula (pronostica) un VaR en que la diferencia es menor que cuando se usa el VaR de RiskMetrics (sobre todo en los casos donde el rendimiento del portafolio lo supera). Es decir, pronostica los peores casos con valores mucho más cercanos a lo que va a suceder. En este resultado reside la utilidad del método propuesto.
Notas al pié de página
1. Para ejemplos adicionales de funciones de autocovarianza, remitimos a Sveshnikov (1968), capítulo 7.
Lista de referencias
Berardi A., Corradin S, Sommacampagna C. Estimating value at risk with the Kalman filter. En IV Workshop in Finanza Quantitativa, 30-31 Gennaio, Torino, Italia. (2003). [ Links ]
Bos T, Newbold P. An empirical investigation of the possibility of stochastic systematic risk in the market model. Journal of Business (1984) 57 (1), 35-41. [ Links ]
Brooks RD, Faff R, McKenzie MD. Time-varying beta risk of australian industry portfolios: A comparision of modelling techniques. Australian Journal of Management (1998) 23 (1), 1-22. [ Links ]
Dowd K. Beyond value at risk. Chichester, England: John Wiley and Sons. (1998). [ Links ]
Fabozzi FJ, Francis JC. Beta as a random coefficient. Journal of Financial and Quantitative Analysis (1978) March, 111-116. [ Links ]
Frances H, Van Dijk D. Nonlinear time series models in empirical finance. Cambridge, UK: Cambridge University Press. (1999). [ Links ]
Ghysels E. On stable factor structures in the pricing of risk: Do time-varying betas help or hurt? The Journal of Finance (1998) 53 (2), 549-573. [ Links ]
Glosten LR, Jagannathan R, Runkle DE. On the relation between expected value and the volatility of the nominal excess return on stocks. The Journal of Finance (1993) 48, 1779-1801. [ Links ]
Harvey AC. Forecasting, structural time series models and the Kalman filter. New York: Cambridge University Press. (1989). [ Links ]
Ruiz E, Sentana E. Unobserved component timeseries models with arch disturbances. Journal of Econometrics (1992) 52 (1-2), 341-349. [ Links ]
Hurtado R, Sandra M. A methodology to calculate value at risk of stock portfolios using Kalman filter. Tesis de maestría no publicada, Universidad Nacional de Colombia, Medellín, Colombia. (2004). [ Links ]
Johnson NL, Kotz S, Kemp AW. Univariate discrete distributions. 2nd edition. New York: John Wiley and Sons. (1992). [ Links ]
Shah A, Moonis SA. Testing for time variation in beta in India. Journal of Emerging Markets Finance (2003) 2 (2), 163-180. [ Links ]
Nelson CR, Kim CJ. State-space models with regime switching: Classical and Gibbs-sampling approaches with applications. Cambridge, Mass: MIT Press. (1999). [ Links ]
Nelson DB. Conditional heteroskedasticity in asset returns: A new approach. Econométrica (1991) 59, 347-370. [ Links ]
RiskMetrics. Technical document. New York: Morgan Guaranty Trust Company. (1996). [ Links ]
Sayed AH. A framework for state-space estimation with uncertain models. IEEE Trans. on Autom. Control (2001) 46 (7), 998-1013. [ Links ]
Shumway RH. Applied statistical time series. Englewood Cliffts: Prentice Hall Internacional. (1988). [ Links ]
Sveshnikov AA. Problems in probability theory, mathematical statistics and theory of random functions. Philadelphia: W. B. Saunders. (1968). [ Links ]
Vilariño SA. Turbulencias financieras y riesgos de mercado. Madrid: Pearson Educación. (2001). [ Links ]
Young P. Stochastic, dynamic modelling and signal processing: Time variable and state dependent parameter estimation. En: W. J. Fitzgerald et al. (Ed.), Nonlinear and nonstationary signal processing. Cambridge, UK: Cambridge University Press. (2000). (pp. 74-114). [ Links ]
Wells C. Variable betas on the Stockholm exchange 1971-1989. Applied Economics (1994).4, 75-92. [ Links ]
The Kalman filter in finance. Dordrechts, The Netherlands: Kluwer Academic Publishers. (1996). [ Links ]


















