Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO  Similars in Google
Similars in Google
Share
Cuadernos de Administración
Print version ISSN 0120-3592
Cuad. Adm. vol.18 no.29 Bogotá June 2005
* Este documento hace parte de los resultados del proyecto de investigación Medición de la eficiencia del CAPM en el mercado bursátil colombiano: una prueba empírica con cuatro activos de riesgo, 2005-2006, financiado por la Pontificia Universidad Javeriana (Registro 1942) y realizado por el grupo de Investigación de Riesgos Financieros y Métodos de Valoración de Empresas (Risval). El artículo se recibió el 29-11-2004 y se aprobó el 24-05-2005.
** BS Economics and Finance, Syracuse University, 1995; MBA Mc Gill University, 2001. Profesor, Departamento de Administración, Facultad de Ciencias Económicas y Administrativas, Pontificia Universidad Javeriana. Correo electrónico: ecayon@javeriana.edu.co.
*** Especialista en Gerencia Financiera de la Pontificia Universidad Javeriana, 2001; administrador de empresas de la Pontificia Universidad Javeriana, 1998. Profesor, Departamento de Administración, Facultad de Ciencias Económicas y Administrativa, Pontificia Universidad Javeriana; coordinador académico, Especialización en Gerencia Financiera, FCEA Pontificia Universidad Javeriana. Correo electrónico: sarmien@javeriana.edu.co.
RESUMEN
En años recientes se ha generado gran interés alrededor de la importancia de la incertidumbre en la evaluación de proyectos de inversión. En este contexto, el análisis de opciones reales, mediante el uso de los supuestos teóricos de la fórmula Black-Scholes, se presenta como una propuesta para que el inversionista cuente con herramientas para la selección y evaluación de proyectos de inversión. El texto ilustra cómo esta fórmula, que inicialmente fue aplicada para valorar opciones financieras, ha mostrado resultados positivos en proyectos de inversión del sector real, así como en la creación de nuevos marcos metodológicos para tal fin. El objetivo principal del artículo es complementar la información que se obtiene de la metodología del sistema de cuadrantes de Luherman para el análisis de opciones reales. Esta información se obtiene aplicando la primera y segunda derivadas parciales de la fórmula Black-Scholes, conocidas como delta y gamma. Se demuestra que, cuando al analizar opciones reales se utilizan estas derivadas para evaluar los resultados de una metodología específica, se generan datos adicionales que complementan la información con que cuenta el inversionista para tomar decisiones frente a proyectos de inversión en el sector real. Finalmente, se plantea la necesidad de investigaciones ulteriores para análisis sectoriales sobre las implicaciones y la validez de la metodología propuesta para clasificar y categorizar proyectos de inversión real.
Palabras clave: finanzas, riesgo, decisiones de inversión, evaluación de proyectos, análisis de opciones reales.
ABSTRACT
Real Option Analysis (ROA) has become a very interesting method to evaluate real investment projects as it supports decision-making on project selection and timing. Black and Scholes' method was initially applied to financial options, but it has turned out an interesting method to evaluate real investment projects and it is a good tool for investors to make their decisions. This paper tries to complement the results obtained on the basis of Luherman's quadrant method for ROA. By applying the first and second partial derivatives from Black and Scholes —delta and gamma—, new information is produced that supplements the investor's information stock available to make a decision on real projects. It is shown that ROA derivative information can be used to evaluate specific results obtained from a given methodology; such data complement information already available for decision-making by real investors. Finally, further research is called to test validity and implications for sector analysis and real project classification.
Key words: Finance, risk, investment decisions, project evaluation, real option analysis.
La importancia que el análisis de opciones reales ha adquirido en la última década se debe a que la metodología más aceptada en la evaluación financiera de proyectos —el flujo de caja descontado basado en proyecciones a futuro— asume que éstas siguen un camino determinado que no incorpora los cambios que nos depara el futuro (Luehrman, 1998). Uno de los problemas que presenta el análisis de opciones reales, aparte de su carácter técnico, es que tiende a sobrevalorar los proyectos, lo que en la mente de muchos puede llevar a decisiones equivocadas sobre la viabilidad real de un proyecto, en contradicción con el enfoque tradicional del flujo de caja descontado (Copeland & Tufano, 2004).
Respecto a los problemas que presentan estas contradicciones, diversos estudios sobre el análisis de opciones reales se han enfocado en desarrollar herramientas metodológicas que ayuden al inversionista a sortear de una manera intuitiva los problemas que presenta la valoración de proyectos de inversión por medio de esta opción.1 Basándose en esto, el propósito del presente artículo es examinar, primero, cuál es el efecto que el uso de la primera y segunda derivadas del modelo Black-Scholes tienen dentro de una metodología comúnmente aceptada para el análisis de opciones reales y, segundo, cuál es el uso de la información adicional que proveen en el proceso de selección de proyectos de inversión.
1. Marco teórico
En su papel seminal de 1973, Fisher Black y Myron Scholes presentaron la prueba matemática para valorar opciones financieras de tipo call,2 con ayuda de un método de arbitraje;3 y aun cuando la prueba de la fórmula está fuera del alcance de este artículo,4 lo importante es la información que nos proveen los componentes de ésta en la evaluación de opciones financieras. La fórmula conocida como el modelo Black-Scholes es la siguiente:
C = precio de la opción call
S = al valor de la acción en el mercado
X = precio de ejercicio de la opción
r = tasa libre de riesgo
σ = volatilidad o desviación estándar que presenta la acción
N(d1) = probabilidad cumulativa de d1 o delta que denota la sensibilidad del precio de la opción a los cambios en el precio de la acción
N(d2) = probabilidad cumulativa de d2 o la probabilidad de que la opción se ejerza a su vencimiento
Basándose en lo anterior, no es difícil hacer el símil entre la fórmula financiera5 para adaptarla a un entorno real de evaluación de proyectos financieros6 (Lara Haro, 2002). En el Cuadro 1 se detalla la equivalencia de la fórmula para su uso en un entorno real:
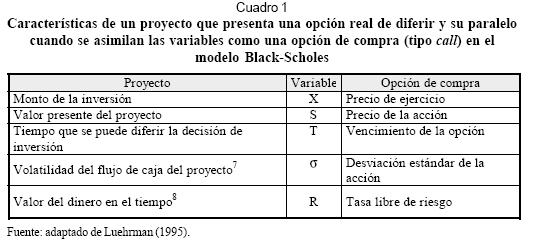
La importancia de ver el valor de las opciones dentro de un proyecto es inmensa: la metodología tradicional del flujo de caja descontado ve la decisión como un problema de ahora o nunca. Es decir, si el flujo de caja descontado (valor presente del proyecto o VP) es menor al monto de inversión requerido (I), esto nos da un VP negativo,9 y en los casos de que I>VP la decisión correcta sería rechazar el proyecto; si pasa lo contrario, se acepta y se procede (Luehrman, 1995). Este enfoque de tipo "ahora o nunca" puede llevarnos a descartar proyectos que en este momento no sean rentables, según la metodología del flujo de caja descontado; pero que dado que no toma el cambio de condiciones futuras en que dicho proyecto pueda volver a ser rentable —ya sea por costos, volatilidad de ingresos, etc.—, se puede estar obviando una oportunidad que, vista desde una óptica que incorpore la flexibilidad (ya que una inversión no se hace en un solo período, sino que puede ser diferida en el tiempo) o la volatilidad (que se ve reflejada en el precio de los bienes y servicios que produzca el proyecto), puede en determinado momento presentar una rentabilidad superior a la actual.
Por esto mismo, aunque un proyecto no ofrezca en este momento la rentabilidad deseada, valorarlo como una opción nos permite verificar, en términos cuantitativos, si la incertidumbre del entorno lo favorece, con lo cual se puede tomar un curso de acción estratégico que favorezca sus prospectos, sin la necesidad de inversiones adicionales, ya que como la opción financiera de compra, la real nos da el derecho, pero no la obligación de realizarla (Bowman & Moskowitz, 2001). Esto se ve claramente reflejado en el modelo Black-Scholes, adaptado para proyectos de inversión, ya que como mencionamos, éste nos permite incorporar la flexibilidad, que se refleja en el tiempo que podemos diferir la inversión, y en la volatilidad, que es un reflejo de la incertidumbre que nos depara el futuro. A continuación describimos cómo sin grandes complejidades matemáticas se puede evaluar el efecto de una opción real de compra en un proyecto de inversión.
2. Marco metodológico
Como lo mencionamos, para el propósito del presente artículo utilizamos la metodología sugerida por Timothy A. Luehrman10 del VPNq, que puede resumirse como una relación beneficio-costo entre los rendimientos del proyecto y el valor presente de la inversión requerida. La diferencia con la relación beneficio-costo tradicional radica en que el valor de la inversión se descuenta por el tiempo de vida de la opción. Para propósitos ilustrativos se puede considerar el ejemplo empleado por Luehrman, que se basa en un proyecto cuya inversión requiere 100 pesos, pero los flujos descontados a hoy son de 90 pesos, lo que nos daría un VPN de -10 pesos. Según la relación beneficio-costo tradicional, el resultado sería:
La lógica del beneficio-costo es bastante sencilla, ya que una razón ≥1 nos dice que el proyecto tiene un VPN positivo, por consiguiente, se acepta; si la razón es ≥1, el proyecto se rechaza, como sería dentro de un marco tradicional. Ahora suponga que el proyecto puede ejecutarse dentro de tres años y que la volatilidad anual de sus ingresos es de un 40% y que los recursos que se invertirían se pueden colocar a una tasa libre de riesgo que renta el 5% anual. Si insertamos todas estas variables en el modelo Black-Scholes, el resultado sería que nuestra opción de compra en este momento tiene un valor de 25,62 pesos, que es claramente superior al VPN de -10 pesos, por lo que vale la pena esperar tres años, pues aunque en este momento no tenga valor, hay una probabilidad muy grande de que tenga rendimientos positivos a futuro. Esto ocurre porque al incorporar el tiempo de espera en la valoración del proyecto, el valor de la inversión a futuro debe disminuir, pues estos recursos, al no ser invertidos en el proyecto, se invierten a la tasa libre de riesgo.11 Tomando en cuenta este hecho, utilicemos el VPNq como lo propone Luehrman:
Lo anterior es coherente con el resultado expresado por Black-Scholes acerca del precio de la opción real: nos dice que hay valor en postergar la decisión hasta que las condiciones mejoren y nos permite evaluar de una manera más sencilla el efecto del precio de la opción en el proyecto y su volatilidad, ya que, según la metodología planteada por Luehrman, se puede elaborar el siguiente marco para asistir al inversionista en la toma de decisiones (Cuadro 2)
Como se puede apreciar, el sistema de cuadrantes12 ayuda a identificar las opciones reales que en realidad pueden generar valor al proyecto y a descartar aquellas que, aunque demuestren algún valor, éste es insignificante con relación a los prospectos futuros del proyecto. Dentro de este marco metodológico deseamos resaltar la importancia de las derivadas parciales delta-gamma en la selección de opciones reales dentro del proyecto.
3. La sensibilidad a variaciones en el valor presente del proyecto delta y gamma
La delta13 de una opción de compra se determina por medio de la probabilidad acumulativa del precio del activo subyacente, y se resume en el modelo Black-Scholes de la siguiente manera:
Como se puede apreciar de la fórmula anterior, mientras mayor sea la volatilidad (s) del activo subyacente, mayor debe ser su valor delta. Por consiguiente, en el caso de una opción de compra, se muestra una relación directa con el precio del activo subyacente (S), que en opciones reales sería el VP, y como delta es N(d1) se demuestra que el valor esperado de S14 depende directamente de los cambios en delta.
La importancia de este hecho radica en que esto nos permite inferir cuál sería el efecto de cómo los cambios futuros en el VP influyen en el precio en la prima de la opción. En nuestro ejemplo anterior el valor de nuestra opción era de 25,62 pesos y la delta respectiva es de 60,50%, es decir, un cambio de 1 peso en el VP causaría un cambio positivo de 0,6050 pesos en la prima de nuestra opción de compra. Esto es de especial importancia, ya que las características de delta y su impacto en las primas de las opciones financieras son ampliamente conocidas (Martin, 2001). Por lo tanto, estas características pueden aplicarse perfectamente dentro del marco metodológico propuesto por Luehrman, de la manera que se detalla a continuación:
• Delta = 100%. El valor de la opción cambia de la misma manera que S o VP, y probablemente será ejercida.
• Delta = 50%. Un cambio en el precio de S o VP causa la mitad de cambio en el precio de la opción: hay un 50/50 de probabilidades que la opción se ejerza o que expire sin valor.
• Delta = 0%. La opción no presenta sensibilidad alguna a cambios de valor de S; por consiguiente, es muy poco probable que se ejerza.
Sin embargo, el problema de delta radica en que no es estable a través del tiempo; por consiguiente, no podemos basarnos sólo en este factor para determinar si ejercemos o descartamos la opción basados en una delta cercano a cero, ya que como la volatilidad cambia durante el tiempo de vida de la opción, tenemos que analizar la estabilidad de la delta con respecto al precio de S, que como podemos ver presenta un problema de circularidad, porque precisamos de uno para poder resolver el otro. Este problema se puede resolver por medio de gamma,15 que se define como:
Para nuestro ejemplo, la delta de nuestra opción era de 0,6050 y la gamma sería de 0,0097, lo que quiere decir que por 1 peso que suba el VP nuestra delta subiría a 0,6147. Esto causaría un cambio de 0,6147 pesos en el precio de la prima de la opción de compra por cada peso que aumente el VP. De igual manera, una gamma menor a 1% muestra una delta estable a cambios en el precio del activo subyacente, una gamma moderada (estabilidad moderada de delta) se considera en el rango de 1% a 10% y una gamma agresiva, que sólo ocurre cuando la opción se encuentra a punto de expirar (poca estabilidad de delta y sensibilidad extrema a cambios en el VP), estaría por encima de estos parámetros (Martin, 2001).
En este contexto, podemos modificar el sistema de cuadrantes desarrollado por Luerhman para incorporar delta gamma de la siguiente manera (Cuadro 3)
Adicionalmente, el uso de la primera y segunda derivadas presenta al administrador una herramienta adicional a la hora de tomar decisiones estratégicas para mejorar los prospectos, tal y como se señala en el cuadrante 3, de una manera que incorpora cuantitativamente el efecto tanto de la flexibilidad como de la volatilidad; además, para lograr que por medio de sus decisiones se emigre ya sea al cuadrante 2 o 1, y de esta manera generar valor mediante una estrategia basada en la prospectiva. A continuación, en el Gráfico 1 se detallan los diferentes valores de delta y gamma en relación con diferentes índices de volatilidad para nuestro ejemplo anterior:
Como se puede apreciar en el gráfico, nuestra opción muestra una serie de gamma estable (cercana a 1); por consiguiente, la volatilidad no tiene un efecto negativo en nuestra delta, lo que sitúa nuestra opción en el cuadrante 2. Esto conlleva a que probablemente nuestra opción se pueda ejercer al vencimiento si utilizamos administración proactiva para situarla en el cuadrante 1.
4. Conclusión
Por medio del presente artículo se demuestra que con el uso de la primera y segunda derivadas (delta y gamma) de la función del precio de la opción real con respecto al precio del subyacente se complementa la conocida relación mayor volatilidad-mayor valor de la opción, y de alguna manera permite evaluarla en más de un punto del tiempo.
La información que se obtiene por medio de este enfoque ayuda a complementar los marcos metodológicos existentes, y a su vez asisten al inversionista en el proceso de identificación y análisis de opciones reales. Esto se propone con el fin de asistir a los inversionistas en la toma estratégica de decisiones, para que tengan como punto de partida los prospectos futuros de la inversión en un entorno de incertidumbre. Por último, y como línea de investigación ulterior, se pueden hacer análisis sectoriales sobre las implicaciones y la validez de esta metodología para la clasificación y categorización de proyectos de inversión real.
Notas al pié de página
1. A efectos de presentar esta propuesta metodológica, nos basamos en la proposición de Timothy A. Luehrman, detallada en su artículo "Investment Opportunities as Real Options: Getting Started on the Numbers" (1998).
2. La fórmula aquí expuesta sirve para valorar opciones financieras de compra tipo europeo, que no generan pagos antes de la expiración de la opción. Una opción de compra sobre una acción da al tenedor el derecho, pero no la obligación de adquirir una acción en una fecha futura a un precio predeterminado hoy.
3. Para una explicación detallada del método de arbitraje para la valoración de opciones recomendamos el libro de Simon Benigna, Financial Modelling (2000).
4. Para una explicación detallada de la prueba de la fórmula recomendamos el libro de Prosper Lamothe Fernández y Miguel Pérez Somalo, Opciones financieras y productos estructurados (2003). Adicionalmente para una prueba de la convergencia de esta fórmula con el modelo binomial, recomendamos el libro de Tom Copeland y Vladimir Antikarov, Real Options: A Practitioner´s Guide (2001).
5. Cabe anotar que mediante el uso de la fórmula no se puede obtener un resultado exacto, ya que para que esto ocurra se deben cumplir los siguientes supuestos: (1) no existen impuestos, costos de transacción y restricciones para jugar a la baja; (2) el activo subyacente no genera dividendos y su rentabilidad histórica exhibe una distribución lognormal con varianza constante; (3) los mercados operan de manera continua, y (4) la tasa de interés es libre de riesgo y constante en el tiempo.
6. Dado que en un entorno de inversión real es imposible que se cumplan los supuestos necesarios para que la fórmula arroje una valoración exacta, su uso en la evaluación de proyectos de inversión real se limita simplemente al de proveer un marco analítico que, desde un punto de vista prospectivo, permite incorporar el efecto y el valor calculado que tiene la incertidumbre con respecto a los resultados futuros del proyecto.
7. Con respecto a cómo se calcula la volatilidad de los flujos, existen múltiples variantes en las que se puede utilizar una o diversas fuentes de volatilidad en los flujos proyectados (por ejemplo: volatilidad histórica de acciones o índices de empresas que pertenezcan al mismo sector de negocios que se está evaluando, materias primas, tasa de cambio, etc.).
8. Con respecto a cómo se puede calcular el valor del dinero en el tiempo y su efecto con relación en el monto de la inversión, existen múltiples variantes en las que se puede utilizar una o diversas fuentes para determinar la tasa (por ejemplo, costo de oportunidad de alternativas existentes, instrumentos de renta fija a plazo determinados, etc.).
9. El valor presente neto (VPN) es simplemente el remanente del valor presente del proyecto menos la inversión requerida (VPN = VP - I).
10. La primera discusión sobre esta metodología fue mencionada en un ensayo de discusión de clase titulado "Capital Projects as Real Options: An Introduction" (1995), que posteriormente fue formalizada en el artículo que se menciona en el pie de página 1.
11. Si recordamos, el modelo Black-Scholes descuenta el precio de ejercicio de la opción, o en el caso de las opciones reales la inversión a la tasa libre de riesgo compuesta. Esto se expresa como Xe-rt (en el caso específico de nuestro ejemplo 100e-3*0,05 = 86), si t = 0 se toma como criterio de decisión el VPN tradicional, que sería en la situación en que no se pueda diferir la decisión de inversión (Benninga, 2001).
12. Aunque en un artículo ulterior del mismo autor titulado "Strategy as a Portfolio of Real Options" (1998) se amplió el sistema de cuatro a seis cuadrantes, por razones de simplicidad en el análisis optamos por la versión del sistema de cuatro cuadrantes.
13. Desde el punto de vista matemático, delta es la primera derivada parcial de la prima (C) con respecto al activo subyacente (S) y se define como delta (d) = dC/ dS (Lamothe Fernández & Pérez Somalo, 2003).
14. Delta es la probabilidad de cambio de precio del activo subyacente, ya que, según Black-Scholes, S*N(d1) denota el valor esperado del activo subyacente durante la vida de la opción.
15. Desde el punto de vista matemático, gamma es la segunda derivada parcial de la primera (D) con respecto a S y se define como gamma = dD/dS. Adicionalmente, como es el caso específico de valorar la opción real como una opción de compra, gamma sería positiva, y si se valorará la opción real como una opción de venta, gamma sería negativa (Lamothe Fernández & Pérez Somalo, 2003).
Lista de referencias
Benninga S. Financial modelling. Boston: MIT Press. (2001). [ Links ]
Bowman EH, Moskowitz GT. Real option analysis and strategic decision making. Organization Science (2001) 12 (6), 772-777. [ Links ]
Copeland T, Antikarov V. Real options: A practitioner´s guide. New York: Texere. [ Links ]
Copeland T, Tufano P. A real world way to manage real options. Harvard Business Review (2004) March, 1-11. [ Links ]
Lara Haro A de. Medición y control de riesgos financieros, México: Limusa. (2002) [ Links ]
Lamothe Fernández P, Pérez Somalo M. Opciones financieras y productos estructurados. Madrid: McGraw Hill. (2003). [ Links ]
Luerhman TA. Capital projects as real options: An introduction. Harvard Business School (1995). Nota de clase 1-11, 9-295-074 [ Links ]
Strategy as a portafolio of real options. Harvard Business Review (1998) september-october, 89-99. [ Links ]
Investments opportunities as real options: Getting started on the numbers. Harvard Business Review (1998) july-august, 1-15. [ Links ]
Martin JS. Aplied math for derivatives. Singapore: John Wiley and Sons. (2001). [ Links ]




















