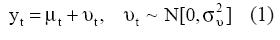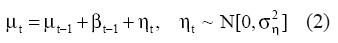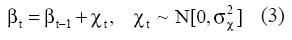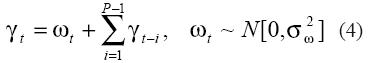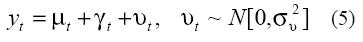Serviços Personalizados
Journal
Artigo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Acessos
Acessos
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares em
SciELO
Similares em
SciELO -
 Similares em Google
Similares em Google
Compartilhar
Cuadernos de Administración
versão impressa ISSN 0120-3592
Cuad. Adm. v.21 n.36 Bogotá jul./dez. 2008
* Artículo de investigación científica y tecnológica. Es producto de la investigación realizada por los grupos Mercados Energéticos e Inteligencia Computacional Aplicada en el modelado y la predicción de variables económicas en mercados de electricidad. Patrocinado por la Facultad de Minas, Universidad Nacional de Colombia, Medellín, Colombia. El artículo se recibió el 03-10-2007 y se aprobó el 18-03-2008.
** Doctor en Ingeniería, Área de Recursos Hidráulicos, Universidad Nacional de Colombia, Medellín, Colombia (2002); Magíster en Aprovechamiento de Recursos Hidráulicos, Universidad Nacional de Colombia (1996); profesor asistente, Escuela de Sistemas, Facultad de Minas, Universidad Nacional de Colombia. Miembro del grupo de investigación Mercados Energéticos, Facultad de Minas, Universidad Nacional de Colombia. Medellín, Colombia. Correo electrónico: cjfranco@unal.edu.co
*** Candidato a Doctor en Ingeniería, Área Sistemas Energéticos, Universidad Nacional de Colombia, Medellín, Colombia. Magíster en Ingeniería de Sistemas, Universidad Nacional de Colombia (1997); profesor asociado, Escuela de Sistemas, Facultad de Minas, Universidad Nacional de Colombia. Director del grupo de investigación Inteligencia Computacional Aplicada, Facultad de Minas, Universidad Nacional de Colombia. Medellín, Colombia. Correo electrónico: jdvelasq@unal.edu.co
**** Doctora en Economía de los Recursos Minerales, Colorado School of Mines, Colorado, USA (2006); Magíster en Ingeniería de Sistemas, Universidad Nacional de Colombia (1999); profesora asistente, Escuela de Sistemas, Facultad de Minas, Universidad Nacional de Colombia, Medellín, Colombia. Miembro del grupo de investigación Mercados Energéticos, Facultad de Minas, Universidad Nacional de Colombia. Medellín, Colombia. Correo electrónico: yolayam@unal.edu.co
RESUMEN
En este artículo se reportan los resultados de ajustar un modelo de componentes no observables a la demanda mensual de electricidad en Colombia entre 1995:8 y 2006:1 con el fin de separar la tendencia subyacente de la componente periódica asociada al ciclo anual y estudiar su comportamiento. Se encontró que la componente periódica tiene un comportamiento estocástico, pero cuya amplitud no crece con el aumento de nivel de la serie; así mismo, el modelo indica que el crecimiento mensual de la demanda posee una componente determínistica lineal, aproximadamente constante durante los últimos años, cuya fase de crecimiento y decrecimiento han coincidido con las del PIB.
Palabras clave: demanda, electricidad, modelos estructurales, series de tiempo.
ABSTRACT
This article reports the results seen from adjusting a model of non-observable components to the monthly electrical power demand in Colombia from 1995:8 to 2006:1 in order to separate the underlying tendency of the periodical component associated with the annual cycle and study its behavior. Findings show that the periodical component has a stochastic behavior but such behavior does not broaden with an increased level in the series; likewise, the model indicates that the monthly growth in demand has a linear deterministic component, approximately constant during recent years, whose rises and falls have coincided with the rises and falls seen in the GDP.
Key Words: demand, electrical power, structural models, time series.
Introducción
La importancia de la electricidad para el progreso económico y el avance tecnológico de una sociedad es indudable (Stoft, 2002) y no es sorpresivo que la energía sea considerada como la base para el progreso de la civilización. La electricidad es un producto final, un bien intermedio o un bien de consumo final; se usa en casi todos los sectores productivos y en algunos de ellos suele representar un costo importante. La atención oportuna de su demanda, asociada con una producción eficiente en términos económicos, ha motivado muchos de los procesos de desregulación y liberalización de sectores eléctricos en las últimas dos décadas (Steiner, 2000). En estos procesos, dicha atención ha deja-do de ser un monopolio natural del Estado (Stoft, 2002, cap. 1) para pasar a la generación, transmisión, distribución y comercialización de electricidad por parte de agentes privados en un ambiente de mercado. En este ambiente, el precio de la electricidad es una medida de los beneficios marginales de cada individuo y del costo marginal de la sociedad (Stoft, 2002).
Por su estrecha relación con todos los sectores económicos, el estudio de la evolución histórica de la demanda de electricidad per-mite establecer diferentes hitos económicos en el desarrollo de una sociedad. Los avances tecnológicos, como los encaminados al uso más eficiente y racional de la energía, cambian la demanda de electricidad, de tal forma que su tasa de crecimiento puede disminuir en función de la rapidez con que se produzcan dichos avances y la socialización que se haga de ellos. Un ejemplo son los programas gubernamentales, como los del uso eficiente de la energía eléctrica en el alumbrado público y en otros sectores, que buscan reducir la demanda para que, en el mediano plazo, se tenga una mayor cobertura de usuarios con la misma demanda; ello contribuye a reducir la tasa de crecimiento de los precios de la electricidad, con el consiguiente beneficio económico. Finalmente, en algunos mercados, la estacionalidad del clima tiene una influencia profunda sobre la demanda, ya que de acuerdo al tipo de estación climática se presentan diferentes patrones típicos de comportamiento.
La demanda de electricidad, junto con la oferta y la regulación, conforman las tres fuerzas fundamentales del mercado eléctrico, las cuales son influenciadas por un gran número de factores de comportamiento complejo que gobiernan su evolución. Dichos facto-res son propios de los mercados energéticos y se distinguen de otros tipos de mercados, como los financieros; esto hace que el precio de la electricidad, como un reflejo de la operación del mercado mismo, presente un comportamiento muy diferente al de otros bienes físicos o de productos financieros. En este sentido, y a diferencia de otros tipos de mercados, el patrón de demanda, sumado a las características particulares de cada sistema de generación y a las tecnologías que lo conforman, induce una estructura económica que puede llegar a ser particular de cada región o país, de tal forma que un diseño de mercado específico no puede ser implantado directamente en otro mercado diferente para el cual fue diseñado, sin tener en cuenta las condiciones particulares.
La modelación del consumo de electricidad ha permitido mejorar la comprensión del impacto de los factores que gobiernan la evolución del consumo en el tiempo y dicho conocimiento ha sido capitalizado en la construcción de modelos de predicción en el corto, mediano y largo plazo (Abdel-Aal y Al-Garni, 1997), en los que se consideran horizontes de hasta un mes, hasta un año y hasta treinta años respectivamente. Desde un punto de vista institucional, la predicción de corto plazo se utiliza para planificar la operación del sistema, mientras que la predicción de largo plazo se usa como un insumo en las decisiones de expansión en la capacidad de generación y del sistema de distribución (Al-Saba y El-Amin, 1999).
En la práctica, estos modelos formales para representar la evolución de la demanda de electricidad han resultado de mucha utilidad, ya que ayudan a los analistas a hacer sus supuestos explícitos y a contrastar las teorías con el mundo real. No obstante, la gran cantidad de simplificaciones en estos modelos y la incertidumbre inherente a los sistemas energéticos generan errores considerables en las proyecciones, las cuales deben ser revisadas constantemente. Más aún, con frecuencia los pronósticos publicados por agencias gubernamentales son documentos políticos que deben ser juzgados por su capacidad de soportar las políticas gubernamentales, más que por su precisión.
En el cuadro 1 se presentan varios estudios representativos del modelado y predicción del consumo de electricidad. Los métodos más usados para explicar el comportamiento de la demanda son: regresión multivariada, cointegración (Beenstock, Goldin y Nabot, 1999; Nasr, Badr y Joun, 2003), funciones de transferencia (Harris y Liu, 1993; Tserkezos, 1992) y modelos ARIMA (Barrientos et al., 2007; Murillo et al., 2003; Castaño, 2007); estos estudios han demostrado que la demanda depende en gran medida de la temperatura (Tserkezos, 1992; Mirasgedis, Sarafidis, Georgopoulou, Lalas, Moschovits, Karagiannis y Papakonstantinou, 2006; Harris y Liu, 1993; Abdel-Aal, Al-Garnib y Al-Nassar, 1997), el tamaño de la población (Egelioglu, Mohamad y Guven, 2001; Al-Saba y El-Amin, 1999), el crecimiento económico (ingreso per cápita o el producto interno bruto) (Tserkezos, 1992; Nasr, Badr y Dibeh, 2000; Medina y García, 2005) y el precio de la electricidad (Abdel-Aal y Al-Garni, 1997; Medina y García, 2005). La predicción es realizada para diferentes escalas de tiempo, dependiendo de las necesidades particulares del agente; así, se ha hecho para datos anuales (Ediger y Tatlidil, 2002; Egelioglu et al., 2001; Mohamed y Bodger, 2005), trimestrales (Tserkezos, 1992; Beenstock et al., 1999), mensuales (Benavente et al., 2005; Abdel-Aal et al., 1997; Chaveza et al., 1999; Harris y Liu, 1993; Mirasgedis et al., 2006; Saab, Badr y Nasr, 2001; Medina y García, 2005), diarios (Mirasgedis et al., 2006) e incluso para cada hora del día (Barrientos et al., 2007; Murillo et al., 2003; Castaño, 2007). Se sabe que para diferentes niveles de agregación temporal, una misma serie puede exhibir complejidades particulares que dificultan el desarrollo de un modelo; este es el caso general de las series de demanda que presentan fuertes patrones cíclicos de periodicidad anual, mensual, semanal, diaria y horaria, eventos atípicos como la presencia de días festivos, así como otras complejidades adicionales. Recientemente, Benavente, Galetovic, Sanhueza y Serra (2005) desarrollaron un método de paneles dinámicos con datos mensuales y procesos de ajuste no instantáneos y estimaron la elasticidad demanda residencial-precio. Así mismo, algunos estudios han demostrado que la respuesta de la demanda ante variaciones en sus determinantes puede ser no lineal.
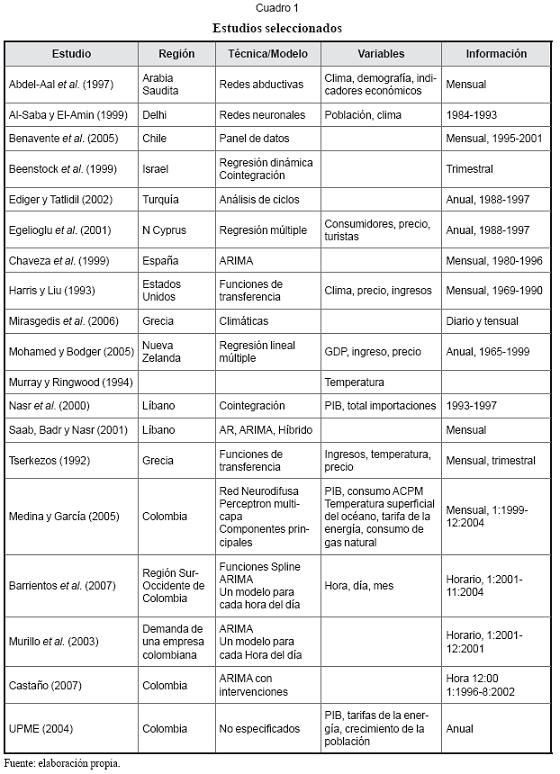
Para el caso colombiano, aunque se sabe que los diferentes agentes del mercado realizan pronósticos, en la literatura científica hay muy poca información relevante. En el cuadro 1 se presentan los estudios que fueron revisados durante esta investigación; en las referencias que aparecen en dichos artículos no se remite a otros estudios para el caso colombiano.
En las predicciones de la demanda en el mediano y en el largo plazo, basadas en modelos explicativos, los errores dependen de la precisión del pronóstico de los factores determinantes, especialmente de aquellos asociados con el crecimiento económico (O'Neill y Desai, 2005). Por esto, a la incertidumbre asociada con el modelo usado para proyectar la demanda, se le debe sumar la incertidumbre de la predicción de sus determinantes.
Estas falencias han motivado el estudio de técnicas univariadas para el modelado y predicción de las series de demanda, pues evitan la inclusión de variables explicativas y los correspondientes supuestos sobre su evolución. De esta forma, con los métodos univariados, las predicciones se hacen a partir de la dinámica propia de la demanda y pueden ser más precisas que las predicciones de los modelos explicativos (Abdel-Aal y Al-Garni, 1997). Una limitación de mucha técnicas univariadas es que los modelos obtenidos usan parámetros constantes en el tiempo, mientras que en la realidad ellos deberían cambiar para reflejar la evolución propia de los sistemas económicos. Sin embargo, no hay evidencias concluyentes de que alguna técnica de predicción sea superior a las otras (Nasr et al., 2003) y, desde un criterio puramente estadístico, aquellos modelos con menor error son de mayor interés (Chaveza, Bernata y Coallab, 1999).
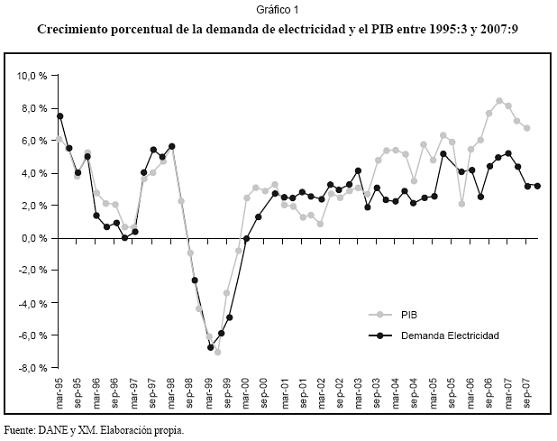
En el caso colombiano se ha encontrado que la demanda es dependiente del producto interno bruto (PIB), de las tarifas de energía y del crecimiento de la población (UPME, 2004). Medina y García (2005) postulan que la demanda también depende del consumo de ACPM y de gas natural así como de fenómenos climáticos extremos. En el gráfico 1 se presentan los crecimientos porcentuales de la demanda y del PIB entre 1995:3 y 2007:9; la inspección visual de dicho gráfico evidencia de manera contundente la relación entre am-bas series. Es importante llamar la atención sobre el decrecimiento de ambas series entre 1998:9 y 2000:9 que obedece a la recesión económica sufrida por el país durante ese período. Cada año la Unidad de Planeación Minero Energética (UPME) emite una reso-lución en la que muestra la proyección oficial de demanda es realizada por la UPME con una resolución anual usando modelos econométricos que relacionan dichas variables, considerando diferentes escenarios para la evolución del PIB y las pérdidas en el sistema de transmisión. Después, las demandas anuales proyectadas son desagregadas mes a mes usando modelos autorregresivos integrados de promedios móviles ARIMA y pronóstico condicional. Estas proyecciones son consideradas como señales del mercado que deben ser interpretadas por los diferentes agentes en sus procesos de toma de decisiones. Dichos modelos no están disponibles a los usuarios, hecho que impide que puedan construir sus propios escenarios de proyección de la demanda; en este sentido, la exploración de alternativas que permitan realizar esta tarea adquiere valor práctico y conceptual, pues brinda la posibilidad de entender mejor la evolución de la demanda de electricidad.
El objetivo principal de este artículo es presentar un modelo para caracterizar la demanda mensual de electricidad en Colombia basado en el desglose en componentes no observables (tendencia, estacionalidad y ruido), y reportar los análisis del comportamiento histórico de la demanda a través de dichos componentes. La ventaja de este tipo de modelos es que incluye un componente adaptativo sustentado en el uso del filtro de Kalman; esto permite que sus parámetros cambien en el tiempo a medida que nuevas observaciones se hacen disponibles; al mismo tiempo, brinda una poderosa capacidad de adaptación haciendo que el modelo recoja cambios puntuales evidenciados en los últimos datos conocidos y los incorpore para realizar los pronósticos de corto plazo.
Ya que el modelo desarrollado en esta investigación no incorpora de forma explícita el efecto de variables exógenas que tienen una fuerte influencia sobre la evolución de la demanda, su uso resulta inapropiado para construir proyecciones de mediano o largo plazo. En este sentido, es importante aclarar que el fin del modelo es el análisis del comportamiento histórico, esto es, su dinámica, más que desarrollar un modelo predictivo; aunque eventualmente podría ser utilizado para esta tarea.
La originalidad de la investigación propuesta está basada en los siguientes aspectos:
1. No se encontraron evidencias de otras investigaciones que abordaran el problema de caracterización de la demanda mensual para el caso colombiano, ni que usaran el modelo propuesto. Tampoco existen publicaciones sobre la calidad de las proyecciones oficiales realizadas por la UPME ni sobre la metodología utilizada por dicha entidad.
2. En las investigaciones de Barrientos et al. (2007), Murillo et al. (2003) y Castaño (2007) se trabaja con la serie de demanda horaria y no mensual, tal como se realiza en esta investigación.
3. Medina y García (2005) se concentran en la predicción de la serie de demanda mensual a partir de un conjunto de variables explicativas usando redes neuronales artificiales y redes neurodifusas; su aproximación reviste el problema de tener que conocer el valor de las variables explicativas para poder realizar la predicción de la demanda. En nuestra investigación, se parte de un modelo univariado cuya concepción metodológica es muy diferente del principio utilizado en las redes neuronales artificiales. Así mismo, en este estudio se parte de una serie de datos mucho más larga que la utilizada por Medina y García (2005), lo que permite un mejor análisis del problema.
En el numeral 1 se describe la información y metodología utilizadas, los resultados obtenidos se muestran en el numeral 2 y, por último, se presentan las principales conclusiones.
1. Información y metodología
1.1 Información utilizada
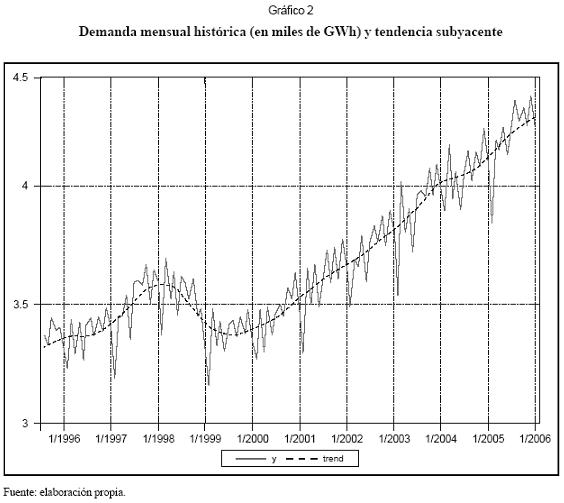
Los datos con los que se elaboró este estudio corresponden a la demanda total de electricidad del sistema interconectado colombiano, en miles de GWh mensuales, entre 1995:8 y 2007:1, que están disponibles en el sistema Neón, y que recogen las características históricas desde la creación de la Bolsa de Energía. La serie se caracteriza por poseer un componente estacional de periodicidad anual, propio de la mayoría de series económicas mensuales. El gráfico 2 presenta su comportamiento histórico.
1.2 Metodología empleada
Los modelos estructurales o de componentes no observables (Harvey, 1989) se basan en capturar las características explícitas más sobresalientes de la serie temporal estudiada, que corresponden a sus movimientos de largo plazo, y sus patrones cíclicos y repetitivos, los cuales son representados por la tendencia y el patrón estacional respectivamente. En estos modelos, dichos componentes pueden variar de manera estocástica en el tiempo, de tal forma que pueden adaptarse a los cambios que sufre la serie.
En el modelo de tendencia local lineal se asume que el comportamiento de la demanda, yt, está determinado por una tendencia estocástica, μt, y un componente irregular, υt, tal que su comportamiento puede ser descrito como:
La tendencia es perturbada en su nivel y en su pendiente, βt, de forma aleatoria, tal que:
donde la notación N[0,σ2] significa que las perturbaciones son independientes y están distribuidas de manera idéntica siguiendo una normal con media 0 y varianza σ2. Cuando las varianzas σ2 η y σ2 χ son 0, la tendencia es determinística y las observaciones oscilan alrededor de ella siguiendo una distribución normal con media 0 y varianza σ2 υ. Cuando σ2 χ = 0 y σ2 η > 0, la pendiente se hace constante y el modelo se reduce a un paseo aleatorio. En el caso contrario, cuando σ2 χ >0y σ2 η = 0 el modelo equivale a un paseo aleatorio integrado.
Cuando la serie estudiada presenta un componente periódico estacional, como en el caso de la demanda mensual de electricidad, este patrón de comportamiento se incorpora dentro del modelo a través de un conjunto de variables ficticias γp cuya suma sobre un período de doce meses es 0; el patrón estacional se puede hacer estocástico considerando que el componente actual γt es perturbado por un ruido aleatorio ωt, y su evolución puede ser descrita como:
así, la demanda actual se obtiene como:
El proceso de extracción de los componentes no observables μt, βt y γt se realiza a partir de la aplicación del filtro de Kalman basado en la información disponible en el momento t. La estimación de los hiperparámetos del modelo (σ2 υ ,σ2 η , σ2 ω y σ2 χ) se hace maximizando la función de verosimilitud de los residuales de la predicción un mes adelante. Los detalles son presentados por Harvey (1989).
2. Resultados obtenidos y discusión
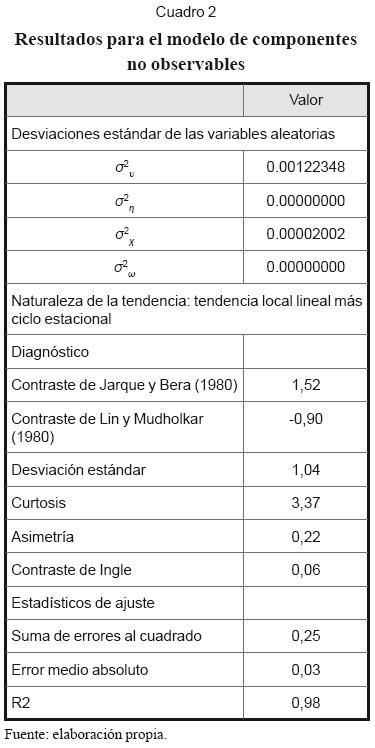
El modelo descrito fue estimado para la demanda mensual de electricidad entre 1995:8 y 2006:1 medida en miles de GWh-mes, el cual permitió obtener los componentes no observables relacionados con la tendencia subyacente, la pendiente, el patrón mensual y la componente irregular (gráfico 3). En general, el modelo se ajusta bien a los datos históricos, pasando una serie de pruebas de especificación. Los parámetros del modelo estimado y los resultados de las pruebas de diagnóstico realizadas son presentados en el cuadro 2. La tendencia estimada es estocástica, mientras que el patrón estacional es determinístico.
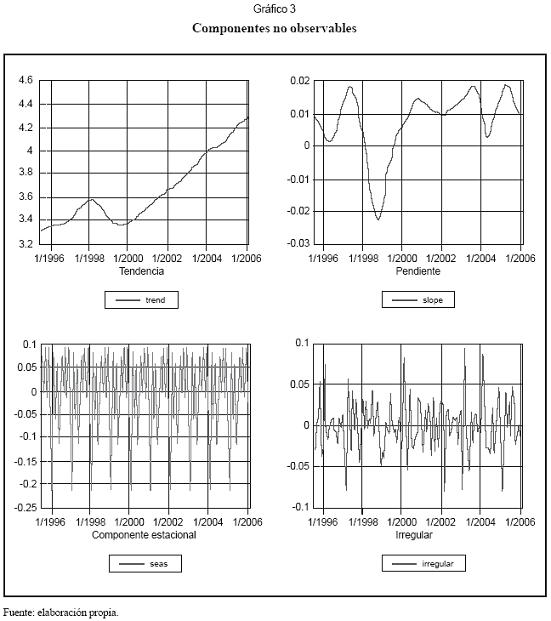
La tendencia subyacente estimada, que se obtiene eliminando el componente estacional, se presenta en el gráfico 3; su tendencia reciente indica que existe un crecimiento sostenido desde el año 2000 hasta ahora; también puede constatarse un crecimiento más acelerado durante 1997, y su posterior caída en 1998, siendo el primer semestre de 1999 una fase de transición hacia la tasa de crecimiento sostenido que se aprecia.
Al comparar la tendencia subyacente con el crecimiento porcentual del PIB y la demanda histórica se aprecia que el modelo detectó el cambio de signo de la pendiente desde el primer trimestre de 1998 anticipándose a la caída en el crecimiento de la demanda que se produjo después de 1998:3 (gráfico 1). Igualmente, la forma en que el modelo captura el efecto de la recuperación de una tasa positiva para el crecimiento de la demanda a partir del primer trimestre de 1999 es adecuada. Esta es una de las características más importantes del modelo, ya que permite extraer el componente de tendencia de largo plazo, una señal oculta en la serie, y hacer inferencias sobre su comportamiento a futuro.
La varianza σ2 η = 0 indica que las variaciones en el nivel subyacente de la serie se deben a los cambios en la pendiente de crecimiento y al componente irregular. La varianza σ2 ω = 0.0 señala que el patrón asociado al ci-clo anual es determinístico; ello implica que los cambios que se perciben mes a mes en la inspección visual son causa de los demás componentes. La varianza de la componente irregular, σ2 υ, es mucho mayor que la varianza de la pendiente, por lo que es responsable de la mayor parte del cambio de la demanda mensual.
El modelo obtenido puede ser usado para predecir la demanda de energía eléctrica sin necesidad de hacer suposiciones sobre el comportamiento futuro de variables causales que podrían explicar su comportamiento. Así mismo, la separación en componentes no observables permite que durante la fase de pronóstico el experto pueda intervenir las predicciones, al considerar por separado los cambios en la tendencia y el patrón estacional, con las consiguientes ventajas durante dicho proceso. El gráfico 4 presenta la predicción extrapolativa para los doce meses posteriores al último dato conocido de la serie. Se observa cómo el modelo muestra un comportamiento acorde con la muestra de datos.
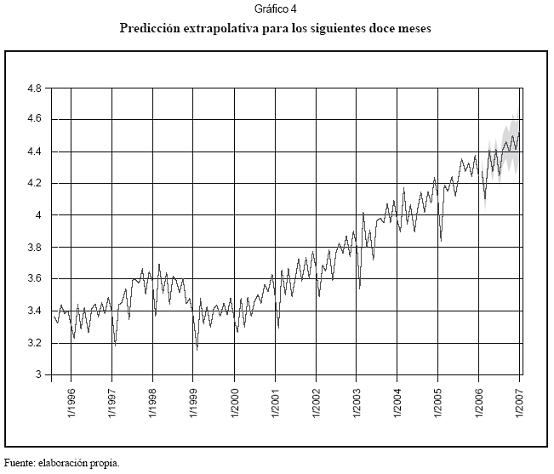
Las varianzas estimadas para los ruidos del modelo de componentes no observables muestran que la mayor fuente de variaciones es el ruido estocástico asociado a la ecuación de nivel (1); esto implica que, aunque existan errores en la predicción de la demanda para los meses siguientes, el componente subyacente (μt) se ve poco afectado y los pronósticos siguen siendo válidos. La evidencia de un error en la predicción no es tan fuerte como para que se revalúe la tasa de crecimiento mensual (βt) de la demanda.
Conclusiones
El análisis del comportamiento histórico de una serie se puede hacer con diferentes tipos de modelos, como losARIMA, estructurales, cointegración y técnicas no lineales. Pese a sus fortalezas, estos modelos no valoran la edad de la información dentro del proceso de estimación. Es decir, no consideran los cambios sutiles en la dinámica de la serie estudiada, razón por la cual resulta más difícil aislar el efecto de hechos puntuales que son de interés para el analista.
En este trabajo se estimaron los componentes no observables de la demanda de electricidad en Colombia; dada la importancia de este indicador dentro de la economía, se hace necesaria una comprensión adecuada de su comportamiento histórico. Para alcanzar este objetivo, se ha presentado un análisis de las características estructurales de la serie de de manda mensual de electricidad entre 1995:8 y 2006:1. Los resultados indican que hay una tendencia de crecimiento subyacente y constante durante los últimos años, y que el patrón estacionario asociado al año es estocástico.
El uso de esta aproximación ha permitido caracterizar el comportamiento mensual de la demanda durante distintas etapas de crecimiento económico que el país ha sufrido en la última década. Así, el modelo de componentes no observables que presentamos aísla el efecto de la recesión económica de finales de la década de los noventa en la demanda de electricidad.
Ya que el modelo desarrollado es univariado, pues no incluye el efecto de las variables exógenas que explican en parte el crecimiento de la demanda, su uso está limitado al análisis de la dinámica de la serie y a la construcción de pronósticos con un horizonte de unos meses adelante. Como trabajo futuro, es necesario reformular el modelo presentado para incorporar variables exógenas, como el PIB y el crecimiento de la población, analizar el comportamiento histórico a la luz de esta nueva información y determinar su capacidad de predicción basada en escenarios que recojan las expectativas que se tengan sobre la evolución de las variables exógenas incorporadas.
Agradecimientos
Los autores expresan sus agradecimientos a dos evaluadores anónimos, cuyos comentarios permitieron mejorar ampliamente la calidad del artículo.
Lista de referencias
1. Abdel-Aal, R. and Al-Garni, A. (1997). Forecasting monthly electric energy consumption in Eastern SaudiArabia using univariate time series analysis. Energy 22 (11), 1059-1069. [ Links ]
2. Abdel-Aal, R., Al-Garnib, A. and Al-Nassar, Y. (1997). ‘Modelling and forecasting monthly electric energy consumption in eastern Saudi Arabia using abductive networks', Energy, 22 (9), 911-921. [ Links ]
3. Al-Saba, T. and El-Amin, I. (1999). ‘Artificial neural networks as applied to long-term demand forecasting', Artificial Intelligence in Engineering, 13 (2), 189-197. [ Links ]
4. Beenstock, M., Goldin, E. and Nabot, D. (1999). ‘The demand for electricity in Israel', Energy Economics, 21 (2), 168-183. [ Links ]
5. Benavente, J., Galetovic, A., Sanhueza, R. y Serra, P. (2005). ‘Estimando la demanda residencial por electricidad en chile: El consumo es sensible al precio', Cuadernos de Economía, 42, 31-61. [ Links ]
6. Barrientos, A.F, Olaya, J., y González, V.M. (2007). ‘Un modelo spline para el pronóstico de la demanda de energía eléctrica', Revista Colombiana de Estadística, 30 (2), 187-202. [ Links ]
7. Castaño, E. (2008). ‘Reconstrucción de datos de series de tiempo: una aplicación a la demanda horaria de electricidad', Revista Colombiana de Estadística, 30 (2), 247-263. [ Links ]
8. Chaveza, S. G., Bernata, J. X. and Coallab, H. L. (1999). ‘Forecasting of energy production and consumption in Asturias (northern Spain ', Energy, 24 (3), 183-198. [ Links ]
9. Ediger, V. and Tatlidil, H. (2002). ‘Forecasting the primary energy demand in turkey and analysis of cyclic patterns', Energy Conversion and Management, 43 (4), 473-487. [ Links ]
10. Egelioglu, F., Mohamad, A. and Guven, H. (2001). ‘Economic variables and electricity consumption in northern cyprus', Energy, 26 (4), 355-362. [ Links ]
11. Harris, J. and Liu, L. M. (1993). ‘Dynamic structural analysis and forecasting of residential electricity consumption', International Journal of Forecasting, 9 (4), 437-455. [ Links ]
12. Harvey, A. (1989). Forecasting, structural time series models and the Kalman filter. Cambridge: University Press. [ Links ]
13. Medina, S. y García, J. (2005). ‘Predicción de demanda de energía en Colombia mediante un sistema de inferencia difuso neuronal', Revista Energética, 33, 15-24. [ Links ]
14. Mirasgedis, S., Sarafidis, Y., Georgopoulou, E., Lalas, D., Moschovits, M., Karagiannis, F. and Papakonstantinou, D. (2006). ‘Models for mid-term electricity demand forecasting incorporating weather influences', Energy, 31 (2-3), 208-227. [ Links ]
15. Mohamed, Z. and Bodger, P. (2005), ‘Forecasting electricity consumption in New Zealand using economic and demographic variables', Energy, 30 (10), 1833-1843. [ Links ]
16. Murillo, J., Trejos, A. y Carvajal, P. (2003). ‘Estudio del pronóstico de la demanda de energía eléctrica utilizando modelos de series de tiempo', Scientia et Technica, 23, 37-42. [ Links ]
17. Murray, F. and Ringwood, J. (1994). ‘Improvement of electricity consumption forecasts using temperature inputs', Simulation Practice and Theory, 2 (2), 121-139. [ Links ]
18. Nasr, G., Badr, E. and Dibeh, G. (2000). ‘Econometric modeling of electricity consumption in post-war Lebanon', Energy Economics, 22 (6), 627-640. [ Links ]
19. Nasr, G., Badr, E. and Joun, C. (2003). ‘Backpropagation neural networks for modeling gasoline consumption', Energy Conversion and Management, 44, 893-905. [ Links ]
20. O'Neill, B. and Desai, M. (2005), ‘Accuracy of past projections of us energy consumption', Energy Policy, 33(8), 979-993. [ Links ]
21. Saab, S., Badr, E. and Nasr, G. (2001), ‘Univariate modeling and forecasting of energy consumption: the case of electricity in Lebanon', Energy, 26(1), 1-14. [ Links ]
22. Steiner, F. (2000), ‘Regulation, industry structure and performance in the electricity supply industry', OECD Economic Studies, (32). [ Links ]
23. Stoft, S. (2002). Power System Economics, Wiley-Interscience. [ Links ]
24. Tserkezos, E. (1992). ‘Forecasting residential electricity consumption in Greece using monthly and quarterly data', Energy Economics 14 (3), 226-232. [ Links ]
25. UPME (2004). Plan de Expansión Preliminar 20042018, UPME. [ Links ]