Serviços Personalizados
Journal
Artigo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Acessos
Acessos
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares em
SciELO
Similares em
SciELO -
 Similares em Google
Similares em Google
Compartilhar
Cuadernos de Administración
versão impressa ISSN 0120-3592
Cuad. Adm. v.22 n.38 Bogotá jan./jun. 2009
* El artículo es producto de la investigación realizada por los grupos de Mercados Energéticos y Computación Aplicada en el modelado y la predicción de variables económicas en mercados de energía. Patrocinado por la Facultad de Minas, Universidad Nacional de Colombia, Medellín, Colombia. El artículo se recibió el 09-10-2007 y se aprobó 30-05-2009.
** Doctor en Ingeniería, Área de Sistemas Energéticos, Universidad Nacional de Colombia, sede Medellín, Colombia, 2009; Magíster en Ingeniería de Sistemas, Universidad Nacional de Colombia, 1997; Ingeniero civil, Universidad Nacional de Colombia, 1994. Profesor asociado, Escuela de Sistemas, Facultad de Minas, Universidad Nacional de Colombia. Director del grupo de investigación Computación Aplicada; miembro del grupo de investigación Mercados Energéticos, Facultad de Minas, Universidad Nacional de Colombia. Medellín, Colombia. Correo electrónico: jdvelasq@unal.edu.co.
*** Doctora en Economía de los Recursos Minerales, Colorado School of Mines, Colorado, Estados Unidos, 2006; Magíster en Ingeniería de Sistemas, Universidad Nacional de Colombia, sede Medellín, Colombia, 1999; Ingeniera de petróleos, Universidad Nacional de Colombia, 1997. Profesora asociada, Escuela de Sistemas, Facultad de Minas, Universidad Nacional de Colombia. Directora del grupo de Mercados Energéticos. Miembro del grupo de Computación Aplicada, Facultad de Minas, Universidad Nacional de Colombia. Medellín, Colombia. Correo electrónico: yolayam@unal.edu.co.
**** Doctor en Ingeniería, Área de Sistemas Energéticos, Universidad Nacional de Colombia, sede Medellín, Colombia, 2002; Magíster en Aprovechamiento de Recursos Hidráulicos, Universidad Nacional de Colombia, 1996; Ingeniero civil, Universidad nacional de Colombia, 1995. Profesor asociado, Escuela de Sistemas, Facultad de Minas, Universidad Nacional de Colombia. Miembro de los grupos de investigación Mercados Energéticos y de Computación Aplicada, Facultad de Minas, Universidad Nacional de Colombia. Medellín, Colombia. Correo electrónico: cjfranco@unal.edu.co.
RESUMEN
El comportamiento del precio del petróleo del West Texas Intermediate (WTI) es complejo y se caracteriza por subidas, bajadas, saltos y tendencias locales. Como resultado, es difícil identificar el impacto de hechos exógenos al mercado en el comportamiento de los precios, y como estos impactos no se pueden aislar fácilmente, la dinámica de la serie se oscurece y dificulta su predicción. La inspección preliminar del gráfico de la serie del logaritmo natural del precio promedio mensual del WTI entre 1986:1 y 2008:8 hace sospechar la presencia de tendencias locales lineales que evidencian cambios en la dinámica. Para validar esta apreciación se desarrolló un algoritmo de búsqueda basado en un particionamiento recursivo para detectar los puntos de ocurrencia de cambios estructurales en la tendencia. Este algoritmo se usó para analizar la dinámica de la serie estudiada. Los principales resultados son: los retornos de los precios siguen un proceso AR(1)-GARCH(2,2) y hay tres cambios estructurales estadísticamente significativos, los cuales son explicados por eventos históricos específicos. Estos cambios de nivel prueban la existencia de tendencias locales lineales en el logaritmo de los precios.
Palabras clave: precio del petróleo, cambios estructurales, GARCH.
ABSTRACT
The comportment of the price of WTI oil is complex, and it is characterised by rises, falls, abrupt changes and local trends. As a result, it is difficult to identify the impact of exogenous events on the market in the comportment of prices, and as these impacts cannot be easily isolated, the dynamics of the series become obscure and difficult to predict. In preliminary inspection of the natural logarithm series of the average monthly price of WTI between 1986:1 and 2008:8 gives rise to suspicion of the presence of local linear trends which ended in evident changes in dynamics. In order to validate this appreciation, an algorithm was developed for research based on a recursive partitioning to detect points of occurrence of structural changes in the trend. The algorithm was used to analyse the dynamics of the series studied. The principal results: returns of prices followed a process AR (1)-GARCH (2, 2), and there are three statistically significant structural changes, which are explained by its specific historic events. These changes of level show the existence of local linear trends in the prices logarithm.
Keywords: Oil price, structural change, GARCH.
RESUMO
O comportamento do preço do petróleo do West Texas Intermediate (WTI) é complexo e se caracteriza por subidas, baixas, saltos e tendências locais. Como resultado, é difícil identificar o impacto de fatores exógenos ao mercado no comportamento dos preços, e como estes impactos não podem ser isolados facilmente, a dinâmica da série se escurece e dificulta sua predição.A inspeção preliminar do gráfico da série do logaritmo natural do preço médio mensal do WTI entre 1986:1 e 2008:8 faz suspeitar a presença de tendências locais lineares que evidenciam mudanças na dinâmica. Para validar esta apreciação desenvolveu-se um algoritmo de busca baseado em um particionamento recursivo para detectar os pontos de ocorrência de mudanças estruturais na tendência. Este algoritmo utilizou-se para analisar a dinâmica da série estudada. Os principais resultados são: os retornos dos preços seguem um processo AR(1)-GARCH(2,2) e há três mudanças estruturais estatisticamente significativas, as quais são explicadas por eventos históricos específicos. Estas mudanças de nível provam a existência de tendências locais lineares no logaritmo dos preços.
Palavras chave: preço do petróleo, mudanças estruturais, GARCH.
Introducción
El estudio de la dinámica de los precios del petróleo está claramente justificado por su rol fundamental en la economía regional y mundial (Álvarez-Ramírez, Álvarez y Rodríguez, 2008), porque es una fuente primaria de energía de la cual depende la sociedad. Se han realizando muchas investigaciones para mejorar la comprensión de la dinámica subyacente de los precios del petróleo, así como para desarrollar metodologías que permitan aplicar este conocimiento a actividades como la valoración de derivados, la formulación de estrategias de cubrimiento de riesgos, la formulación de políticas, la predicción de corto plazo (Askari y Krichene, 2008) y la selección de fuentes alternativas de energía (Gori, Ludovisi y Cerritelli, 2007). Más aún, desde la crisis de los años setenta, se ha analizado el impacto que tienen los cambios en los precios del petróleo en las actividades macroeconómicas en diversos países (Park y Ratti, 2008; Ferderer, 1996; Lee, Ni y Ratti, 1995; Yang, Hwang y Huang, 2002; Chen y Chen, 2007) y, más recientemente, su efecto en el mercado accionario (Yu, Wang y Lai, 2008; Huang, Masulis y Stoll, 1996; Sadorsky, 1999 y 2003). Por ejemplo, Narayan y Narayan (2007) han encontrado indicios de que los altos precios del crudo contribuyen a la inflación y a las recesiones económicas en los países consumidores.
El comportamiento del precio del petróleo es complejo y se caracteriza por la presencia errática de alzas, caídas, saltos y tendencias locales que dificultan la comprensión de su dinámica, y que pueden explicarse mediante diversas teorías económicas (Fan, Liang y Wei, 2008). De acuerdo con la teoría microeconómica, los precios de los commodities regresan en el largo plazo a un nivel normal basado en su costo marginal de producción. En el caso de los recursos agotables, como el petróleo, este costo marginal de producción es total e incluye las rentas por agotamiento (Pindyck, 1999).
El análisis económico fundamental muestra que la complejidad de la evolución de los precios del petróleo en el mundo puede explicarse a través de las relaciones dinámicas y cambiantes entre los países productores, las compañías petroleras, las refinerías individuales, los países importadores y los especuladores (Yu et al., 2008); al igual que por la presencia de eventos económicos, sociales, políticos (Álvarez-Ramírez et al., 2008) y naturales, como los desastres causados por los huracanes Dennis, Katrina y Rita. Así mismo, los precios del petróleo dependen de los niveles de inventarios y cambios en las reservas, la capacidad de producción y refinación y los avances tecnológicos en todos los pasos de la cadena de producción.
La dinámica de los precios del petróleo crudo también se ha analizado usando técnicas estadísticas, ya sea para establecer su tendencia en el tiempo (Álvarez-Ramírez et al., 2008) y realizar pronósticos o para modelar o pronosticar su volatilidad. Respecto a su tendencia en el tiempo, Perron (1989) y Serletis (1992) analizaron los rendimientos de los precios del petróleo crudo con el fin de demostrar si siguen un proceso estacionario o no estacionario. Postali y Picchetti (2006) argumentan que el movimiento browniano geométrico podría ser un buen aproxima-dor de los movimientos del precio, mientras que Panas y Ninni (2000) y Adrangi, Argun, Dhanda y Raffiee (2001) sugieren que los precios siguen un proceso caótico y que existen ineficiencias en el mercado que podrían explotarse con fines económicos.
Gori et al. (2007) construyen escenarios de pronóstico usando diversas metodologías, como la teoría del caos y la lógica difusa. Bernabe, Martina, Álvarez-Ramírez e Ibarra-Valdez (2004) sugieren que existen dos estados competitivos de equilibrio para los precios diarios que pueden modelarse usando un proceso gaussiano de reversión en la media. Este resultado concuerda con los hallazgos analizados por Pindyck (1999), que muestran que los precios de la energía no siguen un paseo aleatorio, sino que siguen un proceso estocástico multivariado, donde la pendiente y el nivel fluctúan en el tiempo.
La importancia del modelado y la predicción de la volatilidad de los precios del petróleo radica en la exposición al riesgo que sufren los productores y los consumidores industriales, lo cual afecta, consecuentemente, las inversiones (Narayan y Narayan, 2007; Pindyck, 2004a) y los costos marginales totales de producción (Pindyck, 2004b). Se ha demostrado ampliamente que la volatilidad de los precios del petróleo, en particular (Regnier, 2007), y de otros energéticos (Pilipovic, 1998), en general, supera ampliamente a muchos commodities.
Narayan y Narayan (2007) han postulado que los precios tienden a cambiar en períodos cortos, basándose en los hallazgos de asimetría y persistencia de choques (shocks) obtenidos al analizar los precios diarios del petróleo crudo. La volatilidad se ha moldeado usando modelos ARIMA-GARCH (Abosedra y Laopodis, 1997; Sadorsky, 2002 y 2006; Morana, 2001; Moshiri y Foroutan, 2006) y ARIMA-EGARCH (Narayan y Narayan, 2007).
Aunque se han realizado importantes esfuerzos para modelar y pronosticar tanto la tendencia como la volatilidad de los precios, el problema está lejos de resolverse de una forma completa y satisfactoria. Si bien muchos de los modelos que se han presentado en la literatura más relevante capturan las principales causas de la variación en el precio del petróleo, no son buenos predictores porque excluyen determinantes del precio que no se observan tan fácilmente, como los factores geopolíticos o las expectativas del mercado.
Por otra parte, la dificultad de predecir la evolución de las variables independientes, como el nivel de inventarios o la capacidad de producción, afecta también la calidad de los pronósticos.
En este contexto, es adecuado y necesario elaborar modelos de predicción que capturen las principales propiedades de la serie histórica de precios a partir de los datos mismos, sin que sea necesario incorporar otras variables explicativas, las cuales deberían ser, a su vez, pronosticadas para construir predicciones de los precios. Sin embargo, un requisito es analizar de forma meticulosa la dinámica de los precios, con el fin establecer sus propiedades, la influencia de las variables que gobiernan su evolución y los principales eventos y hechos atípicos que podrían afectar su dinámica, al introducir cambios estructurales que afectan tanto los modelos desarrollados como las conclusiones que pueden obtenerse del comportamiento de los precios del petróleo. Así, uno de los objetivos de este artículo es verificar si existen dichos cambios estructurales en la dinámica de los precios.
En términos generales, la inspección visual de la evolución en el tiempo del precio del petróleo parece revelar características muy interesantes. Resulta especialmente notoria la existencia de regiones donde los precios presentan una clara tendencia al alza, a la baja o a fluctuar alrededor de un valor fijo. Se dice que en dichas regiones se da la presencia de una tendencia local, la cual es un fenómeno bien conocido en la literatura relacionada con el análisis de series de tiempo. No obstante, los métodos estadísticos tradicionales para la detección de cambios estructurales (cambios de pendiente en esta investigación) no resultan adecuados, ya que los precios del petróleo exhiben una volatilidad cambiante en el tiempo, que debe incorporarse dentro del algoritmo cuando se busca la ocurrencia de un cambio en la pendiente. Consecuentemente, otro objetivo de este artículo es desarrollar una metodología para detectar cambios estructurales que integre los elementos anteriores.
Para lograr los objetivos propuestos, el resto de este artículo está organizado como sigue. En la sección 1 se discute la información utilizada, se realiza su análisis preliminar y se desarrolla una metodología para detectar cambios estructurales. En la sección 2 se discuten los resultados obtenidos. Finalmente, se concluye.
1. Datos y metodología
1.1 Información utilizada
La información utilizada en este estudio corresponde a los precios promedio mensuales del petróleo crudo del West Texas Intermediate (WTI), también conocido como Texas Light Sweet, el cual se transa en la Bolsa de Nueva York y sirve como un referente para valorar contratos de futuros. Los datos con que se elaboró este estudio fueron obtenidos de la página web de la Administración de Información de Energía (EIA), del Departamento de Energía de Estados Unidos (http://tonto.eia.doe.gov/dnav/pet/hist/rwtcM.htm). La información disponible corresponde al período comprendido entre 1986:1 y 2008:8.
1.2 Análisis preliminar
En el Gráfico 1a se presenta la evolución en el tiempo del logaritmo natural del precio promedio mensual en dólares por barril. La inspección visual revela la presencia de varias tendencias lineales mayores: las crecientes correspondientes a los años 1987, 1989, 1995, 1996, 1999, 2000 y 2002 al 2008; mientras que las decrecientes corresponden a 1986, 1988, 1993, 1997, 1998 y 2001. Sin embargo, los precios presentan fluctuaciones rápidas que pueden asociarse a diferentes hitos históricos; la EIA presenta una relación actualizada de diferentes acontecimientos que podrían explicar, al menos en parte, algunas de las fluctuaciones de los precios. Dicha información puede consultarse en http://www.eia.doe.gov/emeu/cabs/AOMC/Overview.html.
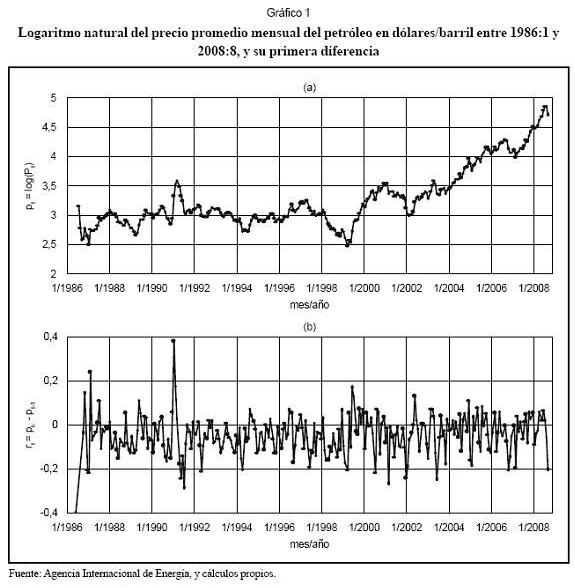
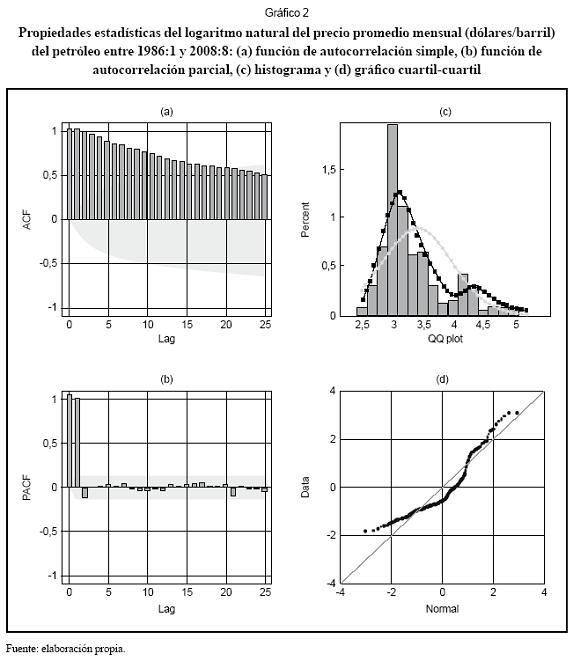
El análisis de las propiedades estadísticas del logaritmo de los precios arroja los siguientes resultados: la función de autocorrelación simple (Gráfico 2a) inicia en un valor muy cercano a la unidad y muere lentamente; entre tanto, la función de autocorrelación parcial (Gráfico 2c) indica que el valor actual depende únicamente del valor anterior. Este -comportamiento es típico de los procesos con raíces unitarias e indica que es posible que el logaritmo de los precios siga un proceso integrado. El histograma (Gráfico 2b) y diagrama Q-Q (Gráfico 2d) señalan que los datos analizados siguen una distribución empírica.
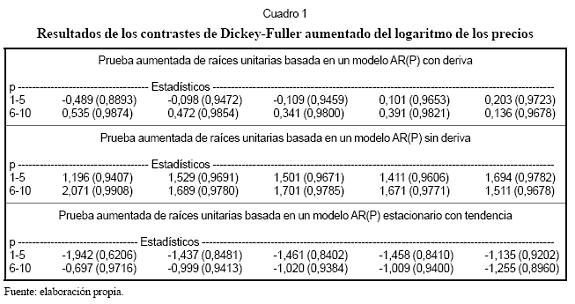
Para verificar la presencia de una raíz unitaria, se aplicó el contraste aumentado de Dickey-Fuller, basado en un modelo autorregresivo de orden P con y sin deriva, y para un modelo autorregresivo estacionario con tendencia. Se consideró que el orden P del modelo varía entre 1 y 10. Los resultados obtenidos se presentan en el Cuadro 1, donde las cantidades entre paréntesis corresponden al valor de p para cada estadístico calculado. Para las tres versiones consideradas del contraste no fue posible rechazar en ningún caso la hipótesis nula en que se considera que el logaritmo de los precios posee una raíz unitaria.
La presencia de una raíz unitaria implica que el modelo debe ser especificado para los rendimientos (rt) de los precios (Pt), los cuales fueron obtenidos como:
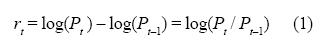
La evolución de los rendimientos en el tiempo se presenta en el Gráfico 1b, mientras que sus propiedades estadísticas, resumidas en sus autocorrelogramas simple y parcial, histograma y gráfico cuartil-cuartil, son presentadas en el Gráfico 3. El análisis de los gráficos indica los rendimientos siguen un proceso autorregresivo de orden uno, AR(1). Aunque la distribución es aparentemente normal, la prueba de Jarque-Bera (1980) permite rechazar la hipótesis nula de normalidad con un valor de p<0,01. La prueba de Lin y Mudholkar (1980) no permite rechazar la hipótesis de normalidad. El gráfico cuartil-cuartil muestra que hay tres outliers que corresponden a dos valores extremos presentados durante 1986 y al pico de los rendimientos que se presenta durante 1990.
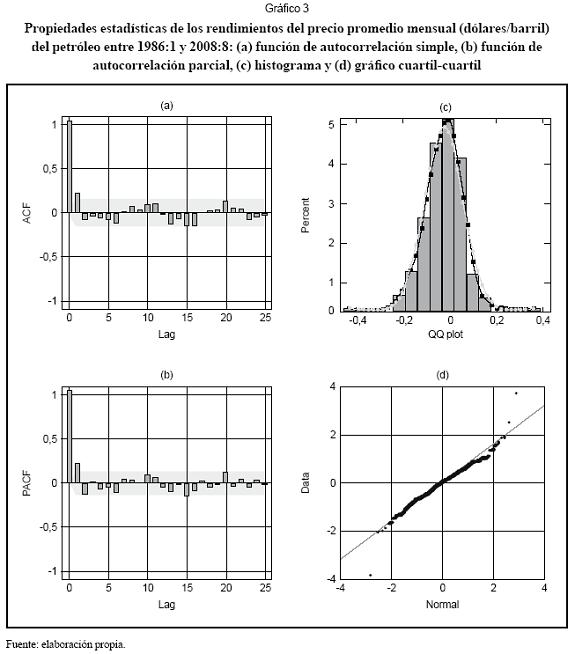
Al continuar con el análisis, se procedió a especificar un modelo que permitiera representar la dinámica de los rendimientos. Por lo tanto, siguiendo el mismo lineamiento sugerido por Abosedra y Laopodis (1997), Sadorsky (2002 y 2006), Morana (2001), Moshiri y Foroutan (2006) y Narayan y Narayan (2007), se formuló un modelo ARMA-GARCH. El mejor modelo encontrado corresponde a unAR(1)-GARCH(2,2):
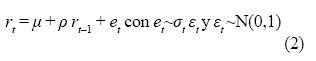
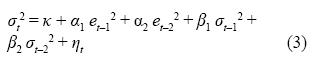
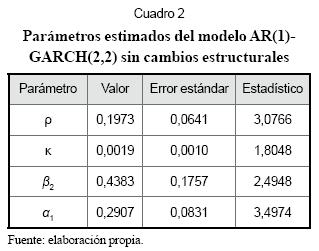
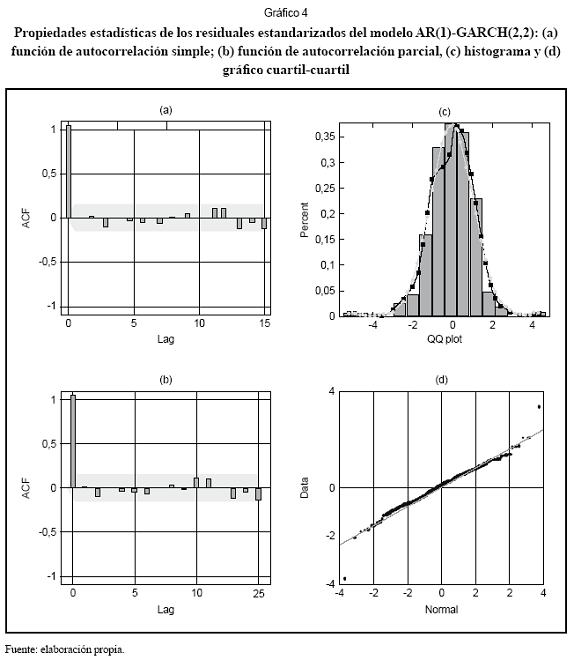
Durante el proceso de especificación se encontró que los valores de los parámetros µ β1y α2 no son significativamente diferentes de cero. En el Cuadro 2 se presentan los valores estimados para los parámetros restantes y sus estadísticos. Entre tanto, en el Gráfico 4 se resumen las propiedades estadísticas de los residuales estandarizados para el modelo seleccionado. Se verificó que no existen autocorrelaciones significativamente diferentes de cero usando los contrastes de Box y Pierce (1970) y Ljung y Box (1978), y que la distribución de los residuales es aproximadamente normal usando los contrastes de Jarque y Bera (1980) y Lin y Mudholkar (1980). El contraste de Engle (1982) permite concluir que no existen componentes heterocedásticos en los residuales estandarizados, mientras que el contraste de McLeod y Lee (1983) indica que no existen componentes no lineales remanentes. No obstante, persisten dos outliers en los residuales normalizados que se identifican a partir del gráfico cuartil-cuartil.
La predicción un mes adelante obtenida usando el modelo AR(1)-GARCH(2,2) se presenta en el Gráfico 5a. La línea continua representa la predicción obtenida para el próximo mes; los puntos indican los logaritmos de los precios reales. La región sombreada corresponde a los intervalos para el 95% de confianza, la cual es función del σt estimado para cada mes. Igualmente, se estimó el pronóstico extrapolativo por fuera de la muestra de datos 36 meses adelante, el cual aparece a la derecha de la línea punteada que indica el fin de los datos históricos.
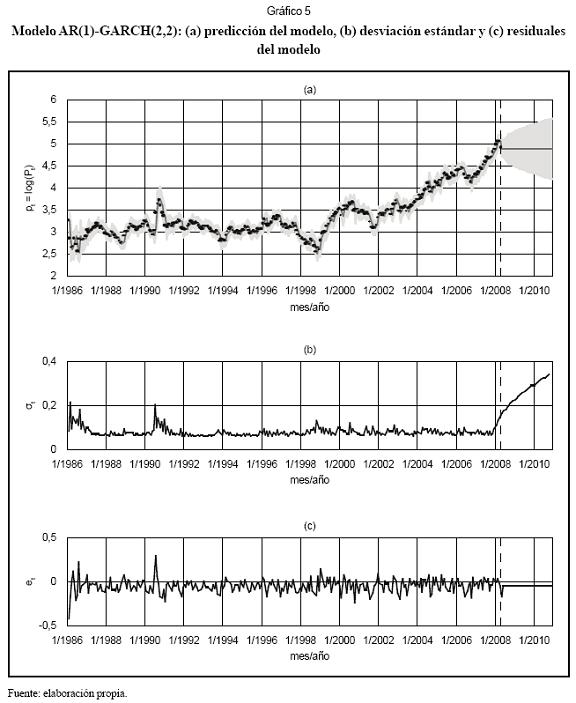
Tres aspectos del Gráfico 5a deben resaltarse. En primer lugar, no se perciben cambios radicales en la volatilidad del logaritmo de los precios para la muestra de datos, excepto para los años 1986 y 1990. En segundo lugar, el modelo pronostica con cierta precisión el valor de la serie para el próximo mes; la sumatoria del error cuadrático medio es de 1,7921, mientras que la sumatoria de errores absolutos es de 15,8582. En tercer lugar, para la predicción extrapolativa no se presenta crecimiento en el logaritmo de los precios, tal como podría esperarse si se sigue la tendencia del período 2002-2008. Este resultado se explica porque el valor esperado de rt es cero; esto es, la constante μ en (2), que representa la tasa de crecimiento de rt de un período a otro, no fue significativamente distinta de cero.
La desviación estándar estimada de los choques se presenta como una función del tiempo en el Gráfico 5b. Se destacan dos regiones donde la desviación estándar es especialmente alta respecto al promedio: la primera de ellas corresponde a 1986, y se explica en parte por varios sucesos: el crecimiento de la producción de la Organization of the Petroleum Exporting Countries (OPEC) y el uso de distintas fórmulas para la valoración del petróleo; y la segunda corresponde al segundo semestre de 1990 y primer semestre de 1991, período durante el cual se dio la invasión de Kuwait por parte de Iraq, y la guerra del Golfo Pérsico. Igualmente, se presentan otros aumentos menores de volatilidad, como el ocurrido a principios de 1999, y que se asocia comúnmente con la crisis asiática. Los choques estimados con el modelo son presentados en el Gráfico 5c; su amplitud está relacionada con la varianza estimada (fig) y dan una visión más clara sobre los cambios en rt.
La inspección visual del logaritmo de los precios señala la posible presencia de tendencias locales que pueden explicarse por diferentes hechos históricos, tal como ya se indicó. En este sentido, el modelo estimado no recoge adecuadamente la dinámica subyacente de los precios. No obstante, los principales eventos históricos podrían modelarse utilizando variables dummy, aunque la gran cantidad de eventos y su corta duración hacen inviable dicha metodología.
1.3 Metodología para detectar cambios de nivel en los rendimientos
En esta subsección se describe la metodología desarrollada para detectar cambios de nivel en el rendimiento de los precios. Se basa en el concepto de partición recursiva de regiones, el cual es la base de muchos procedimientos de regresión no lineal que incluyen Multivariate Adaptive Regression Splines (MARS) (Friedman, 1991) y los árboles de regresión y clasificación (Breiman, Friedman, Olshen y Stone, 1984).
La hipótesis fundamental de la mayoría de los modelos es la estabilidad estructural de la dinámica de la serie.Ante la presencia de uno o más cambios estructurales, los modelos tradicionales se hacen inapropiados y pueden llevar a conclusiones inadecuadas. Para tratar con la presencia de cambios estructurales se han propuesto varias aproximaciones en la literatura (Maddala y Kim, 1998):
-
Modelos cuyos parámetros cambian gradualmente en el tiempo.
-
Modelos que incorporan la presencia de observaciones atípicas.
-
Modelos de varios regímenes, con cambio gradual o abrupto, donde un modelo particular se asocia con cada régimen presente en la dinámica.
Las pruebas estadísticas desarrolladas abarcan diferentes tipos de problemas:
-
Puntos de cambio conocidos contra puntos de cambio desconocidos.
-
Un punto de cambio contra varios puntos de cambio.
Respecto a la clasificación anterior, la metodología propuesta en este artículo permite buscar de forma simultánea e integrada un número desconocido de puntos de cambio en la dinámica de la serie. El algoritmo consta de dos fases: en la primera se realiza la partición recursiva en que los datos se parten en N regiones diferentes; en la segunda, se eliminan las regiones que no aportan al desempeño del modelo. Cada cambio estructural se modela como una variable dummy x que es igual a uno en la región en que se presenta la correspondiente tendencia local, y cero en caso contrario. De esta forma, (2) se reescribe como:
La fase 1 del algoritmo consta de los siguientes pasos :

En el algoritmo anterior, s es el conjunto de puntos que indican un cambio estructural en rt. La búsqueda tiene como objetivo encontrar un máximo de N regiones en que se presentan cambios estructurales (línea 02). La función GetLLF(·,·) calcula el logaritmo de la función de verosimilitud de los residuales obtenidos al estimar el modelo m, especificado por (3) y (4), y los cambios estructurales definidos por s.
En la línea 06 se inicia un ciclo donde se busca un nuevo punto de cambio estructural, t*, tal que se maximice el logaritmo de la función de verosimilitud de los residuales (línea 09). En esta búsqueda se excluyen los puntos de la serie que ya se han seleccionado en iteraciones anteriores (línea 07), y se hace la búsqueda desde t = 3 hasta T-3, donde T es el total de los datos. El nuevo punto de cambio estructural es aceptado o rechazado de acuerdo con el resultado de la prueba del radio de verosimilitud para un nivel de confianza definido de antemano (línea 15). Cuando t* es aceptado como un punto de cambio estructural, se incorpora al conjunto s, y se repite el proceso de búsqueda (línea 02).
La fase 2 tiene como objetivo verificar que todos los puntos de cambio estructural identificados en la fase 1 sean necesarios, y que ninguno de ellos pueda ser eliminado sin degradar el modelo final obtenido. Esta fase consta de los siguientes pasos:

La fase 2 se basa en iterar sobre todos los puntos de cambio estructural definidos en s, tal que ninguno de ellos pueda eliminarse. El ciclo de la línea 04 tiene como objetivo determinar cuál es el punto de cambio estructural en s, t*, tal que al eliminarse maximiza el logaritmo de la función de verosimilitud (línea 07). Una vez se ha identificado dicho punto (t*), se aplica el contraste del radio de verosimilitud para determinar si es estadísticamente significativo. Si el punto t* no es significativo, es eliminado del conjunto s, y se inicia un nuevo proceso de búsqueda; en caso contrario, t* se conserva en s, y el algoritmo se da por terminado. Así, s contiene todos los puntos donde ocurren cambios estructurales que son estadísticamente significativos.
2. Resultados obtenidos y discusión
La metodología descrita en la sección anterior fue aplicada a la serie de rendimientos de los precios promedios mensuales del petróleo del WTI, con un máximo de 10 regiones (N=10). El algoritmo desarrollado detectó cambios de nivel en rt (o cambios de pendiente para los logaritmos de los precios) en 1986:3, 2001:9 y 2002:2.
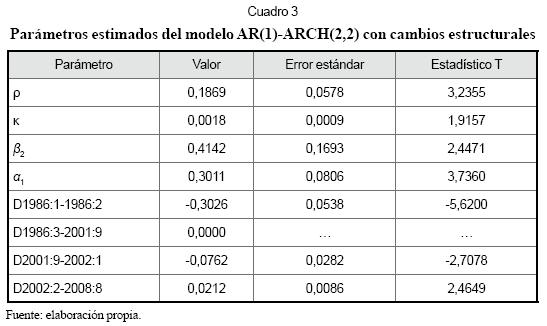
Seguidamente, se estimaron los parámetros de un modelo AR(1)-ARCH(2,2) con cuatro variables dummy que representan las cuatro regiones con diferente nivel. Los parámetros calculados y sus estadísticos se presentan en el Cuadro 3. El coeficiente para la variable que representa el nivel en el período 1986:3 2001:9 no fue significativamente diferente de cero, lo que indica que para dicho lapso no hay una componente determínistica de crecimiento en los precios. Los resultados indican que para los períodos 1986:1-1986:2 y 2001:9-2002:1 se presenta una tendencia decreciente de los precios, mientras que durante el período 2002:2-2008:8 hay un crecimiento del logaritmo de los precios a una tasa mensual de 0,0212.
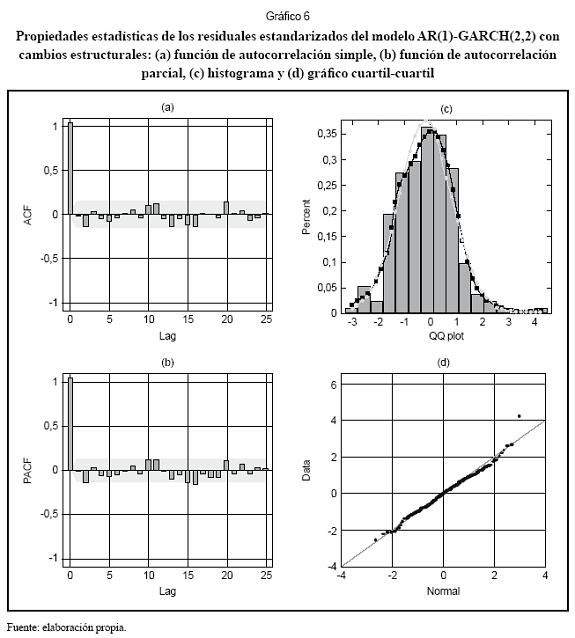
El análisis de las propiedades estadísticas de los residuales estandarizados permiten arrojar las siguientes conclusiones: primero, no existen autocorrelaciones significativamente distintas de cero (gráficos 6a y 6c), y, segundo, los residuales estandarizados siguen una distribución normal (gráficos 6b y 6d).
En el Gráfico 7a se presenta la predicción un mes adelante obtenida al considerar los cambios estructurales (señalados mediante líneas verticales). La mayor diferencia respecto al Gráfico 5a es que el pronóstico extrapolativo presenta un claro componente de tendencia que no estaba presente antes.
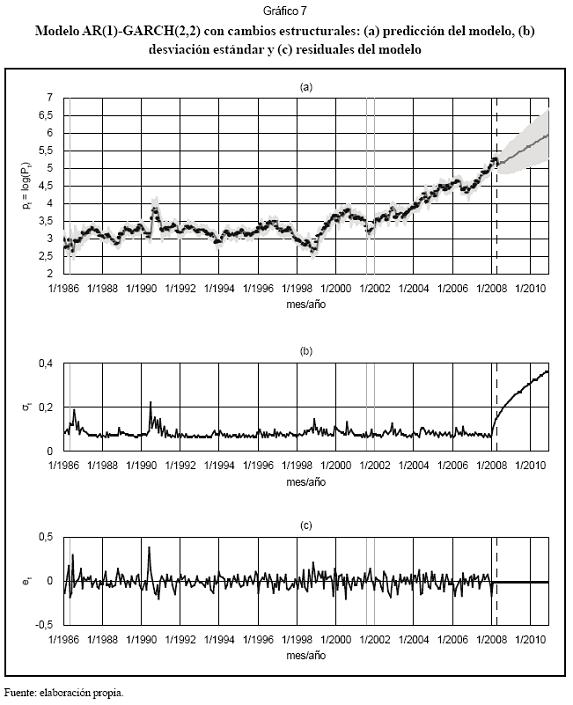
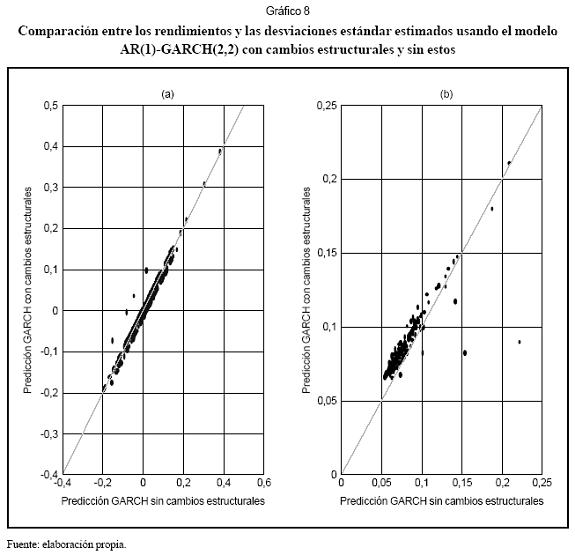
Al comparar los gráficos 5b y 7b se observa una reducción en la volatilidad estimada para el modelo con cambios estructurales. Esto se explica porque los valores de κ y β2 se reducen en un 5% aproximadamente. En los gráficos 5c y 7c no se aprecian cambios. En el Gráfico 8 se comparan para ambos modelos: la predicción un mes adelante para la muestra de calibración (a) y la desviación estándar (b). Los puntos ubicados sobre la línea a 45º indican que ambos modelos estimaron el mismo valor, ya sea para rt o para σt. En el Gráfico 8a se aprecia que el modelo con cambios estructurales produce pronósticos de magnitud inferior a los estimados por el modelo sin cambios. Del Gráfico 8b se concluye que el modelo con cambios estructurales tiende a estimar varianzas inferiores que el modelo sin cambios estructurales.
Finalmente, la sumatoria del error cuadrático medio es 1,5990, y la sumatoria del error medio absoluto es 16,1059. Esto equivale a una reducción del 10% en el error cuadrático medio respecto al modelo sin cambios estructurales.
Conclusiones
En este artículo se analizó la dinámica de los precios promedios mensuales del petróleo del WTI y se demostró que sus rendimientos siguen un proceso AR(1)-GARCH(2,2) con cambios estructurales en su nivel, los cuales ocurren en 1986:3, 2001:9 y 2002:1. Si los cambios estructurales no se tienen en cuenta, la constante del modeloAR(1)-GARCH(2,2) es cero y ello implica que el mejor pronóstico de los precios es el último precio conocido, ya que no existe tendencia.
La inclusión de cambios estructurales permitió detectar regiones donde la esperanza de los rendimientos es diferente de cero, lo que se traduce como la presencia de tendencias locales en los precios. Esto último se capitaliza como la capacidad de extraer la tendencia local para extrapolarla y, así, obtener predicciones de los precios.
Lista de referencias
1. Abosedra, S. and Laopodis, N. (1997). Stochastic behavior of crude oil prices: A GARCH investigation. The Journal of Energy and Development, 21 (2), 283-292. [ Links ]
2. Adrangi, B., Arjun, C., Dhanda, K. K. and Raffiee, K. (2001). Chaos in oil prices? Evidence from future markets. Energy Economics, 23, 405-425. [ Links ]
3. Álvarez-Ramírez, J., Álvarez, J. and Rodríguez, E. (2008). Short-term predictability of crude oil markets:Adetrended fluctuation analysis approach. Energy Economics, 30, 2645-2656. [ Links ]
4. Askari, H. and Krichene, N. (2008). Oil price dynamics (2002-2006). Energy Economics, 30, 2134-2153. [ Links ]
5. Bernabe, A., Martina, E., Álvarez-Ramírez, J. e Ibarra-Valdez, C. (2004). A multi-model approach for describing crude oil price dynamics. Physica A., 338, 567-584. [ Links ]
6. Breiman, L., Friedman, J. H., Olshen, R. A. and Stone, C. J. (1984). Classification and regression trees. Pacific Grove, CA: Wadsworth & Brooks-Cole Advanced Books & Software. [ Links ]
7. Box, G. and Pierce, D. (1970). Distribution of residual correlations in autoregressive-integrated moving average time series models. Journal of American Statistical Association, 65, 1509-1526. [ Links ]
8. Chen, S. S. and Chen, H. C. (2007). Oil prices and real exchange rate. Energy Economics, 29, 390-404. [ Links ]
9. Engle, R. (1982). Autoregressive conditional heterocedasticity with estimates of the variance of United Kingdom inflations. Econometrica, 50, 987-1007. [ Links ]
10. Fan, Y., Liang, Q. and Wei, Y. M. (2008). A generalized pattern matching approach for multi-step prediction of crude oil price. Energy Economics, 30 (3), 889-904. [ Links ]
11. Ferderer, J. P. (1996). Oil price volatility and the macroeconomy. Journal of Macroeconomics, 18, 1-26. [ Links ]
12. Friedman, J. (1991). Multivariate adaptive regression splines (with discussion). Annals of Statistics, 19, 1-141. [ Links ]
13. Gori, F., Ludovisi, D. and Cerritelli, P. F. (2007). Forecast of oil price and consumption in the short term under three scenarios: Parabolic, linear and chaotic behavior. Energy, 32 (7), 1291-1296. [ Links ]
14. Huang, R. D., Masulis, R. W. and Stoll, H. R. (1996). Energy shocks and financial markets. Journal of Futures Markets, 16, 39-56. [ Links ]
15. Jarque, C. and Bera, A. (1980). Efficient tests for normality, homoscedasticy and serial independence of regression residuals. Economic Letters, 6, 255-259. [ Links ]
16. Lee, K., Ni, S. and Ratti, R.A. (1995). Oil shocks and the macroeconomy: The role of price variability. The Energy Journal, 16, 39-56. [ Links ]
17. Lin, C. T. and Mudholkar, G. S. (1980).Asimple test for normality against asymmetric alternatives. Biometrika, 67, 455-461. [ Links ]
18. Ljung, L. and Box, G. (1978). On a measure of lack of fit in time series models. Biometrika, 66, 67-72. [ Links ]
19. Maddala, G. S. and Kim, I.-O. (1998). Unit roots, cointegration and structural change. Cambridge: Cambridge University Press. [ Links ]
20. McLeod, A. and Li, W. (1983). Diagnostic checking ARMAtime series models using squared residual autocorrelations. Journal of Time Series Analysis, 4, 269-273. [ Links ]
21. Morana, C. (2001). A semiparametric approach to short-term oil price forecasting. Energy Economics, 23 (3), 325-338. [ Links ]
22. Moshiri, S. and Foroutan, F. (2006). Forecasting nonlinear crude oil futures prices. The Energy Journal, 27(4), 81-95. [ Links ]
23. Narayan, P. K. and Narayan, S. (2007). Modelling oil price volatility. Energy Policy, 35(12), 6549-6553. [ Links ]
24. Panas, E. and Ninni, V. (2000).Are oil markets chaotic? A non-linear dynamic analysis. Energy Economics, 22, 549-568. [ Links ]
25. Park, J. and Ratti, R. A. (2008). Oil price shocks and stock markets in the U. S. and 13 European countries. Energy Economics, 30, 2587-2608. [ Links ]
26. Perron, P. (1989). The great crash, the oil price shock, and the unit root hypothesis. Econometrica, 57, 1361-1401. [ Links ]
27. Pilipovic, D. (1998). Energy risk: Valuing and managing energy derivates. New York: McGraw Hill. [ Links ]
28. Pindyck, R. (1999). The long-run evolution of energy prices. The Energy Journal, 20 (2), 1-27. [ Links ]
29. Pindyck, R. (2004a). Volatility in natural gas and oil markets. Unpublished Manuscript. Massachusetts Institute of Technology, Cambridge, MA. [ Links ]
30. Volatility and commodity price dynamics. (2004b).Journal of Futures Market, 24, 1029-1047. [ Links ]
31. Postali, F. A. S. and Picchetti, P. (2006). Geometric Brownian motion and structural breaks in oil prices: A quantitative analysis. Energy Economics, 28, 506-522. [ Links ]
32. Regnier, E. (2007). Oil and energy price volatility. Energy Economics, 29 (3), 405-427. [ Links ]
33. Sadorsky, P. (1999). Oil price shocks and stock market activity. Energy Economics, 21, 449-469. [ Links ]
34. Time-varying risk premiums in petroleum futures prices. (2002).Energy Economics, 24 (6), 539-556 [ Links ]
35. The macroeconomic determinants of technology stock price volatility. (2003).Review of Financial Economics, 12, 191-205. [ Links ]
36. Modelling and forecasting petroleum futures volatility. (2006).Energy Economics, 28, 467-488. [ Links ]
37. Serletis,A. (1992). Maturity effects in energy futures. Energy Economics, 14, 150-157. [ Links ]
38. Yang, C. W., Hwang, M. J. and Huang, B. N. (2002). An analysis of factors affecting price volatility of the US oil market. Energy Economics, 24, 107-119. [ Links ]
39. Yu, L., Wang, S. and Lai, K. K. (2008). Forecasting crude oil price with an EMD-based neural network ensemble learning paradigm. Energy Economics, 30 (5), 2623-2635. [ Links ]














