Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Cuadernos de Administración
Print version ISSN 0120-3592
Cuad. Adm. vol.27 no.48 Bogotá Jan./June 2014
Análisis de la correlación de largo plazo del precio spot en el mercado eléctrico colombiano*
An analysis of long range spot price correlation in the Colombian electrical energy market
Análise da correlação de longo prazo do preço Spot no mercado elétrico colombiano
Lilliam Urrego A.**
Santiago Medina H.***
Frederic Heliodore****
Boussaad Ismail*****
Serge Poullain******
Eric Courbon*******
*Este artículo es un producto derivado de la investigación "Desarrollo de modelos de vulnerabilidad del sistema eléctrico de potencia desde un enfoque de riesgos", desarrollada en por Universidad Nacional de Colombia, Facultad de Minas, la empresa XM S.A. y la empresa Alstom Grid. El artículo se recibió el 26-08-13 y se aprobó el 08-04-14. Sugerencia de citación: Urrego, L., Medina, S., Heliodore, F., Ismail, B., Poullain, S. y Courbon, E. (2014). Análisis de la correlación de largo plazo del precio spot en el mercado eléctrico colombiano. Cuadernos de Administración, 27 (48), 153-182.
**Analista especialista en riesgos, XM SA ESP, Universidad Nacional de Colombia, Medellín, Colombia. Hace parte de los grupos de investigación GIFIG: Grupo de Investigación en Ingeniería Financiera y Gestión Empresarial y Risk Team Alstom Grid. Correo electrónico: liurrego@xm.com.co
***Doctor en Fundamentos y técnicas estadísticas para toma de decisiones financieras y actuariales, Universidad Complutense de Madrid, Madrid, España, 2007; DEA Diploma de estudios avanzados del programa de Fundamentos y técnicas estadísticas para toma de decisiones financieras y actuariales, Universidad Complutense de Madrid, Madrid, España, 2003; Especialista en Finanzas, preparación y evaluación de proyectos, Universidad de Antioquia, Medellín, Colombia, 1995; Ingeniero Industrial, Universidad Nacional de Colombia, Medellín, Colombia, 1993. Profesor asociado, Universidad Nacional de Colombia, Medellín, Colombia. Hace parte del grupo de investigación GIFIG: Grupo de Investigacion en Ingeniería financiera y gestion empresarial (U. Nacional) y Risk Team Alstom Grid (Francia). Correo electrónico: smedina@unal.edu.co
****Doctor en Física, Universidad de Lille, Lillre, Francia, 1987. Experto Senior en Investigación y desarrollo "El líder del proyecto", Alstom Grid, La Défense, Francia. Hace parte del grupo de investigación Risk Team Alstom Grid. Correo electrónico: frederic.heliodore@alstom.com
*****Doctor en Proceso de Datos, Universidad de Paris-Est, Créteil, Francia, 2014. Master 2 en Matemática Computacional, Universidad de Paris 13, Paris, Francia, 2009; Ingeniero Diplomado en Investigación Operativa, Universidad de Bugía, Bugía, Argelia, 2006. Investigación y desarrollo: Ph.D, La Défense, Francia. Hace parte del grupo de investigación Risk Team Alstom Grid. Correo electrónico: Boussaad.Ismail@alstom.com
******Doctor en Control de Sistemas, Universidad de Tecnologia, Compiègne, Francia, 1991; Diploma de Estudios Avanzados (DEA) en Control de Sistemas, Universidad de Tecnologia, Compiègne, Francia, 1986; Ingeniero industrial en robótica y electromecánica, Universidad de Tecnología, Compiègne, Francia, 1986; Ingeniero de Investigación y Desarrollo, Senior Expert, Alstom Grid, La Défense, Francia. Hace parte del grupo de investigación Risk Team Alstom Grid. Correo electrónico: serge.poullain@alstom.com
*******Maestría en Ingeniería Mecánica, Institut National des Sciences Appliquées (INSA), Lyon, Francia, 1992; Diploma de Ingeniero, Institut National des Sciences Appliquées (INSA), Lyon, Francia, 1992. Institut National des Sciences Appliquées (INSA), Lyon, Francia, 1992. Alstom Grid, La Défense, Francia. Hace parte del grupo de investigación Risk Team Alstom Grid. Correo electrónico: eric.courbon@alstom.com
Resumen
Este artículo cuestiona los supuestos de los modelos financieros que se suelen usar para analizar el precio de la energía. Parte de un análisis exploratorio de los rendimientos diarios para rechazar las hipótesis de aditividad, volatilidad, independencia y normalidad. Con el uso de herramientas asociadas al análisis fractal y en potencia se detectan varios comportamientos: una reversión de los rendimientos (exponente de Hurst de 0.39 y dimensión fractal de 1.61), ciclos que son múltiplos de 7 días, inexistencia de varianza poblacional, cambios asimétricos, alta probabilidad de ocurrencia de valores extremos y buen ajuste a la distribución α-estable. Estos comportamientos destacan la necesidad de elaborar métodos que incorporen los elementos necesarios para analizar sistemas dinámicos no lineales.
Palabras clave: Exponente de Hurst, series de tiempo no lineales, riesgo financiero.
JEL classification: C46, G17.
Abstract
This paper focuses on the role of the multinational corporations in the Colombian peace process. First a theoretical frame work is built which aims to shed light on the significance of multinationals in this process. The study then presents the specific Colombian experience with relation to the role of multinationals in the peace process. The penultimate section deals with the relation between peace, corporate social responsibility, and the UN Global Compact. Finally it offers a conclusion with regards to the role of multinational companies in the Colombian peace process.
Key words: Hurst exponent, antipersistent, financial risk.
JEL classification: C46, G17.
Resumo
Este artigo questiona as suposições dos modelos financeiros que se costumam usar para analisar o preço da energia. Parte de uma análise exploratória dos rendimentos diários para recusar as hipóteses de aditividade, volatilidade, independência e normalidade. Com o uso de ferramentas associadas à análise fractal e em potência, detectam-se vários comportamentos: uma reversão dos rendimentos (expoente de Hurst de 0,39 e dimensão fractal de 1,61), ciclos que são múltiplos de sete dias, inexistência de variância populacional, mudanças assimétricas, alta probabilidade de ocorrência de valores extremos e bom ajuste à distribuição α-estável. Esses comportamentos destacam a necessidade de elaborar métodos que incorporem os elementos necessários para analisar sistemas dinâmicos não lineares.
Palavras-chave: Expoente de Hurst, séries de tempo não lineares, risco financeiro
Classificação JEL: C46, G17.
Introducción
La estructura actual del mercado eléctrico colombiano es el resultado de un prolongado proceso de intervención estatal que se inició en la década de los treinta, el cual mantenía el poder monopólico en el sector energético prestando los servicios de generación, transmisión y distribución. La industria eléctrica integrada verticalmente funcionó de manera centralizada hasta las reformas efectuadas mediante las leyes 142 y 143 de 1994, como consecuencia de la profunda crisis del sector eléctrico y siguiendo un esquema similar al de los países pioneros en este desarrollo, en especial el Reino Unido. Las reformas introducen la competencia en el sector eléctrico, permite la inversión privada, la privatización de compañías estatales, la eliminación de la integración vertical, y deja al Estado solamente el papel de ente regulador.
Actualmente, el funcionamiento del Mercado Mayorista de Electricidad (MEM) está soportado en la existencia de una Bolsa de Energía donde los agentes generadores y comercializadores realizan intercambios comerciales de energía definidos en el contexto de un mercado de corto plazo o mercado spot, con resolución horaria y un operador central del Sistema (XM SA ESP) encargado de operar el Sistema Interconectado Nacional y administrar el mercado mayorista, incluyendo las transacciones internacionales de electricidad de corto plazo.
En el mercado spot los generadores informan diariamente a la bolsa de energía, sus ofertas de precios y disponibilidad de generación con resolución horaria. La bolsa de energía es entonces, un lugar donde los generadores compiten con sus ofertas de precios para la atención de la demanda del Sistema Interconectado Nacional, de tal manera que la demanda es atendida al mejor precio dado por la competencia entre generadores lo cual define el precio spot de la electricidad. Los comercializadores representantes de los consumidores, no participan activamente en la bolsa dado que no realizan ofertas, pero participan de una manera pasiva en el sentido que sus excedentes y sobrantes de energía respecto a su demanda deben ser vendidos o comprados en bolsa.
Las empresas generadoras y comercializadoras también pueden realizar entre ellas contratos bilaterales de compra y venta de energía con el fin de atender su demanda de mediano y largo plazo. Este mercado opera libremente de acuerdo con las condiciones de oferta y demanda y sin la intervención del operador del mercado. Los contratos se establecen de común acuerdo entre las partes donde se define fecha, hora, precio y cantidad de energía para cubrir su demanda. Estos contratos deben registrarse en el ASIC (Administrador del Sistema de Intercambios Comerciales).
En vista de lo anterior, se definen tres factores fundamentales en el proceso comercial de la electricidad estos son: la demanda de electricidad, los precios de los contratos bilaterales y los precios de la energía en bolsa, cuya predicción y simulación son un insumo requerido por los agentes generadores, los comercializadores, los grandes consumidores y el operador del sistema dentro de los diferentes procesos de decisión que llevan a cabo.
Realizar adecuados pronóstico del precio spot, del precio de contratos y la demanda permite por ejemplo:
- Soportar la toma de decisiones de la negociación de la electricidad en el corto, mediano y largo plazo,
- En la programación de mantenimientos a la red permite medir el impacto financiero de un posible fallo.
- Para estimar la exposición y cobertura en el mercado spot.
- En el largo plazo permite analizar los planes de expansión y los refuerzos necesarios para la red.
- La estructuración del portafolio energético para generadores.
- La cuantificación y cubrimiento de riesgos asociados a la volatilidad de los precios.
- La valoración de derivados con subyacente los precios del spot o los precios de contratos.
Por lo tanto, una buena caracterización y predicción de estas variables trae beneficios técnicos asociados a las decisiones de operación y también financieros asociados a la evaluación económica de las decisiones.
Son varios los trabajos que puntualizan las características de los precios de la electricidad en los diferentes mercados eléctricos tales como la presencia de colas pesadas y sesgos, la curtosis, la presencia de picos y cambios de régimen en la serie, la dinámica de la volatilidad o el análisis del proceso estocástico que captura estas particularidades, también subrayan la influencia de estas características en los modelos de valoración (Schwartz, 1997; Weron, 2005; Johnson y Barz, 1999; Bhanot, 2000; Deidersen y Truck, 2002). Todas estas características son determinantes a la hora de aplicar modelos de pronóstico de las series de tiempo, realizar proyecciones financieras, valorar productos financieros con subyacente los precios de la energía, aplicar modelos de cuantificación de riesgos o realizar procesos de simulación. Todos los estudios subrayan las características particulares del precio de la energía y las dificultades de aplicar per se los modelos de valoración utilizados para el sector financiero.
Desde otra perspectiva, durante los últimos 40 años, los físicos han conseguido resultados importantes en el campo de las transiciones de fase, la mecánica estadística, la dinámica no lineal y el análisis de sistemas caóticos, con el fin de entender el comportamiento de fenómenos físicos y biológicos los cuales se caracterizan por ser discontinuos y no homogéneos. Si bien los trabajos pioneros en esta área se remontan a principios del siglo XX con los trabajos de Henri Poincaré y Max Plank, actualmente el avance en el análisis matemático y estadístico es bastante amplio y conceptos asociados a la ley de potencia, invarianza de escala, correlaciones de largo plazo, dimensión fractal y entropía, entre otros, están disponibles para el entendimiento de fenómenos.
Con el surgimiento de la Geometría Fractal es posible interpretar los objetos y fenómenos de la naturaleza desde una perspectiva diferente, la teoría permite estudiar los patrones que rigen la rugosidad, la discontinuidad y las fracturas en la naturaleza en muchos aspectos, es más natural e intuitiva y permite una mejor comprensión de los fenómenos que el análisis basados en la geometría euclidiana la cual suaviza artificialmente los objetos (Mandelbrot, 1977).
La aplicación de la teoría fractal a la economía fue puntualizada por Mandelbrot a finales del siglo XX. Los análisis basados en el nuevo paradigma rompe con los supuestos de equilibrio general, los supuestos gaussianos y la teoría de los mercados eficientes (Mandelbrot y Hudson, 2010). En el caso de los precios en los mercados financieros, estos no evolucionan según una caminata aleatoria y no son representados adecuadamente como un movimiento Browniano cuyos supuestos han sido la base de modelos como el CAPM, la Teoría Moderna de Portafolios y el modelo Black-Scholes, el Valor en Riesgo, entre otros, sin embargo, el uso extendido de las aproximaciones de la teoría fractal en economía son todavía limitadas (Mandelbrot, 1997).
Con el surgimiento del análisis fractal y la teoría del caos como un subconjunto de una teoría mucho más amplia conocida como Teoría de la complejidad es posible caracterizar el comportamiento de sistemas dinámicos no lineales (Newman, 2003; Kwapieñ y Drozdz, 2012). Respecto a su aplicación en las series de tiempo, algunos investigadores han puntualizado las características no lineales de las series de tiempo de variables económicas y de los precios de la energía mediante el cálculo de indicadores de correlación de largo plazo, el fenómeno de escalamiento asociados a la ley de potencia y su ajuste a la distribución estable (Erzgraber et al., 2008; Norouzzadeh, 2007; Serletis, 2007; Simonsen, 2003; Simonsen, 1998; Weron, 2002; Janicki y Weron, 1994; Weron, 2000), sin embargo la incorporación de los conceptos de la estadística fractal en modelos financieros como el CAPM, la estructuración de portafolios, la cuantificación de riesgos, la valoración de derivados, o en modelos de pronóstico es todavía un proceso en desarrollo debido a su complejidad.
Este artículo resalta las características estadísticas no lineales de la serie de tiempo de los precios spot de la electricidad del mercado eléctrico colombiano, y analiza los efectos sobre los modelos financieros utilizados para la cuantificación de riesgos o la valoración de activos asociados al precio spot de la energía, para ello se hace uso de las herramientas asociadas al análisis fractal de series de tiempo. El artículo está organizado de la siguiente forma, en la primera sección se realiza un análisis exploratorio del precio de bolsa resaltando sus características estadísticas y los posibles efectos en la aplicación de los modelos de economía financiera. Mientras que en la segunda sección se hace un análisis de las características fractales del precio spot y se discuten sus implicaciones sobre los modelos financieros.
1. Análisis exploratorio del precio spot
En la Bolsa de Energía se establece el precio de la electricidad del corto plazo, según las condiciones de la Oferta y la Demanda de electricidad las cuales a su vez son el resultado de una interacción de variables de naturaleza compleja y dinámica. Aunque la variabilidad de los precios es superior a la mayoría de los productos básicos de la economía, la electricidad es considerada como commodity, sin embargo la imposibilidad de almacenar la energía puede aumentar la probabilidad de que haya faltantes, lo cual es un factor que coadyuva al incremento en las fluctuaciones del precio. Dado lo anterior, es fundamental producir la electricidad requerida en el momento necesario de tal manera que la oferta y la demanda estén en todo momento correctamente calzadas. En condiciones ideales se espera que la generación de electricidad cubra exactamente la electricidad que el mercado necesita, en otras palabras, que se consuma exactamente la electricidad producida, sin embargo esta meta no se logra fácilmente, con lo cual se crean fuentes de presión en el precio para uno u otro lado.
Entre los factores que determinan la evolución de los precios se encuentra la oferta de electricidad la cual en el caso colombiano, la producción es mayormente hídrica y está afectada por factores como el niveles de los embalses, el caudal de ríos, la estación climática y factores ambientales, además la capacidad de generación instalada y de transmisión, la seguridad de la red (sistemas de protección, ataques a la infraestructura, etc.), las interconexiones y hasta el poder de mercado por parte de los generadores son variables que afectan los precios (Joskow y Kahn, 2001).
Otro determinante del precio es la demanda eléctrica, la cual está muy relacionada con el incremento o decremento de la actividad económica, factores estacionales y factores climáticos. En mercados en los que el clima cambia drásticamente la demanda es un factor importante de los precios, sin embargo en el mercado colombiano los factores climáticos pesan más sobre el cambio de precios de la oferta. Respecto a la estacionalidad presente en la actividad económica, en la mitad del segundo semestre del año la actividad económica aumenta y a su vez tiende a aumentar el precio de la energía. Por otra parte, en momentos en los que el nivel de demanda está muy cerca al nivel de generación y el nivel de transmisión es máximo, el precio puede aumentar bruscamente al tener que producir electricidad con mayores costos.
El comportamiento de los precios de electricidad a nivel diario y mensual se observa en las gráficas 1 y 2. Dentro de cada resolución, los precios sufren variaciones importantes, los precios mensuales suavizan las variaciones aleatorias de los precios diarios. Se observa una tendencia definida de largo plazo pero es difícil distinguir patrones cíclicos o estacionales en la serie. En las siguientes secciones analizaremos el escalamiento en el tiempo de estadísticos como media y volatilidad, la correlación, la distribución de probabilidad, la presencia de picos en la serie y por último se toman dos ejemplos de modelos financieros para mostrar que los supuestos de los que parten no se cumplen en el caso del precio spot de la energía.
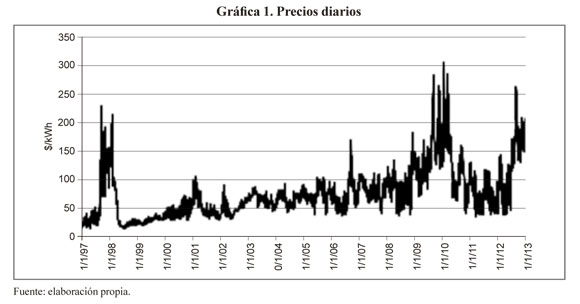
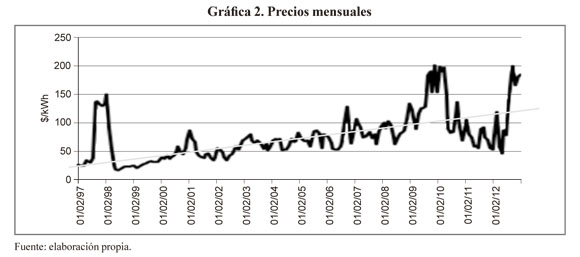
1.1. Aditividad de rendimientos y volatilidad
En medición de riesgos, por lo general, no se trabaja sobre la serie de precios (Pt), sino sobre una transformación de estos, buscando descubrir patrones de comportamientos característicos en el histograma. La transformación logarítmica es la más utilizada por sus propiedades estadísticas ya que genera medidas de tendencia central y desviación más consistentes y además permite centrar la distribución.

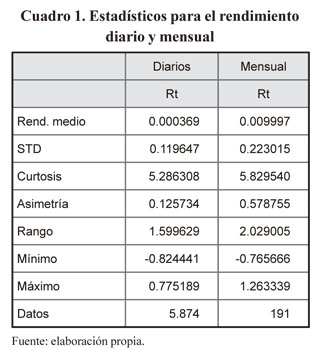
El cuadro 1 indica los estadísticos para rendimientos diarios y mensuales.
En los mercados financieros, por lo general, se asume que los rendimientos del activo se comportan normales mientras que los precios son lognormales. Este supuesto simplifica muchas de las relaciones utilizadas en economía financiera, sin embargo, esto puede subestimar los riesgos inherentes.
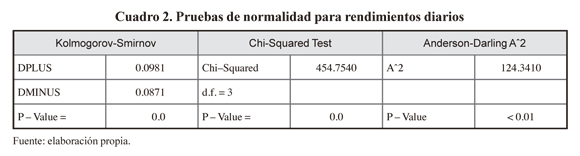
El uso extendido de los rendimientos logarítmicos estriba en dos propiedades fundamentales, por una parte la aditividad de los rendimientos, es decir, la rentabilidad para m días es la suma de las rentabilidades diarias Rm = Ri * m. En nuestro caso para la rentabilidad mensual a partir de la rentabilidad diaria tenemos Rm = 0.000369*30 = 0.0110649 lo cual es diferente de 0.009997 es decir se sobrevalora el rendimiento mensual un 10.67%. Respecto de la rentabilidad mensual calculada directamente de la serie. Por otra parte, asumiendo condiciones de independencia entre las rentabilidades diarias, la varianza de la rentabilidad para m días es equivalente a 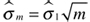 , esto implícitamente está suponiendo que la serie se comporta como ruido blanco. Si verificamos los resultados obtenidos para una volatilidad mensual a partir de la volatilidad diaria se obtiene: am = 0.119647* «¡30 = 0.655334 lo cual es un valor mucho más alto respecto a la volatilidad mensual real calculada directamente de la serie que equivale a 0.223015, es decir se sobrevalora la volatilidad 1.93 veces.
, esto implícitamente está suponiendo que la serie se comporta como ruido blanco. Si verificamos los resultados obtenidos para una volatilidad mensual a partir de la volatilidad diaria se obtiene: am = 0.119647* «¡30 = 0.655334 lo cual es un valor mucho más alto respecto a la volatilidad mensual real calculada directamente de la serie que equivale a 0.223015, es decir se sobrevalora la volatilidad 1.93 veces.
Los resultados anteriores implican que los modelos teóricos para extrapolar la media y la volatilidad subyacentes en el modelo de rendimientos logarítmicos no funcionan adecuadamente para el precio spot. Lo anterior crea inconsistencias en los modelos financieros usados para la valoración de activos, estructuración de portafolios de inversión, o definir modelos de cobertura, etc, en términos económicos los costos asociados al uso de modelos con supuestos que no se cumplen son el pago de mayores costos de cobertura y pago de primas, subvaloración de pérdidas, etc.
La gráfica 3 indica que los rendimientos fluctúan alrededor de un valor medio (μ), lo que podría ser un indicio de que el proceso es estacional en media. También verifica la existencia de un proceso heterocedástico para los rendimientos, lo cual rompe con otro supuesto subyacente en el modelo logarítmico es decir supone que σ = cte.
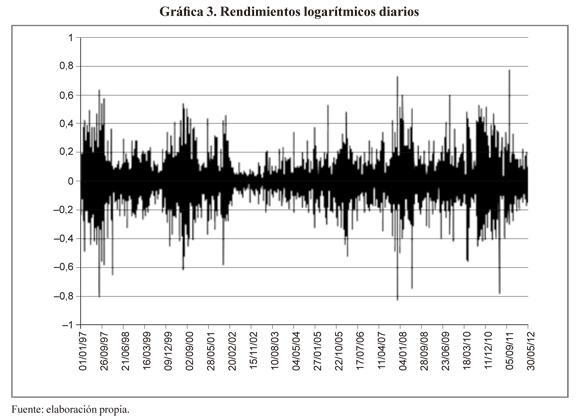
Como un ejemplo podemos presentar dos modelos comúnmente usados en finanzas, el modelo de cuantificación de riesgos de mercado o Valor en Riesgo - VaR1 (relación (2)), y el Movimiento Browniano Geométrico - MBG2 (relación (3)) (Hull, 2006; Winston, 2000).
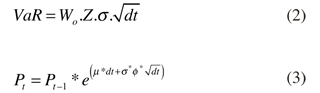
Siendo Wo el valor del portafolio energético. En ambas relaciones, σ es la volatilidad de los rendimientos logarítmicos (asume σ = cte.) y crece con la raíz cuadrada del tiempo Vdt. μ es la tasa promedio de rendimientos la cual se supone constante y normalmente distribuida, además los rendimientos se asumen independientes (ruido blanco). Por lo tanto esta relación presenta problemas con el cumplimiento de los supuestos implícitos como se explica más adelante.
1.2. Análisis de la correlación
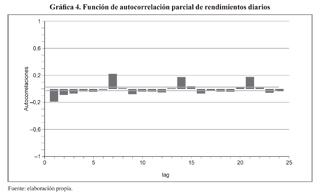
Para verificar las propiedades de independencia o que la serie es ruido blanco se puede calcular la función de autocorrelación parcial de los rendimientos. La gráfica 4 muestra que la autocorrelación entre rendimientos es significativa en el corto plazo. Como puede observarse las correlaciones para los días 1, 2, 3, 4, 5 y 7 superan los límites de confianza al 95% de la prueba de significancia para la correlación. Esto descarta, primero, el supuesto que la serie de rendimientos es ruido blanco. Segundo, el modelo de agregación de volatilidad no es adecuado para m días. Tercero, la correlación es negativa, es decir, si ocurre una subida de precios es probable que al día siguiente haya una caída.
1.3. Distribución de probabilidad
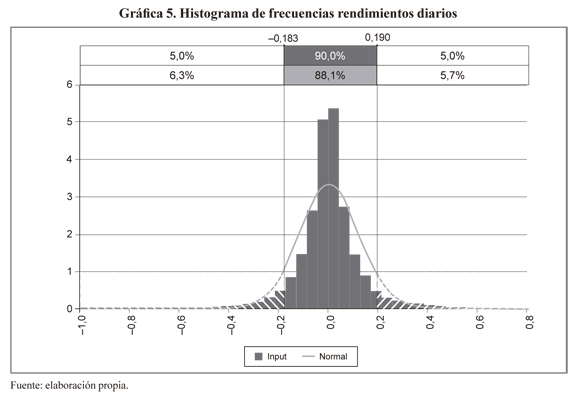
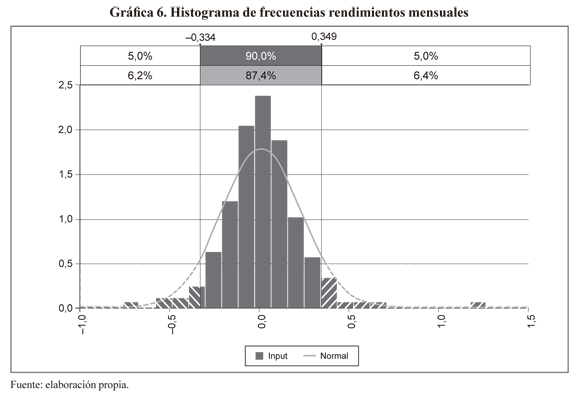
Las gráficas 5 y 6 presentan los histogramas de frecuencia de los rendimientos diarios y mensuales, respectivamente, comparados con la distribución normal. Como puede verse el histograma de los rendimientos se muestra centrado pero exhibe frecuencias muy altas alrededor de la media (leptocurtosis) y presencia de colas pesadas, esto último implica que la probabilidad de tener valores extremos es más alta que la que predice la distribución normal. Por ello es necesario buscar funciones de distribución que ajusten estas características. Un conjunto de distribuciones candidatas para este proceso, es la distribución de valor extremo, la Pareto generalizada, la Cauchy o Weibull. En 1937 Paul Pierre Levy tomó los estudios de Pareto y formuló una distribución generalizada en la cual la normal y la Cauchy son casos especiales. Dicha distribución, conocida como la distribución de Pareto-Levy es más consistente con el comportamiento de los mercados de capitales (Levy, 1937).
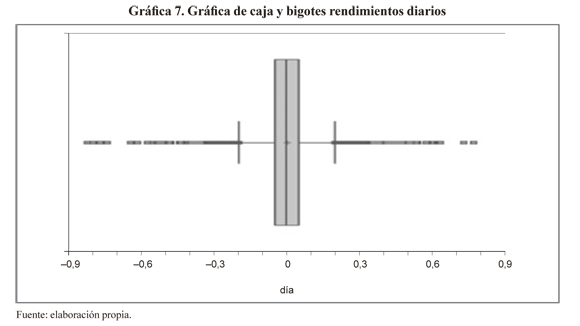
Con el fin de mostrar la presencia de valores extremos en la serie, la gráfica 7 muestra la caja de bigotes de los rendimientos del spot (Tukey, 1977). La gráfica indica la presencia de colas largas en la distribución empírica ya que muchos puntos están por encima y abajo del límite del bigote (1.5 veces el rango intercuarlítico), En términos de probabilidad existe una mayor probabilidad de tener valores extremos que la que predice la distribución normal y por tanto mayor exposición al riesgo.
El cuadro 2 indica las pruebas de normalidad para los rendimientos logarítmicos diarios a un nivel de confianza del 95%. Todas las pruebas tienen un valor-P < 0.05, lo que implica rechazar la hipótesis de normalidad inherente de los rendimientos diarios. Lo anterior desvirtúa la propiedad de aditividad de los rendimientos y la agregación de la volatilidad mediante la ecuación 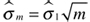 , tal como fue indicado previamente.
, tal como fue indicado previamente.
De igual manera, se ejecutaron las pruebas para determinar el ajuste a las distribuciones de probabilidad más conocidas y no se encontró ajuste. Como resultado, se concluye que los precios diarios de energía no siguen una distribución de probabilidad estándar conocida. Estos mismos resultados se verifican también para los precios mensuales.
1.4. Análisis de la volatilidad
La serie de tiempo de rendimientos exhibe comportamiento heterocedástico (gráfica 3) es decir, existen periodos de alta variación en los precios y otros de baja variabilidad. Este comportamiento puede ser producido por múltiples circunstancias tales como factores hídro-climáticos, condiciones de mercado, factores sociales, cambios en la demanda, el nivel de los embalses, entre otros.
La volatilidad de los precios se debe a la característica inherente a la electricidad transada como activo, las cuales están asociadas a no tener bienes sustitutos directos, la no almacenabilidad o la brecha que existe entre la oferta y la demanda. Por ello se hace indispensable contar con modelos de volatilidad variable que permitan capturar la dinámica de los precios de la energía. Desde un enfoque financiero, la heterocedasticidad afecta la valoración de primas de contratos de derivados financieros, o los modelos de medición de riesgos (Weron, 2006; Longstaff y Wang, 2004). Por tanto, conocer la volatilidad actual y predecir la volatilidad futura, es vital para la gestión del riesgo y del portafolio.
Los modelos ampliamente difundidos corresponden a los desarrollados por Bollerslev (1986) denominados modelos generalizados autoregresivos de heteroscedasticidad condicionada (GARCH). Los modelos GARCH (p,q) se pueden representar por:
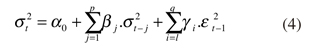
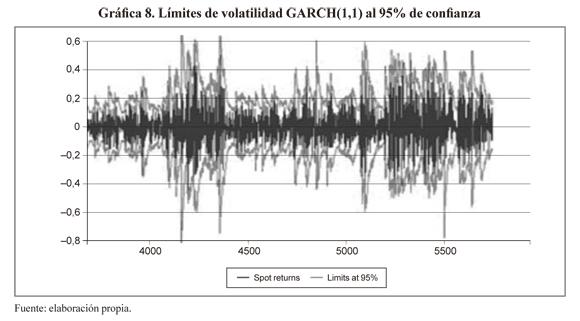
Donde p indica el número de coeficientes GARCH y q el número de coeficientes ARCH. Los parámetros α0, βj, γj. deben estimarse y Rt = μ + εt. El modelo GARCH (1,1) ajustado a los rendimientos diarios del spot se indica en la Gráfica 8 la cual muestra el desempeño del modelo con intervalos de confianza al 95%.
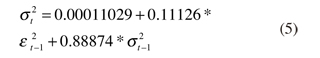
Debido al llamado efecto de apalancamiento se ha desarrollado otra clase de modelos GARCH que son capaces de capturar comportamie ntos asimétricos de la volatilidad e implícitamente de los mercados, es decir, en los mercados no repercuten de igual forma las buenas o malas noticias. Los movimientos a la baja en el mercado vienen acompañados de mayor volatilidad que los movimientos al alza; esto se conoce como asimetría del mercado. El modelo EGARCH (Pagan y Schwert, 1990) captura el efecto de apalancamiento o correlación negativa entre el precio y la volatilidad, y sugiere que la influencia de los residuales sobre la varianza condicional es exponencial y no cuadrática como es asumido por el modelo GARCH. Más adelante se muestra que en el mercado de energía se presenta esta asimetría.
1.5. Estacionalidady presencia de picos
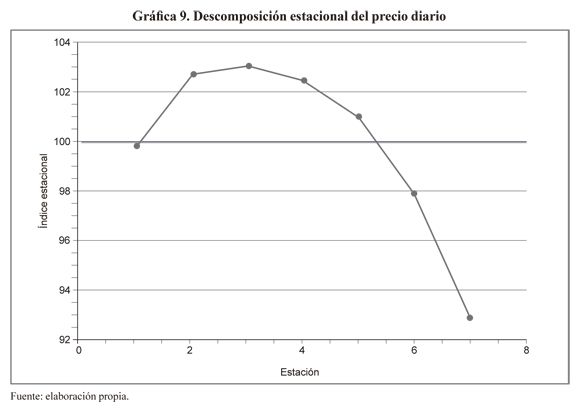
La gráfica 9 muestra los índices estacionales diarios It del precio diario de energía, indicando que a partir del lunes el precio de la energía tiende a incrementarse, mientras que en los fines de semana y días feriados, el precio tiende a decaer, lo cual obedece a que en estos días la demanda es menor. Los índices estacionales nos permiten obtener la serie desdestacionalizada, es decir, nos permite filtrar de la serie la variación periódica o predecible dejando solo el componente de tendencia; esto es posible cuando dividimos los precios sobre el índice Ptd = Pt/It.
La presencia de colas largas indica la presencia de picos en la serie de rendimientos. Con el fin de identificarlos, se utiliza la metodología propuesta por Weron (2006) para caracterizar tanto los picos por movimientos al alza o a la baja del precio spot. Un salto se entiende como todo cambio en el comportamiento "normal" de la serie que sobrepase una tolerancia máxima definida como umbral (Outlier). En el presente trabajo se estableció un umbral de 2.5 veces la desviación estándar de la serie de rendimientos histórica desestacionalizada (ln (Pt/Ptd)). La gráfica 10 muestra la presencia de picos en la serie de rendimientos.
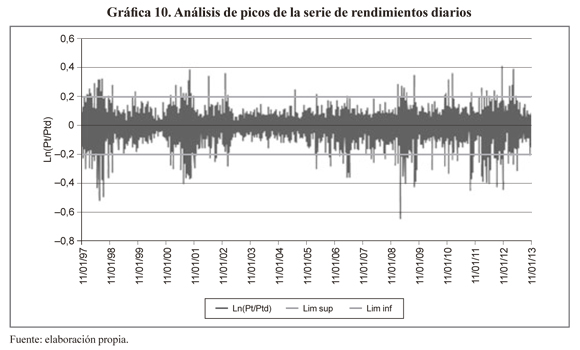
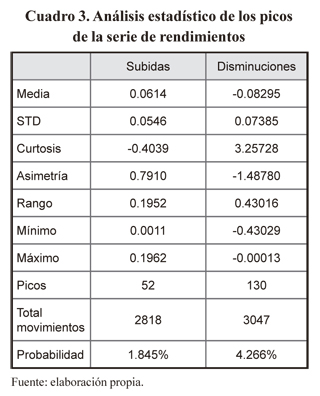
Los valores medios y desviación estándar tanto para picos de subida y disminución de precios se indican en el cuadro 3. La probabilidad de un incremento del precio es 48.04% y una disminución del 51.95%. Se detectaron 182 picos (3.10% del total de rendimientos). La probabilidad de que sea un pico al alza y a la baja dado que se presentó un pico es 28.57% y 71.42% respectivamente, estos resultados reflejan una asimetría del mercado, es decir, los agentes reaccionan de diferente manera cuando se presentan noticias buenas o malas en el mercado. La probabilidad de tener un pico dado que hubo una subida del precios es 1.84% mientras que la probabilidad de tener un pico dado que hubo una caída en el precio es de 4.266%. El análisis previo indica la necesidad de incorporar consideraciones asociadas a la presencia de picos en el análisis del proceso estocástico de la serie de rendimientos.
Como se aprecia, el precio spot de la energía tiene características particulares. Cabe preguntar: ¿cómo se deben modificar las relaciones financieras o qué otras técnicas de análisis se podrían aplicar para recoger adecuadamente las características subyacentes en las series de tiempo y ser utilizados en la práctica? La siguiente sección intenta dar una aproximación a esta pregunta.
2. Análisis fractal del spot
En esta sección se aplican herramientas estadísticas para el análisis de series de tiempo derivadas de la teoría fractal propuesta por Mandelbrot, lo cual nos permitirá hacer una representación más aproximada a las características inherentes de los precios spot de la energía y las cuales deberían ser incorporadas en las herramientas de análisis financieros aplicadas en el sector eléctrico. El presente numeral está fundamentado en los trabajos de Hurst y su análisis del rango reescalado (R/S) (Hurst, 1951), el ajuste de la distribución de cola pesada tipo Pareto-Levy y el análisis espectral de la serie para la detección de ciclos.
El análisis fractal inicialmente intenta detectar si el comportamiento de la serie de tiempo es completamente aleatorio (ruido blanco - comportamiento gaussiano), persistente (hay una correlación de largo plazo y sensibilidad a las condiciones iniciales), o anti persistente (el sistema es amortiguado o existe un proceso de reversión que intenta devolver al equilibrio el sistema ante una perturbación).
2.1. Análisis de la volatilidad
En general las series de tiempo con colas pesadas dan cuenta de procesos de memoria larga producidos por un proceso estocástico no lineal que puede causar una varianza variable en el tiempo o un proceso de memoria larga llamado Pareto-Levy (Peters, 1994). Vimos que a partir del supuesto de normalidad de los rendimientos se deriva que la volatilidad crece con la raíz cuadrada del tiempo (√dt). Sin embargo, puede ocurrir que el crecimiento de la volatilidad sea mayor o menor de esta tasa, lo anterior va en contravía de las caminatas aleatorias y eficiencia del mercado supuestos subyacentes en la teoría financiera moderna.
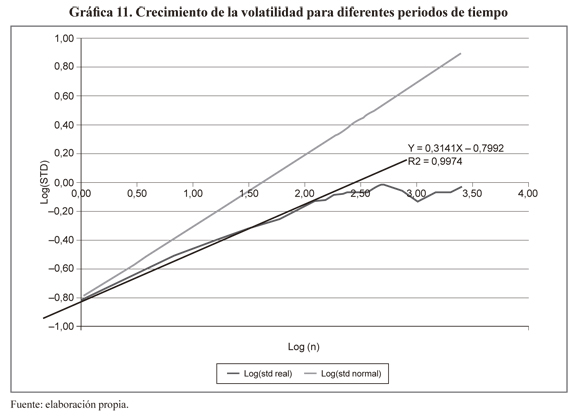
Para el caso de la volatilidad de los rendimientos del precio spot, la gráfica 11 indica el crecimiento de la volatilidad para diferentes periodos de tiempo. Como puede apreciarse, el crecimiento de la volatilidad del spot es menor que la raíz cuadrada del tiempo (αm= α1.m031). Lo anterior refleja un comportamiento antipersistente de la volatilidad (el sistema se "amortigua"), comportamiento que ha sido verificado también en otros mercados eléctricos. (Weron, 2003), es decir, cuando los precios suben (o bajan) el sistema tiende al equilibrio. Este comportamiento está relacionado con flujos turbulentos donde la media y varianza global no pueden ser determinadas con precisión por ser inestables (Peters, 1996). Este resultado tiene importantes consecuencias sobre los modelos financieros ya que son varios los que utilizan la volatilidad y su escalamiento en el tiempo como variable de entrada (ver relación 6). Un escalamiento como caminata aleatoria sobrevaloraría los riesgos de mercado del spot o sobrevaloraría los precios de los derivados, por ejemplo.
2.2. Exponente de Hurst
El resultado sobre el comportamiento de la volatilidad puede ser verificado a partir del cálculo del exponente de Hurst. El análisis permite medir la memoria del proceso y determinar si el proceso es aleatorio, persistente o anti persistente así como la duración de los ciclos. Para ello utilizaremos la metodología del rango reescalado (R/S) (Mandelbrot y Wallis, 1969) basada en los trabajos de Hurst sobre la hidrología del río Nilo (Hurst, 1951). El análisis intenta medir cómo el nivel de una variable fluctúa alrededor de su nivel medio en el tiempo, es decir, el análisis muestra como el rango de la fluctuación cambia dependiendo de la longitud de tiempo utilizada para medir.
Sea Ni la serie de tiempo de los rendimientos diarios calculados mediante la relación (1) y sea N el número de datos de la serie. Si dividimos la serie en A subperiodos de longitud n, tal que N = A χ n, entonces todo dato se puede escribir Nak con a un subperiodo entre los diferentes A subperiodos y k el rango del dato dentro de los n datos de a. Así, el valor promedio de cualquier subperiodos a, escrito como ea estará dado por:
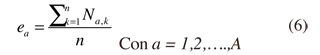
La desviación de cada rendimiento Na,k respecto a la media ea en cada subintervalo a es (Nak - ea) y la acumulación de las desviaciones en a hasta el Nak, escrita Xak está dada por:
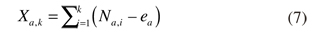
Con a = 1;2;....;A , k = 1;2;.......;n. Asimismo, dentro de a se puede notar en qué medida pasar del rendimiento del periodo k al rendimiento k+1 influye la desviación acumulada. Por lo tanto, se pueden notar las influencias de los rendimientos de diferentes periodos sobre el rendimiento del siguiente periodo. Por ejemplo, si la desviación acumulada aumenta en k+1 respecto a k entonces el rendimiento sigue aumentado/bajando en el tiempo. Lo que ocurre en el pasado influye, en cierta medida, el futuro. De lo contrario, si la desviación acumulada disminuye en k+1 respecto a k hay un proceso de reversión de la subida/bajada en el tiempo. Lo que ocurre en el pasado no necesariamente se realizará en el futuro.
Teniendo en cuenta dichas influencias, se puede establecer la desviación acumulada mínima así como la máxima dentro de a. El rango ajustado de α, escrito Rα, es definido como el máximo menos el mínimo valor en cada subintervalo, esto es:
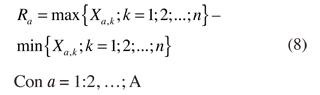
Igualmente, a mayor Rα el proceso de reversión de los rendimientos dentro de es menos frecuente en el tiempo.
Por otra parte, la desviación muestral para cada subperiodo es:
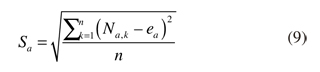
El rango Rα es normalizado dividiendo por la desviación estándar muestral de cada subintervalo Sα, esto es (Rα/Sα). Tenemos α-subperiodos contiguos de longitud n. El valor promedio para la longitud n, es definido como:
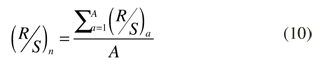
(R/S)n proporciona información sobre la autosimilaridad de todos lo intervalos de tiempo, n. La longitud de los intervalos n, es incrementada hasta n = N/2 y deben seleccionarse valores de n que incluyan los puntos iniciales y finales de la serie. Hurst propuso la siguiente relación derivada de los trabajos de Einstein sobre el movimiento de una partícula:

Tomando logaritmos tenemos:
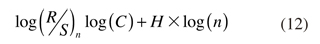
Lo cual significa que la estimación de la pendiente de un gráfico log-log es la estimación del exponente de Hurst. H describe la probabilidad de eventos consecutivos.
El rango reescalado es solo una de las técnicas que actualmente están disponible para la estimación de H, otras técnicas de cálculo han sido propuestas tal como la técnica de ventanas de varianza escalada (Cannon et al., 1997), o el método del periodograma. Sin embargo, el rango reescalado es el análisis más utilizado (Rzeszotko, 2012).
Respecto al significado del exponente, cuando 0.5<H<1, la serie de tiempo es persistente y caracteriza procesos de memoria larga, lo que ocurre hoy impactará en el futuro; si ocurre una subida del precio es más probable que mañana vuelva a subir. Cuando 0<H<0.5 la serie es anti persistente, el proceso se revierte, si ocurre una subida es más probable que el día siguiente ocurra una caída. Si H = 1 la serie es determinística. Si H = 0.5 la serie es ruido blanco. Si H es constante sobre un rango amplio de valores se dice que el proceso es autosimilaridad estadística lo cual es una propiedad de las estructuras fractales.
La gráfica 12 verifica el comportamiento antipersistente del precio spot, con un coeficiente Hurst, H = 0.39 dado por la pendiente de la recta ajustada a la línea punteada que representa el análisis de Hurst para el precio spot. La línea negra representa los cálculos para una serie de ruido blanco simulada normal con media y desviación típica de la serie original.
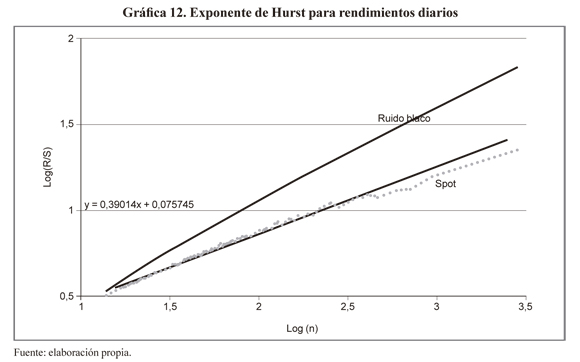
Podemos aplicar la prueba de significancia del exponente de Hurst de la serie (Anis y Lloyd, 1976), calculando un intervalo de confianza al 95% del exponente de una serie de ruido blanco (línea negra). Si consideramos un intervalo de confianza para el valor medio del exponente de Hurst de una serie de ruido blanco normal (HN) podemos determinar si H de la serie de tiempo analizada es significativamente diferente de una serie de ruido blanco. Para la serie de ruido blanco obtenemos (Hurst serie ruido blanco HN = 0.57 y desviación típica stdHN = 0.0132). El resultado indica que el exponente de Hurst para el precio spot es 14,27 = |H - N|/std(HN) veces la desviación estándar de HN. H es significativamente diferente de una caminata aleatoria. Este resultado rompe el supuesto de independencia de las observaciones. Su interpretación puede resumirse en los siguientes puntos:
- H describe la probabilidad de que eventos consecutivos ocurran. Si H = 0.39 significa que si el último evento fue una subida del precio, el siguiente evento tendrá una probabilidad 0.39 de que suba de nuevo y 0.61 de que baje.
- Hay una correlación negativa de los rendimientos, los cambios se revierten (un incremento es seguido de un decremento y viceversa) sin embargo la magnitud del cambio es desconocida. La reversión puede ser más grande o más pequeña que el incremento, es decir, no hay garantía de que la eventual reversión sea suficiente para compensar las pérdidas previas. Eso conlleva a que haya dificultades en identificar la media y varianza del proceso. Los comportamientos antipersistentes están relacionados con procesos en los cuales la media y varianza poblacional no están definidas, lo cual debe ser verificado.
- H está relacionado con la dimensión fractal de la serie de tiempo. La dimensión fractal mide la rugosidad de la serie; es calculada de manera aproximada mediante la relación d = 2 - H (Peters, 1996). Para el precio spot este es d = 2 - 0.39 = 1.61. La interpretación de este resultado hace referencia a la complejidad del sistema bajo estudio. El entero próximo a la dimensión fractal nos habla del número mínimo de variables dinámicas necesarias para modelar el sistema (la cuestión es determinar cuáles son estas variables) y coloca un límite inferior al número de grados de libertad.
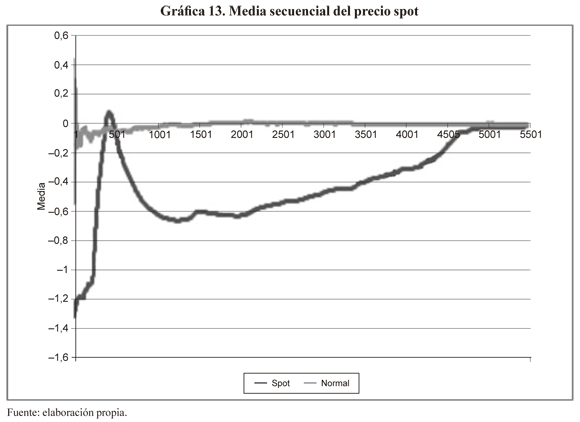
Para verificar la existencia de la media y desviación típica poblacional del precio spot se realiza el cálculo de la media y desviación típica secuencial a la serie de tiempo normalizada. De manera paralela se hace lo mismo para una serie aleatoria normalmente distribuida. Para ello calculamos media y desviación y vamos agregando las observaciones una a la vez hasta cubrir todo el espacio de datos disponibles. Para un proceso normal N(0,1), la media y desviación típica secuencial convergen a la media y desviación típica poblacional, tal y como es previsto en la ley de los grandes números, la cual afirma que a medida que aumentamos el tamaño muestral los parámetros de la muestra convergen a los parámetros de la población.
La gráfica 13 muestra los resultados para la media secuencial indicando que el proceso seguido por el spot tiene problemas de convergencia al valor medio poblacional. Como puede verse la serie normal converge rápidamente a su valor medio (cero) mientras que para el spot el proceso logra estabilizarse a partir la muestra 4786. En nuestro caso la media poblacional para la serie puede ser obtenida.
Las gráficas 14 y 15 muestran el caso de la desviación típica secuencial; como se puede ver, la serie de tiempo no converge hacia una desviación típica poblacional porque existen saltos significativos en la desviación aun usando muestras grandes.
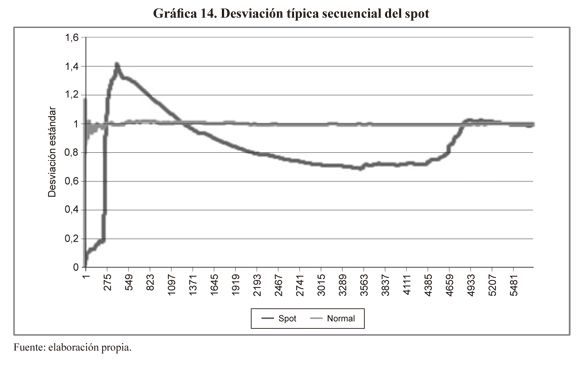
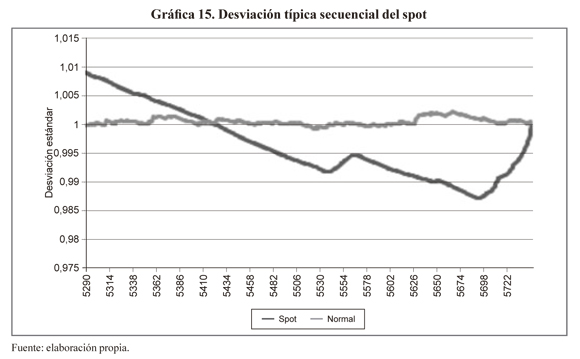
La gráfica 15 muestra una ampliación para los últimos datos de la serie donde se indica que aun con toda la muestra se presentan saltos significativos en el valor de la desviación. Los resultados anteriores permiten concluir que tanto media como desviación típica del spot son inestables (no existen estadísticos poblacionales, sin embargo se pueden calcular estadísticos muestrales) y resalta el hecho de que la distribución normal es inadecuada para describir los rendimientos del spot.
2.3. Ajuste de la distribución Pareto-Levy
De acuerdo con la literatura los fenómenos con distribuciones de cola pesada y leptocurtosis son mejor representados por procesos Pareto-Levy, distribuciones α-estables o distribución fractal (Nolan, 2009). Sea la función F(x) y sea x1 y x2 copias independientes de la variable aleatoria X. X se dice estable si para cualquier constante b1, b2 > 0 la variable aleatoria b1x1+b2x2 tiene la misma distribución de X, bX+c para alguna constante b>0 y c, esto es:
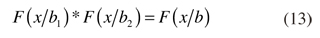
Esta relación existe para todas las funciones de distribución y significa que la combinación lineal de dos copias independientes de la variable tiene la misma distribución, parámetros de escala y localización. La función de distribución está dada por:
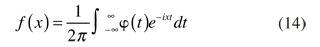
donde φ(t) es la función característica representada por:
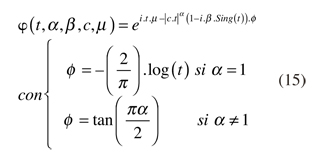
La distribución estable tiene cuatro parámetros: α, β, c, μ
μ = Parámetro de localización. Para el caso normal μ=0
c = Parámetro de escala. Se asemeja a la desviación típica muestral. Es una medida de dispersión y expresa como la distribución se expande o comprime alrededor de μ. Toma valores alrededor de 1.
β = Parámetro de asimetría. Toma valores entre -1<β<1. Si β < 0 la distribución es sesgada a la izquierda y si β > 0 es sesgada a la derecha.
α = Parámetro de altura. Exponente característico, modela la altura y la forma de las colas con 0<α<2. Cuando α = 2 la distribución es normal, si α < 2 el segundo momento o varianza es infinita, si 1 < α < 2 el primer momento o media existe y cuando α < 1 el primer momento o media poblacional es infinita.
La distribución α-estable se dice distribución fractal por sus propiedades de autosimilaridad, es decir, si α, β no cambian y se cambia solo el parámetro c, entonces la distribución se reescala y se mantienen las probabilidades. Esto se conoce como autosimilaridad estadística (las series son divisibles con igual distribución; solo cambia el parámetro c). Por otra parte, el exponente característico α puede tomar valores fraccionarios entre 1 y 2 la cual es la dimensión fractal del espacio de probabilidad.
El ajuste de la distribución α-estable a los rendimientos del precio spot diario de la electricidad se indica en la gráfica 16. Como se indica, la distribución α-estable se ajusta adecuadamente a la serie de rendimientos del spot diario. Utilizamos un método iterativo sobre la función característica con el fin de estimar los parámetros de la distribución (Koutrouvelis, 1981):
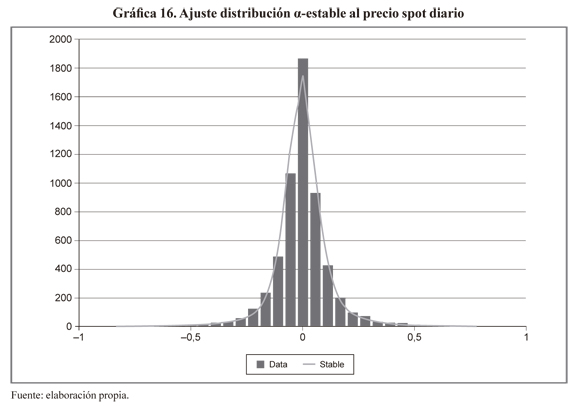
α = 1,391518087, β = 0,04413493, C = 0,05348232, μ = 0,00087231
La prueba de bondad de ajuste Kolmogorov-Smirnov al 95% de confianza tiene los siguientes parámetros: estadístico de prueba (ST)= 0,017023 y nivel crítico (CV)= 0,017951. Como ST<CV aceptamos la hipótesis nula y concluimos que los rendimientos del spot diario se ajustan a una distribución α-estable al 95% de confianza. Además, como α= 1,391518087 < 2, significa que el segundo momento o varianza poblacional de la serie es infinita como habíamos mostrado anteriormente (gráficas 14 y 15) mientras que la media poblacional o primer momento converge.
Los análisis previos (análisis R/S y el ajuste de la distribución α-estable) indican que el precio spot diario es un proceso fractal con varianza incondicional infinita (sin varianza poblacional), sin embargo es posible medir la varianza condicional finita como un efecto local de la distribución fractal utilizando algún modelo de volatilidad dinámica del tipo EGARCH o GARCH (varianza muestral) tal como el que se ajustó antes.
Los resultados obtenidos indican que el uso de la distribución α-estable es más adecuada para la modelación del precio spot de la energía y debe ser considerada en los modelos financieros para la valoración de activos, la identificación del proceso estocástico, la cuantificación de riesgos y la valoración de opciones.
2.4. Análisis espectral
El análisis espectral de la serie spot está relacionado con los análisis previos ya que es otra de las maneras de calcular el exponente de Hurst, por otra parte, el análisis de la serie de tiempo en el dominio de la frecuencia permite descomponer la señal de la serie en una suma de ondas sinusoidales donde es posible identificar los componentes armónicos en la señal o presencia de ciclos. La gráfica 17 muestra el espectro de potencia o transformada de Fourier discreta para el precio spot diario, e indica la presencia de componentes armónicos en la serie de tiempo.
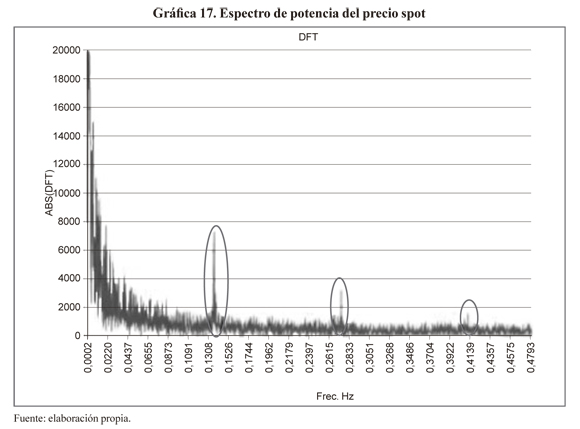
La frecuencia de los componentes cíclicos identificados se indica en el cuadro 4, el cual muestra la presencia de un factor de escalamiento de la frecuencia fundamental de 0,1429 ciclos/día, Hz = 7 días/ciclo, es decir, las otras frecuencias son un múltiplo de la frecuencia fundamental.
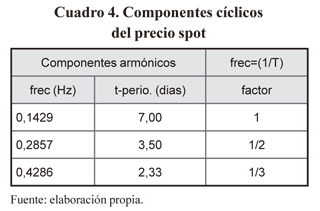
La interpretación de mercado de la presencia de ciclos de siete días en el precio spot muestra que el precio spot está relacionado con el factor estacional de la demanda diaria y debe tenerse en cuenta cuando estamos interesados en realizar pronósticos del precio spot.
El espectro de potencia nos permite, a su vez, determinar si el proceso es persistente o antipersistente para ello es necesario el cálculo del exponente espectral (b), el cual sigue la ley de potencia inversa mediante un gráfico Log-Log (el análisis permite caracterizar el ruido de la serie3). La relación entre el exponente de Hurst y el exponente espectral está dado por b=2H+1. La gráfica 18 nos muestra el inverso del espectro de potencia o periodograma con b=1.4355, el cual corresponde a la pendiente de la línea ajustada al grafico Log-Log. A partir de "b", calculamos el valor H=0.22. Este resultado aunque difiere del análisis R/S, verifica el comportamiento anti persistente de la serie de los precios spot de la energía.
3. Conclusiones
En el mercado de energía mayorista colombiano los precios de la energía eléctrica se ven influenciados por múltiples factores de oferta y demanda que inciden directamente en su comportamiento con características no lineales y complejas.
La serie de tiempo analizada se presenta de dos formas: diaria y mensual. El análisis hace especial énfasis en los precios diarios, sin embargo, se verifican las mismas características para los precios mensuales. Los supuestos acerca del comportamiento de los rendimientos logarítmicos asociados a la agregación de los rendimientos y la volatilidad para m-días además del supuesto de normalidad subyacentes en los modelos financieros, no se cumplen para el precio spot de la electricidad.
La forma de la distribución de los rendimientos está caracterizada por la presencia de valores extremos (colas pesadas) y centrada alrededor de la media, esta característica es propia de las distribuciones de Levy o α-estable. El estudio rechaza el comportamiento normal y verifica el comportamiento α-estable de la distribución de los rendimientos. Este hecho significa que la serie del spot tiene una estructura fractal, con exponente característico α = 1.3915 lo que implica que en la cola, las probabilidades de ocurrencia de valores extremos se comportan como ley de potencia con una probabilidad mayor que la que define la distribución normal. Se descarta el hecho de que la volatilidad de los precios spot crezca con la raíz cuadrada del tiempo el cual es aplicado al caso de las series aleatorias. En cambio, la volatilidad muestra un comportamiento anti persistente, es decir, los choques aleatorios o cambios de precios son amortiguados. El crecimiento de la volatilidad en el tiempo está dado por un factor de 0.31, menor de 0.5, lo que descarta que la serie spot sea una serie aleatoria. Existe una estructura de correlación en la serie y en el corto plazo es negativa.
El exponente de Hurst en 0.39 verifica el comportamiento antipersitente, esto indica que existe probabilidad de 0.61 de que si ocurre un aumento del precio, el siguiente movimiento será una caída. Sin embargo no es posible determinar la magnitud de este cambio con exactitud debido a que no es posible determinar la varianza incondicional de la serie (varianza poblacional) con precisión.
Sin embargo es posible determinar la varianza condicional (varianza muestral) utilizando un modelo de volatilidad dinámica.
El comportamiento antipersitente significa que el sistema cubre menos distancia que una variable completamente aleatoria ya que los movimientos del precio se amortiguan. Debido quizás a la intervención del mercado, o a la participación de inversores con diferentes horizontes temporales los cuales amortiguan las fluctuaciones del precio.
Tradicionalmente la volatilidad se ha utilizado como un indicador de riesgo para la comparación del riesgo entre activos, sin embargo como se explicó, la volatilidad en el caso del precio spot es un indicador inestable incluso aumentando el tamaño de la muestra, esto plantea nuevas preguntas a nivel académico, a saber: ¿Cómo puede utilizarse la dimensión fractal de una serie como un indicador de riesgo en vez de la volatilidad? Tal vez el concepto de dimensión fractal cuente una historia diferente de los procesos subyacentes y sea un mejor indicador que la volatilidad. Esto plantea nuevos retos a nivel académico y práctico. El análisis de la serie en el dominio de la frecuencia permitió detectar la presencia de ciclos en la serie spot de siete días; comportamiento que puede estar asociado a la estacionalidad de la demanda semanal. Aunque se deben realizar más análisis asociados a la estructura del mercado y la formación del precio, esta información es relevante cuando estamos interesados en la realización de pronósticos del precio spot.
Las características fractales de la serie spot identificadas deben ser incorporadas en los modelos financieros de tal manera que permitan la valoración de productos derivados, la cuantificación de riesgos, la estructuración de portafolios, la simulación financiera y la realizar pronósticos donde el subyacente es el spot de energía de una manera más coherente, es decir, debemos trabajar en nuevas aproximaciones, nuevas maneras de entender los mercados que nos permita obtener modelos financieros que capturen las características dinámicas de la serie spot.
Como sugerencia para posteriores desarrollos de este artículo se plantea el reto académico de desarrollar nuevas formas de análisis de los problemas de decisión que considere las características del mercado fractal.
Pie de página
1VaR permite cuantificar la pérdida económica máxima en un intervalo de tiempo y un nivel de confianza dado. Este concepto se utiliza actualmente en la cuan-tificación de pérdidas por riesgos de mercado, riesgo crediticio y riesgos operativos.
2MBG es usada como un proceso estocástico o modelo de dinámica de precios que posibilita la generación de caminos aleatorios en procesos de simulación Monte-carlo de series de tiempo de origen desconocido, para la valoración de activos.
3Para una definición y ampliación de los tipos de ruido asociados a una serie de tiempo, ver Peter (1996).
Referencias
Anis, A. A. and Lloyd, E. H. (1976). The expected value of the Adjusted Rescaled Hurst Range of Independent Normal Summands. Biometrika, 63 (1), 111-116. [ Links ]
Bhanot, K. (2000). Behavior of power prices: Implications for the valuation and hedging of financial contracts. The Journal of Risk, 2 (3), 43-62. [ Links ]
Bollerslev, T. (1986). Generalized autoregressive conditional heteroskedasticity. Journal of Econometrics, 31, 307-327. [ Links ]
Cannon, M., Percival, D., Caccia, D., Raymond, G. and Bassingthwaighte, J. (1997). Evaluating scaled windowed variance methods for estimating the Hurst coefficient of time series. Physica A. 241, 606-626. [ Links ]
Deidersen, J. and Truck, S. (2002). Energy price dynamics quantitative studies and stochastic processes. University of Karlsruhe, Tech. Report TR-ISMW-12/2002. [ Links ]
Erzgraber, H., Strozzi, F., Zaldivar, J., Touchette, H., Gutierrez, E. and Arrowsmith, D. (2008). Time series analysis and long range correlations of Nordic spot electricity market data. Physic A. Statistical Mechanics and its applications, 387, 6567-6574. [ Links ]
Hull, J. (2006). Options, futures and other derivatives. Prentice Hall. [ Links ]
Hurst, H. (1951). Long-term storage capacity of reservoirs, Transactions of the American Society of Civil. Engineers, 116, 770-799. [ Links ]
Janicki, A. and Weron, A. (1994) Simulation and Chaotic Behavior of a-Stable Stochastic Processes. New York: Marcel Dekker. [ Links ]
Johnson, B. and Barz, G. (1999). Selecting stochastic processes for modelling electricity prices. Energy Modeling and the Management of Uncertainty. London: Risk Books. [ Links ]
Joskow, P. and Kahn, E. (2001). A Quantitative Analysis of Pricing Behavior in California's Wholesale Electricity Market during Summer 2000. Working Paper, MIT. [ Links ]
Koutrouvelis, I. A. (1981). An iterative procedure for the estimation of the Parameters of Stable Laws. Commun. Stat. - Simul. Comput. 10 (1), 17-28. [ Links ]
Kwapien, J. and Drozdz, S. (2012). Physical approach to complex systems. Physics Reports, 515, 115-226. [ Links ]
Levy, P. (1937). Theorie de l'addition des variables aleatoires. Paris: Gauthier-Villars. [ Links ]
Longstaff, F. and Wang, A. W. (2004). Electricity forward prices: a high-frequency empirical analysis. Journal ofFinance, 59 (4), 1877-1900. [ Links ]
Mandelbrot, B. B. and Wallis, J. R. (1969). Noah, Joseph and operational hydrology. Water Resources Research, 4, 909-918. [ Links ]
Mandelbrot, B. B. (1997). Fractals and Scaling in Finance. Discontinuity, Concentration, Risk. Springer. Selecta vol. E. [ Links ]
Mandelbrot, B. B. and Hudson, R. L. (2010). Fractales y finanzas. Barcelona: TusQuests. [ Links ]
Mandelbrot, B. B. (1977). The Fractal Geometry of Nature, W.H. San Francisco: Freeman and Co. [ Links ]
Newman, M. E. (2003) The structure and function of complex networks. SIAM Review, 45 (2), 167-256. [ Links ]
Nolan, J. P. (2009). Stable Distributions: Models for Heavy Tailed Data. Switzerland: Birkhauser. [ Links ]
Norouzzadeh, P., Dullaert, W. and Rahmani, B. (2007). Anti-correlation and multifractal features of Spain electricity spot market, Physica A. 380, 333-342. [ Links ]
Peters, E. (1994). Fractal market analysis: Applying chaos theory to investment and economics. New York: Wiley Finances. [ Links ]
Peters, E. (1996). Chaos and order in the capital markets: A new view of cycles, prices, and market volatility. New York: Wiley Finance. [ Links ]
Rzeszotko, Z. (2012). Estimation of the Hurst exponent for market indices by use of rescaled range method and CAS mathematica. Case study: S&P500. Electronic Journal of Mathematics & Technology, 6 (3), 256-267. [ Links ]
Schwartz, E. S. (1997). The stochastic behavior of commodity prices: Implications for valuation and hedging. The Journal of Finance, 52, 923-973. [ Links ]
Serletis, A. and Rosenberg, A. (2007). The Hurst exponent in energy futures prices, Physica A, 380, 325-332. [ Links ]
Simonsen, I. (2003) Measuring anticorrelations in the Nordic electricity spot market by wavelets. Physica A: Statistical Mechanics and its Applications, May 1. [ Links ]
Simonsen, I., Hansen, A. and Nes, O. (1998). Determination of the Hurst exponent by use of wavelet transforms. Physical Review E. 58 (3), 2779-2787. [ Links ]
Tukey, J. W. (1977). Box-and-Whisker Plots. 2C, in Exploratory Data Analysis. Reading, MA: Addison-Wesley. [ Links ]
Weron, R., Simonsen, I. and Wilman, P. (2003). Modeling highly volatile and seasonal markets: evidence from the Nord Pool electricity market. Econometrics 0303007, EconWPA. [ Links ]
Weron, R. (2002). Measuring long-range dependence in electricity prices. In Empirical Science of Financial Fluctuations (pp. 110-119). Tokyo: Springer.
Weron, R., and Przybylowicz, B. (2000). Hurst analysis of electricity price dynamics. Physica A., 283, 462-468. [ Links ]
Weron, R. (2005). Heavy tails and electricity prices. Research Report HSC/05/2. Hugo Steinhaus Center for Stochastic Methods, Institute of Mathematics and Computer Science, Wroclaw University of Technology. Poland. [ Links ]
Weron, R. (2006). Modeling and Forecasting electricity loads and prices. A Statistical Approach. New York: Wiley Finance. [ Links ]
Winston, W. L. (2000). Financial models using simulation and optimization. Palisade Corporation. [ Links ]













