Serviços Personalizados
Journal
Artigo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Acessos
Acessos
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares em
SciELO
Similares em
SciELO -
 Similares em Google
Similares em Google
Compartilhar
Boletín de Ciencias de la Tierra
versão impressa ISSN 0120-3630
Bol. cienc. tierra no.34 Medellín jul./dez. 2013
SIMULACIÓN DE LA DIFUSIÓN DEL Cl- HASTA LA DESPASIVACIÓN DEL ACERO DE REFUERZO EN CONCRETO CON MICROSÍLICE Y EXPUESTO A CARBONATACIÓN
SIMULATION OF ION Cl- DIFFUSION UNTIL DESPASIVACIÓN OF REINFORCING STEEL IN CONCRETE WITH MICROSILICA AS ADDITIVE AND EXPOSED TO CARBONATION
Sergio Alberto Solano Rodríguez
Ing., M.Sc.c., Universidad Industrial de Santander.
Hugo Armando Estupiñán Durán
Ph.D. Profesor Asistente, Universidad Nacional de Colombia, Sede Medellín. haestupinand@unal.edu.co
Custodio Vásquez Quintero
M.Sc. Profesor Titular Laureado, Universidad Industrial de Santander.
Darío Yesid Peña Ballesteros
Ph.D. Profesor Titular, Universidad Industrial de Santander.
Recibido para evaluación: 18 de Octubre de 2012 / Aceptación: 15 de Septiembre de 2013 / Recibida versión final: 02 de Diciembre de 2013
RESUMEN: En este trabajo se simuló la difusión de cloruros y la corrosión de acero de refuerzo embebido en un pilote de concreto afectado por carbonatación en un ambiente marino de la costa pacífica colombiana, teniendo en cuenta, el tiempo de exposición, la carbonatación y la concentración de agregados finos en la preparación de las mezclas de las estructuras de hormigón. La simulación se realizó con la ayuda del software MATLAB Y FEMLAB, mediante ecuaciones diferenciales parciales de transporte de masa, para evaluar el servicio de vida útil de la estructura con acero de refuerzo. Se simularon tres diferentes mezclas 0.4, 0.5 y 0.6 de agua/cemento, con un 10% de microsílice como aditivo, en un ambiente sumergido en agua de mar. Los resultados mostraron la penetración del cloruro en el concreto y del dióxido de carbono y la predicción del tiempo de despasivación de las varillas de refuerzo.
Palabras clave: Difusión, Elementos finitos, Transporte de masa, Concreto
ABSTRACT: In this paper the chloride diffusion and corrosion of reinforcing steel embedded in a concrete pile affected by carbonation in a marine environment of the Colombian Pacific coast was simulated, taking into account the exposure time, carbonation and the concentration of fine aggregate in the preparation of mixtures of concrete structures. The simulation was performed with the help of MATLAB software FEMLAB by partial differential equations of mass transport, to assess the service life of the structure reinforcement. Three different mixtures 0.4, 0.5 and 0.6 water / cement ratio, with 10% of microsilica as an additive were simulated in an environment immersed in seawater. The results showed chloride penetration into concrete and carbon dioxide and prediction time depassivation of the reinforcing rods.
Keywords: finite elements, Mass transport, concrete, diffusion.
1. INTRODUCCIÓN
A nivel mundial existen numerosas estructuras de concreto que se encuentran en medios particularmente agresivos y expuestos al desgaste, como aquellos que se hallan expuestas a ambientes marinos donde el principal responsable de la corrosión es el ión cloruro. Los cloruros al llegar a la superficie del metal, causan que la corrosión se desencadene y se manifieste de diversas maneras: una sobre el metal, con una disminución de su diámetro inicial y por lo tanto de su capacidad mecánica; otra sobre el concreto, debido a que al generarse acumulación de óxidos expansivos en la interface acero-concreto, produciendo fisuras y desprendimientos, y por último sobre la adherencia del concreto al refuerzo (Mejía y Rodriguez, 1999).
El hormigón es uno de los materiales de construcción artificiales más antiguo que se conoce caracterizándose por su durabilidad y estabilidad en el tiempo. Se utiliza para proteger el acero en las armaduras, actuando como una barrera física que lo separa del medio ambiente (Cordero, 2005).
La vida útil de las estructuras con acero de refuerzo está altamente limitada por la acción de la corrosión del refuerzo, por la exposición a ambientes marinos o de sales de deshielo. Esta fenómeno físico de corrosión es producto de la despasivación de dichas varillas de refuerzo a causa de la acción del ion cloruro sobre éstas (Liu y Weyers, 1997; Martin-Perez et al., 2001).
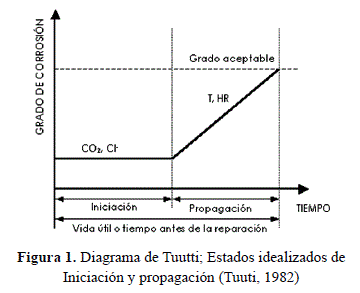
En general, el armazón de acero se encuentra protegido por el concreto de una acción directa, a causa de un ambiente altamente alcalino (pH>13), manteniéndolo en un estado pasivo. El concreto actúa como una barrera física contra el ingreso de agentes agresivos, que aceleran el deterioro y fatiga del acero. En la literatura, la corrosión del acero se idealiza como una secuencia de dos fases separadas: iniciación y propagación. Durante el estado de iniciación, los cloruros migran desde la superficie expuesta, hacia el acero a través del concreto, cuando estas concentraciones exceden un valor umbral, los niveles de pH bajan y toma lugar la despasivación del acero e inicio de la corrosión. Durante el estado de propagación, la corrosión de la varilla se hace presente generando perdidas aceleradas de acero, o hasta que la cubierta de concreto, se fragmente completamente, según el diagrama de Tuutti (1982, Figura 1).
El transporte de especies que participan en el mecanismo de corrosión (cloruro y dióxido de carbono), es afectado por la difusión del ion cloruro, la porosidad, la humedad relativa y la carbonatación. A medida que se difunde el dióxido de carbono, éste reacciona para formar CaCO3 (ec.1) reduciendo gradualmente la porosidad de la matriz cementícia y disminuyendo el tamaño de poro del mismo. Este fenómeno difusivo está regido por el principio de conservación de masa (ley de Fick). En general los procesos corrosivos del acero de refuerzo en el concreto son generalmente considerados como procesos electroquímicos (Havsmann, 1969; Page, 1979).
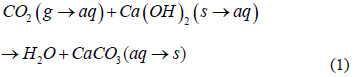
1.1 Mecanismos de Transporte
El transporte de gases (O2, CO2), agua e iones (Cl-) en concreto solo es posible en el sistema poroso del concreto. Este transporte se debe a fuerzas capilares, gradientes de presión (agua, gases) o de concentración (iones), diferencia de presión absoluta (agua, gases) y migración (León y Oróstegui, 2009).
Basado en la conservación de masa (segunda ley de Fick) y difusión en una sola dimensión, la ecuación diferencial parcial que gobierna dichos transportes, tanto del ion cloruro como del dióxido de carbono, se muestra en la ecuación 2. Este fenómeno está afectado por la mezcla agua-cemento equivalente (ec.3) y 10% de microsílice (tabla1).
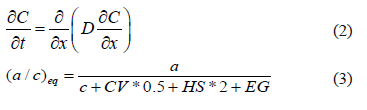
1.2 Transporte de Dióxido de Carbono
Se ha probado que la mitad del dióxido de carbono difundido, reacciona formando una capa carbonatada, mientras la otra mitad continua difundiéndose (Park, 2009), la ecuación 4 representa la difusión del dióxido de carbono a través del concreto, la ecuación 5 representa la difusión y consumo del dióxido de carbono y la ecuación 7 representa la generación de carbonato de calcio.
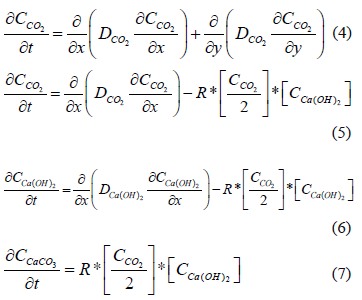
Donde t es el tiempo, x es la distancia de la superficie hacia dentro del concreto, D es el coeficiente de difusión de las especies (ec. 11) (Park, 2007), R es la constante de reacción. Para el estudio se tuvo presente la influencia de R en la difusión del dióxido de carbono, el coeficiente de difusión de la ecuación 10, como función de la humedad relativa, de la porosidad, tal como se presenta en la ecuación 12 y de un coeficiente de difusión inicial, con el fin de realizar una analogía del avance del frente carbonatado, de acuerdo a esto, el modelo en 2D se presenta de la siguiente forma:
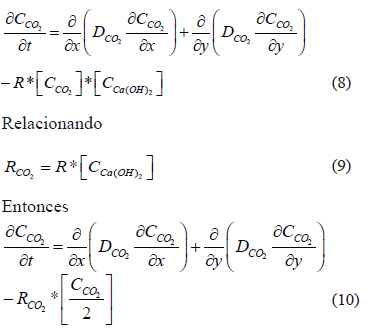
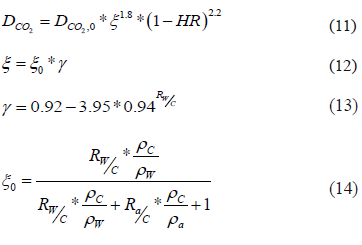
1.3 Transporte del Ion cloruro (Cl-)
El fenómeno difusivo del ion cloruro está gobernado por el modelo matemático de la segunda ley de Fick en dos dimensiones, en el cual el contenido de cloruros, varia respecto al espesor de la estructura y al tiempo de exposición. En este orden de ideas, se plantea la ecuación de Fick aplicada al caso de estudio.
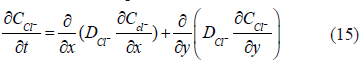
En esta investigación se compararon las evaluaciones de difusión de cloruros, carbonatación y corrosión realizadas a una estructura de concreto de 10 años de construida en la cota del pacífico colombiano, empleada como embarcadero, con resultados de simulación en un pilote de concreto de esta estructura, empleando software comercial y modelos ya establecidos en la literatura. En esta simulación se tuvo en cuenta que el coeficiente de difusión del ión cloruro es no lineal (ec.16 y 17), debido a que es función de la concentración de cloruros en la superficie de la estructura, también de un coeficiente de difusión calculado a un tiempo de referencia (28 días), y del tiempo de exposición de la misma elevado a un valor empírico de envejecimiento para mezclas con agregados m (García, 2009; Margat y Mollot, 1994).
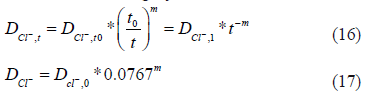
2. METOLOGIA
Para la realización de la investigación fue necesario fijar los parámetros de simulación como: cemento (portland tipo I), relación agua/cemento de 0.4, 0.5 y 0.6, 10% de microsílice como adición, concentraciones típicas de un ambiente marino a la cual se encuentran expuestas como son de 5.4E-4 Kg/m3 de CO2 y de 4 Kg/m3 de cloruros, con una humedad relativa en el ambiente de 78% y temperatura de 15 °C en la interfase varilla-concreto. Además, La figura 2, muestra un corte horizontal de un pilote de 0.4 m de ancho por 0.4 m de profundidad, en el cual se encuentran empotradas 4 varillas metálicas de ½ pulgada de diámetro, cada una de ellas está ubicada a 0.07 m de cada esquina del pilote. Una vez fijados los parámetros anteriormente mencionados, se realizó la simulación por elementos finitos de la difusión del ion cloruro y del dióxido de carbono con los cuales se halla los tiempos de despasivación de la varilla de refuerzo hasta alcanzar el umbral de cloruros y posterior inicio de la corrosión, es decir el cálculo de la densidad de corriente y la resistencia óhmica del concreto.
2.1. Simulación de la difusión de carbonatos y cloruros
Usando el método de elementos finitos, con la herramienta de simulación FEMLAB, se plantea la solución de la ecuación diferencial por la segunda ley de Fick en 2D, mediante ODE15, aplicado al pilote mostrado en la figura 2a. El mallado del modelo, se muestra en la figura 2b. Los perfiles de concentración, tanto del ion cloruro como del CO2 obtenidos en este trabajo, se asumieron diagonalmente (A-B), similares a los perfiles que reportan algunos autores (Martín-Perez et al., 2001; Chen, 2006; Park, 2008; Balaguera, 2009; García, 2009; Leon y Orostégui, 2009; Mike y Hans, 2011; Erhan y Mehmet, 2012).
Condiciones de simulación:
- Simulación del CO2
C (t0)=0 para x>0
C=Cs=5,4x10E-7 (g/cm3) para x=0 cuando t>0
- Simulación del ión Cloruro
C (t0)=0 para x>0
C=Cs=4 Kg/m3 para x=0 cuando t>0
Estas condiciones representan el modelo en 1D, pero pueden ser aplicadas a un modelo en 2D, ya que se asume que el pilote se encuentra rodeado por la atmosfera de simulación.
3. RESULTADOS EXPERIMENTALES
3.1 Perfiles de Concentración en carbonatación
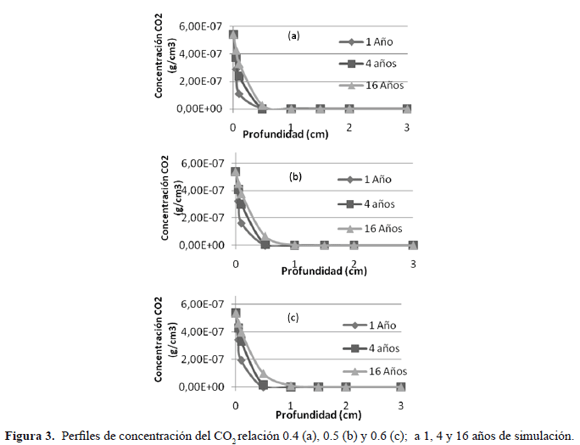
El frente carbonatado avanza simultáneamente con la penetración del dióxido de carbono en el pilote (Figuras 3a, 3b y 3c). Los resultados del modelo difusivo del CO2 obtenidos, se reportan en la tabla 3 y en el modelo resultante para una difusión natural (Ec.18).
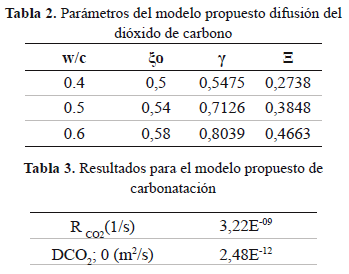
Las tablas 2 y 4 muestran los parámetros de porosidad y reducción de la misma, de acuerdo a la relación agua/cemento para la carbonatación y los coeficientes de difusión iníciales, para la difusión del ion cloruro (García, 2009). Además, la tabla 3 muestra los resultados numéricos del modelo difusivo de carbonatación y la tasa RCO2 que indica el consumo del dióxido de carbono a al difundirse en el concreto.
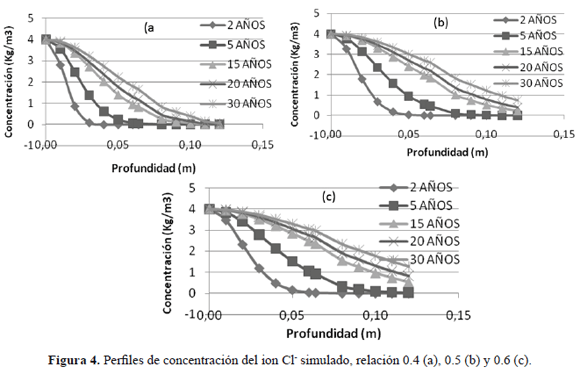
Los perfiles de concentración del ion cloruro se simularon para 2, 5, 15, 20 y 30 años de exposición de la estructura a un ambiente marino. En las Figuras 4a, 4b y 4c se presentan los resultados.
Con los resultados de la simulación y perfiles de concentración del ion cloruro en el pilote se logró calcular el tiempo de despasivación de las varillas al alcanzar el umbral de cloruros anteriormente fijado (0,9 Kg/m3), los resultados fueron 16, 7 y 5 años para relaciones a/c 0.4, 0.5, 0.6 respectivamente.
Los valores reportados en la tabla 4, muestran el coeficiente de difusión aparente Dcl del ion cloruro en el concreto, de acuerdo con la relación agua/cemento equivalente, estos perfiles de concentración, son obtenidos con la solución del coeficiente de difusión evaluado a un año Dcl,1, (Ec.16). La adición de microsílice (10%) en la matriz cementicia, provee una mayor capacidad de resistencia a la permeación de agentes agresivos, hay que agregar que a medida que aumenta la relación a/c, disminuye la resistencia a la permeación, debido a que la porosidad aumenta (aumenta la difusión). Para este estudio se obtuvieron resultados de difusión de dióxido de carbono y de difusión del ion cloruro (tabla 3 y 4). Otros estudios han reportado que el coeficiente de difusión efectivo para cloruros es de 3,5E-12 m2/s para a/c 0,34 y profundidad de carbonatación inferior a 1 mm, luego de 3 años de exposición Arva et al., (2011); un coeficiente de difusión de CO2 de 2,8E-7 m2/s y coeficiente de difusión efectivo para el ión cloruro de 2,03E-9 m2/s, bajo condiciones de humedad relativa superior a 75% para un cemento portland (Sanjuán, 1982); mientras que para a/c 0,5 el DCO2 es de 1,85-8 y 1,15E-13 m2/s para dióxido de carbono gaseoso y acuoso respectivamente (Meier et al., 2005).
Los resultados obtenidos en esta investigación, indican que al agregar microsílice a la mezcla, disminuye el coeficiente de difusión efectivo, lo cual se refleja en una disminución de la penetración de agentes agresivos al concreto, aumentando la vida de servicio de la estructura. Lo anteriormente mencionado, confirma la importancia de una adecuada escogencia de la relación a/c, ya que es directamente proporcional a la penetración del ion en la estructura.
El coeficiente de difusión del CO2 se presenta en el orden de magnitud de 10-14 m2/s, reflejando una muy baja profundidad de penetración del gas en la estructura, lo cual indica, que existe un efecto bajo en la despasivación del refuerzo.
3.1. Simulación de la corrosión en el pilote de hormigón
La resistencia óhmica del concreto puede cambiar significativamente en más 104 ohms cuando hay variaciones entre un ambiente seco y uno húmedo, en los concretos secos, la velocidad de corrosión es muy lenta. Como se sabe, la corrosión del acero de refuerzo requiere una suficiente cantidad de oxígeno para que la reacción catódica suceda, además, la humedad actúa como electrolito de baja resistencia; en este orden de ideas, la velocidad de corrosión del acero en el concreto aumenta, mientras la resistencia del concreto disminuye, en condiciones normales de exposición (Liu y Weyers, 1997).
En esta parte del trabajo se realizó la simulación de la corrosión de un pilote que se encuentra sumergido en el mar, en la costa del pacífico colombiano, con la particularidad de tener en cuenta para esta simulación, la zona de splash, en la cual hay presencia total de oxígeno y un alto nivel de cloruros. Los valores de concentración umbral de cloruros, de acuerdo a los datos experimentales encontrados en pruebas de campo y laboratorio se asumieron entre 0.6 a 1.2 kg/m3 de concreto, para esta investigación, se asumió un valor como concentración umbral 0.9 kg Cl-/m3 sobre la varilla de refuerzo, el cual fue crítico en los resultados de laboratorio. A partir de este umbral, se calculó el tiempo de iniciación de la corrosión, la densidad de corriente de corrosión y la resistencia óhmica del concreto, utilizando las ecuaciones dinámicas de corrosión (19 y 20), propuestas por Liu y Weyers (1997). que en 1998 propusieron un modelo de regresión no lineal, en el que la velocidad de corrosión varía con el contenido de cloruro, la temperatura, la resistencia óhmica, y el tiempo de corrosión activa (Chen, 2004).
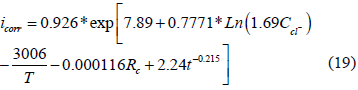
Icorr es la densidad de corriente de corrosión ( mA/cm2); CCl,t, es el contenido total de cloruro (kg/m3 de hormigón); T es la temperatura a la profundidad de refuerzo (Kelvin); Rc es la resistencia óhmica que ofrece la cobertura de concreto (ohmios), y t es el tiempo de la corrosión (años).
El modelo que relaciona la resistencia óhmica del hormigón y el contenido total de cloruro se muestra en la siguiente expresión:
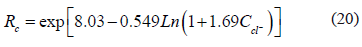
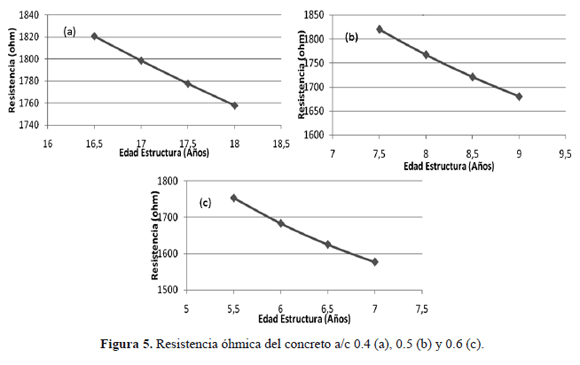
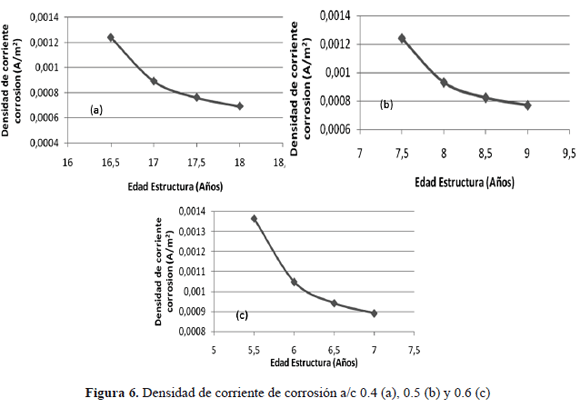
Los resultados obtenidos de resistencia óhmica del concreto (ohm) y de la densidad de corriente de corrosión (A/m2), como función de la concentración de cloruros libres, de la relación a/c y del tiempo de corrosión (años), se presentan en las figuras 5 y 6.
La simulación de la resistencia óhmica del concreto, mostró que esta aumenta al aumentar la relación a/c; sin embargo, la resistencia óhmica disminuye con la edad de la estructura de concreto para los datos experimentales simulados. Este efecto es atribuido al incremento de la concentración de cloruros con el tiempo de exposición, lo cual responde a la relación establecida en el modelo de Liu (Chen, 2006).
Se esperaría que la corrosión en el acero de refuerzo aumentara al disminuir la resistencia óhmica del concreto y por el incremento en la cantidad de cloruros que llegan a la varilla de refuerzo a condiciones normales de exposición; sin embargo, se observa que la densidad de corriente disminuye con la edad de la estructura de concreto de acuerdo al modelo simulado con los datos experimentales tratados. La densidad de corriente de corrosión del acero de refuerzo, muestra una caída significante al inicio de la etapa de propagación; disminuyendo drásticamente durante los primeros años y tendiendo a ser constante para los años subsiguientes. Estos resultados de simulación toman en consideración que existe una reducción en la relación de áreas entre el ánodo y el cátodo, que genera herrumbre en el metal que bloquea la llegada de cloruros a la varilla disminuyendo la migración de iones del acero. La estabilidad de esta herrumbre, en cuanto a su formación uniforme, presencia de picaduras o expansión, no son consideradas en este modelo. Inicialmente el efecto de carbonatación, causa en el acero una corrosión uniforme, cuyo producto al expandirse genera grietas en el concreto, que tampoco son tenidas en cuenta en el modelo planteado por Liu. Se podría predecir que al expandirse el producto de corrosión llenaría los poros que se generan la pérdida de resistencia óhmica del concreto y bloquearía la llegada de cloruros a la varilla, de ahí que se muestre en la simulación un descenso de la densidad de corriente de corrosión, pero, se requiere una mayor verificación de este modelo, que incluya la consideración de corrosión localizada por picadura y efectos de agrietamiento del concreto. Bajo estas mismas consideraciones, en las simulaciones no se presentó un efecto significativo en la densidad de corriente de corrosión con la variación de la relación a/c.
4. CONCLUSIONES
En este trabajo se simuló el transporte de cloruros y dióxido de carbono desde la superficie de hormigón hasta la varilla de refuerzo con datos experimentales obtenidos de una estructura construida en el mar de la costa del pacífico colombiano. Cl y CO2 son especies que favorecen el fenómeno corrosivo, atacando el concreto y la varilla de refuerzo. Los datos de la estructura sometida a ambientes marinos, se simularon bajo la segunda ley de Fick de difusión con la ayuda del software FEMLAB y MATLAB.
Se observó una disminución en la resistencia óhmica del concreto con la edad de la construcción y un incremento notable de esta, cuando aumenta la relación a/c. Esto puede estar relacionado con el incremento en la porosidad del concreto, por las reacciones químicas que generan contracción y deterioro por la acción de los cloruros.
Los tiempos de despasivación de las varillas al alcanzar el umbral de cloruros fijado (0,9 Kg/m3) son 16, 7 y 5 años para las relaciones a/c de 0.4, 0.5, 0.6 respectivamente. Cuando se alcanza el umbral de concentración de cloruros, la densidad de corriente obtenida en la simulación, muestra valores bajos, alrededor de 0,001 A/m2. La disminución en la densidad de corriente de corrosión, obedece a la disminución de la relación entre las áreas del ánodo y el cátodo, debido a la generación de herrumbre, disminuyendo la migración de iones de hierro. Se determinó que se requiere una mayor verificación del modelo empleado que incluya consideraciones de picadura de la superficie y agrietamiento por expansión de los productos de corrosión del acero de refuerzo.
Nomenclatura
OPC: Cemento Portland Ordinario
c: Carga de cemento [Kg]
HS: humo de sílice
EG: Escoria Granular
CV: Ceniza Volante
t = edad actual del concreto [años].
m = valor empírico de envejecimiento para mezclas con agregados
T = Temperatura del medio [Kelvin]
D cl-: Representa el coeficiente de difusión aparente del ión cloruro
D cl,-1: Representa el coeficiente de difusión aparente del ión cloruro a un año
C CO2 Concentración dióxido de Carbono (g/cm3)
C Ca(OH)2 Concentración Hidróxido de calcio (g/cm3)
D CO2 Coeficiente de difusión del dióxido de carbono (cm2/s)
D CO2,0: Coeficiente de difusión inicial del dióxido de carbono (cm2/s)
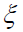 Porosidad total luego de la carbonatación
Porosidad total luego de la carbonatación
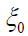 Porosidad del concreto antes de la carbonatación
Porosidad del concreto antes de la carbonatación
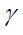 Coeficiente de reducción de la porosidad
Coeficiente de reducción de la porosidad
HR: Humedad relativa (%)
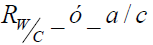 Relación agua-cemento
Relación agua-cemento
REFERENCIAS
[1] Arva, E.A., Morris W., Álvarez M.G, et al. 2003. Corrosión en estructuras de hormigón armado aplicación al contenedor de residuos radioactivos de media actividad. Jornadas SAM 2003/ Congreso CONAMET/Simposio Materia 2003 San Carlos de Bariloche, Río Negro. [ Links ]
[2] Balaguera, D., Porras, B. 2009. Evaluación del efecto de la carbonatación sobre el coeficiente de difusión del ión cloruro en el concreto. Trabajo de Grado, Escuela de Ingeniería Metalúrgica y Ciencia de Materiales, Universidad Industrial de Santander. Colombia. [ Links ]
[3] Bermúdez-Odriozola, M.A. (2007). Corrosión de las armaduras del hormigón armado en ambiente marino: zona de carrera de mareas y zona sumergida. Tesis Doctoral. Departamento de Ingeniería Civil: Construcción / E.T.S.I. Caminos, Canales y Puertos (UPM). Universidad Politécnica de Madrid. España. [ Links ]
[4] Chen, D. 2006. Computational Framework for Durability Assessment of Reinforced Concrete Structures under Coupled Deterioration Processes. PhD Thesis, Civil Engineering. Graduate School of Vanderbilt University. Nashville, Tennessee. [ Links ]
[5] Cordero, M. 2005. Estudio de la vida útil de estructuras de hormigón pretensado frente a la corrosión por cloruros. Tesis Doctoral. Universitat Politècnica de Catalunya Department d'Enginyeria de la Construcción. Barcelona. España [ Links ]
[6] Erhan G., Mehmet G., 2012 Corrosion behavior of reinforcing steel embedded in chloride contaminated concretes with and without metakaolin, Composites: Part B, in Press. [ Links ]
[7] García, N. 2009. Evaluación del efecto de la microsílice sobre el coeficiente de difusión aparente del ión cloruro de concretos expuestos a ambientes con cloruros. Trabajo de Grado, Escuela de Ingeniería Metalúrgica y Ciencia de Materiales, Universidad Industrial de Santander. Colombia. [ Links ]
[8] Havsmann D. A. 1967. Mater. Prot. B, 19. [ Links ]
[9] León, C., Oróstegui, S. 2009. Determinación Experimental del coeficiente de difusión aparente del ión cloruro en concreto expuesto a ambientes con cloruros. Trabajo de Grado, Escuela de Ingeniería Química, Universidad Industrial de Santander. Colombia. [ Links ]
[10] Liu, T., Weyers, R. W. 1997. Modeling the dynamic corrosion process in chloride contaminated concrete structures. Cement Concr. Res. Vol. 28. Issue 3. pp. 365-379. [ Links ]
[11] Mangat T.S., Mollot P.S. 1994. Prediction of long term Chloride concentration in concrete. Materials and Structures. Vol. 27. pp. 338-346. [ Links ]
[12] Martin-Pérez, B., Pantazopoulou, S.J., Thomas, M.D.A. 2001. Numerical solution of mass transport equations in concrete structures. Computers and Structures. Vol. 79. Issue 13. pp. 1251-1264. [ Links ]
[13] Meier, S.A., Peter, M.A., Muntean, A., Böhm, M. 2005. Modelling and simulation of concrete carbonation with internal layers. Berichte aus der Technomathematik No. 05-02, Bremen: Zentrum für Technomathematik, Universität Bremen, 41 pp. [ Links ]
[14] Mejía, R., Rodríguez P. 1999. Durabilidad y Corrosión de Materiales Cementicios. Seminario Internacional CYTED Costa Rica, Universidad de Costa Rica, pp. 185. [ Links ]
[15] Mike, B. O., Hans D. B., 2011. Modelling corrosion propagation in reinforced concrete structures - A critical review, Cement & Concrete Composites. Vol. 33. pp. 240-245. [ Links ]
[16] Page, C. L. 1979. Bull. Inst. Corros. Sci. Technol. 77, 2-7. [ Links ]
[17] Park, D. C. 2008. Carbonatation of concrete in relation to CO2 permeability and degradation of coatings. Construction and building Materials. Vol. 22. pp 260-2268. [ Links ]
[18] Sanjuán, M. A. 1982. Cálculo del periodo de iniciación de la corrosión de la armadura del hormigón. Tesis Doctoral, Instituto de Ciencias de la Construcción "Eduardo Torroja" C.S.I.C. Universidad Complutense de Madrid. España [ Links ]
[19] Tuutti, K. 1982. Corrosion of steel in concrete. Swedish Cement and Concrete Research Institute. Nº F04 Stockholm, Sweden. page. 469. [ Links ]