DOI: http://dx.doi.org/10.15446/rbct.n41.55386

Mathematization of geology

Matematización de la geología

 

Ludger O. Suarez-Burgoa ^a

 

^a Departamento de Ingeniería Civil, Universidad Nacional de Colombia, Medellín, Colombia. losuarezb@unal.edu.co

 

Received: January 26^th, 2016. Received in revised form: October 1^th, 2016. Accepted: November 25^th, 2016

 

This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License.

---

Abstract
This article has the objective to consider about the importance of the mathematization of the geology in the Colombian universities. Even though the analysis and the data were taken for the particular case of the Universidad Nacional de Colombia in Medellin, because of the similitude that the careers of Geology and Engineering Geology have in common, it can be considered possible to extrapolate and generalize the conclusions valid for any university in the territory of Colombia. This article analyses the actual standing, its limitations, and show different obstacles limited the development of this as a strong branch of geology; and projects a better situation for the immediate future. The article begins with an historic review that will help to understand how this branch has been coexisted just from the beginning of the formalization of geology as a science in Europe and North America.

Keywords: Geology; mathematics; Colombian universities.

Resumen
El presente artículo tiene el objetivo de reflexionar sobre la importancia de la matematización de la geología en las universidades colombianas. Si bien el análisis y la toma de datos se hacen para el caso de la Universidad Nacional de Colombia en la sede Medellín, por la semejanza que tienen las carreras de Geología e Ingeniería Geológica en el país es posible extrapolar los resultados y generalizar las conclusiones para toda universidad en el territorio nacional colombiano. El artículo analiza la situación actual, sus limitaciones y las trabas que han limitado el desarrollo de la misma como una fuerte bifurcación de la geología tradicional; y proyecta una mejor posibilidad de desarrollo de ésta hacia el futuro inmediato. El artículo inicia con una reseña histórica que ayuda a entender cómo esta rama ha coexistido casi desde la formalización de la geología como una ciencia en Europa y Norteamérica.

Palabras clave: geología; matemáticas; universidades colombianas.

---

 

1. Introducción

La geología fue dentro de las demás ramas de las Ciencias de la Tierra la que primero se desarrolló en la historia; pese a que su naturaleza fue en su gran trayectoria especialmente una ciencia descriptiva. La geología tuvo a lo largo de su desarrollo histórico un alto manejo de datos de inventario; y solo a finales del siglo XIX fue cuando muchos de esos datos fueron expresados en forma alfa-numérica o numérica.

Sin embargo, el hecho de no haber manejado números en el nacimiento de la geología no necesariamente indicó que no se estaba haciendo ciencias ni matemáticas; debido a que el uso extensivo de los números en las ciencias data de recién poco más de un par de centenas de años (por ejemplo, la geometría Euclidiana se desarrolló en sus inicios sin el uso de números). Hoy en día, la geología ha madurado como ciencia y ahora entró a una etapa hacia su completa matematización.

A finales del siglo pasado (siglo XX) se consolidó el término de Ciencias de la Tierra, abarcando no solo la geología como tal sino las demás ramas. De esta manera, en la actualidad la geología es parte de las Ciencias de la Tierra (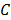), esta última que se conoce como el conjunto interrelacionado de la geología (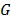), oceanografía (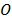), meteorología (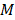), y astronomía (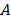); que en lenguaje matemático es .

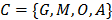Por lo general, las soluciones concretas de la geología (e.g. el problema de los tres puntos) son abordadas siguiendo alguna metodología: un proceso de descripción y reconocimiento del problema; identificación de los objetos matemáticos variables; una caracterización de esos objetos desde el punto de vista de la variabilidad de la variable; el planteamiento de la solución con bases matemáticas (i.e. matematización de la solución); la búsqueda y encuentro de la solución (si existe, si es posible resolverla o si crea una conjetura); la demostración de la solución; y finalmente su implementación. Sin embargo, normalmente, la solución muchas veces no es única en la geología debido a que en la mayoría de las veces se trata de un problema inverso.

Lamentablemente, la actual explotación de la geología en latino América, en muchos de los casos se queda sólo en el primer paso de esta metodología.

La geología matemática no solo enlaza los conocimientos de la geología con las matemáticas, sino también la estadística; porque en todo proceso se trata a las variables no como variables deterministas, sino como variables aleatorias. Y además, debido a que los problemas a resolver no son casos especiales, toda solución de geología matemática necesita de métodos numéricos; y por tanto se necesita tener conocimientos de programación computacional. De ahí que surgen otras dos ramas, que son: la geología estadística y la geología informática; sin embargo, estos dos conceptos no están formalizados como tales, y resulta más bien que la geología matemática ampara a éstos.

Por tanto, la geología matemática es la disciplina científica que concretiza los conocimientos de las matemáticas en problemas de la geología con el uso de la estadística y la aplicación de las ciencias computacionales.

Vistelius define a la geología matemática como una ciencia sobre modelos matemáticos de procesos geológicos [18]. El identificó que las observaciones geológicas implican variables y procesos aleatorios, y manifestaba luego que la geología matemática en principio es una rama de la ciencia sobre modelos estocásticos de procesos geológicos. Bajo esta definición, la geología matemática tiene un alto carácter estadístico.

El término geología matemática tiene otros nombres, algunos usados antes o después del mismo; por ejemplo: geología cuantitativa, geología numérica, y geomatemáticas.

En el presente artículo se hablará de sólo 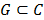y describirá la historia del surgimiento de la geología matemática, para luego pasar a describir el rol, las pretensiones y el potencial de ésta en la región de América latina con el fin de hacer tomar conciencia sobre la necesidad de ésta para la región.

 

2. Reseña histórica

La presente reseña histórica se basa en los relatos hechos por varios autores del mundo occidental. Los conocimientos y los hechos desarrollados en el mundo oriental, en la historia, también han tomado gran parte de este desarrollo. Para no entrar en mucho detalle de la historia de la matemática (que se pueden encontrar en libros más extensos sobre el tema), la reseña histórica se la hace a partir del siglo XVI mostrando algunos hitos relacionados a la geología o ramas afines. La reseña histórica de la evolución de la geología matemática es un ejemplo de la evolución que tuvo todo conocimiento en los últimos 60 años.

2.1. La geología y las matemáticas

A partir de la segunda mitad del siglo XVI los Jesuitas ven la necesidad de impartir las matemáticas en los colegios de La Orden para la formación de futuros jesuitas en el Colegio Romano. En este siglo, las matemáticas se las consideraban como una disciplina inferior a la Filosofía, Medicina o Teología; eran un tema periférico, abstracto y bello, pero alejado de la realidad de la utilidad; y además era una materia que no tomaba examen. En ese entonces el jesuita Christóforus Clavius (1538-1611) -jesuita alemán, matemático autodidacta y reputado astrónomo- critica a sus colegas de Filosofía por no saber suficientes matemáticas, y además, por no saberlas hacer atractivas.

Posteriormente, Vicenzo Figliucci, propone que la comprensión de las matemáticas acerca al hombre al conocimiento divino, permitiéndole descubrir los principios de la naturaleza y remontarse a la causa de los fenómenos. En el siglo XVII se dio las condiciones para que las matemáticas empiecen a tomar control en la explicación de los fenómenos naturales, con los aportes trascendentales de Galileo Gallilei, René Descartes (1596-1650) y Sir Isaac Newton. Los mismos jesuitas empezaron a estudiar la naturaleza de la Tierra, por ejemplo: Athanasius Kircher (1601-1680) escribió el tratado filosófico Mundus subterraneus (1665); donde quiso explicar el origen de los volcanes, y comparó a la Tierra como un organismo viviente.

En estas épocas todo teólogo tenía que tratar dos temas: el concerniente a Dios y el concerniente al entendimiento del mundo natural; porque al entender la creación se logra entender al creador, y esto conllevó a tener que conocer al menos dos tratados: la Biblia y el llamado Libro de la Naturaleza, este último compilado por la congregación de los Dominicos en el siglo XIII. Se dice que ambos libros, si bien fueron compilados por hombres, fueron escritos por Dios.

El estudio de la naturaleza recibió gran interés en el tiempo del Renacimiento, cuando los cristianos empezaron a redescubrir y a acoger los escritos aún remanentes de las culturas antiguas griega, romana y otras que hayan podido sobrevivir a la época Medieval. Aquellos que se especializaron en el estudio de la naturaleza los llamaron filósofos naturales.

Para el siglo XVIII es que se conoce el posible primer tratado de geología del mundo occidental, bajo el nombre de teoría de la Tierra, haciendo una semejanza a un tratado publicado un siglo antes por Newton llamado teoría de los cielos (v.gr. cosmografía). Fue en este siglo donde la experimentación empezó a tener importancia para las apreciaciones; donde se publicaron enciclopedias, y se empezaron a difundir los conocimientos del conocimiento de la Tierra en universidades, bajo el nombre de geometría subterránea. Posiblemente, el primer libro en idioma español sobre temas de las ciencias de la tierra fue del clérigo Antonio Torrubia con su tratado aparato para la historia natural en 1754. Y en este siglo, a finales, es donde se dio la Revolución Industrial. Para ello, la minería demandó hacia el estudio de la Tierra en las universidades.

A inicios del siglo XIX, la geología comenzó a lograr la estructura robusta de una ciencia, con las contribuciones de Abraham G. Werner (1749-1817) en el Neptunismo y mineralogía. En este siglo se tuvo los grandes aportes de James Hutton (1726-1797), quien aportó con la descripción del origen y datación de las rocas; sin embargo, la geología no alcanzó su carácter científico hasta que se logró desarrollar la estratigrafía y la paleontología; logrados a finales del siglo XIX [14]. En esta época se atendía aún la teología natural que muestra aún la influencia que tenía la religión en esta ciencia en el mundo occidental.

Solo hasta el siglo XX se puede decir que la religión y la ciencia recién se separaron completamente, de un proceso que duró al menos dos siglos, cuando al final se empezó a estudiar las Ciencias a partir de los principios físicos y no solo ser un deseo de acercarse a Dios.

Pero ¿Cómo evolucionaron las matemáticas para el siglo XIX en adelante? -A partir del siglo XIX se marca el inicio de las matemáticas modernas; sin embargo, las matemáticas entran a una fase mucho más adelantada de las otras ciencias aplicadas, entra en un campo más abstracto. Se empieza a estudiar la geometría no-euclidiana, geometría hiperbólica, geometría elíptica, geometría de Riemann y los principios de topología con las generalizaciones de las curvas y superficies. También empiezan a tratarse temas del álgebra abstracta como los espacios vectoriales y álgebra booleana. En este siglo se resuelve los problemas matemáticos que no habían sido superados desde los tiempos de la Grecia antigua, como la solución de ecuaciones polinomiales, y problemas de geometría tridimensional.

Para el siglo XX se estableció los fundamentos de la teoría de conjuntos y los fundamentos de las matemáticas. En este siglo se crearon numerosas sociedades nacionales de matemáticas en Inglaterra, Francia, Italia, Escocia y Estados Unidos; y una sociedad limitada especial conocida bajo el seudónimo de Nicolás Bourbaki [10].

En este mismo siglo también se estudia con grandes logros la automatización y computación, tales como: la teoría de la computación de Alan Turing, la teoría de la complejidad, teoría de la información de Claude Shannon, la del procesamiento de señales, de análisis de datos, y de optimización; dando lugar a la ciencia computacionales. Estas teorías computacionales han incrementado el interés en teorías discretas, combinatoria y teoría de grafos, análisis numérico y computación simbólica. Los métodos computacionales en las matemáticas que se destacan en el siglo XX son: el algoritmo simplex, la transformada rápida de Fourier, códigos de corrección de errores, entre otros.

2.2. La geología y las matemáticas

El intento de implementar las matemáticas en la geología se remonta al siglo XVII, con el trabajo del científico francés Pierre Perrault (1611-1680) que trató de explicar el Ciclo Hidrológico de forma cuantitativa en su libro De l'origine des fontaines [19] cuya traducción al español es el origen de las fuentes.

Sin embargo, fue sólo durante el siglo XIX que se creó los fundamentos geológicos para poder aplicar las matemáticas. A esta fase se la conoce la fase formativa de la geología matemática, dado entre los años 1833 a 1895 [13].

Las primeras aplicaciones concretas de las matemáticas a la geología -en ese entonces conocida como geología cuantitativa- fueron más notorias a finales del siglo XIX con las contribuciones del geólogo Charles Lyell, que se considera uno de los padres de la geología moderna [12].

Por ejemplo, la proyección esférica equiángulo -que es una transformación del espacio euclídeo tridimensional al esférico bidimensional, v.gr. una aplicación de la geometría no-Euclidiana- se aplicó en geología a finales del siglo XIX. A principios del siglo XX, en 1917, se publicó en idioma Alemán el trabajo del geólogo Austriaco Walter Schmidt donde se establece un método -con base a la proyección esférica equiárea- para inferir por medio de la estadística las concentraciones de las orientaciones tridimensionales de planos de discontinuidades en la roca, lo que marcaría el inicio de la aplicación de la estadística multidimensional [16]. Luego en 1953, Fisher [5] publicaría la expresión matemática de una distribución espacial axial en la superficie de la esfera, que permitiría el inicio de la aplicación de la estadística paramétrica en esta proyección.

Para mediados del siglo XX se matematizaron algunos fenómenos geológicos, a esta fase se la conoce como la fase de explotación, dada entre los años 1941 a 1985 [13]. En Schaeben [15] se explica un caso particular referente a los primeros logros de la matematización en las Ciencias de la Tierra. Se trata de un modelo matemático para la predicción del clima en meteorología. Inicialmente, en 1922, Richardson planteó las ecuaciones diferenciales para la predicción del clima; sin embargo, las ecuaciones no tenían solución analítica.

Richardson al plantear tal ecuación no previó de la complejidad del problema ni de las condiciones de estabilidad de la solución numérica, él se había adelantado a la época del uso de los computadores. Solo se logró avanzar en el modelo hasta mediados de 1940 donde Neumann tuvo acceso a un computador diseñado especialmente para la predicción del clima; vea [3]. Con esto el autor quiere resaltar, que no existe matematización sin materialización; y la primera no es útil si no procede luego la concretización e implementación.

Para mediados del siglo XX, se pasó a una nueva etapa: la del desarrollo (entre 1941 a 1958 [13]) de los conceptos fundamentales que definen la geología matemática. Importantes personas que impulsaron esta fase fueron: Andrew B. Vistelius (natural del entonces U.R.S.S.) y William C. Krumbein de la Universidad del Noroeste en Illinois (natural de EE.UU.). Vistelius desarrolló formalmente estudios bajo el título de geología matemática en la década de los 50 y 60 de ese siglo (e.g. Vistelius [17]); y Krumbein empezó con estudios de estadística aplicados a la geología (estratigrafía) en la década de los 30, quien fue un pionero en geología computacional (sinónimo de la que Vistelius llamó geología matemática) en los años 60 con la ayuda de la oficina de Investigaciones Navales de EE.UU. (e.g. Krumbein & Sloss [6]).

Entre 1958 a 1970, se desarrollaron los primeros códigos computacionales para solucionar problemas geológicos: v.gr. uso de la matemática y la informática en la geología ayudados por los conceptos e impulso dado en la fase de desarrollo. Esta época es llamada la fase de la computación aplicada a la geología. Esta podría decirse que fue la fase que mayor evolución tuvo, donde ser obtuvieron resultados concretos que hizo ver que este campo era prometedor.

Los grandes problemas con los que se contó en esta fase fueron: la compatibilidad del hardware entre las naciones, y por ende la compatibilidad del software. Sólo por estrategia militar, algunas naciones desarrollaron su propio hardware (v.gr. URSS, EE.UU., Inglaterra, Francia, Dinamarca, Alemania y Suecia) y eso implicaba el desarrollo de sus propios sistemas operativos. Respecto al software, Merrian [11] señala en un comunicado: que los más grandes problemas que se tuvo en esa época para el intercambio de algoritmos fue la compatibilidad del software. Por ejemplo, mientras en EE.UU. se programaba en mayoría las aplicaciones en las Ciencias de la Tierra en FORTRAN; en Europa la tendencia era el uso de ALGOL o AUTOCODE.

Para mediados de los años sesenta se publicaron alrededor de cien artículos relacionados a la aplicación de la informática en la geología; y con la mejora en la disponibilidad y en la velocidad de los computadores, para el inicio de los años setenta se tenían alrededor de mil artículos sobre el tema.

Este gran impulso de la fase de la computación aplicada a la geología se debe a la unificación de los esfuerzos comunes en la temática (e.g. comunicaciones GOSSIP: Geological Oriented Scheme for Sharing Information on Programming) y a la creación de sociedades internacionales; que para el caso en particular fue la Sociedad Internacional de Geología Matemática. Esta sociedad se fundó formalmente en Praga para el año 1968 de la mano de Daniel F. Merrian (del Servicio Geológico del Estado de Kansas en EE.UU.) y Richard Remet de Suecia, que cambió de nombre a la actual Sociedad Internacional de Geociencias Matemáticas (International Association of Mathematical Geosciences, IAMG de las siglas en Inglés).

Todos los desarrollos internacionales permitieron unificarse tras el establecimiento firme de dos revistas exitosas relacionadas a las matemáticas e informática dirigida por la IAMG: Geología Matemática (Mathematical Geology) y Computadores & Geociencias (Computers & Geosciences). En estas dos revistas se publican y se intercambian programas computacionales a nivel de código fuente; sin embargo, ya años atrás a los sesenta (aproximadamente diez años atrás) se intercambiaban códigos de solución de problemas de geología entre colegas, estudiantes e investigadores [9]. Se marcó la lógica del software libre, como ocurrió en otros campos al inicio de la informática.

Ya para la década de los ochenta el lograr un registro impreso de las aplicaciones de la informática a la geología se convirtió en una tarea poco práctica [12]. Se estima que se publicó por el orden los miles de publicaciones y códigos abiertos relacionados a la geología matemática; en revistas indexadas y en congresos especializados al tema. Hoy en día en la red Internet se pueden encontrar la mayoría de estos códigos, muchos de ellos escritos en Fortran; donde la tarea actual puede ser una actualización del código a los lenguajes de programación actuales.

Para la última década del siglo pasado hasta el presente se entra en una fase oscura a causa de la fase de explotación comercial de los códigos computacionales, que la llamaría la fase de la era oculta (v.gr. Digital Dark Age) de los códigos computacionales; apoyado por el concepto que: todo código cerrado compilado necesita de su programa intérprete para descodificarlo, donde muchos de estos programas descodificadores han desparecido en pasar del tiempo y donde los archivos de los códigos ha permanecido.

En esta fase es donde se observa también un interesante gran avance, pero sin tener realmente una visión clara si ese avance podría haber sido mayor si se establecía en el mundo de la informática con mayor impulso el criterio de código libre o abierto.

2.3. La geología matemática del siglo XXI

Para este siglo XXI se tiene anunciado desde el año 2000 los siete problemas sin resolver de las matemáticas, y ya en el 2006 uno de esos problemas -la conjetura de Poincaré- fue resuelta; y por supuesto con la conformación y uso de un programa computacional.

Este inicio de siglo se caracteriza por tener en todas las áreas de investigación grandes cantidades de datos (v.gr. bigdata) para ser procesados; y esto aplica también a la geología, debido a que las computadoras han catalizado la revolución cuantitativa en la geología y ellas posibilitan que se aplique las matemáticas y los modelos estadísticos a estos grandes volúmenes de datos e información [2]. Por ejemplo, en las agencias de la NOAA y la USGS se tiene almacenados grandes cantidades de datos obtenidos por los satélites y sensores terrestres.

La computación es la llave para posiblemente unificar el entendimiento de todo el universo a través del lenguaje matemático. Las grandes potencias con sus científicos asociados están concentrando sus esfuerzos en poder lograr el procesador cuántico eficiente[1]; debido a que el paradigma de la computación cuántica ya fue resuelto. El gran obstáculo en el procesador cuántico es el de aislar el quantum bit (i.e. qubit) de las perturbaciones del mundo físico para que se produzca el entrelazamiento cuántico; que sólo se logra a pocos grados de temperatura absoluta por encima del cero absoluto. Con este procesador eficiente se podrá resolver muchos problemas aún no tratables desde el punto de vista de la implementación; como por ejemplo, problemas de criptografía (v.gr. quantum key distribution), nanotecnología, optimización y aprendizaje automático.

El paradigma de programación para una computadora cuántica es muy diferente que el que se usa para programar una computadora tradicional; consiste en encontrar la relación de un cálculo que menor energía requiera a partir de la búsqueda simultánea de la solución del problema en una vasta cantidad de posibilidades. De este modo, cada cálculo computacional es probabilista más que determinista, donde el computador envía un conjunto de correctas soluciones en un tiempo muy corto (alrededor de millones de respuestas por segundo). Para el caso de las primeras computadoras cuánticas como el D-Wave Two de Dwave Systems, se está desarrollando lenguajes de programación para trabajar bajo este paradigma.

Por otro lado, aparte de tener más hardware eficiente, es necesario cada vez simular más acertadamente mediante software amigable y eficiente, la forma como opera el cerebro humano. Para ello se necesitaría lo siguiente.

1. Incrementar más los métodos inteligentes, i.e. los procesos computacionales en el cual el comportamiento previo del medio geológico se estudie mediante una descripción que va mejorando a medida que se tienen mayores datos, mediante una red informática con nodos interconectados. Esto podría lograrse con redes neurales artificiales a tiempo real.
2. Desarrollar programas computacionales inteligentes que incluyan algoritmos de percepción de la situación que se estudia.
3. Crear el hardware necesario para lograr estas capacidades accesibles a cualquier persona. Hoy en día se puede comprar en un equipo computacional el equivalente del cerebro de un insecto o un ratón por mil dólares; se prevé, que con ese mismo monto dentro de 50 años se pueda comprar el equivalente al cerebro humano.

En lo que respecta la información, se estima que en menos de 20 años se tendrá disponible en la red Internet casi la totalidad de los libros que se han publicado en el pasado y que salgan en ese presente (predicción personal del autor). Se cree que las computadoras serán autores de textos mediante una compilación inteligente y manejo de la información; y los artículos tendrán autores mixtos entre humanos y cibernéticos; surgirá la figura del científico electrónico (e-scientist).

Los computadores tendrán memoria, percepción e inteligencia. La solución de los modelos será en tiempo real con la toma de datos del medio ambiente a través de una red de sensores, y no se necesitará la intervención del hombre para dar los valores de las variables de entrada al modelo. Esto ya se está usando en las exploraciones no tripuladas de Marte, por ejemplo.

El conocimiento siempre dio lugar a las grandes potencias; por tanto, el desarrollo de este nuevo reto está siendo tratado con bastante sigilo y confidencialidad. Es muy probable que se tenga resueltos hitos más avanzados de lo que hoy en día se cree se conoce en los medios comunes de comunicación. El conocimiento humano está creciendo, y el cerebro humano aún está limitado.

 

3. Matematización de la geología

La matematización es un proceso que diseña y desarrolla modelos conceptuales basados en leyes de la naturaleza en notación matemática. Es decir, un proceso por el cual el científico transforma lo observado de la naturaleza en un modelo matemático. En forma sencilla, es la reducción de algún fenómeno a expresiones matemáticas interrelacionadas. Un modelo matemático puede estar planteado inclusive a partir de funciones variables, dando varias formas de solucionar o varias soluciones.

Durante la matematización no sólo se trata de entender el proceso, sino de encontrar las variables que más influyen en el proceso, y las relaciones entre éstas, expresadas a través del correcto lenguaje matemático. La concretización es el proceso inverso a la matematización y es el proceso de transferir un modelo matemático a la realidad.

Mediante la matematización se logra realmente aplicar las matemáticas. Sin embargo, para matematizar la geología es necesario tener conocimientos y pericia en los dos aspectos que involucran esta relación: en las ciencias que describen la naturaleza y en las ciencias matemáticas. Asimismo, el proceso de matematización sugiere seguir un procedimiento o una metodología que involucre una formulación lógica de los hechos, un adecuado uso del lenguaje literal y matemático, una búsqueda de analogías entre la situación estudiada y otras situaciones, y el ordenamiento progresivo del razonamiento. Y esta característica hace que el proceso de matematización no sea una tarea sencilla por ser un proceso elaborado; es más, se ha visto difícil encontrar profesionales con ambas notables capacidades.

Dentro de los pasos del proceso de matematización, uno inicia con un mapa conceptual del problema (que puede ser un esquema hirsuto, un diagrama de flujo con parámetros de entrada y salida), un listado de suposiciones, la introducción de las variables y sus unidades, la identificación de las relaciones de estas, la clasificación de la importancia de las variables y eliminación de algunas innecesarias, y la identificación de uno o más procesos. Por ejemplo, tienen que definirse si realmente los procesos son estáticos o transitorios, y si se las relaciones entrarán en el campo continuo o discontinuo.

Para lograr la matematización de un cierto problema de la naturaleza, se pasa por un proceso largo de entrenamiento, trabajo multidisciplinario, y varias pruebas y errores. Es más, es un trabajo de toda una comunidad científica, que se han trazado el objetivo de ir marcando hitos a través de sus logros.

Para el nivel de los problemas que se quiere resolver en la actualidad en la geología matemática, se ve que el proceso de matematización no se logra con un individuo; hoy en día el trabajo multidisciplinario y conjunto es la única vía de lograr la matematización de problemas.

Se necesita por lo menos tres actores para lograr la matematización de un problema en geología matemática; estos son: un científico de la rama de la geología, un matemático y estadístico, y un desarrollador de software (Fig. 1).

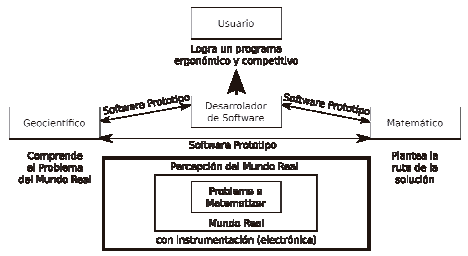
Figura 1. Diagrama de la terna de interacción para solucionar problemas.
Fuente: el autor.

En la Fig. 1, los dos individuos (Usuario y geocinetífico) que no son netamente matemáticos ni estadísticos necesitan tener conocimientos básicos de esas ramas; el matemático y el desarrollador de software necesitan tener conocimientos básicos de las Ciencias de la Tierra; y los tres tienen que saber programar en un lenguaje de programación de prototipaje. Es el desarrollador de software el que agrupará y cumplirá con las necesidades del demandante de la aplicación a partir de todos los insumos logrados por los demás investigadores a partir de los códigos prototipos desarrollados.

En todo ello, se tiene que lograr en el grupo multidisciplinario un interés común y a la vez un beneficio para cada uno de los integrantes. Lo que se observa muchas veces en estos grupos de investigación multidisciplinario es la pérdida rápida de interés por alguno de los especialistas. Normalmente esto sucede con el especialista en matemáticas. El matemático desea aplicar sus conocimientos en geología, pero muchas veces los problemas que plantea la ciencia resultan ser soluciones triviales para las matemáticas; por tanto el matemático pierde el interés en resolver el problema.

Todos los miembros del grupo multidisciplinario tienen que comprender que a medida que se progresa en el problema se llegan a modelos interesantes para todos. La matematización y la solución de un problema en geología matemática toma su tiempo, consume energía y requiere perseverancia de todos sus miembros.

 

4. La geología matemática en Latinoamérica

Los estudiantes y profesores de las universidades latinoamericanas tienen todavía muchos aspectos que frenan el desarrollo de la geología matemática desde la academia; y si desde la academia no se resuelve la implementación de las matemáticas en la geología, muy difícil será poder introducir esta nueva forma de trabajo en la industria.

Los aspectos que frenan este desarrollo en la academia son por ejemplo los siguientes:

1. Muchos estudiantes consideran a la matemática como una disciplina compleja, abstracta y bien desvinculada de su interés profesional. Lo de compleja y abstracta es totalmente cierto, pero lo de desvinculada no lo es.
2. Todavía los estudiantes quieren resolver grandes problemas con herramientas de ofimática, tales como MS-Office.
3. No se posee la experiencia en la manipulación de grandes bases de datos (i.e. bigdata).
4. La enseñanza informática para los geólogos se limita a lo básico y no se les proporciona los conocimientos necesarios para elaborar sus propios programas computacionales.
5. Se les enseña a resolver problemas de forma manual mediante nuevas tecnologías de información, y generalmente se les evalúa para responder con cálculos manuales sin el uso de las nuevas tecnologías de información.

Hace sesenta años la geología no tenía una cercanía alguna con las ciencias exactas y las matemáticas. Inclusive, todavía aquella impresión aún es remanente en el entorno académico de alguna de las universidades latinoamericanas. Se tiene la impresión que tanto las matemáticas como la estadística no son afines con la geología; y esto porque se piensa aún que las matemáticas son abstractas en comparación con la geología que es una ciencia concreta.

Se cree, que esta brecha se está debiendo a las siguientes razones.

1. Las matemáticas tienden a generalizar un comportamiento, mientras que los aspectos que trata la geología son esencialmente singulares y hasta únicos.
2. Los problema en la geología no son únicos, las personas tienden a favorecer más a un modelo que a otro, bien sea por simpatía, por desconocimiento o alguna otra preferencia. Esto causa un gran sesgo en la geología.
3. Similar a lo anterior, la geología bajo una deficiente práctica podría ser hasta cierto punto personal e individual, debido a que a veces ciertas apreciaciones son enteramente de carácter personal.
4. La geología, en contraste con otras ciencias, busca las causas a partir de los efectos; mientras que las ciencias clásicas estudian lo contrario: los efectos con sus causas. Esto resulta en que la mayoría de los problemas en geología son problemas inversos, por tanto no se cumple el principio de la causalidad, y esto tenderá a una respuesta ambigua.
5. La geología tiende a idealizar razonablemente, es decir trata de explicar de forma racional los fenómenos a partir de idealizaciones. Casi como la teología, que parte de ciertos dogmas aún no comprobados. Esto resulta así porque en geología muchos modelos o teorías son modas. Un claro ejemplo es la teoría de sinclinales y geosinclinales, otro ejemplo es el de deriva continental; solo cuando se tomaron datos fue que se favoreció la teoría de tectónica de placas.

 

6. La experimentación en geología es limitada por el efecto escala y tiempo.

La concretización de las matemáticas en la geología se está logrando cada vez más con el uso de la informática; debido a que hoy en día se puede individualizar y singularizar un grupo de cálculos matemáticos (v.gr. un procedimiento) y hasta un modelo. En este aspecto el desarrollo de algoritmos prototipos no triviales son los medios a través de los cuales se están logrando avanzar hacia adelante en temas nuevos e importantes de la geología.

Entonces, corresponde a la academia a nivel universitario la tarea de enlazar nuevamente los siguientes conocimientos: física, química, matemática y estadística, en conjunto con la aplicación de métodos numéricos y técnicas de programación computacional (posiblemente esto resulte en la inclusión de al menos seis nuevos campos del conocimiento) dentro de la enseñanza de la geología, y como consecuencia en la enseñanza de las Ciencias de la Tierra.

La realidad observada en las universidades latinoamericanas es que prácticamente, aquel individuo interesado en enlazar ahora los seis campos del conocimiento científico tiene que volver a estudiar unificando los conocimientos hacia un fin en específico: la solución de un problema real para cubrir una demanda urgente a ser cubierta por el mercado tecnológico del medio, o para desarrollar conocimiento nuevo mediante investigación.

Otro problema que hay destacar es la forma como Latinoamérica accedió a los recursos informáticos y hacia la aplicación de esta en las ciencias. En los últimos treinta años, en Latinoamérica no se percibió claramente la necesidad de unir los conocimientos de física, química, matemática y estadística. Es más, en el transcurrir de estos años no fue un problema catastrófico desde el punto de vista del conocimiento en la región. Todos los profesionales y académicos nos hemos beneficiado con el desarrollo de estas ciencias de la mano de la informática; y esto fue así debido a que la demanda del conocimiento para enlazar todos estos temas se cubrió con los programas computacionales que hacen todo, pero cerrados tipo caja negra, y de llave en mano (en este caso de licencia en mano); que podríamos decir: una solución facilista y a su vez costosa en términos económicos.

Un programa computacional bien desarrollado es capaz de transmitir conocimiento sin mucho esfuerzo hacia el usuario; y sin exigirlo de los pormenores y detalles del conocimiento. Pero esto hizo que en Latinoamérica no se vea la necesidad del desarrollo de software propio; que es una tarea mucho más complicada que requiere un gran proceso de desarrollo.

La solución facilista -pero no consensuada- de la academia (docentes y estudiantes) en las universidades latinoamericanas fue el de tolerar la piratería del software en los pasillos y en las aulas; y no más bien de desarrollar capacidades de su personal académico con el fin de lograr lo más antes posible la unificación de estas ciencias en los niveles académicos más tempranos posibles. Pensado ya en aquellos científicos que han optado por el desarrollo de conocimiento, v.gr. los investigadores, ellos tienen que encarar el reto de enlazar los mencionados seis campos del conocimiento, y como se dijo: lo antes posible y en los niveles académicos más tempranos posibles. A nivel académico, tal enlace es necesario hacerlo en los cursos de post-grado, desde una maestría investigativa hasta el doctorado; teniendo seis años para lograr aquello.

Soluciones para lograr el enlace de los ahora seis conocimientos mencionados emergieron dentro de la geología mediante ramas del conocimiento especializadas. Por ejemplo, la Geofísica que trata de enlazar la Física con la geología; o la Geoquímica, con similar objetivo. Este último par de disciplinas (Geofísica y la Geoquímica) están exigiendo tanto el uso de las matemáticas, estadística y computación; que hicieron surgir lo que trataremos ahora: la geología matemática.

En la reseña histórica referente a las matemáticas y la geología, como las ciencias de la computación direccionados al surgimiento y desarrollo de la geología matemática no se observó ninguna influencia de Latinoamérica, situación que es distinta por ejemplo de los países Europeos.

La reacción que tuvo Latinoamérica ante el surgimiento de la geología matemática hasta finales de los años ochenta del siglo pasado no fue notoria; y solo a partir de la década de los noventa se adopta una política general de introducir los computadores dentro de la geología.

Sin embargo, las malas decisiones de aquel entonces fueron:

• importar programas computacionales de códigos cerrado, todos ellos costosos para el nivel de adquisición de las universidades, empresas públicas y privadas;
• asumir tales herramientas (cajas negras) como insumos fundamentales para desarrollar la investigación local, sin antes percibir que era necesario desarrollar las capacidades de los científicos para lograr aquello.

Otro aspecto que influye en tener profesionales de las Ciencias de la Tierra con pocas capacidades hacia la física, química, matemática y estadística se da en las materias de fundamentación de la educación superior en las carreras que tienen un componente orientados hacia las ingenierías y ciencias. Es una deficiencia aún presente que en los numerosos cursos básicos de física, química, matemática y estadística se aborden temas generales no atractivos para los estudiantes de cada determinada carrera. Muchos de los problemas que se trata y se resuelve en estos cursos se hacen mediante soluciones analíticas bien conocidas; pero largas, engorrosas y de casos especiales: casos especiales que pueden ser simplificaciones poco aplicables de un fenómeno real, o casos especiales cuyas soluciones se apoya en un método de solución específico diseñado solo para esas situaciones. Cuando es el momento de aplicar los conocimientos de física, química, matemática y estadística en temas específicos de las disciplinas relacionadas a la geología, nos encontramos que existe un vacío entre lo aprendido en las materias básicas, y en lo que realmente se necesita conocer.

A continuación, se presenta algunos indicadores de la situación actual de las capacidades de los estudiantes universitarios para aplicar las matemáticas en la geología en Latinoamérica.

El primer aspecto es referente a la percepción de la necesidad de las matemáticas para la geología. En la Universidad Nacional de Colombia se realizó una encuesta a estudiantes de la carrera de ingeniería geológica de la Facultad de Minas, la cual indagaba ¿Cuánta matemática se necesita para ser geólogo o ingeniero geólogo? -Para poder analizar las repuestas, se les pedía a los encuestados que escogieran sólo una opción de las siguientes seis opciones; a nivel:

• avanzado de álgebra, precálculo;
• avanzado de lo anterior y geometría del espacio (geometría tridimensional);
• avanzado de lo anterior y álgebra vectorial, matricial y tensorial;
• avanzado de lo anterior y el análisis matemático de ecuaciones diferenciales parciales, hasta la dimensión ;
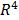• intermedio de lo anterior y estadística descriptiva en 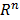; o
• intermedio de lo anterior y topología.

De las 113 respuestas: 2 no respondieron nada (blancos); 4 marcaron más de una opción (nulos); 1 dijo a nivel avanzado de álgebra, pre-cálculo; 2 escogieron a nivel avanzado de lo anterior y geometría del espacio (geometría tridimensional); 11 escogieron para el nivel avanzado de lo anterior y álgebra vectorial, matricial y tensorial; otros 11 para el nivel avanzado de lo anterior y el análisis matemático de ecuaciones diferenciales parciales, hasta la dimensión ; 25 para el nivel intermedio de lo anterior y estadística descriptiva en ; y los restantes 57 optaron por elegir el nivel intermedio de lo anterior y topología.

El segundo aspecto que se indagó fue a ¿Cuáles son las capacidades en el manejo de herramientas computacionales específicas que tienen los estudiantes interesados en la geología matemática? -Para este caso, se convocó a los estudiantes de la Universidad Nacional de Colombia a participar de las actividades del Semillero de Investigación en Geología Matemática y Computacional (GeolMathComp), que se desarrolla en la Facultad de Minas. En dicha reunión se les solicitó que los interesados llenen una encuesta sobre las herramientas computacionales que ellos pueden manejar para el desarrollo de programas aplicados a la geología.

De los 21 encuestados, 8 sabían manejar algún lenguaje de marcas como LaTeX o HTML; sólo 9 reportaban manejar algún lenguaje de programación como C++, Python, Octave o Matlab; 10 indicaron que conocían alguno de los entornos de programación como Eclipse, Qt4 o Visual Basic; y sólo cuatro indican manejar el lenguaje SQL.

A este mismo grupo de interesados, se les solicitó indicar en qué áreas del conocimiento deseaban ayudar dentro del grupo de investigación. De los 21 encuestados, 10 deseaban ayudar únicamente en temas netos de geología (sin matemáticas); mientras que sólo 6 deseaban incursionar en temas de matemáticas o estadística relativos a la geología; el resto quiere ayudar en temas secundarios a los objetivos del grupo como ser desarrollo de documentos de información impresos y/o electrónicos con el uso de herramientas ofimáticas, o en temas administrativos. En este último aspecto, es importante mencionar que un estudiante no debe limitarse al buen y avanzado uso de las herramientas ofimáticas, esto debido a que la necesidad de incursionar en el uso de los lenguajes de programación en los estudiantes de carreras relacionadas a las Ciencias de la Tierra cada vez está siendo más notable [8].

Finalmente a un grupo de 72 estudiantes de pregrado de la misma universidad y facultad se les solicitó matematizar un problema simple de álgebra de vectores en 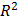. De éstos, sólo 13 usaron diagrama de flujo o pseudocódigo para matematizar el problema; el resto usó lenguaje literario y esquemas para tratar de explicar el procedimiento de la matematización. Estas tres indagaciones (i.e. ¿cuánta matemática se necesita para ser geólogo o ingeniero geólogo?, la capacidad en el manejo de herramientas computacionales específicas, y la capacidad de matematizar un problema) indica que existe muy bajo conocimiento de los alcances que tiene la matemática hacia la geología, muestra la baja formación computacional que se tiene para lograr implementar la matemática a la geología, y el bajo lenguaje matemático y baja capacidad que se tiene para matematizar un problema.

 

5. Epílogo

Varias frases han surgido de los amantes de la matemática; se toma a un autor que escribe mucho sobre ella [1]:

• la matemática es la reina y sirviente de la ciencia, la ciencia de las ciencias, el único y decisivo medio para la formulación y la solución de todos los problemas independientes del campo;
• la matemática es todo un lenguaje, el más preciso lenguaje disponible para las personas de hoy, un lenguaje que con sus fundamentos y desarrollos ha seguido reglas lógicas, un superlenguaje;
• el nivel de una ciencia se determina por la extensión del uso del lenguaje matemático por esta ciencia;
• cualquier ausencia, falta de claridad, imprecisión, o duda que se acredite a las definiciones y el procesamiento de los conceptos en un campo científico se debe sustancialmente al hecho que no se ha triunfado en el uso exclusivo del lenguaje matemático en esos temas;
• la fundamentación axiomática y estricta, así como la preparación para la matematización es una necesidad interna para cualquier rama de la ciencia.

El nivel de conocimiento que se requiere de la física, química, matemática y estadística para el desarrollo de las Ciencias de la Tierra y la geología no es de nivel básico, como se presenta en los cursos de los primeros semestres de las carreras universitarias ya descritas. De este modo se tiene que lograr lo siguiente.

1. En la academia es necesario desarrollar en los profesionales los suficientes conocimientos de las ciencias básicas, las matemáticas y la estadística, para aplicarlas a las Ciencias de la Tierra con el apoyo de las capacidades de desarrollar códigos computacionales.
2. Es necesario establecer un esquema en los centros de investigación de tal modo de lograr software propio y de código abierto, aplicados a solucionar desde los problemas más simples hasta los más complejos que demandan las investigaciones.
3. Actualmente la tecnología de la electrónica y la informática se está transfiriendo de forma eficiente hacia el continente Asiático, quedando al margen de la competencia informática a África y Latinoamérica. Es necesario iniciar con el proceso de empoderamiento de esos conocimientos en la región si se desea ser parte del desarrollo de la ciencia y tecnología en los siguientes 50 años.

En las universidades se necesita lograr lo siguiente.

1. Incentivar hacia el desarrollo de software propio, libre y abierto; y al intercambio de códigos abiertos desarrollados en la academia.
2. Desarrollar más las capacidades de su personal académico con el fin de lograr lo más antes posible la unificación de la física, química, matemática y estadística en los niveles de postgrado: desde una maestría investigativa hasta el doctorado.
3. Transmitir esas capacidades desde los estudiantes de postgrado para entrenar a los de estudiantes de pregrado.

A nivel gubernamental se tendrá que crear la tradición en el desarrollo de esta ciencia y definir políticas educacionales para entrenar esta ciencia a temprana edad.

Y a nivel personal se necesita tener predisposición; paciencia y resiliencia; hacer matemáticas no es fácil ni para el más experto.

 

Referencias

[1] Apostolatos, N., Applied mathematics and parallel computing, Informatics and the internal necessity for the mathematization of the sciences, Physica Verlag, 1, 10, 1996, Munich, 1, Feb.         [ Links ]

[2] Bonham-Carter, G.F., Nemec, V., Merriam, D.F., Pengda, Z., Cheng, W., Bonham-Carter, G. and Cheng, Q., Progress in geomathematics, The role of Frederick Pieter Agterberg in the development of geomathematics, pp. 5-12, Springer, Berlin, 2008.         [ Links ]

[3] Charney, J.G., Fjörtoft, R. and Neumann, J.V, Numerical integration of the barotropic vorticity equation, Tellus, 2, pp. 237-254, 1950.         [ Links ]

[4] Deming, D., Pierre Perrault, the hydrologic cycle and the scientific revolution, Groundwater, 52(1), pp. 156-162, 2014.         [ Links ]

[5] Fisher, R., Dispersion on a sphere, Proceedings of the Royal Society of London, 217(1130), pp. 295-305, 1953.         [ Links ]

[6] Krumbein, W.C. and Sloss, L.L., High-speed digital computers in stratigraphic and facies analysis, Bulletin of the American Association of Petroleum Geologists, 42(11), pp. 2650-2669, 1958.         [ Links ]

[7] Le Bellac, M. A short introduction to quantum information and quantum computation (1 Ed.). Cambridge: Cambridge University Press, 2006.         [ Links ]

[8] Lin, J.W.-B., Why Python is the next wave in earth sciences computing, Bulletin of the American Meteorogical Society, pp. 1823-1824, 2012, DOI: 10.1175/BAMS-D-12-00148.1.         [ Links ]

[9] Loudon, V., Computing techniques in geology, Personal conversation with the author, 2014, Jan, Mathematical Geology.         [ Links ]

[10] Mashaal, M., Bourbaki: A secret society of mathematics. Providence, Rhode Island: American Mathematical Society, 2006.         [ Links ]

[11] Merriam, D.F., Computer use in Europe, Geotimes, 12(9), pp. 14-16, 1967.         [ Links ]

[12] Merriam, D.F., Bibliography of computer applications in the earth sciences, 1948-1970, Computers and Geosciences, 14(6), pp. 5-6, 1988.         [ Links ]

[13] Merriam, D.F., Andrei Borisovich Vistelius: A dominant figure in 20th century mathematical geology, Natural Resources Research, 10(4), pp. 297-304, 2001.         [ Links ]

[14] Puche-Riart, O., R.C. Selley, L.R.M. and Cocks, I.R., Plimer, Encyclopedia of Geology, History of Geology up to 1780, pp. 167-172, Elsevier, London, 2005.         [ Links ]

[15] Schaeben, H., Geology and mathematics: Progressing mathematization of geology, Geologische Rundschau, 77(2), pp. 591-607, 1988.         [ Links ]

[16] Schmidt, W., Statistische methoden zur gefügeuntersuchung kristalliner schiefer. Wien: Sitzungsber. d. k. Akad. d. Wissensch, 1917.         [ Links ]

[17] Vistelius, A.B., Studies in mathematical geology. New York: New York Consultants Bureau. Translation of selected articles of Vistelius form Russian to English, 1967.         [ Links ]

[18] Vistelius, A.B., Mathematical geologists and development of the geological sciences, Mathematical Geology, 8(1), pp. 3-8, 1976.         [ Links ]

[19] Perrault, P., De lórigine des fountaines. Paris: Pierre le Petit, 1674.         [ Links ]

 

L.O. Suarez-Burgoa, es DR. en Geotecnia de la Universidad de Brasilia (UnB), Brasil, MSc. en Ingeniería Geotécnica de la Universidad Nacional de Colombia (UNAL) y graduado como Ingeniero Civil de la Universidad Mayor de San Andrés de Bolivia (UMSA). Es profesor asistente del Departamento de Ingeniería Civil de la Facultad de Minas de la UNAL en Medellín, Colombia. Desarrolló actividades como consultor e investigador por más de quince años en el campo de la geotecnia civil y minera en Bolivia, Chile, Brasil y Colombia, con énfasis en la mecánica de rocas. Actualmente es desarrollador de códigos computacionales en lenguajes intérpretes, tales como MatLab 11 (Octave 4.X) y Python3, en temas relacionados a la geología aplicada y geotecnia; habiendo producido herramientas como: Buzy+, pyCSS, VolteoLab, GeonetDigitizer y SVG-stereographicPlot. Es director del semillero de investigación en geología matemática (www.geomecnica.org), parte del grupo de investigación de geotecnia del Departamento de Ingeniería Civil. ORCID: 0000-0002-9760-0277.