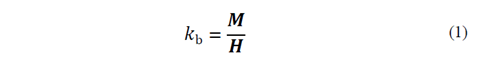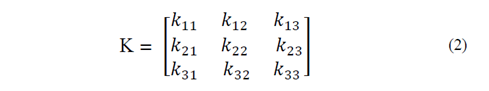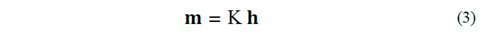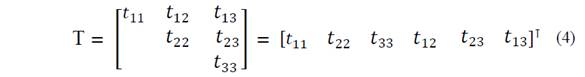1. Introducción
En este artículo se aborda la solución de un cálculo matemático el cual es posiblemente el último paso de una investigación geológica sobre la anisotropía magnética de rocas, i.e., el cálculo matemático-estadístico del Tensor de Anisotropía de Susceptibilidad Magnética (ASM) mediante la aplicación de un programa computacional de licencia libre en el lenguaje de programación Python 3.
Se desarrolla un contexto teórico mínimo necesario para introducir el término del objeto matemático tensor de segundo orden, el cual define la ASM medida en un espécimen. Se presenta el método propuesto por [1] para el tratamiento estadístico básico de una muestra o grupo de n especímenes tomados aleatoriamente y finalmente se presenta el software de aplicación desarrollado para lograr lo anterior; aquí se incluyen sus generalidades, ejecución y objetos de entrada y salida.
Los resultados que retorna el programa computacional son validados con aquellos obtenidos en el estudio de [2] donde se interpreta y analiza eventos deformacionales y depositacionales en el Miembro Superior de la Formación Amagá en el departamento de Antioquia (Colombia).
2. Susceptibilidad magnética y su tensor de anisotropía
2.1. Susceptibilidad magnética
La susceptibilidad magnética (Bulk Magnetic Susceptibility) por unidad de volumen (k b , como escalar y medida global sin tomar en cuenta la posible variación con la orientación espacial) de un sólido (i.e., en este caso una roca homogénea e isótropa en su composición mineralógica desde el punto de vista de reacción al magnetismo) se define como la relación de la magnetización M con la intensidad del campo magnético externo H
La susceptibilidad magnética es una medida del grado de magnetización de un material, por ejemplo, los minerales de la roca, al estar influenciados por un campo magnético externo; en el caso de las rocas, este sería el campo magnético terrestre (CMT) en forma natural.
La susceptibilidad magnética (en la mayoría de los minerales que tienen una respuesta al magnetismo) no es constante en todas las direcciones; por tanto, no se cumple la definición de escalar en un sistema tridimensional. En este caso, la respuesta magnética de la roca M depende de la orientación de la masa con la orientación del campo magnético; es decir, que la roca es ortótropa o anisótropa. De ahí surge el concepto de tensor de anisotropía de susceptibilidad magnética.
La ortotropía o anisotropía en la roca se puede deber a que un solo tipo de minerales que responden al magnetismo están orientados en una de tres posiciones ortogonales en el espacio. También se puede deber a que se tiene más de un mineral que responde al magnetismo, pero que sus propiedades de cada tipo son distintas, y en conjunto todos los minerales manifiestan la anisotropía.
2.2. El tensor de anisotropía de susceptibilidad magnética (ASM)
El tensor de Anisotropía de Susceptibilidad Magnética (i.e., tensor ASM) es uno de orden segundo representado con el símbolo Κ, que se puede expresar en forma de una matriz de 3×3 como Κ.
El tensor de segundo orden (Κ) representa cuánto vale la susceptibilidad magnética para la componente del campo magnético en dirección 𝑥 en tres direcciones x, y, y z: kx= (k 11 ,k 12 ,k 13 ); luego cuánto vale la susceptibilidad magnética para la componente del campo magnético en dirección 𝑦 en las mismas tres direcciones x, y, y z: ky= (k 21 ,k 22 ,k 23 ); y finalmente, cuánto vale la susceptibilidad magnética para la componente del campo magnético en dirección 𝑧 en las tres direcciones x, y, y z: kz= (k 31 ,k 32 ,k 33 ).
De este modo, el tensor de anisotropía de susceptibilidad magnética es
definido por los elementos en sus nueve términos k ij que son escalares.
Sin embargo, ( por definición (de tensor de segundo orden) es simétrico, entonces sus componentes se reducen a seis escalares distintos.
Como todo tensor tipo Cauchy, se aplican las propiedades de este objeto matemático. Por ejemplo, si el sistema coordenado se rota de tal modo que los términos k ij = 0 para i ≠ j y k ij = 0 para i = j, entonces tres magnitudes del tensor se pueden representar en tres direcciones propias. Las tres magnitudes así rotadas se llaman valores propios o valores principales y los vectores de las direcciones cuando actúan los valores propios se llaman vectores propios o vectores principales.
El tensor de ASM entonces se puede también definir como un tensor simétrico de segundo orden en el cual la magnitud de sus tres orientaciones propias del tensor (k 1 ,k 2 ,k 3 ) reflejan las respuestas más influyentes en las tres direcciones ortogonales de los dipolos magnéticos dentro de un campo magnético; modificado de [3].
El tensor ASM tiene una variedad de escalares estadísticos para su caracterización, los cuales eventualmente podrían ser de interés para el usuario que manipule este tipo de datos; en [4] (Seccs. 1.5.1 a 1.5.2, Tab. 1.1) se profundiza esto.
2.3. Representaciones gráficas del tensor de ASM
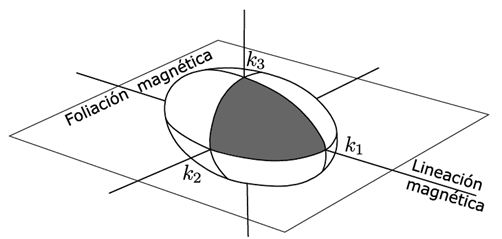
Si las direcciones propias del tensor simétrico del segundo orden ( se colocan mutuamente ortogonales, y a partir del origen de estas tres direcciones se trazan tres semiejes paralelos a los ejes coordenados y en el sentido positivo de estos ejes, tal que: para la dirección propia mayor se coloca un semieje de longitud igual al valor propio mayor del tensor, para la dirección propia intermedia un semieje de longitud igual al valor propio intermedio y para la dirección propia menor la longitud igual al valor propio menor, entonces se obtiene un octante positivo de un elipsoide. Con el octante se completa todo el elipsoide por simetría ortogonal; donde finalmente se construye el elipsoide de susceptibilidad magnética.
La Fig. 1 muestra esquemáticamente el octante y el elipsoide del tensor de anisotropía de susceptibilidad magnética, donde el eje mayor es la línea del alineamiento magnético y el plano cuyo vector ortogonal es la dirección propia menor del tensor corresponde a la foliación magnética.
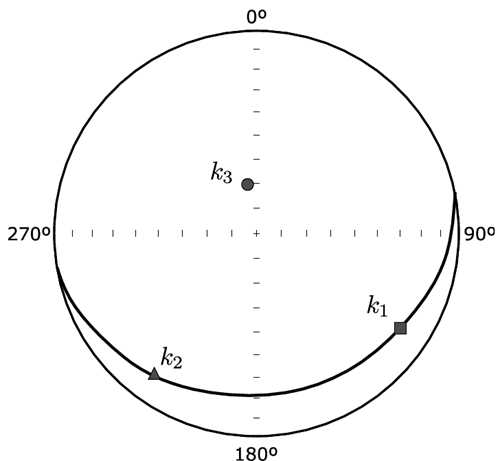
La Fig. 2 muestra esquemáticamente los tres puntos en la proyección estereográfica equiangular que representan las tres orientaciones propias del tensor de anisotropía de la susceptibilidad magnética. Estos tres puntos tienen una particularidad gráfica en esta proyección que está relacionada al tensor: los puntos que representan la orientación propia de mayor e intermedia definen un plano (en la proyección) cuyo polo corresponde al punto que representa la orientación propia menor. Esto se debe a la ortogonalidad de las direcciones propias de un tensor de segundo orden y es una de las propiedades bases dentro del desarrollo estadístico presentado más adelante.
2.4. Relación del tensor ASM con H y M
Como H y M son realmente vectores en el espacio, se representarían más adecuadamente con los símbolos h y m La relación que tiene el tensor ASM con la dirección del campo magnético h (que es generalmente un punto en el CMT) y el grado de magnetización m se puede explicar del siguiente modo:
La roca tiene minerales que responden al magnetismo y están orientadas en el espacio dado por un vector d.
Estas rocas están dentro de un campo magnético H que en el punto donde está la roca tiene una cierta dirección h.
Debido a que estos minerales están todos orientados, estos generan en un volumen de roca un campo magnético m, i.e., la magnetización.
¿Qué objeto matemático relacionará h con m? --El tensor ASM, , con la operación tensorial
Debido a que m y h son ambos campos magnéticos por unidad de volumen, entonces en el sistema internacional de unidades, el tensor ( tiene dimensión uno, i.e., [2] (erróneamente llamado adimensional).
2.5. Cálculo del tensor ASM
La operación directa de la relación entre los vectores indica que conocido 𝐡 y Κ se puede conocer 𝐦. Sin embargo, la operación contraria indica que se tiene que hallar Κ a partir de 𝐡 y 𝐦; y este aspecto implica un proceso de inversión de datos.
Lo anterior implica que existe un procedimiento tal que a partir de las medidas de h y m (para diferentes orientaciones relativas de h y m) se calcule el tensor Κ.
Debido a que las medidas tienen errores sistemáticos, que convierte a Κ en una variable aleatoria y su estimación se convierte entonces en un proceso estadístico como lo es el método de [1] el cual se usa en este artículo para la solución del cálculo inverso.
3. Estadística del tensor ASM, método de Jelínek
Como se vio arriba, el tensor Κ se puede reducir a tres direcciones propias; que si se tiene varios datos de medidas para cada una de esas tres orientaciones se tendrá una nube de puntos muy cercanos.
Inicialmente se puede aplicar la estadística de vectores a cada una de estas direcciones según lo propuesto por Fisher en [5], pero no es correcto porque la distribución alrededor de cada orientación propias no es de tipo esférica y las tres orientaciones no son estadísticamente independientes, ya que las tres están relacionadas entre sí por la condición geométrica de ortogonalidad.
Para corregir este inconveniente y poder seguir usando la estadística de Fisher, Jelínek en [1], con base al trabajo de Hext en [6] (por tanto debería llamarse el método de Hext-Jelínek pero la literatura sólo toma a uno de los autores y especialmente al segundo), desarrolla un método estadístico que se basa en el promedio de todos los tensores medidos que constituyen la muestra después de un proceso de normalización con el promedio de sus valores principales; lo que hace de este método un método fácil y preciso.
Con este método se estima entonces el tensor ASM promedio de la muestra, 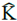 , su matriz de covarianza
, su matriz de covarianza 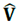 y los límites de variabilidad de los valores propios y vectores propios (k
1
,k
2
,k
3
) de
y los límites de variabilidad de los valores propios y vectores propios (k
1
,k
2
,k
3
) de 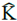 para un nivel de confiabilidad dado, siendo en el segundo caso una región que define la forma de una elipse que se localiza ortogonalmente al respectivo vector propio.
para un nivel de confiabilidad dado, siendo en el segundo caso una región que define la forma de una elipse que se localiza ortogonalmente al respectivo vector propio.
Las consideraciones de [1] indican que los errores de las medidas de las muestras son bajos y que están distribuidos de forma gaussiana, además, los tensores de la muestra de donde se estima 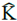 están normalmente distribuidos. Bajo estas suposiciones se estiman las regiones de confiabilidad a través de un esquema de propagación lineal de las incertidumbres en la descomposición de los valores propios del tensor. Para el manejo de los valores redundantes se basa en la teoría de mínimos cuadrados; y el marco de los cálculos es la teoría estándar multivariada.
están normalmente distribuidos. Bajo estas suposiciones se estiman las regiones de confiabilidad a través de un esquema de propagación lineal de las incertidumbres en la descomposición de los valores propios del tensor. Para el manejo de los valores redundantes se basa en la teoría de mínimos cuadrados; y el marco de los cálculos es la teoría estándar multivariada.
Sin embargo, el método de Jelínek falla si las direcciones propias no están distribuidas simétricamente, si las orientaciones propias están intermezcladas o si las orientaciones propias no oscilan alrededor de cada una de las orientaciones promedio de las medidas. Cuando se dice intermezcladas, se refiere por ejemplo a que un espécimen 𝑎 de la muestra puede tener una orientación 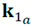 que representa el valor propio mayor y que un espécimen 𝑏 de la misma muestra puede tener una orientación
que representa el valor propio mayor y que un espécimen 𝑏 de la misma muestra puede tener una orientación 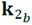 que representa el valor propio intermedio (o menor) muy cercana a
que representa el valor propio intermedio (o menor) muy cercana a 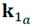 ([4] citando a [7]).
([4] citando a [7]).
4. Software de Aplicación jelinekstat
Como software se define al conjunto de programas computacionales, procedimientos y posiblemente documentación asociada y datos pertinentes para la operación de un sistema computacional [8]; mientras que software de aplicación (desde ahora con la sigla SA) es aquel diseñado para ayudar a los usuarios a llevar a cabo tareas o encargarse de ciertos tipos de problemas, distinto de aquel software que controla el computador [8]. Siendo un programa computacional una unidad sintáctica que engloba a las reglas de un particular lenguaje de programación y que está compuesto de declaraciones, sentencias condicionales e instrucciones necesarias para una función, tarea o solución de un problema [9].
A continuación, se presenta el SA desarrollado para el presente artículo, jelinekstat, el cual se encuentra empaquetado y enlazado en el repositorio PyPI (siglas del idioma inglés de the Python Package Index). para su instalación mediante el manejador de paquetes PIP con la siguiente instrucción en consola:
El SA jelinekstat es un software de aplicación libre (licencia académica BSD-2) y de código abierto que se ha desarrollado por los autores del presente artículo con el fin de analizar bajo el marco de la estadística, los datos cuyo objeto matemático es un tensor de segundo orden que representa un tensor ASM.
El SA jelinekstat logra obtener mediante cálculos: el tensor promedio y sus valores y vectores propios (también llamados principales), los intervalos de confianza de los valores propios del tensor promedio y finalmente las regiones de confianza de las direcciones propias del tensor promedio a partir del método propuesto por Jelínek en [1]; todo esto englobado y presentado en un diagrama de proyección esférica equiareal.
Este SA fue escrito en el lenguaje de programación Python 3 bajo el paradigma funcional; de este modo, son 17 funciones seccionadas en 2 módulos (un módulo es cada archivo en lenguaje Python con extensión .py) con el fin de realizar los cálculos con los datos de tensores de ASM de una muestra de 𝑛 especímenes medidos.
La división de la aplicación en dos módulos se realiza por la necesidad de separar las funciones asociadas a las ecuaciones presentadas por Jelínek en [1] para el desarrollo del proceso estadístico (jelinekstat.py) y el grupo de herramientas que soportan a la metodología para su completo desarrollo tales como operaciones del algebra lineal, transformaciones de sistemas coordenados y operaciones sobre la red estereográfica (tools.py). El esquema de la Fig. 3 muestra la organización del directorio del SA.
La documentación (i.e., explicación de parámetros de entrada, salida, uso, y ejemplos) de cada una de las funciones se amplían en el Manual de Usuario cuyo enlace electrónico se muestra en el Anexo B del presente artículo.
Para facilitar el uso del módulo se debe crear un archivo de lotes con los datos de entrada de las medidas, y con ello ir estructurando el procedimiento de cálculo llamando a cada una de las 17 funciones de forma apropiada.
Como modelo de archivo de lotes, el usuario consulta el archivo shortSCR.py que tiene las oraciones de código mínimas necesarias para hacer un completo cálculo desde los datos de entrada, hasta los datos de salida incluyendo gráficas.
En caso de no ser muy experto en el manejo de programas en Python 3, esta tarea está agrupada en una sola función llamada tensorStat.
Para que el programa corra se requiere en el intérprete de ese mismo lenguaje de programación importe a los paquetes NumPy y SciPy, además, si se quiere tener capacidades de graficación en la proyección esférica equiárea, se debe tener también los paquetes Matplotlib y mplsteronet; todos ellos disponibles en línea en el repositorio PyPI.
A continuación, se describe cada uno de los objetos computacionales que hacen los datos de entrada y salida del SA.
4.1. Objetos de entrada
Lo más importante para el uso de este programa es introducir correctamente los datos de los valores medidos de las componentes de los n tensores ASM / que constituyen la muestra aleatoria (grupo de n especímienes que se usan para estimar los estadísticos de la población).
Un tensor cualquiera Τk de segundo orden que representa una medida ASM es un tensor simétrico compuesto por seis componentes que por comodidad se pone en un vector columna:
Los componentes de los 𝑛 tensores se reúnen en un objeto (definición desde el punto de vista computacional) que resulta bien sea de la importación de un archivo de texto, una lista anidada o un arreglo matricial en NumPy.
Si el objeto de entrada de los datos va a ser un archivo, los datos se preparan en cualquier editor de texto y se graban con la extensión .txt. Este archivo tendrá un arreglo de números tal que que formará una matriz de 𝑛 filas y 𝑚 columnas, siendo 𝑛 el tamaño de la muestra, es decir, el número de tensores (dato que se tiene disponible de las mediciones) y siendo 𝑚 las 6 componentes de cada tensor en su forma vectorial con el estricto orden que se muestra en la ecuación 4; la exigencia final para la importación del archivo es que el separador de columnas sea el espacio tabulador.
El siguiente listado muestra los datos de ocho tensores en el archivo exampledata.txt del subdirectorio de ejemplos del SA (examples/).
Para importar los datos del archivo de texto se usa la función del programa extractdata con las siguientes líneas de comando:
donde sample es un objeto del tipo array del módulo NumPy de Python que agrupa los objetos de arreglo matriciales que representan los tensores; y numTensors es el número de tensores en la muestra.
Por otro lado, si la entrada de los datos no es desde un archivo de texto, se puede lograr con un objeto lista con estructura anidada de la siguiente forma:
Eventualmente, se tendría el mismo resultado como un arreglo matricial del paquete NumPy mediante un objeto de tipo array a partir de la lista anidad así:
El segundo objeto de entrada para el programa es el valor numérico del estadístico que indica el nivel de confianza. Este debe ser almacenado en la variable confLevel; por ejemplo, confLevel = 0.95 indica un nivel de confianza del 95% Por lo regular se calcula para niveles de confianza de 50%, 95% y 99.5%.
4.2. Ejecución del programa
La ejecución del programa se puede hacer de varias formas.
-
Embebiendo el intérprete de Python 3 en el código de programa externo mediante una interfaz de alto nivel. Por ejemplo, desde el lenguaje C++ se crea las siguientes líneas de comandos
-
Desde la consola de cualquier sistema operativo abierta en la carpeta donde reside el script de ejecución (por ejemplo el presentado en el Apéndice C) mediante la siguiente instrucción:
Desde un Entorno de Desarrollo Integrado (IDE, acrónimo del idioma inglés de Integrated Development Environment) ejecutando allí el script.
Escribiendo línea a línea cada comando del script directamente en el intérprete de Python 3 abierto en consola.
-
Haciendo uso de cualquiera de las opciones anteriores importando la función tensorStat así:
Todas estas opciones se tienen disponible en un SA de código abierto, y esa es la ventaja referente a los códigos cerrados, porque en código abierto se puede acoplar lo que ya está desarrollado aquí en otro programa más específico.
4.3. Objetos de salida
Una vez que el programa es ejecutado con los objetos de entrada descritos arriba, este arroja una estructura de tipo diccionario con las siguientes claves.
El tensor promedio dado en forma de matriz 3×3, K.
El tensor promedio dado en forma de vector, k.
El número de tensores con el que se realizó el cálculo, n.
El valor propio mayor de K, k1, en una estructura de tipo diccionario cuyas claves son su valor, value y su variabilidad, variability.
El valor propio intemedio de K, k2, en una estructura de tipo diccionario cuyas claves son su valor, value y su variabilidad, variability.
El valor propio menor de K, k3, en una estructura de tipo diccionario cuyas claves son su valor, value y su variabilidad, variability.
El vector propio mayor de K, p1, en una estructura de tipo diccionario cuyas claves son las siguientes:
coordenadas ℝ 3 , coords;
cabeceo o inclinación (plunge), plg;
dirección respecto al norte (trend), trd;
longitud del eje mayor de la elipse de la región de confianza, majAx;
longitud del eje menor de la elipse de la región de confianza, minAx;
inclinación del eje mayor de la elipse de la región de confianza respecto al eje vertical en el sentido de las manecillas del reloj, incl.
El vector propio intermedio de K, p2, en una estructura de tipo diccionario cuyas claves son las mismas de p1.
El vector propio menor de K, p3, en una estructura de tipo diccionario cuyas claves son las mismas de p1.
Además de lo anterior, el SA permite obtener dos resultados gráficos para visualizar tras la ejecución o como archivos exportables con cualquier extensión permitida por Matplotlib bien sea de tipo vectorial o rasterizado.
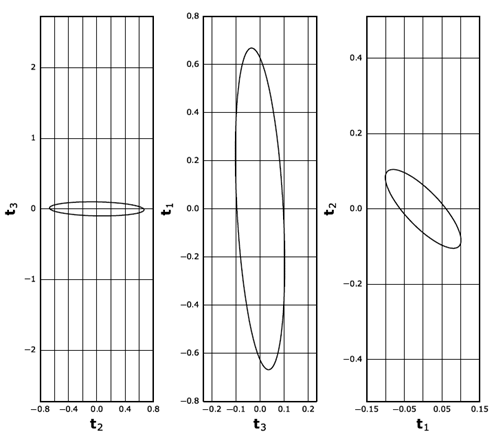
El primer resultado gráfico corresponde a una figura fraccionada en tres, donde se observan las tres regiones de confianza de las direcciones principales del tensor promedio en planos ortogonales a cada una. Ejemplo de este resultado se observa en la Fig. 4.
Fuente: Los autores.
Figura 4 Elipses de confianza del 95% en el plano ortogonal a cada vector propio.
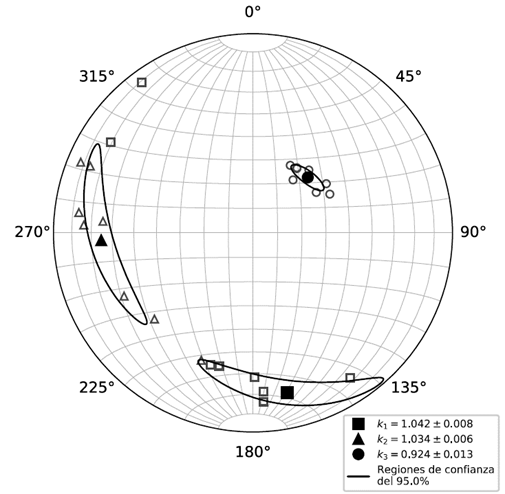
El segundo resultado gráfico corresponde a una figura en proyección esférica equiárea que contiene las orientaciones principales del tensor promedio y las elipses de sus regiones de confianza proyectadas en este sistema; también proyecta las orientaciones principales de cada una de las medidas de la muestra con la que se estimó el tensor promedio. En la gráfica, el símbolo que representa el vector principal mayor es un cuadrado, el que representan el vector principal intermedio es un triángulo, y el que representa el menor es un círculo. Si el símbolo está relleno de color negro está representando el promedio, mientras que si no está relleno es únicamente el dato de entrada. Ejemplo de este resultado se observa en la Fig. 5.
Fuente: Los autores.
Figura 5 Ejemplo de la proyección esférica equiárea del SA jelinekstat: cuadrados, direcciones principales mayores; triángulos, direcciones principales intermedias; círculos, direcciones principales menores. Los valores en la leyenda son los valores propios con su respectivo límite de variabilidad para una confianza del 95%; las elipses proyectadas son las regiones de variabilidad de la misma confianza para cada dirección principal del tensor promedio.
Otros resultados intermedios del proceso estadístico planteado en [1] se encuentran disponibles si se ejecuta con el archivo de lotes en su versión extendida que se encuentra en el directorio de ejemplos del SA con el nombre de longSCR.py del subdirectorio de ejemplos.
A partir de todos los objetos de salida se puede diseñar un programa para colocar en un reporte de una hoja en formato pdf si se interactúa con el programa LaTeX, por ejemplo; y esta es otra ventaja de tener un código abierto.
5. Validación
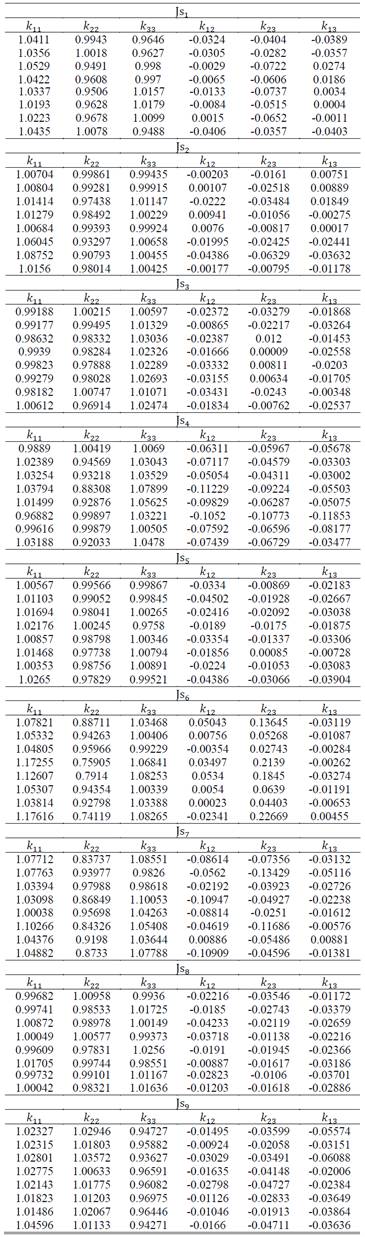
La validación del SA se hizo con nueve muestras de mediciones del tensor ASM del estudio de [2], 𝐉𝐬 1 , 𝐉𝐬 2 , …, 𝐉𝐬 9 , cada una de ellas con un total de 𝑛=8 especímenes, las cuales se presentan en el Apéndice A.
Dichos datos para la validación del SA fueron otorgados a los autores del presente artículo por gentileza los autores del trabajo de campo y laboratorio que generaron los datos de entrada de ASM usados en [2].
Debido a que los autores del mencionado estudio usaron como herramienta de análisis el programa computacional gratuito (pero en código cerrado) llamado Anisoft 4.2, que es un programa validado desde hace varios años y frecuentemente usado hoy en día en la industria; entonces simplemente la validación radicará en comparar los resultados de ambos SA, y si las gráficas de resultados son las mismas, entonces los programas realizan la misma tarea.
5.1. Origen geológico de las muestras e interpretación
El trabajo de [2], sobre la ASM fue desarrollado en rocas sedimentarias de la unidad Geológica denominada formalmente como Formación Amagá, la cuál ha sido objeto de múltiples estudios desde hace ya casi 100 años cuando E. Grosse realizó su estudio sobre la unidad carbonífera del suroccidente antioqueño de Colombia a la cual denominó el Terciario Carbonífero de Antioquia [10].
El ejemplo mostrado previamente en las secciones 4.1 y 4.3, se desarrolló con los datos de la muestra  extraída de un estrato de 10m de espesor de una arenisca con laminación plana-paralela perteneciente a la unidad estratigráfica número cuatro del levantamiento presentado por [11] de la sección expuesta en la Quebrada Sabaleticas, donde aflora el Miembro Superior de la Formación Amagá [12].
extraída de un estrato de 10m de espesor de una arenisca con laminación plana-paralela perteneciente a la unidad estratigráfica número cuatro del levantamiento presentado por [11] de la sección expuesta en la Quebrada Sabaleticas, donde aflora el Miembro Superior de la Formación Amagá [12].
Los datos de mediciones del tensor de anisotropía de susceptibilidad magnética en el estudio de [2], se usaron con el objeto de interpretar y analizar eventos deformacionales y depositacionales en el Miembro Superior de la Formación Amagá en el departamento de Antioquia (Colombia). Por lo anterior, en el presente estudio no se realiza una interpretación geológica de los datos, debido a que esto ya fue hecho.
5.2. Comparación de resultados
Los datos de entrada puestos en el SA Anisoft 4.2 arrojan un diagrama en proyección estereográfica equiárea con la síntesis del resultado; similarmente ocurre al hacerlo con el SA jelinekstat también arroja un diagrama igual como síntesis.
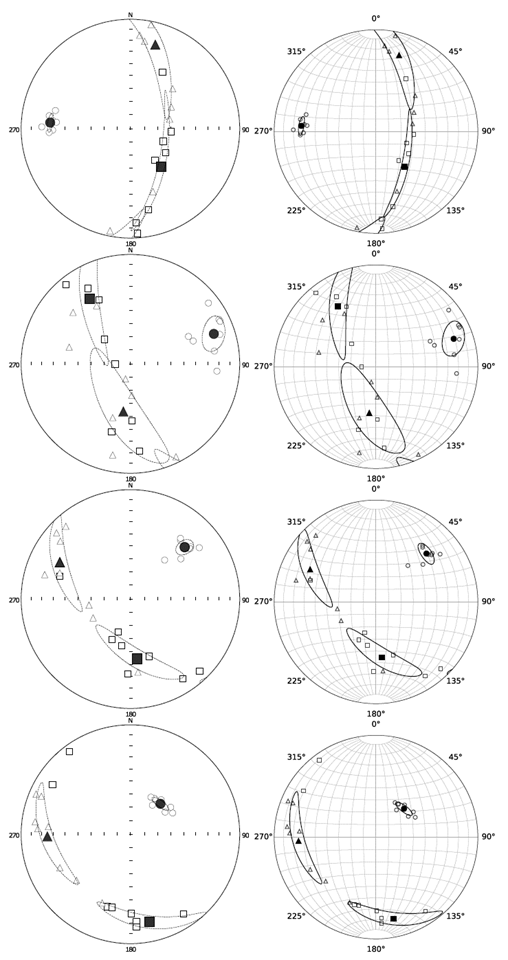
Las Figs. 6 y 7 están estructuradas de tal forma que las obtenidos con el programa Anisoft 4.2 del estudio original se encuentran en la subcolumna izquierda, mientras que las obtenidas con el código que se ha descrito en este artículo, el SA jelinekstat, se encuentran en la subcolumna derecha.
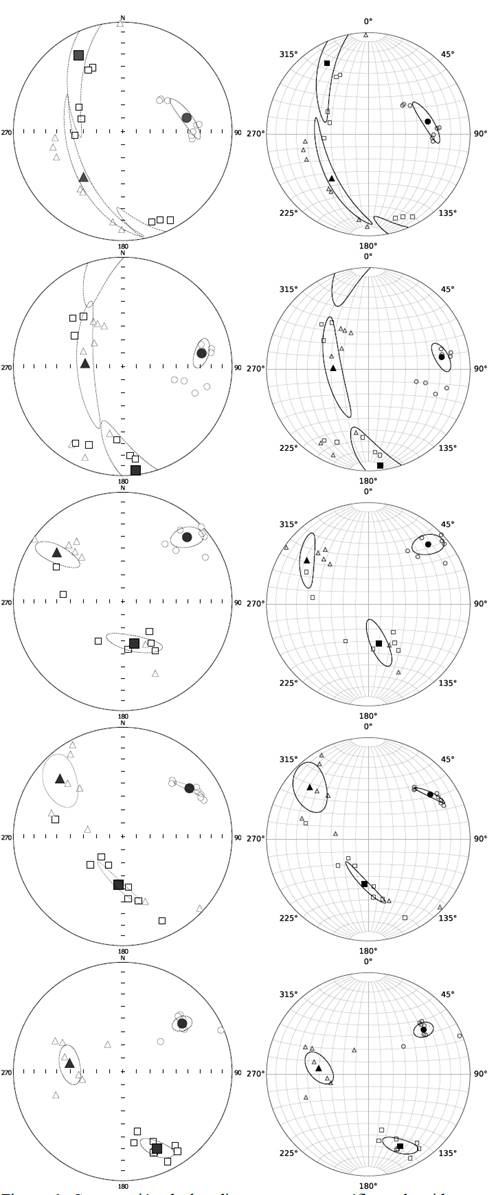
Fuente: Los autores.
Figura 6 Comparación de los diagramas estereográficos obtenidos por Anisoft 4.2 (izquierda) y el SA jelinekstat: (derecha). Muestras 𝐉𝐬 1 a 𝐉𝐬 5 .
5.3. Discusión
Aunque los programas computacionales comerciales o aquellos que acompañan a los instrumentos de laboratorio son de gran utilidad para el desarrollo de las labores científicas e ingenieriles para una producción industrial, es fundamental conocer la concepción teórica que hay detrás de todo cálculo y resultado, y más aún, la forma en que se desarrollan los cálculos internamente para asegurar la confiabilidad de los resultados y además para a partir de esos datos hacer más cálculos.
Dado que en el software Anisoft no es posible visualizar las componentes del tensor promedio 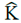 o los productos intermedios del cálculo de Jelínek como la matriz de covarianza
o los productos intermedios del cálculo de Jelínek como la matriz de covarianza 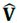 , se pueden comparar únicamente la localización de los vectores propios del tensor promedio y la forma de las regiones de confianza de los mismos en los diagramas estereográficos de las nueve muestras; tal como se observa en las Figs. 6 y 7. Con este paralelo se aprecia entonces, que los diagramas son similares dando un buen argumento para la validación del programa desarrollado.
, se pueden comparar únicamente la localización de los vectores propios del tensor promedio y la forma de las regiones de confianza de los mismos en los diagramas estereográficos de las nueve muestras; tal como se observa en las Figs. 6 y 7. Con este paralelo se aprecia entonces, que los diagramas son similares dando un buen argumento para la validación del programa desarrollado.
El SA jelinekstat es potencialmente más útil porque no es un programa cerrado y además porque no solo arroja objetos gráficos, sino que también los datos intermedios del proceso estadístico presentado por [1] que pueden ser empleados en otras aplicaciones o para otro tipo de interpretaciones.
6. Conclusiones
El código abierto y libre desarrollado por los autores y expuesto en el presente artículo, jelinekstat, posibilita al usuario que a partir de un grupo 𝑛 de tensores simétricos y balanceados (de segundo orden), se calcule el tensor promedio y la variabilidad de sus valores y direcciones principales, estas últimas expresadas como elipses de confiabilidad.
Con el SA, también posibilidad la obtención de una gráfica en proyección esférica que sintetiza lo anterior, así como la representación de los tensores de la muestra introducidos. También es posible obtener los demás resultados intermedios del método de cálculo de Jelínek para la estadística de tensores de segundo orden.
La funcionalidad del SA es validada con datos medidos en las muestras estudiadas por [2], muestras que pertenecen al Miembro Superior de la Formación Amagá.
El programa es útil para la academia, investigación y la industria; puede ser estudiado, modificado, mejorado o ampliado bajo licencia BSD-2 según las necesidades específicas requeridas.