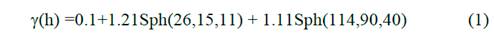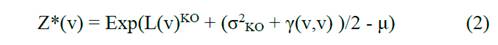1. Introducción
En el noroeste de la provincia de Pinar del Río, Cuba, existen un grupo de yacimientos minerales, así como otras pequeñas acumulaciones clasificadas como tipo Bechi. Los más importantes son: “Hierro Mantua”, “Unión 1”, “Juan Manuel”, “Unión 2”, “Flanco Este”. Algunos de ellos se encuentran en la etapa de factibilidad para futura explotación. Los mismos están asociados a rocas de la Formación Esperanza (J3ox - K1ne).
Según [9], la faja esperanza ha sido considerada por algunos autores como una sub-zona independiente y por otros como una prolongación de la secuencia de Rosario Norte. Su corte puede dividirse en dos partes:
Corte inferior: Secuencia carbonatada- terrígena constituida por calizas arenosas, a veces micro - organógenas, calizas fragmentarias o gravelíticas, calizas arcillosas con material orgánico, calizas dolomitizadas. Entre las calizas aparecen capas finas a medias de areniscas y limolitas cuarcíferas. Se intercalan a veces paquetes de dolomitas y anhidritas, además de cuerpos de diabasas o basaltos toleíticos.
Corte superior: Secuencia terrígena- carbonatada constituida por areniscas y limolitas cuarcíferas, con intercalaciones de capas de arcillas con material orgánico, calizas arenosas, gravelitas calcáreas y calizas micro-organógenas.
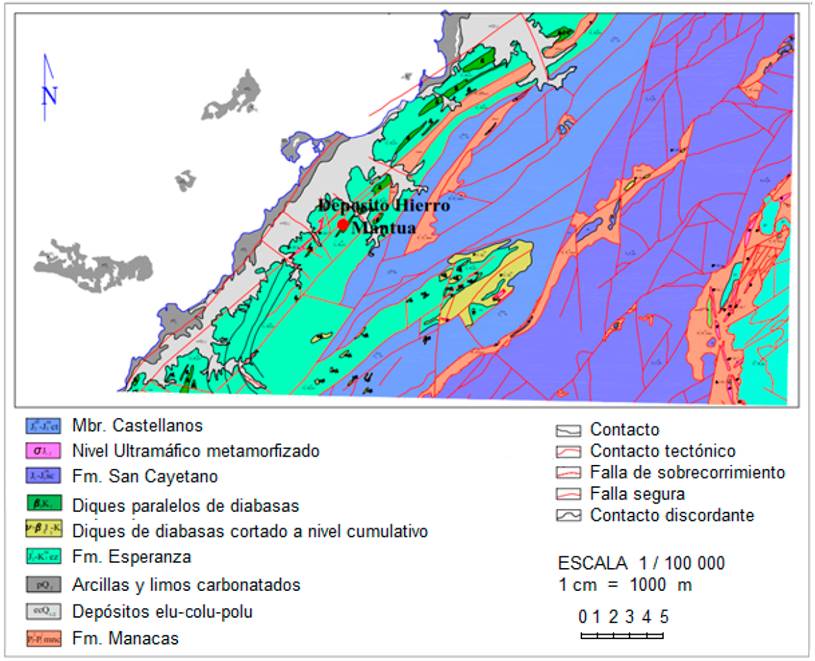
El cuerpo mineral es un lente alargado, que se asocia a una colina de dirección NE, paralela a la costa, con alturas entre 60 y 75 metros sobre el nivel del mar (msnm) (Fig. 1), este aflora a la superficie, concordante con las rocas encajantes, donde los procesos de enriquecimiento secundario alcanzan un desarrollo total, como resultado de un proceso de extrema oxidación, lixiviación y concentración del Cu, de la mineralización sulfurosa primaria de origen vulcanógeno - sedimentario, tipo Bechi.
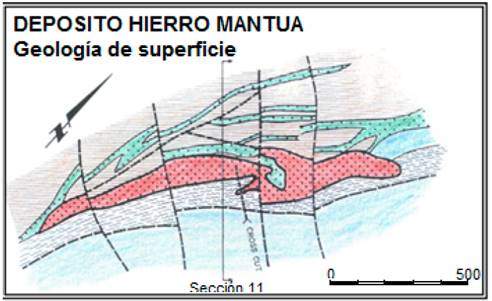
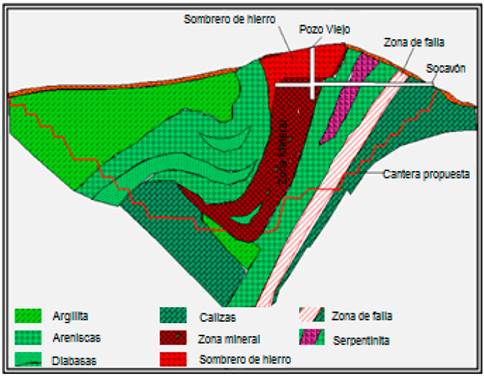
En las Figs. 2 y 3 se muestran un esquema geológico de superficie y un corte transversal típico del yacimiento, respectivamente, en ellos se destaca la gran complejidad geólogo estructural representada por numerosas fallas e intensos plegamientos acompañado de una oxidación total y posterior enriquecimiento de todos los sulfuros primarios.
Históricamente, se utilizaron métodos clásicos para la estimación de recursos en estos yacimientos, pero como es conocido estos métodos no garantizan la precisión necesaria, lo que se acentúa por las complejidades geológicas de la región. Con el objetivo de lograr la precisión adecuada en la estimación de recursos en el yacimiento “Hierro Mantua” dos objetivos son tratados en este trabajo: obtener la Unidad de Selección Minera (USM) racional para cuantificar los recursos minerales en el yacimientos en estudio, y aplicar métodos de la Geoestadística no lineal para la estimación de recursos minerales, específicamente el Krigeado Lognormal por la presencia de distribuciones asimétricas en los contenidos de Cu, particularmente por la ocurrencia de pocos valores altos de esta variable en el yacimiento Hierro Mantua.
En relación al Krigeado Lognormal, existen algunas publicaciones relativas a este método de estimación, clasificado dentro de la Geoestadística no lineal, algunos de los más importantes son: [20; 19; 22; 14; 15; 8; 16; 25; 2; 23; 18; 17; 24; 4; 6; 26; 27; 21]. Algunas ideas discutidas en estos trabajos son: la sensibilidad del semivariograma experimental con relación a pequeños valores altos [14], los altos valores causan deformidades en el semivariograma que impiden el uso del Krigeado lineal. De acuerdo con [4], “…los problemas potenciales en el Krigeado Lognormal están relacionados en la transformación inversa de las estimaciones logarítmicas a la escala de valores originales, con relación a la cual han existido desacuerdos en la literatura Geoestadística en cuanto a cómo se debe desarrollar la transformación inversa. En este sentido no es fácil encontrar en la bibliografía Geoestadística una expresión para la transformación inversa en el caso del Krigeado de Bloques. Un resumen sobre la estimación del Krigeado Lognormal en una forma ordenada es presentado en [23], este autor concluye que la ecuación de transformación inversa para la estimación de bloques no es teóricamente óptima. [24] concluye que “…los especialistas deben decidir si el Krigeado Lognormal es factible para las estimaciones locales. [6], puntualiza “…que los datos que describen una distribución asimétrica pueden ser satisfactoriamente modelados a partir de procesos espaciales log-normales. De una forma práctica la transformación inversa puede ser obtenida por la exponencial de las estimaciones de Krigeado más un término de no sesgo ([26]. Finalmente, en nuestro trabajo los valores de Cu son estimados siguiendo las ideas presentadas en [23], específicamente la ecuación de transformación inversa, ecuación 6 de la página 218. La precisión de este método ha sido probada por algunos autores en diferentes yacimientos minerales y otros estudios cuando la distribución asimétrica ha sido encontrada.
2. Materiales y métodos
La calidad de la información primaria es uno de los elementos más importantes para la estimación de recursos usando el Krigedo como interpolador, este aspecto determina la calidad de los resultados [1]. La base de datos del yacimiento “Hierro Mantua” usada en este trabajo fue validada en el 2008 por la compañía “Coffey Mining” a solicitud de RSG Global de la Empresa “Cobre Mantua S.A.” [3]. Una revisión exploratoria inicial de las muestras fue desarrollada determinándose que la longitudes de las muestras varían entre 0.05 m a 4.65 m, con un promedio de 1.22 m. Se realizó una regularización en compósitos de 1 m de longitud en el interior del cuerpo mineral. Se estudiaron los valores de Cu de 318 pozos regularmente distribuidos en dos campañas de exploración de 100x100 m y 50x50 m, creando 5304 compósitos de 1 m longitud.
2.1. Análisis exploratorio de datos
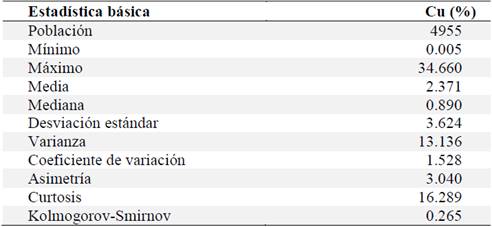
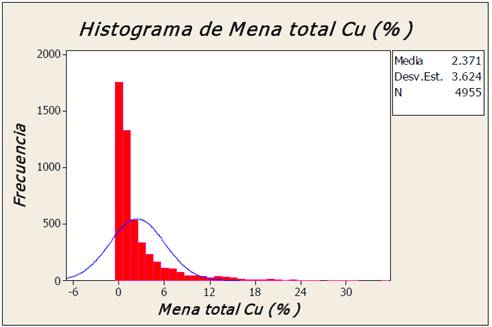
La Tabla 1 muestra la estadística descriptiva de los valores de Cu. Se puede observar que la media y la mediana presentan valores muy diferentes y muy pequeños con relación al valor máximo, el coeficiente de variación es mayor que 1. Por lo que se puede inferir que la distribución de los contenidos de Cu es asimétrica, lo cual puede ser observado en el histograma, Fig. 4. El valor de la prueba de normalidad Kolmogorov-Smirnov es de 0.265, el cual es mayor que 0.05 Los resultados muestran un comportamiento no normal de los valores de Cu. Por esta razón los procedimientos de la Geoestadística lineal, Krigeado Simple o Krigeado Ordinario no pueden ser aplicados, es más apropiado usar métodos no lineales de la Geoestadística [13; 12; 23].
2.2. Metodología
El procedimiento propuesto para la solución del problema planteado consiste en transformar los datos de forma logarítmica, de modo que se obtenga una nueva variable que sea estacionaria, posteriormente aplicar el Krigeado Simple o Krigeado Ordinario, se utiliza en este caso la segunda variante. Posteriormente los datos son anti-transformados para devolverlos a su rango original. Este procedimiento se conoce como Krigeado Log-normal. Con el objetivo de lograr una mayor precisión en la estimación de recursos, se propone además, un procedimiento para determinar la Unidad de Selección Minera racional a utilizar en la estimación, en cual consiste en usar la simulación Geoestadística para obtener una realización de la variable transformada y probar la calidad de la estimación por Krigeado para diferentes tamaños de los bloques de estimación. Para esto se logra obtener un posible valor real a través de los valores medios simulados por ventanas móviles con igual tamaño que los bloques propuestos, y comparar la estimación con lo posibles valores reales utilizando el criterio del erro cuadrático medio. Las estimaciones obtenidas utilizando la variable transformada de forma logarítmica unido al tamaño racional de la Unidad de Selección Minera proporciona una valor más preciso.
3. Resultados y discusión
3.1. Transformación Lognormal
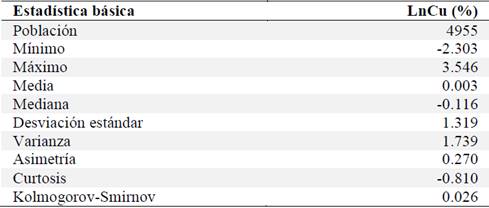
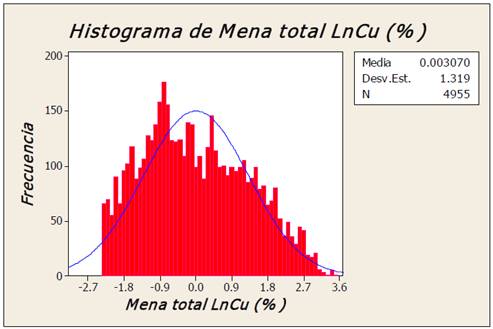
Los valores de Cu fueron transformados logarítmicamente, obteniéndose una nueva variable LnCu (LnCu = Ln[Cu]), la Tabla 2 muestra la estadística básica y la Fig. 5 el histograma de los datos transformados. Se puede observar una distribución normal en correspondencia con la estadística básica. Los valores de la media y la mediana de la nueva variable LnCu son ahora cercanos. La prueba Kolmogorov-Smirnov es 0.026, la cual es menor que 0.05, lo que asegura un comportamiento normal en los valores de LnCu. Adicionalmente, la estadística de ventanas móviles muestra valores estables de la media de los valores de LnCu. El rango calculado por la diferencia de los valores máximos y mínimos de la media de las ventanas móviles es de 1/5 del rango de los valores de LnCu. Por lo anterior la estacionaridad puede ser asumida en el comportamiento de la variable transformada LnCu, el Krigeado Lognormal puede ser aplicado [13; 12; 5].
3.2. Análisis de variabilidad
La distancia entre las localizaciones más alejadas por el rumbo es de 650 m, 230 m por le buzamiento y 60 en la dirección vertical. Los parámetros para el cálculo del semivariograma se presentan en la Tabla 3. En todas las direcciones, la variabilidad fue estudiada hasta aproximadamente la mitad de la distancian máxima.
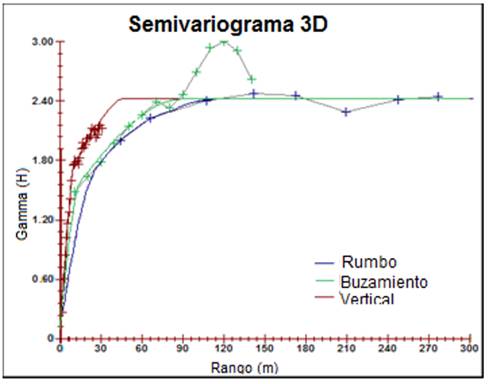
El semivariograma experimental y el modelo ajustado son mostrados en la Fig. 6. Todos los semivariogramas fueron calculados con el sistema automatizado GEMCOM. Se observa una anisotropía geométrica. El ajuste del semivariograma experimental fue realizado por un modelo imbricado, compuesto por dos modelos esféricos con un efecto de pepita. La expresión analística de modelo de variabiliad y correlación especial obtenida se muestra en la siguiente ecuación (Ec. 1):
Dónde:
0.10 = Efecto de Pepita
Sph = Modelos Esférico
1.22 = Meseta de la primera estructura
(25,20,10) = Alcances para la primera estructura según el rumbo, el buzamiento y pozo abajo
1.19 = Meseta de la segunda estructura
(110,90,30) = Alcances de la segunda estructura según el rumbo, el buzamiento y pozo abajo
3.3. Validación del modelo
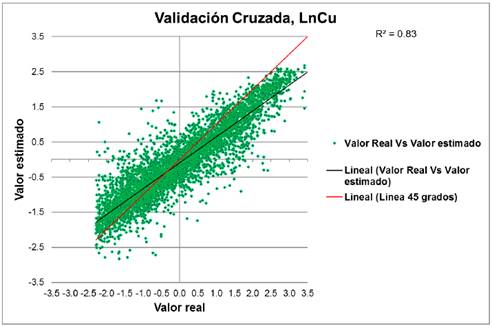
El modelo de variabilidad obtenido fue validado usando el procedimiento de la validación cruzada. La correlación entre estimados y valores medidos es buena (Fig. 7), esta figura muestra una alta concentración de valores alrededor de la pendiente 45°, el coeficiente de Pearson es de 0.92. Este resultado muestra que el modelo de variabilidad obtenido en el análisis estructural describe adecuadamente la variabilidad y correlación espacial de la transformación log-normal de los contenidos de Cu en el fenómeno mineralizado bajo estudio.
Con los resultados de la validación cruzada, valores reales y estimados, se desarrolló un análisis de los errores de estimación, se obtuvo que el 94.34% de los datos reales están incluidos en el intervalo de predicción (Zi ± 2*σ) considerando σ como la desviación estándar de los errores de estimación, y el 87.11% de los datos reales están incluidos en este intervalo de predicción considerando σ como la desviación estándar de Krigeado.
3.4. Determinación de la unidad de selección minera
Por medio de la simulación Geoestadística se aplicó un procedimiento para la determinación de la unidad de selección minera. Una realización de la variable regionalizada estudiada (LnCu) fue obtenida utilizando la simulación secuencial gaussiana (SSG) por medio de la librería Geoestadística GsLib [7], particularmente por medio del programa “sgsim”. La SSG es una técnica ponderosa y la más utilizada para obtener valores simulados de forma regionalizada [11]. En este sentido como los valores de Cu muestran una extrema distribución asimétrica, la nueva variable obtenida por transformación logarítmica LnCu, fue simulada en una red densa con el objetivo de reproducir posibles valores reales. Estos posibles valores reales fueron calculados a partir del promedio de los valores simulados en el interior de bloques con diferentes tamaños de USM.
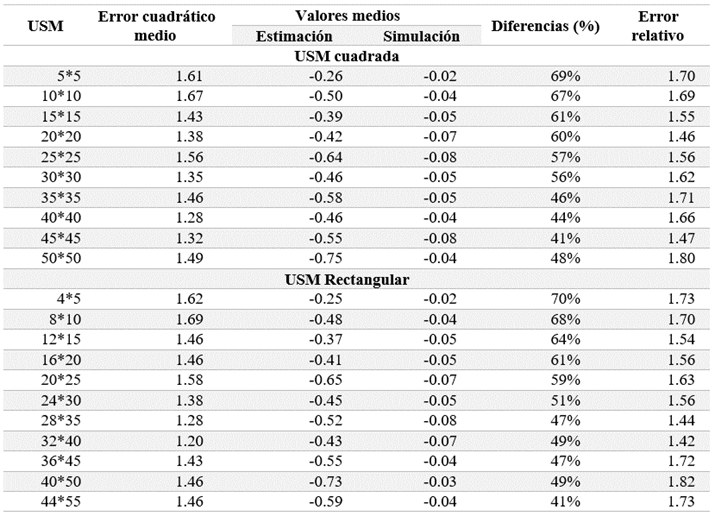
Este procedimiento consiste en comparar posibles valores reales con los valores estimados por Krigeado Ordinario para un conjunto de USM propuestas (Tabla 4). Posteriormente se utiliza el criterio del Error Cuadrático Medio para obtener el tamaño racional de los bloques de estimación. De esta forma se garantiza una alta precisión en la estimación de recursos tanto a nivel global como local. El tamaño racional obtenido como racional fue de 32x40m.
El procedimiento propuesto fue repetido para otras realizaciones obtenidas a partir de la Simulación Secuencial Gaussiana, los resultados obtenidos fueron similares, es decir se obtuvo 32x40m cómo tamaño racional de la USM. [10] desarrollaron una primera investigación para un yacimiento no metálico, basados en la opinión de que el equipamiento minero no debe ser el factor determinante del tamaño de la USM, sino debe ser el resultado de aplicar adecuadamente el método de estimación desde el punto de vista matemático, el cual tiene en cuenta el comportamiento natural del fenómeno regionalizado. Finalmente, se emplea el Krigeado Lognormal para la estimación de recursos utilizando el tamaño de la unidad de selección minera obtenido anteriormente.
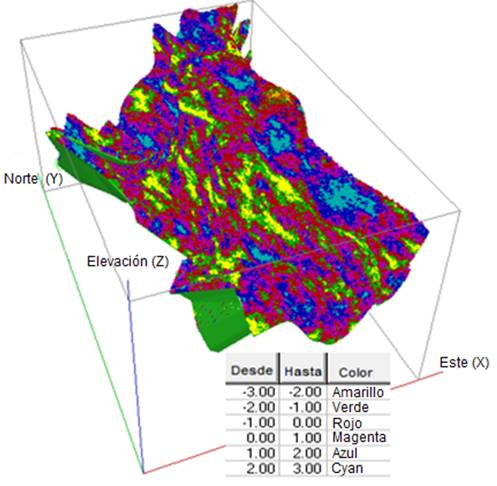
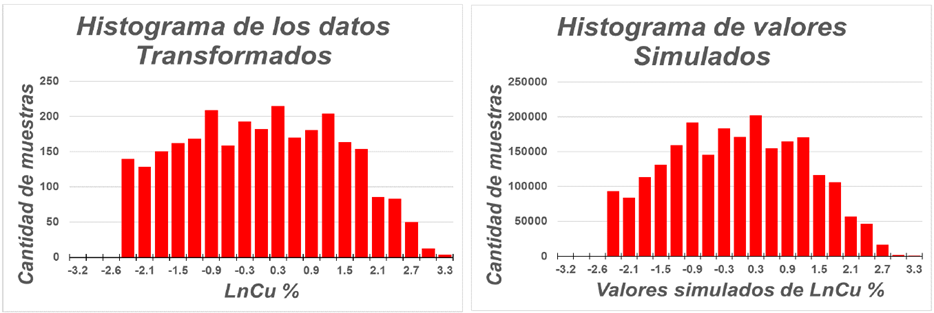
La simulación desarrollada con los datos transformados, LnCu, se presenta en la Fig. 8, usando el modelo de variabilidad especial representados por la Ec. 1 en una red de simulación de (1x1x1 m). Esta simulación fue verificada, la estadística básica de los datos reales y simulados son iguales, así como que el histograma y el semivariograma de éstos, que muestran un comportamiento similar, Fig. 9.
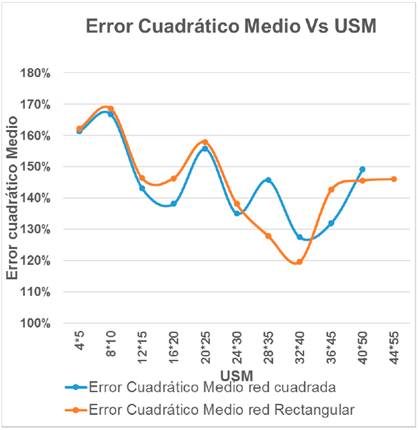
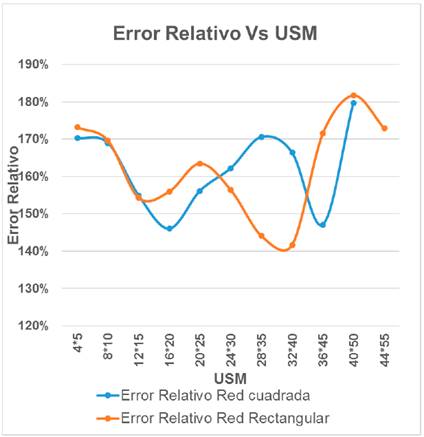
La red de simulación fue muy densa con el objetivo de obtener los posibles valores reales en el interior de cada USM propuesta (Tabla 4). Los valores estimados fueron obtenidos por el Krigeado Ordinario para cada USM propuesta, los errores fueron calculados comparando los posibles valores reales con los valores estimados para cada USM. Los resultados se muestran en la Tabla 4 y Fig. 9. El error cuadrático medio y errores relativos fueron utilizados en la comparación. La Fig. 9 muestra los nomogramas de los errores cuadráticos medios y relativos contra el tamaño dela USM. Las USM fue propuesta en dos formas: la cuadrada y la rectangular, para tomar en cuenta la anisotropía.
La influencia de la forma de la USM fue verificada (Fig. 10a y 10b). El menor valor del error cuadrático medio se presenta en la USM de 32x40m, la cual es la más precisa para la estimación de recursos. Usando esta USM como racional se aplicó el Krigeado Lognormal sobre el cuerpo mineralizado (Fig. 9). La transformación inversa fue realizada por la siguiente expresión [23].
donde:
L(v)KO = Estimación de los valores transformados por Krigeado Ordinario.
σ2 KO = Varianza de Krigeado.
γ(v,v) = Semivariograma medio Bloque-Bloque.
μ = Multiplicador de Lagrange.
La Tabla 5 muestra la estadística básica entre los contenidos originales y estimados después de la transformación inversa. Los valores medios son próximos. La varianza tiene valores adecuados, en correspondencia con las características de suavizado de los métodos de interpolación. No se obtuvieron valores extremos en la estimación. Otra variante a emplear cuando la trasformación logarítmica no garantiza la estacionaridad necesaria es el Krigeado Multigaussiano.
4. Conclusiones
En este artículo se muestra como obtener una adecuada estimación de recursos cuando los datos exhiben una distribución asimétrica, la cual es muy común en estudios mineros. Las complejidades geológicas en la región del yacimiento indican que los métodos de la Geoestadística lineal no pueden ser aplicados. La no normalidad de los de los contenidos de Cu en el yacimiento “Hierro Mantua” fue probada por la estadística descriptiva, por la prueba de bondad de ajuste Kolmogorov-Smirnov y la no estacionalidad por la estadística de ventanas móviles. El Krigeado Lognormal ha sido ampliamente aplicado en diversos estudios mineros, así como en otros problemas de las geo-ciencias.
Los contenidos de Cu fueron transformados logarítmicamente en una nueva variable, LnCu, para la cual la estadística básica y de ventanas móviles, muestran normalidad y estacionalidad. El análisis estructural de los datos transformados muestra anisotropía geométrica, in la dirección N-S y E-O. El modelo ajustado es una estructura imbricada compuesta por un efecto pepita más dos modelos esféricos, el cual fue validado por validación cruzada.
La USM obtenida como racional muestra los valores mínimos del error cuadrático medio cuando comparamos los valores reales y estimados, usando diferentes USM. Este procedimiento se basa en la idea de que el equipamiento minero no debe ser el factor determinante de tamaño de la USM, sino resultado de aprovechar las potencialidades adecuadamente un método de estimación matemático, el cual toma en cuenta el comportamiento natural del fenómeno.
La estimación desarrollada por Krigeado Lognormal es adecuada para la estimación de recursos en el caso de estudio presentado. La estadística básica de los valores reales y estimados muestra proximidad en los valores de la media y adecuados valores de la varianza.