Serviços Personalizados
Journal
Artigo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Acessos
Acessos
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares em
SciELO
Similares em
SciELO -
 Similares em Google
Similares em Google
Compartilhar
Revista Integración
versão impressa ISSN 0120-419X
Integración - UIS vol.31 no.1 Bucaramanga jan./jun. 2013
Operadores pseudodiferenciales definidos en
medidas de Borel
DUVÁN CARDONA*
Universidad del Valle, Departamento de Matemáticas, A.A 25360, Cali, Colombia.
Resumen. En este trabajo se introduce un tipo de operadores pseudodiferenciales definidos en medidas de Borel. Clásicamente la definición de operadores pseudodiferenciales se extiende al espacio de las distribuciones temperadas; sin embargo, en su representación no interviene el análisis de Fourier en espacios de medidas. El objetivo principal es definir tales operadores en un ángulo diferente y establecer resultados de continuidad entre espacios normados adecuados, además de proporcionar una conexión con la teoría de operadores pseudodiferenciales con símbolos en las clases 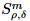 definidas en ℝn y el toro Tn.
definidas en ℝn y el toro Tn.
Palabras claves: Operadores pseudodiferenciales,Medidas de Borel, Teorema de Radon-Nikodým, Continuidad y compacidad de operadores, Distribuciones, Operadores elípticos.
MSC2010: 47G30, 65R10.
Pseudo-differential operators defined
on Borel measures
Abstract. In this paper we introduce a type of pseudo-differential operators defined on Borel measures. Classically the definition of pseudo-differential operators extends the tempered distributions space, but in its representation does not intervene the Fourier analysis in measures spaces. The main objective is to define such operators at a different angle and establish boundedness results on suitable normed spaces, in addition to providing a connection with the pseudo-differential operators theory with symbols in the classes 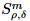 defined on ℝn and the torus Tn.
defined on ℝn and the torus Tn.
Keywords: Pseudo-differential operators, Borel measures, Radon-Nikodým Theorem, Boundedness and compactness of operators, Distributions, Elliptic operators.
Texto Completo disponible en PDF
Referencias
[1] Ashiro R., Nagase M. and Vaillancourt R., "Pseudo-differential operators in Lp(ℝn) spaces", Cubo 6 (2004), no. 3, 91-129. [ Links ]
[2] Conway J., A Course in Functional Analysis, Springer-Verlag, New York, 1997. [ Links ]
[3] Calderón A. and Vaillancourt R., "On the boundedness of pseudo-differential operators", J. Math. Soc. Japan 23 (1971), 374-378. [ Links ]
[4] Dieudonné J., "Recent development in the theory of linear partial differential equations", Internat. J. Math. Math. Sci. 3 (1980), no. 1, 1-14. [ Links ]
[5] Duoandikoetxea J., Fourier Analysis, 29. American Mathematical Society, Providence, 2000. [ Links ]
[6] Guzmán M., "Representación de medidas vectoriales", Rev. Soc. Colombiana de Mat. 44 (2010), no. 2, 129-147. [ Links ]
[7] Hörmander L., The Analysis of Linear Partial Differential Operators III, Springer-Verlag, Berlín, 1985. [ Links ]
[8] Hwang I., "The L2-boundedness of pseudo-differential operators", Trans. Amer. Math. Soc. 302 (1987), no. 1, 55-76. [ Links ]
[9] Kohn J. and Nirenberg L., "An Algebra of pseudo-differential operators", Comm. Pure Appl. Math. 18 (1965), 269-305. [ Links ]
[10] Molahajloo S., "Pseudo-differential Operators on ℤ", Oper. Theory Adv. Appl. 205 (2010), no. 1, 213-221. [ Links ]
[11] Restrepo G., Teoría de la Integración, Universidad del Valle, Colombia, 2004. [ Links ]
[12] Rodriguez C., "P-Estimates for Operators on ℤn", J. Pseudo-Differ. Oper. Appl. 1 (2010), no. 2, 367-375. [ Links ]
[13] RuzhanskyM. and Turunen V., Pseudo-differential Operators and Symmetries: Background Analysis and Advanced Topics, Pseudo-Differential Operators. Theory and Applications 2, Birkhäüser-Verlag, Basel, 2010. [ Links ]
[14] Schwartz L., Radon Measures on Arbitrary Topological Spaces and Cylindrical Measures, Oxford University Press, London, 1973. [ Links ]
[15] Stein E., Harmonic Analysis: Real-Variable Methods, Orthogonality, and Oscillatory Integrals, Princeton University Press, Princeton, New Jersey, 1993. [ Links ]
[16] Stein E., Introduction to Fourier Analysis on Euclidean Spaces, Princeton University Press, Princeton, New Jersey, 1971. [ Links ]
[17] Taylor M., Partial differential equations III. Non linear equations, Springer-Verlag, New York, 2011. [ Links ]
[18] Wong M.W., An Introduction to pseudo-differential operators. World Scientific Publishing, New Jersey, 1991. [ Links ]
*E-mail: duvan.cardona@correounivalle.edu.co.
Recibido: 10 de febrero de 2013, Aceptado: 20 de mayo de 2013.













