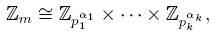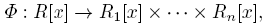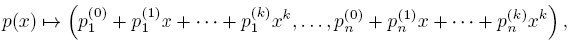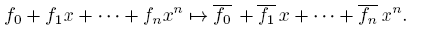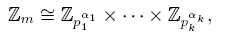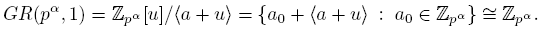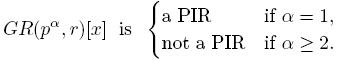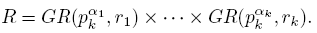1. Introduction and preliminaries

Polynomials with coefficients in a finite commutative ring R with identity arise naturally, for instance, in practical applications dealing with coding theory, cryptography and algebraic combinatorics, e. g. [¹], [²], [³], [⁴], [⁶]. For some of these applications, it is important to know the algebraic structure of either the ring of polynomials R[x] or the quotient ring R[x]/A, where A is an ideal of R[x]. In particular, often one wants to know when such rings are principal ideal rings (PIR’s). Motivated by this question, in this paper we examine when R[x] is a PIR. We prove that R[x] is a principal ideal ring if and only if R is a finite direct product of finite fields. To this end, let us start remembering some facts about commutative finite rings with identity.

The most familiar example of a finite commutative ring with identity is the ring Z _m of integers modulo m ≥ 2. When m is a composite number, the Chinese Remainder Theorem assures that

where m = p ₁ ^α1 · · · p_k ^αk is the prime factorization of m, and Z _p1 ^α1 ×· · ·× Z_pk ^αk is the direct product of the rings Z_pi ^αi , 1 ≤ i ≤ n. Remember that for each i (1 ≤ i ≤ k), Z_pi ^αi is a finite local ring with maximal ideal 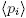(see [⁵]). In particular, note that if α = 1, then Z_p is a finite field (see [⁴]). Consequently, the Chinese Remainder Theorem establishes that Z_m is isomorphic to a direct product of finite local rings. This is the simplest case of the following result.

Theorem 1.1 (Structure of Finite Commutative Rings, [⁵], Theorem VI.2). Every finite commutative ring with identity is isomorphic to a direct product of finite commutative local rings with identity. This decomposition is unique up to the order of the factors.

In view of the previous theorem, if R is a finite commutative ring with identity and R ₁ × · · · × R_n is the unique decomposition of R as a direct product of local rings, then there exists a ring isomorphism φ: R → R ₁ × · · · × R_n which maps each element r ∈ R into a unique n-tuple φ(r) = (r ₁, . . . , r_n ) ∈ R ₁ × · · · × R_n . This map extends to a ring isomorphism

defined by

(1)

where p(x) = p ₀ + p ₁ x + · · · + p_kx^k and φ(p_i ) = (p ₁ ⁽ⁱ⁾ , . . . , p_n ⁽ⁱ⁾), 0 ≤ i ≤ k.

Proposition 1.2. Let R₁, . . . ,R_n be commutative rings with identity. Then their direct product R = R₁ × · · · × R_n is a PIR if and only if Ri is a PIR for each i, 1 ≤ i ≤ n.

Proof. Let A be an ideal of R and for each i, 1 ≤ i ≤ n, define A_i = {a_i ∈ R_i : (a ₁, . . . , a_i , . . . , a_n ) ∈ A}. Then A_i is an ideal of R_i and we claim that A = A ₁×· · ·×A_n . The inclusion A ⊆ A ₁ × · · · × A_n is clear. To prove the reverse inclusion, let a = (a ₁, . . . , a_n ) be an element in A ₁ × · · · × A_n . It follows from the definition of A_i that there exist α ₁, . . . , α_n ∈ A such that a = α ₁ e ₁+· · ·+α_ne_n , where e_i denotes the element of R with a 1 in the ith coordinate and 0’s elsewhere. Hence, using that A is an ideal of R ₁×· · ·×R_n , we have that a ∈ A. 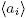Therefore A = A ₁×· · ·×A_n , and so A = if and only if A_i = for every i, 1 ≤ i ≤ n.

In light of Proposition 1.2 and the isomorphism Φ given in (1), R[x] is a PIR if and only if R_i [x] is a PIR for each i, 1 ≤ i ≤ n. Hence, in order to determine whenever R[x] is a PIR, it is natural to ask when R_i [x] is a PIR. This is the purpose of the next section. To illustrate the results of Section 2, we present in Section 3 three families of finite rings with identity that are relevant in the theory of finite commutative rings.

2. Ideals of R[x]

First of all, by a ring R we will always mean a commutative ring with identity 1 ≠ 0, and remember that a ring R is called local if it has a unique maximal ideal, or equivalently, R is a local ring with maximal ideal M if and only if M = R\U(R), where U(R) denotes the group of units of R. We usually write (R,M) or (R,M, F) to denote a local ring R, its maximal ideal M and its residue field F = R/M (using that M is a maximal ideal of R, the quotient ring R/M is indeed a field).

The simplest case of a finite local ring R is when R is a finite field. In this case the ring R[x] of polynomials with coefficients in R is a PIR. In fact, R[x] is a principal ideal domain (PID). Therefore, in what follows we focus our attention on a finite local ring R which is not a field.

Let (R,M, F) be a finite local ring which is not a field. Note that the natural surjective homomorphism − : R → F induces a surjective polynomial ring homomorphism μ: R[x] → F[x] given by

This ring homomorphism lets us deduce some facts about polynomials f(x) = Σ ⁿ _{i =0} f_ixⁱ ∈ R[x] by using the structure of F[x]. In particular, note that μ(f(x)) = 0 if and only if f_i ∈ M for all i, 0 ≤ i ≤ n and so, it follows that ker μ is a proper ideal of R[x] (indeed, ker μ is a prime ideal of R[x] because R[x]/ ker μF[x] is an integral domain).

On the other hand, remember that an element r of a ring R is called irreducible if it is neither 0 nor a unit in R and the condition r = ab, for some a, b ∈ R, implies that a ∈ U(R) or b ∈ U(R).

Having remembered the above, if f(x) ∈ R[x] is such that μ(f(x)) is irreducible in F[x], then f(x) is also irreducible in R[x]. Since for every finite field K and every positive integer n there exists an irreducible polynomial in K[x] of degree n (see [4]), we conclude that irreducible polynomials in R[x] of degree n exist for every positive integer n. It is worth to mention that the converse of this fact does not hold in general. That is, if f(x) is an irreducible polynomial in R[x] then μ(f(x)) is not necessarily irreducible in F[x]. For instance, if p ≥ 2 is a prime number, then p ∈ Z _p² [x] is irreducible in Zp² [x] but μ(p) = 0̅ ∈ (Z _p²/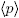 [x] is not irreducible by definition. Furthermore, if f(x) = x ² + 2x + 3 ∈ Z₄[x] then f(x) is irreducible in Z₄[x]; whereas μ(f(x)) = x ² + 1̅ = (x + 1̅)² ∈ (Z₄/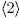) [x] is not irreducible.

Lemma 2.1. Let (R,M) be a local ring which is not a field, p(x) an irreducible polynomial in R[x] and θ ∈ M \ {0}. Then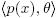is a proper ideal of R[x].

Proof. If μ(p(x)) = 0̅, then p(x) ∈ ker μ, so that 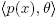⊆ ker μ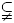R[x]. If μ(p(x)) ≠ 0̅, then we proceed by contradiction. Assume then the existence of some polynomials f(x), g(x) ∈ R[x] such that 1 = f(x)θ + g(x)p(x). This implies that 1̅ = μ(g(x))μ(p(x)), which contradicts the irreducibility of p(x). Hence, for every irreducible polynomial p(x) in R[x] and θ ∈ M \ {0}, 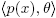is a proper ideal of R[x].

If p(x) = p ₀ + p ₁ x + · · · + p_nxⁿ ∈ R[x] is an irreducible polynomial in R[x] such that μ(p(x)) ≠ 0̅, then deg(μ(p(x))) = k ≥ 1, since μ(p(x)) can not be a unit in F[x]. This implies that p_k ∈ U(R) and p_{k +1}, . . . , p_n ∈ M and so, for each nonzero polynomial a(x) ∈ R[x] we have that deg(p(x)a(x)) ≥ k ≥ 1. Consequently, every nonzero polynomial in 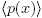⊂ R[x] is not a constant polynomial, and so M .

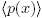Theorem 2.2. Let (R,M) be a local ring which is not a field. Then R[x] is not a PIR.

Proof. Let p(x) ∈ R[x] be an irreducible polynomial in R[x] such that μ(p(x)) ≠ 0̅, and let θ ∈ M \ {0}. Then we claim that 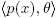is not a principal ideal of R[x]. Assume the contrary; that is, suppose that there is a polynomial h(x) ∈ R[x] such that 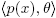= 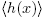. Then there exists f(x) ∈ R[x] such that p(x) = f(x)h(x). Using that p(x) is irreducible, we have that f(x) ∈ U(R[x]) or h(x) ∈ U(R[x]). It follows immediately from Lemma 2.1 that h(x) 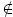U(R[x]), and so f(x) ∈ U(R[x]). This implies that 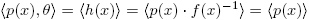, which is a contradiction since θ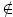 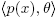. In consequence, 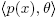is not a principal ideal in R[x].

Note that we have proved implicitly in Theorem 2.2 that for every local ring (R,M, F) which is not a field, the family of ideals 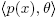, where p(x) is an irreducible element in R[x] such that μ(p(x)) ≠ 0̅, and θ is a nonzero element in M, consists entirely of non-principal ideals of R[x]. This family contains an infinite number of elements since irreducible polynomials of degree n in R[x] exist for every integer n ≥ 1.

Theorem 2.3. Let R be a finite ring. The following statements are equivalent:

Proof. It follows immediately from Proposition 1.2 and Theorems 1.1, 2.2.

An equivalent way to state Theorem 2.3 is as follows: R[x] is a not a PIR if and only if R is isomorphic to a direct product R ₁×· · ·×R_i ×· · ·×R_n of finite local rings such that at least one of them is not a finite field, say (R_i ,M_i , F_i ). In this case, for all θ ∈ M_i \ {0} and for all irreducible polynomials p(x) ∈ R_i [x] with μ_i (p(x)) ≠ 0̅ in F_i [x] we have that 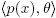⊂ R_i [x] is not a principal ideal in R_i [x]. In consequence, by using the ring isomorphism Φ defined in (1), one can easily show that 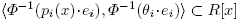is not a principal ideal in R[x].

Another equivalent way to state Theorem 2.3 is derived from the structure theorem for commutative PIR’s due to Zariski-Samuel (see [⁷, Theorem 33]). This result states that every commutative PIR is (isomorphic to) a direct sum of PID’s and of special PIR’s. Therefore, Theorem 2.3 shows that Zariski-Samuel theorem can be expressed for the ring of polynomials over a finite ring R as follows: R[x] is a PIR if and only if R[x] is isomorphic to a direct product of PID’s. Moreover, the isomorphism Φ given in (1) presents one decomposition of R[x] as a direct product of PID’s. In addition, Theorem 2.2 also implies that for a local ring (R,M) which is not a field, the ring of polynomials R[x] cannot be a special PIR.

3. Examples

As a first example we present the one that we used to motivate Theorem 1.1. Let m ≥ 2 be an integer. Then

where m = p ₁ ^α1 · · · p_k ^αk is the prime factorization of m. Since Z _piαi is a finite field if and only if α_i = 1, it follows from Theorem 2.3 that Z _m [x] is a PIR if and only if α ₁ = · · · = α_k = 1.

In order to generalize the previous example, let us to consider the ring Z _pᵅ , where p is a prime number and α is a positive integer. Let f(u) be a monic polynomial of degree r ≥ 1 in Z _pᵅ [u] such that μ(f(u)) is irreducible in (Z _pᵅ/) [u]. Then the Galois ring of characteristic p^α and cardinality p^αr is definied as the quotient ring

This ring is a finite local ring with maximal ideal , and residue field isomorphic to 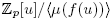(see [⁵] for more details). Note that if r = 1 then

Consequently, GR(p, 1) 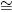Z _p is a finite field, and for any integer α ≥ 2, GR(p^α , 1) is a finite local ring which is not a field. Furtheremore, if r ≥ 2 and α = 1, then GR(p, r) = Z _p [u]/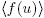 is a finite field with p^r elements (see [⁴]). Hereof it follows from Theorem 2.2 that

(2)

Let p ₁, p ₂, . . . , p_k be prime numbers, α_i , r_i positive integers for 1 ≤ i ≤ k, and consider the following ring which is a natural generalization of Z _m :

In the examples given above we have presented infinite families of finite rings for which the ring of polynomials with coefficients in these rings are not PIR. The common ground in both families of rings is that they are finite products of local rings whose ideals are principal and they are linearly ordered by inclusion. Any local ring satisfying these conditions is called a finite chain ring (see [¹]). In general, if R is a finite chain ring that is not a field, then R[x] is not a PIR by Theorem 2.2, and so for every finite ring R such that it is isomorphic to a direct product of finite chain rings (of which at least one is not a field), the ring R[x] is not a PIR by Theorem 2.3.

In the following lines, we are going to present a family of finite local rings which was introduced in [²].

Let p be a prime number, α a positive integer and denote by F_q the unique finite field with q = p^α elements (see [⁵]). Then for every integer k ≥ 1, the quotient ring R_k = F_q [u ₁, u ₂, . . . , u_k ]/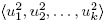 is a commutative ring with identity. Furthermore, it is proved in [²] that R_k is a finite local ring with maximal ideal and residue field Rk/M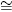F ₂. In consequence, Theorem 2.3 shows that R_k [x] is not a PIR for any integer k ≥ 1.

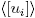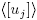Since k ≥ 2, the ring R_k described above is neither a PIR nor a chain ring in view of M is not a principal ideal and and are not linearly ordered by inclusion for i ≠ j. However, it was pointed out in [²] that R_k is a finite Frobenius ring.