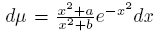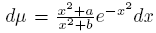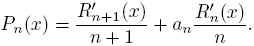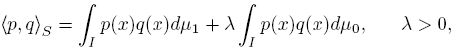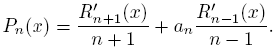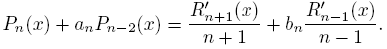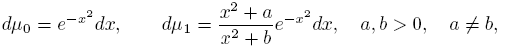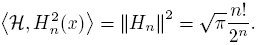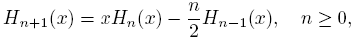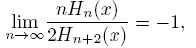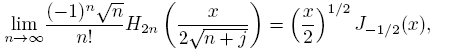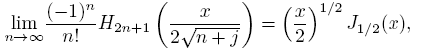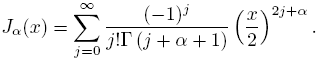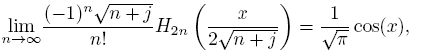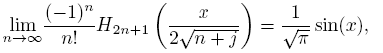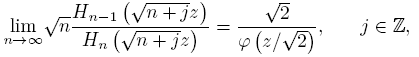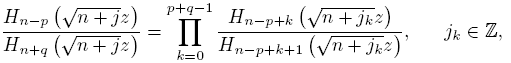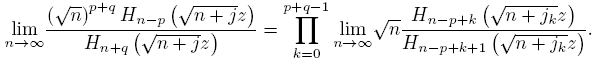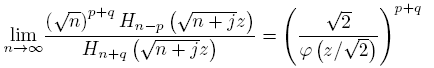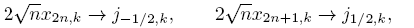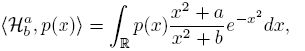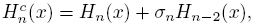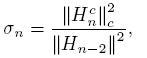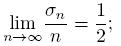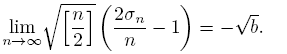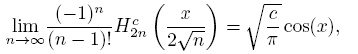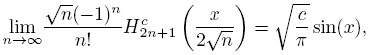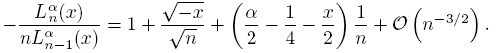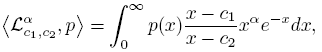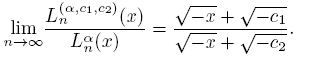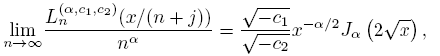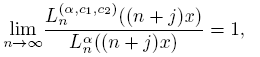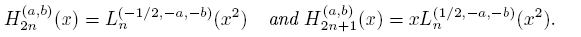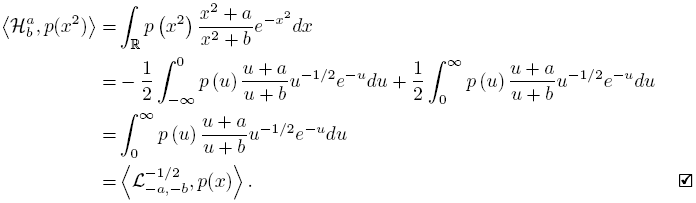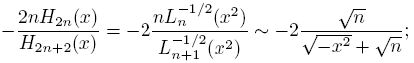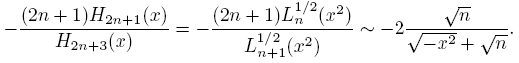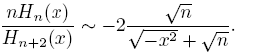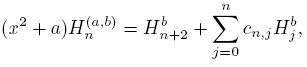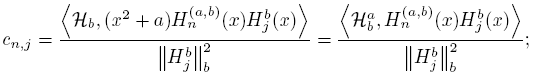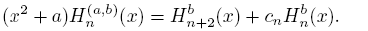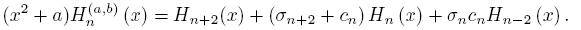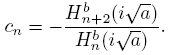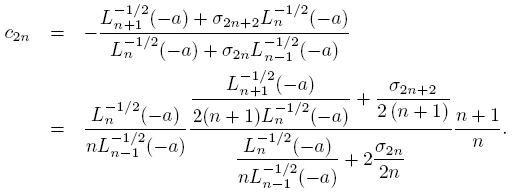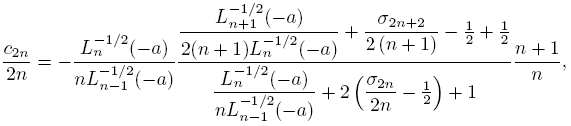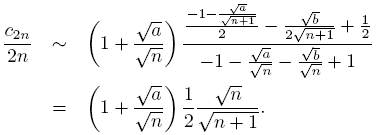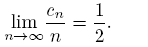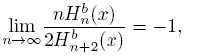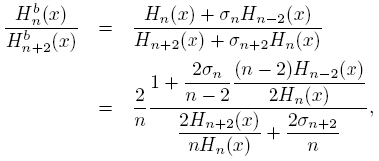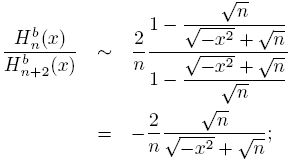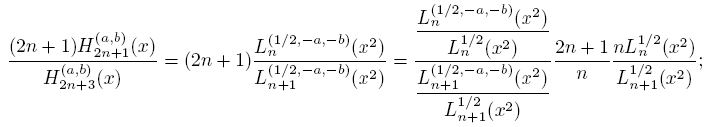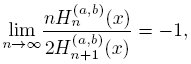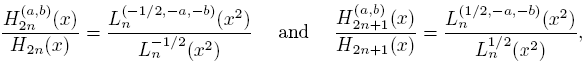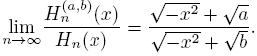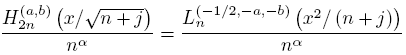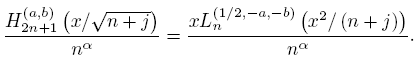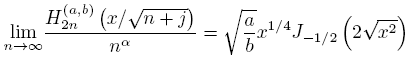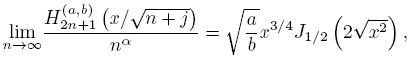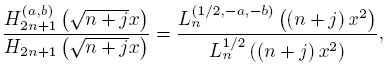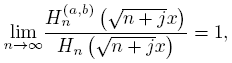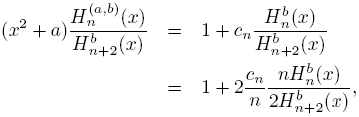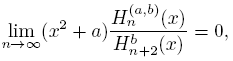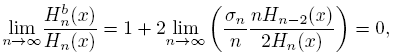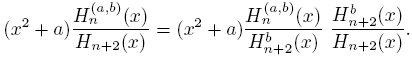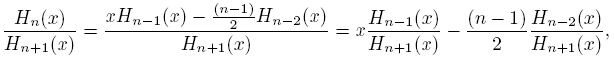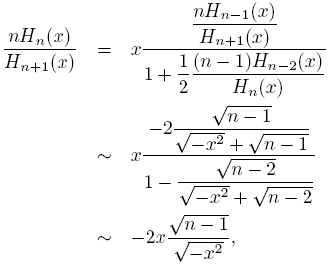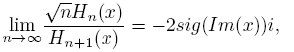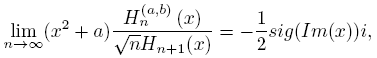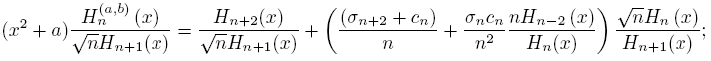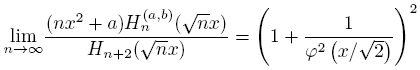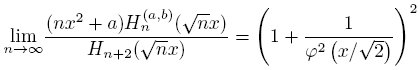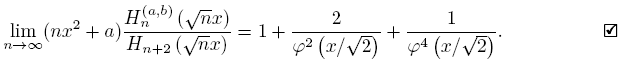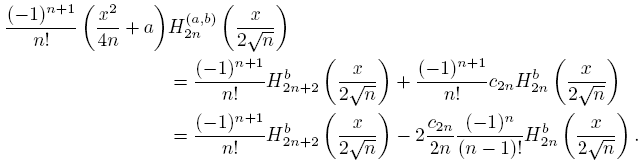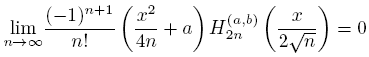1. Introduction
Let U and V be quasi-definite linear functionals and let {Pn } n∈N and {Rn } n∈N be their sequences of monic orthogonal polynomials (SMOP), respectively. (U, V ) is a coherent pair if there exists a sequence (an ), an ≠ 0, such that
This concept is introduced in [7] where it is studied its connection with polynomials orthogonal with respect to Sobolev inner products like
where μ 0 and μ 1 are positive Borel measures supported on an infinite subset I ⊆ R, with U and V as the associated functionals, respectively. In this way, among others, it is studied an algebraic connection between the Sobolev polynomials and the sequence {Rn } n∈N , in such a way that the coefficients of connection are independent of the degree; an algorithm is presented for to compute Fourier coefficients using as basis the Sobolev polynomials. Likewise, if U and V are symmetric, (U, V ) is a symmetric coherent pair if there exists a sequence (an ) , an ≠ 0, such that
In [8] all coherent pairs and symmetric coherent pairs are determined and it is shown that at least one of the functionals has to be classical (Hermite or Gegenbauer in the symmetric case); moreover, if ξ > 0, the symmetric coherent pair dμ
0 = e
−x2
dx, 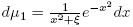 is obtained. In connection with this particular case, in [2] the outer relative asymptotics of Sobolev polynomials orthogonal with respect to (1) is found; besides, in [9] Mehler-Heine type formulas are established with respect to rational modification of the Hermite polynomials. Under the same assumptions, (U, V ) is a symmetric (1, 1)−coherent pair if there exist sequences (an
)
n∈N and (bn
)
n∈N , bn ≠ 0, such that the respective SPOM satisfies
is obtained. In connection with this particular case, in [2] the outer relative asymptotics of Sobolev polynomials orthogonal with respect to (1) is found; besides, in [9] Mehler-Heine type formulas are established with respect to rational modification of the Hermite polynomials. Under the same assumptions, (U, V ) is a symmetric (1, 1)−coherent pair if there exist sequences (an
)
n∈N and (bn
)
n∈N , bn ≠ 0, such that the respective SPOM satisfies
About this subject, in [4] is presented the algebraic relation between the Sobolev polynomials and the polynomials {Rn } n∈N ,; besides, the particular case where V is classical is studied, and the respective symmetric (1, 1)−coherent companion is found. In particular, we focus on the symmetric (1, 1)−coherent pair
and we will study the asymptotic behavior of the orthogonal polynomials associated with dμ 1. Thus, the structure of this manuscript is as follows: In the section 2 we present some basic facts about of asymptotic behavior of Hermite orthogonal polynomials. In section 3 we present an algebraic connection between the Hermite polynomials and the SMOP associated with dμ 1, as well as the asymptotic behavior of the respective connection coefficients. Finally, in section 4 some asymptotics properties are studied.
2. Preliminaries
From now on, and as it is usual, {Hn
}
n∈N will represent the sequence of monic Hermite polynomials, orthogonal with respect to the weight e
−x² on (−∞,∞). The classical Hermite linear functional will be denoted by H and 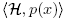 will be the application of H on any polynomial p. The norm of the monic Hermite polynomials is defined as
will be the application of H on any polynomial p. The norm of the monic Hermite polynomials is defined as
On the other hand the sequence {Hn } n∈N is defined via the three terms recurrence relation
with the initial conditions H 0(x) = 1 and H −1(x) = 0. With respect to the asymptotic behavior of Hermite polynomials we present the next results.
Theorem 2.1 (See [10]).
uniformly on compact sets of C\R.
Theorem 2.2 (Mehler-Heine). (See [1]). For j ∈ Z fixed,
and
uniformly on compact sets of the complex plane, where Jα represents Bessel’s function of the first kind defined by
Theorem 2.3 (Mehler-Heine). (See [10]).
and
uniformly on compact subsets of C and uniformly on j ∈ N ∪ {0} .
Theorem 2.4 (See [11]). For j ∈ Z fixed,
holds uniformly on compact subsets of C\ [−√2,√2]. Here, φ (z) = z + √z 2 − 1 is the conformal mapping of C\ [−1, 1] onto the exterior of the closed unit disk.
If i = 0 and if p and q are non-negative integers such that n > p − 1, then
and as a consequence,
The above proves the next
Corollary 2.5. For j ∈ Z fixed, and non-negative integers p and q such that n > p − 1,
holds uniformly on compact subsets of C\ [−√2,√2].
The zeros of Hn are real, simples and symmetric; that is, for every n, Hn(t) = 0 is equivalent to Hn (−t) = 0. Let {xn ,k }[n/2] n=1 be the positive zeros of Hn in increasing order. It is well known that the zeros of Hn and Hn −1 are interlaced and for k fixed, xn ,k → 0 when n → ∞. Besides, given that Jα has a countably infinite set of real and positive zeros if α > −1, as a consequence of Mehler-Heine formulas and the Hurwitz’s theorem, if n → ∞ and k ≥ 1 then
and 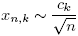 , where ck
> 0 and {jα
,k
}
n∈N are the zeros of Jα
when α > −1.
, where ck
> 0 and {jα
,k
}
n∈N are the zeros of Jα
when α > −1.
On the other hand, let {Hn (a,b)} n∈N be the sequence of monic polynomials orthogonal with respect to the positive definite linear functional Ha b , defined as
where a, b > 0, and a ≠ b. As it is usual, let ║.║(a,b) be the induced norm. If c > 0, then {Hc
n
} will be the sequence of monic polynomials orthogonal with respect to the positive definite functional Hc
defined by 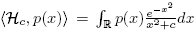 , and ║.║
c
the respective induced norm. On the algebraic connection between the sequence {Hc
n
} and the classical Hermite polynomials we get the next result.
, and ║.║
c
the respective induced norm. On the algebraic connection between the sequence {Hc
n
} and the classical Hermite polynomials we get the next result.
Lemma 2.6 (See [2]). There exists a sequence of real numbers (σn ) such that
with
and
moreover,
With respect to asymptotic behavior and Mehler-Heine type formulas for the sequence {Hc n } n∈N , we get the next
Theorem 2.7 (See [9]).
and
both uniformly on compact subsets of C.
Let Lα be the classical Laguerre functional, α > −1, and let {Lα n (x)} be the respective SMOP. We present the next result about asymptotics behavior of ratios of Laguerre polynomials that will be necessary in our work. The proof can be see in [5].
Lemma 2.8. For x ∈ C\R+,
In this paper also will be important to deal with rational perturbations of the Lα and the asymptotic behavior of the associated SPOM. About this topic, in [6] is made an exhaustive study of asymptotic behavior of orthogonal polynomials associated to this kind of perturbations. Indeed, given c 1, c 2 < 0, let {Ln (α,c₁,c₂) (x)} be the SMOP associated to positive definite linear functional Lα c ₁,c₂ defined on the space of polynomials as
and about the asymptotic behavior of the sequence {Ln (α,c₁,c₂) (x)},we get the next
Theorem 2.9 (See [6]).
a). Uniformly on compact subsets of C\[0,∞),
b). Uniformly on compact subsets of C,
where j ∈ N ∪ {0} .
c). (Plancherel-Rotach type exterior asymptotics).
uniformly on compact subsets of C\[0, 4], and uniformly on j ∈ N ∪ {0} .
3. Some basic results
Given that H is a symmetric linear functional, it is well known that there is a relation between the classical Laguerre and Hermite polynomials, namely
In this way, the next result is an extension of the above relations.
Lemma 3.1. For every n ∈ N,
Proof. Given that Ha
b is symmetric, there exists an unique quasi-definite linear functional v, with {Pn
} as the associated SPOM and such that H
2n
(a,b) (x) = Pn
(x
2) and H
(a,b)
2n+1(x) = xPn
(x
2) (see [3]), moreover, 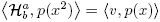 .We will see that v = L
−1/2
−a,−b
. Indeed, with the change of variable u = x
2 we get
.We will see that v = L
−1/2
−a,−b
. Indeed, with the change of variable u = x
2 we get
On the other hand, from (22) we have 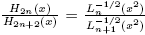 , and given that (see (18))
, and given that (see (18)) 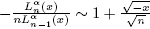 , we get
, we get
in the same way, in the odd case we get
Then we have deduced the next
Lemma 3.2. For x ∈ C\R we get
By using of {Hb n } n∈N as a basis we get
where
then, cn
,j
= 0, for j = 0, ..., n − 1, and 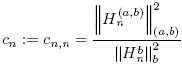 . So we get
. So we get
As a consequence of (12), we have
In order to obtain the behavior limit of the sequence (cn ), we choose x = i√a in (25), and then for every n
By using (12) we get
In the even case,
From (12) we obtain
and by using of (18) we get
Given that H
2n+1(x) = xLn
1/2 (x
2), and following the same arguments in the odd case for the subsequence 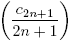 , we get the next
, we get the next
Lemma 3.3.
4. Asymptotic Properties
We want to obtain formulas of the kind (4) associated to the ratios 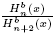 and
and 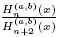 . First, we will deduce the next
. First, we will deduce the next
Lemma 4.1.
uniformly on compact sets of C\R.
Proof. From (12), we get that
and by using of (24) we get
In the above result we have obtained a formula of the type (4) for the sequence {Hb n } n∈N . Now we will get the same one for the sequence {Hn (a,b)} n∈N. Indeed, in the odd case and from (23) we get
as before, the even case is similar. Then, as a consequence of (18) and (19) we get the next
Proposition 4.2.
uniformly on compact subsets of C\R.
Moreover, from (23) we get
and as a consequence of (19) we obtain
Lemma 4.3. Uniformly on compact subsets of C\R,
On the other hand, scaling the variable, and by (23), we get
and
And from (20) we deduce
Lemma 4.4. Uniformly on compact subsets of C,
and
where j ∈ N ∪ {0} .
Finally, given that
and
as a consequence of (21) we have
Lemma 4.5 (Plancherel-Rotach type exterior asymptotics).
uniformly on compact subsets of C − [−2, 2], and uniformly on j ∈ N ∪ {0} .
In our search of information about of asymptotic behavior of the sequence {Hn (a,b)} n∈N, it is very useful to consider the sequence {(x 2 + a)Hn (a,b)} and the results obtained in the above lemmas. In this way, using (25) we obtain
then, the next proposition is a consequence of (27) and (28).
Proposition 4.6. The sequence {Hn (a,b)} satisfy
uniformly on compact sets of C\R.
Naturally, it is possible to obtain a similar result for the ratio 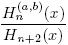 . It is enough to consider (4) and (12) to obtain
. It is enough to consider (4) and (12) to obtain
uniformly on compact sets of C\R, and to use the above theorem for the expression
On the other hand, using recurrence relation (3) we get
and as a consequence, 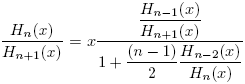 . As before, for x ∈ C\R, and from (24), it follows
. As before, for x ∈ C\R, and from (24), it follows
and as a consequence, 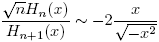 . Then we get the next
. Then we get the next
Lemma 4.7.
uniformly on compact subsets of C\R.
Now, we will see the importance of above lemma in the following theorems.
Theorem 4.8.
uniformly on subsets compact of C\R.
Proof. From (26) we get
then, using (4) and (29) the result holds. 
Theorem 4.9 (Scaled Relative Asymptotics).
holds uniformly on compact subsets of C\ [−√2,√2].
Proof. Making the scaling x → √nx in (26), we have
Then, using (9) and (14) we obtain
Now we will deduce Mehler-Heine type formulas for the polynomials {Hn
(a,b)}. Making 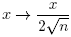 in (25), for the even case we get
in (25), for the even case we get
Then, using (16) and following a similar procedure in the odd case, we get the next
Proposition 4.10 (Mehler-Heine type formulas).
and
uniformly on compact subsets of the complex plane.




![When is R[x] a principal ideal ring?](/img/pt/prev.gif)
![Theorem of Dirichlet on F q [t]](/img/pt/next.gif)