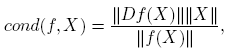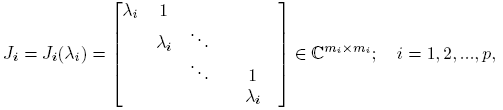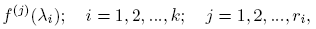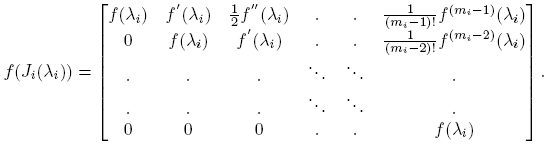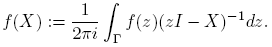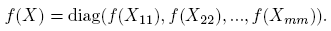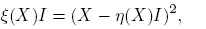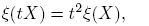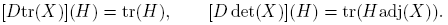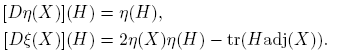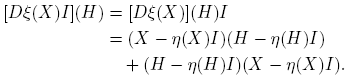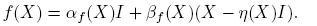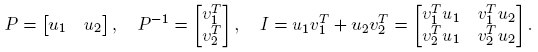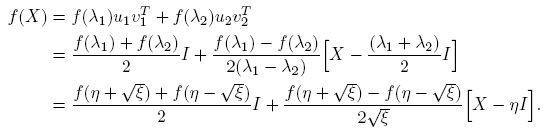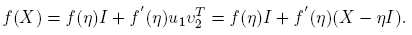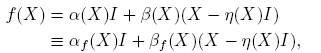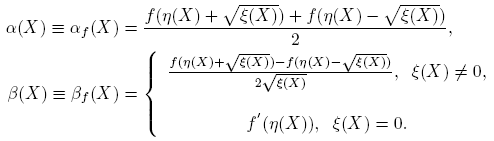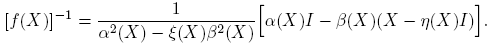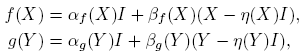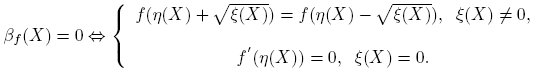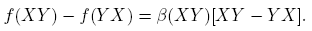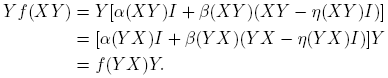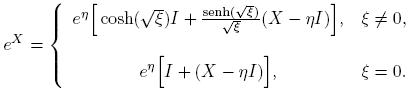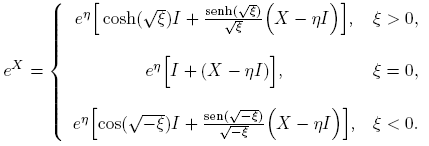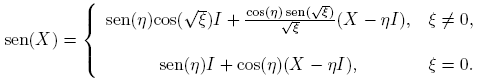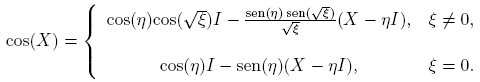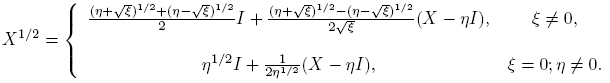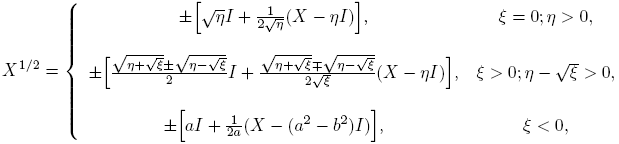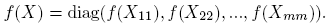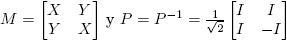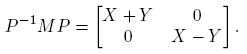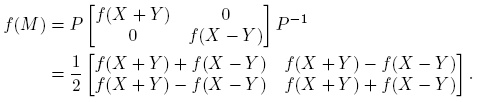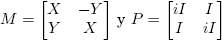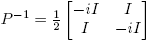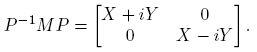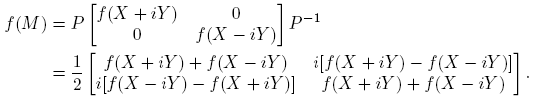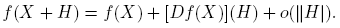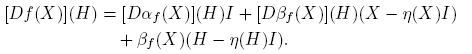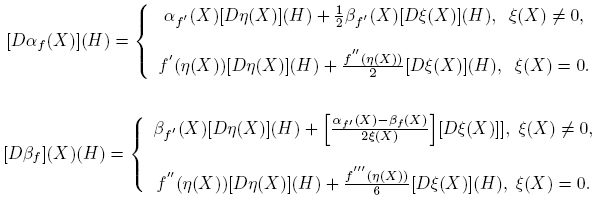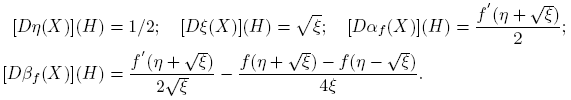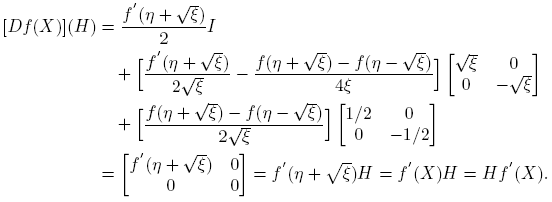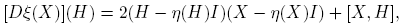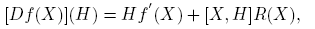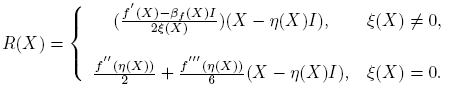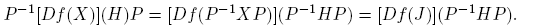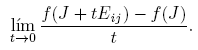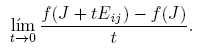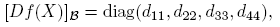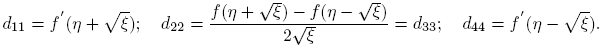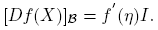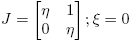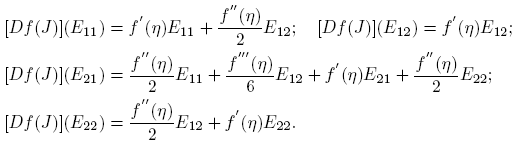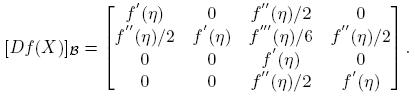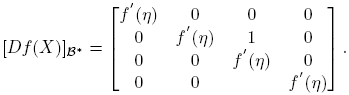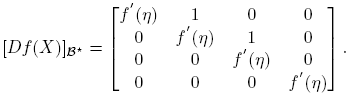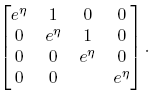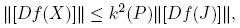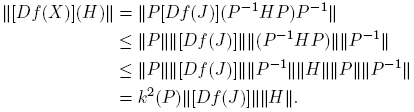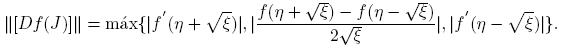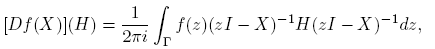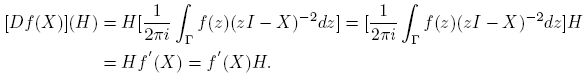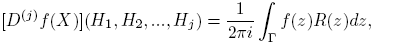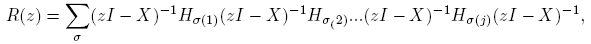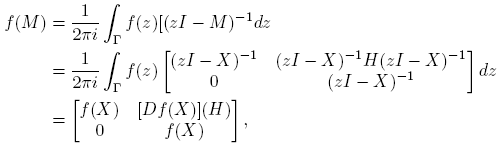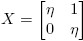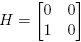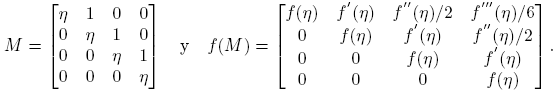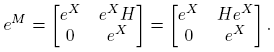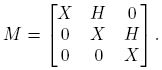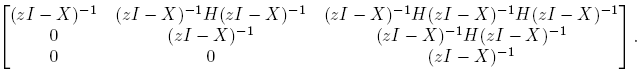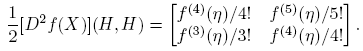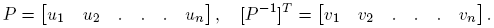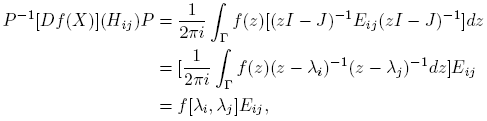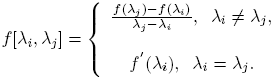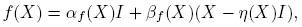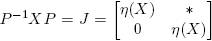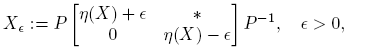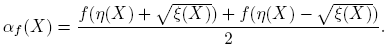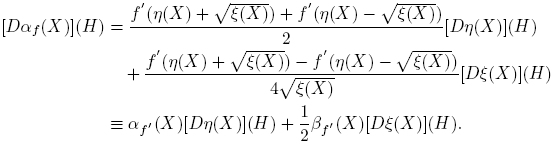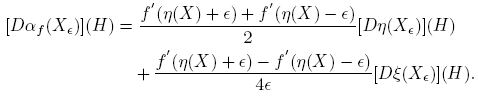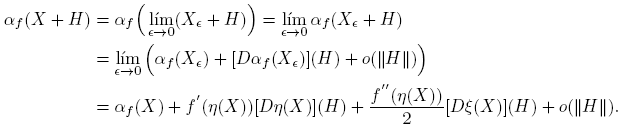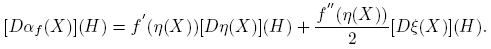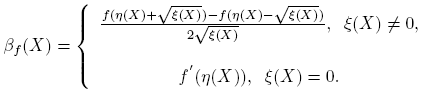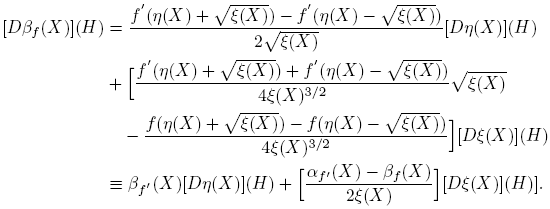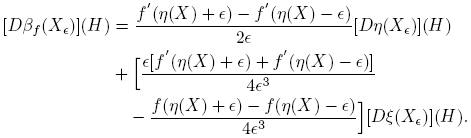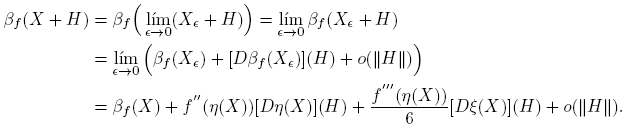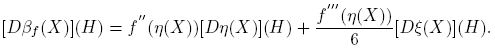1. Introducción

La norma de la derivada de Fréchet de una función matricial f : A ⊂ C ^n×n → C ^n×n aparece explícitamente en una expresión que da el número de condición relativo de f en X. De manera precisa (ver la Sección 3.1 de Higham [⁴], o la Sección 3.3 de Higham and Lijing [⁶]):

siendo ║ · ║ una norma matricial y 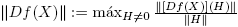. Este número mide la sensibilidad de f(X) a pequeños cambios en X. Hay trabajos recientes dedicados a la estimación de cotas para este número de condición en situaciones particulares; ver por ejemplo, Cardoso y Sadeghi [¹], Deadman y Relton [²] o Kandolf y Relton [⁸], entre otros.

Es entonces conveniente disponer de expresiones concretas de la derivada de Fréchet de tales funciones. En este contexto, el problema de investigación 3.11 en Higham [⁴] consiste en determinar la forma de Jordan de la derivada de Fréchet de funciones matriciales X → f(X); X ∈ A ⊂ C ^n×n , en términos de la de X. Cuando X es diagonalizable, el Corolario 3.12 en Higham [⁴] implica que la forma canónica de Jordan de dicha derivada es también diagonal (esto se demuestra en la Sección 6 para funciones analíticas). En este artículo se presenta una fórmula para evaluar funciones de matrices 2 × 2, la cual se usa para determinar su derivada de Fréchet. La principal contribución de este trabajo consiste en dar la forma canónica de Jordan de la derivada de Fréchet de funciones matriciales en el caso n = 2.

El resto del trabajo está organizado como sigue. En la Sección 2 se dan dos definiciones de la matriz f(X); X ∈ C ^n×n . Para matrices 2 × 2 se introducen dos funciones de valor escalar, que serán fundamentales para el desarrollo del resto del trabajo. En la Sección 3 se deduce una expresión para f(X), X ∈ C^2×2 (Teorema 3.1); como aplicación, se dan condiciones necesarias y suficientes para que f(X)g(Y ) = g(Y )f(X), se presentan fómulas explícitas para calcular las matrices e^X , sen(X), cos(X) y X ^1/2 y, finalmente, se considera la evaluación de funciones de algunas matrices particionadas. La Sección 4 se dedica a la derivada de Fréchet de funciones X → f(X); X ∈ A ⊂ C^2×2 y, la Sección 5, a dar su forma canónica de Jordan (Teorema 5.1). Por último, en la Sección 6, se considera la derivada de Fréchet de funciones matriciales en el caso en que f(·) es analítica y X ∈ C ^n×n ; se demuestra que si X es diagonalizable, entonces la forma canónica de Jordan de la derivada de Fréchet es diagonal (Teorema 6.3).

2. Preliminares

Se establecen aquí la terminología, las definiciones y los resultados básicos, que se utilizarán a lo largo del trabajo.

2.1. Definiciones de f(X)

Hay varias maneras equivalentes de definir f(X), X ∈ C ^n×n (ver, por ejemplo, Rinehart [¹⁰], el Capítulo 6 de Horn y Johnson [⁷], el Capítulo 11 de Golub y Van Loan [3] o el Capítulo 1 de Higham [⁴]). En este artículo presentamos dos definiciones; la primera, en términos de la forma canónica de Jordan y, la segunda, en términos de la integral de Cauchy.

Supóngase que los distintos valores propios de X ∈ C ^n×n son λ ₁, λ ₂, ..., λ_k , es decir, σ(X) = {λ ₁, λ ₂, ..., λ_k } es el espectro de X, que m_X (λ) = (λ−λ ₁) ^r1(λ−λ ₂) ^r2 ...(λ−λ_k ) ^rk es su polinomio mínimo, y que X tiene forma canónica de Jordan J = P ⁻¹ XP, donde J = diag(J ₁, J ₂, ..., J_p ),

y m ₁ + m ₂ + ... + m_p = n. Aunque la matriz P no es única, la matriz de Jordan J es única, salvo el orden en que aparecen los bloques en su diagonal.

Supóngase además que f(t) es una función con valores escalares, de variable real o compleja t. Con estas notaciones se establecen las siguientes definiciones (ver Higham [⁴], Definiciones 1.1 y 1.2, p. 3).

Definición 2.1. Se dice que f está definida en el espectro de X, si existen los valores

denominados valores de f en el espectro de X. Aquí, f ^(j)(·) indica la derivada j-ésima de f.

Definición 2.2. Supóngase que f está definida en el espectro de X. Se define f(X) := Pdiag(f(J ₁), f(J ₂), ..., f(J_p ))P ⁻¹, donde el bloque diagonal f(J_i ) es la matriz C ^mi×mi dada por

La matriz f(X) no depende de la forma de Jordan usada (ver Horn y Johnson [⁷], Teorema 6.2.9-(b), p. 412). Para funciones multivaluadas como f(t) = t ^1/2 y f(t) = log(t), se sobreentiende que sólo una rama se escoge en la evaluación de los bloques corrrespondientes a un mismo λ_i ; i = 1, 2, ..., k (ver el Ejemplo 4 del Apartado 3.5). En este caso, f(X) se denomina función matricial primaria.

La definición más corta y elegante de función matricial es la que sigue (Definición 1.11, p. 8, en Higham [⁴]).

Definición 2.3. Sea f(t) una función analítica dentro y sobre un contorno cerrado Γ que encierra a λ_i ; i = 1, 2, ..., k. Se define

Cuando se pueden aplicar, las definiciones anteriores son equivalentes (ver Horn y Johnson [7], Teorema 6.2.28, p. 427, o Rinehart [¹⁰], Teorema 1, p. 405).

Propiedades generales sobre f(X) pueden ser consultadas en Horn y Johnson [⁷] (Teorema 6.2.9, p. 412), o en Higham [⁴] (Sección 1.3). Se resaltan las siguientes, que serán usadas en la Sección 3.

Proposición 2.4. Suponga que f está definida en el espectro de X y que Q es una matriz invertible. Entonces,

1. f(Q ⁻¹ XQ) = Q ⁻¹ f(X)Q;

2. Si X = diag(X ₁₁,X ₂₂, ...,X_mm ) es diagonal por bloques, entonces

2.2. Las funciones escalares η, ξ : C^2×2 → C

En lo que sigue, C^2×2 denota el espacio de Banach de las matrices complejas 2 × 2 con la norma de Frobenius. La traza, el determinante y la matriz adjunta de X ∈ C^2×2 se denotarán por tr(X) , det(X) y adj(X), respectivamente. Cuando existe, la derivada de Fréchet de una función k : C^2×2 → C en el punto X ∈ C^2×2 es la única transformación lineal [Dk(X)] : C^2×2 → C tal que para todo H ∈ C^2×2 se cumple

Considérense ahora las funciones η, ξ: C^2×2 → C definidas por

Se sabe que η es lineal y que para cada matriz invertible Q se cumplen η(X) = η(Q ⁻¹ XQ) y ξ(X) = ξ(Q ⁻¹ XQ). De inmediato se verifican las identidades

(1)

(2)

donde I es la matriz idéntica y t ∈ C. Nótese que los valores propios de X son precisamente η(X) + √ξ(X) y η(X) − √ξ(X). Aquí, √ξ(X) indica la raíz cuadrada principal de ξ(X).

De otra parte, es bien conocido que las funciones X → tr(X) y X → det(X) son continuamente diferenciables según Fréchet, y que para H ∈ C^2×2 se cumplen las igualdades

De esto se sigue que las funciones X → η(X) y X → ξ(X) son continuamente diferenciables según Fréchet, y que para H ∈ C^2×2,

(3)

También, de la ecuación (1) se obtiene

(4)

3. Funciones matriciales para matrices 2 × 2

En esta sección se muestra que si f(·) está definida en el espectro de X ∈ C^2×2, entonces f(X) es un polinomio de la forma

Esta expresión se usa para establecer algunas propiedades de f(X) y para dar fórmulas explícitas a fin de calcular las matrices e^X , sen(X), cos(X) y X ^1/2. Por último, se muestra la utilidad de esta expresión en la evaluación de funciones de algunas matrices particionadas.

De acuerdo con lo establecido en la Sección 2, los valores propios de una matriz X ∈ C^2×2 son λ ₁ = η(X) + √ξ(X) y λ ₂ = η(X) − √ξ(X). Sea J = P ⁻¹ XP la forma canónica de Jordan de X. Si se describen P por columnas y P ⁻¹ por filas, entonces

Utilizando la Definición 2.2, a continuación se da una expresión para f(X). Se escribe η ≡ η(X) y ξ ≡ ξ(X).

Caso 1. J = diag(λ ₁, λ ₂); λ ₁ ≡ η + √ξ ≠ η − √ξ ≡ λ ₂, i.e., ξ ≠ 0. En este caso, X = λ ₁ u ₁ v ₁ ^T + λ ₂ u ₂ v ₂ ^T , f(X) = Pdiag(f(λ ₁), f(λ ₂))P ⁻¹, y se puede escribir

Caso 2. J = λI ≡ ηI; ξ = 0. De inmediato se ve que f(X) = f(λ)I ≡ f(η)I.

Caso 3.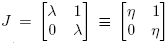; ξ = 0. En este caso, X = ηI + u ₁ v ₂ ^T y 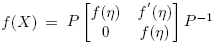. Por tanto,

En resumen, se tiene el siguiente teorema.

Teorema 3.1. Si f(·) está definida en el espectro de X ∈ C^2×2, entonces

(5)

donde

Cuando sea claro el contexto, se escribe α(X) y β(X), en lugar de α_f (X) y β_f (X).

Observación 3.2. De la Fórmula (5) se siguen fácilmente los siguientes hechos.

3.1. Conmutatividad

Sean X, Y ∈ C^2×2.

• 1. Sean f(·) y g(·) funciones tales que f(X) y g(Y ) están definidas. Escribiendo

• se deduce que f(X)g(Y ) − g(Y )f(X) = β_f (X)β_g (Y )[XY − Y X]. De esto se sigue que f(X)g(Y ) = g(Y )f(X) si y sólo si β_f (X) = 0 o β_g (Y ) = 0 ó XY = Y X. Nótese que cuando β_f (X) = 0 se obtiene f(X) = α_f (X)I, que es un múltiplo de la matriz identidad. Ahora,

• 2. Puesto que η(XY ) = η(Y X) y ξ(XY ) = ξ(Y X), si f(XY ) está definida, entonces f(Y X) está definida, y

• Por tanto f(XY ) = f(Y X) si y sólo si, β(XY ) = 0 ó XY = Y X. También (confróntese con el Corolario 1.34, p. 21, de Higham [⁴]),

3.2. Ejemplos

En este apartado se usa la Fórmula (5) para dar formas explícitas para evaluar e^X , sen(X), cos(X) y X ^1/2; X ∈ C^2×2. Propiedades generales sobre estas matrices aparecen en Higham [⁴], Golub y Van Loan [³] y Horn y Johnson [⁷], entre otros.Métodos numéricos para evaluar funciones matriciales pueden consultarse en Higham y Al-Mohy [⁵], así como las referencias ahí citadas. En estos ejemplos se escribe η ≡ η(X), ξ ≡ ξ(X).

Ejemplo 3.3. La función X → e^X ,

Cuando X es real, i.e., X ∈ R^2×2, entonces e^X es real. En efecto, usando las identidades cosh(ix) = cos(x) y senh(ix) = i sen(x), se obtiene

Ejemplo 3.4. La función X → sen(X),

Si X es real, i.e., X ∈ R^2×2, entonces sen(X) es real. En efecto, las identidades cos(ix) = cosh(x) y sen(ix) = i senh(x), permiten escribir la correspondiente expresión real.

Ejemplo 3.5. La función X → cos(X),

Cuando X es real, cos(X) es real. Para dar la fórmula correspondiente, basta usar las identidades cos(ix) = cosh(x) y sen(ix) = i senh(x).

Utilizando las fórmulas anteriores, cálculos directos permiten comprobar las identidades sen²(X) + cos²(x) = I y cos(X) + i sen(X) = e^iX . Si además se tiene en cuenta que η(2X) = 2η(X) y ξ(2X) = 4ξ(X), entonces es fácil comprobar las identidades cos²(X)− sen²(X) = cos(2X) y 2 sen(X)cos(X) = sen(2X).

Ejemplo 3.6. La función X → X ^1/2 .

Si X = 0, entonces X ^1/2 = 0. Para X ≠ 0 se tiene la siguiente expresión general:

Para 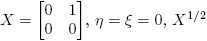no está definida. Cuando X ∈ R^2×2 no tiene valores propios reales negativos, entonces X ^1/2 toma valores reales. En efecto, con esta condición

donde, en el caso ξ < 0 (X tiene dos valores propios complejos conjugados), se ha escrito: (η+√ξ)^1/2 = a+ib; a, b ∈ R, (η−√ξ)^1/2 = a−ib; η = a ²−b ² y √ξ = 2abi. Además, en este caso, X ^1/2 toma los valores complejos 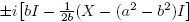(Confrontar con el Lema 6.4 de Higham [⁴]).

3.3. Matrices particionadas

En este apartado se muestra que la Fórmula (5) sirve para el cálculo de funciones de matrices particionadas con estructura especial. En particular, si X = diag(X ₁₁,X ₂₂, ...,X_mm ) y las matrices X_ii , i = 1, 2, ...,m tienen tamaño menor que 3, entonces el cálculo de f(X) es inmediato, pues, por la Proposición 2.4,

Supóngase ahora que X, Y ∈ C^2×2.

• 1. Si , entonces

• La Proposición 2.4 conduce a

• 2. Si , entonces y

• Ahora, por la Proposición 2.4,

4. La derivada de Fréchet de funciones matriciales 2 × 2

En adelante, O es un conjunto abierto de R ó C, f(·) es una función escalar tres veces continuamente diferenciable en O y A es el conjunto abierto de las X ∈ C^2×2 tales que η(X) + √ξ(X) y η(X) − √ξ(X) están en O. La derivada de Fréchet de f: A → C^2×2 en el punto X ∈ A es la única transformación lineal Df(X) : C^2×2 → C^2×2 tal que para H ∈ C^2×2,

Bajo las condiciones sobre f(·) estipuladas arriba, la derivada de Fréchet [Df(X)](H) existe y es continua en las variables X y H; ver Higham [⁴] (Teorema 3.8 pg. 60). Ahora se da una fórmula para esta derivada.

A partir de la expresión f(X) = α_f (X)I + β_f (X)(X − η(X)I), usando las reglas de derivación, se llega a que, para cada H ∈ C^2×2,

(6)

Esta fórmula se completa cuando se expliciten las derivadas de Fréchet de las funciones X → α_f (X) y X → β_f (X). Los cálculos de estas derivadas, que se presentan en el apéndice de este artículo, conducen a los siguientes resultados:

Por ejemplo, para 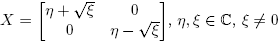, y 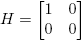se obtiene:

Reemplazando en la fórmula (6) se llega a

Observación 4.1. De la Fórmula (4) se sigue que

donde [X,H] ≡ XH − HX. Usando esta representación se obtiene

(7)

siendo

Asi las cosas, si XH = HX ó f(x) = ax+b, a, b ∈ C; entonces [Df(X)](H) = f ^′(X)H = Hf ^′(X).

5. Forma canónica de Jordan de la derivada de Fréchet

Sea J = P ⁻¹ XP la forma canónica de Jordan de X ∈ C^2×2, donde P = [u ₁ u ₂] y 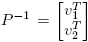. Es fácil ver que B: = {H_ij = u_iv_j ^T ; i, j = 1, 2} es una base de C^2×2. La matriz de la tranformación lineal [Df(X)] en esta base se denotará por [Df(X)] _B . Se deduce fácilmente de la fórmula (6) que para cada H ∈ C^2×2

(8)

Ahora, si H = H_ij = u_iv_j ^T , entonces P ⁻¹ HP = e_ie_j ^T = E_ij , donde I = [e ₁ e ₂], es decir, {E_ij ; i, j = 1, 2} es la base estándar de C^2×2. Para calcular [Df(J)](E_ij ), podemos usar la Fórmula (6) o determinar directamente las derivadas direccionales:

De cualquier forma se obtienen los siguientes resultados.

Caso 1. J = diag(η + √ξ, η − √ξ); ξ ≠ 0. En este caso (confronte con el Teorema 3.11; p. 62 de Higham [⁴]),

Esto significa que la matriz de [Df(X)] en la base B es la matriz diagonal:

donde

Caso 2. J = ηI; ξ = 0. En este caso, [Df(J)](E^ij ) = f ^′(η)(E^ij ) y la matriz que representa a [Df(X)] en la base B (y en cualquier otra base de C^2×2) es la matriz diagonal

Caso 3.. En este caso

Esto quiere decir que la matriz de [Df(X)] en la base B es:

La forma canónica de Jordan de la matriz [Df(X)] depende de f ^′(η) y f ^′′(η).

Caso f ^′′(η) = f ^′′′(η) = 0. Es claro que [Df(X)]B = f ^′(η)I.

Caso f ^′′(η) = 0; f ^′′′(η) ≠ 0. En la base 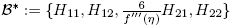se tiene

Caso f ^′′(η) ≠ 0. En la base B* = {R ₁₁,R ₁₂,R ₂₁,R ₂₂}, donde 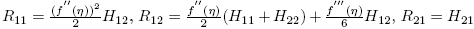y R ₂₂ = H ₁₁ −H ₂₂, se tiene

El análisis anterior se resume en el siguiente teorema.

Teorema 5.1. La forma canónica de Jordan de [Df(X)], X ∈ C^2×2 posee las siguientes propiedades:

Ejemplo 5.2. Si f(x) = e^x , la forma de Jordan de Df(X)] es diagonal si y sólo si X es diagonalizable. Cuando X tiene forma de Jordan 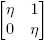, entonces [Df(X)] tiene forma de Jordan

Observación 5.3. En relación con la norma de la derivada de Fréchet, se cumple la siguiente desigualdad:

donde k(P) = ║P║║P ⁻¹║. En efecto, de la expresión (8) se obtiene

Ahora bien, de las expresiones anteriores se puede determinar ║[Df(J)]║. En particular, si J = diag(η + √ξ, η − √ξ), ξ ≠ 0, entonces

Si J = ηI o si J = 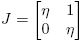y 0 = f ^′′(η) = f ^′′′(η), entonces ║[Df(J)]║ = |f ^′(η)|.

6. Derivada de Fréchet de funciones matriciales de matrices n × n

En esta sección se considera el caso en que f(·) es analítica y X es una matriz n × n. Cuando f(·) es analítica dentro y sobre un contorno cerrado Γ que encierra a λ_i , i = 1, 2, ..., k, la fórmula más compacta de la derivada de Fréchet de X → f(X); X ∈ C ^n×n es la de Stickel (ver Stickel [¹¹], Teorema 1, p. 84):

(9)

la cual, cuando XH = HX, conduce a

Más aún, para la j-ésima derivada de Fréchet, j = 2, 3, ..., se obtiene (ver el Teorema 4.1 de Deadman y Relton [²]):

(10)

siendo

donde la suma se hace sobre las j! permutaciones σ de {1, 2, ..., j}.

Los siguientes ejemplos ilustran la utilidad de estas fórmulas.

6.1. Ejemplos

En esta subsección X,H ∈ C ^n×n .

Ejemplo 6.1. Supóngase que 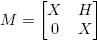. Entonces la Definición 2.3 y la Fórmula (9) conducen a la siguiente identidad (confronte con la fórmula (3.16), p. 60 de Higham [⁴]):

la cual se puede usar para obtener [Df(X)](H)] a partir de f(M), o para calcular f(M) a partir de f(X) y [Df(X)](H).

Si, por ejemplo, y , entonces

De aquí que 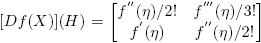. De otra parte; cuando f(x) = e^x y X conmuta con H, entonces

Ejemplo 6.2. Supóngase ahora que

Entonces, cuando existe, la matriz (zI −M)⁻¹ es

La Definición 2.3 y la Fórmula (10) llevan a

expresión que permite calcular [D ² f(X)](H,H) a partir de f(M). Como en el ejemplo anterior, cuando 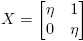y 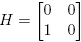, se obtiene

Estos ejemplos constituyen una generalización de la matrix f(J_i ) que aparece en la Definición 2.2 (ver Najfeld and Havel [⁹], Teorema 4.13, p. 350).

Se termina esta sección con el siguiente resultado anunciado en la introducción.

Teorema 6.3. Si X es diagonalizable y f(·) es analítica dentro y sobre un contorno cerrado Γ que encierra el espectro de X, entonces la forma canónica de Jordan de la derivada de Fréchet es diagonal.

Demostración. Supóngase que X ∈ Cn×n es diagonalizable y que P ⁻¹ XP = J = diag(λ ₁, λ ₂, ..., λ_n ), donde

Entonces B := {H_ij = u_iv_j ^T ; i, j = 1, 2, ..., n} es una base de C ^n×n y P ⁻¹ H_ijP = e_ie_j ^T = E_ij , donde I = [e ₁ e ₂ . . . e_n ], es decir, {E_ij ; i, j = 1, 2, ..., n} es la base estándar de C ^n×n . Con estas notaciones se puede escribir

donde

De esto se sigue que [Df(X)](H_ij ) = f[λ_i , λ_j ]H_ij , por lo que la matriz que representa la tranformación lineal [Df(X)](·) en la base B es diagonal. ☑

7. Conclusiones

En este artículo se ha mostrado que si f(X) está definida, X ∈ C^2×2, entonces

donde las funciones α_f (·), β_f (·) y η(·) dependen de la traza y el determinante de X. Se ha usado esta expresión para dar fórmulas explícitas para evaluar las matrices e^X , sen(X), cos(X) y X ^1/2, para evaluar funciones de ciertas matrices particionadas y para determinar la derivada de Fréchet de la función X → f(X); X ∈ A ⊂ C^2×2. Como resultado central, se ha calculado la forma canónica de Jordan de su derivada de Fréchet. La determinación de la forma de Jordan de la derivada de Fréchet en el caso n ≥ 3 queda abierta y, para funciones analíticas se puede abordar con la fórmula de Stickel (9).