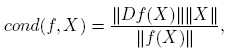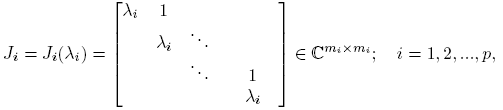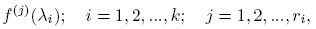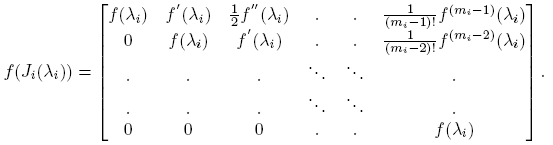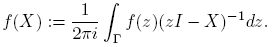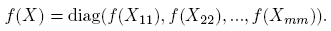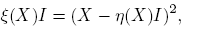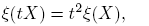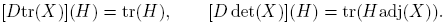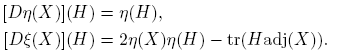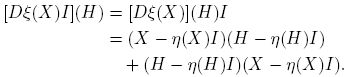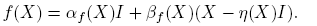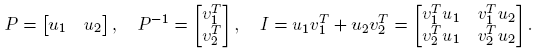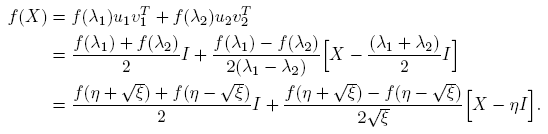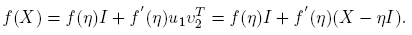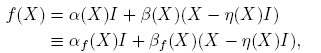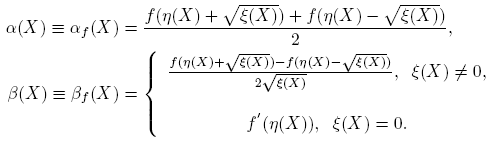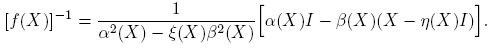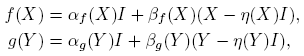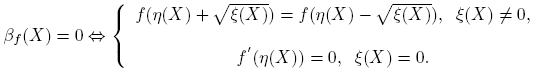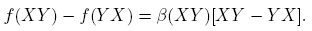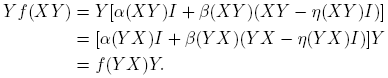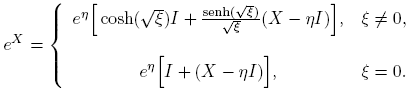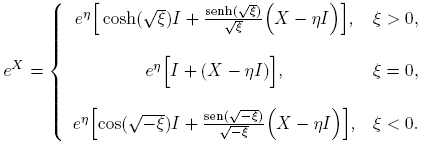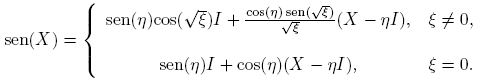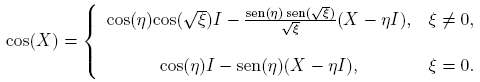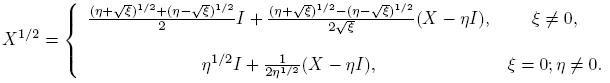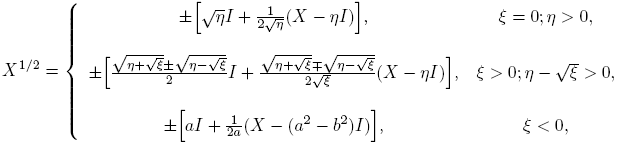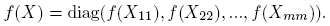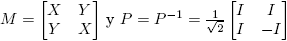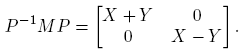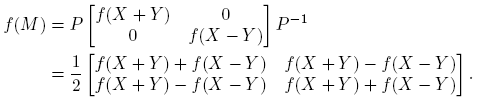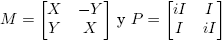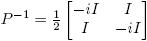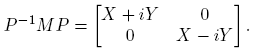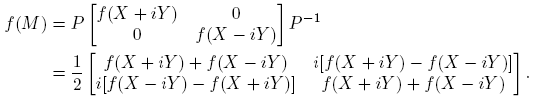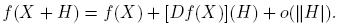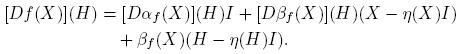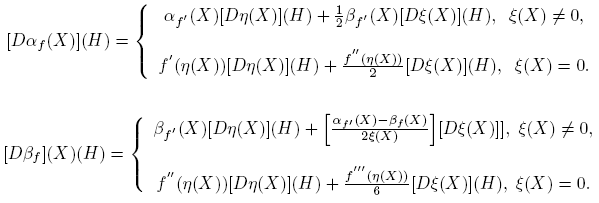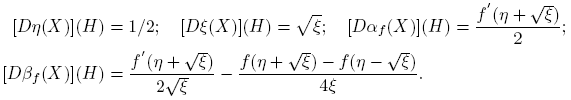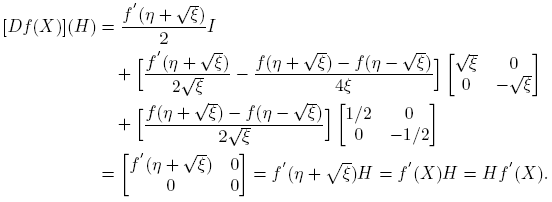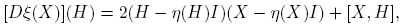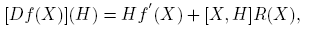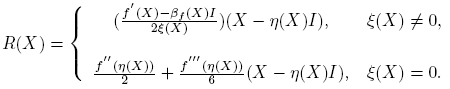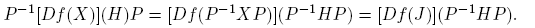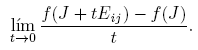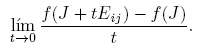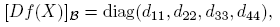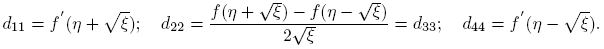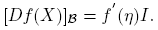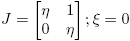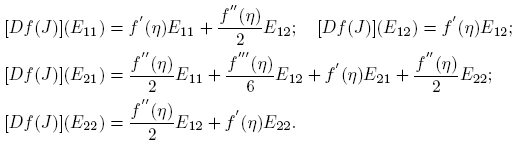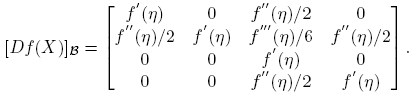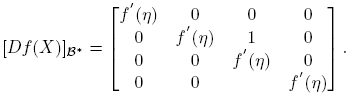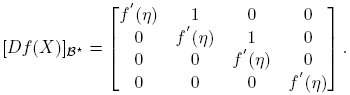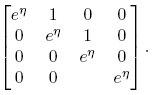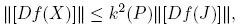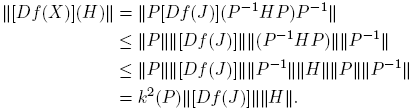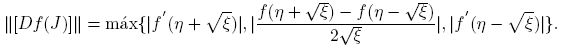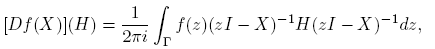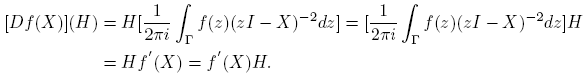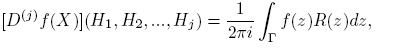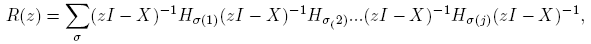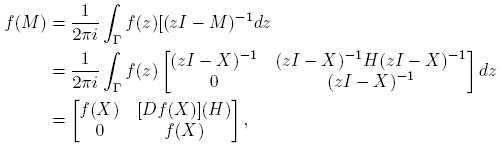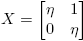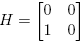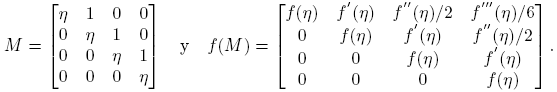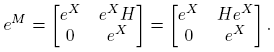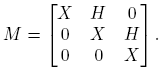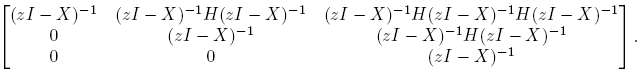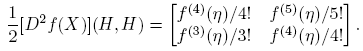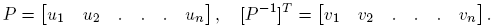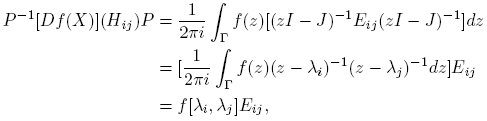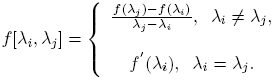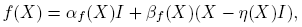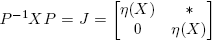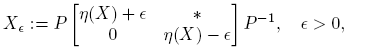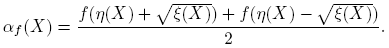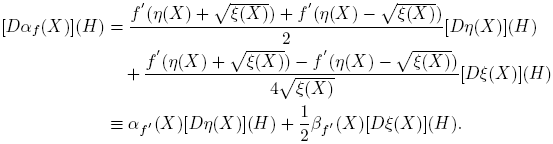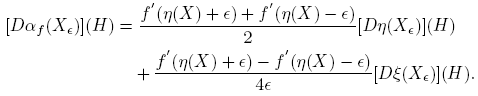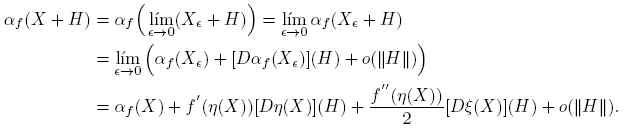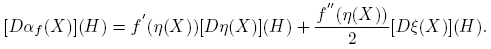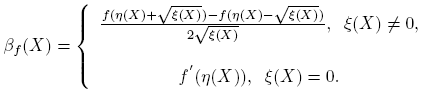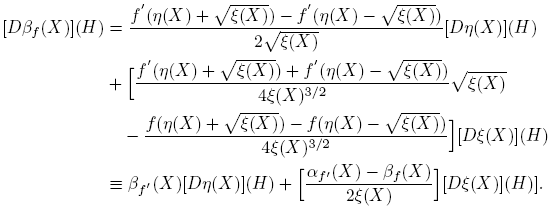1. Introducción
La norma de la derivada de Fréchet de una función matricial f : A ⊂ C n×n → C n×n aparece explícitamente en una expresión que da el número de condición relativo de f en X. De manera precisa (ver la Sección 3.1 de Higham [4], o la Sección 3.3 de Higham and Lijing [6]):
siendo ║ · ║ una norma matricial y  . Este número mide la sensibilidad de f(X) a pequeños cambios en X. Hay trabajos recientes dedicados a la estimación de cotas para este número de condición en situaciones particulares; ver por ejemplo, Cardoso y Sadeghi [1], Deadman y Relton [2] o Kandolf y Relton [8], entre otros.
. Este número mide la sensibilidad de f(X) a pequeños cambios en X. Hay trabajos recientes dedicados a la estimación de cotas para este número de condición en situaciones particulares; ver por ejemplo, Cardoso y Sadeghi [1], Deadman y Relton [2] o Kandolf y Relton [8], entre otros.
Es entonces conveniente disponer de expresiones concretas de la derivada de Fréchet de tales funciones. En este contexto, el problema de investigación 3.11 en Higham [4] consiste en determinar la forma de Jordan de la derivada de Fréchet de funciones matriciales X → f(X); X ∈ A ⊂ C n×n , en términos de la de X. Cuando X es diagonalizable, el Corolario 3.12 en Higham [4] implica que la forma canónica de Jordan de dicha derivada es también diagonal (esto se demuestra en la Sección 6 para funciones analíticas). En este artículo se presenta una fórmula para evaluar funciones de matrices 2 × 2, la cual se usa para determinar su derivada de Fréchet. La principal contribución de este trabajo consiste en dar la forma canónica de Jordan de la derivada de Fréchet de funciones matriciales en el caso n = 2.
El resto del trabajo está organizado como sigue. En la Sección 2 se dan dos definiciones de la matriz f(X); X ∈ C n×n . Para matrices 2 × 2 se introducen dos funciones de valor escalar, que serán fundamentales para el desarrollo del resto del trabajo. En la Sección 3 se deduce una expresión para f(X), X ∈ C2×2 (Teorema 3.1); como aplicación, se dan condiciones necesarias y suficientes para que f(X)g(Y ) = g(Y )f(X), se presentan fómulas explícitas para calcular las matrices eX , sen(X), cos(X) y X 1/2 y, finalmente, se considera la evaluación de funciones de algunas matrices particionadas. La Sección 4 se dedica a la derivada de Fréchet de funciones X → f(X); X ∈ A ⊂ C2×2 y, la Sección 5, a dar su forma canónica de Jordan (Teorema 5.1). Por último, en la Sección 6, se considera la derivada de Fréchet de funciones matriciales en el caso en que f(·) es analítica y X ∈ C n×n ; se demuestra que si X es diagonalizable, entonces la forma canónica de Jordan de la derivada de Fréchet es diagonal (Teorema 6.3).
2. Preliminares
Se establecen aquí la terminología, las definiciones y los resultados básicos, que se utilizarán a lo largo del trabajo.
2.1. Definiciones de f(X)
Hay varias maneras equivalentes de definir f(X), X ∈ C n×n (ver, por ejemplo, Rinehart [10], el Capítulo 6 de Horn y Johnson [7], el Capítulo 11 de Golub y Van Loan [3] o el Capítulo 1 de Higham [4]). En este artículo presentamos dos definiciones; la primera, en términos de la forma canónica de Jordan y, la segunda, en términos de la integral de Cauchy.
Supóngase que los distintos valores propios de X ∈ C n×n son λ 1, λ 2, ..., λk , es decir, σ(X) = {λ 1, λ 2, ..., λk } es el espectro de X, que mX (λ) = (λ−λ 1) r1(λ−λ 2) r2 ...(λ−λk ) rk es su polinomio mínimo, y que X tiene forma canónica de Jordan J = P −1 XP, donde J = diag(J 1, J 2, ..., Jp ),
y m 1 + m 2 + ... + mp = n. Aunque la matriz P no es única, la matriz de Jordan J es única, salvo el orden en que aparecen los bloques en su diagonal.
Supóngase además que f(t) es una función con valores escalares, de variable real o compleja t. Con estas notaciones se establecen las siguientes definiciones (ver Higham [4], Definiciones 1.1 y 1.2, p. 3).
Definición 2.1. Se dice que f está definida en el espectro de X, si existen los valores
denominados valores de f en el espectro de X. Aquí, f (j)(·) indica la derivada j-ésima de f.
Definición 2.2. Supóngase que f está definida en el espectro de X. Se define f(X) := Pdiag(f(J 1), f(J 2), ..., f(Jp ))P −1, donde el bloque diagonal f(Ji ) es la matriz C mi×mi dada por
La matriz f(X) no depende de la forma de Jordan usada (ver Horn y Johnson [7], Teorema 6.2.9-(b), p. 412). Para funciones multivaluadas como f(t) = t 1/2 y f(t) = log(t), se sobreentiende que sólo una rama se escoge en la evaluación de los bloques corrrespondientes a un mismo λi ; i = 1, 2, ..., k (ver el Ejemplo 4 del Apartado 3.5). En este caso, f(X) se denomina función matricial primaria.
La definición más corta y elegante de función matricial es la que sigue (Definición 1.11, p. 8, en Higham [4]).
Definición 2.3. Sea f(t) una función analítica dentro y sobre un contorno cerrado Γ que encierra a λi ; i = 1, 2, ..., k. Se define
Cuando se pueden aplicar, las definiciones anteriores son equivalentes (ver Horn y Johnson [7], Teorema 6.2.28, p. 427, o Rinehart [10], Teorema 1, p. 405).
Propiedades generales sobre f(X) pueden ser consultadas en Horn y Johnson [7] (Teorema 6.2.9, p. 412), o en Higham [4] (Sección 1.3). Se resaltan las siguientes, que serán usadas en la Sección 3.
Proposición 2.4. Suponga que f está definida en el espectro de X y que Q es una matriz invertible. Entonces,
2.2. Las funciones escalares η, ξ : C2×2 → C
En lo que sigue, C2×2 denota el espacio de Banach de las matrices complejas 2 × 2 con la norma de Frobenius. La traza, el determinante y la matriz adjunta de X ∈ C2×2 se denotarán por tr(X) , det(X) y adj(X), respectivamente. Cuando existe, la derivada de Fréchet de una función k : C2×2 → C en el punto X ∈ C2×2 es la única transformación lineal [Dk(X)] : C2×2 → C tal que para todo H ∈ C2×2 se cumple
Considérense ahora las funciones η, ξ: C2×2 → C definidas por
Se sabe que η es lineal y que para cada matriz invertible Q se cumplen η(X) = η(Q −1 XQ) y ξ(X) = ξ(Q −1 XQ). De inmediato se verifican las identidades
donde I es la matriz idéntica y t ∈ C. Nótese que los valores propios de X son precisamente η(X) + √ξ(X) y η(X) − √ξ(X). Aquí, √ξ(X) indica la raíz cuadrada principal de ξ(X).
De otra parte, es bien conocido que las funciones X → tr(X) y X → det(X) son continuamente diferenciables según Fréchet, y que para H ∈ C2×2 se cumplen las igualdades
De esto se sigue que las funciones X → η(X) y X → ξ(X) son continuamente diferenciables según Fréchet, y que para H ∈ C2×2,
También, de la ecuación (1) se obtiene
3. Funciones matriciales para matrices 2 × 2
En esta sección se muestra que si f(·) está definida en el espectro de X ∈ C2×2, entonces f(X) es un polinomio de la forma
Esta expresión se usa para establecer algunas propiedades de f(X) y para dar fórmulas explícitas a fin de calcular las matrices eX , sen(X), cos(X) y X 1/2. Por último, se muestra la utilidad de esta expresión en la evaluación de funciones de algunas matrices particionadas.
De acuerdo con lo establecido en la Sección 2, los valores propios de una matriz X ∈ C2×2 son λ 1 = η(X) + √ξ(X) y λ 2 = η(X) − √ξ(X). Sea J = P −1 XP la forma canónica de Jordan de X. Si se describen P por columnas y P −1 por filas, entonces
Utilizando la Definición 2.2, a continuación se da una expresión para f(X). Se escribe η ≡ η(X) y ξ ≡ ξ(X).
Caso 1. J = diag(λ 1, λ 2); λ 1 ≡ η + √ξ ≠ η − √ξ ≡ λ 2, i.e., ξ ≠ 0. En este caso, X = λ 1 u 1 v 1 T + λ 2 u 2 v 2 T , f(X) = Pdiag(f(λ 1), f(λ 2))P −1, y se puede escribir
Caso 2. J = λI ≡ ηI; ξ = 0. De inmediato se ve que f(X) = f(λ)I ≡ f(η)I.
Caso 3.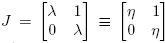 ; ξ = 0. En este caso, X = ηI + u
1
v
2
T
y
; ξ = 0. En este caso, X = ηI + u
1
v
2
T
y 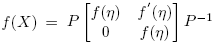 . Por tanto,
. Por tanto,
En resumen, se tiene el siguiente teorema.
Teorema 3.1. Si f(·) está definida en el espectro de X ∈ C2×2, entonces
donde
Cuando sea claro el contexto, se escribe α(X) y β(X), en lugar de αf (X) y βf (X).
Observación 3.2. De la Fórmula (5) se siguen fácilmente los siguientes hechos.
2. Para cada t ∈ C se verifican las relaciones η(X+tI) = η(X)+t y ξ(X+tI) = ξ(X). Por tanto, si f(·) y f ′(·) son funciones t-periódicas, entonces f(X + tI) = f(X), siempre que estas matrices estén definidas. Por ejemplo: sen(X + 2πI) = sen(X), cos(X + 2πI) = cos(X) y eX +2πiI = eX .
3. Como η(−X) = −η(X) y ξ(−X) = ξ(X), si para cada t en el dominio de f(·) se cumple f(−t) = ±f(t), entonces f(X) = ±f(X).
4. Sean O un subconjunto abierto de R o C y A el conjunto abierto de las X tales que η(X)+ √ξ(X) y η(X)− √ξ(X) están en O. Si f(·) es continuamente diferenciable en O, entonces las funciones X → αf (X) y X → βf (X), X ∈ A, son continuas. Resulta entonces que la función X → f(X) es continua en A (ver también Horn y Johnson [7], Teorema 6.2.27-(1), p.425).
3.1. Conmutatividad
Sean X, Y ∈ C2×2.
se deduce que f(X)g(Y ) − g(Y )f(X) = βf (X)βg (Y )[XY − Y X]. De esto se sigue que f(X)g(Y ) = g(Y )f(X) si y sólo si βf (X) = 0 o βg (Y ) = 0 ó XY = Y X. Nótese que cuando βf (X) = 0 se obtiene f(X) = αf (X)I, que es un múltiplo de la matriz identidad. Ahora,
2. Puesto que η(XY ) = η(Y X) y ξ(XY ) = ξ(Y X), si f(XY ) está definida, entonces f(Y X) está definida, y
Por tanto f(XY ) = f(Y X) si y sólo si, β(XY ) = 0 ó XY = Y X. También (confróntese con el Corolario 1.34, p. 21, de Higham [4]),
3.2. Ejemplos
En este apartado se usa la Fórmula (5) para dar formas explícitas para evaluar eX , sen(X), cos(X) y X 1/2; X ∈ C2×2. Propiedades generales sobre estas matrices aparecen en Higham [4], Golub y Van Loan [3] y Horn y Johnson [7], entre otros.Métodos numéricos para evaluar funciones matriciales pueden consultarse en Higham y Al-Mohy [5], así como las referencias ahí citadas. En estos ejemplos se escribe η ≡ η(X), ξ ≡ ξ(X).
Ejemplo 3.3. La función X → eX ,
Cuando X es real, i.e., X ∈ R2×2, entonces eX es real. En efecto, usando las identidades cosh(ix) = cos(x) y senh(ix) = i sen(x), se obtiene
Ejemplo 3.4. La función X → sen(X),
Si X es real, i.e., X ∈ R2×2, entonces sen(X) es real. En efecto, las identidades cos(ix) = cosh(x) y sen(ix) = i senh(x), permiten escribir la correspondiente expresión real.
Ejemplo 3.5. La función X → cos(X),
Cuando X es real, cos(X) es real. Para dar la fórmula correspondiente, basta usar las identidades cos(ix) = cosh(x) y sen(ix) = i senh(x).
Utilizando las fórmulas anteriores, cálculos directos permiten comprobar las identidades sen2(X) + cos2(x) = I y cos(X) + i sen(X) = eiX . Si además se tiene en cuenta que η(2X) = 2η(X) y ξ(2X) = 4ξ(X), entonces es fácil comprobar las identidades cos2(X)− sen2(X) = cos(2X) y 2 sen(X)cos(X) = sen(2X).
Ejemplo 3.6. La función X → X 1/2 .
Si X = 0, entonces X 1/2 = 0. Para X ≠ 0 se tiene la siguiente expresión general:
Para 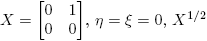 no está definida. Cuando X ∈ R2×2 no tiene valores propios reales negativos, entonces X
1/2 toma valores reales. En efecto, con esta condición
no está definida. Cuando X ∈ R2×2 no tiene valores propios reales negativos, entonces X
1/2 toma valores reales. En efecto, con esta condición
donde, en el caso ξ < 0 (X tiene dos valores propios complejos conjugados), se ha escrito: (η+√ξ)1/2 = a+ib; a, b ∈ R, (η−√ξ)1/2 = a−ib; η = a
2−b
2 y √ξ = 2abi. Además, en este caso, X
1/2 toma los valores complejos 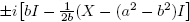 (Confrontar con el Lema 6.4 de Higham [4]).
(Confrontar con el Lema 6.4 de Higham [4]).
3.3. Matrices particionadas
En este apartado se muestra que la Fórmula (5) sirve para el cálculo de funciones de matrices particionadas con estructura especial. En particular, si X = diag(X 11,X 22, ...,Xmm ) y las matrices Xii , i = 1, 2, ...,m tienen tamaño menor que 3, entonces el cálculo de f(X) es inmediato, pues, por la Proposición 2.4,
Supóngase ahora que X, Y ∈ C2×2.
4. La derivada de Fréchet de funciones matriciales 2 × 2
En adelante, O es un conjunto abierto de R ó C, f(·) es una función escalar tres veces continuamente diferenciable en O y A es el conjunto abierto de las X ∈ C2×2 tales que η(X) + √ξ(X) y η(X) − √ξ(X) están en O. La derivada de Fréchet de f: A → C2×2 en el punto X ∈ A es la única transformación lineal Df(X) : C2×2 → C2×2 tal que para H ∈ C2×2,
Bajo las condiciones sobre f(·) estipuladas arriba, la derivada de Fréchet [Df(X)](H) existe y es continua en las variables X y H; ver Higham [4] (Teorema 3.8 pg. 60). Ahora se da una fórmula para esta derivada.
A partir de la expresión f(X) = αf (X)I + βf (X)(X − η(X)I), usando las reglas de derivación, se llega a que, para cada H ∈ C2×2,
Esta fórmula se completa cuando se expliciten las derivadas de Fréchet de las funciones X → αf (X) y X → βf (X). Los cálculos de estas derivadas, que se presentan en el apéndice de este artículo, conducen a los siguientes resultados:
Por ejemplo, para 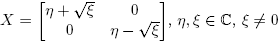 , y
, y  se obtiene:
se obtiene:
Reemplazando en la fórmula (6) se llega a
Observación 4.1. De la Fórmula (4) se sigue que
donde [X,H] ≡ XH − HX. Usando esta representación se obtiene
siendo
Asi las cosas, si XH = HX ó f(x) = ax+b, a, b ∈ C; entonces [Df(X)](H) = f ′(X)H = Hf ′(X).
5. Forma canónica de Jordan de la derivada de Fréchet
Sea J = P
−1
XP la forma canónica de Jordan de X ∈ C2×2, donde P = [u
1
u
2] y  . Es fácil ver que B: = {Hij
= uivj
T
; i, j = 1, 2} es una base de C2×2. La matriz de la tranformación lineal [Df(X)] en esta base se denotará por [Df(X)]
B
. Se deduce fácilmente de la fórmula (6) que para cada H ∈ C2×2
. Es fácil ver que B: = {Hij
= uivj
T
; i, j = 1, 2} es una base de C2×2. La matriz de la tranformación lineal [Df(X)] en esta base se denotará por [Df(X)]
B
. Se deduce fácilmente de la fórmula (6) que para cada H ∈ C2×2
Ahora, si H = Hij = uivj T , entonces P −1 HP = eiej T = Eij , donde I = [e 1 e 2], es decir, {Eij ; i, j = 1, 2} es la base estándar de C2×2. Para calcular [Df(J)](Eij ), podemos usar la Fórmula (6) o determinar directamente las derivadas direccionales:
De cualquier forma se obtienen los siguientes resultados.
Caso 1. J = diag(η + √ξ, η − √ξ); ξ ≠ 0. En este caso (confronte con el Teorema 3.11; p. 62 de Higham [4]),
Esto significa que la matriz de [Df(X)] en la base B es la matriz diagonal:
donde
Caso 2. J = ηI; ξ = 0. En este caso, [Df(J)](Eij ) = f ′(η)(Eij ) y la matriz que representa a [Df(X)] en la base B (y en cualquier otra base de C2×2) es la matriz diagonal
Esto quiere decir que la matriz de [Df(X)] en la base B es:
La forma canónica de Jordan de la matriz [Df(X)] depende de f ′(η) y f ′′(η).
Caso f ′′(η) = f ′′′(η) = 0. Es claro que [Df(X)]B = f ′(η)I.
Caso
f
′′(η) = 0; f
′′′(η) ≠ 0. En la base 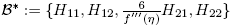 se tiene
se tiene
Caso f
′′(η) ≠ 0. En la base B* = {R
11,R
12,R
21,R
22}, donde 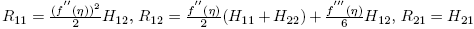 y R
22 = H
11 −H
22, se tiene
y R
22 = H
11 −H
22, se tiene
El análisis anterior se resume en el siguiente teorema.
Teorema 5.1. La forma canónica de Jordan de [Df(X)], X ∈ C2×2 posee las siguientes propiedades:
Es diagonal cuando X es diagonalizable, o cuando X no es diagonalizable pero f ′′(η) = f ′′′(η) = 0.
Tiene un bloque de tamaño 2 y dos bloques de tamaño 1 cuando X no es diagonalizable, f ′′(η) = 0 y f ′′′(η) ≠ 0.
Tiene un bloque de tamaño 3 y uno de tamaño 1 cuando X no es diagonalizable y f′′(η) ≠ 0.
Ejemplo 5.2. Si f(x) = ex
, la forma de Jordan de Df(X)] es diagonal si y sólo si X es diagonalizable. Cuando X tiene forma de Jordan 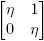 , entonces [Df(X)] tiene forma de Jordan
, entonces [Df(X)] tiene forma de Jordan
Observación 5.3. En relación con la norma de la derivada de Fréchet, se cumple la siguiente desigualdad:
donde k(P) = ║P║║P −1║. En efecto, de la expresión (8) se obtiene
Ahora bien, de las expresiones anteriores se puede determinar ║[Df(J)]║. En particular, si J = diag(η + √ξ, η − √ξ), ξ ≠ 0, entonces
Si J = ηI o si J = 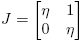 y 0 = f
′′(η) = f
′′′(η), entonces ║[Df(J)]║ = |f
′(η)|.
y 0 = f
′′(η) = f
′′′(η), entonces ║[Df(J)]║ = |f
′(η)|.
6. Derivada de Fréchet de funciones matriciales de matrices n × n
En esta sección se considera el caso en que f(·) es analítica y X es una matriz n × n. Cuando f(·) es analítica dentro y sobre un contorno cerrado Γ que encierra a λi , i = 1, 2, ..., k, la fórmula más compacta de la derivada de Fréchet de X → f(X); X ∈ C n×n es la de Stickel (ver Stickel [11], Teorema 1, p. 84):
la cual, cuando XH = HX, conduce a
Más aún, para la j-ésima derivada de Fréchet, j = 2, 3, ..., se obtiene (ver el Teorema 4.1 de Deadman y Relton [2]):
siendo
donde la suma se hace sobre las j! permutaciones σ de {1, 2, ..., j}.
Los siguientes ejemplos ilustran la utilidad de estas fórmulas.
6.1. Ejemplos
En esta subsección X,H ∈ C n×n .
Ejemplo 6.1. Supóngase que 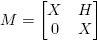 . Entonces la Definición 2.3 y la Fórmula (9) conducen a la siguiente identidad (confronte con la fórmula (3.16), p. 60 de Higham [4]):
. Entonces la Definición 2.3 y la Fórmula (9) conducen a la siguiente identidad (confronte con la fórmula (3.16), p. 60 de Higham [4]):
la cual se puede usar para obtener [Df(X)](H)] a partir de f(M), o para calcular f(M) a partir de f(X) y [Df(X)](H).
De aquí que 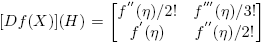 . De otra parte; cuando f(x) = ex
y X conmuta con H, entonces
. De otra parte; cuando f(x) = ex
y X conmuta con H, entonces
Ejemplo 6.2. Supóngase ahora que
Entonces, cuando existe, la matriz (zI −M)−1 es
La Definición 2.3 y la Fórmula (10) llevan a
expresión que permite calcular [D
2
f(X)](H,H) a partir de f(M). Como en el ejemplo anterior, cuando 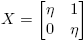 y
y 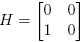 , se obtiene
, se obtiene
Estos ejemplos constituyen una generalización de la matrix f(Ji ) que aparece en la Definición 2.2 (ver Najfeld and Havel [9], Teorema 4.13, p. 350).
Se termina esta sección con el siguiente resultado anunciado en la introducción.
Teorema 6.3. Si X es diagonalizable y f(·) es analítica dentro y sobre un contorno cerrado Γ que encierra el espectro de X, entonces la forma canónica de Jordan de la derivada de Fréchet es diagonal.
Demostración. Supóngase que X ∈ Cn×n es diagonalizable y que P −1 XP = J = diag(λ 1, λ 2, ..., λn ), donde
Entonces B := {Hij = uivj T ; i, j = 1, 2, ..., n} es una base de C n×n y P −1 HijP = eiej T = Eij , donde I = [e 1 e 2 . . . en ], es decir, {Eij ; i, j = 1, 2, ..., n} es la base estándar de C n×n . Con estas notaciones se puede escribir
donde
De esto se sigue que [Df(X)](Hij ) = f[λi , λj ]Hij , por lo que la matriz que representa la tranformación lineal [Df(X)](·) en la base B es diagonal. ☑
7. Conclusiones
En este artículo se ha mostrado que si f(X) está definida, X ∈ C2×2, entonces
donde las funciones αf (·), βf (·) y η(·) dependen de la traza y el determinante de X. Se ha usado esta expresión para dar fórmulas explícitas para evaluar las matrices eX , sen(X), cos(X) y X 1/2, para evaluar funciones de ciertas matrices particionadas y para determinar la derivada de Fréchet de la función X → f(X); X ∈ A ⊂ C2×2. Como resultado central, se ha calculado la forma canónica de Jordan de su derivada de Fréchet. La determinación de la forma de Jordan de la derivada de Fréchet en el caso n ≥ 3 queda abierta y, para funciones analíticas se puede abordar con la fórmula de Stickel (9).