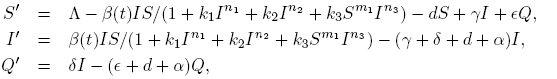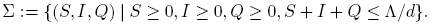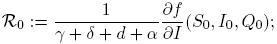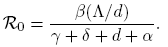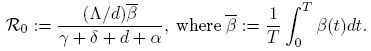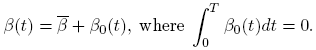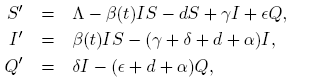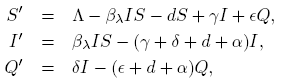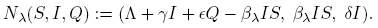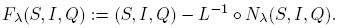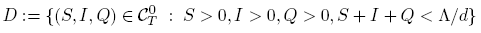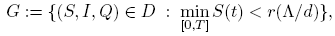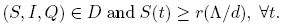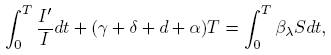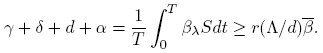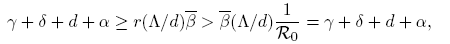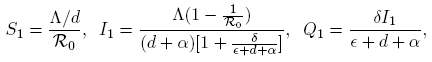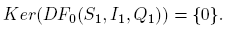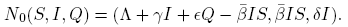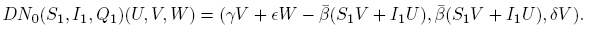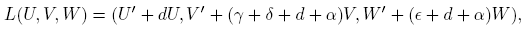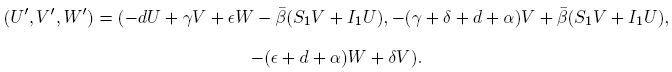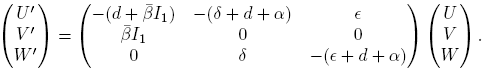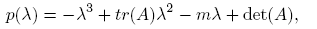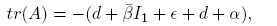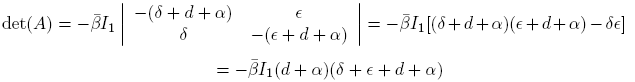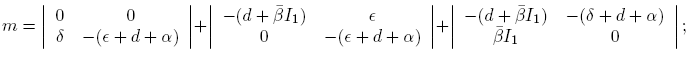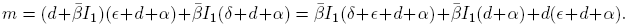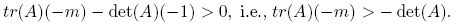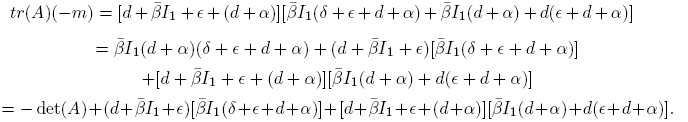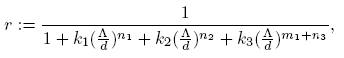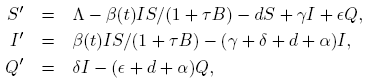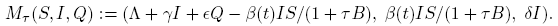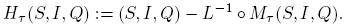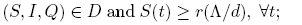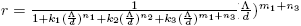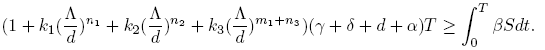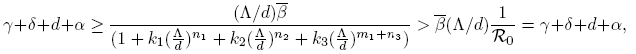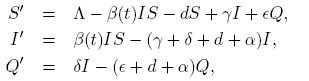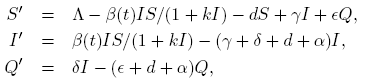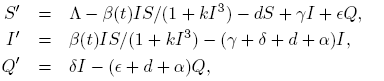1. Introduction
In epidemiological models it is of importance the consideration of possible ways of controlling infectious diseases, such as vaccination or quarantine. Hence the addition of a compartment consisting of quarantined individuals gives a way of exploring possible mitigation effects for controlling or eliminating the disease. We consider a disease model in a population in the following way. At any given time, t, the total population N is divided into three compartments with N(t) = S(t)+I(t)+Q(t) where S is the number of individuals in the susceptible class, I is the number of individuals who are infectious but not quarantined, and Q is the number of individuals who are quarantined. Based in the autonomous bilinear model with quarantine of [5], we formulate a quarantined models with seasonally-dependent saturated incidence rate given by
where parameters Λ, δ, d and α are positive constants; γ, ki , ∊ are non-negative constants, and ni ,m 1 ≥ 1, i = 1, 2, 3. The constant Λ is the recruitment rate of susceptibles corresponding to births and immigration, d is the per capita natural mortality rate, δ is the rate constant for individuals leaving the infective compartment I for the quarantine compartment Q, α is the disease-related death rate constant in compartments I and Q, and γ and ǫ are the rates at which individuals recover and return to susceptible compartment S from compartments I and Q, respectively. In short, we call these models as SIQS models.
The case of a bilinear autonomous SIQS model with β-constant was considered in [5], where thresholds, equilibria, and their stability are studied. In [10] a bilinear nonautonomous epidemic model with quarantine was studied and some conditions for thresholds and eradication of the infectious disease were obtained. In this work, we assume that the interactions between susceptible and infected individuals are modeled by the incidence function β(t)IS/(1 +k
1
In
1 +k
2
In
2 +k
3
Sm
1
In
3 ), where β(t) is a non constant non-negative continuous T -periodic function. Since several time-dependent factors are very important for the spread of diseases, with the use of a periodic incidence function we can take into account the variability of diseases according to climate seasons, school calendars, etc. Besides with the saturated term 1+k
1
In
1+k
2
In
2+k
3
Sm
1
In
3 , we measure the inhibition effect from the behavioral change of the susceptible or infected individuals when the number of infected increases. In the case autonomous (with β-constant), several different saturated incidence rates have been proposed by authors, for example: Capasso and Serio [2] introduced a saturated incidence function 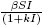 in an epidemic model when they studied the cholera epidemic in 1973. Xiao and Ruan [12] proposed an SIRS epidemic model with non-monotonic incidence function
in an epidemic model when they studied the cholera epidemic in 1973. Xiao and Ruan [12] proposed an SIRS epidemic model with non-monotonic incidence function 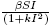 . A general saturation incidence function
. A general saturation incidence function 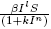 was proposed by Liu and coworkers [8], [9] and used by a number of authors. A incidence function with form
was proposed by Liu and coworkers [8], [9] and used by a number of authors. A incidence function with form 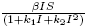 was studied in [6]. In [1] was introduced a model with incidence function
was studied in [6]. In [1] was introduced a model with incidence function 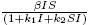 . So with our incidence rate can analyze similar situations, but in the non-autonomous case.
. So with our incidence rate can analyze similar situations, but in the non-autonomous case.
In this paper we are interested in the existence of periodic orbits for system (1). To do so, we shall use the Leray-Schauder degree theory, we reformulate the problem in a functional setting, in our development we generalize the Katriel’s frame [7] to our context of quarantined system with saturated incidence rate making appropriate adjustments. In particular, we must adapt its scheme to three dimensional systems, use a Hurwitz condition to control the roots of a characteristic polynomial, also we need use a second homotopy to deal with the term of saturation. In the study of epidemiological models the analysis of periodic solutions is seen as an important goal as this periodicity reveals the recurrence of an epidemic in a population. Hence, determining existence of such solutions under different parameter configurations and incidence functions is crucial.
2. Existence of periodic orbits
The total population size N is variable with N ′ = Λ − dN − α(I + Q). Following [5] we can see that, in the absence of disease, the population size N approaches the carrying capacity Λ/d. The differential equation for N implies that solutions of (1) starting in the positive orthant R 3 + either approach, enter, or remain in the subset of R 3 defined by
Thus it suffices to consider solutions in the region Σ.
The system (1) always has the disease-free equilibrium (S 0, I 0,Q 0) = (Λ/d, 0, 0). The basic reproductive number R 0 has been defined as the average number of secondary infections that occur when one infective is introduced into a completely susceptible host population. When β is constant, it is easily computed by the van den Driessche and Watmough approach [11]: for system (1) we have that
a direct calculation yields
Motivated by this, we consider R 0 for system (1) as follows:
We write
The proof of the existence of periodic orbits for systems of type (1) will be done in two steps. First, we consider the bilinear case ki = 0,
and prove the existence of solutions on this system. Then, we construct an homotopy between (2) and (1).
For λ ∈ [0, 1] we define the homotopy
where βλ: = β̅ + λβ0(t).
To show the existence of a positive periodic solution, we shall use the Leray-Schauder degree theory. To do so, we need to reformulate our system as a functional problem defined on an adequate Banach space where periodic solutions correspond to the zeroes of convenient family of operators. Then, we need to find an open bounded subset on the Banach space such that the family of operators does not support zeroes on the boundary of such open set. After that, we can proceed to determine the Leray-Schauder degree and, if applicable, establish the existence of periodic solutions. In our methods, we are following the approach used in [7], but we establish suitable modifications for the nonlinear incidence case, in particular, we need to use a double homotopy, in the first we work with the linear incidence case, so, we must adapt its scheme to three dimensional systems unlike [7] where it was possible to reduce the problem to a two-dimensional system; after that, for to estimate the Leray-Schauder degree we use a Hurwitz condition to control the roots of a characteristic polynomial; later in our context, we shall use a second homotopy to deal with the saturation term.
We start the proof by introducing for l = 0, 1 the Banach spaces
Cl T : = {(S, I,Q) : S, I,Q ∈ Cl (R,R), S(t + T ) = S(t), I(t + T ) = I(t),Q(t + T ) = Q(t)}.
Let L: C 1 T → C 0 T and Nλ : C 0 T → C 0 T be the operators given by
and
Since L is invertible we define
Since C 1 T is compactly embedded in C 0 T , we can think of L −1 as going from C 0 T to C 0 T ; therefore, L −1 ◦ Nλ : C 0 T → C 0 T is a compact operator. In a similar fashion, we can consider Fλ : C 0 T → C 0 T . Thus, (5) is a functional reformulation of problem (3); in particular, periodic solutions of (3) correspond to zeroes of Fλ .
We consider the open sets
and
for a fixed r.
Recall that the existence of a solution for F 1 in G via Leray-Schauder degree is guaranteed if deg(F 0,G) ≠ 0 and Fλ is an admissible homotopy, i.e., 0 ∉ Fλ (∂G), ∀ λ ∈ [0, 1]. The next result says that Fλ is admissible.
Lemma 2.1.
If R
0 > 1 and r is such that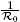 < r < 1, then for any λ ∈ [0, 1] there are no solutions (S, I,Q) of (3) on ∂G.
< r < 1, then for any λ ∈ [0, 1] there are no solutions (S, I,Q) of (3) on ∂G.
Proof. First note that (S 0, I 0,Q 0) is the only solution of (3) on ∂D for any λ ∈ [0, 1]. If (S, I,Q) ∈ ∂G, then (S, I,Q) ∉ ∂D, so
By integrating the second equation in (3) on the interval [0, T ], we have that
but 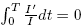 because I is T -periodic; using the inequality (6) one gets
because I is T -periodic; using the inequality (6) one gets
Now, from our hypothesis,
which is a contradiction. ☑
By Theorem 2 in [5], when λ = 0, the system (3) has exactly two periodic orbits in Σ being these: S 0 = Λ/d, I 0 = 0,Q 0 = 0 and
which in fact are critical points.
We recall that a polynomial is Hurwitz if its eigenvalues have negative real parts. It is well known that if the characteristic polynomial of a linear differential equation is Hurwitz, then any solution converges to the origin, therefore the unique possible periodic solution that a linear system with Hurwitz characteristic polynomial can have is the origin. The following lemma, which is a direct consequence of the Routh-Hurwitz stability criterion, gives us a characterization so that a cubic polynomial is Hurwitz.
Lemma 2.2. The polynomial p(z) = a 0 z 3 + a 1 z 2 + a 2 z + a 3 is Hurwitz if and only if ai have the same sign and a 1 a 2 − a 3 a 0 > 0.
The following result determine the degree of F 0 on G.
Proposition 2.3. For the open set G, we have that deg(F 0,G) ≠ 0.
Proof. Note that if R 0 > 1, then (S 1, I 1,Q 1) is the unique periodic solution of F 0(S, I,Q) = 0 in G. So, to establish the degree deg(F 0,G) ≠ 0 we need only to prove that DF 0(S 1, I 1,Q 1) is invertible. We have that F0 is a compact perturbation of the identity, so by the Fredholm alternative it is enough to prove that
Consider (U, V,W) ∈ C 0 T so that (U, V,W) ∈ Ker(DF 0(S 1, I 1,Q 1)); by the definition of F 0, we get that L(U, V,W) = DN 0(S 1, I 1,Q 1)(U, V,W), since
Then, we obtain
Using the definition of
we get
Rewriting and substituting S 1, we have
Thus any possible periodic element (U, V,W) ∈ Ker(DF 0(S 1, I 1,Q 1)) is in fact a solution of the linear system (9). Therefore it would be enough for us to see that the characteristic polynomial of (9) is Hurwitz.
Denoting by A = (aij ) the above matrix, we have that its characteristic polynomial is given by
where m: = M 11 + M 22 + M 33, the sum of the minors for the elements of the main diagonal. We have
and
hence,
Note that tr(A),−m and det(A) are negative, thus all coefficients of the characteristic polynomial are negative; therefore, to apply Lemma 2.2 we need to verify that
So,
Thus the inequality (14) is valid, and by Lemma 2.2 the characteristic polynomial of system (9) is Hurwitz. So the periodic element (U, V,W) is solution of (9) and as any solution of this system converges to the origin by having a characteristic Hurwitz polynomial, then the only option is that (U, V,W) = (0, 0, 0), which proves the result. ☑
Thus we have established our first result
Theorem 2.4. If R 0 > 1, then the system (2) admits a non-trivial periodic solution.
Proof. Using the invariance of the Leray-Schauder degree under homotopy by Lemma 2.1 and Proposition 2.3 we obtain that deg(F 1,G) ≠ 0, then the system (2) admits a non-trivial periodic solution, which proves Theorem 2.4. ☑
2.1. Saturated case
We now establish the existence of periodic solutions in the case of saturated system (1), when k > 0. Assume that 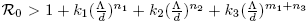 ; then, by taking (and for the rest of the work) in Theorem 2.4
; then, by taking (and for the rest of the work) in Theorem 2.4
we obtain that deg(F 1,G) ≠ 0.
For τ ∈ [0, 1] we define the homotopy
where B: = k 1 In 1 + k 2 In 2 + k 3 Sm 1 In 3 . We consider the operator Mτ : C 0 T → C 0 T given by
Taking L as (4), we define
Thus, (17) is a functional reformulation of problem (1); in particular, periodic solutions of (1) correspond to zeroes of Hτ . Note that H 0 = F 1, therefore deg(H 0,G) ≠ 0. Recall that the existence of a solution for H 1 in G is guaranteed via Leray-Schauder degree if deg(H 0,G) ≠ 0 and Hτ is an admissible homotopy, i.e., 0 ∉ Hτ (∂G), ∀τ ∈ [0, 1]. So we need only establish that Hτ is an admissible homotopy.
Lemma 2.5.
If , then for any τ ∈ [0, 1] there are no solutions (S, I,Q) of (16) on ∂G.
, then for any τ ∈ [0, 1] there are no solutions (S, I,Q) of (16) on ∂G.
Proof. Note that if (S, I,Q) ∈ ∂G, then (S, I,Q) ∉ ∂D; therefore,
Multiplying by (1 + τB)/I and integrating the second equation in (16) on the interval [0, T ], we have that
Now, from our hypothesis,
which is a contradiction. Hence Hτ is an admissible homotopy. ☑
By combining our observations we get:
Theorem 2.6.
If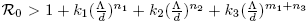 , then there is at least one T -periodic orbit of (1) whose components are positive.
, then there is at least one T -periodic orbit of (1) whose components are positive.
2.2. Examples
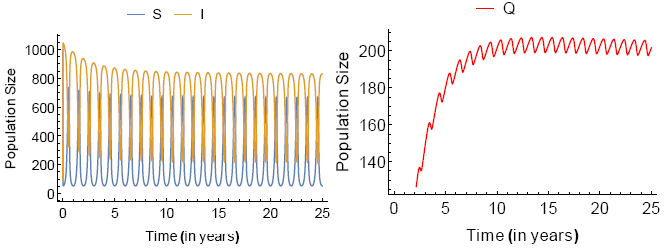
We now provide numerical evidence of the existence of periodic solutions.
Example 2.7.
where parameters are determined by Λ = 22, d = 0.0001, γ = 15, δ = 0.095, ∊ = 0.28999 and α = 0.026. The incidence function is determined by β(t) = 0.15 (1 + 0.92 cos(2πt)).
Example 2.8.
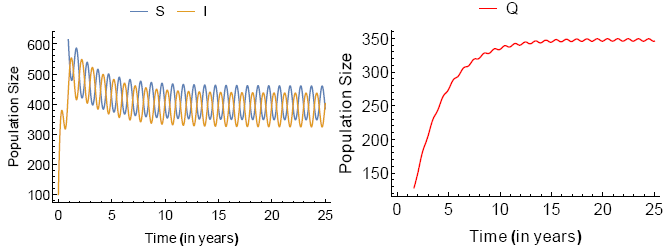
where parameters are determined by Λ = 22, d = 0.001, γ = 0.8, δ = 0.2, ∊ = 0.19, k = 0.8 and α = 0.029. The incidence function is determined by β(t) = 0.8 (1 + 0.92 cos(2πt)).
Example 2.9.
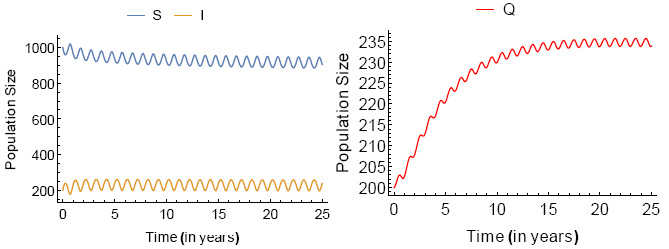
where parameters are determined by Λ = 1.5, d = 0.0001, γ = 0.2, δ = 0.199, ∊ = 0.19, k = 0.0009 and α = 0.005. The incidence function is determined by β(t) = 0.5 (1 + 2 cos(2πt)).
3. Conclusions
Public health policies have consequences in the behaviour of infectious diseases; in particular, the strategy of quarantine. Feng and Thieme pointed out in [3], [4], that the quarantine process could contribute to sustained oscillations in diseases by combining with other factors such as seasonal variation in the contact rates, stochastic effects, and density dependent demographics.
In our work, we establish analytically the occurrence of sustained oscillations in the some epidemiological model with the quarantine and periodic contact rate. We exhibit numerical evidence of the existence of such periodic solutions by means of numerical simulations of convenient SIQS epidemiological models.