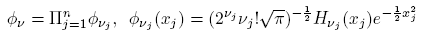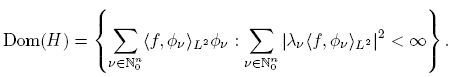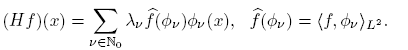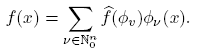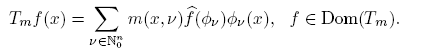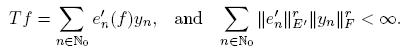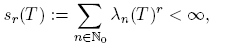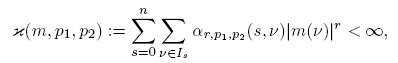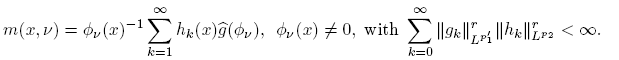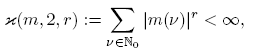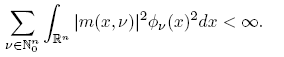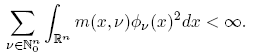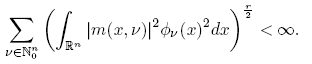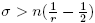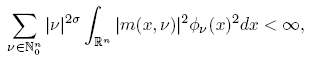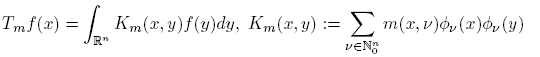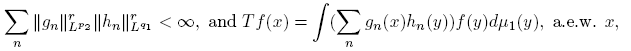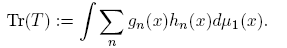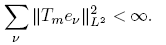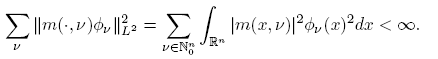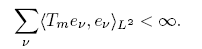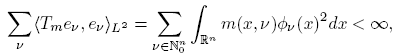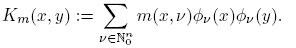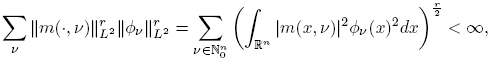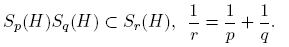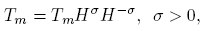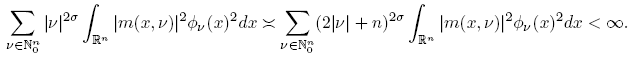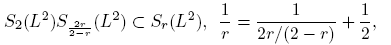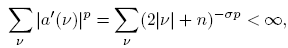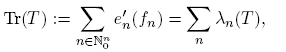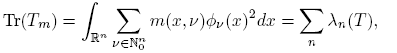1. Introduction
1.1. Outline of the paper
Pseudo-multipliers and multipliers associated to the harmonic oscillator arise from the study of Hermite expansions for complex functions on R n (see Thangavelu [23], [24], [25], [26] [27], [28], Epperson [11] and Bagchi and Thangavelu [1]). At the same time, we note that pseudo-multipliers are pseudo-differential operators on R n in view of the quantization process developed by Ruzhansky and Tokmagambetov in [17] and [18] when the reference operator is the harmonic oscillator. In this note, we are interested in the membership of pseudo-multipliers associated to the harmonic oscillator (also called Hermite pseudo-multipliers) in the Schatten classes, Sr (L 2) on L 2(R n ). With this paper we finish the classification of pseudo-multipliers in classes of r-nuclear operators on Lp -spaces (see Barraza and Cardona [2], [3]), which on L 2(R n ) coincide with the Schattenvon Neumann classes of order r. Our main result is Theorem 1.1 where we establish some criteria in order that pseudo-multipliers belong to the classes Sr (L 2), 0 < r ≤ 2. In order to present our main result we recall some notions. Let us consider the sequence of Hermite functions on R n ,
where x = (x 1, ・ ・ ・ , xn ) ∈ R n , ν = (ν 1, ・ ・ ・ , νn ) ∈ N n 0 , and Hνj (xj ) denotes the Hermite polynomial of order νj . It is well known that the Hermite functions provide a complete and orthonormal system in L 2(R n ). If we consider the operator L = −Δ + |x|2 acting on the Schwartz space S(R n ), where Δ is the standard Laplace operator on R n , then we have the relation LΦν = λνΦν , ν ∈ N n 0 . The operator L is symmetric and positive in L 2(R n ) and admits a self-adjoint extension H whose domain is given by
So, for f ∈ Dom(H), we have
The operator H is precisely the quantum harmonic oscillator on R n (see [15]). The sequence {fˆ(Φv )} determines the Fourier-Hermite transform of f, with corresponding inversion formula
On the other hand, pseudo-multipliers are defined by the quantization process that associates to a function m on R n × N n 0 a linear operator Tm of the form
The function m on R n × N n 0 is called the symbol of the pseudo-multiplier Tm . If in (5), m(x, ν) = m(ν) for all x, the operator Tm is called a multiplier. Multipliers and pseudomultipliers have been studied, for example, in the works [1], [20], [21], [22], [23], [24] (and references therein) principally by its mapping properties on Lp spaces. In order that the operator Tm : L 2(R n ) → L 2(R n ) belongs to the Schatten class Sr (L 2), in this paper we provide some (sharp) conditions on the symbol m.
1.2. Pseudo-multipliers in Schatten classes
By following A. Grothendieck [12], we can recall that a linear operator T: E → F (E and F Banach spaces) is r-nuclear, if there exist sequences (e′n ) n∈N₀ in E′ (the dual space of E) and (yn ) n∈N₀ in F such that
The class of r−nuclear operators is usually endowed with the quasi-norm
In addition, when E = F is a Hilbert space and r = 1 (resp. r = 2), the definition above agrees with the concept of trace class operators (resp. Hilbert-Schmidt). For the case of Hilbert spaces H, the set of r-nuclear operators agrees with the Schatten-von Neumann class of order r (see Pietsch [13], [14]). We recall that a linear operator T on a Hilbert space H belong to the Schatten class of order r, Sr(H), if
where {λn (T )} denotes the sequence of singular values of T, which are the eigenvalues of the operator √T ∗T. It was proved in [2] that a multiplier Tm , with symbol satisfying conditions of the form
where {Is } n s =0 is a suitable partition of N n 0 , and αr ,p₁,p₂(s, ν) is a suitable kernel, can be extended to a r-nuclear operator from Lp ₁(R n ) into Lp ₂ (R n ). Although is easy to see that similar necessary conditions apply for pseudo-multipliers, the r-nuclearity for these operators in Lp -spaces was characterized in [3] by the following condition:
a pseudo-multiplier Tm can be extended to a r-nuclear operator from Lp ₁ into Lp ₂ if and only if there exist functions hk and gk satisfying
If we consider p 1 = p 2 = 2, and a multiplier Tm , the conditions above can be replaced by the following more simple one,
because the set of singular values of a multiplier Tm
consists of the elements in the sequence 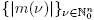 . The condition (10) characterizes the membership of pseudomultipliers in Schatten classes in terms of the existence of certain measurable functions. However, in this paper we provide explicit conditions on m in order to guarantee that Tm
∈ Sr
(L
2), because explicit conditions allow us to known information about the distribution of the spectrum of these operators. Our main result is the following theorem.
. The condition (10) characterizes the membership of pseudomultipliers in Schatten classes in terms of the existence of certain measurable functions. However, in this paper we provide explicit conditions on m in order to guarantee that Tm
∈ Sr
(L
2), because explicit conditions allow us to known information about the distribution of the spectrum of these operators. Our main result is the following theorem.
Theorem 1.1. Let Tm be a pseudo-multiplier with symbol m defined on R n × N n 0 . Then we have:
In general, on a Banach space compact linear operators are bounded operators. Taking into account that Schatten-von Neumann classes on Hilbert spaces are families of compact operators, our main theorem gives conditions for the L 2(R n )-continuity of pseudomultipliers. The problem of finding “satisfactory” conditions for the L 2(R n )-boundedness of pseudo-multipliers remains open, and it was proposed by Bagchi and Thangavelu in [1]; with our main result and the conditions proposed in Cardona and Barraza [3], we solve partially such problem. However, Bagchi-Thangavelu’s problem will be “satisfactorily” solved in the work Cardona and Ruzhansky [4].
1.3. Related works
Now, we include some references on the subject. Sufficient conditions for the r-nuclearity of spectral multipliers associated to the harmonic oscillator, but in modulation spaces and Wiener amalgam spaces, have been considered by J. Delgado, M. Ruzhansky and B. Wang in [8], [9]. The Properties of these multipliers in Lp -spaces have been investigated in the references S. Bagchi, S. Thangavelu [1], J. Epperson [11], K. Stempak and J.L. Torrea [20], [21], [22], S. Thangavelu [23], [24] and references therein. Hermite expansions for distributions can be found in B. Simon [19]. The r-nuclearity and Grothendieck-Lidskii formulae for multipliers and other types of integral operators can be found in [7], [9]. On Hilbert spaces the class of r-nuclear operators agrees with the Schatten-von Neumann class Sr (H); in this context operators with integral kernel on Lebesgue spaces and, in particular, operators with kernel acting of a special way with anharmonic oscillators of the form Ea = −Δ x + |x| a , a > 0, has been considered on Schatten classes on L 2(R n ) in J. Delgado and M. Ruzhansky [10]. A complete treatment for Lp -boundedness and Lp -compactness properties in terms of the Littlewood-Paley theory and the Hörmander condition will be considered in Cardona and Ruzhansky [4]. The proof of our results will be presented in the next section.
2. Pseudo-multipliers in Schatten-von Neumann classes
In this section we prove our main result for pseudo-multipliers Tm . Our criteria will be formulated in terms of the symbols m. First, let us observe that every pseudo-multiplier Tm is an operator with kernel Km (x, y). In fact, straightforward computation shows that
for every f ∈ D(R n ). We will use the following result (see J. Delgado [5], [6]).
Theorem 2.1.
Let us consider 1 ≤ p
1, p
2 < ∞, 0 < r ≤ 1 and let qi be such that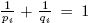 . Let (X
1, μ
1) and (X
2, μ
2) be σ-finite measure spaces. An operator T: Lp
₁(X
1, μ
1) →Lp
₂ (X
2, μ
2) is r-nuclear if and only if there exist sequences (gn
)
n in Lp
₂(μ
2), and (hn
) in Lp
₁ (μ
1), such that
. Let (X
1, μ
1) and (X
2, μ
2) be σ-finite measure spaces. An operator T: Lp
₁(X
1, μ
1) →Lp
₂ (X
2, μ
2) is r-nuclear if and only if there exist sequences (gn
)
n in Lp
₂(μ
2), and (hn
) in Lp
₁ (μ
1), such that
for every f ∈Lp ₁ (μ 1). In this case, if p 1 = p 2 (see Section 3 of [5]) the nuclear trace of T is given by
Now, we prove our main theorem.
Proof of Theorem 1.1. Let us consider a pseudo-multiplier Tm . By definition, Tm is a Hilbert-Schmidt operator if and only if there exists an orthonormal basis {eν } ν of L 2(R n ) such that
In particular, if we choose the system of Hermite functions {Φν }, which provides an orthonormal basis of L 2(R n ), from the relation Tm (Φν ) = m(x, ν)Φν we conclude that Tm is of Hilbert-Schmidt type, if and only if
So, we have proved the first statement. Now, if we assume that Tm is positive, then Tm is of class trace if and only if there exists an orthonormal basis {eν } ν of L 2(R n ) such that
As in the first assertion, if we choose the basis formed by the Hermite functions, Tm is of class trace if and only if
which proves the second assertion. Now, we will verify that (14) implies that Tm ∈ Sr (L 2) for 0 < r ≤ 1. For this, we will use Delgado’s Theorem (Theorem 2.1) to the representation (16) of Km ,
So, Tm ∈ Sr (L 2) if
where we have used that the L 2−norm of every Hermite function Φν is normalised. In order to finish the proof, we only need to prove that (15) assures that Tm ∈ Sr (L 2) for 1 < r < 2. This can be proved by using the following multiplication property on Schatten classes:
So, we will factorize Tm as
where H is the harmonic oscillator. Let us note that the symbol of A = TmHσ is given by a(x, ν) = m(x, ν)(2|ν| + n) σ . So, from the first assertion, A ∈ S 2(L 2) if and only if
In order to prove that Tm ∈ Sr (L 2), in view of the multiplication property
we only need to prove that H
−σ
∈ Sp
(L
2) with 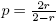 . The symbol of H
−σ
is given by a′(ν) = (2|ν| + n)−σ
. By using the hypothesis
. The symbol of H
−σ
is given by a′(ν) = (2|ν| + n)−σ
. By using the hypothesis 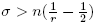 we have that
we have that
because 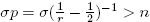 . So, we finish the proof. ☑
. So, we finish the proof. ☑
2.1. Trace class pseudo-multipliers of the harmonic oscillator
In order to determinate a relation with the eigenvalues of Tm we recall the following result (see [16]).
Theorem 2.2.
Let T: Lp
(μ) → Lp
(μ) be a r-nuclear operator as in (6). If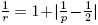 , then,
, then,
where λn (T ), n ∈ N, is the sequence of eigenvalues of T with multiplicities taken into account.
As an immediate consequence of the preceding theorem (or the classical Grothendieck-Lidskii Theorem), if Tm : L 2(R n ) → L 2(R n ) is trace class (1-nuclear) then,
where λn (T ), n ∈ N, is the sequence of eigenvalues of Tm with multiplicities taken into account.