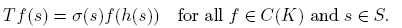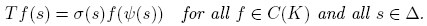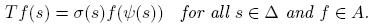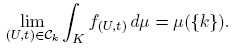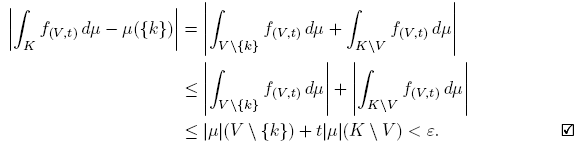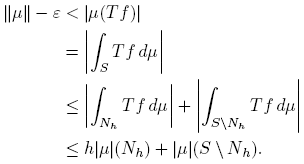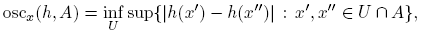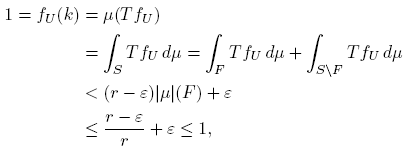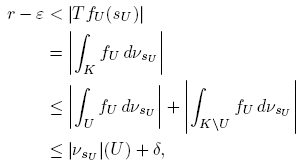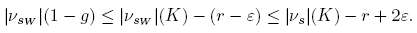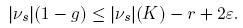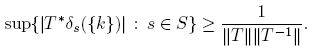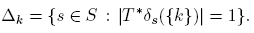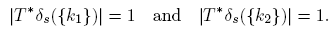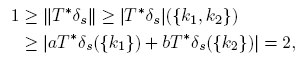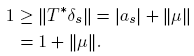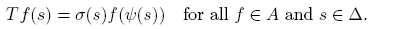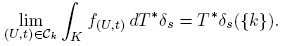1. Introduction and main theorems
We will use the standard terminology and notation of Banach space theory. For unexplained definitions and notation we refer to [1], [2], [3], [4], [5], [6], [7], [8], [9], [10]. As usual K stands for the field R or C. For a compact Hausdorff space K, we denote by C(K) the Banach space of K-valued continuous functions on K, provided with the supremum norm.
The classical Banach-Stone theorem states that the Banach space C(K) determines the topology of K [3], [4], [5], [11]. More precisely, if T: C(K) → C(S) is an onto isometry, then there are a homeomorphism h: S → K and a continuous function σ: S → K with |σ(s)| = 1 for all s ∈ S such that
The conclusion of the Banach-Stone theorem is too far to be valid when we consider into isomorphisms between C(K) spaces. Thus it seems natural to ask for topological properties which are preserved under into isomorphisms of C(K) spaces. In this direction, Holsztyński [8] proved:
Theorem 1.1. Let K and S be compact Hausdorff spaces. If T: C(K) → C(S) is an into isometry, then there are a closed subset Δ of S, a continuous surjection ψ: Δ → K and a continuous function σ: Δ → K with |σ(s)| = 1 for all s ∈ Δ such that
In [2], it is established the following generalization of Theorem 1.1 for extremely regular spaces. According to [6], a closed subspace A of C(K) is called extremely regular if for each k ∈ K and each neighborhood U of k and each 0 < ε < 1, there exists f ∈ A satisfying ║f║ = f(k) = 1 and |f(w)| < ε for all w ∈ K \ U.
Theorem 1.2. Let K and S be compact Hausdorff spaces. Let A be an extremely regular subspace of C(K) and B a closed subspace of C(S). Suppose that T: A → B is an into isometry. Then there exist a closed subset Δ of S, a continuous function ψ from Δ onto K and a continuous function σ: Δ → K with |σ(s)| = 1 for all s ∈ Δ such that
The aim of this note is to give an alternative proof of Theorem 1.2. The paper is divided as follows: in the second section we generalize a result which is proved by Plebanek in the setting of C(K) spaces (see [9, Theorem 3.3]). In third section, we prove Theorem 1.2.
2. Preliminaries
Following [7, p. 222], we identify dual space C(K)* with the space of regular countably additive bounded measures, and we denote it by M(K). We always consider M(K) equipped with the weak* topology inherited from C(K)*. The total variation of a measure μ ∈ M(K) on a Borel set E is denoted by |μ|(E), and its norm by ║μ║ = |μ|(K).
Let K and S be compact Hausdorff spaces. Throughout the paper A denotes an extremely regular subspace of C 0(K). Also B will be a closed subspace of C(S). If s ∈ S is fixed and T: A → B is an embedding, νs will denote any norm-preserving extension to C(K) of the functional T*δs : A → R defined as T*δs (f) = T f(s) for f ∈ A. Also let us assume that T satisfies r║f║ ≤ ║T f║ ≤ ║f║ for all f ∈ A, where r > 0. Analogously if E = TA ⊂ B and k ∈ K is given, let μk be any norm-preserving extension to C(S) of the functional (T −1)*δk : E → R.
Before stating our first result, we need to establish a notation.
Let k ∈ K be given and Vk any fundamental system of open neighborhoods of k. Consider the set Ck = Vk × (0,∞). In Ck we define a partial order as follows: (U, t) ≺ (V, s) iff V ⊂ U and s < t. Note that (Ck ,≺) is a directed set. It is easy to see that there exists a net (f (U,t))(U,t)∈Ck in A satisfying
We will write {(U, t), f (U,t)}(U,t)∈Ck ↔ {k} to indicate that the above conditions are satisfied.
Lemma 2.1. Let A be an extremely regular subspace of C(K) and k ∈ K given. Suppose that {(U, t), f (U,t)}(U,t)∈Ck ↔ {k}. If μ ∈ M(K), then
Proof. The statement is obvious if ║μ║ = 0, so we assume that ║μ║ ≠ 0. Let ε > 0 be given. Since |μ| is regular, there is W ⊂ K open with k ∈ W such that |μ|(W\{k}) < ε/2. Let U 0 ∈ Vk be such that U 0 ⊂ W. If (U 0, ε/2║μ║) ≺ (V, t), we have
The next two results are proved in [9] for C(K) spaces. However, we noted that they are also valid for extremely regular subspaces of C(K). So, for sake of completeness we include a proof here.
Lemma 2.2. Let k ∈ K be fixed. If μ = μk , then ║νs ║ ≥ r μ-almost everywhere.
Proof. Let N = {s ∈ S: ║δs | E ║ < 1}. We show that μ(N) = 0. For 0 < h < 1, define Nh = {s ∈ S: ║δs | E ║ ≤ h}; then Nh is closed and N = ∪ h<1 Nh . It suffices to prove that |μ|(Nh ) = 0 for all h ∈ (0, 1). If ε > 0 is given, then there is f ∈ A with ║T f║ ≤ 1 such that ║μ║ − ε < |μ(T f)|. Thus,
Since ║μ║ = |μ|(Nh ) + |μ|(S \ Nh ), we infer that |μ|(Nh ) ≤ ε/1 − h. Thus, |μ|(Nh ) = 0, by the arbitrariness of ε.
Now let s ∈ S \ N; then ║δs | E ║ ≥ 1. For a positive number ε there exists f ∈ A with ║T f║ ≤ 1 such that |T f(s)| > 1 − ε. From the fact ║f║ ≤ 1/r, we infer that r(1 − ε) < ║νs ║. So, the result follows when ε → 0. ☑
If h is a real valued function defined on a topological space X, the oscillation of h at x on a set A is
where the infimum is taken over all open neighborhoods U of x.
Lemma 2.3. Let k ∈ K and ε > 0 be fixed. Consider the measure μ = μk. Suppose that there is a compact subset F of S such that
Then, there is s ∈ F such that |νs ({k})| ≥ r − 2ε.
Proof. Let δ > 0 be given and let U ⊂ K be open with k ∈ K. Since A is extremely regular, there exists fU ∈ A such that ║fU ║ = fU (k) = 1 and |fU (w)| < δ for all w ∈ K \ U. We will show that there is sU ∈ F satisfying |T fU (sU )| > r − ε. Indeed, if |T fU (s)| < r − ε for all s ∈ F, then
which is absurd. Now if sU ∈ F satisfies |T fU (sU )| > r − ε, then
since ║νsU ║ = ║T *δsU ║ ≤ 1. So if δ → 0, then r−ε ≤ |νsU |(U). Let Vk be a fundamental system of open neighborhoods of k and consider the net (sU ) U∈ Vk in F. Since F is compact, there is a subnet (sU ) U∈W converging to s ∈ F. By (2), so we may assume that ║νsU ║ ≤ ║νs ║ + ε for all U ∈ W.
Now, if U ⊂ K is open with k ∈ U, then we have |νs |(U) ≥ r − 2ε. Indeed, by Urysohn Lemma [7, Proposition 4.32] there exists g: K → [0, 1] continuous such that g = 1 on an open set V containing k and g = 0 outside U. Thus, if W ∈ W satisfies W ⊂ V , then |υsW |(g) ≥ |υsW |(W) ≥ r − ε. Whence,
Since νsW → νs in the weak* topology, by [9, Lemma 2.1] and the above inequality we have
Therefore, |νs |(U) ≥ |νs |(g) ≥ r − 2ε. Regularness of νs implies |νs ({k})| ≥ r − 2ε, and the proof is complete. ☑
The proof of the next result follows as in [9, Theorem 3.3] by using Lemmas 2.2 and 2.3.
Theorem 2.4. Let K and S be compact Hausdorff spaces. Suppose that T : A → B is an embedding. For each k ∈ K we have
3. Proof of Theorem 1.2
Since T is an isometry we have ║T ║ = ║T −1║ = 1. For k ∈ K we set
By Theorem 2.4 we have Δ k ≠ ∅ for each k ∈ K.
Claim 3.1. If k 1, k 2 ∈ K and k 1 ≠ k 2, then Δ k₁ ∩ Δ k₂ = ∅.
If not, let s ∈ S be such that s ∈Δ k₁ ∩ Δ k₂ . Then
By taking a, b ∈ K with aT*δs ({k 1}) = 1 and bT *δs ({k 2}) = 1, we infer from definition of variation that
which is absurd. This proves the claim.
Claim 3.2. Let k ∈ K be given. If s ∈ Δ k , then there is as ∈ K with |as | = 1 such that T f(s) = asf(k) for all f ∈ A.
Indeed, if s ∈ Δ k , then as = T *δs ({k}) ∈ K and |as | = 1. On the other hand, T *δs = asδk + μ, where μ ∈ M(K) satisfies μ({k}) = 0. So, it follows that
So, ║μ║ = 0, which means that μ = 0. Hence T *δs = asδk , that is, T f(s) = asf(k) for all f ∈ A, as claimed.
Set Δ = ∪ k∈K Δ k , and let ψ: Δ → K and σ: Δ → K be defined as ψ(s) = k and σ(s) = as , respectively, iff s ∈ Δ k , where as is determined as in Claim 3.2. Note that ψ is well-defined by Claim 3.1. The surjectivity of ψ is consequence from the fact Δ k ≠ ∅ for each k ∈ K. Clearly, |σ(s)| = 1 for all s ∈ S. Also, by Claim 3.2 we have
Claim 3.3. ψ: Δ → K and σ: Δ → K are continuous.
Let s ∈ Δ be given and (sα ) a net in Δ such that sα → s. Suppose that ψ(sα ) = kα ↛ ψ(s) = k. Thus, there is a compact neighborhood V ⊂ K of k such that for all α, there is α ′ ≥ α with kα ′ ∉ V . Since A is extremely regular, there exists f ∈ A such that ║f║ = f(k) = 1 and |f(w)| < 1/2 for all w ∈ K \ V . Note that |T f(s)| = |f(ψ(s))| = |f(k)| = 1. By continuity of T f, there is α0 such that |T f(sα )| > 1/2 for all α ≥ α 0. By taking α ′ ≥ α 0 with kα′ ∉ V , we have 1/2 > |f(kα ′ )| = |f(ψ(sα ′ ))| = |T f(sα ′)| > 1/2, which is impossible.
Now we prove continuity of σ. Let s ∈ Δ be given and ψ(s) = k. Take f ∈ A such that ║f║ = f(k) = 1. By Equation (2) we have σ(s) = T f(s), and continuity follows immediately.
Claim 3.4. Δ is closed.
Let (sα ) be a net in Δ and suppose that sα → s for some s ∈ S. Write ψ(sα ) = kα for all α. By compactness of K, we may assume that kα → k for some k ∈ K. By Claim 3.2 we have |T f(sα )| = |f(ψ(sα ))| = |f(kα )| for all f ∈ A. Thus, |T f(s)| = |f(k)| for all f ∈ A. Let (f (U,t))(U,t)∈Ck be a net in A such that {(U, t), f (U,t)}(U,t)∈ Ck ↔ {k}. Then |T f (U,t)(s)| = |f (U,t)(k)| = 1 for all (U, t) ∈ Ck . Once again by Lemma 2.1, we have
So, |T *δs ({k})| = 1, that is, s ∈ Δ.