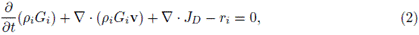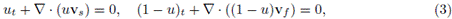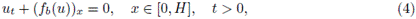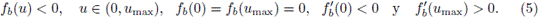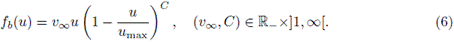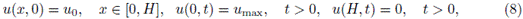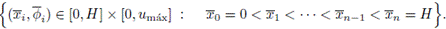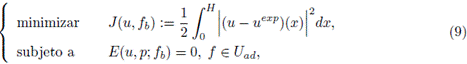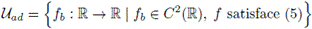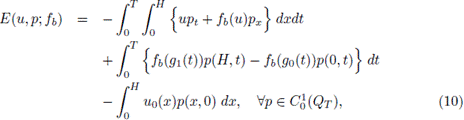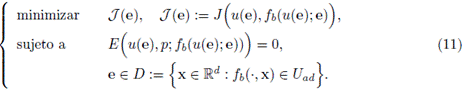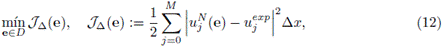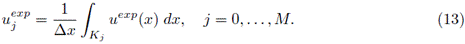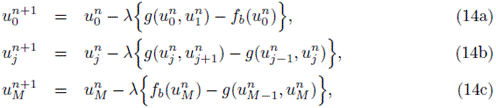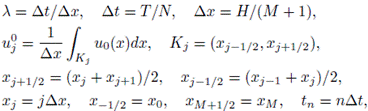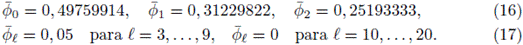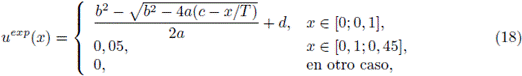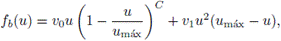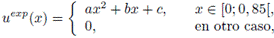Español (pdf)
Articulo en XML
Referencias del artículo
Traducción automática
Enviar articulo por email
Citado por SciELO 
Citado por Google 
Similares en
SciELO 
Similares en Google 
Permalink
1. Introducción
La sedimentación es un proceso mecánico utilizado para la separación de una mezcla de tipo sólido-fluido. Su gran utilidad en los procesos industriales la convierte en un fenómeno relevante para la investigación científica (ver [5]). Los lineamientos de la teoría de sedimentación para materiales incompresibles fueron establecidos inicialmente por Kynch [16]. Esta teoría introduce las condiciones bajo las cuales los procesos de sedimentación pueden ser modelados utilizando una ecuación de transporte no lineal unidimensional, o más precisamente una ley de conservación escalar. Estas hipótesis, a pesar de ser ideales, fundamentan de manera muy razonable la explicación del fenómeno. Actualmente, existen diversas extensiones de esta teoría; los principales aspectos históricos de la evolución de esta teoría aparecen detallados en [4], [5], [6].
La componente principal de una ley de conservación es la función flujo, la cual describe las propiedades del material utilizado dependiendo de la concentración de sólidos como una variable desconocida. En el problema de calibración del modelo se inicia con un perfil de concentración de sólidos en un tiempo fijo, bajo el supuesto de una forma paramétrica del flujo. La parametrización de la función flujo es una consecuencia de las ecuaciones constitutivas comprobadas empíricamente. El problema de calibración se formula como un problema de optimización, donde se busca un vector de parámetros que minimiza la distancia entre el perfil solución del modelo y el perfil observado.
El problema de calibración ha recibido una atención notable (ver [1], [2], [3], [20], [22], [24]). En [1], [2], [3] el problema de optimización fue resuelto numéricamente por un método de gradiente. En cambio, en [20], [22], [24] se aplican otras técnicas para la solución del problema inverso. La rigurosidad de la aproximación por el método de gradiente no ha sido tratada, porque se sabe que las soluciones entrópicas de las leyes de conservación escalares son funciones discontinuas, incluso bajo condiciones de alta regularidad en la condición inicial y la función de flujo. La baja regularidad de la solución de la ecuación de estado implica una baja regularidad en la función objetivo. En particular, la diferenciabilidad de la función objetivo es un asunto complicado.
En este artículo el problema de optimización se resuelve aplicando un algoritmo genético continuo. La función objetivo es discretizada utilizando la solución numérica del problema directo. La aproximación numérica natural del problema directo se obtiene mediante un método de volúmenes finitos, donde el flujo numérico es el de Engquist and Osher [7]. La función objetivo construida numéricamente no corresponde a un problema de optimización discreta. Por lo tanto, la aplicación de un algoritmo genético codificado de manera binaria conduce a un proceso de cálculo muy lento, y por ello se opta por utilizar un algoritmo genético codificado de manera continua (para mayores detalles consultar el libro de Haupt and Haupt [13] y también las referencias [10], [11], [14], [18]). El algoritmo propuesto para la calibración es aplicado a datos sintéticos. Este artículo es una versión sucinta de uno más extenso, donde el comportamiento del algoritmo es puesto a prueba en varios ejemplos.
El presente artículo está organizado en cuatro secciones. En la Sección 2 se presentan las hipótesis de modelamiento de Kynch, se establece el modelo matemático para la sedimentación y se esboza el algoritmo genético continuo. En la Sección 3 se presentan los resultados numéricos de la identificación de parámetros. Finalmente, en la Sección 4 se presentan algunas conclusiones.
2. Teoría
2.1. Balance de masa y momentum en una mezcla
La fundamentos de la teoría de mezclas dentro de la mecánica del medio continuo se establecen en los trabajos de Fick, Stefan y Maxwell. Sin embargo, la formalización en el marco teórico conocido actualmente fue establecida por Truesdell. Esta teoría supone que cada punto del espacio puede ser ocupado por un número finito de partículas diferentes, una para cada componente del sistema. En consecuencia, la mezcla puede ser representada como la superposición de varios medios continuos, cada uno de los cuales mantiene su propio movimiento junto con las restricciones impuestas por las interacciones. En la teoría de mezclas cada componente satisface una ecuación de equilibrio. Si se denota por Gi una propiedad extensiva por unidad de masa de la i-ésima componente de la mezcla con densidad pi, entonces
donde Ji es el flujo de densidad y ri es la razón de generación de la i-ésima componente por unidad de volumen. El flujo puede ser dividido en su parte convectiva y difusiva para establecer la ecuación
donde v es la velocidad promedio de la mezcla y J D es el flujo de difusión. La ecuación de equilibrio (2) se puede utilizar para derivar balances de masa y momento en varias aplicaciones.
2.2. Modelo matemático para la sedimentación
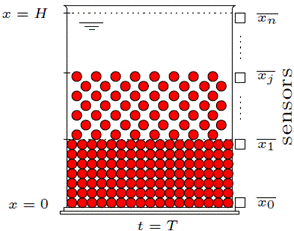
El modelo matemático de la sedimentación describe una mezcla de partículas sólidas sumergidas en un fluido (ver Figura 1 para una ilustración del proceso). Se asume que la mezcla satisface las siguientes propiedades:
(A1) Todas las partículas sólidas tiene el mismo tamaño, forma y densidad.
(A2) El sólido y el fluido de la mezcla son incompresibles. No hay transferencia de masa entre sus componentes.
(A3) La velocidad relativa sólido-líquido es vr = vs - vf, donde vs es la velocidad del sólido y vf es la velocidad del líquido, que depende solamente de la concentración local de sólidos u.
(A4) Los efectos de pared son despreciables.
Los balances de masa para la fase sólida y líquida son
respectivamente. Definiendo la velocidad volumétrica promedio
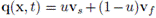y sumando ambas ecuaciones se obtiene que
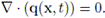A partir de las ecuaciones de balance de masa para las fases sólida y líquida se puede deducir que la ecuación diferencial del modelamiento de la sedimentación bath tiene la forma
donde H denota la altura de la mezcla contenida en la columna. De acuerdo con las evidencias empíricas, las propiedades que debe satisfacer la función de flujo son
En la práctica, esta restricción se impone de manera implícita mediante la elección de la forma paramétrica del flujo. En el ejemplo numérico se considera la función de flujo
Nótese que la negatividad
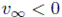satisface la restricción fb(u) < 0. Los tres parámetros identificados se establecen en el vector de parámetros
La ecuación (4) es hiperbólica no lineal de primer orden y debe ser complementada con condiciones iniciales y de frontera adecuadas. Bajo los supuestos de que la suspensión tiene una concentración inicial homogénea u0 y en la parte inferior del recipiente existe un incremento continuo pero rápidamente creciente de la concentración, iniciando desde u0 hasta la concentración máxima umax, se tienen las siguientes condiciones inicial y de frontera:
donde u0 y umax son constantes tales que 0 < u0 < umax < 1. En consecuencia, el modelo de sedimentación en la columna es dado por la ecuación (4) con condiciones inicial y de frontera dadas por (8) con la función de flujo satisfaciendo (6).
2.3. Problema inverso
Para la calibración del modelo (4),(5),(8) se dispone de un conjunto de datos experimentales medidos a lo largo de la columna en un tiempo fijo t = T (ver Figura 2). Los n sensores son asociados a localizaciones específicas denotadas por
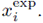. Los valores de la concentración de sólidos medidos en esos puntos son
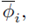lo cual significa que el conjunto de datos para la calibración del flujo es el siguiente:
En la práctica este conjunto de datos es ajustado por una curva, es decir se define
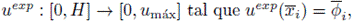que es denominado el perfil experimental. En términos de la información experimental el problema inverso de determinar la función de flujo es formulado en un ambiente abstracto como el problema de optimización
donde U ad es el conjunto admisible definido como
y E(u, p; f b ) es la formulación débil del problema (4),(5),(8), más precisamente,
donde
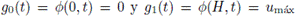son las soluciones en la frontera del intervalo [0, H], y p es una función test [1]. La forma débil (10) es obtenida a partir de (4) multiplicando por la función test p, integrando sobre [0,H] x [0, T] y utilizando integración por partes.
El problema (9) se reduce al problema de identificación de parámetros, donde se supone que la función de flujo es parametrizada por el vector de parámetros
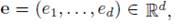, que significa que
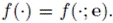En consecuencia, la identificación de parámetros se formula como el siguiente problema de optimización en varias variables:
2.4. Discretización de la función costo y del problema directo
La discretización de la función costo (11) es dada por
donde
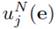para j ∈ {0,..., M} es la solución numérica de (4),(5),(8) en t = T, y los valores de
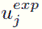son los correspondientes datos experimentales calculados por promediar la función interpolada u
exp sobre los intervalos
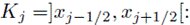
En efecto, en este trabajo, para determinar
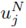se sigue lo detallado en [8], [17], [23] para la metodología de volúmenes finitos en leyes de conservación, y se considera el siguiente esquema de volúmenes finitos:
definida para n = 0,..., N y j = 1,..., M - 1, donde
y g es un flujo numérico de Engquist-Osher [7], es decir,
Además, por razones de estabilidad y convergencia del esquema numérico (14) es necesario considerar la condición de Courtant-Friedrichs-Lewy (abreviadamente condición CFL)
la cual limita el tamaño del paso de tiempo para el esquema explícito.
2.5. Algoritmo genético
Las técnicas de computación evolutiva imitan los principios de la selección natural (o la supervivencia de los más aptos) y la evolución. La base de la computación evolutiva está en los siguientes cuatro paradigmas: algoritmos genéticos [14], programación genética [15], estrategias evolutivas [19] y programación evolutiva [9]. Entre estas técnicas, los algoritmos genéticos son los más populares porque son, computacionalmente, más fáciles de implementar. Complementariamente, bajo ciertas condiciones, proporcionan convergencia global y otras venta jas detalladas en [21].
En lo que sigue se utilizará la terminología estándar de algoritmos genéticos. Para completar, presentamos algunas definiciones básicas; cromosoma, gen, población y generación. Mayores detalles se pueden consultar [13], [21].
Definición 2.1. Un cromosoma es un arreglo de los parámetros que deben ser identificados, es decir, donde la función objetivo es evaluada.
Definición 2.2. Un gen es cada una de las componentes del vector de parámetros.
Definición 2.3. Una población es un conjunto de cromosomas.
Definición 2.4. Una generación es la población que existe al final de cada iteración del algoritmo genético.
Los algoritmos genéticos más utilizados seleccionan entre una representación binaria o una continua (punto flotante) de los parámetros a identificar. En este artículo se opta por una representación continua, principalmente, porque son más rápidos cuando la función objetivo y las variables son continuas. Mayores detalles respecto de ventajas y desventajas de ambas representaciones se pueden encontrar, por ejemplo, en [13].
En este artículo se considera el siguiente algoritmo genético:
(a) Problación inicial. Se define la matriz que representa a la población aleatoria inicial
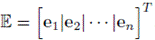donde cada fila
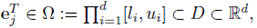con
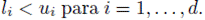Sea G el número máximo de iteraciones o de generaciones. Se inicializa el contador
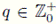en q = 0 y comienza una iteración de los pasos siguientes:
(b) Costo de la población. Se define el vector
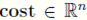mediante la evaluación de la función objetivo para cada cromosoma de la población
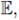es decir
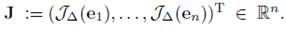Se define la matriz
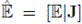Dado J
mín como una tolerancia preestablecida para la evaluación de la función objetivo, si existe
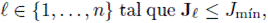entonces la solución del problema de minimización discreto es aproximada por
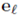y se detiene la iteración.
(c) Selección de los padres. Se escogen los padres en tres etapas. Primero, se actualiza
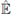permutando sus columnas hasta satisfacer la propiedad
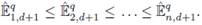. Segundo, si s ∈ (0,1] denota la tasa de selección, entonces se seleccionan las primeras [ns] columnas de
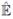y se almacena la submatriz en la denominada mating pool matrix F. Aquí, [·] denota al mayor entero más cercano. Tercero, aplicando la regla de la ruleta, se seleccionan los padres desde los cromosomas de
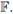
(d) Apareamiento. Se define la regla algebraica para el cruzamiento de los padres. En este artículo, se obtienen los nuevos cromosomas aplicando una combinación convexa aleatoria de los genes de los padres seleccionados mediante un punto de cruzamiento. El proceso de apareamiento se detiene cuando n - [ns] cromosomas son generados. Aquí, en este paso, la matriz de población
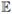se actualiza considerando que los padres se almacenan en las primeras [ns] filas y los nuevos en las siguientes.
(e) Mutación. Si µ ∈ [0,1] denota la tasa de mutación, se define el número total de mutaciones como m := [µ(n - 1)d]. Se repite m veces el siguiente proceso de mutación: el gen aleatorio
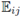se reemplaza por un número aleatorio perteneciente al intervalo [l
j, u
j]. Nótese que después de que finaliza la mutación, la matriz de población
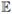se encuentra actualizada. Se incrementa q = q +1. Si q ≤ G, entonces ir al ítem (b), si no, calcular el vector J, y la solución es el cromosoma
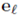tal que
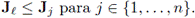
El hipercubo Ω considerado en el ítem (a) se puede reemplazar por un conjunto convexo tal que Ω ⊂ D. La hipótesis de convexidad se requiere para la combinación convexa utilizada en el ítem (d).
3. Resultados de la identificación
En esta sección se presenta la aplicación del algoritmo genético continuo para la identificación de parámetros de la función flujo fb. Para la identificación se utilizó la configuración de parámetros sugerida por Haupt y Haupt en [13]:
Se consideran dos ejemplos. En el Ejemplo 1 se estudian algunas propiedades del algoritmo genético, y en el Ejemplo 2 se identifica una función de flujo con mayor complejidad.
3.1. Ejemplo 1
Se supone que los sensores están ubicados en
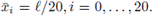En el ejemplo se considera la función de flujo definida en (6), donde se identifican los parámetros
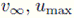y C, de acuerdo con (7). Para obtener los datos experimentales sintéticos se considera una simulación del problema directo con T = 3500, u
0
(x) = 0, 05, M = 800, v∞ = -2, 7 x 10-4, u
max = 0, 5 y C = 5. El conjunto de valores numéricos para la concentración que se obtiene mediante la simulación del problema directo son
Así se obtiene la siguiente función ajustada como perfil de observación en T = 3500:
Íb 2 - Jb 2 -4a(c-x/T) -y.-^-^ + xe[0;0,l], 0,05, a x G [0,1;0,45], [18] 0, en otro caso,
con a = 8, 29285e - 4, b = 7, 52058e - 4, c = 1, 69437 y d = 4,40647e - 1. Los valores numéricos de a, b, c, d se eligen de tal manera que la función (18) sea el mejor ajuste a los datos (16)-(17). Para el algoritmo genético se consideró
Ω = [-5e - 4, -5e - 5] x [2, 7] x [0, 1, 0, 6]
como el rango de búsqueda para el vector de parámetros a identificar e = (v∞, C, u max). En lo que sigue se reportan seis experimentos (desde (i) hasta (vi)) que muestran varias propiedades del algoritmo.
(i) Identificación de e = (v∞, C, u max)
En este ejemplo se identifica la función de flujo definida en (6). Para ser precisos se considera la identificación de e = (v∞, C, u max) a partir de los datos experimentales dados en (18). Los resultados fueron obtenidos con una malla de tamaño espacial M = 200, el valor del vector de parámetros identificado es e = (-2, 6e - 4; 4,910062;0,483) y el valor de la función costo es 9,7161e - 5. En la Figura 3-(a) se muestra la comparación del perfil obtenido con el mejor cromosoma y el perfil observado.
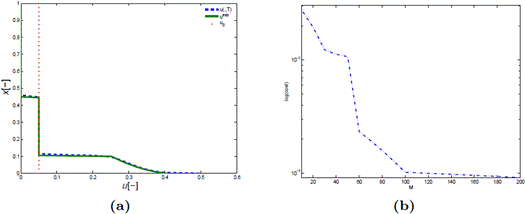
Figura 3 Experimentos numéricos (i) y (ii). En (a) se muestra el perfil identificado, la observación y la condición inicial, y en (b) la convergencia en términos del refinamiento.
(ii) Evolución de la función costo en términos de las generaciones
Se estudia la convergencia en términos de las generaciones con una longitud de espacio fija M = 50. Se encuentran los cromosomas de las primeras 100 iteraciones y se grafica la generación vs. la función de costo del mejor cromosoma en la Figura 3-(b).
(iii) Convergencia con respecto al refinamiento de la malla
En este experimento se estudia la convergencia del algoritmo en términos del refinamiento. En este caso, se considera que el número total de iteraciones es fijo e igual a 200 y se desarrolla la identificación con tamaños de malla M i = 10 i para i ∈ {1,..., 20}. Se encuentran los mejores cromosomas en términos del tamaño de malla y se grafica el tamaño de malla M i vs. la evaluación de la función de costo de esos cromosomas. Los resultados se muestran en la Figura 4-(a).
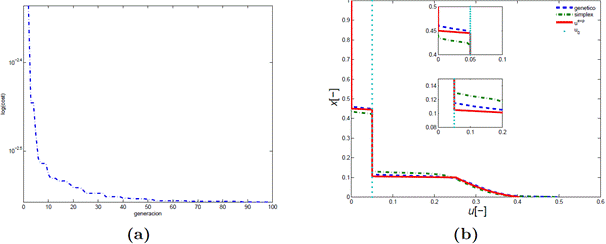
Figura 4 Experimentos numéricos (iii) y (iv). En (a) se muestra la evolución de la función costo en las distintas generaciones y en (b) la comparación de los perfiles identificados por el algoritmo genético y por el método símplex.
(iv) Comparación con el método símplex
En este experimento se compara el algoritmo genético con el método de busqueda llamado Símplex, que es implementado en la función fminsearch de Matlab. La selección del método Símplex es hecha al seguir las sugerencias de Hansen y colaboradores [12]. Para el método simplex el punto inicial es (-2, 3400e - 4; 4,4191; 4, 6). Otros puntos iniciales también fueron considerados, pero la convergencia fue muy lenta y la ejecución fue abortada cuando el tiempo cpu superó las 11 horas. Los valores de la función costo obtenidas por el método símplex y el algoritmo genético, después de 50 iteraciones, son 1, 94322e - 4 y 6,43343e - 4, respectivamente. Los valores correspondientes del tiempo cpu fueron de 8,56 horas en el caso del algoritmo genético, y en el caso del símplex de 9,32 horas. La comparación de los perfiles se muestra en la Figura 4-(b). De hecho, en las pruebas, el método símplex es muy lento cuando el punto inicial se escoge lejos del óptimo.
(v) Tiempo cpu del algoritmo.
En este experimento numérico se consideran medidas del tiempo CPU. Las simulaciones fueron hechas utilizando Matlab R(2010a) en un computador personal Dell Vostro 3500 con las siguientes propiedades: Intel Core I5 M520 con un procesador 2.40Ghz, 4Gb de RAM, 500 Gb de disco duro con 720 rpm, y con Windows 7 como sistema operativo. La identificación con el algoritmo genético es hecho con un cantidad de pasos de espacio M = 30 y con diferentes tamaños de población n = 10i para i = 1,..., 10. El tiempo CPU es medido en generación 10 y 15. Los resultados se muestran en la Figura 5-(a).
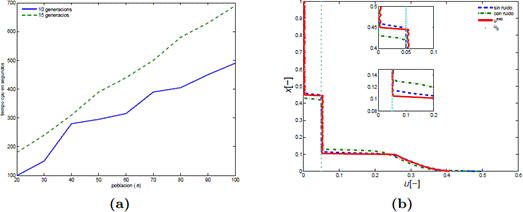
Figura 5 Experimentos numéricos (v)-(vi). En (a) se muestra la medida del tipo CPU en segundos y en (b) la comparación de los perfiles identificados para la observación sin ruido y la observación con ruido.
(vi) Identificación con ruido
En este ejemplo se muestra la identicación con el algoritmo genético en la presencia de un ruido en la observación. Se consideró que la observación es perturbada con 0, 5 % de ruido aleatoriamente distribuido. Los resultados fueron obtenidos con una malla de tamaño espacial M = 200. El valor del vector de parámetros identificados para la observación sin el ruido es e = (-2, 6e - 4; 4, 910062; 0, 483), y el valor de la función costo es 9, 7161e - 5. El valor del vector de parámetros identificados para la observación con el ruido es e = (-2, 91e-4; 5, 501051; 0, 494) y el valor de la función costo es 3, 5463e-04. En la Figura 3-(b) se muestra la comparación del perfil obtenido para el mejor cromosoma con ruido, el perfil para el mejor cromosoma sin ruido y el perfil observado perturbado.
3.2. Ejemplo 2
En este ejemplo la función de flujo que se identificará es definida por
donde
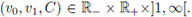El parámetro u
máx
= 0,64156 es considerado fijo y se identifican los otros tres, es decir e = (v
0
, v
1
, C). Para obtener el perfil observado se consideró una simulación del problema directo con T = 235, M = 200, el flujo y la condición inicial definidas por
Se supone que los sensores están ubicados en
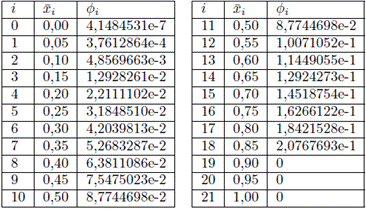
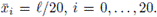El conjunto de valores para la concetración que se obtiene mediante la simulación del problema directo se muestra en la Tabla 1. Luego, utilizando un ajuste de los datos se obtiene como perfil de observación en T = 235, el cual es dado por la siguiente función:
donde a = 0,1796, b = 0,08979 y c = -0,002797.
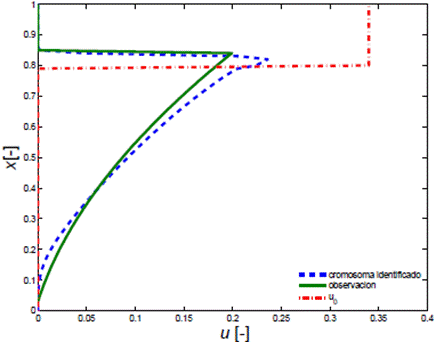
Para el algoritmo genético se consideró: Ω = [-5e - 3, -1e - 3] x [1e - 4, 5e - 4] x [1.1,4]. Los resultados de la identificación con M = 100 se muestran en la Figura 6, y los valores de los parámetros identificados son v0 = -2, 5726e - 3, v1 = 4, 2527e - 4 y C = 1, 8929 con el valor de la función costo 1, 8238e - 4.
4. Conclusiones
En esta contribución se ha validado exitosamente un algoritmo genético continuo para resolver numéricamente el problema de calibración de una función de flujo en una ley de conservación que modela el fenómeno físico de la sedimentación de partículas sólidas inmersas en un fluido, donde la función de flujo satisface las consideraciones físicas introducidas por Kynch en [16]. La distancia entre perfiles observados e identificados permite concluir que el algoritmo genético resuelve adecuadamente el problema de identificación de parámetros para leyes de conservación escalares no convexas.
Además, se observa que este nuevo algoritmo supera las conocidas desventajas de los métodos de tipo gradiente aplicadas en [1], [2], [3], entre las cuales se destacan; (a) El algoritmo genético elige aleatoriamente el punto de partida para la iteración, y (b) El algoritmo genético no necesita ninguna hipótesis de diferenciabilidad de la función objetivo.
Finalmente, el algoritmo genético de identificación considerado resultó ser estable a pesar de los datos de observación sintéticos utilizados. El problema inverso estudiado es sobredeterminado, ya que, en el ejemplo numérico, así como en situaciones prácticas relevantes, existen más datos de observación (aquí 20, en aplicaciones industriales hasta 1000) que parámetros libres para ajustarse (normalmente nunca mayores de 5).
