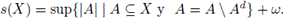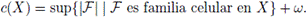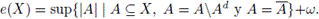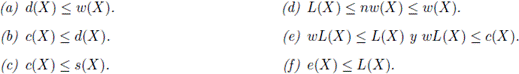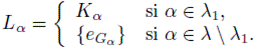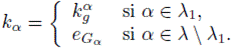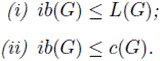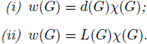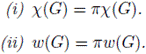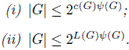1. Introducción
En el presente artículo abordamos el tema de las funciones cardinales en grupos topológicos, enfocándonos en el índice de acotamiento. Como se sabe, la teoría de los grupos topológicos conjuga dos ramas de la matemática: la Teoría de grupos y la Topología. El concepto matemático de grupo topológico en sí fue aceptado a principios de los años treinta del siglo XX con la publicación de diversos artículos [14], y desde entonces se ha convertido en un área de gran interés para su estudio. En palabras, un grupo topológico es un grupo abstracto dotado con una topología que hace a las operaciones del grupo funciones continuas. Como podemos notar en [14], la teoría de los grupos topológicos es bastante extensa e interesante. Más aún, el estudio de las funciones cardinales dentro de los grupos topológicos despierta gran interés en vista de que su comportamiento en estos espacios es, desde un cierto punto de vista, mucho mejor que en espacios topológicos, incluso compactos. Ejemplo de esto es que en la clase de los grupos topológicos el carácter y el n-carácter, así como el peso y el n-peso, coinciden, cuando en general no sucede en espacios topológicos, aún en presencia de compacidad.
Una función cardinal importante definida para grupos topológicos es el índice de acotamiento o también llamado índice de estrechez, función que denotamos por ib. En este artículo exponemos algunas de sus propiedades básicas que consideramos útiles y representativas, dentro de la teoría de invariantes cardinales para grupos topológicos. Por ejemplo, la función ib nos ayuda a obtener cotas para la cardinalidad de un grupo topo-lógico; más aún, el índice de acotamiento refleja fuertemente todo cardinal infinito en la clase de los grupos topológicos.
Destacamos que para poder hacer accesibles los resultados de este escrito a un amplio número de lectores, presentamos las definiciones y, en buena medida, las demostraciones de los hechos utilizados referentes a funciones cardinales topológicas, así como un resumen de los conceptos de grupos topológicos. Con esto en mente, hemos dividido el artículo en cinco secciones. Después de la Introducción, en la Sección 2 recordamos las notaciones básicas de espacios topológicos y damos la mayor parte de las definiciones de las funciones cardinales, globales y locales, así como las demostraciones de casi todas las igualdades y desigualdades requeridas en el desarrollo del trabajo. La Sección 3 está dedicada a presentar lo fundamental de grupos topológicos para la lectura del trabajo. En la Sección 4 brindamos los resultados sobre el índice de acotamiento que, como hemos mencionado, consideramos que son los más útiles y representativos de esta función cardinal. Finalmente, en la Sección 5 exponemos un resultado de la teoría de reflejo en grupos topológicos para la función ib. Los lectores interesados en este tema pueden ampliar su lectura en las referencias [2], [11], [12], [13], [14], [16], en las cuales los autores han basado principalmente este estudio.
2. Funciones cardinales
Sea (X, T) un espacio topológico. Dado un punto x ∈ X, llamamos vecindad de x en X a un conjunto abierto U ⊆ X tal que x ∈ U. Denotamos por VX (x) la colección de todas las vecindades de x en el espacio X. Una familia B de subconjuntos de X es una base para T, si B ⊆ T y para todo x ∈ X y cualquier V ∈ V
X
(x), existe U ∈ B tal que x ∈ U ⊆ V .Si x ∈ X, decimos que una familia B
x ⊆ VX (x) es una base local de x en X, si para toda V ∈ Vx(x), existe U ∈ B
x tal que x ∈ U ⊆ V. Denotamos por A y por A
d la clausura de A en X y el conjunto derivado de A, respectivamente. Un subconjunto D ⊆ X es denso en X si
 = X. Dada una familia de espacios {X
α
| α ∈ λ}, consideramos el espacio producto Πα∈λXα con la topología producto o Tychonoff; esto es, aquella topología que tiene por base la familia
= X. Dada una familia de espacios {X
α
| α ∈ λ}, consideramos el espacio producto Πα∈λXα con la topología producto o Tychonoff; esto es, aquella topología que tiene por base la familia
 es finito y U
α
abierto en Xα, para cada α ∈ λ1}, donde
es finito y U
α
abierto en Xα, para cada α ∈ λ1}, donde
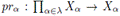 es la proyección sobre el factor Xα.
es la proyección sobre el factor Xα.
Para poder definir las primeras funciones cardinales que utilizamos a lo largo del trabajo, señalamos que la notación empleada es la misma que se usa en [8], [10]. El símbolo ω denota tanto el menor ordinal como el cardinal infinito. Si K es un cardinal, entonces K+ denota el menor cardinal mayor que K y le llamamos sucesor de K. Cada ordinal es el conjunto de los ordinales menores que él; de donde si β y α son ordinales, entonces β < α y β ∈ α significan lo mismo. Dado un conjunto E y un número cardinal K, denotamos con P(E) el conjunto potencia de E. La colección de todos los subconjuntos de E con cardinalidad ≤ K (respectivamente, con cardinalidad = K), la denotamos con [E]≤K (respectivamente, con [E]K).
Una función cardinal es una función ϕ, de la clase de los espacios topológicos (o de una subclase bien definida) hacia la clase de los cardinales infinitos, de tal forma que si X y Y son espacios homeomorfos, entonces ϕ(X) = ϕ (Y). Un ejemplo sencillo de una función cardinal es la función cardinalidad de un espacio X, denotada por |X|, y que es igual al número de elementos de X más ω. Decimos que una función cardinal ϕ es monótona si para todo subespacio Y de X, se cumple ϕ (Y) ≤ ϕ (X).
Recordemos que una familia celular en un espacio topológico X es una colección no vacía de conjuntos abiertos no vacíos y ajenos por pares. Entendemos por red en X una familia N ⊆ P(X) tal que todo conjunto abierto no vacío de X es la unión de elementos de N.
Definición 2.1. Sea X un espacio topológico. Se define:
La densidad de X como d(X) = mín{|D| | D ⊆ X y D es denso en X} + ω.
El grado o número de Lindelöf de X, denotado por L(X), como el menor cardinal infinito K tal que toda cubierta abierta de X tiene una subcubierta de cardinalidad ≤ K.
El número débil de Lindelöf de X, denotado wL(X), como el menor cardinal infinito K tal que para toda cubierta abierta
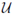 de X, existe
de X, existe
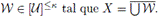
El peso de X como w(X) = mín{|B| | B es base de X} + w.
El peso red de X como nw(X) = mín{|N| | N es red para X} + w.
El resultado que exponemos a continuación está en [5, Theorem 3.2-(3)], del cual incluimos una demostración. Requerimos recordar los conceptos siguientes: orden parcial, cota superior de un conjunto, elemento maximal y cadena; además, el Lema de Zorn.
Lema 2.2. Sean X un espacio topológico, n = c(X) y F una colección de abiertos no vacíos en X. Existe
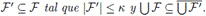
Demostración. Sea
 la colección de los abiertos no vacíos en X, los cuales son subconjuntos de algún elemento de F. Sea P la colección de los subconjuntos G ⊆
la colección de los abiertos no vacíos en X, los cuales son subconjuntos de algún elemento de F. Sea P la colección de los subconjuntos G ⊆
 tal que G es familia celular en X. Nótese que si U ∈
tal que G es familia celular en X. Nótese que si U ∈
 , entonces G = {U} ∈ P. De donde, P es no vacía. Más aún, no es difícil verificar que toda cadena en (P, ⊆) tiene una cota superior en P. De aquí, por el Lema de Zorn, P tiene un elemento maximal, digamos
, entonces G = {U} ∈ P. De donde, P es no vacía. Más aún, no es difícil verificar que toda cadena en (P, ⊆) tiene una cota superior en P. De aquí, por el Lema de Zorn, P tiene un elemento maximal, digamos
 '. Puesto que
'. Puesto que
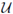 ' es una familia celular en X, |
' es una familia celular en X, |
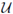 '| ≤ k. Además, si
'| ≤ k. Además, si
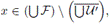 entonces x ∈ U, para algún
entonces x ∈ U, para algún
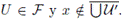 Luego, existe una vecindad abierta U
x de x tal
Luego, existe una vecindad abierta U
x de x tal
que
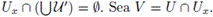 Notemos que, por construcción, V ∈
Notemos que, por construcción, V ∈
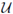 ; además,
; además,
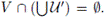 De aquí que la familia
De aquí que la familia 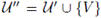 es una familia celular tal que
es una familia celular tal que
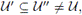 lo que contradice la maximalidad de
lo que contradice la maximalidad de
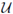 '. Por tanto,
'. Por tanto,
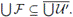 Sea F' la familia formada por los U ∈ F para los cuales existe V ∈
Sea F' la familia formada por los U ∈ F para los cuales existe V ∈
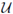 ', con V ⊆ U. Claramente
', con V ⊆ U. Claramente
En la Proposición 2.3 recordamos algunas relaciones bien conocidas entre las funciones cardinales dadas en la Definición 2.1. Las utilizamos más adelante y, con el afán de hacer este trabajo lo más autosuficiente posible, incluimos una demostración.
Proposición 2.3. Dado un espacio topológico X, se cumple lo siguiente:
Demostración. (a) Sea B0 una base para X tal que |B0| = mín{|B| | B es base de X}. Entonces |B0| + ω = w(X). Consideremos el conjunto D0 = {xB | B ∈ B0}. Es fácil ver que D0 es denso en X. Así, mín{|D| | D ⊆ X y D es denso en X} ≤ |D0|. Además, como |D0| ≤ |B0|, obtenemos que d(X) ≤ |D0| + ω ≤ |B0| + ω = w(X). Por lo tanto, d(X) ≤ w(X).
(b) Sea D0 un subconjunto denso de X tal que |D0| = mín{|D| | D ⊆ X y D es denso en X}, y supongamos que existe al menos una familia celular F en X. Notemos que |D0| + ω = d(X). Como D0 es denso en X, para cualquier U ∈ F, existe xU ∈ U ∩ D0. Sea A = {xU | U ∈ F}. Se tiene que |A| ≤ |D0|. Además, es claro que si U ≠ V , entonces xU ≠ xV . Luego, |F| = |A|. Por lo que |F| ≤ |D0| y, así, |F| ≤ d(X). Se sigue que d(X) es cota superior de {|F| | F es familia celular en X} + ω. Por lo tanto, c(X) ≤ d(X).
(c) Sea F una familia celular en X. Para cada F ∈ F, consideremos xF ∈ F. Luego, el conjunto E = {xF | F ∈ F} es no vacío y tal que E = E \ Ed. Además, |E| = |F|. De aquí, |F| + ω ≤ s(X). Por lo tanto, c(X) ≤ s(X).
(d) La demostración de que nw(X) ≤ w(X) se sigue del hecho de que toda base es una red. Para demostrar que L(X) ≤ nw(X), veamos que se cumple lo siguiente:
(∗) Si nw(X) ≤ k entonces para cualquier colección de abiertos en X, {U
s | s ∈ S}, existe S0 ∈ [S]≤k tal que
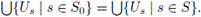
En efecto, tomemos una red N para X tal que |N | ≤ nw(X) y consideremos el conjunto N0 = {N ∈ N | N ⊆ Us para algún s ∈ S}. Para cada N ∈ N0, fijamos r(N) ∈ S, de tal forma que N ⊆ Ur(N). Esto nos define una función r : N → S. Ponemos S0 = r(N0). Veamos que el conjunto S0 cumple con lo requerido en (∗). Claramente |S0| ≤ |N0| ≤ nw(X). Además, si
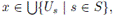 entonces x ∈ Us para algún s ∈ S. Como N es una red, existe N ∈ N tal que x ∈ N ⊆ Us. Para tal N hemos fijado r(N) ∈ S tal que N ⊆ Ur(N). Luego
entonces x ∈ Us para algún s ∈ S. Como N es una red, existe N ∈ N tal que x ∈ N ⊆ Us. Para tal N hemos fijado r(N) ∈ S tal que N ⊆ Ur(N). Luego
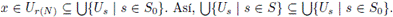 Por lo tanto,
Por lo tanto,
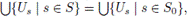 y la afirmación en (∗) queda demostrada. Ahora es inmediato de (∗) que L(X) ≤ nw(X).
y la afirmación en (∗) queda demostrada. Ahora es inmediato de (∗) que L(X) ≤ nw(X).
(e) La desigualdad wL(X) ≤ L(X) se obtiene directamente de las definiciones. Por otra parte, del Lema 2.2 tenemos que wL(X) ≤ c(X).
(f) Sean K = L(X) y A un subconjunto cerrado y discreto en X. Demostremos que |A| ≤ K. Supongamos que |A| > K. Para cada x ∈ A, existe un abierto Ux en X tal que A ∩ Ux = {x}. Puesto que A es cerrado, X \ A es abierto. Así, la colección
{Ux | x ∈ A}∪{X \ A}
es una cubierta abierta de X que no admite subcubiertas de cardinalidad menor que | A| . Esto es una contradicción. Por tanto, e(X) ≤ L(X). 0
Cabe señalar que un aspecto común entre las funciones cardinales definidas anteriormente es que son de carácter global; esto es, su definición depende o está dada a través de propiedades globales del espacio. Por otra parte, las siguientes funciones (excepto el π-peso) son de carácter local, es decir, su definición concierne a propiedades locales y puntuales del espacio.
Recordemos que dado un espacio topológico X, una colección B de subconjuntos abiertos no vacíos en X es una π-base para X, si para cualquier abierto U en X, existe V ∈ B tal que V ⊆ U. Claramente toda base de un espacio X es una π-base para X. Por otro lado, dado un punto p ∈ X y una colección B
p de conjuntos abiertos no vacíos en X, se dice que B
p
es π-base local de p, si para toda U ∈ VX(p), existe V ∈ Bp tal que V ⊆ U. Notemos que toda base local de un espacio X es una π-base local de X. Dado x ∈ X, una pseudobase local de x es una colección V de subconjuntos abiertos en X tal que para cualquier V ∈ V, se cumple que
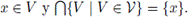
Definición 2.4. Sea X un espacio topológico. Se define:
El carácter de un punto x ∈ X como (x,X) = mín{|Bx| | Bx es base local de x}, y el carácter de X como (X) = sup{ (x,X) | x ∈ X} + ω.
El π-carácter de un punto x ∈ X como πX (x,X) = mín{|Bx| | Bx es π-base local de x}, y el π-carácter de X como πX(X) = sup{πX (x,X) | x ∈ X} + ω.
El π-peso de X como πw(X) = mín{|B| | B es π-base de X} + ω.
Si X es un espacio T1, se define el pseudocarácter de un punto x ∈ X como ψ(x,X) = mín{|V| | V es pseudobase local de x}. Además, el pseudocarácter de X se define como ψ (X) = sup{ ψ(x,X) | x ∈ X} + ω.
En la Proposición 2.5 encontramos relaciones que se cumplen entre algunas funciones cardinales, locales y globales. Serán empleadas posteriormente.
Proposición 2.5. Dado un espacio topológico X, se cumple:
Demostración. (a) Sean x0 ∈ X y B0 una base para X tal que |B0| = mín{|B| |B es base de X}. Así, |B0| + ω = w(X). Sea B(x0) = {B ∈ B0 | x0 ∈ B}. Se tiene que B(x0) es una base local de x0. Luego, (x0,X) ≤ |B(x0)|. Como |B(x0)| ≤ |B0|, obtenemos que (x0,X) ≤ |B0|. De aquí, sup{ (x,X) | x ∈ X} ≤ |B0|. Luego, (X) ≤ |B0|+ω. Por lo tanto, (X) ≤ w(X).
(b) Por (a) previo se sigue que d(X)x(X) ≤ d(X)w(X). Por lo tanto, de la Proposición 2.3-(a), obtenemos que d(X)x(X) ≤ w(X).
(c) Por (a) previo notamos que L(X)x(X) ≤ L(X)w(X). De aquí, en vista de la Proposición 2.3-(d), concluimos que L(X)x(X) ≤ w(X).
(d) Se sigue del hecho de que toda base local de un espacio X es una π-base local de X.
(e) Sea B0 una π-base para X tal que |B0| = mín{|B| | B es π-base de X}. Se sigue que |B0| + ω = πw(X). Consideremos el conjunto D0 = {xV | V ∈ B0}. Es fácil ver que D0 es denso en X. Así, mín{|D| | D ⊆ X y D es denso en X} ≤ |D0|. Además, como |D0| ≤ |B0|, obtenemos que d(X) ≤ |D0| + ω ≤ |B0| + ω = πw(X). Por lo tanto, d(X) ≤ πw(X).
(f) Sea B una π -base de X tal que |B| ≤ π w(X). Sea x un punto arbitrario en X. Puesto que B es π-base, para cada U ∈ VX(x), existe V ∈ B de tal forma que V ⊆ U. Denotemos por Bx la colección de los elementos de B con esta propiedad. Claramente, Bx ⊆ B y Bx es una π-base. Notemos que (x,X) ≤ |Bx| ≤ |B| ≤ πw(X). Así, dado que x lo tomamos de forma arbitraria, tenemos que πw(X) es cota superior del conjunto { πX (x,X) | x ∈ X}, y por lo tanto πX (X) = sup{ πX (x,X) | x ∈ X} ≤ πw(X). Esto es, πX (X) ≤ πw(X).
(g) Es consecuencia de que toda base de un espacio X es una π-base para X.
Terminamos la sección con lo siguiente. Para un espacio X de Tychonoff, se dice que un espacio de Tychonoff Y es una condensación de X si existe una función biyectiva f: X → Y tal que f es continua. El i-peso de X se define como iw(X) = mín{w(Y ) |Y es una condensación de X}.
Proposición 2.6. Para cualquier espacio de Tychonoff X se cumple que |X| ≤ 2iw[X].
Demostración. Puesto que X es T0, se sigue que |X| ≤ 2 nw[X] (véase pág. 17 de [8]). Luego, por la parte (d) de la Proposición 2.3, |X| ≤ 2w[X]. Sea K = iw(X) y sea Y una condensación de X tal que K = w(Y). Notemos que |X| = |Y|. Además, como Y es de Tychonoff, |Y| ≤ 2w[Y]. Así, |X| ≤ 2K. Es decir, |X| ≤ 2iw[X]. 0
3. Grupos topológicos
Ahora presentamos algunas definiciones y resultados de la teoría de los Grupos topológicos, que utilizamos en el desarrollo del artículo. Las demostraciones de los hechos indicados a continuación, así como un estudio más detallado sobre grupos topológicos, pueden consultarse en [2], [15].
Recordemos que un grupo algebraico (G,) dotado con una topología T se llama grupo topológico cuando las funciones cuya regla de correspondencia es (x, y) → x · y y x - x-1 son continuas respecto a T. Esto último es equivalente a decir que la función ф : G×G → G definida por ф(x, y) = x · y
−1 es continua. En lo que sigue, escribimos xy en lugar de x · y. Dados un grupo topológico
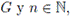 , ponemos xn para el producto de x consigo mismo n veces. Denotamos por e
G
el elemento identidad de G. En caso de que el espacio G quede subentendido, escribimos simplemente e. De acuerdo a nuestras notaciones que hemos indicado para espacios topológicos, denotamos por VG(e) la colección de todas las vecindades de la identidad en G. Dados dos subconjuntos A y B de un grupo topológico G, se define el producto de A y B en G como el conjunto AB = {xy | x ∈ A, y ∈ B}. Para g ∈ G escribimos gB en lugar de {g}B, o bien Ag en lugar de A{g}. Observemos que AB = S{xB | x ∈ A}. Cuando A = B escribimos A2 en vez de AA. En general, para
, ponemos xn para el producto de x consigo mismo n veces. Denotamos por e
G
el elemento identidad de G. En caso de que el espacio G quede subentendido, escribimos simplemente e. De acuerdo a nuestras notaciones que hemos indicado para espacios topológicos, denotamos por VG(e) la colección de todas las vecindades de la identidad en G. Dados dos subconjuntos A y B de un grupo topológico G, se define el producto de A y B en G como el conjunto AB = {xy | x ∈ A, y ∈ B}. Para g ∈ G escribimos gB en lugar de {g}B, o bien Ag en lugar de A{g}. Observemos que AB = S{xB | x ∈ A}. Cuando A = B escribimos A2 en vez de AA. En general, para
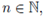 , denotamos con A
n el producto de A consigo mismo n veces. Además, A
−1 denota el conjunto {x
−1 | x ∈ A}. Por otra parte, un subconjunto V ⊆ G es simétrico si V = V
−1.
, denotamos con A
n el producto de A consigo mismo n veces. Además, A
−1 denota el conjunto {x
−1 | x ∈ A}. Por otra parte, un subconjunto V ⊆ G es simétrico si V = V
−1.
Sean G un grupo topológico y H ⊆ G. Se dice que H es un subespacio de G, si H es un grupo topológico con la topología de subespacio. Más aún, dado un grupo topológico G, se define el subgrupo generado por un conjunto S como la intersección de todos los subgrupos de G que contienen a S.
Recordemos que dados un grupo topológico G y g ∈ G fijo, se definen las funciones φg, σg : G → G por φg(x) = xg y σg(x) = gx, para cada x ∈ G. Estas funciones reciben el nombre de traslación de g derecha y traslación de g izquierda, respectivamente. La función f : G → G dada por f(y) = y −1, para cada y ∈ G, se llama inversión. Una propiedad importante de los grupos topológicos es que son espacios homogéneos [15, Corolario 1.4]. Es decir, si G es un grupo topológico, entonces para cualesquiera x, y ∈ G, existe un homeomorfismo f : G → G tal que f(x) = y. La demostración de este resultado, se basa en el hecho de que las traslaciones derecha e izquierda, así como las inversiones, son homeomorfismos [15, Teorema 1.3]. La homogeneidad de un grupo topológico G nos permite estudiar las propiedades topológicas locales de G en un único punto, que por conveniencia se toma la identidad e de G.
Es sabido que si G es un grupo topológico, g ∈ G y A ⊆ G, entonces para cualquier subconjunto abierto U de G los conjuntos gU, Ug, U
−1, AU y UA son abiertos en G [15, Teorema 1.10]. Además, si B
e es una base local de e en G y U ∈ VG(e), entonces para cada
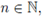 existe V ∈ B
e tal que V
n ⊆ U [15, Lema 1.9-(1)]. Más aún, en este mismo sentido se tiene que los conjuntos que son abiertos y simétricos forman una base para la identidad de G [15, Lema 1.8].
existe V ∈ B
e tal que V
n ⊆ U [15, Lema 1.9-(1)]. Más aún, en este mismo sentido se tiene que los conjuntos que son abiertos y simétricos forman una base para la identidad de G [15, Lema 1.8].
Si G es un grupo topológico de Hausdorff, entonces existe una base local Be que satisface lo siguiente [15, Teorema 1.13]:
para cada U ∈ V G (e), existe V ∈ Be tal que V V −1 ⊆ U;
para cada U ∈ V G (e) y para cada x ∈ U, existe V ∈ B e tal que xV ⊆ U .
Luego, {xV | V ∈ B e} es base local de x.
Por otro lado, sean G y G' dos grupos. Una función f : G → G' es inyectiva si y sólo si el núcleo de f, ker(f), es el conjunto {eG}. Decimos que una función f : G → G' es un homomorfismo si f es suprayectiva y si para cada x,y ∈ G se cumple f (xy) = f (x)f (y).
Cuando f : G → G’ es una función biyectiva entre grupos topológicos, se dice que f es un isomorfismo topológico si f y f-1 son homomorfismos continuos.
Finalmente, mencionamos que en este artículo consideramos grupos topológicos T 0. De hecho, todo grupo topológico T 0 es un espacio de Tychonoff, es decir, completamente regular y T 1 ([15, Teorema 4.14]).
4. El índice de acotamiento
Como hemos mencionado en la introducción, una función cardinal importante definida en la clase de los grupos topológicos es el índice de acotamiento, o también llamado índice de estrechez, que la denotamos por ib. En esta sección exponemos las relaciones que existen entre el índice de acotamiento y otras funciones cardinales. Además, vemos la utilidad de la función ib dentro de la teoría de los invariantes cardinales de grupos topológicos. Por ejemplo, el ib es útil para demostrar que el peso y el π-peso de un grupo topológico son iguales (Proposición 4.15). Además, sirve para estimar el i-peso de un grupo topológico (Teorema 4.17) y obtener cotas para la cardinalidad de estos espacios (Teorema 4.18 y Corolario 4.19).
Definición 4.1. Sean G un grupo topológico y k un cardinal infinito. Decimos que G es k-acotado, si para cada U ∈ VG(e), existe K ∈ [G]≤k tal que G = KU. El índice de acotamiento para un grupo topológico G es el menor cardinal infinito k ≥ ω tal que G es k-acotado.
El índice de acotamiento de G es denotado con ib(G). De esta manera, podemos escribir:
ib(G) = mín{k ≥ ω | G es k-acotado} + ω.
Claramente, si ib(G) > k, para algún cardinal infinito k, entonces existe U ∈ VG(e) tal que para todo K ∈ [G]≤k se tiene que G ≠ KU.
Antes de mostrar ejemplos de grupos topológicos con un determinado índice de acotamiento, presentamos algunas propiedades de esta función cardinal.
Proposición 4.2. Sean G y G' grupos topológicos. Las siguientes afirmaciones son verdaderas:
(i) El índice de acotamiento ib es una función monótona;
(ii) Si f : G → G' es un homomorfismo continuo, entonces ib(G') ≤ ib(G);
(iii) Si {Gα | α ∈ λ} es una colección de grupos topológicos tales que para todo α ∈ λ, ib(Gα) ≤ k, entonces
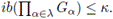
Demostración. (i) Ponemos k = ib(G). Dado un subespacio H de G, veamos que ib(H) ≤ ib(G). Para cualquier U ∈ VH(e), existen V,W ∈ VG(e) tales que U = V ∩H y W−1W ⊆ V . Puesto que ib(G) = k, existe K ∈ [G]≤k tal que G = KW. Para cada x ∈ K, tomamos ax ∈ H de la siguiente manera:
(∗) Si xW ∩ H ≠ ∅, entonces ax ∈ xW ∩ H; en otro caso, ax = e.
Sea A el conjunto formado por tales puntos. Claramente A ∈ [H]≤k. Veamos que H = AU. Como AU ⊆ H, resta verificar que H ⊆ AU. Sea y ∈ H. Puesto que G = KW y y ∈ G, tenemos que existe x ∈ K tal que y ∈ xW. Así, y ∈ (xW) ∩ H. De aquí, xW ∩ H ≠ ∅. Luego, por (∗), ax ∈ xW. En consecuencia, x ∈ axW−1. Por consiguiente, xW ⊆ axW−1W ⊆ axV. Así, y ∈ axV. De donde, ax −1 x y ∈ ax −1 x axV = V. Además, dado que y ∈ H y ax ∈ H, obtenemos que ax −1 x y ∈ H. Luego, ax −1 x y ∈ V ∩ H = U. Se sigue que y ∈ axU ⊆ AU. Con todo, concluimos que H ⊆ AU. Con esto, H es k-acotado. Por lo tanto, ib(H) ≤ k.
(ii) Supongamos que f : G → G′ es un homomorfismo continuo. Sea V ∈ VG′(e). Es claro que U = f−1(V ) ∈ VG(e). Luego, existe K ∈ [G]≤ib[G] tal que G = KU. Ponemos L = f(K). Claramente L ∈ [G′]≤ib[G]. Por otro lado, LV = f(K)f(U) = f(KU) = f(G) = G′. Con esto se tiene que G′ es ib(G)-acotado. Por lo tanto, ib(G′) ≤ ib(G).
(iii) Sea
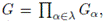 donde para todo
donde para todo
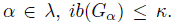 Veamos que para cada U ∈ VG(e), existe K ∈ [G]-K tal que G = KU. Dado U ∈ VG(e) cualquiera, podemos suponer, sin perder generalidad, que existe un subconjunto finito λ1 ⊆ λ tal que U =
Veamos que para cada U ∈ VG(e), existe K ∈ [G]-K tal que G = KU. Dado U ∈ VG(e) cualquiera, podemos suponer, sin perder generalidad, que existe un subconjunto finito λ1 ⊆ λ tal que U =
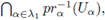 donde para cada α ∈ λ1, Uα ∈ TGα. Notemos que para cada a ∈ λ1, eGα ∈ Uα. Para cada α ∈ λ1, sea Vα una vecindad de eGα en Gα tal que VαVα
-1 ⊆ Uα. Ahora, por hipótesis, para todo α ∈ λ1, existe Kα ∈ [Gα]≤K tal que Gα = KαVα. Notemos que Gα = KαUα. Sea
donde para cada α ∈ λ1, Uα ∈ TGα. Notemos que para cada a ∈ λ1, eGα ∈ Uα. Para cada α ∈ λ1, sea Vα una vecindad de eGα en Gα tal que VαVα
-1 ⊆ Uα. Ahora, por hipótesis, para todo α ∈ λ1, existe Kα ∈ [Gα]≤K tal que Gα = KαVα. Notemos que Gα = KαUα. Sea
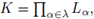 donde
donde
Claramente, K ∈ [G]≤k. Afirmamos que G = KU. En efecto, si g ∈ G, entonces para todo α ∈ λ1, tenemos que prα(g) ∈ Gα. Como Gα = KαKα, existe
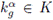 que
que
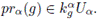 Ponemos
Ponemos
Sea
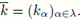 Es claro que
Es claro que
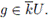 Así, G = KU. Por lo tanto, ib(G) ≤ k.
Así, G = KU. Por lo tanto, ib(G) ≤ k.
Proposición 4.3. Sean G un grupo topológico y H un subespacio denso de G. Se tiene que ib(G) = ib(H).
Demostración. Sea k = ib(H). Por Proposición 4.2-(i), sólo demostremos que ib(G) ≤ k. Sea U ∈ VG(e). Existe V ∈ VG(e) tal que V V −1 ⊆ U. Como V ∩ H ∈ VH(e), existe K ∈ [H]≤k tal que H = K(V ∩ H). De aquí, H ⊆ KV . Entonces, como H es denso en G, obtenemos que KV es denso en G. Veamos que G = KU. Dado x ∈ G cualquiera, se tiene que xV ∈ VG(x). Luego, (xV ) ∩ (KV ) ≠ ∅. Así, existen v1, v2 ∈ V y c ∈ K tales que xv1 = cv2. De aquí, x = cv2v1 −1 1 ∈ KV V −1 ⊆ KU. Luego, G = KU. Por lo tanto, ib(G) ≤ k.
En el siguiente resultado vemos la relación que guarda el índice de acotamiento de un grupo topológico con otras funciones cardinales, a saber con el grado de Lindelöf y la celularidad.
Proposición 4.4. Para cualquier grupo topológico G:
Demostración. (i) Sean k = L(G) y U ∈ VG(e). Es claro que la familia U = {xU | x ∈ G} es una cubierta abierta de G. Luego, como = L(G), existe K ∈ [G]≤tal que G =
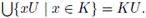 Así, G es k-acotado. Por lo tanto, ib(G) ≤ k.
Así, G es k-acotado. Por lo tanto, ib(G) ≤ k.
(ii) Pongamos k = c(G). Supongamos que ib(G) > k. Así, existe U ∈ VG(e) tal que para todo K ∈ &·091;G&·093;≤k se tiene que G ≠ KU. Consideremos V ∈ VG(e) tal que V V −1 ⊆ U. Con inducción transfinita, construimos una sucesión de puntos en G, {xα | α ∈ k+}, con la siguiente propiedad:
(∗) Si β < α < k+, entonces xα ∉ xβU.
Como para cada K ∈ [G]≤k, G ≠ KU, en particular G ≠ eU. Luego, existe x0 ∈ G\ eU. Claro que |{x0}| ≤ k. Así, G ≠ x0U. De donde, existe x1 ∈ G\x0U. Ahora, sea 0 < α < k y supongamos construido el elemento para cada β < α Notemos que el elemento xα queda construido como sigue. En vista de que
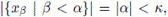 tenemos que
tenemos que
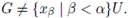 Así, existe
Así, existe
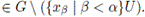
Afirmamos que la familia F = {xαU | α ∈ k+} es celular. Supongamos que no. Luego, existen α, β ∈ k+ tales que β < α y (xαV ) ∩ (xβV ) ≠ ∅. Luego, existen v1, v2 ∈ V tales que xβv2 = xαv1. De donde, xα ∈ xβV V −1 ⊆ xβU. Así, xα ∈ xβU, lo que contradice la propiedad (∗). Por lo tanto, F es celular. Puesto que |F| > k, obtenemos una contradicción con k = c(G). Por lo tanto, ib(G) ≤ k.
Como consecuencia de la Proposición 4.4 y de los incisos (b)-(d) de la Proposición 2.3, obtenemos el siguiente corolario.
Corolario 4.5. Sea G un grupo topológico. Para cualquier función cardinal ф ∈ {d, s, nw, w}, se cumple que ib(G) ≤ ф (G).
En particular, del Corolario 4.5 obtenemos lo siguiente:
Ejemplo 4.6. Sea
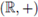 el grupo topológico de los números reales con la suma usual. Es bien sabido que
el grupo topológico de los números reales con la suma usual. Es bien sabido que
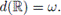 . Así, por el Corolario 4.5, obtenemos que
. Así, por el Corolario 4.5, obtenemos que
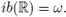
Por otro lado, dado que para cualquier espacio topológico X, se cumple que e(X) ≤ L(X) (vea parte (f) de la Proposición 2.3), una pregunta natural es si la desigualdad en la parte (i) de la Proposición 4.4 se sigue cumpliendo si cambiamos la función L por la función e. En el siguiente resultado vemos que la respuesta es afirmativa.
Proposición 4.7. Para cada grupo topológico G se cumple que ib(G) ≤ e(G).
Demostración. Sea G un grupo topológico tal que K = e(G). Es suficiente con demostrar que podemos cubrir a G con a lo más K-traslaciones de toda vecindad simétrica U de e.
(*) Supongamos que existe una vecindad simétrica U0 de G tal que para cada D ∈
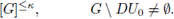
Con la suposición en (*), construimos una sucesión X = {xa | a < K+} en G que cumple: (**) Si α < β < K+, entonces
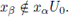
En efecto, sea 0 < a < K+ y supongamos que para todo β < α hemos construido xβ tal que se cumple la condición (**). Dado que |{xβ: β < α}| ≤ K, se sigue de (*) que G \ {xβ | β < α}U0 α ≠ ∅. Luego, existe xα ∈ G \ {xβ | β < α}U0, lo que completa la construcción de la sucesión deseada.
Ahora demostremos que para cualesquiera
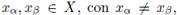 se cumple que
se cumple que
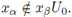 En efecto, sean xα, xβ ∈ X tales que
En efecto, sean xα, xβ ∈ X tales que
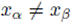 y supongamos que
y supongamos que
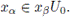 Luego de la condición en (**) tenemos que α < β. Además, como
Luego de la condición en (**) tenemos que α < β. Además, como
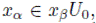 entonces existe u ∈ U0 tal que xα = xβu. Luego
entonces existe u ∈ U0 tal que xα = xβu. Luego
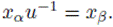 Así,
Así,
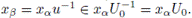 Pero esto es una contradicción, pues α < β .
Pero esto es una contradicción, pues α < β .
Finalmente, sea V una vecindad simétrica de e tal que V4 ⊆ U0. Por [2, Lemma 1.4.22], {xαV | α < K+} es una familia discreta (es decir, para cada g ∈ G existe una vecindad que interseca a lo más un elemento de {xαV | α < K+} [6, p. 16]). De este hecho se sigue que X es un conjunto cerrado y discreto en G con |X| = K+, una contradicción. Por lo tanto, ib(G) ≤ e(G).
Para poder contar con más ejemplos del índice de acotamiento de grupos topológicos, recordemos lo siguiente. Dado un espacio topológico X, se dice que x ∈ X es un punto de acumulación completo de un subconjunto E ⊆ X si para todo V ∈ V(x), se cumple que |V∩E| = |E|. Por otra parte, para un cardinal infinito K, se dice que un espacio topológico X es inicialmente K-compacto si para toda cubierta abierta U de X con |U| ≤ K, existe V ∈ [U]<ω, tal que V cubre a X . De hecho, un espacio X es inicialmente K-compacto si y sólo si todo subconjunto infinito de cardinalidad a lo más K tiene un punto de acumulación completo [1]. Esta equivalencia nos ayuda a obtener lo siguiente:
Teorema 4.8. Si X es un espacio topológico inicialmente K-compacto, entonces e(X) ≤ K.
Demostración. Para ver que e(X) ≤ K basta demostrar que si A es un subconjunto infinito de X con |A| > K, entonces A tiene un punto de acumulación. Sea A ⊆ X tal que |A| > K. Tomemos B ∈ [A]K. Por la equivalencia mencionada en el párrafo previo, B tiene un punto de acumulación completo, de donde A tiene al menos un punto de acumulación. Por lo tanto, e(X) ≤ K.
Se sigue de la Proposición 4.7 y del Teorema 4.8 lo siguiente.
Ejemplo 4.9. Si G es un grupo inicialmente K-compacto, entonces ib(G) ≤ k.
En particular, puesto que para cualquier K, todo espacio compacto es inicialmente K-compacto, obtenemos del Ejemplo 4.9 el siguiente hecho.
Ejemplo 4.10. Para un grupo topológico compacto G, se tiene que ib(G) = w.
Las siguientes dos proposiciones nos muestran la relación entre el índice de acotamiento con otras funciones cardinales. La primera de ellas mejora las desigualdades en la Proposición 4.4, pues involucra el número débil de Lindelöf (vea Proposición 2.3-(e)). La segunda proposición nos relaciona el índice de acotamiento con el peso y el carácter de un grupo topológico.
Proposición 4.11. Para cualquier grupo topológico G se cumple que ib(G) ≤ wL(G).
Demostración. Sea G un grupo topológico tal que K = wL(G). Veamos que ib(G) ≤ K. Sea U ∈ VG(e). Existe V ∈ VG(e) tal que VV-1 = V2 ⊆ U. Sea U = {xV | x ∈ G}. Claramente U es una cubierta abierta de G. Luego, como k = wL(G), existe K ∈ [G]
≤K
tal que
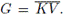 Veamos que G = KU. Sea g ∈ G. Puesto que KV es denso en G obtenemos que ( gV) ∩ ( KV) ≠ ∅. Entonces, existe x ∈ K tal que (gV) ∩ ( xV) ≠ ∅. De aquí, existen v1,v2 ∈ V tales que gv1 = xv2. De donde, g = xv2v1
-1 ∈ xVV-1 = xV2. Con esto, g ∈ xV2 ⊆ xU. Así, G ⊆ KU. Se concluye que G = KU. Por lo tanto, ib(G) ≤ K. 0
Veamos que G = KU. Sea g ∈ G. Puesto que KV es denso en G obtenemos que ( gV) ∩ ( KV) ≠ ∅. Entonces, existe x ∈ K tal que (gV) ∩ ( xV) ≠ ∅. De aquí, existen v1,v2 ∈ V tales que gv1 = xv2. De donde, g = xv2v1
-1 ∈ xVV-1 = xV2. Con esto, g ∈ xV2 ⊆ xU. Así, G ⊆ KU. Se concluye que G = KU. Por lo tanto, ib(G) ≤ K. 0
Proposición 4.12. Para cualquier grupo topológico G, w(G) = ib(G)x(G).
Demostración. Sea G un grupo topológico. Notemos que por el Corolario 4.5, ib(G) ≤ w(G). De aquí, por la parte (a) de la Proposición 2.5, se sigue que ib(G)x(G) ≤ w(G).
Por otro lado, sea K = ib(G)x(G). Veamos que w(G) ≤ K. Como x(G) ≤ K, existe una base local Be de la identidad e de G tal que |Be| ≤ K. Puesto que ib(G) ≤ K, para todo B ∈ Be existe DB ∈ [G]≤K tal que G = DBB. Sean
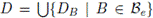 y B = {xB | x ∈ D y B ∈ Be}. Afirmamos que B es base de G. Sean g ∈ G y U un abierto que contiene a g. Así, existe V ∈ VG (e) tal que gV ⊆ U. Consideremos W ∈ VG (e) tal que W-1W ⊆ V y sea B ∈ Be tal que B ⊆ W. Puesto que G = DB B existe x ∈ DB con g ∈ xB. De aquí, xB ∈ gB-1B. Como gB-1B ⊆ gW-1W ⊆ gV ⊆ U, obtenemos que g ∈ xB ⊆ U. Por tanto, B es base de G. Finalmente, como |D| = Σ{|DB| | B ∈ Be} ≤ |Be| ≤ K, se tiene que |B| ≤ K. Con todo w(G) ≤ K. Por lo tanto, w(G) = ib(G)x(G).
y B = {xB | x ∈ D y B ∈ Be}. Afirmamos que B es base de G. Sean g ∈ G y U un abierto que contiene a g. Así, existe V ∈ VG (e) tal que gV ⊆ U. Consideremos W ∈ VG (e) tal que W-1W ⊆ V y sea B ∈ Be tal que B ⊆ W. Puesto que G = DB B existe x ∈ DB con g ∈ xB. De aquí, xB ∈ gB-1B. Como gB-1B ⊆ gW-1W ⊆ gV ⊆ U, obtenemos que g ∈ xB ⊆ U. Por tanto, B es base de G. Finalmente, como |D| = Σ{|DB| | B ∈ Be} ≤ |Be| ≤ K, se tiene que |B| ≤ K. Con todo w(G) ≤ K. Por lo tanto, w(G) = ib(G)x(G).
La Proposición 4.13 que presentamos a continuación la demostramos utilizando algunos de los resultados que hemos expuesto del índice de acotamiento. Esta proposición es de suma importancia en la teoría de los grupos topológicos, por la siguiente razón. Es bien sabido que todo espacio topológico segundo numerable es primero numerable y separable; además, todo espacio segundo numerable es de Lindelöf. Sin embargo, en general, un espacio primero numerable y separable no es segundo numerable; más aún, un espacio primero numerable y de Lindelöf no siempre es segundo numerable (vea [6, Example 3.8.14]). La situación es muy distinta en la teoría de los grupos topológicos. De hecho, como consecuencia de la Proposición 4.13, obtenemos que todo grupo topológico primero numerable y separable sí es segundo numerable; y, además, todo grupo topológico primero numerable y de Lindelöf resulta ser segundo numerable.
Proposición 4.13. Todo grupo topológico G satisface que:
Demostración. (i) Se sigue del Corolario 4.5, la Proposición 4.12 y de la parte (b) de la Proposición 2.5.
(ii) Se sigue de la parte (i) de la Proposición 4.4, de la Proposición 4.12 y de la parte (c) de la Proposición 2.5. 0
Se desprende de la Proposición 4.13 lo siguiente.
Corolario 4.14. Dado un grupo topológico G, se cumple:
(i) Si G es primero numerable y separable, entonces G es segundo numerable;
(ii) Si G es primero numerable y de Lindelöf, entonces G es segundo numerable.
Cabe señalar que una propiedad importante que poseen algunas funciones cardinales definidas en grupos topológicos es que coinciden, incluso cuando en espacios compactos pueden ser distintas (vea [8, Example 7.22]). Mostramos esto en el siguiente resultado.
Proposición 4.15. Para cualquier grupo topológico G se cumple:
Demostración. Sea G un grupo topológico. Podemos suponer que G no es discreto.
(i) Por la parte (d) de la Proposición 2.5 es suficiente verificar que x(G) ≤ πx(G). Sea B una π-base local de e tal que |B| = πx(e, G). Se tiene que B' = {BB-1 | B ∈ B} es una base local de e. En efecto, sea U un abierto tal que e ∈ U. Consideremos V ∈ VG (e) tal que VV-1 ⊆ U. Puesto que B es π-base local de e, existe B ∈ B tal que B ⊆ V. De donde, e BB-1 ⊆ U, lo que demuestra la afirmación. Observemos que |B'| ≤ |B|. Así, x(e, G) ≤ πx(e, G). Puesto que todo grupo topológico es homogéneo, concluimos que x(G) ≤ πx(G).
(ii) Por la parte (i) de la Proposición 4.13 y por (i) previo, tenemos que w(G) = d(G)πx(G). Se sigue de la parte (e) de la Proposición 2.5 que w(G) ≤ πw(G)πx(G). Luego, de (f) de la Proposición 2.5, w(G) ≤ πw(G). Por lo tanto, de la parte (g) de la Proposición 2.5, obtenemos que w(G) = πw(G).
Para terminar esta sección, en el Teorema 4.18, empleamos el índice de acotamiento para establecer una cota superior para la cardinalidad de un grupo topológico. Para destacar la importancia de este resultado, previamente recordamos algunas desigualdades de la teoría de los invariantes cardinales topológicos:
(A) Hajnal-Juhász: |X| ≤ 2s[X]ψ[X], para X un espacio T1.
(B) Hajnal-Juhász: |X| ≤ 2c[X]x[X], para X un espacio T2.
(C) Arhangel'skiĭ: |X| ≤ 2L[X]x[X], para X un espacio T2.
Es bien sabido que con el resultado en (C), Arhangel'skiĭ resuelve el problema de Alexandroff-Urysohn. El lector interesado en conocer más detalles sobre las desigualdades en (A) y en (B), así como las contribuciones de la desigualdad de Arhangel’skiĭ en (C) a la teoría de los invariantes cardinales topológicos, puede consultar [7].
En la actualidad aún existen problemas que podrían continuar abiertos relacionados con la desigualdad de Arhangel'skii. Por ejemplo:
(I) ¿Existe una generalización común para las desigualdades en (B) y en (C)?
Una respuesta parcial y afirmativa a esta pregunta es la desigualdad de Bell, Ginsburg y Woods, que nos dice que si X es un espacio T4, entonces |X| ≤ 2wL[X]x[X] [3].
A su vez, el mismo Arhangel’skiĭ cuestiona (vea [7]):
(II) ¿Qué se puede decir de la cardinalidad de un espacio X que es T1, de Lindelöf y con pseudocarácter numerable?
Finalmente, un problema en cierto sentido más natural es el siguiente:
(III) Si X es un espacio T1, de Lindelöf y primero numerable; entonces, ¿es cierto que |X| ≤ 2w?
Si bien la desigualdad que presentamos en el Teorema 4.18 es interesante por sí sola, es importante destacar que, por un lado, es una generalización común, en la clase de los grupos topológicos, para las desigualdades dadas en (B) y (C), lo que notamos en el Corolario 4.19. Por otro lado, de la desigualdad del Teorema 4.18 se obtienen respuestas a las preguntas en (II) y (III), para la clase de los grupos topológicos.
A continuación, presentamos lo requerido para la demostración del Teorema 4.18.
Lema 4.16 ([12, p. 191]). Sea G un grupo topológico T-acotado y sea U una vecindad de la identidad e ∈ G. Entonces existe un homomorfismo continuo sobre un grupo topológico H, f : G → H, con w(H) ≤ T, y existe una vecindad V de la identidad de H tal que f-1(V) ⊆ U.
Teorema 4.17. Para cualquier grupo topológico G, existe un isomorfismo continuo de G sobre un grupo topológico H tal que w(H) ≤ ib(G)ψ(G). En consecuencia, cualquier grupo topológico G satisface que iw(G) ≤ ib(G)ψ(G).
Demostración. Sea G un grupo topológico. Sea K = ib(G)ψ(G). Como ψ(G) ≤ K, existe una pseudobase local de eG en G, digamos B = {Uα | α ∈ K}. Puesto que ib(G) ≤ K, se sigue del Lema 4.16 que, para cada α < K, existen un grupo topológico Hα y un homomorfismo continuo y suprayectivo fα: G → Hα tales que w(Hα) ≤ K, y existe una vecindad Vα de la identidad eHα tal que f-1(Vα) ⊆ Uα. Sea
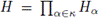 y definamos la función F: G → H por
y definamos la función F: G → H por
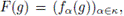 para cada g ∈ G. Es claro que F es suprayectiva. Además, por [6, Proposition 2.3.6] F es continua. Veamos que F es inyectiva. Para esto, demostramos que ker(F) = { eG } . Supongamos que g ∈ G es tal que F (g) = eH, donde eH es la identidad de H. Si g ≠ eG, entonces por ser B pseudobase local de eG, existe a < K tal que
para cada g ∈ G. Es claro que F es suprayectiva. Además, por [6, Proposition 2.3.6] F es continua. Veamos que F es inyectiva. Para esto, demostramos que ker(F) = { eG } . Supongamos que g ∈ G es tal que F (g) = eH, donde eH es la identidad de H. Si g ≠ eG, entonces por ser B pseudobase local de eG, existe a < K tal que
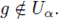 Se tiene que
Se tiene que
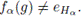 En efecto, si fα(g) = eHα , entonces fα(g) ∈ Vα. De aquí, g ∈ fα
-1(Vα) ⊆ Uα. Así, g ∈ Uα, lo que es una contradicción. Luego
En efecto, si fα(g) = eHα , entonces fα(g) ∈ Vα. De aquí, g ∈ fα
-1(Vα) ⊆ Uα. Así, g ∈ Uα, lo que es una contradicción. Luego
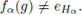 Con esto,
Con esto,
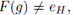 de donde ker(F) = {eG}. Con todo, hemos demostrado que F es una biyección continua entre G y H. Es claro que w(H) ≤ K.
de donde ker(F) = {eG}. Con todo, hemos demostrado que F es una biyección continua entre G y H. Es claro que w(H) ≤ K.
Resta probar que iw(G) ≤ ib(G)ψ(G). Para esto, notemos que H es una condensación de G tal que w(H) ≤ ib(G)ψ(G). Por lo tanto, de la definición de iw, obtenemos que iw(G) ≤ ib(G)ψ(G).
Teorema 4.18 ([12]). Para cualquier grupo topológico G, se cumple que |G| ≤ 2ib[G]ψ[G].
Demostración. Se sigue de la Proposición 2.6 y del Teorema 4.17.
Corolario 4.19 ([12]). Para cualquier grupo topológico G, se cumple:
Demostración. Por la Proposición 4.4, obtenemos las desigualdades ib(G)ψ(G) ≤ c(G)ψ(G) y ib(G)ψ(G) ≤ L(G)ψ(G). Así, (i) y (ii) se siguen del Teorema 4.18.
5. Reflejo y el índice de acotamiento
Concluimos este trabajo mostrando que el índice de acotamiento refleja todo cardinal infinito en la clase de los grupos topológicos. Antes daremos algunas definiciones y resultados, sin demostración, referentes a la teoría de reflejo para funciones cardinales topológicas. Cabe mencionar que esta teoría es una manera muy natural para estudiar las propiedades de un espacio topológico dado. Básicamente, el problema de reflejo tiene la siguiente forma: ¿es cierto que si para todo subespacio Y de X tal que |Y| ≤ K y Y satisface la propiedad P, entonces X tiene la propiedad P? El lector interesado en el tema o en conocer una demostración para los resultados que presentamos a continuación puede consultar [9].
Definición 5.1. Sean X un espacio topológico, ф una función cardinal y K ≥ w un cardinal. Se dice que:
(1) ф refleja a K, cuando se verifica la condición: si ф(X) ≥ K, entonces existe Y ∈ [X]≤K tal que ф(Y) > K.
(2) ф refleja fuertemente a K, cuando se verifica la condición: si ф(X) ≥ K, entonces existe Y ∈ [X]≤K tal que para todo subespacio Z de X tal que Y C Z, se cumple ф(Z) ≥ K.
Observemos que ф refleja a K si y sólo si para todo Y ∈ [X]≤K tal que ф(Y) < K, se cumple que ф(X) < K. En ocasiones, cuando se desean obtener teoremas de reflejo, para ciertas funciones cardinales, es necesario restringir la clase de espacios en consideración. En un caso así, la definición de reflejo apropiada es: ф refleja a K para la clase C, si dado X ∈ C con ф (X) ≥ K, existe Y ∈ [X]≤K tal que ф(Y) ≥ K. Es claro que las condiciones de la Definición 5.1 se satisfacen cuando K = w. Por esta razón suponemos que K > w.
Las relaciones entre reflejo y reflejo fuerte se resumen en el resultado siguiente.
Teorema 5.2. Sean ф una función cardinal y K ≥ w.
(i) Si ф refleja fuertemente a K, entonces ф refleja a K. Cuando ф es monótona, el recíproco también se cumple.
(ii) Si ф refleja fuertemente todo cardinal sucesor, entonces ф refleja fuertemente todo cardinal infinito. En particular, si ф es monótona y refleja todo cardinal sucesor, entonces ф refleja fuertemente todo cardinal infinito.
En seguida vemos que el índice de acotamiento refleja todo cardinal infinito. La demostración del siguiente resultado sigue las ideas de [16, Proposition 2.3].
Teorema 5.3 ([4]). La función ib refleja fuertemente todo cardinal infinito en la clase de los grupos topológicos.
Demostración. Sea G un grupo topológico. Puesto que ib es monótona (vea parte (i) de la Proposición 4.2) tenemos que, en vista del Teorema 5.2-(ii), es suficiente demostrar el resultado para un cardinal sucesor K+. Supongamos que para todo subgrupo H de G, con |H| ≤ K+, se tiene que ib(H) ≤ K. Si ib(G) > K (es decir, si ib(G) ≥ K+), entonces existe U ∈ VG(e) tal que para todo K ∈ [G]≤K, se tiene que G ≠ KU.
Vamos a construir ahora una sucesión {pα | 0 ≤ a < K+} de puntos en G tal que:
(∗) pβ ∈ G \ (({pp | p<β})U).
Para esto tomemos 0 < α < K+, y supongamos que pβ se tiene construido para cada β ∈ α. Puesto que α < K+, tenemos que |α| < K. Así, por nuestra hipótesis, existe pα ∈ G \ ({pβ | β < α})U, lo cual completa la construcción.
Ahora, sea Y = {pα | 0 < α < K+} y denotemos con H el subgrupo de G generado por Y. Notemos que |H| ≤ |[Y]≤W| = |Y| ≤ K+.
Para terminar la demostración probemos que ib(H) = K+. Para esto, supongamos que ib(H) = µ ≤ K, y sea V una vecindad abierta y simétrica de la identidad de H de tal forma que V2 ⊆ U. Luego existe F ⊆ H con |F| ≤ µ tal que H = F(V∩H). Ahora, para cada α < K+, existen gα ∈ F y va ∈ V tales que pα = gαvα. Puesto que |F| < K+, se tiene que, por la regularidad de K+, existe β < α < K+ tal que gβ = gα = g. Luego, pβ = gvβ y pα = gvα. Así, pα = (pβ)(vβ -1)(vα) ∈ (pβ)V-1V ⊆ (pβ)V2 ⊆ ({pβ | β < α})U, lo cual es una contradicción con (∗). De esta contradicción obtenemos que ib(G) ≤ K. Por lo tanto, ib refleja a K+, y dado que ib es monótona, tenemos que ib refleja todo cardinal infinito.