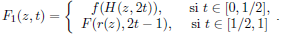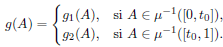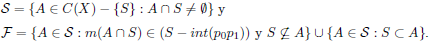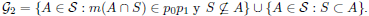Espanhol (pdf)
Artigo em XML
Referências do artigo
Tradução automática
Enviar este artigo por email
Citado por SciELO 
Citado por Google 
Similares em
SciELO 
Similares em Google 
Permalink
1. Introducción
La unicoherencia es una propiedad topológica que surge de trabajos de distintos autores, entre los cuales podemos mencionar a L. E. J. Brouwer (1910), F. Hausdorff (1914), Z. Janiszewsky (1913), S. Mazurkiewicz (1922) y R. L. Moore (1924). El primero en definirla y llamarla tal y como la conocemos fue K. Kuratowski (ver [21] y [22]). En [11], K. Borsuk introduce el uso de funciones continuas de un espacio al círculo unitario, y con esto encuentra una nueva forma de estudiar a la unicoherencia de un espacio topológico. Un excelente trabajo que podemos recomendar acerca de la unicoherencia es [17].
De manera intuitiva podemos decir que un espacio es unicoherente si no tiene "agujeros". Podemos pensar que un espacio topológico conexo Z tiene un "agujero", si podemos "cubrir" con dos cerrados y conexos a Z de tal forma que su intersección sea no conexa. Con esta idea intuitiva podemos ver que el círculo unitario en el plano y el toro son ejemplos de espacios que tienen un "agujero". Siguiendo de manera intuitiva, podemos preguntarnos: ¿qué le pasa a un espacio topológico unicoherente si le quitamos un elemento? Si pierde la propiedad de la unicoherencia entonces vemos que "agujerea". Esta es básicamente la idea que abrió paso a una nueva rama de la Teoría de Continuos y sus Hiperespacios.
Durante todo el trabajo nos referiremos al autor o los autores de los resultados que se irán mencionando, evitando así llenar la lectura con los nombres de ellos. Dividimos al trabajo en cinco partes. La primera es esta en la que estamos. En la segunda parte damos las definiciones y resultados que necesitamos en el desarrollo del trabajo. En la tercera parte mostramos las herramientas que se utilizan en las demostraciones, y mostramos cómo se relacionan los conceptos de propiedad b) y de unicoherencia. En la cuarta parte se enuncian los resultados que se conocen de la búsqueda de los elementos que agujerean un espacio, y en cada resultado hacemos una descripción sistemática de la prueba que presentan los autores. Finalmente, la quinta parte consiste de las conclusiones de este trabajo.
2. Conceptos generales
Vamos a representar el conjunto de los enteros positivos como N, el conjunto de los números reales como R, al intervalo [0,1] como I, a la n- celda como In (para n ∈ N), al cubo de Hilbert I x I x... como I∞ y a la n- esfera como Sn (para n ∈ N). La cardinalidad de un conjunto A la denotaremos por |A|.
Sea Z un espacio topológico y A ⊂ Z; denotaremos por cl(A) la cerradura de A, bd(A) la frontera de A y int(A) el interior de A, todos estos en Z. A los elementos de int(A) se los llama puntos interiores. Dados dos espacios topológicos Y y Z formamos el espacio producto Y x Z, con la topología producto. Otro espacio que formaremos a partir espacios topológicos Y y Z es el espacio cociente, y lo escribiremos como Y/Z, dotado con la topología cociente. Cuando dos espacios topológicos Y y Z sean homeomorfos, lo denotaremos como Y ≈ Z.
Una variedad de dimensión n o n-variedad es un espacio de Hausdorff M en el cual cada uno de sus puntos tiene una vecindad homeomorfa a Rn. Una n-variedad compacta se llama cerrada. Una n-variedad con frontera es un espacio de Hausdorff M en el cual cada uno de sus puntos tiene una vecindad homeomorfa a Rn o a
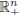= {x1,...,xn) ∈ Rn: xn ≥ 0}.
Una propiedad topológica P es hereditaria en Z, si cada subespacio de Z tiene la propiedad en cuestión. Al referirnos como "Z hereditariamente P", será porque P es hereditaria en Z.
Un espacio topológico X es un continuo si es un espacio métrico compacto conexo no degenerado, con métrica d. A lo largo del trabajo, X siempre denotará un continuo.
Diremos que un subespacio Y ⊂ X es un subcontinuo de X, si es por sí mismo un continuo.
Un arco es un espacio topológico homeomorfo a I. Un arco pq en un espacio topológico Z, con puntos finales p y q, es llamado arco libre si pq - {p, q} es un subconjunto abierto en Z. Sabemos que una curva cerrada simple es un espacio topológico homeomerfo a S1. Una curva cerrada simple S es llamada curva cerrada simple libre en Z si S ≠ Z y existe p ∈ S tal que S - {p} es un subconjunto abierto de Z.
Un espacio topológico Z es localmente conexo si para cualquier x ∈ Z y una vecindad abierta U de x existe un conjunto abierto conexo C tal que x ∈ C ⊂ U. Un espacio de Peano es un espacio localmente conexo.
Sea Y un subespacio de un espacio topológico Z. Una retracción de Z en Y es una función continua r: Z → Y tal que, para toda y ∈ Y, r(y) = y. Decimos que Y es un retracto por deformación de Z si existen una retracción r: Z → Y y una función continua H: Z x I → Z tales que para cada z ∈ Z tenemos: H(z, 0) = z y H(z, 1) = r(z). Decimos que un espacio topológico Z es contráctil si existe z ∈ Z, tal que {z} es un retracto por deformación de Z.
Un elemento z en un espacio topológico conexo Z es un punto de corte de Z si Z - {z} no es conexo. El conjunto de puntos de corte de Z se denota por Cut(Z). Un punto final z ∈ Z es un elemento tal que no es punto de corte de un arco que lo contenga. Consideremos E(Z) el conjunto de puntos finales. Un elemento z de Z es un punto de ramificación, siempre que z sea un punto final de tres o más arcos en Z. El conjunto de todos los puntos de ramificación se denota por R(Z).
Un continuo X es un abanico si es arcoconexo, hereditariamente unicoherente y con exactamente un punto de ramificación. A ese punto de ramificación se lo llama vértice del abanico. Un continuo de Peano X se dice que es una dendrita si no contiene curvas cerradas simples. Una gráfica finita es un continuo que se compone de un número finito de arcos, tales que cualesquiera dos de ellos son ajenos, o se intersecan en un solo punto o en sus puntos finales.
Una compactación del rayo R = [0, ∞) con residuo un arco J es llamada un Elsa continuo, y se denota X = J ∪ R. Esta clase de continuos fue definida por S. B. Nadler Jr., en [28]. Se sabe que existe una cantidad no numerable de Elsa continuos (ver [26, p. 184]), entre los cuales se encuentra el conocido sin (1/x)-continuo. A partir de esta familia podemos construir otras dos familias no numerables de continuos. La primer familia es la de los Elsa círculos (ver [5, Definition 4.19]): se considera un Elsa continuo J ∪ R y se identifica un extremo de J con el extremo R. Un ejemplo de este es el círculo de Varsovia. La segunda es la de los doble Elsa círculos (ver [5, Definition 4.20]): se considera la compactación de dos rayos con el mismo residuo J y los extremos de los rayos se identifican.
Los conceptos que no mencionamos en esta sección y que lleguemos a usar se definirán en el lugar adecuado.
3. Unicoherencia y Propiedad b)
Iniciemos con el siguiente concepto, que es una herramienta muy útil en la búsqueda de agujeros. Sea Z un espacio topológico. Decimos que Z tiene la propiedad b) si para cada función continua ƒ: Z → S1, existe una función continua h: Z → R tal que ƒ = exp oh, donde exp es la función de R sobre S1 definida por exp(t) = (cos(2πt), sin(2πt)). A la función h se la llama levantamiento de ƒ.
Esta sección tiene dos propósitos. El primero es mostrarle al lector algunos de los resultados que sirven como herramientas para la búsqueda de agujeros. El segundo es mostrar la relación que hay entre la propiedad b) y la unicoherencia.
Proposición 3.1 ([1, Proposition 8, p. 2001]). Sea Z un espacio topológico tal que Z = A ∪ B, donde A y B son cerrados y conexos. Si A y B tienen la propiedad b) y A ∩ B es conexo, entonces Z tiene la propiedad b).
El siguiente resultado fue probado por S. Mardesic (1958).
Teorema 3.2 ([25, Lemma 5, p. 39]). Sea Z un espacio topológico y ƒ: Z → S1 una función continua. Entonces ƒ tiene un levantamiento si, y sólo si, ƒ es homotópica a una función constante.
Proposición 3.3. Sea Z un espacio topológico y sea Y un retracto por deformación de Z. Entonces Z tiene la propiedad b) si, y sólo si, Y tiene la propiedad b).
Demostración. Dado que Y es un retracto por deformación de Z, existen una retracción r: Z → Y y una función continua H: Z x I → Z tales que para cada z ∈ Z tenemos H(z, 0) = z y H(z, 1) = r(z).
Probemos la necesidad: sea ƒ: Y → S1 una función continua. Como Z tiene la propiedad b), existe un levantamiento h: Z → R de ƒ or. Consideremos h | Y: Y → R. Dado y ∈ Y, tenemos que exp oh | Y (y) = ƒ o r(y) = ƒ (y). Esto prueba que ƒ tiene un levantamiento, y por tanto Y tiene la propiedad b).
Para la suficiencia, consideremos una función continua ƒ: Z → S1. Probaremos que f es homotópica a una constante. Dado que Y tiene la propiedad b), por el Teorema 3.2, ƒ |Y es homotópica a una constante. De manera que existen s0 ∈ S1 y una función F: Y x I → S1 tales que, para cada y ∈ Y, F(y, 0) = ƒ |Y(y) y F(y, 1) = s0. Definimos F1: Z x I → S1 por
Como f (H(z, 1)) = ƒ (r(z)) y F(r(z), 0) = ƒ (r(z)), para toda z ∈ Z, tenemos que F1 es continua. Además, para cada z ∈ Z tenemos que F1 (z, 0) = ƒ (H(z, 0)) = ƒ (z) y F1(z, 1) = F(r(z), 1) = s0. De tal manera que ƒ es homotópica a una constante y por el Teorema 3.2 ƒ tiene un levantamiento, así concluimos que Z tiene la propiedad b).
Proposición 3.4. Cada espacio topológico contráctil tiene la propiedad b).
Demostración. Si Z es contráctil, entonces existe z ∈ Z tal que {z} es un retracto por deformación de Z. Dado que {z} tiene la propiedad b), por la Proposición 3.3, Z tiene la propiedad b).
Ahora hablaremos de la unicoherencia y la relación que tiene con la propiedad b).
Teorema 3.5 ([14, Théorème 2 and 3, p. 69 and 70] o [30, Theorem 7.3, p. 227]). Sea Z un espacio topológico normal. Si Z tiene la propiedad b), entonces es unicoherente.
Ejemplo 3.6. Tenemos que el intervalo I tiene la propiedad b); resulta ser un agradable ejercicio probar que esto es verdad. La circunferencia S1 no la tiene; para ver esto se puede probar que la identidad iS1: S1 → S1 no tiene un levantamiento. Una familia de continuos que tiene la propiedad b) es la de los Elsa continuos (ver [27, 12.66, p. 269]) y por el Teorema 3.5 es unicoherente. Por otro lado, es posible probar directamente que el intervalo 1 es unicoherente, mientras que la circunferencia S1 no es unicoherente.
Observación 3.7. La implicación en la otra dirección del Teorema 3.5 no siempre es cierta; un ejemplo de esto es X = S1 ∪ {[1 + 1/t]exp(it): t ≥ 1}, representado en el plano complejo. Este continuo es una compactación del rayo R = [0, ∞) con residuo S1. Al estudiar este continuo, podemos ver que sólo hay cuatro tipos de subcontinuos: puntos, arcos, S1 y homeomorfos a X. Con esto es fácil probar que X es unicoherente. Por otro lado, se puede probar que una función ƒ: X → S1, tal que ƒ |S1 = iS1, no tiene levantamiento.
Existe una equivalencia para estas dos propiedades.
Teorema 3.8 ([13, Theorem 3, p. 70]). Sea Z es un espacio topológico T1, normal y localmente conexo. Z es unicoherente si, y sólo si, Z tiene la propiedad b).
Sean Y y Z dos continuos. Sea ƒ: Y → Z una función continua; decimos que ƒ es monótona si para cada y ∈ Y se tiene que ƒ -1(y) es un continuo.
Teorema 3.9 ([30, Theorem 2.21, p. 138]). La unicoherencia es invariante bajo funciones monótonas entre continuos.
Teorema 3.10 ([30, Corollary 7.41, p. 228]). La propiedad b) es invariante bajo funciones monótonas entre continuos localmente conexos.
Teorema 3.11 ([30, Theorem 7.5, p. 228]). Si dos continuos Z y Y tienen la propiedad b), entonces Z x Y también la tiene.
Teorema 3.12. Sea Y un espacio conexo. Si X x Y es unicoherente, entonces X es unicoherente.
Demostración. Supongamos que X x Y es unicoherente. Consideremos la proyección πX: X x Y → X dada por πX (x,y) = x para cualquier (x,y) ∈ X x Y. Nótese que πX es monótona. Por [17, Theorem 3.6, p. 40] tenemos que πX (X x Y) = X es unicoherente.
El recíproco del teorema anterior no se sabe si es cierto; de hecho pertenece a un problema abierto más general del cual se sabe en algunos casos. K. Kuratowsky (1930) propuso el problema: ¿es unicoherente el producto de dos continuos unicoherentes de Peano? Bursuk en [11] contestó afirmativamente este problema. S. Eilenberg [14] dio una prueba para un caso más general: el producto de dos espacios métricos unicoherentes localmente conexos es unicoherente. Fue T. Ganea en [15, Theorem 1.3, p. 35] que dio una generalización de esto: el producto de una familia arbitraria de espacios unicoherentes localmente conexos es unicoherente. Se sabe que el continuo X de la observación 3.7 cumple que X x X no es unicoherente (ver [17, Example 5.5, p. 48 and 49]).
4. Búsqueda de agujeros
Consideremos los siguientes espacios topológicos H(X):
2X = {A ⊂ X: A es cerrado y no vacío}, el hiperespacio de los cerrados de X.
Cn(X) = {A ∈ 2X: A tiene a lo más n componentes}, el hiperespacio de los cerrados con a lo más n componentes de X.
Fn(X) = {A ∈ 2X: A tiene a lo más n elementos}, el n-ésimo producto simétrico de X.
Cono(X) = (X x I)/(X x {1}), el cono topológico de X.
Sus(X) = Cono(X)/(X x {0}), la suspensión topológica de X.
Si n = 1, entonces a C1 (X) lo escribiremos como C(X) y lo llamaremos el hiperespacio de subcontinuos, a F1(X) lo llamaremos el hiperespacio de los unipuntuales y a F2(X) lo llamaremos el segundo producto simétrico de X. A los primeros tres los consideramos con la métrica de Hausdorff (ver [20]). En los últimos dos se consideran la topología producto y la topología cociente.
Presentamos ahora la definición de nuestro interés: sea Z un espacio topológico unicoherente y sea z ∈ Z. Decimos que z agujera (o hace agujero) en Z si Z - {z} no es unicoherente.
Para ilustrar la importancia de la busqueda de elementos que agujeran, mencionamos el siguiente caso que sirvió para distinguir diferencias entre espacios topológicos. En [19, lemmas 2.1 and 2.2, p. 348 and 349] A. Illanes probó que C2([0,1]) - {A} es unicoherente para cada A ∈ C2([0,1]), mientras que C2(S1) - {S1} no es unicoherente. Como consecuencia, A. Illanes obtuvo que C2 ([0, 1]) y C2 (S1) no son homeomorfos; esto contrasta con el hecho de que C([0,1]) y C(S1) son homeomorfos: ambos son homeomorfos a I2 (ver [20, Example 5.1 y Example 5.2, p. 33-36]). Este tr es el primero en donde se estudia la unicoherencia de un espacio topológico sin un elemento, aunque no es ahí en donde se le da el nombre. El primer trabajo que aborda el problema de manera directa y que define el concepto es [1].
Por definición vemos que para buscar elementos que agujeren un espacio debemos tener necesariamente que este espacio sea unicoherente. En [29, Corollary 1.176, p. 178] S. B. Nadler Jr. probó que los hiperespacios 2X y C(X) son unicoherentes para cualquier X. En [24] S. Macías probó que el hiperespacio Cn(X) tiene la propiedad b) y que es unicoherente, para cualquier X y para todo n ≥ 1. El mismo autor en [23] probó que el hiperespacio Fn(X) es unicoherente, para cualquier X y para todo n ≥ 3. Para el cono y la suspensión tenemos lo siguiente. Al considerar a Z como espacio métrico, tenemos que Cono(Z) y Sus(Z) son espacios normales (ver [5, Proposition 3.2]). Por otro lado, se prueba con cierta facilidad que si v es el vértice del cono, entonces {v} es un retracto por deformación de Cono(Z), así que Cono(Z) es contráctil. Por la Proposición 3.4 tenemos que Cono(Z) tiene la propiedad b), y en consecuencia es unicoherente por el Teorema 3.5. Ahora, por [17, Theorem 3.6, p. 40] tenemos que Sus(X) es unicoherente. Como habrá notado el lector, el caso de F2(X) es uno aparte. Se sabe que F2(S1) es homeomorfo a la Banda de Moebius (ver [20, Exercise 1.26, p. 9]), la cual no es unicoherente, como es fácil de ver. También se conoce un continuo que es unicoherente, pero cuyo segundo producto simétrico no lo es (ver [12]). Esto lleva a estudiar la generalización de la unicoherencia en este hiperespacio (ver las conclusiones al final).
Antes de iniciar con la descripción de los resultados vamos a ver un poco de las herramientas que se usan en los hiperespacios.
Una función continua μ: 2X → [0, ∞) es llamada una función de Whitney si μ ({p}) = 0 para p ∈ X y μ (A) < μ (B) si A ⊂ B. Si agregamos la condición μ (X) = 1 podemos definir a la función sobre I. Además podemos hacer la restricción a C(X). La existencia de funciones de Whitney se garantiza en [20, Theorem 13.4, p. 107]. Un nivel de Whitney es un subconjunto de C(X) de la forma μ-1(t) para t ∈ I. Un bloque de Whitney es un subconjunto de C(X) de la forma μ-1([a, b]) para [a, b] ⊂ I. Se sabe que los niveles y bloques de Whitney son sobcontinuos de C(X) (ver [20, Theorem 19.9, p. 160]).
4.1. Para C(X)
En [1] el autor prueba los siguientes resultados.
Teorema 4.1 ([1, Theorem 1, p. 2001]). Si pq es un arco libre en X tal que p y q no son puntos interiores de pq, entonces pq agujera a C(X).
Demostración. Sea Y = X - int(pq). Consideremos los siguientes subconjuntos de C(X): D1 = {A ∈ C(X) - {pq}: A ⊂ pq} y D2 = {B ∈ C(X) - {pq}: B ∩ Y ≠ ∅}. Tenemos que D1 y D2 son subconjuntos cerrados y conexos de C(X) - {pq}, y además D1 ∪ D2 = C(X) - {pq}. Veamos qué sucede con la intersección. Sean ε1 = {pr ⊂ pq: r ∈ pq - {q}} y ε2 = {tq ⊂ pq: t ∈ pq - {p}}. Es fácil ver que ε1 ∩ ε 2 = ∅. Como D1 ∩ D2 = ε1 ∪ ε2, podemos concluir que C(X) - {pq} no es unicoherente, y por lo tanto pq agujera a C(X).
Teorema 4.2 ([1, Theorem 2, p. 2001]). Si X es un continuo localmente conexo y X no es una curva cerrada simple, entonces X no agujera a C(X).
Demostración. Consideremos una función de Whitney μ: C(X) → I. Por [18, Theorem D, p. 253] tenemos que existe s < 1 tal que μ-1(s) es unicoherente. Por [18, Theorem A, p. 252] tenemos que μ-1(t) es unicoherente para cada t ∈ [s, 1]. Ahora, por [29, Theorem 14.9, p. 408] tenemos que μ-1(t) es localmente conexo para cada t ∈ I. Por Teorema 3.8 tenemos que μ-1(t) tiene la propiedad b), para cada t ∈ [s, 1]. Se puede probar que μ 1(t) es un retracto por deformación de μ-1([0,t]) (el lector interesado puede usar la función continua definida en [29, 0.65.1, p. 37]). Así, por la Proposición 3.3 tenemos que μ-1([0,t]) tiene la propiedad b) para t ∈ [s, 1].
Sea ƒ: (C(X) - {X}) - S1 una función continua. Fijemos a un punto x0 ∈ X y a un número t0 ∈ exp-1(ƒ({x0})). Sea {tn} una sucesión real estrictamente creciente tal que t1 = s y {tn} → 1. Para cada n ∈ N, sea ƒn = ƒ|μ −1 ([0,tn ]). Para cada n ∈ N, considere hn: μ-1([0,tn]) → R el único levantamiento de ƒn tal que hn({x0}) = t0. Definamos ahora h:
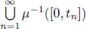→ R dada por h(A) = hn(A), si A ∈ μ-1([0,tn]). No es difícil ver que h está bien definida y que es continua. También es sencillo ver que si A ∈
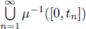, entonces h(A) = exp(ƒ (A)). Dado que C(X) - {X} =
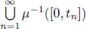, podemos concluir que h es un levantamiento de ƒ. Por lo tanto X no agujera a C(X).
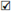
Si X ≈ S1, entonces X ∈ int(C(X)) considerada como una 2-variedad (ver [20, Example 5.2, p. 35]). En este caso tenemos que X agujera a C(X).
Sea H ∈ {2X, C(X)} y sea KA = {B ∈ H: A ⊂ B}, para A ∈ H.
Lema 4.3 ([1, Lemma 13, p. 2004]). Sea K un subconjunto no vacío de H. Si KA C K, para cada A ∈ K, entonces K tiene la propiedad b).
La prueba del siguiente resultado se sigue de manera natural del lema anterior, considerando a K = H - {x}
Teorema 4.4 ([1, Theorem 3, p. 200.1]). Si x ∈ X, entonces {x} no agujera a 2X y {x} no agujera a C(X).
Para la demostración del siguiente teorema el autor usa la siguiente afirmación: Sea p un elemento de X y Y1, Y2 ∈ C(X) tales que Y1, Y2 son no degenerados, X = Y1 ∪ Y2 y Y1 ∩ Y2 = {p}. Entonces existe una función de Whitney μ: C(X) → I tal que μ (Y1) < μ (Y2) y μ-1(μ(Y1)) - {Y1} es conexo. (Ver [1, Lemma 14, p. 2005]).
Teorema 4.5 ([1, Theorem 4, p. 2001]). Si pq es un arco libre en X tal que p no es un punto interior de pq y q es un punto interior de pq, entonces pq no agujera a C(X).
Demostración. Sea ƒ: (C(X) - {pq}) → S1 una función continua. Probando que ƒ tiene un levantamiento podemos concluir que C(X) - {pq} tiene la propiedad b). Sea Y = X - int(pq). Notemos que X = Y ∪ pq y Y ∩ pq = {p}. Así que Y es conexo (ver [1, Proposition 7, p. 2001]). Por lo tanto pq y Y cumplen las condiciones de la afirmación previa a este teorema, y tenemos que existe una función de Whitney μ: C(X) → I tal que μ-1(μ(pq)) - {pq} es conexa. Sea t0 = μ(pq). Consideremos las siguientes funciones ƒ1 = ƒ |μ-1 ([t0,1])-{pq} y ƒ2 = ƒ |μ-1([0, t0])-{pq}. Ahora se puede probar que existen funciones continuas g1: (μ-1([t0,1]) - {pq}) → R y g2: (μ-1([0,t0]) - {pq}) → R, tales que ƒ1 = exp °g1, ƒ2 = exp °g2 y g1 |μ-1 (t0)-{pg} = g2 |μ-1 (t0)-{pq}. Ya para finalizar se define la función g: (C(X) - {pq}) → R dada por
Entonces g es un levantamiento de f, y con esto se concluye la prueba.
Teorema 4.6 ([1, Theorem 5, p. 2001]). Si S es una curva cerrada libre en X, entonces S agujera a C(X).
Demostración. Sea S una curva cerrada libre, e identifiquémosla con el círculo unitario de R2. Como suponemos que S es libre, existe p ∈ S tal que p ∉ int(S) y S - {p} es un subconjunto abierto de X. Denotemos como p0 el punto diametralmente opuesto a p, y tomemos un punto fijo p1 ∈ S - {p,p0}. Sea p0p1 el arco en S que cumple que p ∉ p0p1.
Definamos la función m: C(S) - {S} → S tal que m(B) es el punto de B que lo divide en dos subarcos de igual longitud, siempre que B sea un arco. Si B es un singular, entonces m(B) = B.
Sean
Dado que S es un subconjunto cerrado de C(X) - {S}, por [1, Lemma 15, p. 2006] tenemos que F es un subconjunto cerrado conexo de C(X) - {S}. Por otro lado, por [1, Proposition 7, p. 2001] tenemos que Y = X - int(S) es conexo y por lo tanto un subcontinuo de X. Más aún, C(Y) es cerrado en C(X) - {S}. Entonces G1 = F ∪ C(Y) es cerrado en C(X) - {S}. También se puede ver que es conexo.
Definamos ahora
Tenemos que G2 es un cerrado conexo de C(X) - {S}. De aquí es sencillo ver que C(X) - {S} = G1∪G2, y que G1∩G2 no es conexo. Por lo tanto, C(X) - {S} no es unicoherente.
Con respecto a los Teoremas 4.1 y 4.5, el autor hace notar que no se considera el caso cuando p y q son puntos interiores del arco libre pq. En este caso tenemos que pq es abierto y cerrado en X, así X es un arco y C(X) es una 2-celda (ver [20, Example 5.1, p. 33]). Como X ∈ bd(C(X)) considerada como 2-variedad, tenemos que pq no agujera a C(X).
En [2] el autor da la clasificación de los elementos que agujeran a C(X) cuando X es un continuo localmente conexo. El teorema de clasificación es el siguiente.
Teorema 4.7 ([2, Theorem 7.1, p. 13]). Supongamos que X es localmente conexo y sea A un subcontinuo de X. Tenemos que A agujera a C(X) si, y sólo si, A es de una de las siguientes formas:
A = X y X es una curva cerrada simple;
A es una curva cerrada simple libre, o
A = pq es un arco libre tal que p,q ∉ int(A).
Demostración. Probemos primero la necesidad. Sea A un subcontinuo de X y supongamos que A agujera a C(X). Si A = X, por el Teorema 4.2 tenemos que X es una curva cerrada. Supongamos que A ≠ X. Por [2, Proposition 6.2, p. 12] A es localmente conexo. Ahora, por [2, Proposition 3.5, p. 8] A es una curva cerrada simple o es un arco libre. Si es el caso de que sea una curva cerrada simple, por [2, Proposition 5.4, p. 11] A es una curva cerrada libre. En el caso de que A sea un arco libre con puntos finales p y q, por el Teorema 4.5 p,q ∉ int(A).
Para la suficiencia, supongamos que A = X y X es una curva cerrada. Es un resultado conocido que C(X) es homeomorfo al disco unitario, y dado que A está en el interior del disco unitario considerado como una variedad, tenemos que A agujera a C(X). Los dos casos restantes se siguen de los teoremas 4.1 y 4.6.
En [4] los autores estudian los agujeros en dos tipos de continuos: estos son los abanicos suaves y los Elsa continuos.
Tenemos que un abanico X con vértice v se le llama suave si siempre que {xn} → x en X, entonces {vxn} → vx en C(X). Además, decimos que un arco A es un arco simple si A∩E(X) = ∅, y si existe {An} en C(X) tal que {An} → A y para cada n ∈ N se cumple que v ∉ An, int(An) ≠ ∅ y A ∩ An ≠ ∅.
El siguiente teorema da la clasificación de los elementos que agujeran a C(X) cuando X es un abanico suave.
Teorema 4.8 ([4, Theorem 3.8, p. 136]). Sea X un abanico suave con vértice v y A ∈ C(X). Entonces A hace agujero en C(X) si, y sólo si, A es un arco simple.
Demostración. Para la necesidad. Sea A un subcontinuo de X y supongamos que A agujera a C(X). Por el Teorema 4.4 y por [4, Theorem 3.3, p. 134], tenemos que A es un arco pq. Por [4, Theorem 3.6, p. 135] y [4, Theorem 3.7, p. 136], vemos que pq ⊂ ve - {v,e}, donde e ∈ E(X). Además, qe es un arco libre en X. Con esto resulta fácil de ver que A es un arco simple.
La suficiencia se sigue de [4, Theorem 3.5, p. 135].
El siguiente teorema da la clasificación de los elementos que agujeran a C(X) cuando X es un Elsa continuo.
Teorema 4.9 ([4, Theorem 4.4, p. 138]). Sea X = J∪R un Elsa continuo y sea A ∈ C(X). Tenemos que A agujera a C(X) si, y sólo si, A es un arco libre pq tal que p,q ∉ int(pq).
Demostración. Para la necesidad. Sea A un subcontinuo de X y supongamos que A agujera a C(X). Por el Teorema 4.4, por [4, Theorem 4.2, p. 137] y por [4, Theorem 4.3, p. 138], A es un arco contenido en R. Así, A es un arco libre en X. Por el Teorema 4.5 debemos tener que p,q ∉ int(pq).
La suficiencia se sigue del Teorema 4.1.
4.2. Para F2(X)
En [9] los autores estudian los agujeros en el segundo producto simétrico en dos tipos de continuos. El siguiente teorema da la clasificación de los elementos que agujeran a F2(X), cuando X es una dendrita.
Teorema 4.10 ([9, Theorem 2.7, p. 86]). Sea X una dendrita y sea {x,y} ∈ F2(X). Tenemos que {x,y} hace agujero en F2(X) si, y sólo si, x ≠ y y ni x ni y son puntos finales de X, o si x = y y x es un punto de ramificación.
Demostración. Sean x,y ∈ X tales que {x,y} agujera a F2(X). Si x = y, por [9, Theorem 2.6, p. 86] y por [9, Corollary 2.5, p. 86] tenemos que x es un punto de ramificación de X. Si x ≠ y, entonces por [9, Corollary 2.5, p. 86] ninguno de los puntos pueden ser finales en X. El recíproco lo tenemos por [9, Theorem 2.1, p. 84] y [9, Theorem 2.2, p. 84].
El siguiente teorema da la clasificación de los elementos que agujeran a F2(X) cuando X es un abanico que es homeomorfo a un cono sobre un compacto.
Teorema 4.11 ([9, Theorem 3.10, p. 91]). Sea X un abanico que es homeomorfo a un cono sobre un compacto, sea {x,y} ∈ F2(X) y sea v el punto de ramificación. Tenemos que {x,y} hace agujero en F2(X) si, y sólo si, x = y = v, o y ≠ x y x,y ∈ Cut(X) ∪{v}.
Demostración. Sean x,y ∈ X tales que {x,y} agujeran a F2(X). Si x = y, por [9, Theorem 3.4, p. 87] y [9, Theorem 3.8, p. 87] tenemos que x = v. Si x ≠ y, entonces por [9, Theorem 3.6, p. 87] y [9, Theorem 3.9, p. 89] tenemos que x,y ∈ Cut(X) ∪{v}. El recíproco lo tenemos por [9, Theorem 3.2, p. 87], [9, Theorem 3.3, p. 87] y [9, Theorem 3.5, p. 87].
En [10] los autores estudian los agujeros en el segundo producto cuando X es un continuo unicoherente localmente conexo. Para la prueba de que este hiperespacio es unicoherente, ver [16, Theorem 1].
Teorema 4.12 ([10, Theorem 3.5, p. 258]). Sea X un continuo unicoherente localmente conexo y sean x,y ∈ X. Tenemos que {x,y} agujera a F2(X) si, y sólo si, ocurre una de las situaciones siguientes: x = y y X - {x} tiene al menos tres componentes; o x ≠ y y x y y son puntos de corte de X.
Demostración. Sean x,y ∈ X tales que {x,y} agujeran a F2(X). Por [10, Theorem 3.3, p. 257] tenemos que x,y ∈ Cut(X). Si x = y, por [10, Theorem 3.4, p. 257] vemos que X - {x} tiene al menos tres componentes. El recíproco lo tenemos por [10, Theorem 3.1, p. 256] y [10, Theorem 3.2, p. 256].
4.3. Para Cono(X) y Sus(X)
En [5] los autores estudian los agujeros en el cono topológico y la suspensión topológica. Antes de enunciar los resultados demos la notación que se usa. Consideremos Z como espacio métrico. El vértice del Cono(Z) se denota por v y es el punto donde se identifica Z x {1}. Un elemento de Cono(Z) - {v} será denotado por [z,t]c, con z ∈ Z y t ∈ [0,1). La base del Cono(Z) es el conjunto B(Z) = {[z,0]c: z ∈ Z}. Para la Sus(Z), el punto de identificación es denotado por BZ. Para todo [z,t]c ∈ Cone(Z) - {B(Z),v} su clase en Sus(Z) es denotada por [z,t]s. Los resultados que los autores encuentran son los siguientes.
Proposición 4.13 ([5, Proposition 3.4]). Sea Z un espacio métrico. Entonces ningún z ∈ Z, [z,0]c agujera a Cono(Z).
Demostración. Se puede probar con cierta facilidad que Cono(Z) - {[z, 0]c} es contráctil, y por la Proposición 3.4 tiene la propiedad b). Ahora, por [5, Proposition 3.2] este espacio es normal y por el Teorema 3.5 tenemos que es unicoherente.
Observación 4.14. Como una aplicación del resultado anterior consideremos a I2. Es sabido que I2 ≈ Cono(S1), así que si Z ≈ I2 tenemos que para todo z ∈ ∂(Z) se cumple que Z - {z} es unicoherente y tiene la propiedad b), ya que es localmente conexo, donde ∂(Z) denota la frontera de Z vista como una variedad.
Proposición 4.15 ([5, Proposition 3.6]). Sea Z un espacio métrico y supongamos que pq es un arco libre en Z tal que p,q ∈ int(pq). Si r ∈ pq, entonces para todo t0 ∈ (0,1) tenemos que [r,t0]c agujera a Cono(Z).
Demostración. Sea r0 ∈ pq tal que r0 ≠ r. Consideremos un arco rr0 de r a r0 contenido en pq. Se consideran ahora los subconjuntos C1 = {[s,t]c: s ∈ rr0,t ∈ [0,t0]} - {[r,t0]c} y C2 = cl(Cone(Z) -C1) - {[r,t0]c}. Entonces C1 ∪C2 = Cone(Z) - {[r,t0]c} y C1∩C2 = {[r,t]c: t ∈ [0,t0)}∪{[r0,t]c: t ∈ [0,t0]} ∪{[s,t0]c: s ∈ rr0, s ≠ r}, la cual no es conexa. Así, podemos concluir que [r,t0]c agujera a Cone(Z).
Proposición 4.16 ([5, Proposition 3.7]). Sea Z un espacio métrico y supongamos que pq es un arco libre en Z. Si p ∈ int(pq), entonces para todo t0 ∈ (0,1) tenemos que [p,t0]c no agujera a Cono(Z).
Demostración. Tenemos que Cone(Z) tiene la propiedad b) por ser contráctil. Por otro lado, Cone(pq) es una vecindad conexa de [p,t0]c en Cone(Z) y bd(Cone(pq)) es conexa. Por la Observación 4.14, Cone(pq) - {[p,t0]c} tiene la propiedad b). Por lo tanto, por [2, Theorem 2.4, p. 3] tenemos que Cone(Z) - {[p,t0]c} tiene la propiedad b), y por el Teorema 3.5 es unicoherente.
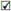
Proposición 4.17 ([5, Proposition 3.8]). Sean Z un espacio métrico y z0 ∈ Z tal que Z - {z0} es conexo. Si Z tiene la propiedad b), entonces para todo t0 ∈ (0,1) tenemos que [p,t0]c no agujera a Cono(Z).
Demostración. Sea z0 ∈ tal que Z - {z0} es conexo, y sea t0 (0,1). La idea de la demostración es usar la Proposición 3.1. Los subconjuntos que se usan son C1 = {[z,t]c: z ∈ Z,t ∈ [0,t0]} - {[z0,t0]c} y C2 = cl{Cone(Z) - C1} - {[z0,t0]c}, los cuales son cerrados y conexos en Cone(Z) - {[z0,t0]c}. De estos podemos ver que C1 ∪ C2 = Cone(Z) - {[z0,t0]c} y C1 ∩ C2 = Z x {t0} - {[z0,t0]c}. Por hipótesis tenemos que Z tiene la propiedad b), por la Proposición 3.3 C1 tiene la propiedad b) y por la Proposición 3.4 C2 tiene la propiedad b). Como C1 ∩ C2 es conexo, podemos concluir la prueba.
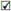
Para la prueba de la siguiente proposición basta usar el Teorema 3.12.
Proposición 4.18 ([5, Proposition 3.9]). Sea Z un espacio métrico. Si Z no es unicoherente, entonces v agujera a Cono(Z).
Los anteriores son los resultados que se presentan para el cono; para la suspensión son los siguientes.
Proposición 4.19 ([5, Proposition 3.10 and Proposition 3.11]). Para todo espacio métrico Z, ni BZ ni v agujeran a Sus(Z).
Demostración. Haremos la prueba sólo para BZ, ya que Sus(Z) - {v} ≈ Sus(Z) - BZ. Nótese que {v} es un retracto por deformación de Cone(Z) - B(Z). Así, Cone(Z) - B(Z) es contráctil, por la Proposición 3.4 tiene la propiedad b) y por el Teorema 3.5 es unicoherente. El resultado se sigue del hecho de que Cone(Z) -B(Z) ≈ Sus(Z) -BZ.
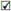
A diferencia del cono, si se cuenta con un teorema de clasificación para la suspensión, es el siguiente.
Teorema 4.20 ([5, Proposition 3.12]). Sean Z un espacio métrico y z ∈ Z. Tenemos que Z - {z} es conexo si, y sólo si, cualquiera que sea t0 ∈ (0,1), [z,t0]s no agujera a Cono(Z).
Demostración. Supongamos que Z - {z} es conexo. Para esta implicación se usa la Proposición 3.1 de la siguiente forma. Dado que {v} es un retracto por deformación de C1 = (Zx [t0,1]/Zx{1}) - {[z,t0]s} y {BZ}, lo es para C2 = (Zx [0,t0]/B(Z)) - {[z,t0]s}, y por la Proposición 3.4 ambos tienen la propiedad b). Como (Z x {t0}) - {[z,t0]s} ≈ Z - {z}, entonces C1 ∩ C2 es conexo. Por lo tanto C1 ∪ C2 tiene la propiedad b).
Para la otra implicación, sean z ∈ Z y t0 ∈ (0,1) tales que [z,t0]s no agujera a Sus(Z). Sean C1 = (Z x [t0,1]/Z x {1}) - {[z,t0]s} y C2 = (Z x [0,t0]/B(Z)) - {[z,t0],}. Ambos son subconjuntos cerrados y conexos de Sus(Z) - {[z, t0]s}. Además, C1 ∪ C2 = Sus(Z) - {[z,t0]s}. Así, por la unicoherencia de Sus(Z) - {[z, t0]s} tenemos que C1 ∩ C2 ≈ Z - {z} es conexa.
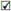
Como una aplicación de los resultados obtenidos sobre el cono y la suspensión, en el mismo trabajo los autores dan teoremas de clasificación para el cono y la suspensión de las siguientes familias de continuos.
gráficas finitas (ver [5, Subsection 4.1]);
n-celdas y el cubo de Hilbert (ver [5, Subsection 4.2]);
variedades cerradas conexas y variedades cerradas conexas con frontera (ver [5, Subsection 4.3]);
Elsa continuos (ver [5, Subsection 4.4]), y
Elsa círculos y doble Elsa círculos (ver [5, Subsection 4.5]).
4.4. Otros hiperespacios
En esta sección presentamos los resultados que se conocen para otros hiperespacios diferentes a los que ya se mencionaron.
Sabemos que si X es localmente conexo, entonces 2X ≈ I∞ (ver [20, Theorem 11.3, p. 89]). También sabemos que si X es localmente conexo sin arcos libres, entonces Cn(X) ≈ I∞ (ver [24, Theorem 7.1, p. 250]). En [5, Lemma 4.9] los autores prueban que en el cubo de Hilbert ningún elemento lo agujera, así que tenemos los siguientes dos teoremas.
Teorema 4.21 ([5, Theorem 5.1]). Si X es un continuo localmente conexo, entonces ningún A ∈ 2X agujera a 2X.
Teorema 4.22 ([5, Theorem 5.2]). Si X es un continuo localmente conexo sin arcos libres, entonces ningún A ∈ Cn(X), cualquiera que sea n ∈ N, puede agujerar a Cn(X).
Un resultado que presentan los autores en este trabajo es el siguiente.
Teorema 4.23 ([5, Theorem 5.5]). Sea Y un espacio métrico compacto. Consideremos X = Cono(Y) y a H(X) ∈ {2X,Cn(X),Fn(X)}, para n ∈ N. Entonces H(X) ≈ Cono(Z), donde Z es un continuo.
Para finalizar damos un corolario, consecuencia de este interesante resultado. Nótese que la prueba es una consecuencia directa de la Proposición 4.13.
Corolario 4.24 ([5, Corollary 5.6]). Sea Y un espacio métrico compacto. Consideremos X = Cono(Y) y a H(X) ∈ {2X, Cn(X), Fn(X)}, para n ∈ N. Si A ∈ Z = {A ∈ H(X): A ∩ B(Y) ≠ ∅}, entonces A no agujera a H(X). En particular, X no agujera a H(X).
4.5. Conclusiones
Hemos presentado los resultados que son el inicio de esta área de estudio, la cual continúa activamente. Por ejemplo, podemos mencionar dos trabajos más que están por aparecer. El primero es el estudio de los agujeros en el hiperespacio suspensión H(X) = C(X)/F1(X), ver [6]. El segundo aborda este problema para C(X) de den-droides suaves, ver [3]. La existencia de otras clases de continuos y de otros tipos de hiperespacios, abre una gran gama de posibles objetos de estudio. Aunada a todo esto, tenemos la posibilidad de estudiar los agujeros respecto al grado de multicoherencia (ver [27, Section 13.32, p. 292]) de un espacio topológico dado. Ejemplos de esto son los trabajos [7] y [8]. En [7] los autores estudian los agujeros respecto al grado de multicoherencia en el segundo producto simétrico de los subcontinuos del continuo conocido como Figura 8. En [8] los autores dan un teorema de clasificación de los agujeros respecto al grado de multicoherencia del segundo producto simétrico de gráficas conexas cíclicas.
