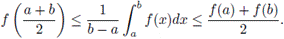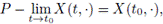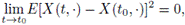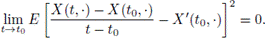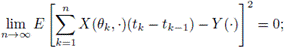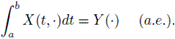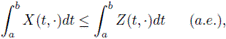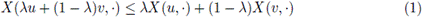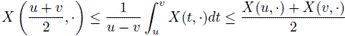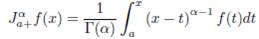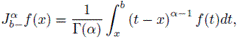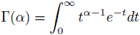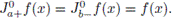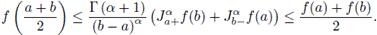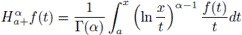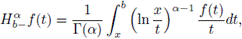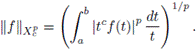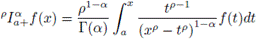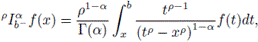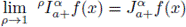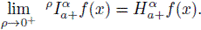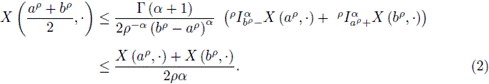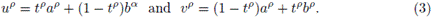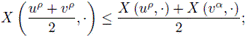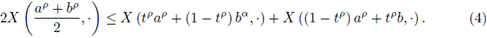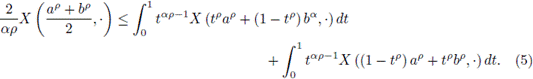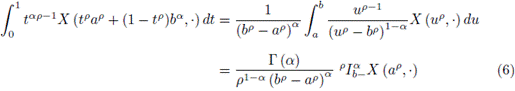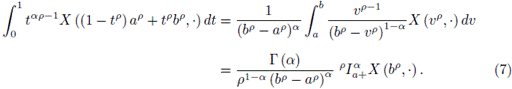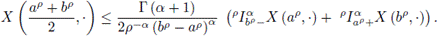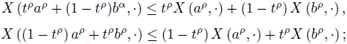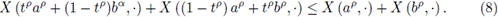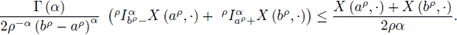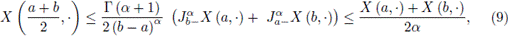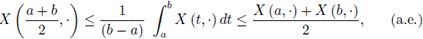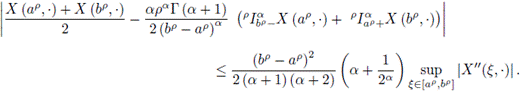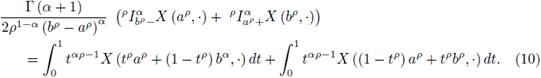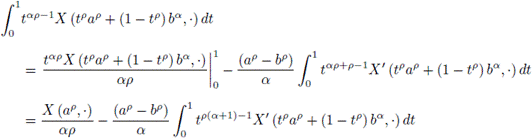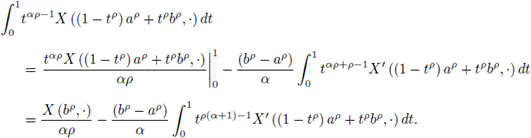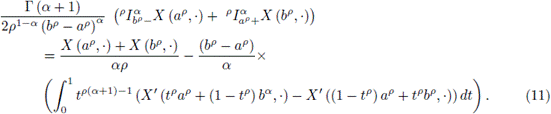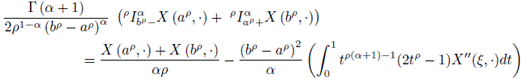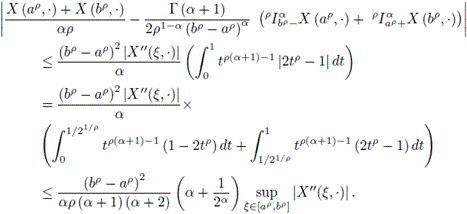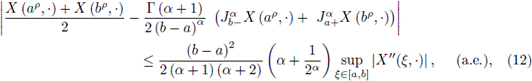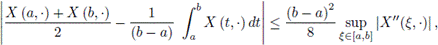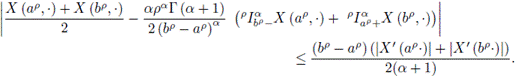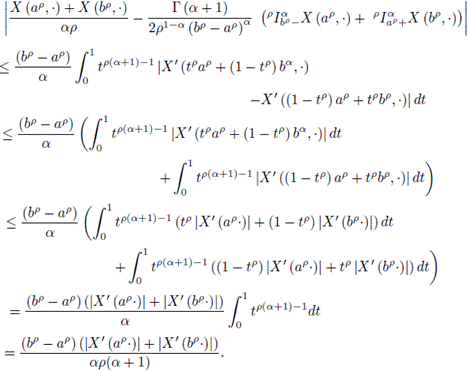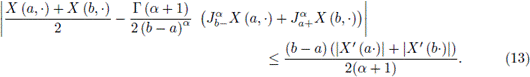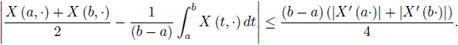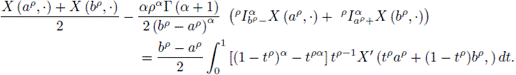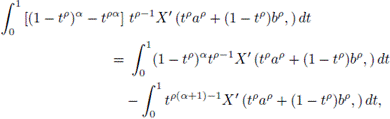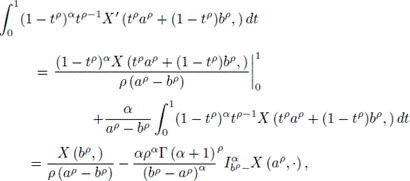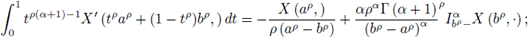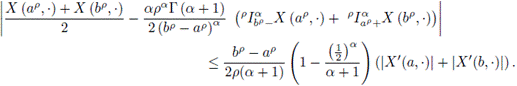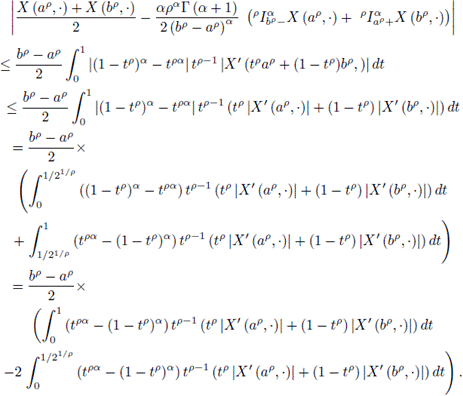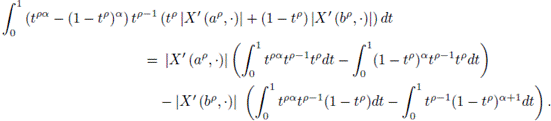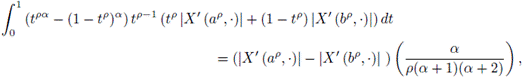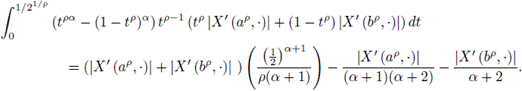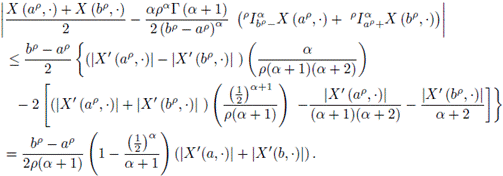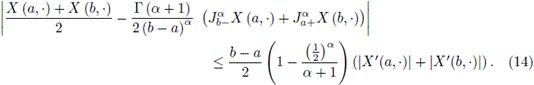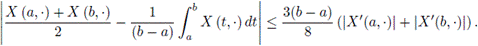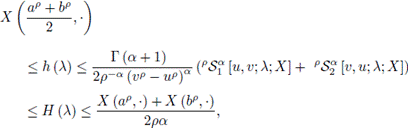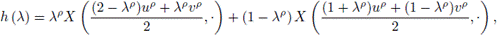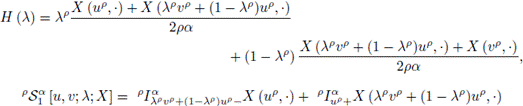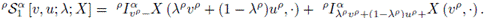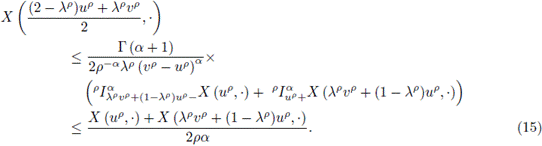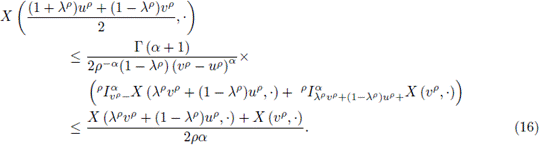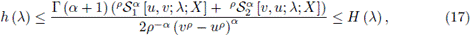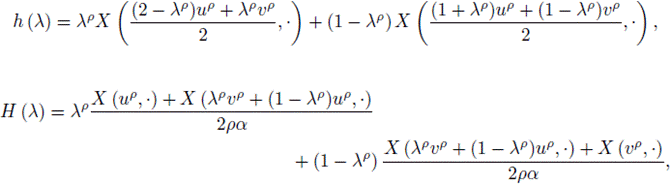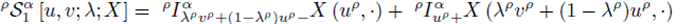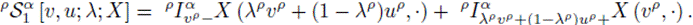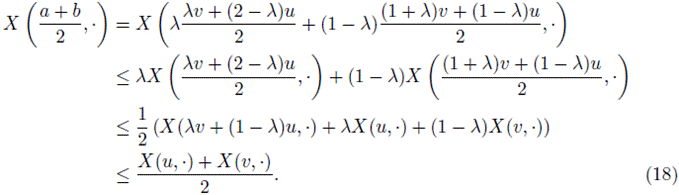Espanhol (pdf)
Artigo em XML
Referências do artigo
Tradução automática
Enviar este artigo por email
Citado por SciELO 
Citado por Google 
Similares em
SciELO 
Similares em Google 
Permalink
1. Introduction
The study of convex functions has been of interest for mathematical analysis based on the properties that are deduced from this concept. Due to generalization requirements of the convexity concept in order to obtain new applications, in the last years great efforts have been made in the study and investigation of this topic.
A function
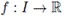is said to be convex if for all x,y ∈ I and t ∈ [0,1] the inequality
f (tx +(1 - t)y) ≤ tf (x) + (1 - t)f (y)
holds.
Numerous works of investigation have been realized extending results on inequalities for convex functions towards others much more generalized, using new concepts such as E-convexity [35], quasi-convexity [28], s-convexity [3], logarithmically convexity [2], and others.
A compendium about the history of the Hermite-Hadamard inequality can be found in the work of D.S. Mitrinovic and I.B. Lackovic [22]. The formulation of this result is as follows:
(Hermite-Hadamard Inequality). Let
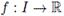be a convex function, and a, b ∈ I with a < b, then
The inequality of Hermite-Hadamard has become a very useful tool in the Theory of Probability and Optimization (See [18]).
The study on convex stochastic processes began in 1974 when B. Nagy, in [23], applied a characterization of measurable stochastic processes to solving a generalization of the (additive) Cauchy functional equation. In 1980 Nikodem [24] considered convex stochastic processes. In 1992 and 1995 Skowronski [31], [32] obtained some further results on convex stochastic processes which generalize some known properties.
In the year 2014, E. Set et. al. in [27] investigated Hermite-Hadamard type inequalities for stochastic processes in the second sense (For other results related to stochastic processes see [4], [9], [20], [29], [30], where further references are given).
Also, Fractional calculus [10], [21] was introduced at the end of the nineteenth century by Liouville and Riemann, the subject of which has become a rapidly growing area and has found applications in diverse fields ranging from physical sciences and engineering to biological sciences and economics.
In 2011, U. Katugampola presented a new fractional integral operator in [12], which generalizes the Riemann-Liouville and the Hadamard integrals into a single form, and various researchers have made use of this result in the field of convexity, generalized convexity and others ([5], [7], [8], [33]).
Recently, several Hermite-Hadamard type inequalities [19], [34] associated with fractional integrals have been investigated. Here, it is established some generalized Hermite-Hadamard type integral inequalities for stochastic processes using Katugampola fractional integral operator, which generalize, in a single form those found using Riemann-Liouville fractional integral and Hadamard fractional integral. Also, it is proposed a refinement of the inequality object of study using the aforementioned fractional integral. Application areas of the results found are optimization, especially in optimal designs, and also useful for numerical approximations when there exist probabilistic quantities [29].
2. Preliminaries
2.1. About calculus of stochastic processes.
The following notions corresponds to ordinary and convex Stochastic Process (References about can be found in [16], [17], [20], [31], [32].
Definition 2.1. Let (Ω, A, P) be an arbitrary probability space. A function
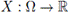is called a random variable if it is A-measurable.
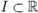be an interval indicating time. A function
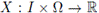is called a stochastic process if for every t ∈ I the function X(t, ·) is a random variable.
1. If X(t,w) takes values in
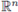it is called vector-valued stochastic process.
2. If the time I can be a discrete subset of
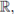then X(t,w) is called a discrete time stochastic process.
3. If the time I is an interval,
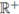or
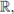it is called a stochastic process with continuous time.
Definition 2.2. Let (Ω,A,P) be a probability space and
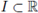be an interval. A stochastic process
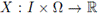is called:
1. Increasing (decreasing) if for all u,v ∈ I such that u < v,
X(u, ·) < X(v, ·), (X(u, ·) > X(v, ·)), (a.e.);
2. Monotonic, if it's increasing or decreasing;
3. Continuous in probability in the interval I, if for all t0 G I the following limit holds:
where P - lim denotes the limit in probability;
4. Mean square continuous in the interval I, if the limit for all t0 ∈ I
where E [X(t, ·)] denotes the expectation value of the random variable X(t, ·);
5. Mean square differentiate in I, if there exist a stochastic process X'(t, ·) (the derivative of X) such that for all t0 ∈ I we have
Definition 2.3. Let (Ω,A, P) be a probability space,
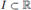be an interval with E [X(t)]2 < ∞ for all t ∈ I.
Let [a, b] ⊂ I, a = t0 < t1 < ... < tn = b be a partition of [a, b] and θk ∈ [tk-1, tk] for k = 1, 2,…,n.
A random variable
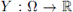is called mean-square integral of the process X(t, ·) on [a, b], if the following identity holds:
in such a way, it can be written
Also, mean square integral operator is increasing, that is,
where X(t, ·) ≤ Z(t, ·) in [a, b].
Throughout this paper, it will be considered mean square continuous stochastic processes.
Important theorems as the mean value theorem for mean square derivatives and integrals for stochastic processes have been proved in the work of J.C. Cortés et. al. The reader can find these results in [6, Lemma 3.1,Theorem 3.2].
In 1980 K. Nikodem introduced the following definition [24].
Definition 2.4. Set (Ω, A, P) be a probability space and
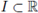be an interval. The stochastic process
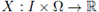is said to be a convex stochastic process if
holds almost everywhere for all u, v ∈ I and λ ∈ [0,1].
One of the results of interest for the present work is the following.
Theorem 2.5. Every Jensen-convex stochastic process and continuous in probability is convex.
Using Definition 2.4, D. Kotrys presented, in 2012, the Hermite-Hadamard integral inequality version for Stochastic Processes [16].
Theorem 2.6. If
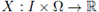is convex and mean square continuous in the interval T x Ω, then for any u, v ∈ T, the inequality
holds almost everywhere.
2.2. About generalized fractional integral operators
Before establishing the main results, it will be given some necessary notions and mathematical preliminaries of fractional calculus theory which are used further in this paper. For more details, consult [10], [15], [21], [25].
Definition 2.7. Let f ∈ L1 ([a, b]). The Riemann-Liouville integrals
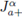and
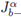of order α > 0 with a ≥ 0 are defined by
and
respectively, where Γ(α) is the Euler's Gamma function defined by
Note that
Using the Riemann-Liouville fractional integral, Sarikaya et all [26] established the Hermite-Hadamard inequalities version.
Theorem 2.8. Let
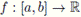be a positive function with a < b and f ∈ L1 ([a, b]). If / is a convex function on [a, b], then, with α > 0,
Also, J. Hadamard in 1892 introduced the following fractional integral operator ([11]).
Definition 2.9. Let α > 0 with
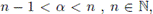and a < x < b. The left and right-side Hadamard fractional integrals of order α > 0 of a function f, are given by
and
respectively.
As it was mentioned in the introductory section, Katugampola introduced a new fractional integral that generalizes the Riemann-Liouville and Hadamard fractional integrals into a single form (see [12], [13], [14]).
In the following will denote the space
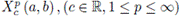of those complex valued Lebesgue measurable functions f on [a, b] for which
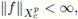where
Katugampola in [13] established the following definition and property.
Definition 2.10. Let
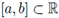be a finite interval. The left and right sides of Katugampola fractional integral of order
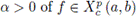are defined by
and
respectively, with a < x <b and p > 0, if the integrals exist.
Theorem 2.11. Let α > 0 and p > 0. Then, for x > a,
and
Similar results also hold for the right-sided operators.
The purpose of this paper is to derive some inequalities of type Hermite-Hadamard for convex stochastic processes using the Katugampola fractional integrals.
3. Main Results
Theorem 3.1. Let α > 0 and p > 0. Let
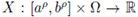be a positive stochastic process with 0 ≤ a < b and
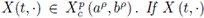is convex, the following inequality holds almost everywhere:
Proof. Let t ∈ [0,1], and u,v ∈ [a, b] defined by
Since X is a convex stochastic process,
using (3), it can be rewritten as
Multiplying both sides of (4) by tαp-1, (α, p > 0) and integrating over t ∈ [0,1], it is obtained that
Now, from (3) and the Definition 2.10, it is obtained that
and
Replacing (6) and (7) in (5), it is obtained the left side of the inequality (2)
In order to obtain the right side of the inequality(2) , it is used the convex property of the stochastic process X:
adding these inequalities it is obtained
Multiplying both sides of (8) by tαp-1, (a, p > 0) and integrating over t ∈ [0,1], it is attained that
The proof is complete.
Remark 3.2. Using the Theorem 2.11 we get the Hermite Hadamard inequality version for the Riemann Liouville fractional integral,
almost everywhere, making coincidence with the result proved by H. Aghahi and A. Babakhani in [1]. Letting α =1 in (9), it is obtained the Hermite Hadamard inequality for the ordinary Riemann integral
making coincidence with the result proved by Kotrys in [16].
Theorem 3.3. Let
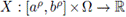be a square mean differentiable stochastic process with 0 ≤ a <b. If X' is a square mean differentiate stochastic process, then the following inequality holds almost everywhere:
Proof. From the proof of Theorem 3.1 we get
Integrating by parts each of the integrals we have
and
So,
Applying the Mean Value Theorem for X' it is obtained
for some ξ ∈ [ap, bp].
Now, it can be written
The proof is complete.
Remark 3.4. Using Theorem 2.11 and taking limit when p → 1 in Theorem 3.3, it is obtained the version for the Riemann-Liouville fractional integral
and letting α = 1 in (12) it is obtained the version for the ordinary Riemann integral
Theorem 3.5. Let α > 0 and p > 0. Let
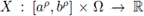be a mean square differentiate stochastic process with 0 ≤ a < b and
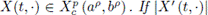is convex, then the following inequality holds almost everywhere:
Proof. Using equality (11), the triangular inequality and the convexity of
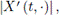it is obtained that
The proof is complete.
Remark 3.6. With the same reasoning used in Remarks 3.2 and 3.4, it is obtained the following inequality almost everywhere, for the Riemann-Liouville fractional integral:
Letting α = 1 in (13), it is obtained the inequality for the ordinary Riemann integral
Lemma 3.7. Let
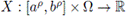be a mean square differentiate stochastic process; then the following equality holds:
Proof. First, it must be noted that
and using integration by parts it is obtained
and similarly,
adding these last results we get the desired result.
The proof is complete.
Theorem 3.8. Let
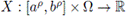be a mean square differentiate stochastic process on
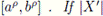is a convex stochastic process, then the following inequality holds almost everywhere:
Proof. Using Lemma 3.7 and the convexity of |X′|, it is obtained that
Making the corresponding substitution in the previous inequalities, we have:
With the change of variable x = tp it is obtained
and similarly,
So,
The proof is complete.
Remark 3.9. With the same reasoning used in Remarks 3.2, 3.4 and 3.6, it is obtained the following inequality almost everywhere, for the Riemann-Liouville fractional integral:
Letting α = 1 in (14), it is obtained the following inequality, almost everywhere, for the ordinary Riemann integral:
Next theorem proposes a refinement of the Hermite-Hadamard inequality using Katugam-pola fractional integral.
Theorem 3.10. Let α > 0 and p > 0. Let
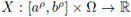be a positive stochastic process with 0 ≤ a < b and
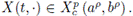If X (t, ·) is Jensen-convex and mean square continuous in the interval [ap, bp], the following inequality holds almost everywhere:
where
and
Proof. Applying (2) in the interval
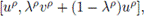we have:
Now, for the interval
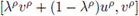we have:
Multiplying (15) by λp and (16) by (1 - λp), and adding these inequalities, we have
where
and
Using Theorem 2.5 it is seen that
From (17) and (18) it is attained the desired result. The proof is complete.
4. Conclusions
In the present article, the fractional integral of Katugampola was used to find the Hermite-Hadamard inequality for convex stochastic processes (Theorem 3.1), as well as some other results that estimate the difference between the value of the fractional integral and the right side of such inequality (Theorems 3.3, 3.5, 3.8), as well as a refinement of the aforementioned inequality (Theorem 3.10). From the results found, the same were deduced for the particular cases of Riemann-Liouville fractional integral and Riemann integral. The authors hope that this work will serve as a stimulus for future research in the area.
