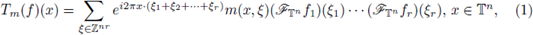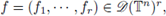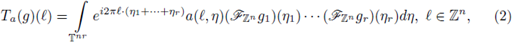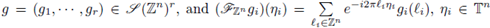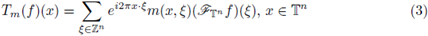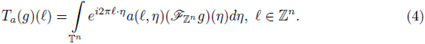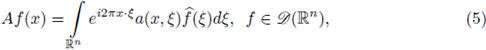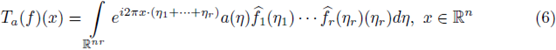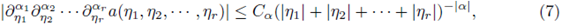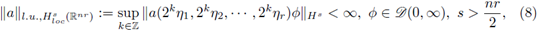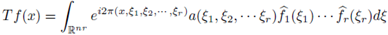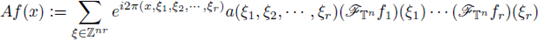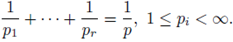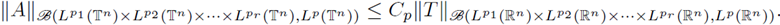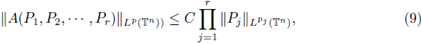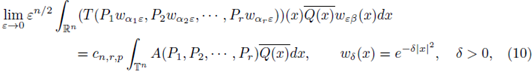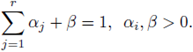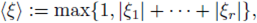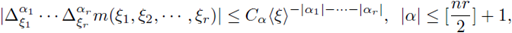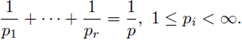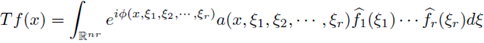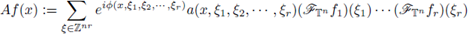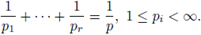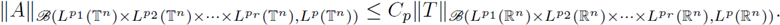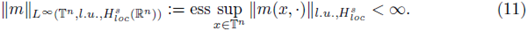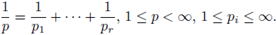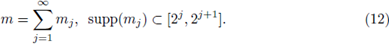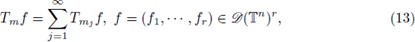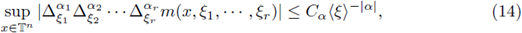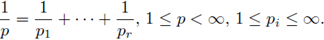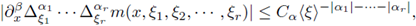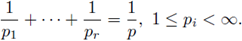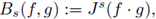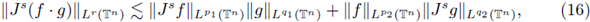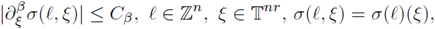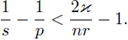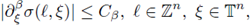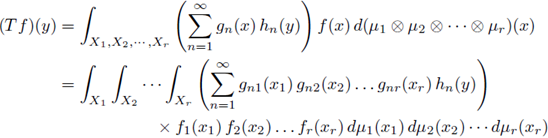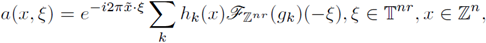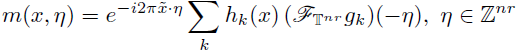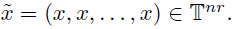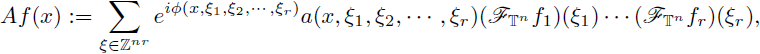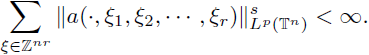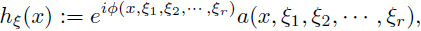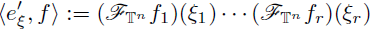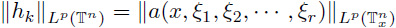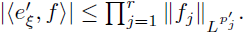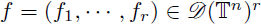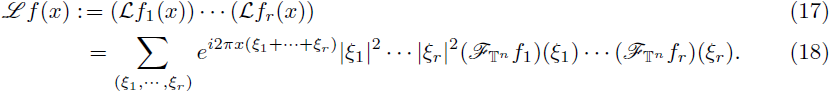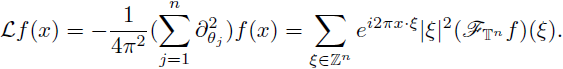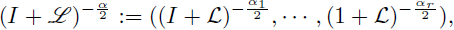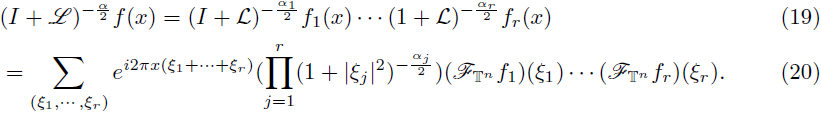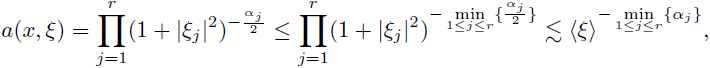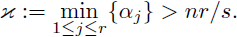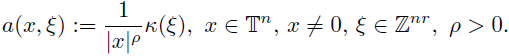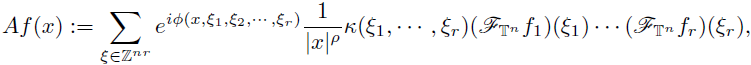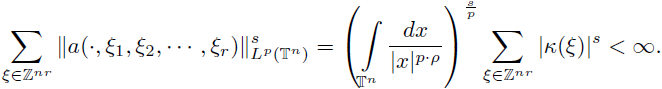1. Introduction
The goal of this note is to announce the main results about the Lp-multilinear analysis developed by the authors in [10] for periodic and discrete pseudo-differential operators. These operators can be defined by using the multilinear Fourier transform as follows. If
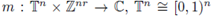 is a suitable function, then the periodic multilinear-pseudo-differential operator associated to m is the operator defined as
is a suitable function, then the periodic multilinear-pseudo-differential operator associated to m is the operator defined as
is the periodic multilinear Fourier transform of f. We have denoted by
 the space of smooth functions on the torus
the space of smooth functions on the torus
 endowed with its usual Fréchet structure. On the other hand, if α:
endowed with its usual Fréchet structure. On the other hand, if α:
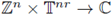 is a measurable function, then the discrete multilinear-pseudo-differential operator associated to α is the multilinear operator defined by
is a measurable function, then the discrete multilinear-pseudo-differential operator associated to α is the multilinear operator defined by
the discrete Fourier transform of gi. For r ≥ 2, these operators have been studied by V. Catană in [12]. If r = 1, these quantization formulae can be reduced to the known expressions
and
Periodic pseudo-differential operators (see (3)) were defined by Volevich and Agranovich [1]. The subsequent works of McLean [29], Turunen and Vainikko [47], and Ruzhansky and Turunen [44] developed a periodic analysis from Hörmander classes to applications to periodic equations, although the symbolic calculus was consistently developed by Ruzhansky and Turunen [44]. Nevertheless, the references Ruzhansky and Turunen [44], [45], Cardona [6], [7], [8], Delgado [15] and Molahajloo and Wong [34], [35], [36] provide some complementary results for the subject. Mapping properties for more general operators as periodic Fourier integral operators appear in Ruzhansky and Turunen [45] and Cardona, Messiouene and Senoussaoui [11].
In a more recent approach, pseudo-differential operators on
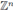 (discrete pseudo-differential operators) were introduced by Molahajloo in [36], and some of its properties were developed in the last years in the references [9], [17], [28], [38], [39], [40], [41], [43]. However, only the fundamental work L. Botchway, G. Kibiti, and M. Ruzhansky [5] includes properties about a discrete pseudo-differential calculus and applications to difference equations. The reference [9] discusses those relations of the theory of discrete pseudo-differential operators with important problems in number theory as the Waring problem and the hypothesis K
*
by Hooley.
(discrete pseudo-differential operators) were introduced by Molahajloo in [36], and some of its properties were developed in the last years in the references [9], [17], [28], [38], [39], [40], [41], [43]. However, only the fundamental work L. Botchway, G. Kibiti, and M. Ruzhansky [5] includes properties about a discrete pseudo-differential calculus and applications to difference equations. The reference [9] discusses those relations of the theory of discrete pseudo-differential operators with important problems in number theory as the Waring problem and the hypothesis K
*
by Hooley.
An overview to the mapping properties for pseudo-differential operators on
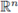 provides the expected results in the discrete and periodic setting. On
provides the expected results in the discrete and periodic setting. On
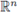 these operators have the form
these operators have the form
with
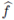 the euclidean Fourier transform of f (see Hörmander [25]). The nuclearity of pseudo-differential operators on
the euclidean Fourier transform of f (see Hörmander [25]). The nuclearity of pseudo-differential operators on
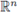 has been treated in Aoki and Rempala [2], [42]. In a context closely related to our work, multilinear pseudo-differential operators have been treated in Bényi, Maldonado, Naibo, and Torres, [3], [4], Michalowski, Rule and Staubach, Miyachi and Tomita [30], [31], [32], [33] and references therein. The multilinear analysis for multilinear Fourier multipliers
has been treated in Aoki and Rempala [2], [42]. In a context closely related to our work, multilinear pseudo-differential operators have been treated in Bényi, Maldonado, Naibo, and Torres, [3], [4], Michalowski, Rule and Staubach, Miyachi and Tomita [30], [31], [32], [33] and references therein. The multilinear analysis for multilinear Fourier multipliers
born with the works of Coifman and Meyer [13], [14], where the condition
for sufficiently many multi-indices α = (α1,α2, · · · , ar), was proved to be sufficient for the boundedness of Ta from
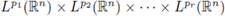 into
into
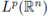 provided that 1/p = 1/p1 + 1/p2 + · · · + 1/pr, and 1 ≤ pi, p < ∞. A generalization for this result was obtained by Tomita in [46], where it was proved that the multilinear Hörmander condition
provided that 1/p = 1/p1 + 1/p2 + · · · + 1/pr, and 1 ≤ pi, p < ∞. A generalization for this result was obtained by Tomita in [46], where it was proved that the multilinear Hörmander condition
implies the boundedness of Ta from
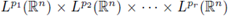 into
into
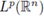 provided that 1/p = 1/p1 + 1/p2 + · · · + 1/pr, and 1 ≤ pi, p < ∞. The case r = 1 is known as the Hörmander-Mihlin theorem. These multilinear theorems have been generalized to Hardy spaces
provided that 1/p = 1/p1 + 1/p2 + · · · + 1/pr, and 1 ≤ pi, p < ∞. The case r = 1 is known as the Hörmander-Mihlin theorem. These multilinear theorems have been generalized to Hardy spaces
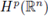 for suitable values of 0 < pi, p < ∞, in the works of Grafakos, Torres, Miyachi, Fujita, Tomita, Kenig, Stein, Muscalo, Thiele and Tao [19], [21], [22], [23], [24], [27], [37]. The main novelty of this work is that we provide discrete and periodic analogues for these works in the multilinear setting.
for suitable values of 0 < pi, p < ∞, in the works of Grafakos, Torres, Miyachi, Fujita, Tomita, Kenig, Stein, Muscalo, Thiele and Tao [19], [21], [22], [23], [24], [27], [37]. The main novelty of this work is that we provide discrete and periodic analogues for these works in the multilinear setting.
This note is organized as follows. In section 2 we provide those results on the boundedness of pseudo-differential operators on
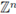 and the torus. Later, in Section 3 we classify those s-nuclear multilinear integral operators on arbitrary σ-finite measure spaces and we apply this classification to periodic and discrete multilinear pseudo-differential operators.
and the torus. Later, in Section 3 we classify those s-nuclear multilinear integral operators on arbitrary σ-finite measure spaces and we apply this classification to periodic and discrete multilinear pseudo-differential operators.
2. Boundedness of pseudo-differential operators on 𝕋n and ℤn
In this section we explain in detail the main results of our investigation on the bounded-ness of the multilinear operators considered. Our starting point is the following multilinear version of the Stein-Weiss multiplier theorem (see Theorem 3.8 of Stein and Weiss [48]). Sometimes we denote (x,ξ) := (x, ξ1, · · · , ξr) = x · (ξ1 + · · · + ξr).
Theorem 2.1. Let 1 <p < ∞
and let
α:
 be a continuous bounded function. If the multilinear Fourier multiplier operator
be a continuous bounded function. If the multilinear Fourier multiplier operator
extends to a bounded multilinear operator from
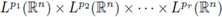 into
into
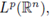 then the periodic multilinear Fourier multiplier
then the periodic multilinear Fourier multiplier
also extends to a bounded multilinear operator from
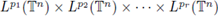 into
into
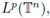 provided that
provided that
Moreover, there exists a positive constant C p such that the following inequality holds:
Remark 2.2. Theorem 2.1 can be proved in the following way. By the density of the trigonometric polynomials, we can prove that under the conditions of this theorem, we have the estimate
where the constant C does not dependent of every trigonometric polynomial Pi. For this, we will prove that
for some positive constant cn,r,p > 0. We will assume that
Observe that by linearity, we only need to prove (10) when
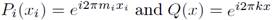 for k and mi in
for k and mi in
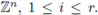 The main step in our proof (see Cardona and Kumar [10]) is to show (10) and how it implies (9).
The main step in our proof (see Cardona and Kumar [10]) is to show (10) and how it implies (9).
With the help of the previous result we prove the following fact. We use the notation
for all
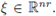 Now, we provide the following discrete version of the known result of Coifman and Meyer mentioned in the introduction.
Now, we provide the following discrete version of the known result of Coifman and Meyer mentioned in the introduction.
Theorem 2.3. Let Tm be a periodic multilinear Fourier multiplier. Under the condition
the operator
T
m
extends to a bounded multilinear operator from
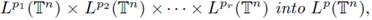 provided that
provided that
If we consider Fourier integral operators (FIOs) with periodic phases, we can recover the following multilinear version for FIOs of the multiplier theorem of Stein and Weiss.
Theorem 2.4. Let 1 < p < ∞
and let ф be a real valued continuous function defined on
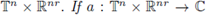 is a continuous bounded function, and the multilinear Fourier integral operator
is a continuous bounded function, and the multilinear Fourier integral operator
extends to a bounded multilinear operator from
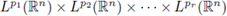 into
into
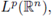 then the periodic multilinear Fourier integral operator
then the periodic multilinear Fourier integral operator
also extends to a bounded multilinear operator from
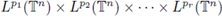 into
into
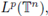 provided that
provided that
Moreover, there exists a positive constant CP such that
Now, we present some results about the boundedness of periodic multilinear pseudodifferential operators where explicit conditions on the multilinear symbols are considered.
Theorem 2.5. Let us assume that m satisfies the Hörmander condition of order s > 0,
Then the multilinear periodic pseudo-differential operator Tm
associated with m extends to a bounded operator from
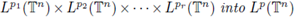 provided that
provided that
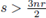 and
and
Remark 2.6. The proof of Theorem 2.5 is based on a suitable Littlewood-Paley decomposition of the symbol m. Indeed, we decompose m as
We prove that by assuming (11), we can decompose the operator Tm as
where every operator T
mj is associated to the symbol m
j, and we prove that the operator norm of every Tmj is less than
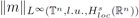 multiplied by a factor proportional to
multiplied by a factor proportional to
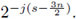 We conclude our proof in [10] by observing that
We conclude our proof in [10] by observing that
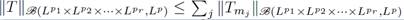
The following theorem is an extension of the Coifman-Meyer result presented above in the multilinear pseudo-differential framework.
Theorem 2.7. Let us assume that m satisfies the discrete symbol inequalities
sup |A|1 1 A|2 ··· A|; m(xfe, ··· ,ξr )| < Cafe-H (14)
for all
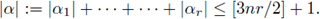 Then the periodic multilinear pseudo-differential operator
Tm
extends to a bounded operator from
Then the periodic multilinear pseudo-differential operator
Tm
extends to a bounded operator from
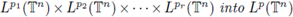 provided that
provided that
Remark 2.8. We prove Theorem 2.7 by observing that (14) implies (11). We develop this delicate argument in [10] where we use, among other things, the periodic analysis developed by Ruzhansky and Turunen.
The condition on the number of discrete derivatives in the preceding result can be relaxed if we assume regularity in x. We show it in the following theorem.
Theorem 2.9. Let Tm be aperiodic multilinear pseudo-differential operator. If m satisfies toroidal conditions of the type
where
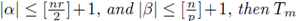 extends to a bounded multilinear operator from
extends to a bounded multilinear operator from
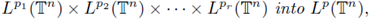 provided that
provided that
Example 2.10. Theorem 2.7 applied to the bilinear operator
where Js
is the periodic fractional derivative operator
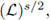 or the periodic Bessel potential of order
or the periodic Bessel potential of order
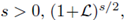 implies the (well known) periodic Kato-Ponce inequality:
implies the (well known) periodic Kato-Ponce inequality:
where
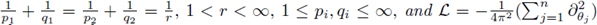 is the Laplacian on the torus.
is the Laplacian on the torus.
Boundedness of discrete multilinear pseudo-differential operators. Our main results about the boundedness of discrete multilinear pseudo-differential operators are stated as follows.
Theorem 2.11. Let
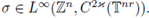 If
σ
satisfies the discrete inequality
If
σ
satisfies the discrete inequality
for all β
with
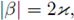 then
Tσ
extends to a bounded operator from
then
Tσ
extends to a bounded operator from
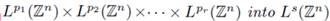 provided that
1 ≤ pj ≤ p ≤ ∞,
and
provided that
1 ≤ pj ≤ p ≤ ∞,
and
The following result can be derived of the previous result with r = 1 and s = p.
Corollary 2.12. Let
 If
σ
satisfies the discrete inequality
If
σ
satisfies the discrete inequality
for all β
with
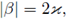 then
Tσ
extends to a bounded operator from
then
Tσ
extends to a bounded operator from
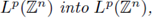 provided that
provided that
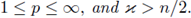
3. s-Nuclearity, 0 < s ≤ 1, of pseudo-differential operators on 𝕋n and ℤn
In this section we study the s-nuclearity, 0 < s ≤ 1 of multilinear discrete and periodic pseudo-differential operators. We prove Theorem 3.1 regarding the characterization of s-nuclear multilinear operators on abstract σ-finite measure spaces, and Theorem 3.2 and Theorem 3.3 regarding the characterization of s-nuclearity of periodic and discrete pseudo-differential operators. Although these theorems are multilinear extensions of the results due to Delgado [16], Delgado and Wong [17], JamalpourBirgani [26] and Ghaemi, JamalpourBirgani and Wong [20], we can recover their results from our results by considering r = 1. In order to study these multilinear operators admitting s-nuclear extensions, we prove the following multilinear version of a result by Delgado, on the nuclearity of integral operators on Lebesgue spaces (see [16], [18]). So, in the following multilinear theorem we characterize those s-nuclear (multilinear) integral operators on arbitrary (σ-finite) measure spaces (X,μ).
Theorem 3.1. Let (Χί,μί), 1 ≤ i ≤ r
and
(Y, ν)
be σ-finite measure spaces. Let
1 ≤
P
i
,ρ < ∞, 1 ≤ i ≤ r and let
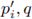 be such that
be such that
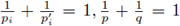 for
1 ≤
i ≤ r. Let
for
1 ≤
i ≤ r. Let
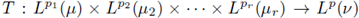 be a multilinear operator. Then
T
is a s-nuclear,
0 < s ≤ 1,
operator if, and only if, there exist sequences
{gn}n
with
gn = (gn1,gn2,...,gnr)
and
be a multilinear operator. Then
T
is a s-nuclear,
0 < s ≤ 1,
operator if, and only if, there exist sequences
{gn}n
with
gn = (gn1,gn2,...,gnr)
and
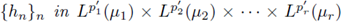 and
LP(v),
respectively, such that
and
LP(v),
respectively, such that
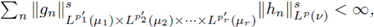 and for all f = (f1, f2,...,fr) ∈ LP1 (μ) χ LP2 (μ2) χ ··· χ LPr (μr )
we have
and for all f = (f1, f2,...,fr) ∈ LP1 (μ) χ LP2 (μ2) χ ··· χ LPr (μr )
we have
for almost every y ∈ Y.
Remark 3.2. The proof of Theorem 3.1 is based on an important lemma proved in [10, Lemma 4.1]. The proof of the if part of Theorem 3.1 follows using the definition of nuclear operators, Lemma 4.1 (iv) of [10] and the fact that Lp-convergence of a sequence implies the convergence of a sequence almost everywhere.
The only if part of Theorem 3.1 is a straightforward using the part (iv) of [10, Lemma 4.1] and applications of monotone convergence theorem of B. Levi and Lebesgue dominated convergence theorem.
This criterion applied to discrete and periodic operators gives the following characterizations (for the proof we refer the reader to [10]).
Theorem 3.3. Let a be a measurable function defined on
 .
The multilinear pseudo-differential operator
.
The multilinear pseudo-differential operator
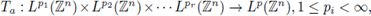 for all 1 ≤ i ≤ r,
is a
s
-nuclear,
0 < s ≤ 1,
operator if, and only if, the following decomposition holds:
for all 1 ≤ i ≤ r,
is a
s
-nuclear,
0 < s ≤ 1,
operator if, and only if, the following decomposition holds:
where
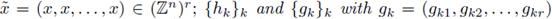 are two sequences in
are two sequences in
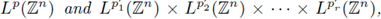 respectively, such that
respectively, such that
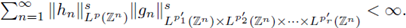
Similarly, we can classify the s-nuclearity of periodic multilinear operators.
Theorem 3.4. Let m
be a measurable function on
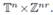 Then the mutlilinear pseudo-differential operator
Then the mutlilinear pseudo-differential operator
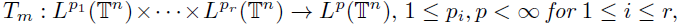 is a
s
-nuclear,
0 < s ≤ 1,
operator if, and only if, there exist two sequences
{gk}k
with
is a
s
-nuclear,
0 < s ≤ 1,
operator if, and only if, there exist two sequences
{gk}k
with
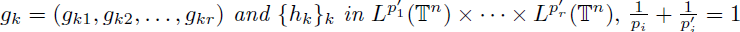 for
1 ≤ i ≤ r and
for
1 ≤ i ≤ r and
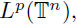 respectively, such that
respectively, such that
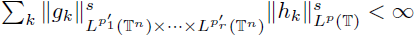 and
and
Now, we present the following sharp result on the s-nuclearity of periodic Fourier integral operators.
Theorem 3.5. Let us consider the real-valued function
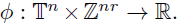 Let us consider the Fourier integral operator
Let us consider the Fourier integral operator
with symbol satisfying the summability condition
Then A extends to a s-nuclear,
0 < s ≤ 1,
operator from
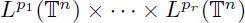 into
into
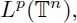 provided that
1 ≤ p
j < ∞, and 1 ≤ p ≤ ∞.
provided that
1 ≤ p
j < ∞, and 1 ≤ p ≤ ∞.
Remark 3.6. The proof of Theorem 3.5 follows using Theorem 3.1 by considering the function
the functional
and their estimates
Example 3.7. In order to illustrate the previous conditions, we consider the multilinear Bessel potential. This can be introduced as follows. Consider the periodic multilinear Laplacian denoted by
For r = 1, we recover the usual periodic Laplacian
The
multilinear Bessel potential of order
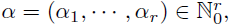
can be defined by the Fourier analysis associated to the torus as
From the estimate
Theorem 3.5 applied to
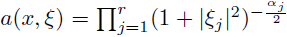 implies that the multilinear Bessel potential
implies that the multilinear Bessel potential
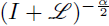 extends to a s-nuclear operator from
extends to a s-nuclear operator from
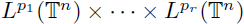 into
into
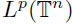 for all
1 ≤ pj < ∞ and 1 ≤ p ≤ ∞,
provided that
for all
1 ≤ pj < ∞ and 1 ≤ p ≤ ∞,
provided that
This conclusion is sharp, in the sense that if we restrict our analysis to r = 1
and
p1 = ρ = 2, the operator
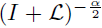 extends to a s-nuclear operator on
extends to a s-nuclear operator on
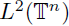 if, and only if,
if, and only if,
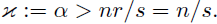
Example 3.8. Now, we consider FIOs with symbols admitting some type ofsingularity at the origin. In this general context, let us choose a sequence
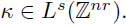 Let us consider the symbol
Let us consider the symbol
we consider the Fourier integral operator associate to α(·, ·),
the condition
0 < ρ < n/p
implies that the periodic Fourier integral operator A
extends to a
s
-nuclear multilinear operator from
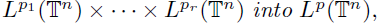 for all
1 ≤ pj < ∞ and 1 ≤ p ≤ ∞. In
fact, by Theorem 3.5, we only need to verify that
for all
1 ≤ pj < ∞ and 1 ≤ p ≤ ∞. In
fact, by Theorem 3.5, we only need to verify that
But, for every ρ > 0, this happens if, and only if, 0 < ρ < n/p.