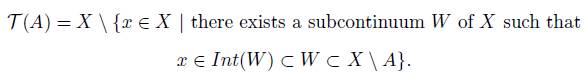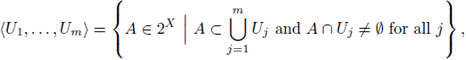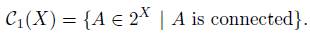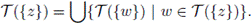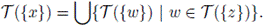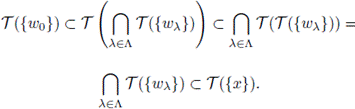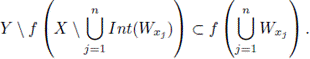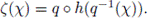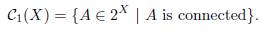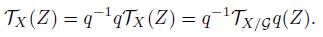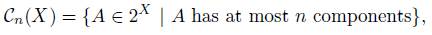1. Introduction

The first person to investigate contractibility of hyperspaces was M. Wojdyslawski ^[20] in 1938. The next investigation was done by J. L. Kelley ^[7] in 1942. Kelley defined a property as a sufficient condition to guarantee the contractibility of some of the hyperspaces of metric continua. This property has been known as property 3.2, property [K] and property of Kelley. It turns out that this property has been very important in the study not only of hyperspaces, but of metric continua, too [18, Chapter XVI]. In 1999 W. J. Charatonik ^[3] and W. Makuchowski ^[14] defined the property of Kelley for Hausdorff continua. Charatonik presented a homogeneous Hausdorff continuum without the property of Kelley, and Makuchowski generalized some local connectedness properties to hyperspaces of Hausdorff continua. We present Hausdorff version of several results known in the metric case. We also establish a weak Hausdorff version of Jones' Aposyndetic Decomposition Theorem.

2. Definitions

If Z is a topological space, then given a subset A of Z, the interior of A is denoted by Int(A) and the closure of A by Cl(A). We write Int_z(A) and Cl_z(A), respectively, if there is a possibility of confusion.

A map is a continuous function. A surjective map f: X → Y between topological spaces is monotone provided that f^-1(C) is connected for every connected subset C of Y. The surjective map f is open (closed, respectively) if f (U) is open (closed, respectively) in Y for each open (closed, respectively) set U of X. If f: X → Y is a surjective map and Z is a nonempty subset of X, then f |_z: Z → Y denotes the restriction of f to Z. Given a space Z, 1_z denotes the identity map on Z.

Given a topological space Z, a decomposition of Z is a family G of nonempty and mutually disjoint subsets of Z such that G = Z. A decomposition G of a topological space Z is said to be upper semicontinuous if for each element G of G and each open subset U of Z such that G ⊂ U, there exists an open subset V of Z such that G ⊂ V, and for every G' ∈ G such that G' ∩ V ≠ 0, we have that G' ⊂ U. The decomposition G of Z is lower semicontinuous provided that for each G ∈ G any two points z ₁ and z₂ of G and any open subset U of Z containing z₁, there exists an open subset V of Z such that z₂ ∈ V and for each G' ∈ G such that G' ∩ V ≠ 0, we obtain that G' ∩ U ≠ 0. The decomposition G is continuous if it is both upper and lower semicontinuous.

A continuum is a compact connected Hausdorff space. A subcontinuum of a space Z is a continuum contained in Z. A continuum is decomposable if it is the union of two of its proper subcontinua. A continuum is indecomposable if it is not decomposable. A continuum X is homogeneous provided that for each pair of points x₁ and x₂ of X, there exists a homeomorphism h: X → X such that h(x₁) = x₂.

Given a continuum X, we define the set function T as follows: if A is a subset of X, then

We write T_X if there is a possibility of confusion. Let us observe that for any subset A of X, T(A) is a closed subset of X and A ⊂ T(A). A continuum X is aposyndetic provided that T({p}) = {p} for every p ∈ X.

The set function T is idempotent on X (idempotent on closed sets of X, on subcontinua of X, respectively) provided that T²(A) = T(A) for each subset A of X (for every nonempty closed subset A of X, for each subcontinuum A of X, respectively), where T² = T o T. The set function T is idempotent on singletons if T²({x}) = T({x}) for all x ∈ X.

We say that T is continuous for a continuum X provided that T: 2^X - 2^X is continuous, where 2^X is the hyperspace of nonempty closed subsets of X, topologized with the Vietoris topology ^[15] (or the Hausdorff metric if X is metric ^[18]). A base for the Vietoris topology for 2^X is given by the sets of the form

where U₁,..., U_m are open subsets of X. If f: X → Y is a map, then 2^f: 2^X → 2^Y given by 2^f(A) = f(A) is a map [18, (1.168)]. Observe that there exists a copy of X inside 2^X, namely, F₁(X) = {{x} | x e X}. The map ξ: X → F₁(X) given by ξ(x) = {x} is an embedding. We say that T is continuous on singletons provided that T|_F1(X): F₁(X) → 2^X is continuous. For more information about the set function T see [8, Chapter 3]

Let X be a continuum. Then C₁(X) denotes the hyperspace of subcontinua of X; i.e.,

If U₁,...,U_m are open subsets of X, then 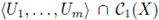is denoted by 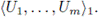Note that if K is a subcontinuum of X, then T(K) is a subcontinuum of X (Theorem 3.5).

3. Preliminaries

The following result is known as The Boundary Bumping Theorem. It has many applications in continuum theory and in hyperspaces. A proof of this theorem may be found in [6, Theorem 2-16]. Bd(U) denotes the boundary of a set U in a space X.

Theorem 3.1. Let X be a continuum and let U be a nonempty, proper, open subset of X. If K is a component of Cl(U), then K ∩ Bd(U) ≠ ∅.

Let X be a continuum and let K be a subcontinuum of X. Then K is a terminal subcontinuum of X if for each subcontinuum L of X such that L ∩ K ≠ ∅, then either L ⊂ K or K ⊂ L.

Lemma 3.2. Let X be a continuum. If W is a proper terminal subcontinuum of X, then Int(W) = ∅.

Proof. Suppose W is a proper terminal subcontinuum of X and Int_X (W) ≠ ∅. Note that Bd_X(Int_X(W)) ⊂ W. Let x ∈ X \ W and let C be the component of X \ Int_X(W) containing x. By Theorem 3.1, C ∩ Bd_X(Int_X(W)) ≠ ∅. Hence, C ∩ W ≠ ∅, and C \ W ≠ ∅. Since W is a terminal subcontinuum of X, W ⊂ C, a contradiction to the fact that C ∩ Int_X (W) = ∅. Therefore, Int_X (W) = ∅.

Lemma 3.3. If X is a continuum, then T is upper semicontinuous.

Proof. Let U be an open subset of X and let 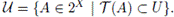We show that 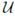is open in 2^X. Let B ∈ Cl₂x (2^X \U). Then there exists a net {B_λ}_λ∈Λ of elements of 2^X \ converging to B [5, 1.6.3]. Note that for each λ ∈ Λ, T(B_λ) ∩ (X \ U) ≠ ∅. Let x_λ ∈ T(B_λ) ∩ (X \ U). Without loss of generality, we assume that {x_λ}_λ∈Λ converges to a point x ∈ X [5, 3.1.23 and 1.6.1] and [17, Theorem 4]. Note that x ∈ X \ U. We assert that x ∈ T(B). Suppose x ∈ X \ T(B). Then there exists a subcontinuum W of X such that x ∈ Int(W) ⊂ W ⊂ X \ B. Since {B_λ}_λ∈Λ converges to B and {x_λ}_λ∈Λ converges to x, there exists λ₀ ∈ Λ such that for each λ ≥ λ₀, B_λ ⊂ X \ W and X _λ ∈ Int(W).

Let λ ≥ λ₀. Then x ∈ Int(W) ⊂ W ⊂ X \ BA. This implies that Xλ ∈ X \ T(Bλ), a contradiction. Thus, x ∈ T(B) ∩ (X \ U). Hence, B ∈ 2^X\ . Therefore, 2^X\ is closed in 2^X and is open.

Lemma 3.4. Let X and Y be continua and let h: X → Y be a homeomorphism. If A is a subset of X, then h(T_X(A)) = T_Y(h(A)).

Proof. Let A be a closed subset of X. Let y ∈ Y\ h(T_X(A)). Then h^-1(y) ∈ X \T_X(A). Hence, there exists a subcontinuum W of X such that h^-1(y) ∈ Int(W) ⊂ W ⊂ X \ A. This implies that y ∈ Int(h(W)) ⊂ h(W) ⊂ Y \ h(A). Thus, y ∈ Y \ T_Y(h(A)).

Now, let y ∈ X \ T_Y(h(A)). Then there exists a subcontinuum K of Y such that y ∈ Int(K) ⊂ K ⊂ Y\h(A). This implies that h^-1(y) ∈ Int(h^-1(K)) ⊂ h^-1(K) ⊂ X\A. Thus, h^-1(y) ∈ X \T_X(A). Hence, y ∈ Y \ h(T(A)).

Therefore, h(T(A)) = T(h(A)).

Theorem 3.5. Let X be a continuum. If W is a subcontinuum of X, then T(W) is a subcontinuum ofX.

Proof. Let W be a subcontinuum of X. We already know that T(W) is a closed subset of X.

Suppose T( W) is not connected. Then there exist two disjoint closed subsets A and B of X such that T(W) = A ∪ B. Since W is connected, without loss of generality, we assume that W ⊂ A. Since X is a normal space, there exists an open subset U of X such that A ⊂ U and Cl(U) n B = ∅.

Note that Bd(U) ∩ T(W) = ∅. Hence, for each z ∈ Bd(U), there exists a subcontinuum K_z of X such that z ∈ Int(K_z) ⊂ K_z ⊂ X \ W. Since Bd(U) is compact, there exist z₁,...,z_n ∈ Bd(U) such tha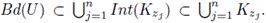t Let 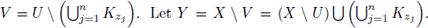By Theorem 3.1, Y has only a finite number of components. Observe that B ⊂ X \ Cl(U) ⊂ X \ U ⊂ Y. Hence, B ⊂ Int(Y). Let b ∈ B, and let C be the component of Y such that b ∈ C. Note that b ∈ Int(C). By construction, C ∩ W = ∅. Thus, b ∈ X \ T(W), a contradiction. Therefore, T(W) is connected.

Let X be a continuum and let z ∈ X. We say that T({z}) has property BL [9, p. 167] provided that T({z}) c T({x}) for each x ∈ T({z}).

Lemma 3.6. Let X be a decomposable continuum for which T is idempotent on singletons, and let z ∈ X. If T({z}) has property BL, then T({w}) = T({z}) for every w ∈ T({z}).

Proof. Let z ∈ X be such that T({z}) has property BL, and let w ∈ T({z}). Since w ∈ T({z}) and T is idempotent on singletons, T({w}) ⊂ T(T({z})) = T({z}). Hence, T({w}) ⊂ T({z}). Since T({z}) has property BL, T({z}) ⊂ T({w}). Therefore, T({w}) = T({z}).

Corollary 3.7. Let X be a decomposable continuum for which T is idempotent on singletons. If z₁ and z₂ are two points of X such that both T({z₁}) and T({z₂}) have property BL, then either T({z₁) = T({z₂}) or T({z₁) ∩ T({z₂}) = ∅.

Proof. Let z₁ and z₂ be points of X such that both T({z₁}) and T({z₂}) have property BL. Suppose T({z₁}) nT({z₂}) = ∅. Let z₃ eT({z₁}) nT({z₂}). Then, by Lemma 3.6, T ({z₁})= T({z₃}) = T({z₂}).

Lemma 3.8. Let X be a decomposable continuum for which T is idempotent on singletons. If z ∈ X, then

Proof. Let z e X and let w₀ ∈ T({z}). Since T is idempotent on singletons T({w₀}) ⊂ T(T({z})) = T({z}). Hence, 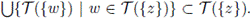The other inclusion is clear.

The proof of the following theorem is based on a technique of Bellamy and Lum [1, Lemma 5].

Theorem 3.9. If X is a decomposable continuum for which T is idempotent on singletons, then for each x e X, there exists z e T({x}) such that T({z}) has property BL.

Proof. Let x ∈ X. By Lemma 3.8, we have that

Let G_x = {T({w}) | w ∈ T({x})}. Partially order G_x by inclusion. Let H = {T({W_Λ})}_λ∈Λ be a (set theoretic) chain of elements of G_x. We show that H has a lower bound in G_x.

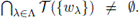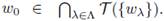Since H is a chain of continua (Theorem 3.5), Let Then

Hence, by Kuratowski-Zorn Lemma, there exists z ∈ T({x}) such that T({z}) is a minimal element; i.e., each w ∈ T({z}) satisfies that T({z}) ⊂ T({w}). Therefore, T({z}) has property BL.

Lemma 3.10. Let X and Y be continua and let f: X → Y be a surjective map. If f is monotone, then T_Y(B) = f T_Xf^-1(B), for all B ∈ 2^Y .

Proof. Let y ∈ Y\f T_Xf^-1(B). Then f^-1(y) ∩T_Xf^-1(B) = ∅. Thus, for each x ∈ f^-1(y), there exists a subcontinuum W_x of X such that x ∈ Int(W_x) ⊂ W_x ⊂ X \ f^-1(B). Since f^-1(y) is compact, there exist x₁,..., x_n ∈ f^-1(y) such that

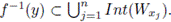
Note that 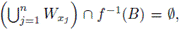and for each j ∈ {1,...,n}, f^-1(y) ∩ W_xj. = ∅.

Hence, 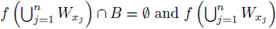is a continuum (y ∈ f (W_xj) ∩ f (W_xk) for every j, k ∈ {1, 2,..., n}).

Observe that 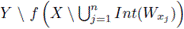is an open set of Y and it is contained in 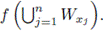To see this, note that, since Then 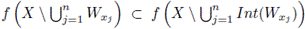and, consequently, 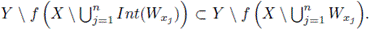Since f is a surjection, 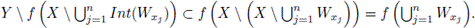Thus,

Also, since 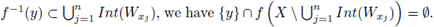Hence, 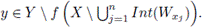Therefore, y ∈ Y \ T_Y(B).

Let x ∈ X \ f^-1TY(B). Then f (x) ∈ Y \ TY(B). Hence, there exists a subcontinuum W of Y such that f (x) ∈ Int(W) ⊂ W ⊂ Y \ B. This implies that x ∈ f^-1(f (x)) ⊂ f^-1(Int(W)) ⊂ f^-1(W) ⊂ X\f^-1(B). Since f is monotone, f^-1(W) is a subcontinuum of X. Therefore, x ∈ X \ T_Xf^-1(B).

We know that T_Y(B) ⊂ fT_Xf^-1(B). Since T_Xf^-1(B) ⊂ f^-1T_Y(B), by previous paragraph, fT_Xf^-1(B) ⊂ ff^-1T_Y(B) = T_Y(B). Therefore, fT_Xf^-1(B) = T_Y(B).

4. Property of Kelley

The property of Kelley for Hausdorff continua is defined independently in ^[3] and ^[14]. In ^[3], a homogeneous continuum without the property of Kelley is given, showing that the fact that homogeneous metric continua have the property of Kelley ([8, 4.2.36] or [19, (2.5)]) is not true in this more general setting. It is also mentioned that hereditarily indecomposable continua have the property of Kelley [3, Proposition 2.7]. In ^[14], the property of Kelley is used to study points of various types of local connectedness in the hyperspace of subcontinua of a continuum. In fact, if a continuum X has the property of Kelley, then local connectedness of C₁(X) is proved to be equivalent to some stronger kinds of local connectedness and of local arcwise connectedness ^[14].

A continuum X has the property of Kelley at a point x₀ if for every subcontinuum K of X containing x₀ and each open subset U of C₁(X) containing K, there exists an open subset V of X such that x₀ e V, and if x e V, then there exists a subcontinuum L of X such that x e L and L eU. The open set V is called a Kelley set for U and x₀. The continuum X has the property of Kelley if X has the property of Kelley at each of its points.

Theorem 4.1. Let X be a continuum with the property of Kelley. Let A be a nonempty closed subset of X and let W be a subcontinuum of X such that Int(W) = ∅ and W∩A = ∅. If w ∈ W, then there exists a subcontinuum K of X such that w ∈ Int(K) and K ∩ A = ∅.

Proof. Let w ∈ W. Since X is normal, there exists an open subset U of X such that W ⊂ U and Cl(U) ∩ A = ∅. Let 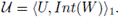Note that 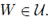Also observe that if L ∈ 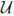, then L ⊂ U and L ∩ W = ∅. Since X has the property of Kelley at w, there exists a Kelley set V for 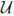and w. Let v ∈ V \ {w}. Then there exists a subcontinuum L_v of X such that v ∈ L_v and L_v ∈ U. Let L_w = W, and let 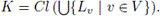Then K is a subcontinuum of X, w ∈ V ⊂ K and K ⊂ Cl(U) ⊂ X \ A.

Corollary 4.2. Let X be a continuum with the property of Kelley, let W be a subcontinuum of X, with non-empty interior, and let A be a non-empty closed subset of X such that W ∩ A = ∅. Then there exists a subcontinuum M of X such that W ⊂ Int(M) and M ∩ A = ∅.

Proof. Let w ∈ W. By Theorem 4.1, there exists a subcontinuum K_w such that w ∈ Int(K) and K ∩ A = ∅. Note that {Int(K_w) | w ∈ W} forms an open cover of W, so that by compactness, there exist w₁,..., w_n in W such tha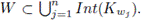t Let 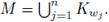Then M is a subcontinuum of X, W ⊂ Int(M) and M ∩ A = ∅.

The proof of the following result is different from the one given in [12, Theorem 5.2].

Theorem 4.3. Let X be a continuum with the property of Kelley and let W₁ and W₂ be disjoint subcontinua with non-empty interior. Then T(W₁) ∩ T(W₂) = ∅.

Proof. By Corollary 4.2, there exists a subcontinuum M₁ such that W₁ ⊂ Int(M₁) and M₁ ∩ W₂ = ∅. This implies that W₁ ∩ T(W₂) = ∅. By Corollary 4.2, there exists a subcontinuum M₂ such that T(W₂) ⊂ Int(M₂) and M₂ ∩ W₁ = ∅. Hence, T(W₂) ∩ T(W₁) = ∅.

Theorem 4.4. If X is a continuum with the property of Kelley, then T is idempotent on closed sets.

Proof. Let A be a nonempty closed set of X. We know that T(A) ⊂ T²(A). Let x ∈ X \ T(A). Then there exists a subcontinuum W of X such that x ∈ Int(W) ⊂ W ⊂ X \ A. By Corollary 4.2, there exists a subcontinuum M of X such that W ⊂ Int(M) and M ∩ A = ∅. Since Int(M) ⊂ X \ T(A), x ∈ Int(W) ⊂ W ⊂ X \ T(A). Hence, x ∈ X \ T²(A). Therefore, T is idempotent on closed sets.

Remark 4.5. Theorem 4.4 cannot be improved to obtain that the function T is idempo-tent, even for metric continua. Let X be the product of a solenoid and a simple closed curve. Then X is a homogeneous metric continuum. By [8, 4.2.32], T_X is idempotent on closed sets and, by [10, Theorem 3.3], T_X is not idempotent.

Theorem 4.6. Let X be a continuum. If G = {T_X({x}) | x e X} is a decomposition of X, then G is upper semicontinuous. Hence, X/G is a continuum.

Proof. By Lemma 3.3, T is upper semicontinuous. Hence, G is an upper semicontinuous decomposition. To show that X/G is Hausdorff, let q: X → X/G be the quotient map and let x₁ and x₂ be two distinct points of X/G. Then q^-1(x₁) and q^-1(x₂) are two disjoint closed subsets of X. Since X is normal, there exist two disjoint open subsets U₁ and U₂ of X such that q^-1(x₁) ⊂ U₁ and q^-1(x₂) ⊂ U₂. Note that, since G is an upper semicontinuous decomposition, there exist two saturated open subsets W_U1 and W_U2 of X such that q^-1(x₁) ⊂ W_U1 ⊂ U₁ and q^-1(x₂) ⊂ W_U2 ⊂ U₂. Then q(W_U1) and q(W_U2) are two disjoint open subsets of X/G such that x₁ ∈ q(W_U1) and x₂ ∈ q(W_U2). Therefore, X/G is a Hausdorff space.

Corollary 4.7. Let X be a continuum such that TX is idempotent on singletons. If G = {T_X({x}) | x ∈ X} is a decomposition of X, then X/G is an aposyndetic continuum.

Proof. By Theorem 4.6, G is an upper semicontinuous decomposition and X/G is a continuum. Let q : X → X/G be the quotient map. Then q is a monotone map. Let X ∈ X/G and let x ∈ X be such that T_X({x}) = q^-1(x). Since q is a monotone map, by Lemma 3.10, T_X/G({X}) = qT_Xq ^-1(x) = qT_X(T_X({x})) = qT_X({x}) = qq^-1(x) = {x}; the third equality is true because T_X is idempotent on singletons. Therefore, X/G is an aposyndetic continuum.

Theorem 4.8. Let X be a continuum with the property of Kelley. If G = {T_X ({x}) | x ∈ X} is a decomposition of X, then T({x}) is a terminal subcontinuum of X for all x ∈ X.

Proof. Suppose there exists a point x₀ in X such that T({x₀}) is not a terminal sub-continuum of X. Then there exists a subcontinuum L of X such that L ∩ T({x0}) ≠ ∅, L \ T({x₀}) = ∅ and T({xo}) \ L ≠ ∅. Let p ∈ L \ T({x₀}) and 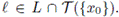Since G is a decomposition, without loss of generality, we assume that x₀ ∈ T({x₀}) \ L. Since p ∈ L \ T({x₀}), there exists a subcontinuum W of X such that p ∈ Int(W) ⊂ W ⊂ X \ {x₀}. Let K = L ∪ W. Then K is a subcontinuum of X, p ∈ Int(K) and K ⊂ X \ {x₀}. By Theorem 4.1, there exists a subcontinuum M of X such that 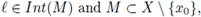a contradiction to the choice of 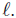Therefore, T({x}) is a terminal subcontinuum of X for all x ∈ X.

Let X and Z be continua and let f: X → Z be a map. Then, f is an atomic map if for each subcontinuum K of X such that f (K) is not degenerate, then K = f^-1(f (K)).

Next we prove a weak version of F. Burton Jones Aposyndetic Decomposition Theorem. Note that we obtain that the decomposition is only upper semicontinuous.

Theorem 4.9. Let X be a homogeneous continuum with the property of Kelley. If G = {T({x}) | x ∈ X}, then G is an upper semicontinuous terminal decomposition of X, X/G is an aposyndetic homogeneous continuum, and the quotient map q: X → X/G is an atomic map.

Proof. Let X be a point of X. We show that if z ∈ T({x}), then T({z}) = T({x}). Since X the property of Kelley, by Theorem 4.4, T is idempotent on closed sets. Hence, T({z}) ⊂ T({x}). Also, by Theorem 3.9, there exists x₀ ∈ T({x}) such that T({x₀}) has property BL. Since X is homogeneous, there exists a homeomorphism h: X → X such that h(x₀) = x. Since z e T({x}), h^-1(z) e T({x₀}). Hence, by Lemma 3.6, T({h^-1(z)}) = T({xo}). Thus, by Lemma 3.4, T({x}) = h(T({xo})) = h(T({h^-1(z)})) = T({z}). Therefore, G is a decomposition of X. By Theorem 4.6, G is upper semicontinuous. The fact that each element of G is a terminal subcontinuum of X follows from Theorem 4.8. Also, by Corollary 4.7, X/G is an aposyndetic continuum. We show that X/G is homogeneous. Let q: X → X/G be the quotient map. Let x₁ and x₂ be two elements of X/G. We define Z: X/G → X/G as follows: Let x₁ and x₂ be elements of X such that q(x₁) = x₁ and q(x₂) = x₂. Since X is homogeneous, there exists a homeomorphism h: X → X such that h(x1) = x2. Note that, by Lemma 3.4, h(T({x₁}) = T({x2}); i.e., h(q^-1(x₁)) = q^-1(x₂). Define

Then ζ is well defined and ζ(x₁) = x₂. To see that ζ is continuous, let 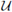be an open subset X/G. Then q^-1( 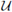) is a saturated open subset of X. Since h is a homeomorphism, h^-1(q^-1( 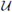)) is a saturated open subset of X. Hence, q(h^-1(q^-1( 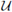))) = ζ^-1( 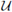) is an open subset of X/G. Thus, ζ is continuous. Similarly, ζ^-1 is defined and is continuous. Therefore, X/G is homogeneous. To see the quotient map is atomic, let K be a subcontinuum of X such that q(K) is nondegenerate. Clearly, K ⊂ q^-1q(K). Let x e q^-1q(K). Then there exists k e K such that q(k) = q(x). Thus, q^-1q(x) n K ≠ ∅. Since q^-1q(x) is a terminal subcontinuum of X, from Theorem 4.8 and the fact that q(K) is nondegenerate, we have that x e q^-1q(x) ⊂ K. Hence, q^-1q(K) ⊂ K. Therefore, q is an atomic map.

In the following theorem we extend to (nonmetric) continua [2, Theorem 5.4].

Theorem 4.10. Let X be a decomposable continuum with the property of Kelley. If T_X is continuous on singletons and

then T_X (Z) = q^-1T_X/Gq(Z) for each nonempty closed subset Z of X, where q: X → X/G is the quotient map.

Proof. Without loss of generality, we assume that X is not aposyndetic. Note that by Theorem 4.4 and [11, Theorem 3.4], G is a decomposition of X. Let Z be a nonempty closed subset of X. We divide the proof in six steps.

Step 1. q^-1q(Z) ⊂ Tx(Z).

Let x ∈ q^-1q(Z). Then q(x) ∈ q(Z). Thus, there exists z ∈ Z such that q(z) = q(x). This implies that T_X({z}) = T_X({x}). Hence, since TX is idempotent on closed sets (Theorem 4.4), T_X({x}) = TX({z}) ⊂ T_X(Z). Therefore, x ∈ T_X(Z), and q^-1q(Z) ⊂ T_X(Z).

Step 2. T_X(Z) = q^-1qTx(Z).

Clearly, T_X(Z) ⊂ q^-1qTX(Z). Let x ∈ q^-1qT_X(Z). Then q(x) ∈ qT_X(Z). Hence, there exists y ∈ T_X(Z) such that q(y) = q(x). This implies that T_X({y}) = T_X({x}). Thus, since TX is idempotent on closed sets (Theorem 4.4), we have that T_X ({y}) ⊂ T_X (Z). Hence, x ∈ T_X(Z), and q^-1qTx(Z) ⊂ TX(Z). Therefore, T_X(Z) = q^-1qTx(Z).

Step 3. If Z is connected and Int_X(Z) = 0, then Z = q^-1q(Z).

Clearly, Z ⊂ q^-1q(Z). Let x ∈ q^-1q(Z). Then q(x) ∈ q(Z). Thus, there exists z ∈ Z such that q(z) = q(x). This implies that TX({z}) = TX({x}). Since TX({x}) is a nowhere dense terminal subcontinuum of X (Lemma 3.2, Lemma 3.4 and Theorem 3.5), TX({x}) ∩ Z ≠ ∅ and Int_X(Z) ≠ ∅, we have that TX({x}) ⊂ Z. In particular, x ∈ Z. Therefore, Z = q^-1q(Z).

Step 4. qT_x(Z) CT_X/Gq(Z).

Let x ∈ X/G \ T_X/Gq(Z). Then there exists a subcontinuum W of X/G such that x ∈ Int_X/G (W) ⊂ W ⊂ X/G \ q(Z). From these inclusions we obtain that q^-1(x) ⊂ Intx (q^-1(W)) ⊂ q^-1(W) ⊂ X \ q^-1q(Z) ⊂ X \ Z. Hence, since q is monotone (Theorem4.9), q^-1(x) ∩ Tx(Z) ≠ ∅. Thus, qq^-1(x) ∩ qTX(Z) ≠ ∅. Therefore, x ∈ X/G\qTX(Z), and qTx (Z) ⊂ TX/Gq(Z).

Step 5. T_X/Gq(Z) ⊂ qTx(Z).

Let x ∈ X/G\ qTX (Z). Then {x}∩ qTX (Z) = ∅. This implies that q^-1(x) ∩ q^-1qTX (Z) = ∅. Hence, by Step 2, q^-1(x) ∩ TX (Z) = ∅. Since TX is idempotent on closed sets (Theorem 4.4), 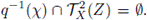Thus, there exists a subcontinuum W of X such that q^-1(x) ⊂ Int_X (W) ⊂ W ⊂ X \ T_X (Z) ⊂ X \ Z. From these inclusions, since q is an open map (G is a continuous decomposition), we obtain that {x} = qq^-1(x) ⊂ Int_X/G (q(W)) ⊂ q(W) ⊂ q(X \ Z). To finish, we need to show that q(W) ∩ q(Z) = ∅. Suppose there exists x' ∈ q(W) ∩ q(Z). Then, by Steps 3 and 1, q^-1(x') ⊂ q^-1q(W) ∩ q^-1q(Z) = W ∩ q^-1q(Z) ⊂ W ∩ TX(Z), a contradiction to the election of W. Hence, q(W) ∩ q(Z) = ∅, and x ∈ X/G \ T_X/Gq(Z). Therefore, T_X/Gq(Z) ⊂ qTx(Z).

Step 6. qTx(Z) = T_X/Gq(Z).

The equality follows from Steps 4 and 5.

From Steps 2 and 6, we have that

Therefore, .

The property of Kelley weakly is introduced in ^[13] to study points of connectedness im kleinen of the n-fold hyperspaces of metric continua. Next, we extend this property to continua.

A continuum X has the property of Kelley weakly, if there exists a dense subset A of C₁(X) such that X has the property of Kelley at some point of each element A ∈ A.

Let X be a continuum and let n be a positive integer. Then C_n(X) denotes the n-fold hyperspace of X; i.∈.,

with the Vietoris topology. If U₁,..., U_m are open subsets of X, then 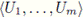∩ C_n (X) is denoted by

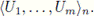
Lemma 4.11. Let X be a continuum with the property of Kelley weakly and let n be a positive integer. Then for each open subset U of C_n(X), there exists A ∈ 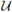such that X has the property of Kelley at some point a of A.

Proof. Let 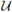be an open subset of C_n(X), let K ∈ 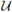and let V₁,..., V_t be open subsets of X such that K ∈ 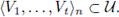Let L be a component of K and let 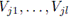denote all the elements of {V₁,...,V_t} that L intersects. Then 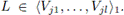Since X has the property of Kelley weakly, there exists M ∈ C₁(X) such that M ∈ 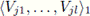and X has the property of Kelley at some point a of M. Let A = (K \ L) ∪M. Then 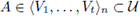and X has the property of Kelley at a ∈ M ⊂ A.

Part (2) of the following theorem is known for the hyperspace of subcontinua of a continuum [14, Theorem 11].

Theorem 4.12. Let X be a continuum and let U be an open subset of C_n(X).

(1) If X has the property of Kelley weakly, then

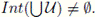
(2) If X has the property of Kelley, then 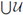is an open subset of X.

Proof. We prove (1). By Lemma 4.11, there exists A ∈ U such that X has the property of Kelley at some point a of A. Let V₁,...,V_t be open subsets of X such that A ∈ 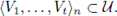Let A₁ be the component of A containing a. Let V_j1,...,V_jl denote all the elements of {V₁,...,V_t} that A₁ intersects. Since X has the property of Kelley at a, there exists a Kelley set V for a and 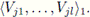We show that 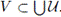Let z ∈ V. Then there exists D ∈ C₁(X) such that z ∈ D and 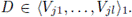Let B = (A \ A1) ∪ D. Then B ∈ C_nX) and 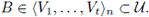Hence, 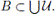Since 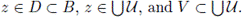Therefore,

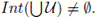
To prove (2), let 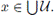Then there exists C ∈ 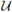such that x ∈ C. Let C₁,...,C_t be the components of C. Without loss of generality, we assume that x ∈ C₁. Let V₁,...,V_t be open subsets of X such that 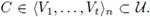Let V_j1,...,V_jl denote all the elements of {V₁,...,V_t} that C₁ intersects. Since X has the property of Kelley at x, there exists a Kelley set V for x and 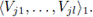We show that 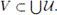Let z ∈ V. Then there exists L ∈ C₁(X) such that z ∈ L and 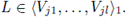Let R = (C \ C₁) U L. Then R ∈ C_n(X) and 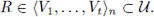Since 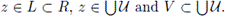Thus, x is an interior point of 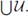Therefore, 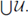is open in X. 0

Lemma 4.13. Let X be a continuum. If 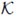is a subcontinuum of 2^X and 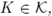then each component of 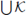intersects K.

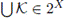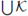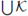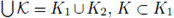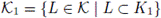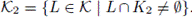Proof. First, note that [15, 2.5.2]. Suppose that there exists a component C of such that K ∩ C = ∅. Hence, by [4, (4.A.11)], there exist two closed subsets K₁ and K₂ of such that and C ⊂ K₂. Let and Then 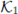and 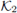are disjoint closed subsets of 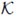. Also, 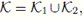a contradiction to the fact that 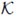is connected. Therefore, each component of 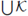intersects K.

As a consequence of Theorem 4.12 part (1) and Lemma 4.13, we have the following corollary:

Corollary 4.14. Let X be a continuum that has the property of Kelley weakly, and let n ≥ 1. If W is a subcontinuum of C_n(X) such that 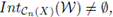then

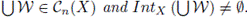
Theorem 4.15. Let X be a continuum that has the property of Kelley weakly, and let n ≥ 1. If X is indecomposable, then C_n(X) is locally connected only at X.

Proof. Let 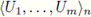be a basic open subset of C_n(X) containing X. Then, by [16, Theorem 2.4 and (1.4)], we have that 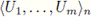is arcwise connected. Therefore, C_n(X) is locally connected at X.

Assume that C_n(X) is locally connected at A and A ≠ X. Then there exists a continuum neighborhood 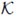of A such that 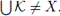By part (1) of Theorem 4.12, 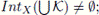also, by Lemma 4.13, 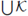is compact and has at most n components. Hence, by the Baire Theorem [6, Theorem 2-82], some component C of has nonempty interior in X. Therefore, since C ≠ X, X is decomposable by [6, Theorem 3-41].

Corollary 4.16. Let n be a positive integer. If X is a hereditarily indecomposable continuum, then X is the only point at which C_n(X) is locally connected.

Proof. By [3, Proposition 2.7], hereditarily indecomposable continua have the property of Kelley. The corollary now follows from Theorem 4.15.