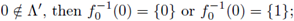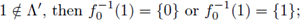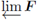1. Introduction
In 2013 the author was invited to give a mini-course at a meeting in Puebla, México. The theme of that series of lectures was traditional continuum theory arising in inverse limits with set-valued functions. Here we revisit that theme and survey some results on the topic of traditional continuum theory in inverse limits with set-valued functions. We include a discussion of some additional results that have been obtained in the five years since the Puebla meeting and we raise questions, some old and some new, suggested by our theme.
Roughly following the outline of the Puebla talks, this article is divided into sections. In Section 2 we provide some of the background for the remainder of the paper. In Section 3 we briefly discuss compactness and connectedness in inverse limits with set-valued functions. In Section 4 we turn our attention to a very traditional topic in the theory of continua, chainability. We follow this in Section 5 with a look at treelikeness, another quite traditional property. We close in Section 6 with a look at a more recent topic of parameterized families of inverse limits with set-valued functions that arises out of the interaction between continuum theory and dynamical systems. Questions and problems are sprinkled throughout the paper. For the perspective of a member of the audience for the talks in Puebla, see [6].
2. Definitions and Notation
A compactum is a compact metric space; a continuum is a connected compactum. If X is a compactum, 2X denotes the collection of all compact subsets of X. If each of X and Y is a compactum, a function f : X → 2Y, herein denoted f : X
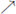 Y, is said to be upper semi-continuous at the point x of X provided that if V is an open subset of Y that contains f (x) then there is an open subset U of X containing x such that if t is a point of U then f (t) ⊆ V .A function f : X
Y, is said to be upper semi-continuous at the point x of X provided that if V is an open subset of Y that contains f (x) then there is an open subset U of X containing x such that if t is a point of U then f (t) ⊆ V .A function f : X
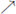 Y is called upper semi-continuous provided it is upper semi-continuous at each point of X. If f : X
Y is called upper semi-continuous provided it is upper semi-continuous at each point of X. If f : X
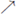 Y is continuum-valued, we often denote this by f : X → C(Y), where C(Y) denotes the connected elements of 2Y. If f : X
Y is continuum-valued, we often denote this by f : X → C(Y), where C(Y) denotes the connected elements of 2Y. If f : X
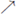 Y is a set-valued function, by the graph of f, denoted G(f), we mean
Y is a set-valued function, by the graph of f, denoted G(f), we mean
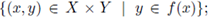 if f : X
if f : X
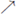 Y and g : Y
Y and g : Y
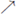 Z, then g o f : X
Z, then g o f : X
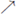 Z denotes the function given by z ∈ g o f (x) if and only if there is a point y of Y such that y ∈ f (x) and z ∈ g(y). It is known that if X and Y are compacta and M is a subset of X x Y such that X is the projection of M to its set of first coordinates, then M is closed if, and only if, M is the graph of an upper semi-continuous function [21, Theorem 2.1] or [13, Theorem 1.2, p. 3]. We call an upper semi-continuous function f : X
Z denotes the function given by z ∈ g o f (x) if and only if there is a point y of Y such that y ∈ f (x) and z ∈ g(y). It is known that if X and Y are compacta and M is a subset of X x Y such that X is the projection of M to its set of first coordinates, then M is closed if, and only if, M is the graph of an upper semi-continuous function [21, Theorem 2.1] or [13, Theorem 1.2, p. 3]. We call an upper semi-continuous function f : X
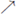 Y surjective provided for each point y of Y there is a point x in X such that y ∈ f (x). If s = s1, s2, s3,… is a sequence, we normally denote the sequence in boldface type and its terms in italics. Suppose X is a sequence of compacta and fn : Xn+1
Y surjective provided for each point y of Y there is a point x in X such that y ∈ f (x). If s = s1, s2, s3,… is a sequence, we normally denote the sequence in boldface type and its terms in italics. Suppose X is a sequence of compacta and fn : Xn+1
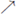 Xn is an upper semi-continuous function for each
Xn is an upper semi-continuous function for each 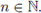 By the inverse limit of f, denoted
By the inverse limit of f, denoted
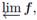 we mean
we mean
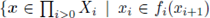 for each positive integer i}. The spaces in the sequence X are referred to as factor spaces while the functions in the sequence f are called bonding functions. If
for each positive integer i}. The spaces in the sequence X are referred to as factor spaces while the functions in the sequence f are called bonding functions. If
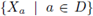 is a collection of sets and A is a subset of D, we denote by πA the natural projection of
is a collection of sets and A is a subset of D, we denote by πA the natural projection of
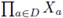 onto
onto
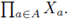 If a and b are two numbers, we denote the interval with endpoints a and b by [a, b], whether or not a is smaller. For the most part, throughout this article we assume the factor spaces are continua.
If a and b are two numbers, we denote the interval with endpoints a and b by [a, b], whether or not a is smaller. For the most part, throughout this article we assume the factor spaces are continua.
Inverse limits with mappings have been employed in continuum theory for almost sixty years dating back at least to 1959, when Anderson and Choquet made use of inverse limits to construct a continuum in the plane no two of whose nondegenerate subcontinua are homeomorphic [1]. The ease with which complicated continua can be constructed from simple objects led to an explosion of results involving inverse limits. Detailing even a few of these significant developments in continuum theory is beyond the scope of the present article.
Inverse limits with set-valued functions are extensions of inverse limits with mappings. The only change involves replacing the continuous functions for bonding functions with upper semi-continuous set-valued functions. Inverse limits with set-valued functions subsume inverse limits with mappings. As a consequence the author distinguishes between the notions simply by making reference to the nature of the bonding functions in the system. We actually object to the term "generalized inverse limit" and never make use of it; any generalization is with respect to the bonding functions with only a slight adjustment in the definition of the inverse limit to accommodate this change.
3. Compactness and connectedness
Fundamental to the study of any topic in mathematics is an existence theorem that demonstrates that there are structures in the area under consideration. For inverse limits with set-valued functions our interests in continuum theory extend beyond the existence to compactness and connectedness. A set traditionally used in the proof that
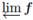 is nonempty and compact is
is nonempty and compact is
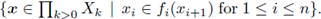 This set was originally denoted Gn in the early papers on this topic and it is easy to see that the inverse limit is
This set was originally denoted Gn in the early papers on this topic and it is easy to see that the inverse limit is
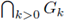 thus reducing the question of existence and compactness of the inverse limit to the question of the compactness of a nonempty Gn. In case the bonding functions in an inverse limit with set-valued functions are upper semi-continuous, places to find a discussion of the compactness of a nonempty Gn include [13, Theorem 1.6, p. 9] and [21, Theorem 111, p. 81]. Connectedness of the inverse limit is characterized by the connectedness of the set Gn for n =1, 2, 3,... as seen in our first theorem.
thus reducing the question of existence and compactness of the inverse limit to the question of the compactness of a nonempty Gn. In case the bonding functions in an inverse limit with set-valued functions are upper semi-continuous, places to find a discussion of the compactness of a nonempty Gn include [13, Theorem 1.6, p. 9] and [21, Theorem 111, p. 81]. Connectedness of the inverse limit is characterized by the connectedness of the set Gn for n =1, 2, 3,... as seen in our first theorem.
Theorem 3.1. Suppose that X is a sequence of continua and f: Xi+1
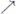 Xi
is upper semi-continuous for each positive integer i. Then,
Xi
is upper semi-continuous for each positive integer i. Then,
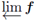 is connected if, and only if, G
n
is connected for each positive integer n.
is connected if, and only if, G
n
is connected for each positive integer n.
It quickly became clear that the projection of Gn into the finite product
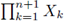 holds an equally important place in the area and these projections, especially
holds an equally important place in the area and these projections, especially
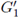 and
and
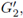 possess an advantage in that in many instances we are able to represent them with meaningful pictures. As a consequence of the importance of these projections and because when the factor spaces are continua they are connected if, and only if, the sets Gn are connected, we adopt and use throughout this article the notation
possess an advantage in that in many instances we are able to represent them with meaningful pictures. As a consequence of the importance of these projections and because when the factor spaces are continua they are connected if, and only if, the sets Gn are connected, we adopt and use throughout this article the notation
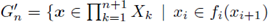 for 1 ≤ i ≤ n} for the projection of Gn into the product of the first n+1 factor spaces, i.e.,
for 1 ≤ i ≤ n} for the projection of Gn into the product of the first n+1 factor spaces, i.e.,
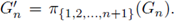 Also, when the bonding functions are upper semi-continuous, these sets G’n are precisely the "approximations" whose compactness yields compactness of the inverse limit. In the literature G’n has also been denoted by G'(f1, f2,…,fn) and we shall make use of both means of denoting this important set. In an effort to honor Bill Mahavier (an effort the author applauds) for his introduction of set-valued bonding functions into the study of inverse limits [24], some have suggested and some authors have even used the term 'Mahavier product' for the sets This author has pointed out to anyone who will listen that these sets are not actually products in any traditional sense and should not be called products.
Also, when the bonding functions are upper semi-continuous, these sets G’n are precisely the "approximations" whose compactness yields compactness of the inverse limit. In the literature G’n has also been denoted by G'(f1, f2,…,fn) and we shall make use of both means of denoting this important set. In an effort to honor Bill Mahavier (an effort the author applauds) for his introduction of set-valued bonding functions into the study of inverse limits [24], some have suggested and some authors have even used the term 'Mahavier product' for the sets This author has pointed out to anyone who will listen that these sets are not actually products in any traditional sense and should not be called products.
Examples show that even when the factor spaces are all [0,1] and the graph of the only bonding function in the system is connected, the inverse limit may not be connected; for example, see [13, Example 2.1, p. 15]. However, by assuming the bonding functions are continuum-valued we obtain a connected inverse limit, see [20] or [21, Theorem 125].
Theorem 3.2. Suppose that X is a sequence of continua and fi: Xi+1 → C(Xi) is upper semi-continuous for each positive integer i. Then,
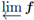 is a continuum.
is a continuum.
In case the factor spaces are the interval [0,1], Greenwood and Kennedy have characterized connectedness of inverse limits with set-valued functions, [9]. The Greenwood-Kennedy result is complicated to state so we omit it and its proof is long. As a consequence, the search continues for other simple sufficient conditions on the bonding functions for connectivity of the inverse limit.
4. Chainable inverse limits
It is known that inverse limits with mappings on chainable continua produce chainable continua. Unlike inverse limits with mappings, even on the interval [0,1] inverse limits with upper semi-continuous bonding functions need not produce chainable continua. Such inverse limits may fail to be connected [13, Example 1.2], be infinite dimensional [13, Example 1.1], contain triods [13, Example 2.4], or contain simple closed curves as seen in Example 5.1 below. In this section we discuss some results that show some set-valued functions on [0, 1] that are not mappings produce chainable inverse limits.
Like chainability and connectedness, many of the properties that researchers in inverse limits with mappings are accustomed to obtaining in the inverse limit space fail to hold when the bonding functions are set-valued even in the case where the factor spaces are [0, 1]. As already mentioned, with set-valued bonding functions on [0, 1] the inverse limit can even be infinite dimensional. See [13] for more information on such differences. The tools available from the theory of inverse limits with mappings are available in the literature and many of them can be found in these sources ([12] and [21]). The following theorem is quite easy to prove, but it is very useful in attacking certain problems in inverse limits with set-valued functions, specifically because it allows us to bring the power of inverse limits with mappings to bear on the problems we are trying to solve.
Theorem 4.1. Suppose X is a sequence of compacta and f: Xi+1
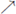 Xi
is a surjective upper semi-continuous function for each positive integer i. Then,
Xi
is a surjective upper semi-continuous function for each positive integer i. Then,
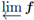 is homeomorphic to an inverse limit on the sequence of spaces X1, G'(f1), G'(f1, f2), G'(f1, f2, f3),… with bonding functions that are mappings.
is homeomorphic to an inverse limit on the sequence of spaces X1, G'(f1), G'(f1, f2), G'(f1, f2, f3),… with bonding functions that are mappings.
The bonding mappings in Theorem 4.1 are restrictions of projections, π{1,2…n}, of products to the factor spaces. This theorem is useful in proving that the inverse limit has certain properties that are preserved by inverse limits with mappings by showing that the sets G’n possess the given property. Such properties include, but are not limited to: chainability, treelikeness, dimension not greater than n, atrioidicity, and hereditary unicoherence. Recent applications of Theorem 4.1 include our next two theorems where inverse limits are shown to be chainable. In the proof of Theorem 4.2 the sets G’n are shown to be arcs, while in Theorem 4.4 the sets G’n are shown to be chainable continua. Theorem 4.2 may be found in [17, Section 7]. Theorem 4.4 is found in a recent manuscript currently available in preprint form, [18].
Theorem 4.2. Suppose a is a number 0 ≤ a < 1 and fa
is the upper semi-continuous function whose graph consists of three straight line intervals, one from (0, 0) to (1/2,1), one from (1/2,1) to (1/2, a), and one from (1/2, a) to (1,1). Then,
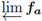 is a chainable continuum ifand only if
is a chainable continuum ifand only if
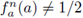 for each positive integer n.
for each positive integer n.
We require some definitions to state Theorem 4.4. Suppose z0, z1, z2,… is a sequence of numbers from [0, 1] such that
Z0 = 1;
zi+1 > zi if i is odd and z i + 1 < z i otherwise;
some subsequence of z converges to 0 and another subsequence of z converges to 1.
Let f : [0,1]
 [0,1] be the upper semi-continuous function defined as follows:
[0,1] be the upper semi-continuous function defined as follows:
We call G( f) the sinusoid determined by z, or, simply, a sinusoid. Sinusoids include a traditional sin(1/x)-curve and the curve shown by Dorothy Sher-ling [25] not to be homeomorphic to an inverse limit on intervals with a single mapping. Her example from [25] is the sinusoid determined by the sequence 1,0,1/2,0,1,0,1,0,1/2,0,1,0,1,0,1,0,1/2,0,…. The proof of Theorem 4.4 may be found in [18]. It employs an old theorem of R. H. Bing that characterizes chainability among hereditarily deomposable continua [3]. A continuum M is hereditarily unicoherent provided if A and B are subcontinua of M with a point in common then A ∩ B is connected. A continuum M is a triod provided there is a subcontinuum H of M such that M - H has (at least) three components; a continuum is atriodic provided it does not contain a triod. The following theorem of Bing [3] is key in the proof of Theorem 4.4 in [18].
Theorem 4.3 (Bing). Suppose M is an hereditarily decomposable continuum. Then M is chainable if, and only if, it is atriodic and hereditarily unicoherent.
Theorem 4.4. Suppose f is a sequence of upper semi-continuous functions such that, for each positive integer i, fi: [0,1]
 [0,1] has a graph that is a sinusoid. Then
[0,1] has a graph that is a sinusoid. Then
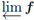 is chainable.
is chainable.
4.1. C-sets and monotone mappings
The proof of Theorem 4.4 also makes use of the notions of a C-set, terminal subcontinua, and monotone mappings. A subset K of a continuum M is a C-set in M provided it is true that if H is a subcontinuum of M containing a point of K and a point of M - K, then K ⊆ H (see [11] for more on C-sets). A subcontinuum C of a continuum M is said to be terminal in M provided if H and K are subcontinua of M each intersecting C, then H ⊆ K ∪ C or K ⊆ H ∪ C. Terminal continua were introduced by Fugate; for more information on terminal continua see [10]. Some results needed to establish Theorem 4.4 include many of the following theorems.
Theorem 4.5. If A and B are chainable continua and A ∩ B is a continuum that is terminal and a C-set in both A and B, then A ∪ B is chainable. Moreover, A ∩ B is a C-set in A ∪ B.
Theorem 4.6. Suppose H is a subcontinuum of the continuum M and K is a C-set in H. If there is an open subset U of M such that K ⊆ U ⊆ H, then K is a C-set in M.
A mapping between continua is called monotone provided point inverses are connected. It is well known that preimages of continua under monotone maps are continua. Below are listed some results from [18] that relate monotone maps and C-sets.
Theorem 4.7. Suppose each of M and N is a continuum and f : M
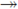 N is a mapping. If x is a point of N such that f-1(x) is a C-set in M, and H is a subcontinuum of M containing a point of f-1(x) such that f (H) is nondegenerate, then f-1(x) is a subset of H.
N is a mapping. If x is a point of N such that f-1(x) is a C-set in M, and H is a subcontinuum of M containing a point of f-1(x) such that f (H) is nondegenerate, then f-1(x) is a subset of H.
Theorem 4.8. Suppose each of M and N is a continuum and f : M
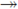 N is a monotone mapping such that f-1(x) is a C-set in M for each x in N. If H is a subcontinuum of M and f (H) is nondegenerate, then f-1(f (H)) = H.
N is a monotone mapping such that f-1(x) is a C-set in M for each x in N. If H is a subcontinuum of M and f (H) is nondegenerate, then f-1(f (H)) = H.
Theorem 4.9. Suppose a and b are numbers with a < b, M is a continuum and f
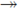 M : [a, b] is a monotone mapping such that f -1(t) is a C-set in M for each t in [a, b]. Then, f -1(a) and f -1(b) are terminal in M.
M : [a, b] is a monotone mapping such that f -1(t) is a C-set in M for each t in [a, b]. Then, f -1(a) and f -1(b) are terminal in M.
Theorem 4.10. Suppose M and N are continua, N is hereditarily decomposable, and f : M → N is a monotone mapping such that f-1(x) is a C-set in M for each x in N. If H is a subcontinuum of M such that f(H) is nondegenerate, then H is decomposable.
Theorem 4.11. Suppose M and N are continua, N is hereditarily decomposable, and f : M → N is a monotone mapping such that f-1(x) is an hereditarily decomposable C-set in M for each x in N. Then, M is hereditarily decomposable.
Theorem 4.12. Suppose M and N are continua, N is atriodic, and f : M → N is a monotone mapping such that f-1(x) is an atriodic C-set in M for each x in N. Then, M is atriodic.
Theorem 4.13. Suppose M and N are continua, N is hereditarily unicoherent, and f : M → N is a monotone mapping such that f-1(x) is an hereditarily unicoherent C-set in M for each x in N. Then, M is hereditarily unicoherent.
4.2. Theorems and questions about C-sets
Bing's theorem and the preceding results on C-sets and monotone mappings lead to Theorem 4.14 and Question 4.15 from [18]. More information on the question and its background is contained in [18].
Theorem 4.14. Suppose M is a continuum, N is an hereditarily decomposable chainable continuum, and f : M
 N is a monotone mapping such that f -1(x) is an hereditarily decomposable chainable C-set in M for each x in N. Then, M is chainable.
N is a monotone mapping such that f -1(x) is an hereditarily decomposable chainable C-set in M for each x in N. Then, M is chainable.
Traditionally, questions abound about the chainability of a continuum when its image under a monotone mapping is chainable (see [5, Problem 105, p. 382] or [8] for more on such questions). The result in Theorem 4.14 suggests the following question along these lines. This question is posed in [18].
Question 4.15. If M is a 1-dimensional atriodic continuum and f is a monotone mapping of M onto a chainable continuum N such that point-inverses are chainable C-sets in M, is M chainable?
Theorem 4.14 yields that the answer to Question 4.15 is "yes" in case N as well as all point inverses are hereditarily decomposable chainable continua even without assuming M is atriodic and 1-dimensional.
4.3. More on chainability
In a nice paper in 2014, Kelly [22] showed that a class of set-valued functions that he calls irreducible functions produce chainable continua in systems on [0, 1] with a single bonding function. His results confirm the chainability of Example 5.4 of [15] and extend it considerably. We conclude this section with Kelly's result. Notably, he is able to characterize chainability in systems with a single irreducible bonding function by the chainability of G’2 as well as by conditions on the graph of the function that are easy to check.
Let A be a closed subset of [0,1] containing 0 and 1 such that
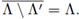 A collection of mappings
A collection of mappings
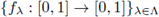 is called irreducible provided:
is called irreducible provided:
0 ∈ fλ([0,1]) if, and only if, λ = 0; and 1 ∈ fA ([0,1] if, and only if, λ =1;
if λ, μ ∈ Λ with λ < μ, then fλ(y) ≠ fμ(y) for all y ∈ (0,1), and G(fλ) ∩ G(fμ) ≠∅ if, and only if, (λ,μ) ∩ Λ = ∅; and
if λ is a sequence of points of Λ that converges to λ, then the sequence fλ1, fλ2, fλ3,… converges uniformly to fλ.
A function F : [0,1]
 [0,1] is called irreducible provided there is an irreducible collection
[0,1] is called irreducible provided there is an irreducible collection
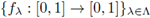 such that
such that
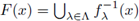 for each x in [0,1].
for each x in [0,1].
Theorem 4.16 (Kelly). If F : [0,1]
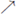 [0,1] is an irreducible function, then the following are equivalent:
[0,1] is an irreducible function, then the following are equivalent:
5. Treelikeness
Many inverse limits with set-valued functions that are continua but not chainable turn out to be treelike. Early in its development, treelikeness was defined by covers by tree chains. Treelikeness has been characterized in a number of ways including being homeomorphic to an inverse limit on trees. In order for the reader to appreciate the complexities of the problem of determining treelikeness we mention the following example of an upper semi-continuous function on [0,1] whose graph is the union of two surjective homeomorphisms yet the inverse limit is not treelike.
Example 5.1. Let h1
be the homeomorphism of [0,1] whose graph consists of two straight line intervals, one from (0,0) to (1/2, 3/4) and one from (1/2, 3/4) to (1,1). Let h2
be the homeomorphism whose graph consists of two straight line intervals, one from (0, 1) to (1/2, 3/4) and one from (1/2, 3/4) to (1,0). Let f : [0,1]
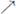 [0,1] be the function whose graph is h1 ∪ h2
. Then,
[0,1] be the function whose graph is h1 ∪ h2
. Then,
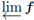 contains a simple closed curve and consequently is not treelike.
contains a simple closed curve and consequently is not treelike.
In [17] the author demonstrated the chainability of inverse limits with many members of a parameterized family of upper semi-continuous functions. The functions in the family were first mentioned above in Theorem 4.2 and may be described as follows: for 0 ≤ a < 1 let fa: [0,1] → C([0,1]) be the function whose graph consists of three straight line intervals, one from (0, 0) to (1/2, 1), one from (1/2, 1) to (1/2, a), and one from (1/2, a) to (1,1). It is known that
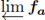 is treelike for each a ∈ [0,1] ([16, Corollary 4.1]). See also Theorem 5.8 below. Had we allowed the parameter a to be 1, the graph consists of only two straight line intervals and the inverse limit is an arc.
is treelike for each a ∈ [0,1] ([16, Corollary 4.1]). See also Theorem 5.8 below. Had we allowed the parameter a to be 1, the graph consists of only two straight line intervals and the inverse limit is an arc.
Theorem 5.2. If 0 ≤ a < 1 then
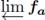 is treelike.
is treelike.
One class of set-valued functions that has received some attention is the class of functions whose graphs are a union of two mappings. Example 5.1 above is such a function. In our next example we consider another member of the class. It is known that treelike continua are unicoherent. Thus, we can demonstrate that an inverse limit is not treelike by showing that it is not unicoherent. Consider the following example from [14, Example 4.3].
Example 5.3. Let f1
be the identity on [0,1] and f2
be the piecewise linear map that passes through (0,1/2), (1/4,1), (1/2,1/2), and (1,0). Let f = f1 ∪ f2. Then, M =
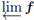 is not unicoherent.
is not unicoherent.
Proof. Let H be the subcontinuum of M that is the inverse limit of the sequence f2, f2, f1, f1, f1, … and K be the inverse limit of f1, f2, f1, f1, f1,.... Then, H n K = {(1/2,1/2,1/2,…), (1/2,1/2,0, 0,--.)}.
A sufficient condition for the treelikeness of an inverse limit of a set-valued function that is the union of two mappings is found in the following theorem from [14, Theorem 3.4, p, 20].
Theorem 5.4. If f1
and f2
are mappings of [0,1] into [0,1] whose only coincidence point is a common fixed point p such that
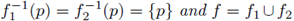 is surjective, then
is surjective, then
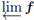 is treelike.
is treelike.
Relative to this theorem, note that the only coincidence point of the maps f1 and f2 in Example 5.3 is a common fixed point 1/2 but f2 -1(1/2) = {0,1/2)}.
Some traditional continuum theory is used in the proof of Theorem 5.4, the notion of clumps that Howard Cook introduced in 1974 in [4]. Stating all of the definitions to give full details on clumps and their use in the proof is beyond the scope of this survey. The interested reader is referred to the Cook's paper for more details about clumps along with [14] for the way they are used in obtaining treelikeness in Theorem 5.4.
One quite useful characterization of treelikeness comes from the theory of shape where treelikeness is characterized by the properties of trivial shape and having dimension one. Charatonik and Roe proved a vital theorem to demonstrating treelikenss of inverse limits on [0, 1] when they proved the following theorem [7], which reduces the treelikeness problem for inverse limits on [0, 1] with interval-valued functions to a dimension problem.
Theorem 5.5. Suppose f: [0,1] → C([0,1]) is upper semi-continuous for each positive integer i. Then,
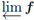 has trivial shape.
has trivial shape.
Nall observed that a companion theorem to the Charatonik-Roe theorem holds (see [19], where one can find a different but equivalent statement of Nall's theorem along with its proof).
Theorem 5.6 (Nall). Suppose f: [0,1] → C([0,1]) is upper semi-continuous for each positive integer i. Then,
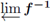 has trivial shape.
has trivial shape.
There are several results in the literature having the flavor of Theorems 5.5 and 5.6. For example it is known that if f : [0,1]
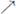 [0,1] is a surjective upper semi-continuous function, then
[0,1] is a surjective upper semi-continuous function, then
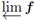 is connected if, and only if,
is connected if, and only if,
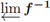 is connected ([13, Theorem 2.3, p. 16]). Thus, we pose the following question.
is connected ([13, Theorem 2.3, p. 16]). Thus, we pose the following question.
Question 5.7. Suppose f : [0,1]
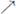 [0,1] is a surjective upper semi-continuous function such that
[0,1] is a surjective upper semi-continuous function such that
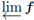 is treelike. Is
is treelike. Is
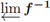 treelike?
treelike?
A major obstacle to controlling dimension in inverse limits with set-valued functions is found in graphs that contain horizontal intervals (flat spots). This has been known for virtually the entire life of the study of these inverse limits. One of the earliest examples that was considered was the function f : [0,1]
 [0,1] such that f (t) =0 for t > 0 and f (0) = [0,1], where
[0,1] such that f (t) =0 for t > 0 and f (0) = [0,1], where
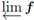 is infinite dimensional. For interval-valued functions, roughly speaking, we get treelikeness provided flat spot values do not iterate to a point with a nondegenerate value. The simplest theorem we know along these lines is the following.
is infinite dimensional. For interval-valued functions, roughly speaking, we get treelikeness provided flat spot values do not iterate to a point with a nondegenerate value. The simplest theorem we know along these lines is the following.
Theorem 5.8. If f : [0,1] → C([0,1]) is upper semi-continuous and G(f) contains no horizontal interval, then
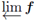 is treelike.
is treelike.
Recently, Mark Marsh [27] has looked further into treelikenss of inverse limits on [0,1] with interval-valued functions and subsequently he has established a characterization in [28].
6. Inverse limits with parameterized families
A topic somewhat less traditional in continuum theory than the properties we have examined thus far is the study of inverse limits with members of parameterized families of functions. However, the topic has now been under scrutiny for close to twenty-five years or more. Closer ties between continuum theory and the theory of dynamical systems are chiefly responsible for the increased interest in parameterized families. In 1967 Smale published an article, [29], in the Bulletin of the American Mathematical Society in which he described his famous horseshoe. Continuum theorists were struck by the similarity to a construction of the familiar Brouwer-Janiszewski-Knaster continuum (B-J-K continuum), [23, Example 1, pp. 204-205] (n.b., footnote (3) on page 204). In the 1980s questions from the theory of dynamical systems began to appear in continuum theory. The author's first recollection of such a question was by Marcy Barge regarding whether the Henón attractor at certain parameter values is homeomorphic to the B-J-K continuum. In 1996 Barge and the author published a paper [2] containing an investigation of inverse limits on [0, 1] using single bonding maps chosen from the parameterized logistic family of mappings. Over the years many research articles have been devoted to the topology of inverse limits with bonding maps from the parameterized tent family of maps, fλ: [0,1] → [0,1] given by fλ(t) = min{2λt, 2λ(1 - t)}. Although the maps from the tent family have been shown to produce different inverse limits for differing parameter values, current research is still involved in deciding whether this remains true of the core maps in the tent family. For inverse limits with set-valued functions, in [17] the author has studied the effects of changing the parameter in a parameterized family of set-valued functions inspired by the family of tent maps. The members of the family studied in [17] all produce treelike continua so the article concentrated on determining when the inverse limits are chainable.
Let a be a number, 0 ≤ a < 1 and let fa be the upper semi-continuous set-valued function whose graph consists of three straight line intervals, one from (0, 0) to (1/2,1), one from (1/2,1) to (1/2, a), and one from (1/2, a) to (1,1). We have already seen in the section on treelikeness, Section 5, that each fa produces an inverse limit that is treelike. Theorem 4.2 characterizes chainability in terms of the parameter. Our next theorem addresses the nature of the continua in this family that are chainable (see [17, Example 7.1]).
Theorem 6.1. Suppose a is a number, 0 ≤ a < 1/2 and
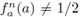 for each positive integer n. Then,
for each positive integer n. Then,
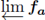 is the closure of a topological ray with remainder
is the closure of a topological ray with remainder
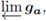 where
where
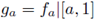
There are uncountably many values for a, 0 ≤ a < 1/2 such that 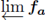 is chainable ([17, Remark 7.1, p.65]). We pose the following question from that same article ([17, Question 7.1, p. 65]).
is chainable ([17, Remark 7.1, p.65]). We pose the following question from that same article ([17, Question 7.1, p. 65]).
Question 6.2. If 0 ≤ a ≤ b < 1/2, are
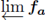 and
and
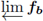 topologically different?
topologically different?
It is known for the parameterized tent family of mappings that two maps with different parameters greater than 1/2 produce topologically different continua. Even though maps with parameter values above 1/2 in that family produce an inverse limit that is a topological ray with remainder the core of the inverse limit, the question of whether the cores are all topologically different remains unsettled. This fact leads us to look at cores for the family of Theorem 6.1. Changing fa|[a, 1] into an upper semi-continuous function on [0, 1] leads us to the following two-parameter family of maps and a companion to Question 6.2.
Let b, c be numbers, 0 ≤ b < 1 and 0 < c < 1. Define gb,c to be the upper semi-continuous set-valued function whose graph consists of three straight line intervals, one from (0, b) to (c, 1), one from (c, 1) to (c, 0), and one from (c, 0) to (1, 1). Theorem 5.8 yields that each member of this two-parameter family produces a treelike continuum in its inverse limit. We pose the following question, see [17, Question 8.1].
Question 6.3. Suppose c is a number, 0 < c < 1. If a, b are numbers, 0 ≤ a < b < 1, are
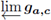 and
and
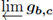 topologically different?
topologically different?
It is known that if
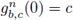 for some positive integer n, then
for some positive integer n, then
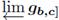 is a decomposable continuum that is not chainable even though it is treelike (see [17, Example 9.1]).
is a decomposable continuum that is not chainable even though it is treelike (see [17, Example 9.1]).
7. Additional topics
After reviewing a draft of this article, Mark Marsh suggested that the author mention something about two other traditional topics in continuum theory as they relate to inverse limits with set-valued functions, plane embeddings and the fixed point property. Not much is known about either of these topics.
One of the few published results on plane embeddings is found in a discussion of a surprisingly complicated inverse limit on [0,1] where the only bonding function has a graph consisting of two straight line intervals, one from (0,0) to (0,1) and one from (0, 1) to (1, 0), see [13, p. 33]. There it is shown that the inverse limit is nonplanar because it contains uncountably many mutually exclusive triods.
There are published questions about the fixed point property in [13, Problems 6.53, 6.54, and 6.55] but, insofar as the author knows, the only results are found in Marsh's papers, [26] and [27]. We refer the interested reader to Marsh's papers for further information. Marsh poses the following interesting question in [26, Question 19, p. 225].
Question 7.1 (Marsh). Do all treelike continua obtainable as inverse limits on [0,1] with interval-valued functions have the fixed point property?
Other traditional topics in continuum theory get some mention in [13, Chapter 6]. These include hyperspaces (Problems 6.47 and 6.48), span (Problem 6.52), and the Property of Kelley (Problem 6.56). The author knows of no progress on any of these topics.