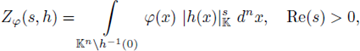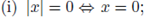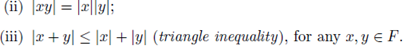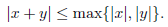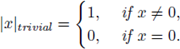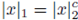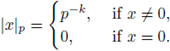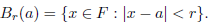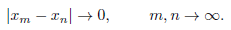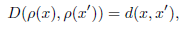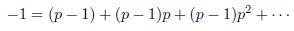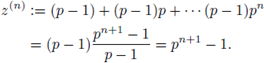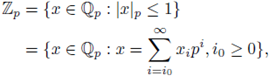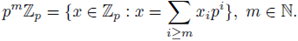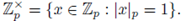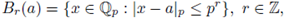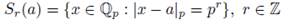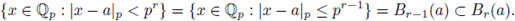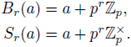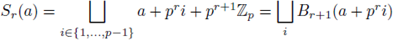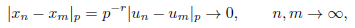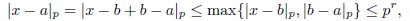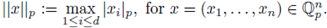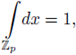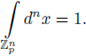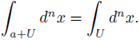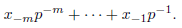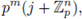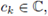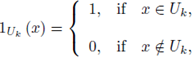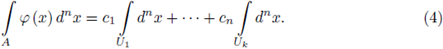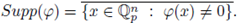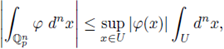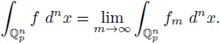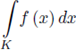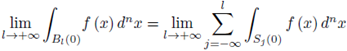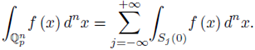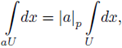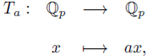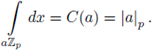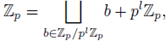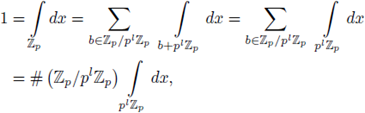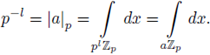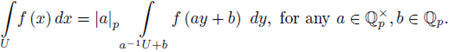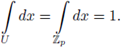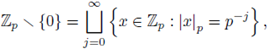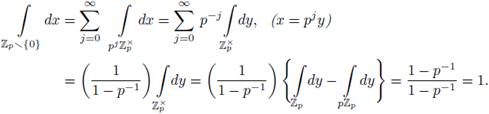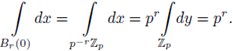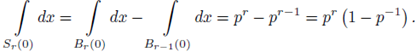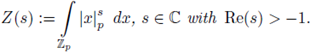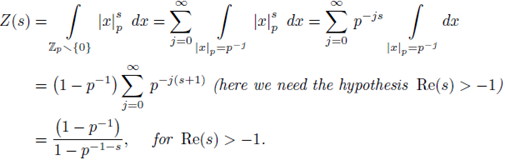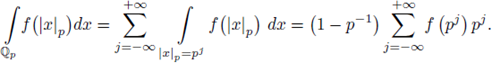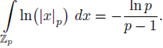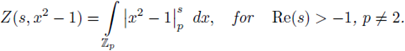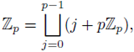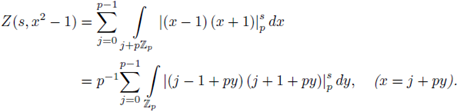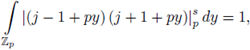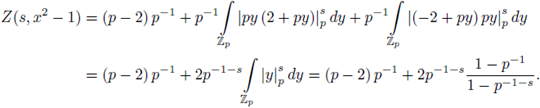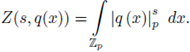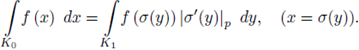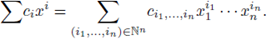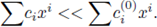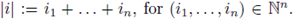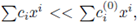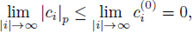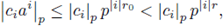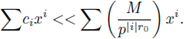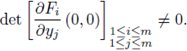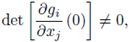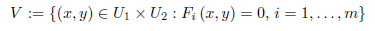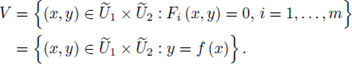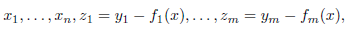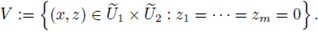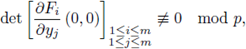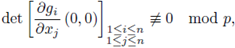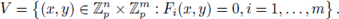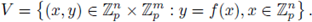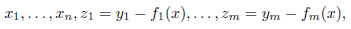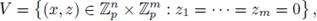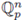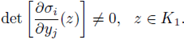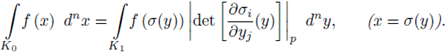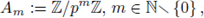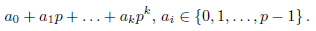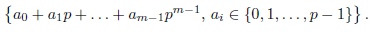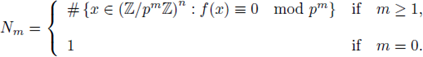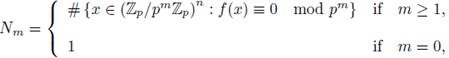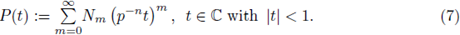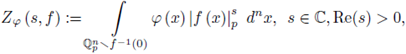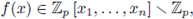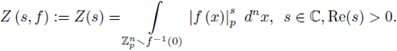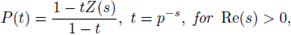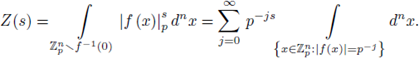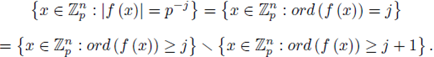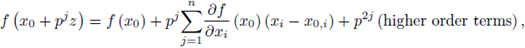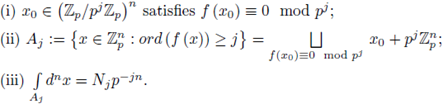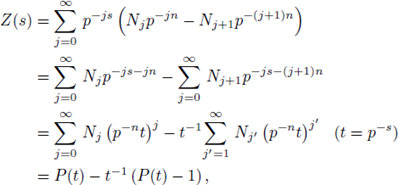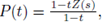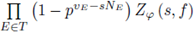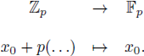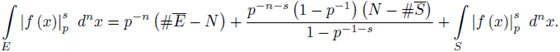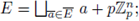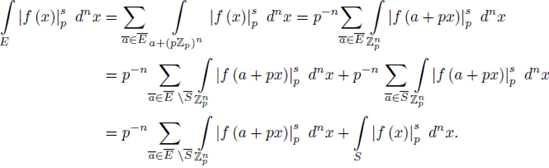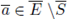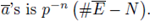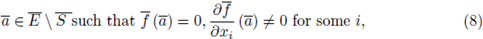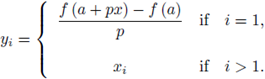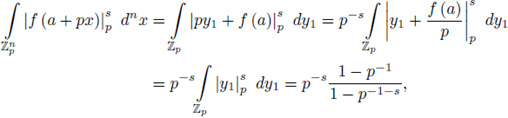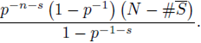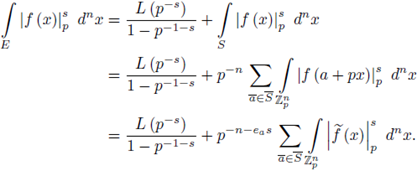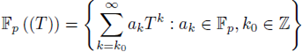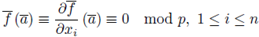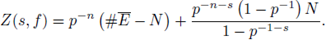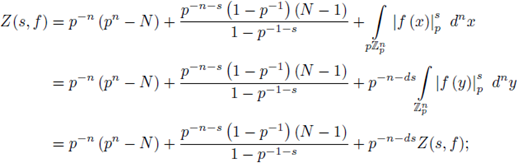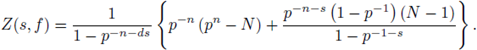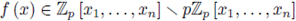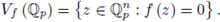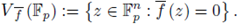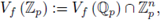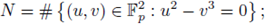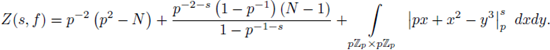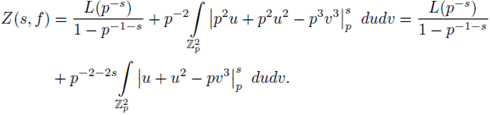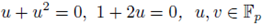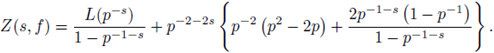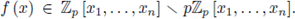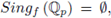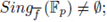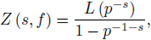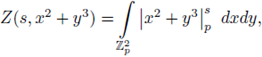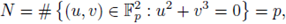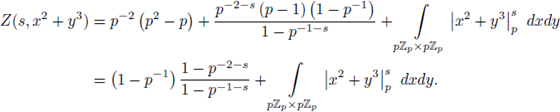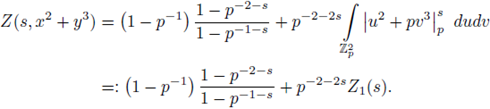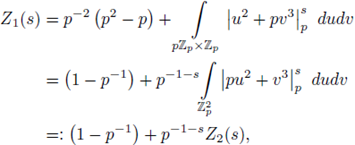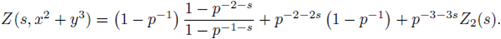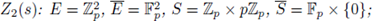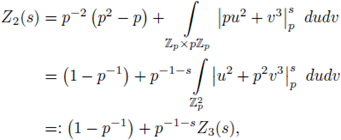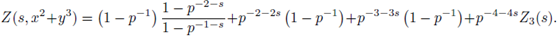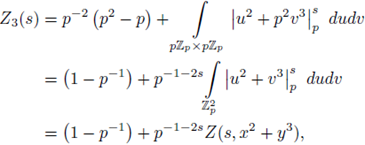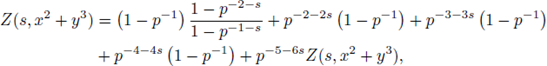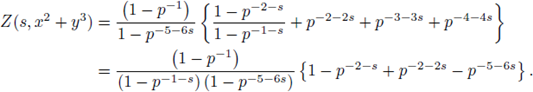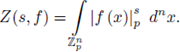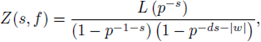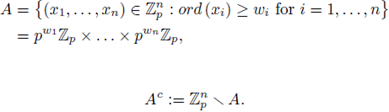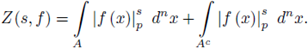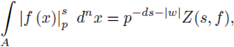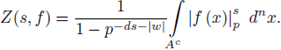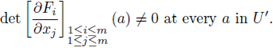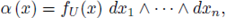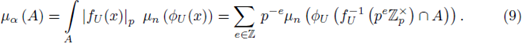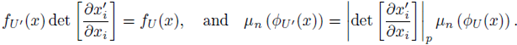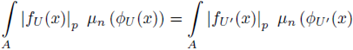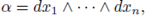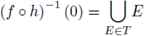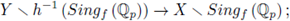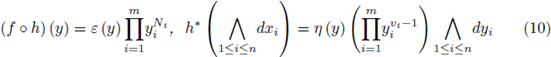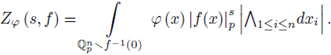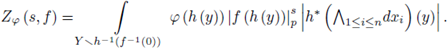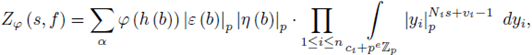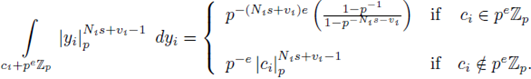1. Introduction
In these notes we provide an introduction to the theory of local zeta functions from scratch. We assume essentially a basic knowledge of algebra, metric spaces and basic analysis, mainly measure theory. Let
 be a local field, for instance
be a local field, for instance
 the field of p-adic numbers, or
the field of p-adic numbers, or
 the field of formal Laurent series with coefficients in a finite field with p elements. Let
the field of formal Laurent series with coefficients in a finite field with p elements. Let
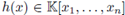 be a non-constant polynomial and let 92 be a test function. The local zeta function attached to the pair (h, 9) is defined as
be a non-constant polynomial and let 92 be a test function. The local zeta function attached to the pair (h, 9) is defined as
where
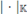 denotes the absolute value of
denotes the absolute value of
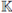 , s ∈ C, and d
n
x denotes a normalized Haar measure of the topological group (
, s ∈ C, and d
n
x denotes a normalized Haar measure of the topological group (
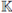 n, +). These integrals give rise to holomorphic functions of s in the half-plane Re(s) > 0. If
n, +). These integrals give rise to holomorphic functions of s in the half-plane Re(s) > 0. If
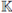 has characteristic zero, then
has characteristic zero, then
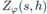 admits a meromorphic continuation to the whole complex plane. The p-adic local zeta functions (also called Igusa's local zeta functions) are connected with the number of solutions of polynomial congruences mod pm and with exponential sums mod pm (see e.g., [14], [28], [31]).
admits a meromorphic continuation to the whole complex plane. The p-adic local zeta functions (also called Igusa's local zeta functions) are connected with the number of solutions of polynomial congruences mod pm and with exponential sums mod pm (see e.g., [14], [28], [31]).
In the Archimedean case,
 the study of local zeta functions was initiated by Gel'fand and Shilov 21]. The meromorphic continuation of the local zeta functions was established, independently, by Atiyah [4] and Bernstein [6] (see also [31, Theorem 5.5.1 and Corollary 5.5.1]). The main motivation was that the meromorphic continuation of Archimedean local zeta functions implies the existence of fundamental solutions (i.e. Green functions) for differential operators with constant coefficients. It is important to mention here, that in the p-adic framework, the existence of fundamental solutions for pseudo differential operators is also a consequence of the fact that the Igusa local zeta functions admit a meromorphic continuation (see [33, Chapter 10] and [62, Chapter 5]).
the study of local zeta functions was initiated by Gel'fand and Shilov 21]. The meromorphic continuation of the local zeta functions was established, independently, by Atiyah [4] and Bernstein [6] (see also [31, Theorem 5.5.1 and Corollary 5.5.1]). The main motivation was that the meromorphic continuation of Archimedean local zeta functions implies the existence of fundamental solutions (i.e. Green functions) for differential operators with constant coefficients. It is important to mention here, that in the p-adic framework, the existence of fundamental solutions for pseudo differential operators is also a consequence of the fact that the Igusa local zeta functions admit a meromorphic continuation (see [33, Chapter 10] and [62, Chapter 5]).
On the other hand, in the middle 60s, Weil initiated the study of local zeta functions, in the Archimedean and non-Archimedean settings, in connection with the Poisson-Siegel formula [59]. In the 70s, Igusa developed a uniform theory for local zeta functions over local fields of characteristic zero [28], [30]. More recently, Denef and Loeser introduced in [15] the topological zeta functions, and in [16] they introduce the motivic zeta functions, which constitute a vast generalization of the p-adic local zeta functions.
In the last thirty-five years there has been a strong interest on p-adic models of quantum field theory, which is motivated by the fact that these models are exactly solvable. There is a large list of p-adic type Feynman and string amplitudes that are related with local zeta functions of Igusa-type, and it is interesting to mention that it seems that the mathematical community working on local zeta functions is not aware of this fact (see e.g. [2], [5], [7], [10]-[13], [18]-[20], [22]-[24], [27], [38], [39], [42], [48]-[52], and the references therein).
The connections between Feynman amplitudes and local zeta functions are very old and deep. Let us mention that the works of Speer [50] and Bollini, Giambiagi and González Domínguez [11] on regularization of Feynman amplitudes in quantum field theory are based on the analytic continuation of distributions attached to complex powers of polynomial functions in the sense of Gel'fand and Shilov [21] (see also [5], [7], [10] and [42], among others). This analogy turns out to be very important in the rigorous construction of quantum scalar fields in the p-adic setting (see [43] and the references therein).
The local zeta functions are also deeply connected with p-adic string amplitudes. In [8], the authors proved that the p-adic Koba-Nielsen type string amplitudes are bona fide integrals. They attached to these amplitudes Igusa-type integrals depending on several complex parameters and show that these integrals admit meromorphic continuations as rational functions. Then they used these functions to regularize the Koba-Nielsen amplitudes. In [9], the authors discussed the limit p approaches to one of tree-level p-adic open string amplitudes and its connections with the topological zeta functions. There is empirical evidence that p-adic strings are related to the ordinary strings in the limit p → 1. Denef and Loeser established that the limit p → 1 of a Igusa's local zeta function gives rise to an object called topological zeta function. By using Denef-Loeser's theory of topological zeta functions, it is showed in [9] that limit p → 1 of tree-level p-adic string amplitudes give rise to certain amplitudes, that we have named Denef-Loeser string amplitudes.
Finally, we want to mention about the remarkable connection between local zeta functions and algebraic statistics (see [40], [58]). In [58] is presented an interesting connection with machine learning.
This survey article is based on well-known references, mainly Igusa's book [31]. The work is organized as follows. In Section 2, we introduce the field of p-adic numbers, and we devote Section 3 to the integration theory over
 Section 4 is dedicated to the implicit function theorems on the p-adic field. In Section 5, we introduce the simplest type of local zeta function and show its connection with number of solutions of polynomial congruences mod pm. In Section 6, we introduce the stationary phase formula and use it to establish the rationality of local zeta functions for several type of polynomials. Finally, in Section 7, we state Hironaka's resolution of singularities theorem, and we use it to prove the rationality of the simplest type of local zeta functions in Section 8.
Section 4 is dedicated to the implicit function theorems on the p-adic field. In Section 5, we introduce the simplest type of local zeta function and show its connection with number of solutions of polynomial congruences mod pm. In Section 6, we introduce the stationary phase formula and use it to establish the rationality of local zeta functions for several type of polynomials. Finally, in Section 7, we state Hironaka's resolution of singularities theorem, and we use it to prove the rationality of the simplest type of local zeta functions in Section 8.
For an introduction to p-adic analysis the reader may consult [1], [25], [32], [35], [46], [47], [53] and [56]. For an in-depth discussion of the classical aspects of the local zeta functions, we recommend [3], [14], [21], [28], [30], [31], [41]. There are many excellent surveys about local zeta functions and their generalizations. For an introduction to Igusa's zeta function, topological zeta functions and motivic integration we refer the reader to [14], [16], [17], [44], [45], [55]. A good introduction to local zeta functions for pre-homogeneous vector spaces can be found in [30], [31] and [34]. Some general references for differential equations over non-Archimedean fields are [1], [33], [56], [62]. Finally, the reader interested in the relations between p-adic analysis and mathematical physics may enjoy [12], [13], [19], [20], [22]- [24], [27], [33], [37]- [39], [43], [48], [49], [52], [54], [56], [57] and [62].
2. p-adic Numbers- Essential Facts
2.1. Basic Facts
In this section we summarize the basic aspects of the field of p-adic numbers, for an in-depth discussion the reader may consult [1], [25], [32], [35], [46], [47], [53] and [56].
Definition 2.1. Let F be a field. An absolute value on F is a real-valued function, | · |, satisfying
Definition 2.2. An absolute value | · | is called non-Archimedean (or ultrametric), if it satisfies
Example 2.3. The trivial absolute value is defined as
From now on we will work only with non trivial absolute values.
Definition 2.4. Given two absolute values | · |1, | · |2 defined on F, we say that they are equivalent, if there exists a positive constant c such that
for any x ∈ F.
Definition 2.5. Let p be a fixed prime number, and let x be a nonzero rational number. Then,
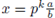 for some a ,b, k ∈
for some a ,b, k ∈
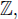 with p ∤ ab. The p-adic absolute value of x is defined as
with p ∤ ab. The p-adic absolute value of x is defined as
Lemma 2.6. The function | · |p
is a non-Archimedean absolute value on
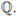
The proof is left to the reader. In fact, we kindly invite the reader to prove all the results labeled as Lemmas in these notes.
Theorem 2.7 (Ostrowski, [35]). Any non trivial absolute value on
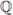 is equivalent to | · |p
or to the standard absolute value | · |∞.
is equivalent to | · |p
or to the standard absolute value | · |∞.
An absolute value | · | on F allow us to define a distance d(x, y) := |x − y|, x, y ∈ F. We now introduce a topology on F by giving a basis of open sets consisting of the open balls B r (a) with center a and radius r > 0:
A sequence of points
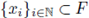 is called Cauchy if
is called Cauchy if
A field F with a non trivial absolute value | · | is said to be complete if any Cauchy sequence
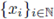 has a limit point x* ∈ F, i.e. if |xn - x*| → 0, n → ∞. This is equivalent to the fact that (F, d) , with d(x, y) = | x - y| , is a complete metric space.
has a limit point x* ∈ F, i.e. if |xn - x*| → 0, n → ∞. This is equivalent to the fact that (F, d) , with d(x, y) = | x - y| , is a complete metric space.
Remark 2.8. Let (X, d), (Y, D) be two metric spaces. A bijection p : X → Y satisfying
is called an isometry.
The following fact is well-known (see e.g. [36]).
Theorem 2.9. Let (M, d) be a metric space. There exists a complete metric space
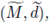 such that M is isometric to a dense subset of
such that M is isometric to a dense subset of
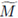
The field of p-adic numbers
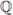 p is defined as the completion of
p is defined as the completion of
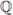 with respect to the distance induced by | · |p. Any p-adic number x ≠ 0 has a unique representation of the form
with respect to the distance induced by | · |p. Any p-adic number x ≠ 0 has a unique representation of the form
where
 The integer γ is called the p-adic order of x, and it will be denoted as ord(x). By definition ord(0) = +∞.
The integer γ is called the p-adic order of x, and it will be denoted as ord(x). By definition ord(0) = +∞.
Lemma 2.10. Let (F, | · |) be a valued field, where | · | is a non-Archimedean absolute value. Assume that F is complete with respect to | · |. Then, the series
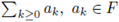 converges if, and only if, limk→∞ |ak | = 0.
converges if, and only if, limk→∞ |ak | = 0.
Since |xipi+r |p = p-i-r → 0, i → ∞, from Lemma 2.10 we conclude that series (1) converges in | · |p.
Example 2.11.
Indeed, set
Then limn→∞ z(n) = limn→∞ pn+1 - 1 = 0 - 1 = -1, since = |pn+1|p = p−n−1.
The unit ball
is a ring, more precisely, it is a domain of principal ideals. Any ideal of Zp has the form
Indeed, let
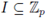 be an ideal. Set
be an ideal. Set
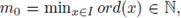 , and let x0 ∈ I such that ord(xo) = m0. Then
, and let x0 ∈ I such that ord(xo) = m0. Then
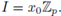
From a geometric point of view, the ideals of the form
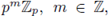 constitute a fundamental system of neighborhoods around the origin in
constitute a fundamental system of neighborhoods around the origin in
 The residue field of
The residue field of
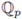 is
is
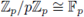 (the finite field with p elements).
(the finite field with p elements).
Lemma 2.12. x = x0 + x1p + ... ∈
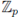 is a unit if, and only if, x
0
≠ 0. Moreover if x ∈
is a unit if, and only if, x
0
≠ 0. Moreover if x ∈
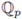 \ {0}, then
\ {0}, then
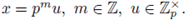
2.2. Topology of Q p
As we already mentioned,
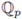 with d(x,y) = |x → y|p is a complete metric space. Define
with d(x,y) = |x → y|p is a complete metric space. Define
as the ball with center a and radius pr, and
as the sphere with center a and radius pr.
The topology of
 is quite different from the usual topology of
is quite different from the usual topology of
 First of all, since
First of all, since
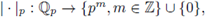 the radii are always integer powers of p; for the sake of brevity we just use the power in the notation Br(a) and Sr(a). On the other hand, since the powers of p and zero form a discrete set in
the radii are always integer powers of p; for the sake of brevity we just use the power in the notation Br(a) and Sr(a). On the other hand, since the powers of p and zero form a discrete set in
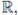 in the definition of Br (a) and Sr (a) we can always use '≤'. Indeed,
in the definition of Br (a) and Sr (a) we can always use '≤'. Indeed,
Remark 2.13.
We declare Br(a), r ∈
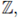 a ∈
a ∈
 , are open subsets; in addition, these sets form a basis for the topology of
, are open subsets; in addition, these sets form a basis for the topology of
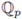 .
.
Proposition 2.14. Sr (a), Br (a) are open and closed sets in the topology of
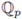 .
.
Proof. We first show that Sr(a) is open. Note that
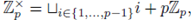 then
then
is an open set.
In order to show that Sr (a) is closed, we take a sequence
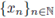 of points of Sr (a) converging to
of points of Sr (a) converging to
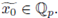 We must show that
We must show that
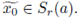 Note that
Note that
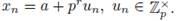 Since {xn} is a Cauchy sequence, we have
Since {xn} is a Cauchy sequence, we have
thus
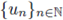 is also Cauchy, and since QP is complete, un →
is also Cauchy, and since QP is complete, un →
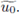 Then
Then
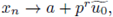 so in order to conclude our proof we must verify that
so in order to conclude our proof we must verify that
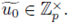 Because um is arbitrarily close to
Because um is arbitrarily close to
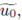 their p-adic expansions must agree up to a big power of p, hence
their p-adic expansions must agree up to a big power of p, hence
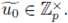
A similar argument shows that B r (a) is closed.
Proposition 2.15. f b ∈ B r (a) then B r (b) = B r (a), i.e., any point of the ball B r (a) is its center.
Proof. Let x ∈ Br (b); then,
i.e., Br(b) ⊆ B r (a). Since a ∈ Br(b) (i.e. |b - a|p = |a - b|p ≤ pr), we can repeat the previous argument to show that Br (a) ⊆ Br (b). 0
Lemma 2.16. The following assertions hold:
(i) any two balls in
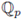 are either disjoint or one is contained in another;
are either disjoint or one is contained in another;
(ii) the boundary of any ball is the empty set.
Theorem 2.17 ([1, Sec. 1.8]). A set K ⊂
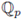 is compact if, and only if, it is closed and bounded in
is compact if, and only if, it is closed and bounded in
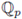 .
.
2.3. The n-dimensional p-adic space
We extend the p-adic norm to
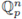 by taking
by taking
We define
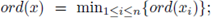 then, ||x||p = p-ord(x). The metric space
then, ||x||p = p-ord(x). The metric space
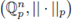 is a separable complete ultrametric space (here, separable means that
is a separable complete ultrametric space (here, separable means that
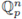 contains a countable dense subset, which is
contains a countable dense subset, which is
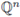 ).
).
For r ∈
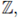 denote by
denote by
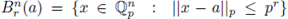 the ball of radius p
r
the ball of radius p
r
with center at a = (a1,...,an) ∈
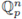 and take
and take
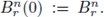 Note that
Note that
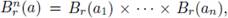 where
where
 is the one-dimensional ball of radius pr with center at
is the one-dimensional ball of radius pr with center at
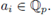 The ball
The ball
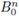 equals the product of n copies of Bo =
equals the product of n copies of Bo =
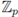 . We also denote by
. We also denote by
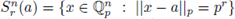 the sphere ofradius pr
with center at a = (a1, . . . , an) ∈
the sphere ofradius pr
with center at a = (a1, . . . , an) ∈
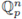 , and take
, and take
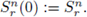 We notice that
We notice that
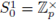 (the group of units of
(the group of units of
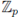 ), but
), but
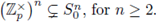
As a topological space
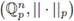 is totally disconnected, i.e., the only connected subsets of
is totally disconnected, i.e., the only connected subsets of
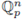 are the empty set and the points. Two balls in
are the empty set and the points. Two balls in
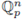 are either disjoint or one is contained in the other. As in the one dimensional case, a subset of
are either disjoint or one is contained in the other. As in the one dimensional case, a subset of
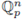 is compact if, and only if, it is closed and bounded in
is compact if, and only if, it is closed and bounded in
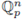 . Since the balls and spheres are both open and closed subsets in QJ, one has that
. Since the balls and spheres are both open and closed subsets in QJ, one has that
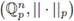 is a locally compact topological space.
is a locally compact topological space.
3. Integration on Q p
For this section we assume a basic knowledge of measure theory (see e.g. [26]).
Theorem 3.1 ([26, Thm B. Sec. 58]). Let (G, ·) be a locally compact topological group. There exists a Borel measure dx, unique up to multiplication by a positive constant, such that
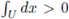 for every non empty Borel open set U, and
for every non empty Borel open set U, and
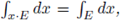 for every Borel set E.
for every Borel set E.
The measure dx is called a Haar measure of G. Since (
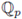 , +) is a locally compact topological group, by Theorem 3.1 there exists a measure dx, which is invariant under translations, i.e., d(x + a) = dx. If we normalize this measure by the condition
, +) is a locally compact topological group, by Theorem 3.1 there exists a measure dx, which is invariant under translations, i.e., d(x + a) = dx. If we normalize this measure by the condition
then dx is unique.
For the n-dimensional case we use that (
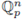 , +) is a locally compact topological group. We denote by d
n
x the product measure dxi ... dx
n
such that
, +) is a locally compact topological group. We denote by d
n
x the product measure dxi ... dx
n
such that
This measure also satisfies that d
n
(x + a) = d
n
x, for a ∈
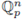 The open compact balls of ,
The open compact balls of ,
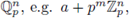 , generate the Borel σ-algebra of
, generate the Borel σ-algebra of
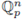 The measure d
n
x assigns to each open compact subset U a nonnegative real number
The measure d
n
x assigns to each open compact subset U a nonnegative real number
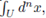 which satisfies
which satisfies
for all compact open subsets U
k
in
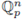 , which are pairwise disjoint, and verify
, which are pairwise disjoint, and verify
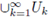 is still compact. In addition,
is still compact. In addition,
3.1. Integration of locally constant functions
A function
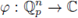 is said to be locally constant if for every x ∈
is said to be locally constant if for every x ∈
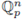 there exists an open compact subset U, containing x, and such that f (x) = f (u) for all u ∈ U.
there exists an open compact subset U, containing x, and such that f (x) = f (u) for all u ∈ U.
Lemma 3.2. Every locally constant function is continuous.
Remark 3.3. Set
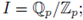 then I is countable. We fix a set of representatives for the elements of I of the form
then I is countable. We fix a set of representatives for the elements of I of the form
If V is an open subset of
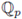 , then for any x ∈ V there exists a ball contained in V of the form
, then for any x ∈ V there exists a ball contained in V of the form
for some j ∈ I
n
and m ∈
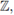 containing x. Consequently,
containing x. Consequently,
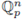 is a second-countable space.
is a second-countable space.
Any locally constant function
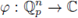 can be expressed as a linear combination of characteristic functions of the form
can be expressed as a linear combination of characteristic functions of the form
and
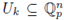 is an open compact for every k. In the proof of this fact one may use Remark 3.3.
is an open compact for every k. In the proof of this fact one may use Remark 3.3.
Let
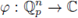 be a locally constant function as in (3). Assume that
be a locally constant function as in (3). Assume that
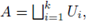 with Ui open compact. Then we define
with Ui open compact. Then we define
We recall that, given a function
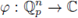 the support of 9 is the set
the support of 9 is the set
A locally constant function with compact support is called a p-adic test function or a Bruhat-Schwartz function. These functions form a C-vector space denoted as D. From (2) and (4) one has that the mapping
is a well-defined linear functional.
3.2. Integration of continuous functions with compact support
We now extend the integration to a larger class of functions. Let U be a open compact subset of
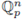 . We denote by C(U,
. We denote by C(U,
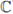 ) the space of all the complex-valued continuous functions supported on U, endowed with the supremum norm. We denote by
) the space of all the complex-valued continuous functions supported on U, endowed with the supremum norm. We denote by
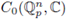 the space of all the complex-valued continuous functions vanishing at infinity, endowed also with the supremum norm. The function 9 vanishes at infinity, if given ε > 0, there exists a compact subset K such that
the space of all the complex-valued continuous functions vanishing at infinity, endowed also with the supremum norm. The function 9 vanishes at infinity, if given ε > 0, there exists a compact subset K such that
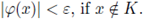
It is known that
 is dense in
is dense in
 (see, e.g., [53, Prop. 1.3]). We identify C(U,
(see, e.g., [53, Prop. 1.3]). We identify C(U,
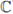 ) with a subspace of
) with a subspace of
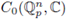 , therefore
, therefore
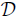 is dense in C(U,
is dense in C(U,
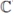 ).
).
We fix an open compact subset U and consider the functional (5), since
This means that if f ∈ C(U,
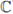 ) and
) and
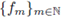 is any sequence in
is any sequence in
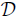 approaching f in the supremum norm, then
approaching f in the supremum norm, then
3.3. Improper Integrals
Our next task is the integration of functions that do not have compact support. A
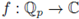 is said to be locally integrable,
is said to be locally integrable,
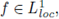 if
if
exists for every compact K.
Example 3.4. The function |x|p is locally integrable but not integrable.
Definition 3.5 (Improper Integral). A function
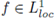 is said to be integrable in
is said to be integrable in
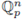 if
if
exists. If the limit exists, it is denoted as
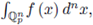 and we say that the improper integral exists.
and we say that the improper integral exists.
Note that
3.4. The change of variables formula in dimension one
Let us start with the formula
which means the following:
for every Borel set
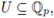 for instance an open compact subset. Consider
for instance an open compact subset. Consider
with
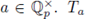 is a topological and algebraic isomorphism. Then
is a topological and algebraic isomorphism. Then
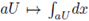 is a Haar measure for (
is a Haar measure for (
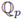 , +), and by the uniqueness of such measure, there exists a positive constant C(a) such that
, +), and by the uniqueness of such measure, there exists a positive constant C(a) such that
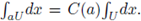 To compute C(a) we can pick any open compact set, for instance
To compute C(a) we can pick any open compact set, for instance
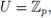 and then we must show
and then we must show
Let us consider first the case
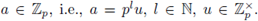 Fix a system of representatives
Fix a system of representatives
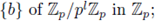 then,
then,
And
i.e.,
The case
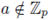 is treated in a similar way.
is treated in a similar way.
Now, if we take
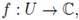 where U is a Borel set, then
where U is a Borel set, then
The formula follows by changing variables as x = ay + b. Then we get dx = d (ay + b) = d(ay) = | a|p dy, because the Haar measure is invariant under translations and formula (6).
Example 3.6. Take U =
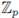 \ {0}. We show that
\ {0}. We show that
Notice that U is not compact, since the sequence
 converges to 0 ∈ U. Now, by using
converges to 0 ∈ U. Now, by using
we have
This calculation shows that
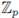 \ {0} has Haar measure 1 and that {0} has Haar measure 0.
\ {0} has Haar measure 1 and that {0} has Haar measure 0.
Example 3.9. Set
We prove that Z(s) has a meromorphic continuation to the whole complex plane as a rational function of p -s .
Indeed,
We now note that the right hand-side is defined for any complex number s ≠ -1, therefore, it gives a meromorphic continuation of Z(s) to the half-plane Re(s) < -1. Thus we have shown that Z(s) has a meromorphic continuation to the whole
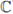 with a simple pole at Re(s) = -1.
with a simple pole at Re(s) = -1.
Example 3.10. Let
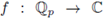 be a radial function, i.e., f(x) = f(|x|p). If
be a radial function, i.e., f(x) = f(|x|p). If
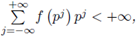 then
then
Example 3.11. By using
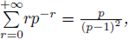 one may show that
one may show that
Example 3.12. We compute
Let us take
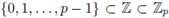 as a system of representatives of
as a system of representatives of
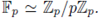 Then,
Then,
and
Let us consider first the integrals in which
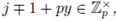 i.e., the reduction mod p of j ∓ 1 is a nonzero element of
i.e., the reduction mod p of j ∓ 1 is a nonzero element of
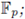 in this case,
in this case,
and since p ≠ 2, there are exactly p - 2 of those j's; then,
Lemma 3.13. Take q (x) = FJ (x → a¿)ei ∈ Zp [x], a¿ ∈ Zp, ej ∈ N \ {0}. Assume that
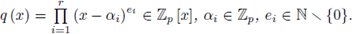 Assume that
Assume that
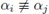 mod p. Then by using the methods presented in examples 3.9 and 3.12, one can compute the integral
mod p. Then by using the methods presented in examples 3.9 and 3.12, one can compute the integral
3.5. Change of variables (general case)
A function
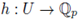 is said to be analytic on an open subset U ⊆
is said to be analytic on an open subset U ⊆
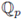 , if there exists a convergent power series
, if there exists a convergent power series
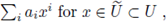 with
with
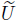 open, such that
open, such that
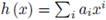 for
for
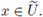 In this case,
In this case,
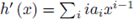 is a convergent power series. A function f is said to be bi-analytic if f and f-1 are analytic.
is a convergent power series. A function f is said to be bi-analytic if f and f-1 are analytic.
Let K
0
, K
1
⊂
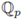 be open compact subsets. Let σ : K
1
→ K
0
be a bi-analytic function such that σ '(y) ≠ 0, y ∈ K
1
. Then, if f is a continuous function over K0,
be open compact subsets. Let σ : K
1
→ K
0
be a bi-analytic function such that σ '(y) ≠ 0, y ∈ K
1
. Then, if f is a continuous function over K0,
4. Implicit Function Theorems on Q p
Let us denote by
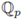 [[x1,..., xn]], the ring of formal power series with coefficients in
[[x1,..., xn]], the ring of formal power series with coefficients in
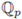 . An element of this ring has the form
. An element of this ring has the form
A formal series
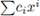 is said to be convergent if there exists r ∈ Z such that
is said to be convergent if there exists r ∈ Z such that
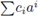 converges for
converges for
 satisfying ||a||p = maxi |a
i
|
p
< p
r
. The convergent series form a subring of
satisfying ||a||p = maxi |a
i
|
p
< p
r
. The convergent series form a subring of
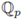 [[x1,...,xn]], which will be denoted as
[[x1,...,xn]], which will be denoted as
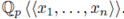
If for
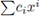 there exists
there exists
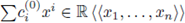 such that
such that
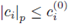 for all
for all
 we say that
we say that
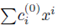 is a dominant series for
is a dominant series for
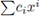 and write
and write
Proposition 4.1. A formal power series is convergent if, and only if, it has a dominant series.
and thus
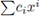 is convergent by Lemma 2.10.
is convergent by Lemma 2.10.
If
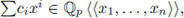 then there exists r ∈
then there exists r ∈
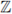 such that
such that
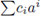 converges for any ||a|| p < pr. Choose r0 ∈
converges for any ||a|| p < pr. Choose r0 ∈
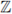 such that 0 < pr0 < pr. Then for every a ∈
such that 0 < pr0 < pr. Then for every a ∈
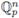 satisfying ||a|| p < pr0 , we have
satisfying ||a|| p < pr0 , we have
and thus
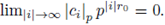 Hence,
Hence,
 for some positive constant M. Finally,
for some positive constant M. Finally,
We say that
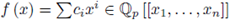 is a special restricted power series, abbreviated SRP, if f (0) = 0, i.e., c0 = 0, and ci = 0 mod p
|i|−1
, for any
is a special restricted power series, abbreviated SRP, if f (0) = 0, i.e., c0 = 0, and ci = 0 mod p
|i|−1
, for any
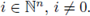
Lemma 4.2. Assume that f (x) is a SRP; then the following assertions hold: (i) f (x) ∈
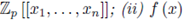 is convergent at every a in
is convergent at every a in
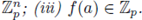
Theorem 4.3 (First Version of the Implicit Function Theorem). (i) Take F (x,y) = (Fi (x,y),..., Fm (x, y)), with
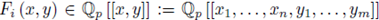 such that F
i
(0, 0) = 0, and
such that F
i
(0, 0) = 0, and
Then there exists a unique f (x) = (f
i
(x),..., f
m
(x)), with
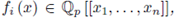 f
i
(0) = 0, satisfying F (x, f (x)) = 0, i.e., F
i
(x, f (x)) = 0 for all i.
f
i
(0) = 0, satisfying F (x, f (x)) = 0, i.e., F
i
(x, f (x)) = 0 for all i.
(ii) If each Fi (x, y) is a convergent power series, then every fi (x) is a convergent power series. Furthermore, if a is near 0 in
 then f (a) is near 0 in
then f (a) is near 0 in
 and F (a, f (a)) = 0; and if (a, b) is near (0, 0) in
and F (a, f (a)) = 0; and if (a, b) is near (0, 0) in
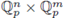 and F (a, b) = 0, then b = f (a).
and F (a, b) = 0, then b = f (a).
For a proof of this result the reader may consult [31, Thm. 2.1.1].
Corollary 4.4 ([31, Cor. 2.1.1]).
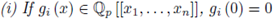 for 1 ≤ i ≤ n, and
for 1 ≤ i ≤ n, and
then there exists a unique f (x) = (f
i
(x),...,f
n
(x)) with f
i
(x) ∈
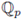 [[x
i
,...,x
n
]], fi (0) = 0, for all i, such that g (f(x)) = x.
[[x
i
,...,x
n
]], fi (0) = 0, for all i, such that g (f(x)) = x.
(ii) If
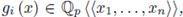 then
then
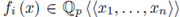 for all i. Furthermore, if b is near 0 in
for all i. Furthermore, if b is near 0 in
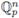 and a = g(b), then a is also near 0 in
and a = g(b), then a is also near 0 in
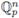 and b = f(a). Therefore, y = f (x) gives rise to a bi-continuous map from a small neighborhood of 0 in
and b = f(a). Therefore, y = f (x) gives rise to a bi-continuous map from a small neighborhood of 0 in
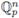 to another neighborhood of 0 in
to another neighborhood of 0 in
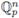 .
.
Remark 4.5. (i) Take
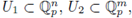 open subsets containing the origin. Assume that each F
i
(x,y) : U
1
x U
2
→
open subsets containing the origin. Assume that each F
i
(x,y) : U
1
x U
2
→
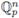 is a convergent power series. A set of the form
is a convergent power series. A set of the form
is called an analytic set. In the case in which all the Fi (x, y) are polynomials and
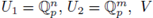 is called an algebraic set. If all the
is called an algebraic set. If all the
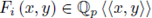 satisfy the hypotheses of the implicit function theorem, V has a parametrization, possible after shrinking U1, U2, i.e. there exist open subsets containing the origin
satisfy the hypotheses of the implicit function theorem, V has a parametrization, possible after shrinking U1, U2, i.e. there exist open subsets containing the origin
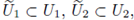 such that
such that
(ii) If we now use as coordinates
we have
We say that such V is a closed analytic submanifold of
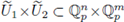 of codimension m. The word 'closed' means that V is closed in the p-adic topology.
of codimension m. The word 'closed' means that V is closed in the p-adic topology.
In the next version of the implicit function theorem we can control the radii of the balls involved in the theorem.
Theorem 4.6 (Second Version of the Implicit Function Theorem). (i) If F
i
(x,y) ∈
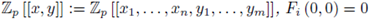 for all i and
for all i and
then there exists a unique solution f (x) = (f
1
(x),..., f
m
(x)), with f
i
(x) ∈
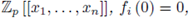 of F (x,f (x)) = 0, i.e. Fi (x, f (x)) = 0 for all i.
of F (x,f (x)) = 0, i.e. Fi (x, f (x)) = 0 for all i.
(ii) If every F
i
(x, y) is an SRP in x
1
,..., x
n
,y
1
,...,y
m
, then every f
i
(x) is an SRP in x
1
,...,x
n
. Furthermore, if a ∈
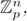 then f (a) ∈
then f (a) ∈
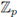 and F (a, f (a)) = 0, and if (a, b) ∈
and F (a, f (a)) = 0, and if (a, b) ∈
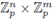 satisfies F(a, b) = 0, then b = f (a).
satisfies F(a, b) = 0, then b = f (a).
For a proof of this result the reader may consult [31, Thm. 2.2.1].
Corollary 4.7 ([31, Cor. 2.2.1]). (i) If
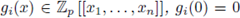 for all i, and further
for all i, and further
then every f
j
(x) in the unique solution of g
i
(f
1
(x),..., f
n
(x)) = x satisfying f
j
(0) = 0 is also in
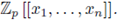
(ii) If every gi(x) is a SRP in x1, . . . , xn, then every fj(x) is also a SRP in the same variables, and, y = f(x) gives rise to a bi-continuous map from
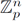 to itself.
to itself.
Remark 4.8. Assume that every F i (x,y) is a SRP in x,y. Take
Under the hypotheses of the second version of the implicit function theorem, we have
By using the coordinate system
V takes the form
and we will say V is a closed analytic submanifold of
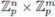 of codimension m.
of codimension m.
5. The Igusa local zeta functions
Let p be a fixed prime number. Set
the ring of integers modulo p m . Recall that any integer can be written in a unique form as
Thus we can identify, as sets, Am with
Take f (x) ∈
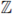 [x1,..., xn] \
[x1,..., xn] \
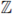 , and define
, and define
A basic problem is to study the behavior of the sequence N m as m → ∞.
More generally, we can take f (x) ∈
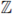 p [x1,... ,xn] \
p [x1,... ,xn] \
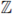 p (recall that
p (recall that
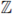 ⊂
⊂
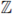 p and that
p and that
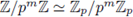 ), and
), and
where x = y mod pm means x → y ∈ pm
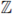 p. To study the sequence
p. To study the sequence
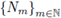 we introduce the following Poincaré series:
we introduce the following Poincaré series:
We expect that the analytic properties of P(t) provide information about the asymptotic behavior of the sequence
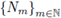 . A key question is the following:
. A key question is the following:
In what follows we will use the convention: given a > 0 and s ∈
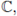 we set
we set
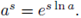
Definition 5.1. Let
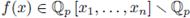 and let 92 be a locally constant function with compact support, i.e., an element of
and let 92 be a locally constant function with compact support, i.e., an element of
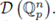 The local zeta function (also called Igusa's local zeta function) attached to (f, φ) is
The local zeta function (also called Igusa's local zeta function) attached to (f, φ) is
where dnx is the Haar measure of (
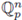 , +) normalized such that
, +) normalized such that
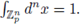
Remark 5.2. Z φ (s, f) is an holomorphic function on the half-plane Re(s) > 0. For the proof of this fact the reader may consult [31, Lemma 5.3.1].
Proposition 5.3. With the above notation,
where P(t) is the Poincaré series defined in (7).
Proof. We first note that
On the other hand,
Now, take
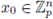 satisfying ord (f (x0)) ≥ j, then, by using Taylor expansion,
satisfying ord (f (x0)) ≥ j, then, by using Taylor expansion,
we have ord (f (x0 + pjz)) ≥ j, for all z ∈
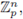 i.e.
i.e.
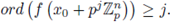 This fact implies:
This fact implies:
Therefore,
Theorem 5.4 (Igusa, [31, Thm. 8.2.1]). Let f (x) be a non-constant polynomial in
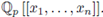 There exist a finite number of pairs
There exist a finite number of pairs
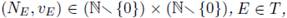 such that
such that
is a polynomial in p -s with rational coefficients.
The proof of this theorem will be given in Section 8. From Theorem 5.4 and Proposition 5.3, we get:
Corollary 5.5. P(t) is a rational function of t.
The rationality of P(t) was conjectured in the sixties by Borevich and Shafarevich. Igusa proved this result at middle of the seventies. The rationality of Z φ (s, f) also allows us to find bounds for the Nm's (see e.g. [28] and [31]).
The proof of Theorem 5.4 given by Igusa depends on a deep result in algebraic geometry known as Hironaka's resolution of singularities theorem. Now we introduce the stationary phase formula, which is an elementary method for computing p-adic integrals like Z φ (s, f), Igusa has conjectured in [29] that this method will conduct to a new elementary proof of the rationality of Z φ (s, f).
6. The Stationary Phase Formula
Let us identify Fp, set-theoretically, with {0,1,... ,p - 1}. Let '-' denote the reduction mod p map, i.e.,
This map can be extended to
 The reduction mod p of a subset
The reduction mod p of a subset
 will be denoted as
will be denoted as
 denotes its reduction mod p.
denotes its reduction mod p.
Proposition 6.1 (Stationary Phase Formula). Take
 and denote by
and denote by
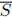 the subset consisting of all
the subset consisting of all
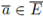 such that
such that
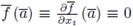 mod p, for 1 ≤ i ≤ n. Denote by E, S the preimages of
mod p, for 1 ≤ i ≤ n. Denote by E, S the preimages of
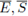 under reduction mod p map
under reduction mod p map
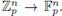 and by N the number of zeros of
and by N the number of zeros of
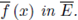 Then
Then
Take now
say i = 1. Define
Then yi's are SRP's and
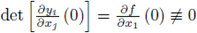 mod p; hence, the map x → y gives rise to a measure-preserving map from
mod p; hence, the map x → y gives rise to a measure-preserving map from
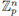 to itself (cf. Corollary 4.7). Therefore,
to itself (cf. Corollary 4.7). Therefore,
and the contribution of the points of the form (8) is
Set
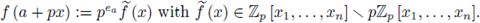 The stationary phase formula, abbreviated SPF, can be re-written as
The stationary phase formula, abbreviated SPF, can be re-written as
We can now apply SPF to each
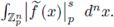 Igusa has conjectured that by applying recursively SPF, it is possible to establish the rationality of integrals of type
Igusa has conjectured that by applying recursively SPF, it is possible to establish the rationality of integrals of type
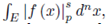 in the case in which the polynomial f has coefficients in a non-Archimedean complete field of arbitrary characteristic.
in the case in which the polynomial f has coefficients in a non-Archimedean complete field of arbitrary characteristic.
The arithmetic of the Laurent formal series field
is completely analog to that of
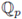 . In particular, given a polynomial with coefficients in
. In particular, given a polynomial with coefficients in
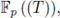 we can attach to it a local zeta function, which is defined like in the p-adic case. The rationality of such local zeta functions is an open problem. The main difficulty here is the lack of a theorem of resolution of singularities in positive characteristic. The above-mentioned conjecture can be re-stated saying that the rationality of local zeta functions for polynomials with coefficients in
we can attach to it a local zeta function, which is defined like in the p-adic case. The rationality of such local zeta functions is an open problem. The main difficulty here is the lack of a theorem of resolution of singularities in positive characteristic. The above-mentioned conjecture can be re-stated saying that the rationality of local zeta functions for polynomials with coefficients in
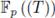 should follow by applying recursively SPF.
should follow by applying recursively SPF.
Remark 6.2. Take
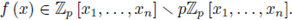 If the system of equations
If the system of equations
has no solutions in
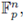 then S = ∅, and by SPF,
then S = ∅, and by SPF,
Example 6.3. Let
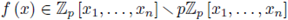 be a homogeneous polynomial of degree d, such that
be a homogeneous polynomial of degree d, such that
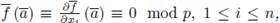 implies
implies
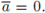 We now compute Z(s, f). We use SPF with
We now compute Z(s, f). We use SPF with
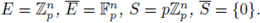
therefore,
6.1. Singular points of hypersurfaces
Take
and define
Vf (
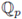 ) is the set of
) is the set of
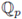 -rational points of the hypersurface defined by f. This notion can be formulated on an arbitrary field K. Set
-rational points of the hypersurface defined by f. This notion can be formulated on an arbitrary field K. Set
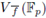 is the set of Fp-rational points of the hypersurface defined by
is the set of Fp-rational points of the hypersurface defined by
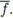 If
If
then
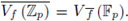 A point a ∈ Vf (
A point a ∈ Vf (
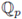 ) is said to be singular if
) is said to be singular if
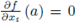 for 1 ≤ i ≤ n. The set of singular points of Vf (
for 1 ≤ i ≤ n. The set of singular points of Vf (
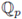 ) is denoted as Sing
f
(
) is denoted as Sing
f
(
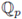 ). We define
). We define
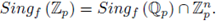 In a similar form we define
In a similar form we define
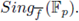
Note that
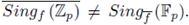 . In fact, it may occur that
. In fact, it may occur that
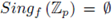 and that
and that
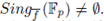 For instance, if f (x,y) = px + x
2
→ y
3
, then
For instance, if f (x,y) = px + x
2
→ y
3
, then
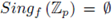 , but
, but
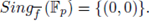
Example 6.4. We compute Z(s, f) for f (x, y) = px + x2 - y
3
by using SPF. Note that
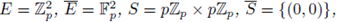
then, by applying SPF,
By changing variables in the last integral as x = pu, y = pv, we have
We now apply SPF to the last integral. Take
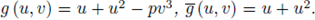 Since the system ofequations
Since the system ofequations
has no solutions,
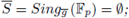 by applying SPF we get
by applying SPF we get
where L (p
-s
) is a polynomial in p-s with rational coefficients (see [60]- [61]). The denominator of Z (s, f) is controlled by
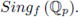 Nowadays the numerator is not fully understood, but it depends strongly on
Nowadays the numerator is not fully understood, but it depends strongly on
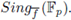 The lack of
The lack of
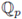 -singular point, i.e. Sing
f
(
-singular point, i.e. Sing
f
(
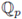 ) = ∅, makes the denominator of Z (s,f) 'trivial': 1 or 1 → p-1-s.
) = ∅, makes the denominator of Z (s,f) 'trivial': 1 or 1 → p-1-s.
Example 6.6. We now compute
by using SPF. Note that
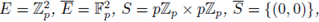 and that
and that
because the set
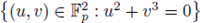 can be parametrized as u = α
3
, v = α
2
, with
can be parametrized as u = α
3
, v = α
2
, with
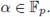 By applying SPF we have
By applying SPF we have
By changing variables in the last integral as x = pu, y = pv, dxdy = p -2 dudv,
We now apply SPF to
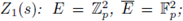 since
since
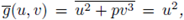 the solution set of u
2
= 2u = 0 is
the solution set of u
2
= 2u = 0 is
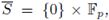 then
then
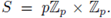 In addition,
In addition,
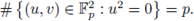 Therefore,
Therefore,
and
and
Finally, we apply SPF to
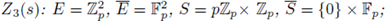 then,
then,
and
i.e.,
6.2. Quasi-homogenous singularities
Take
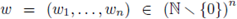 and
and
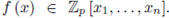 We say that f(x) is a quasi-homogeneous polynomial of degree d with respect to w if: (1)
We say that f(x) is a quasi-homogeneous polynomial of degree d with respect to w if: (1)
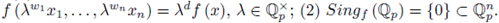 .
.
Set |w| := w1 + ... + wn, and
Proposition 6.7. With the above notation and hypotheses,
where L (p-s) is a polynomial in p -s with rational coefficients.
Proof. Set
Then,
By changing variables in the first integral as 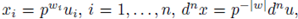 we have
we have
And
We now note that
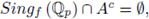 but it may occur that
but it may occur that
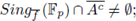 this makes the computation of the integral on Ac not simple. By using SPF recursively and some ideas on Néron p-desingularization, one can show that
this makes the computation of the integral on Ac not simple. By using SPF recursively and some ideas on Néron p-desingularization, one can show that
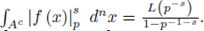 For a detailed proof, including the most general case of the semiquasi-homogeneous singularities, the reader may consult [60].
For a detailed proof, including the most general case of the semiquasi-homogeneous singularities, the reader may consult [60].
7. p-adic Analytic Manifolds and Resolution of Singularities
This section is based on [31, Sec. 2.4]. Let
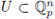 be a non-empty open set, and let f : U →
be a non-empty open set, and let f : U →
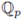 be a function. If at every point a = (a1,...,an) of U there exists an element
be a function. If at every point a = (a1,...,an) of U there exists an element
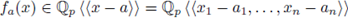 such that f (x) = fa(x) for any point x near to a, we say that f is an analytic function on U. It is not hard to show that all the partial derivatives of f are analytic on U.
such that f (x) = fa(x) for any point x near to a, we say that f is an analytic function on U. It is not hard to show that all the partial derivatives of f are analytic on U.
Let U be as above and let h = (h1,..., hm) : U →
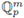 be a mapping. If each h
i
is an analytic function on U, we say that h is an analytic mapping on U.
be a mapping. If each h
i
is an analytic function on U, we say that h is an analytic mapping on U.
Let X denote a Hausdorff space and n a fixed non-negative integer. A pair (U, ф
U
), where U is a nonempty open subset of X and ф
U
: U → ф
u
(U) is a bi-continuous map (i.e., a homeomorphism) from U to an open set
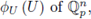 is called a chart. Furthermore ф
U
(x) = (x1,..., xn), for a variable point x of U are called the local coordinates of x. A set of charts {(U, ф
U
)} is called an atlas if the union of all U is X and for every U, U' such that U ∩ U' ≠ ∅ the map
is called a chart. Furthermore ф
U
(x) = (x1,..., xn), for a variable point x of U are called the local coordinates of x. A set of charts {(U, ф
U
)} is called an atlas if the union of all U is X and for every U, U' such that U ∩ U' ≠ ∅ the map
is analytic. Two atlases are considered equivalent if their union is also an atlas. This is an equivalence relation and any equivalence class is called an n-dimensional p-adic analytic structure on X. If {(U, ф U )} is an atlas in the equivalence class, we say that X is an n-dimensional p-adic analytic manifold, and we write n = dim (X).
Suppose that X, Y are p-adic analytic manifolds respectively, defined by {(U, ф U )}, {(V, ψv)}, and f : X → Y is a map. If for every U, V such that U ∩ f-1 (V) ≠ ∅ the map
is analytic, then we say that f is an analytic map. This notion does not depend on the choice of atlases.
Suppose that X is a p-adic analytic manifold defined by {(U, ф U )} and Y is a nonempty open subset of X. If for every U' = Y ∩ U ≠ ∅ we put ф U' = ф U | U’ , then {(U', ф U’ ')} gives an atlas on Y, which makes Y a p-adic analytic open submanifold of X, with dim(X) = dim(Y).
If U, U' are neighborhoods of an arbitrary point a of X, and f, g are p-adic analytic functions respectively on U, U' such that f |W = g |W for some neighborhood W of a contained in U ∩ U', then we say that f, g are equivalent at a. An equivalence class is
said to be a germ ofanalytic functions at a. The set of germs of analytic functions at a form a local ring denoted by
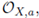 or simply
or simply
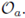
Suppose that Y is a nonempty closed subset of X, a p-adic analytic manifold as before, and 0 < m ≤ n such that an atlas {(U, ф U )} defining X can be chosen with the following property: If ф U (x) = (x1,...,xn) and U' = Y ∩ U ≠ ∅, there exist p-adic analytic functions F1,..., Fm on U such that firstly U' becomes the set of all x in U satisfying F1 (x) = ... = Fm (x) = 0, and secondly,
Then by Corollary 4.4-(ii) the mapping x → (F1 (x),..., Fm (x), xm+1,..., xn) is a bi-analytic mapping from a neighborhood of a in U to its image in
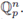 If we denote by V the intersection of such neighborhood of a an Y, and put ΨV (x) = (xm+1,... , xn) for every x in V, then {(V, ΨV)} gives an atlas on Y. Therefore Y becomes a p-adic analytic manifold with dim (Y) = n - m. We call Y a closed submanifold of X of codimension m.
If we denote by V the intersection of such neighborhood of a an Y, and put ΨV (x) = (xm+1,... , xn) for every x in V, then {(V, ΨV)} gives an atlas on Y. Therefore Y becomes a p-adic analytic manifold with dim (Y) = n - m. We call Y a closed submanifold of X of codimension m.
Let µn denote the normalized Haar measure of
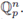 Take X and {(U, ф
U
)} as before. Set a a differential form of degree n on X; then α |U has an expression of the form
Take X and {(U, ф
U
)} as before. Set a a differential form of degree n on X; then α |U has an expression of the form
in which fU is an analytic function on U. If A is an open and compact subset of X contained in U, then we define its measure µ α (A) as
We note that the above series converges because fu (A) is a compact subset. If (U', ф
U’
) is another chart and A ⊂ U’ then we will have the same µα (A) relative to that chart. In fact, if
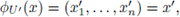 then
then
Actually, the previous equations just give account of the change of variables rule as x → x', in the integral (9), that is
(see [31, pg. 112 and Proposition 7.4.1]). Note that if
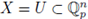 and
and
then µα is the normalized Haar measure of
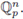
Theorem 7.1 (Hironaka). Take f (X) a nonconstant polynomial in
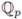 [x1,...,xn], and put X =
[x1,...,xn], and put X =
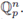 Then there exist an n-dimensional p-adic analytic manifold Y, a finite set T = {E} of closed submanifolds of Y of codimension 1 with a pair of positive integers (N
E
,V
E
) assigned to each E, and a p-adic analytic proper mapping h : Y → X satisfying the following conditions: (i) h is the composition of a finite number of monoidal transformations each one with a smooth center; (ii)
Then there exist an n-dimensional p-adic analytic manifold Y, a finite set T = {E} of closed submanifolds of Y of codimension 1 with a pair of positive integers (N
E
,V
E
) assigned to each E, and a p-adic analytic proper mapping h : Y → X satisfying the following conditions: (i) h is the composition of a finite number of monoidal transformations each one with a smooth center; (ii)
and h induces a p-adic bianalytic map
(iii) at every point b of Y, if E1,...,Em are all the E in T containing b with local equations y 1 ,...,y m around b and (N i , v i ) = (NE , v E ) for E = Ei, then there exist local coordinates of Y around b of the form (y 1 ,...,y m ,y m+1 ,…,y n ) such that
on some neighborhood of b, in which ε (y), r, (y) are units of the local ring
 of Y at b. In particular,
of Y at b. In particular,
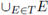 has normal crossings.
has normal crossings.
8. Proof of Theorem 5.4
We want to end this notes by proving Igusa's Theorem about the meromorphic continuation of Z φ (s, f) (see Theorem 5.4 in Section 5). We follow the proof given by Igusa in [31, Thm. 8.2.1].
Let
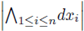 denote the measure induced by the differential form
denote the measure induced by the differential form
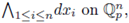 which agrees with the Haar measure of
which agrees with the Haar measure of
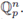 Then
Then
Pick a resolution of singularities h : Y → Xi for f -1 (0) as in Theorem 7.1; we use all the notation introduced there. Then Y \ h -1 (f -1 (0)) → X \ f -1 (0) is a p-adic bianalytic proper map, i.e., a proper analytic coordinate change; then,
At every point b of Y \ h
-1
(f
-1
(0)) we can choose a chart (U, (ф
U
) such that (10) holds. Since h is proper and the support of φ, say A, is compact, we see that h
-1
(A) := B is compact. Then we can cover B by a finite disjoint union of open compact balls B
a
such that each of these balls is contained in some U above. Since φ is locally constant, after subdividing B
α
we may assume that
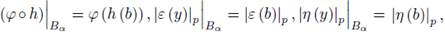 and further that
and further that
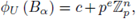 for some c = (c
1
,..., c
n
) in
for some c = (c
1
,..., c
n
) in
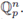 and
and
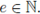 Then,
Then,
with the understanding that N i = 0,v i = 1 in the case E i is not crossing through b. Finally one has by [31, Lemma 8.2.1] that